滤波算法是一种能在非线性离散时间内估计后验状态的算法。在目标跟踪中,滤波算法是在贝叶斯滤波(Bayesian filter)框架下,给定当前时刻的观测信息,估计目标的后验状态并预测下一时刻的先验状态。当前应用广泛且较为成熟的滤波算法有卡尔曼滤波(Kalman filter,KF)、扩展卡尔曼滤波(extended Kalman filter,EKF)、无迹卡尔曼滤波(unscented Kalman filter,UKF)和粒子滤波(particle filter,PF)等。KF算法只能用来解决线性问题,而在目标跟踪中大多数情况下都是非线性问题,因而适用度不高[1]。EKF算法将非线性系统局部线性化,对于较弱的非线性系统可以获得很好的滤波效果,但对于较强非线性系统,效果并不理想。UKF算法采用无极变换和EKF算法框架,其思想是近似高斯分布比近似非线性方程要容易;UKF算法虽然能够得到三阶矩的后验均值及协方差估计,但由于其与EKF一样,假设非线性系统的后验状态服从高斯分布,因而对一般的模型仍不适用[2],因此并不适用于目标跟踪。
在目标跟踪中用于估计后验状态的最著名的方法为粒子滤波算法(particle filter,PF)。PF算法采用序贯蒙特卡洛方法(sequential Monte Carlo methods,SMC),采用一组样本(即粒子)近似表示非线性系统的后验分布,再使用这一近似表示估计系统的状态。与其他几种算法相比,PF算法更适用非线性系统,适用范围更广,实际效果也较好。在当前主流的视觉跟踪算法中,如L1APG算法[3]、CNT算法[4]和IOPNMF算法[5]等皆是以粒子滤波为框架的跟踪算法。然而粒子滤波算法无法避免粒子退化[6]现象,这是因为粒子权值的方差会随着时间而递增。为解决退化问题,一般有两种措施:1)增加采样数量,2)重采样[7]方法。增加采样数量会相应地增加计算量,降低算法的运行效率。重采样的思想是舍弃权值较小的粒子,繁殖权值较大的粒子。然而过度地重采样会产生新的问题:由于大权值粒子被反复地选择,粒子多样性很快丧失,导致样本贫化问题[8]。粒子滤波算法存在的另一个问题是要求在状态转移过程中,进化后的粒子需要能够涵盖目标所有的可能状态,否则跟踪的结果就会逐渐偏离目标的真实位置,导致跟踪失败。解决的方法一般有两种:1)增加粒子数,显然这种方法会增加计算量,导致算法的实时性降低;2)设计合适的状态转移方程,以提高每个粒子对于状态预测的准确率。
智能群体(又称为群智能[9], swarm intelligence,SI)是一类仿生物行为计算技术,源于生物群体的行为规律。例如观察蚂蚁、蜜蜂、鸟类、鱼群等社会性群居动物可以发现,它们分工合作、各司其职像有思维有意识一样地筑巢、觅食。同时人们也观察到不同生物群体有着不同的行为特征,例如,鱼群会向有食物源的地方聚集;蜂群在离开蜂巢寻找食物时会向周围分离;而蚁群则会共同地搬动食物并排列运送至蚁巢。在对这些行为特征总结归纳后发现这些群体行为具有群集共性[10]。动物的群集共性给人们解决新问题带来启发,例如,Cheng等[11]利用群智能优化分析大数据,并设计出一个更加有效的数据分析算法;Xia[12]利用群智能优化解决网络覆盖优化问题,提高了无线传感器网络(wireless sensor network)的网络覆盖率;Devi等[13]将群智能优化技术用于增强语音计算技术,相比于传统的梯度算法,提高了语音系统的信噪比。
在目标跟踪中,后验概率估计的准确度直接影响到跟踪结果的精确度。因此,本文将贝叶斯滤波理论与智能群体优化算法结合,提出一种新颖的智能群体优化滤波算法。相比于传统的粒子滤波算法,本文算法能够有效地应对粒子退化问题,提高跟踪算法的准确度。
1 贝叶斯滤波理论给定离散时间动态系统的状态空间模型(dynamic state-space model,DSSM)可描述为
| $\left\{ {\begin{array}{*{20}{l}} {{x_k} = f\left( {{x_{k - 1}}, {v_{k - 1}}} \right)} \\ {{{\textit{z}}_k} = h\left( {{x_k}, {n_k}} \right)} \end{array}} \right.$ | (1) |
式中:
假设
由
| $\begin{gathered} p({x_k}, {x_{k - 1}}|{{\textit{z}}_{1:k - 1}}) = p({x_k}|{x_{k - 1}}, {{\textit{z}}_{1:k - 1}})p({x_{k - 1}}|{{\textit{z}}_{1:k - 1}})= \\ p({x_k}|{x_{k - 1}})p({x_{k - 1}}|{{\textit{z}}_{1:k - 1}}) \end{gathered} $ | (2) |
等式两端对
| $p({x_k}|{{\textit{z}}_{1:k - 1}}) = \int {p({x_k}|{x_{k - 1}})p({x_{k - 1}}|{{\textit{z}}_{1:k - 1}}){\rm{d}}{x_{k - 1}}} $ | (3) |
式中:
在获得k时刻的测量值
| $\begin{gathered} p({x_k}|{{\textit{z}}_{1:k}}) = \frac{{p({{\textit{z}}_{1:k}}|{x_k})p({x_k})}}{{p({{\textit{z}}_{1:k}})}} {\frac{{p({{\textit{z}}_k}, {{\textit{z}}_{1:k}}|{x_k})p({x_k})}}{{p({{\textit{z}}_k}, {{\textit{z}}_{1:k - 1}})}}} = \\ {\frac{{p({{\textit{z}}_k}|{{\textit{z}}_{1:k - 1}}, {x_k})p({x_k}|{{\textit{z}}_{1:k - 1}})}}{{p({{\textit{z}}_k}|{{\textit{z}}_{1:k - 1}})}}} \\ \end{gathered} $ | (4) |
若观测是相互独立的,则
| $p({x_k}|{{\textit{z}}_{1:k}}) = \frac{{p({{\textit{z}}_k}|{x_k})p({x_k}|{{\textit{z}}_{1:k - 1}})}}{{p({{\textit{z}}_k}|{{\textit{z}}_{1:k - 1}})}}$ | (5) |
式中:
| $p({{\textit{z}}_k}|{{\textit{z}}_{1:k - 1}}) = \int {p({{\textit{z}}_k}|{x_k})p({x_k}|{{\textit{z}}_{1:k - 1}}){\rm{d}}{x_k}} $ | (6) |
贝叶斯滤波方法主要分为更新和预测两个阶段。更新的目的是为了利用最新观测值对先验滤波概率密度进行修正,得到后验滤波概率密度,预测的目的则是根据当前状态预测下一时刻先验滤波概率密度。由于式(3)和式(6)的积分难以计算,所以按照经典蒙特卡洛模拟方法:将后验概率密度转化为累积概率密度分布,然后在区间[0,1]中随机抽取N个数值,每个值对应一个目标状态,由此得到N个独立同分布的样本
| $p({x_k}|{{\textit{z}}_{1:k}}) \approx \frac{1}{N}\sum\limits_{i = 1}^N {\delta ({x_k} - x_k^i)} $ | (7) |
然而实际应用时,真实的后验概率密度是无法知道的,因此通过CDF采集样本是不现实的。这启发了我们可以结合实际情况有选择的采样,即结合智能群体优化方法,充分利用最新的观测信息,将移动粒子至高似然区,得到可靠的建议分布作为重要性密度函数进行重要性采样[14]。假设经过智能群体优化后的建议分布为
| $q({x_k}|{{\textit{z}}_{1:k}}) \approx \sum\limits_{i = 1}^N {\delta ({x_k} - x_k^i)w_k^*\left( {x_k^i} \right)} $ | (8) |
其中:
| $w_k^*(x_k^i) = \frac{{p({{\textit{z}}_{1:k}}|x_k^i)p(x_k^i)}}{{q(x_k^i|{{\textit{z}}_{1:k}})}}$ | (9) |
为k时刻第i个粒子所对应的权值,由相应的观测模型[15]求出。则后验滤波概率密度:
| $ p({x_k}|{{\textit{z}}_{1:k}}) = \frac{{q({x_k}|{{\textit{z}}_{1:k}})p({x_k}|{{\textit{z}}_{1:k}})}}{{q({x_k}|{{\textit{z}}_{1:k}})}}= { \frac{{q({x_k}|{{\textit{z}}_{1:k}})w_k^*({x_k})}}{{p({{\textit{z}}_{1:k}})}}} $ | (10) |
又因为:
| $\begin{gathered} p({{\textit{z}}_{1:k}}) = \int {p({{\textit{z}}_{1:k}}, {x_k}){\rm{d}}{x_k}} =\\ { \int {\frac{{p({{\textit{z}}_{1:k}}|{x_k})p({x_k})q({x_k}|{{\textit{z}}_{1:k}})}}{{q({x_k}|{{\textit{z}}_{1:k}})}}} } {\rm{d}}{x_k}\approx \\ w_k^*({x_k})\sum\limits_{i = 1}^N {\int {w_k^*(x_k^i)} \delta ({x_k} - x_k^i){\rm{d}}{x_k}} = \\ w_k^*(x_k^i)\sum\limits_{i = 1}^N {w_k^*(x_k^i)} \end{gathered} $ | (11) |
联立式(8)、式(10)、式(11),可得:
| $\begin{gathered} p({x_k}|{{\textit{z}}_{1:k}}) = \frac{{w_k^*({x_k})\displaystyle\sum\limits_{i = 1}^N {w_k^*(x_k^i)\delta ({x_k} - x_k^i)} }}{{w_k^*(x_k^i)\displaystyle\sum\limits_{i = 1}^N {w_k^*(x_k^i)} }} =\\ \sum\limits_{i = 1}^N {\delta ({x_k} - x_k^i){w_k}(x_k^i)} \end{gathered} $ | (12) |
式中:
由以上推导可知,在贝叶斯滤波中,求得后验滤波概率密度之前,可以根据最新的观测信息,结合智能群体优化方法,通过粒子分层后,将权值较低的粒子移动到高似然区,即将粒子移动到权值更大的区域,再结合蒙特卡洛模拟产生可靠的重要性密度函数,进行重要性采样,即可估计出后验状态。
2.1 粒子分层通过设定的阈值
| ${\rm{layer}}({x_k}):\left\{ {\begin{array}{*{20}{l}} {x_k^i \in {\psi _h}, \quad{w_k^*(x_k^i) \geqslant {\tau _h}} } \\ {x_k^i \in {\psi _m}, \quad{{\tau _h} > w_k^*(x_k^i) \geqslant {\tau _l}}} \\ {x_k^i \in {\psi _l}, \quad {{\tau _l} > w_k^*(x_k^i)} } \end{array}} \right.$ | (13) |
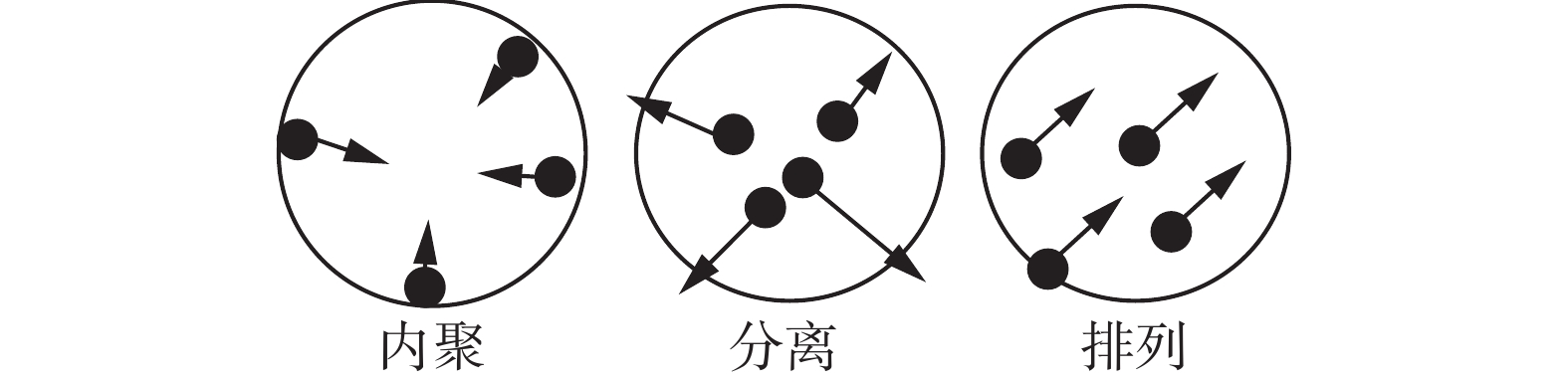
群集共性表现在3个方面:内聚、分离和排列。内聚运动时,各成员朝着一个平均的中心位置进行聚合;分离运动时,各成员远离一个平均的中心位置;排列运动时,各成员朝着一个平均的方向共同运动,如图1所示。
|
Download:
|
| 图 1 群集共性示意图 Fig. 1 Sketch of swarm intelligence | |
根据已有粒子的权值,让权值较低的粒子移动至权值较大的区域,从而产生更可靠的重要性密度函数。为了提高鲁棒性,粒子的移动方法如下:
| ${\rm{coh}}({x_k}):{x_k} = {x_{k - 1}} + \left( {a + (b - a) \times {\rm{rand}}} \right) \times ({x_{k - 1}} - {x_c})$ | (14) |
式中:
在当前时刻无法准确确定目标位置时,让所有粒子进行分离运动,目的是为了下一时刻能够尽可能多地涵盖目标的可能状态。粒子的移动方法如下:
| ${\rm{spa}}({x_k}):{x_k} = {x_{k - 1}} +{\textit{λ}} \times \bar v \times {\rm{rand}} \times ({x_c} - {x_{k - 1}})$ | (15) |
式中:
排列运动目的是在当前时刻能够准确估计目标位置的情况下,预测下一时刻目标位置。采用状态转移概率密度作为排列运动的运动模型,即
| ${x_k}\sim p({x_k}|{x_{k - 1}})$ | (16) |
在实际运用于目标跟踪中,系统状态转移的运动模型有很多种,诸如匀速运动模型,自由漫步运动模型和匀加速运动模型等。这里采用匀速运动模型,它的优点是计算简单高效:
| ${x_k} = {x_{k - 1}} + {\textit{λ}} \times {\rm{rand}} \times \bar v$ | (17) |
可根据最小均方误差(minimum mean squared error, MMSE)准则或极大后验(maximum A posterior,MAP)准则,即将条件均值或具有极大后验概率密度的状态作为系统状态的估计值。MAP准则计算公式为
| $\hat x_k^{{\rm{MAP}}} = \mathop {\arg \max }\limits_{{x_k}} p({x_k}|{{\textit{z}}_{1:k}}) = \mathop {\arg \max }\limits_{{x_k}} {w_k}({x_k})$ | (18) |
式中:
1)局部最小均方误差(local minimum mean squared error,LMMSE)准则。
通过设定一个范围R,计算该范围内的粒子数M,在对目标状态后验估计时,仅对范围内的粒子样本进行加权求和,其计算公式为
| $\hat x_k^{{\rm{LMMSE}}} = \int {{x_k}} p({x_k}|{{\textit{z}}_{1:k}}){\rm{d}}{x_k} = \sum\limits_{i = 1}^M {\left( {x_k^i{w_k}(x_k^i)} \right)} \in {\rm{R}}$ | (19) |
式中:
2)全局最小均方误差(global minimum mean squared error,GMMSE)准则。
对总数为N的粒子集中所有粒子整体加权求和,计算公式为
| $\hat x_k^{{\rm{GMMSE}}} = \int {{x_k}} p({x_k}|{{\textit{z}}_{1:k}}){\rm{d}}{x_k} = \sum\limits_{i = 1}^N {x_k^i{w_k}(x_k^i)} $ | (20) |
式中:
更新的目的是要充分利用当前时刻粒子的位置和权值信息,找出目标最可能的状态,即生成合适的建议分布,从而准确地估计目标在当前时刻的位置。虽然权值较高的粒子比权值较低的粒子更能充分表示目标的位置状态,但当高权值粒子数量较少时,容易陷入局部最优解。因此,设计以下4条准则自适应地更新粒子状态。
准则1 当高权值粒子集
准则2 当高权值粒子集
准则3 当高权值粒子集
准则4 当高权值粒子集
预测的目的是为了下一时刻能更准确地估计目标的状态,即设计出合适的先验分布函数。在SIF算法中,遵循以下两条准则:
准则5 若当前时刻满足更新准则的条件,表明当前时刻能够判断目标的位置状态。则根据GMMSE准则估计目标的后验状态,再将粒子集进行排列运动预测下一时刻的先验状态。
准则6 若当前时刻不满足更新准则中的任一条件,即当高权值粒子集
本文算法的流程如图2所示,其具体实现步骤如算法1所示。

|
Download:
|
| 图 2 智能群体优化滤波算法流程 Fig. 2 Algorithm flow of SIF | |
算法1 智能群体优化滤波算法
输入 图像序列共T帧,初始位置;
输出 跟踪位置。
1) 初始化:设定粒子数N,阈值为mpts,threshold,threshold;
2) for
3) 由观测函数计算每个粒子的权值
4) 状态更新
| $\!\!\!\!\!\!\!\! \begin{array}{l} {\rm{if}}\left( {{\rm{length}}\left( {{\psi _h}} \right) > {\rm{threshold}}} \right)\\ \qquad {{\hat x}_k} =\displaystyle \sum\limits_{i = 1}^N {x_k^i} {w_k}\left( {x_k^i} \right)\\ {{\rm{elseif(length}}({\psi _h}) > {\rm{mpts}}}\\ \qquad {\& \& {\rm{length}}({\psi _m}) > {\rm{threshold}})}\\ \qquad {{\hat x}_k} = \displaystyle\sum\limits_{i = 1}^M {\left( {x_k^i{w_k}\left( {x_k^i} \right)} \right)} {x_k^i}, \in {\psi _h}\\ {{\rm{elseif(length}}({\psi _h}) > {\rm{mpts}}}\\ \qquad {\& \& {\rm{length}}({\psi _m}) < {\rm{threshold}})}\\ \qquad {{\hat x}_k} = \displaystyle\sum\limits_{i = 1}^M {\left( {x_k^i{w_k}\left( {x_k^i} \right)} \right)} {x_k^i}, \in {\psi _h}\\ \qquad {\psi _m}\sim {\rm{coh}}\left( {{{\hat x}_k}} \right)\\ {\rm{else}}\\ \qquad {{\hat x}_k} = \displaystyle\sum\limits_{i = 1}^M {\left( {x_k^i{w_k}\left( {x_k^i} \right)} \right)} , {x_k^i \in {\psi _m}}\\ {\rm{endif}}\\ {\psi _l}\sim {\rm{coh}}\left( {{{\hat x}_k}} \right) \end{array} $ |
5) 重新计算粒子的权值
| $ {\tilde x_k} = \sum\limits_{i = 1}^N {x_k^i} {w_k}\left( {x_k^i} \right) $ |
6) 状态预测
| $ \begin{array}{l} {if({\rm{length}}({\psi _h}) < {\rm{mpts}}} \\ \qquad {\& \& {\rm{length}}({\psi _m}) < {\rm{threshold}})} \\ \qquad{x_k}\sim {\rm{spa}}\left( {{{\tilde x}_k}} \right) \\ {\rm{else}} \\ \qquad{x_k}\sim p({x_k}\left| {{x_{k - 1}}} \right.) \\ {\rm{endif}} \end{array} $ |
7)
注:
为了证明本文算法的理论可靠性和实际可行性,分别进行了仿真实验和目标跟踪模拟实验,实验平台为IntelCore3.2 GHz,2 GB内存,MATLAB2014a。
3.1 仿真模拟实验为了说明智能优化滤波算法在非线性系统中估计后验状态的性能,选择文献[16]中广泛使用的一维非静态增长模型进行模拟仿真实验,此模型状态的后验分布具有双峰特征且非线性很强,是标准的验证模型。其状态空间模型定义如下:
| $\left\{ {\begin{aligned} & {{x_k} = {f_k}({x_{k - 1}}, k) + {v_{k - 1}}} \\ & {{{\textit{z}}_k} = \frac{{x_k^2}}{{20}} + {n_k}} \end{aligned}} \right.$ | (21) |
式中:
| ${f_k}({x_{k - 1}}, k) = \frac{{{x_{k - 1}}}}{2} + \frac{{25{x_{k - 1}}}}{{1 + x_{k - 1}^2}} + 8\cos (1.2k)$ | (22) |
式中:
|
Download:
|
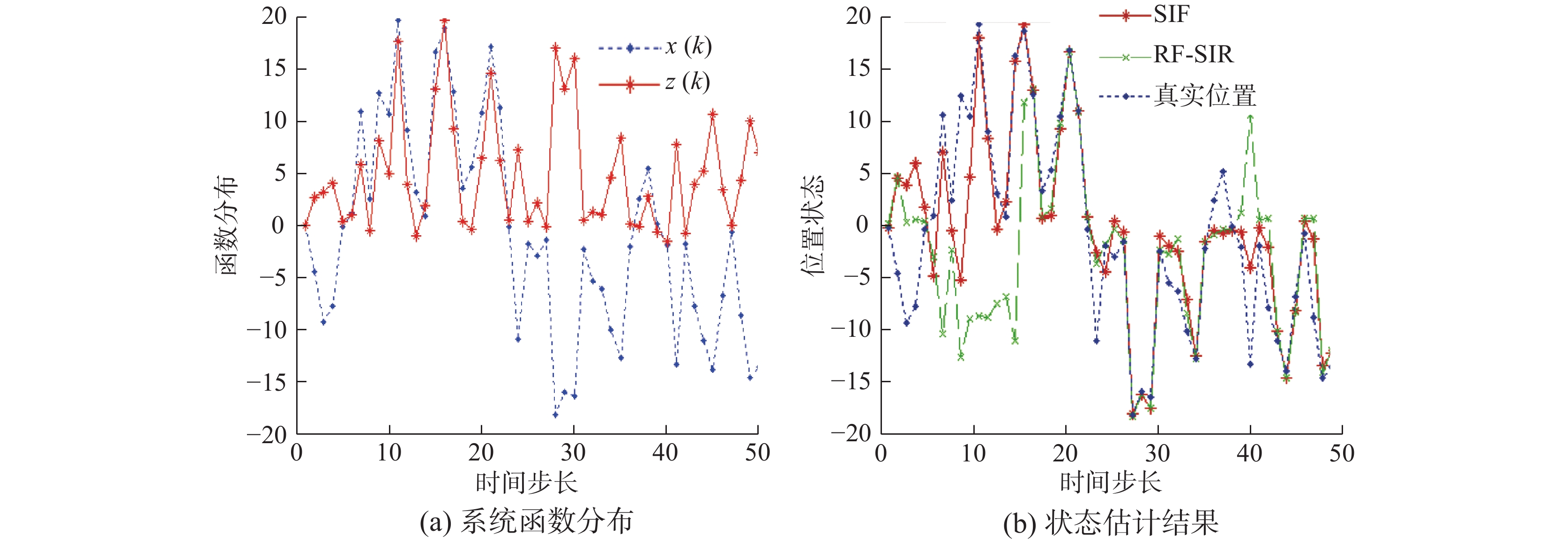
| 图 3 Monte Carlo仿真结果 Fig. 3 Results of Monte Carlo simulations | |
图3(a)为状态函数
定义状态估计的均方根误差(root mean squared error,RMSE)为
| ${\rm{RMSE}} = \sqrt {\frac{1}{T}\sum\limits_{k = 1}^T {{{({x_k} - {{\hat x}_k})}^2}} } $ | (23) |
用来定量衡量状态估计的准确度。
表1列出了两种算法的RMSE误差和运行时间。由表中数据可以看出,SIF算法状态估计的RMSE误差值小于PF-SIR算法,但是运行时间要多与PF-SIR算法。这是因为本文算法充分考虑到当前时刻的观测信息,在更新过程中,将权值较低的粒子进行内聚运动,并且更新后重新计算了权值。因此所花费时间要比PF-SIR算法多。
| 表 1 Monte Carlo仿真的RMSE误差和运行时间 Tab.1 RMSE and runtime of Monte Carlo simulations |
为了证明SIF算法在目标跟踪中实际应用价值,将智能提群体优化滤波算法分别嵌入到IVT[17]算法和IOPNMF[5]算法中。出于定性的比较,保留IVT算法和IOPNMF算法所采用的特征和模型更新[15],将两种算法的运动模型由粒子滤波算法改成智能群体优化滤波算法。分别在David3、Faceocc1、Faceocc2、Singer、Girl_head、Basketball、Liquor1、ShopAssistant2cor (以下简称SA2c)和EnterExitCrossingPaths1cor (以下简称EECP1c)视频集中进行比较,以上前7个视频集都来源于ObjectTrackingBenchmark[18],而SA2c和EECP1c视频集来源于标准数据库PETS2004。上述视频序列涵盖了的光照变化、平面内外旋转、快速运动、尺度变化、运动模糊、背景干扰及遮挡等复杂干扰情况,具体情况如表2所示。
| 表 2 各视频集中的主要干扰因素 Tab.2 Main challenges in each sequences |
参数设定为:粒子数N=600。阈值
| ${\tau _h} = \frac{1}{5}\sum\limits_{m = k - 5}^k {(\max w_m^*({x_m}) - \frac{1}{N}\sum\limits_{i = 1}^N {w_m^*(x_m^i)} )} $ | (24) |
| ${\tau _l} = \frac{1}{5}\sum\limits_{m = k - 5}^k {(\frac{1}{N}\sum\limits_{i = 1}^N {w_m^*(x_m^i)} - \min w_m^*({x_m}))} $ | (25) |
式中:k为当前帧;
为了充分比较算法的总体性能,除了将改进后的SIF_IOPNMF算法和SIF_IVT算法与原算法比较外,还与L1APG[3]、CNT[4]、ASLA[19]、LOT[20]、MTT[21]算法进行比较,以上5种经典的目标跟踪算法皆是基于粒子滤波框架下。定义中心误差为
| $e = \sqrt {{{({x_t} - {x_s})}^2} + {{({y_t} - {y_s})}^2}} $ | (26) |
式中:
9种算法在各视频集中逐帧的中心误差如图4所示,其左上角标签栏为平均中心误差。定义重叠率(Overlap rate)为

|
Download:
|
| 图 4 9种算法在各视频集上的中心误差 Fig. 4 Center error of 9 algorithms in each sequences | |
| ${\rm{score}} = \frac{{{\rm{area}}({R_t} \cap {R_s})}}{{{\rm{area}}({R_t} \cup {R_s})}}$ | (27) |
式中:
| 表 3 9种算法在各视频集中的平均重叠率(最优值加粗表示) Tab.3 Average overlap rate of 9 algorithms in each sequences |
由图4中的标签栏和表1中数据可以看出,嵌入SIF算法后的SIF_IVT与SIF_IOPNMF算法与原算法相比,每个视频集中的平均中心误差皆有所降低,平均重叠率皆有所提高。其中在Faceocc2、Singer和Faceocc1这3个视频序列中,IVT算法总体表现较好。在David3、Faceocc1、Singer和Faceocc2这4个视频序列中,IOPNMF算法跟踪效果总体表现良好。表2列出了这几个视频集的主要干扰因素,从中可以看出,IVT算法所采用的特征适合处理部分遮挡和小尺度旋转等干扰因素,而IOT与SIFPNMF算法的模型更新准则适合处理部分遮挡和光照变化等干扰因素。此时嵌入SIF算法后的SIF_IVT和SIF_IOPNMF算法与原算法相比,跟踪效果略有上升。由实验结果可知:在目标跟踪中,所选取的特征和模型更新起着重要作用;当所提取的特征和模型更新适合应对一些简单的跟踪环境时,采用智能群体优化滤波的算法与采用粒子滤波的算法跟踪效果相当。
图5列出9种算法在部分视频集中实验结果部分帧截图。在Girl_head、Liquor1、Basketball、SA2c及EECP1c这5个视频序列中,采用粒子滤波的IOPNMF和IVT算法都出现了漂移和跟踪失败的情况,而采用智能群体优化滤波的SIF_IOPNMF和SIF_IVT算法跟踪效果有着明显的进步。图5列出了视频序列中部分帧的实验结果截图,从图中可以看出,Girl_head视频序列(图5(a))中,由于目标在80帧后出现了平面内旋转、平面外旋转和尺度变化等干扰因素,IOPNMF、IVT和LOT算法皆出现了漂移,SIF_IOPNMF和SIF_IVT通过准则2,忽略低权值粒子集,择取高权值粒子集估计目标的位置,因而避免了漂移现象。在Liquor(图5(b))视频序列中,目标在330帧后出现快速移动、运动模糊和尺度变化等干扰因素,此时IOPNMF、IVT、L1APG和LOT算法皆跟踪失败;SIF_IOPNMF和SIF_IVT通过准则6将粒子集进行分离运动,能够有效地增加粒子多样性,并根据最大后验准则成功地估计了目标的后验状态。在Basketball(图5(c))视频序列中,在20帧之后,由于目标出现大幅度遮挡,IOPNMF算法出现了漂移;SIF_IOPNMF通过准则3对高权值粒子集里的粒子进行局部加权,有效地处理了遮挡问题。在85帧左右,目标出现快速移动,此时CNT算法跟踪失败;在250帧之后,由于目标出现大尺度平面外旋转,此时MTT和L1APG算法皆出现漂移;而在480帧之后,由于目标大尺度的非刚性变形,只有SI_IOPNMF、SI_IVT和LOT算法仍未丢失目标。在David3(图5(e))视频序列中,20帧左右时,跟踪目标出现小幅度遮挡,此时MTT算法跟踪失败;在110帧后,目标出现大尺度平面内旋转,L1APG和ASLA算法皆出现漂移;在200帧左右时,由于出现了背景干扰和大幅度遮挡,IVT和CNT算法皆丢失目标。SIF_IVT通过准则4对中权值粒子集进行局部加权计算出中心位置,能够应对大幅度遮挡导致的局部最优化,再对低权值粒子集进行内聚运动,有效地处理了背景干扰问题。SA2c(图5(d))和EECP1c(图5(f))两个视频序列中,目标皆出现大幅度遮挡和尺度变换,只有SI_IOPNMF、SIF_IVT、CNT和ASLA算法跟踪效果良好,CNT和ASLA由于利用了局部特征模块,对遮挡有着良好的鲁棒性,而SI_IOPNMF和SIF_IVT则通过结合内聚运动和局部加权准则,增加了算法的遮挡和尺度变化的适应性。由以上实验结果可以看出,在所提取的特征和更新准则不能很好地应对复杂多变的跟踪环境时,采用智能群体优化滤波算法比采用粒子滤波算法更加适应多变的跟踪环境。

|
Download:
|
| 图 5 9种算法在部分视频集中的实验结果截图 Fig. 5 Sampling tracking results of 9 trackers in some sequences | |
针对目标跟踪的运动模型,本文提出了一种智能群体优化滤波(SIF)算法。在贝叶斯滤波的基础上,本文提出的算法融入了智能群体优化中的3种智能群体优化思想,即内聚、分离和排列运动。在当前时刻能够准确地估计后验状态的情况下,内聚运动是将权值较低的粒子聚合在高权值粒子周围,以增加其权值并保留了粒子多样性,再结合排列运动准确地预测下一时刻的先验状态,能够有效地增加算法对遮挡和形变的适应性。分离运动是在当前时刻无法准确估计后验状态的情况下,通过扩大搜索范围来增加粒子多样性,能够有效处理快速移动和运动模糊导致的粒子权值退化问题,提高了下一时刻的先验滤波概率密度。
实验结果表明,相比于广泛使用的粒子滤波算法,智能群体优化滤波算法更能准确地估计后验状态,当实际运用在目标跟踪中,更加有效地应对复杂多变的跟踪环境。同时本文提出的算法思想还可以使用在任何基于采样的跟踪算法中,因此该算法具有很好的适用性。本文的实验只将算法应用到了IPONMF算法和IVT算法中,为了进一步提高跟踪效果,下一步的工作将考虑将智能群体优化滤波算法应用到其他的跟踪算法中。
| [1] |
LGUENSAT R, TANDEO P, FABLET R, et al. Non-parametric Ensemble Kalman methods for the inpainting of noisy dynamic textures[C]//Proceedings of 2015 IEEE International Conference on Image Processing. Quebec City, Canada, 2016: 4288–4292.
( 0) 0)
|
| [2] |
王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37(8): 1679-1694. WANG Fasheng, LU Mingyu, ZHAO Qingjie, et al. Partilce filtering algorithm[J]. Chinese journal of computers, 2014, 37(8): 1679-1694. (  0) 0)
|
| [3] |
BAO Chenglong, WU Yi, LING Haibin, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 1830–1837.
( 0) 0)
|
| [4] |
ZHANG Kaihua, LIU Qingshan, WU Yi, et al. Robust visual tracking via convolutional networks without training[J]. IEEE transactions on image processing, 2016, 25(4): 1779-1792. ( 0) 0)
|
| [5] |
WANG Dong, LU Huchuan. On-line learning parts-based representation via incremental orthogonal projective non-negative matrix factorization[J]. Signal processing, 2013, 93(6): 1608-1623. DOI:10.1016/j.sigpro.2012.07.015 ( 0) 0)
|
| [6] |
吴昊, 孙晓燕, 郭玉堂, 等. 保持粒子多样性的非退化粒子滤波方法研究[J]. 电子学报, 2016, 44(7): 1734-1741. WU Hao, SUN Xiaoyan, GUO Yutang, et al. Non-degeneracy particle filtering method research for particle diversity preserving[J]. Acta electronica sinica, 2016, 44(7): 1734-1741. DOI:10.3969/j.issn.0372-2112.2016.07.031 (  0) 0)
|
| [7] |
常天庆, 李勇, 刘忠仁, 等. 一种改进重采样的粒子滤波算法[J]. 计算机应用研究, 2013, 30(3): 748-750. CHANG Tianqing, LI Yong, LIU Zhongren, et al. Particle filter algorithm based on improved resampling[J]. Application research of computers, 2013, 30(3): 748-750. DOI:10.3969/j.issn.1001-3695.2013.03.026 (  0) 0)
|
| [8] |
CAO Bei, MA Caiwen, LIU Zhentao. Particle filter with fine resampling for bearings-only tracking[J]. Procedia engineering, 2012, 29: 3685-3690. DOI:10.1016/j.proeng.2012.01.553 ( 0) 0)
|
| [9] |
DU Kelin, SWAMY M N S. Swarm intelligence[M]//DU Kelin, SWAMY M N S. Search and Optimization by Metaheuristics. Cham: Birkhäuser, 2016.
( 0) 0)
|
| [10] |
彭喜元, 彭宇, 戴毓丰. 群智能理论及应用[J]. 电子学报, 2003, 31(S1): 1982-1988. PENG Xiyuan, PENG Yu, DAI Yufeng. Swarm intelligence theory and applications[J]. Acta electronica sinica, 2003, 31(S1): 1982-1988. (  0) 0)
|
| [11] |
CHENG Shi, ZHANG Qingyu, QIN Quande. Big data analytics with swarm intelligence[J]. Industrial management and data systems, 2016, 116(4): 646-666. DOI:10.1108/IMDS-06-2015-0222 ( 0) 0)
|
| [12] |
XIA Junbo. Coverage optimization strategy of wireless sensor network based on swarm intelligence algorithm[C]//Proceedings of 2016 International Conference on Smart City and Systems Engineering. Hunan, China, 2016: 179–182.
( 0) 0)
|
| [13] |
DEVI K U, SARMA D, LAISHRAM R. Swarm intelligence based computing techniques in speech enhancement[C]//Proceedings of 2015 International Conference on Green Computing and Internet of Things. Noida, India, 2015: 1199–1203.
( 0) 0)
|
| [14] |
KRONANDER J, SCHÖN T B. Robust auxiliary particle filters using multiple importance sampling[C]//Proceedings of 2014 IEEE Workshop on Statistical Signal Processing. Gold Coast, Australia, 2014: 268–271.
( 0) 0)
|
| [15] |
WANG Naiyan, SHI Jianping, YEUNG D Y, et al. Understanding and diagnosing visual tracking systems[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 3101–3109.
( 0) 0)
|
| [16] |
ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on signal processing, 2002, 50(2): 174-188. DOI:10.1109/78.978374 ( 0) 0)
|
| [17] |
ROSS D A, LIM J, Lin R S, et al. Incremental learning for robust visual tracking[J]. International journal of computer vision, 2008, 77(1/2/3): 125-141. ( 0) 0)
|
| [18] |
WU Yi, LIM J, YANG M H. Online object tracking: a Benchmark[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA, 2013: 2411–2418.
( 0) 0)
|
| [19] |
JIA Xu, LU Huchuan, YANG M H. Visual tracking via adaptive structural local sparse appearance model[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 1822–1829.
( 0) 0)
|
| [20] |
ORON S, BAR-HILLEL A, LEVI D, et al. Locally orderless tracking[J]. International journal of computer vision, 2015, 111(2): 213-228. DOI:10.1007/s11263-014-0740-6 ( 0) 0)
|
| [21] |
ZHANG Tianzhu, GHANEM B, LIU Si, et al. Robust visual tracking via multi-task sparse learning[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 2042–2049.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


