2. 北京建筑大学 电气与信息工程学院,北京 100044
2. School of Electrical and Information Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
MicroRNAs(miRNAs)是一类很小的内源性非编码RNA,长度约为20~24个核苷酸,通过碱基配对与其靶向的mRNA的3'端非编码区相结合,导致靶mRNA的降解或翻译抑制,从而在转录后水平上调控基因表达[1-3]。越来越多的证据表明,miRNA在免疫反应、转录、增殖、分化、信号传导和胚胎发育等[4-7]生物过程中起着重要的作用,miRNA突变、miRNA的生物合成和miRNA与其靶mRNA的功能失调可能会导致各种疾病。因此,识别miRNA与疾病之间的互作关系至关重要。早期研究采用生物学实验方法确定miRNA与特定疾病的关系,然而生物学实验方法实验周期长、成本高。因此计算生物学方法分析、预测miRNAs和疾病的关联问题成为了当前的研究热点。
1 相关工作目前,miRNA和疾病的关联预测主要分为基于网络拓扑结构的方法和机器学习的方法。
基于网络拓扑结构的研究方法建立在“功能相似的miRNA调控的疾病也比较相似,反之亦然[8-9]”这个假设基础上,文献[10-19]就此展开了一系列研究工作。2010年,Jiang等[10]首次提出一种计算方法,构建功能相关miRNA网络和人类疾病表型-miRNA网络,将人类的miRNA组按照与疾病关联得分的大小排序,预测miRNA与疾病的关联。这是以前用基于网络的方法预测与疾病相关的编码蛋白基因的合理延伸。2010年,Jiang等[11]又提出一种基于基因组数据融合的新方法,用朴素贝叶斯模型融合多种来源的数据,构建一个模型预测基因之间的功能相关性。分别用两个向量表示疾病与基因之间的关联、miRNA与靶基因之间的关联。对于给定的疾病,计算其与每个miRNA的相似得分,并从高到低排序,最高得分为与该疾病相关的miRNA。Chen等[12]将随机游走算法应用到miRNA-miRNA功能相似网络,在给定的种子结点处开始,将已知的关联关系的大小作为转移概率,模拟网络中当前结点扩散到其邻结点的过程,以此来挖掘网络中可能潜在的关联关系。Chen等[13]在2013年又提出一种基于相似度的方法,分为3个策略:基于miRNA的相似度推断 (miRNA-based similarity inference,MBSI)、基于表型的相似度推断(phenotype-based similarity inference,PBSI)和基于网络一致性的推断(network-consistency-based inference,NetCBI);Shi等[14]于2013年提出一种基于可重启的随机游走 (random walk with restart,RWR)算法的新方法,将疾病基因和miRNA靶基因映射到蛋白质−蛋白质互作 (protein-protein interaction,PPI)网络上,设置不同的种子应用RWR算法;Xuan等[15]后又提出名为HDMP的方法——基于加权最相似k近邻的方法,预测与疾病相关的miRNA;Xu等[16]主要通过比对miRNA与mRNA表达谱融合多种疾病的表型关联,预测与癌症相关的miRNA;2013年,Mork等[17]提出一种蛋白质介导的预测方法,通过miRNA与蛋白质之间的关联、蛋白质与疾病之间的关联预测miRNA与疾病之间的关系;2016年,Sun等[19]提出了基于已知的miRNA-疾病网络拓扑相似性,以挖掘更多潜在的与疾病相关的miRNA,利用二分投影的方法,来完成miRNA与疾病的关联预测工作。
到目前为止,基于网络拓扑结构的研究方法处理miRNAs和疾病的关联预测问题上,更多的倾向于基于已知的关联关系来挖掘其中潜在的关系,而对缺少已知关联信息的miRNAs和疾病,其结果往往呈现随机化。
在机器学习方法研究上。2012年,Xu等[20]首先使用机器学习方法预测miRNA与疾病之间的关系。这种方法旨在从大规模的反例中分辨出正例关联,核心是从miRNA-疾病网络中提取特征,训练一个SVM分类器。2013年,Jiang等[21]又通过构建不同于Xu的特征集——一个关于miRNA信息的特征集和一个关于疾病表型信息的特征集,应用此方法得到相近的结果。2014年,Chen等[22]提出一种半监督的全局化方法(regularized least squares for mirna-disease association,RLSMDA),在没有负例集的情况下预测miRNA与疾病的关联。用正则化最小二乘法构建一个连续的分类函数,表示每个miRNA与给定疾病相关的概率,对于未知相关miRNA的疾病,该方法也适用。
基于机器学习的方法能够取得与“基于网络拓扑结构方法”相近或者更好结果,有的甚至很好地处理未知miRNA的疾病,例如RLSMDA。而机器学习主要受制于miRNAs与疾病特征的表示,以及对如何处理有正样本数据的模型设计。
基于矩阵分解的算法用高维空间的向量解决了特征表示的问题,算法同时构建miRNAs和疾病在高维空间的表示,并以此为基础获得其关联关系,用迭代最小二乘法求解出最终的miRNA-疾病关联关系的概率。这个求解思路来源于推荐系统中当前所流行的矩阵分解方法,对解决类似的关联关系预测问题在近年来也被证明非常有效。Shen[23]在2017年首次提出基于矩阵分解的方法对miRNAs和疾病的关联关系进行预测,并取得了比Chen[22]更好的效果,但在其迭代求解的过程中,受到其损失函数的影响无法使用最小二乘法,导致其每个变量都需要迭代求解,这在同时要求多个变量迭代求解的情况下,其结果很大程度上依赖于初始解的选择,在很多的情况下甚至无法收敛,算法的稳定性难以保证。
本文提出的LMFMDA算法,首先构建miRNAs相似性网络、疾病相似性网络和miRNA-疾病关联网络;进而构建矩阵分解算法模型,算法在利用迭代最小二乘法优化求解的过程中,通过引入辅助miRNAs和疾病变量的方法,提高计算速度,解决收敛结果最优的问题,确保算法的稳定性。
2 实验数据在本节介绍LMFMDA算法所使用的数据和处理方法。数据来源如表1所示。
| 表 1 数据材料及其来源表题 Tab.1 Data materials and the sources |
直接从MISIM数据库获得miRNAs的功能相似度网络MS,网络中miRNA之间的相似度被表示为[0, 1]的实数。
2.2 疾病语义相似性网络疾病的语义相似性通过MeSH得到,计算方法来自Wang[24],假设疾病t是疾病d的一个祖先,或者d=t,令:
| ${C_d}(t) = \left\{ \begin{array}{l}1,\;\;\;\;t = d\\\max \{ 0.5 \times {C_d}(t')|t' \in {\rm{childrenoft}}\} ,\;\;\;\;t \ne d\end{array} \right.$ | (1) |
疾病1和疾病2之间的语义相似性DS(d1, d2)即
| ${\rm{DS}}(d_1,d_2) = \displaystyle\frac{{\displaystyle\sum\nolimits_{t \in T(d_1) \cap T(d_2)} {({C_{d_1}}(t) + {C_{d_2}}(t))} }}{{\displaystyle\sum\nolimits_{t \in T(d_1)} {{C_{d_1}}(t) + \sum\nolimits_{t \in T(d_2)} {{C_{d_2}}(t)} } }}$ | (2) |
在HMDD数据库下载了现有的miRNAs-疾病关联关系网络。网络包含了378个疾病、571个miRNAs及其构成的10 381个关联关系。关联矩阵R中,如果miRNA m(i)和疾病 d(j)被认为有关,则R(m(i)、d(j))为1,否则,为0。
2.4 数据融合将上述3个数据库的数据进行融合,最终得到了重合的446个miRNAs和322个疾病,和已经确认的5 152条miRNAs-疾病关联关系。
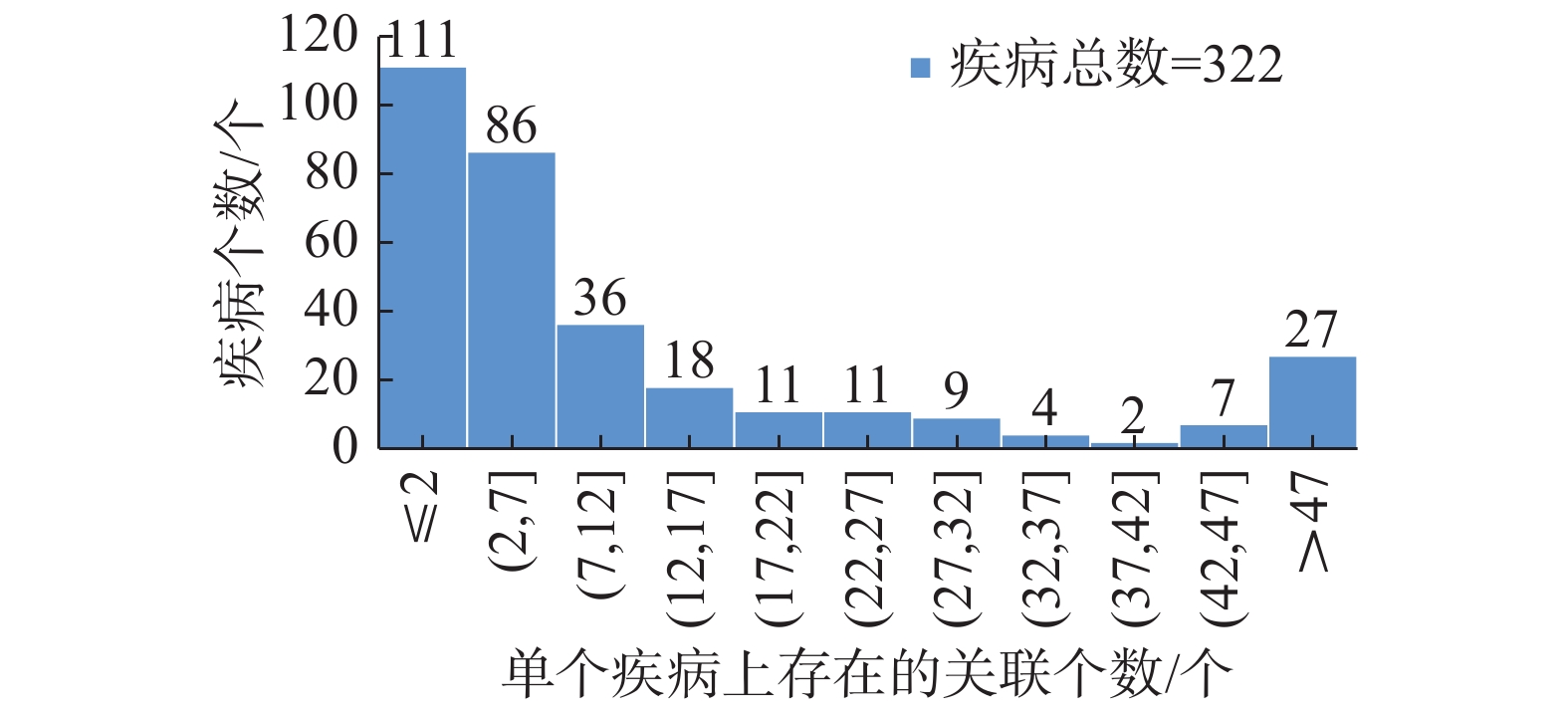
在疾病上的分布如图1所示。
|
Download:
|
| 图 1 miRNAs-疾病关联关系在疾病中的分布图 Fig. 1 Distribution map of the miRNAs-disease association in diseases | |
在miRNA上的分布如图2所示。

|
Download:
|
| 图 2 miRNAs-疾病关联关系在miRNA中的分布图 Fig. 2 Distribution map of the miRNAs-disease association in miRNAs | |
本文中,引入了矩阵分解的思想来解决miRNAs-疾病关联关系预测问题。
首先,通过整合miRNAs功能相似度网络和疾病语义相似性网络得到最终的miRNAs相似度矩阵MS和疾病相似度矩阵DS,以及已经被实验验证的miRNAs-疾病关联网络R。
首先,对每个miRNA和疾病,给定它们在固定长度为k的维度空间的初始化投影向量,并以其内积来表示miRNAs和疾病的关联关系,可以用式(3)表示:
| ${{{R}}'} = {{{M}}^{\rm{T}}}{{D}}$ | (3) |
式中:M是由m(本文中m=446)个k维列向量组成的k行m列的矩阵,同样的,D是k行d列(本文中d=322)的矩阵。我们的目标即是通过求解合适的M和D来最小化R′和真实关系R的距离,即
| $\min {\lambda _1}\left\| {{{{M}}^{\rm{T}}}{{M}}- {\bf{MS}}} \right\|_F^2 + {\lambda _2}\left\| {{{{D}}^{\rm{T}}}{{D}} - {\bf{DS}}} \right\|_F^2$ | (4) |
考虑到这样的函数是二次的形式,在迭代优化时很难化简为不含有自身变量的等式,这会使得在迭代的过程中无法取得最优解,我们引入了辅助矩阵X和Y来进行优化,式(4)可以变形为
| $\begin{array}{c}\min {\lambda _1}\left\| {{{{M}}^{\rm{T}}}{{X}} - {\bf{MS}}} \right\|_F^2 + {\mu _1}\left\| {{{M}} - {{X}}} \right\|_F^2 + \\ {\lambda _2}\left\| {{{{D}}^{\rm{T}}}{{Y}} - {\bf{DS}}} \right\|_F^2 + {\mu _2}\left\| {{{D}} - {{Y}}} \right\|_F^2\end{array}$ | (5) |
经验性地,我们对需要约束的M、D加入二范数的约束,以防止模型陷入过拟合。最终的损失函数如式(6)所示:
| $\begin{array}{c}{ L} = \left\| {{{{M}}^{\rm{T}}}{{D}} - {{R}}} \right\|_F^2 + {\lambda _0}\left( {\left\| {{M}} \right\|_F^2 + \left\| {{D}} \right\|_F^2} \right) + \\ {\lambda _1}\left\| {{{{M}}^{\rm{T}}}{{X}} - {\bf{MS}}} \right\|_F^2 + {\mu _1}\left\| {{{M}} - {{X}}} \right\|_F^2 + \\ {\lambda _2}\left\| {{{{D}}^{\rm{T}}}{{Y}} - {\bf{DS}}} \right\|_F^2 + {\mu _2}\left\| {{{D}} - {{Y}}} \right\|_F^2\end{array}$ | (6) |
我们采用迭代最小二乘的方式来优化这个问题,先固定D、X、Y,求解M。对M求导,有
| $\begin{array}{c}\displaystyle\frac{{{ \partial }}{{L}}}{{{ \partial }}{{M}}} = 2 \cdot {{D}} \cdot {\left( {{{{M}}^{\rm{T}}}{{D}} - {{R}}} \right)^{\rm{T}}} + 2 \cdot {\lambda _0} \cdot {{M}} + \\ 2 \cdot {\lambda _1} \cdot {{X}} \cdot {\left( {{{{M}}^{\rm{T}}}{{X}} - {\bf{MS}}} \right)^{\rm{T}}} + 2 \cdot {\mu _1}\left( {{{M}} - {{X}}} \right)=\\ 2 \cdot {{D}}{{{D}}^{\rm{T}}}{{M}} - 2 \cdot {{D}}{{{R}}^{\rm{T}}} + 2 \cdot {\lambda _0} \cdot {{M}} + 2 \cdot {\lambda _1} \cdot {{X}}{{{X}}^{\rm{T}}}{{M}} - \\ 2 \cdot {\lambda _1} \cdot {{X}} \cdot {\bf{M}}{{\bf{S}}^{\rm{T}}} + 2 \cdot {\mu _1} \cdot {{M}} - 2 \cdot {\mu _1} \cdot {{X}}\end{array}$ | (7) |
令
| $\begin{array}{c}{{M}} = {\left( {{{D}}{{{D}}^{\rm{T}}} + \left( {{\lambda _0} + {\mu _1}} \right) \cdot {{{I}}_k} + {\lambda _1} \cdot {{X}}{{{X}}^{\rm{T}}}} \right)^{ - 1}}\cdot\\\left( {{{D}} \cdot {{{R}}^{\rm{T}}} + {\lambda _1} \cdot {{X}} \cdot {\bf{MS}} + \mu {}_1 \cdot {{X}}} \right)\end{array}$ | (8) |
同样,固定其他参数,分别求解D、X、Y,有:
| $\begin{array}{c}{{D}} = {\left( {{{M}}{{{M}}^{\rm{T}}} + ({\lambda _0} + {\mu _2}) \cdot {{{I}}_k} + {\lambda _2} \cdot {{Y}}{{{Y}}^{\rm{T}}}} \right)^{ - 1}}\\\left( {{{M}} \cdot {{R}} + {\lambda _2} \cdot {{Y}} \cdot {\bf{DS}} + {\mu _2} \cdot {{Y}}} \right)\\{{X}} = {\left( {{\lambda _1} \cdot {{M}}{{{M}}^{\rm{T}}} + {\mu _1}{{{I}}_k}} \right)^{ - 1}}\left( {{\lambda _1} \cdot {{M}} \cdot {\bf{MS}} + {\mu _1}{{M}}} \right)\\{{Y}}= {\left( {{\lambda _2} \cdot {{D}}{{{D}}^{\rm{T}}} + {\mu _2}{{{I}}_k}} \right)^{ - 1}}\left( {{\lambda _2} \cdot {{D}} \cdot {\bf{DS}} + {\mu _2}{{D}}} \right)\end{array}$ | (9) |
利用得到的M和D,用其内积得到新的关联关系矩阵
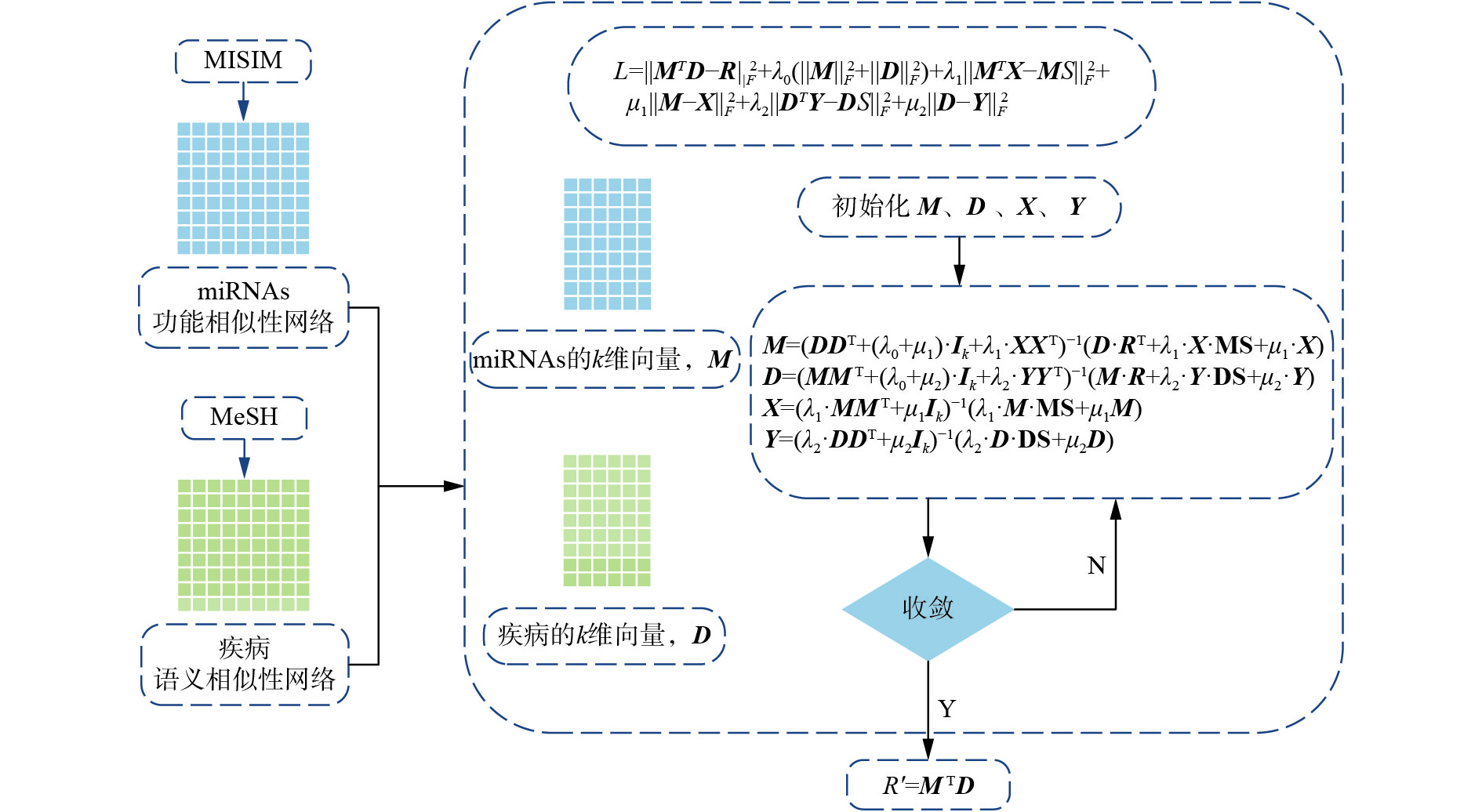
具体算法步骤如下:
1) 初始化miRNAs和疾病的向量矩阵M、D,以及辅助向量X、Y,并构建损失函数;
2) 用迭代最小二乘法求解M和D;
3)根据M和D预测miRNAs-疾病的关联关系。
| ${{{R}}'} = {{{M}}^{\rm{T}}}{{D}}$ |
算法框架如图3所示。
|
Download:
|
| 图 3 LMFMDA算法模型框图 Fig. 3 The flow chat of LMFMDA algorithm model | |
时间复杂度上,对于每次迭代,我们以M的求解为例,
同样地,求解D、X、Y的时间复杂度分别为
空间复杂度上,LMFMDA要求MS、DS、R、M、D、X和Y的存储空间,其空间复杂度为
实验采用留一交叉验证方式进行,对每个关系,将同一疾病下的未知关联视为负例,当前关联视为正例,最终得到的AUC作为评价结果。
4.1 实验参数通过对不同的参数进行实验对比,得到了以下参数组合:
miRNAs与疾病的向量矩阵M与D初始化为取值在[0, 1]上的随机向量,X与Y分别初始化为等同于M和D。
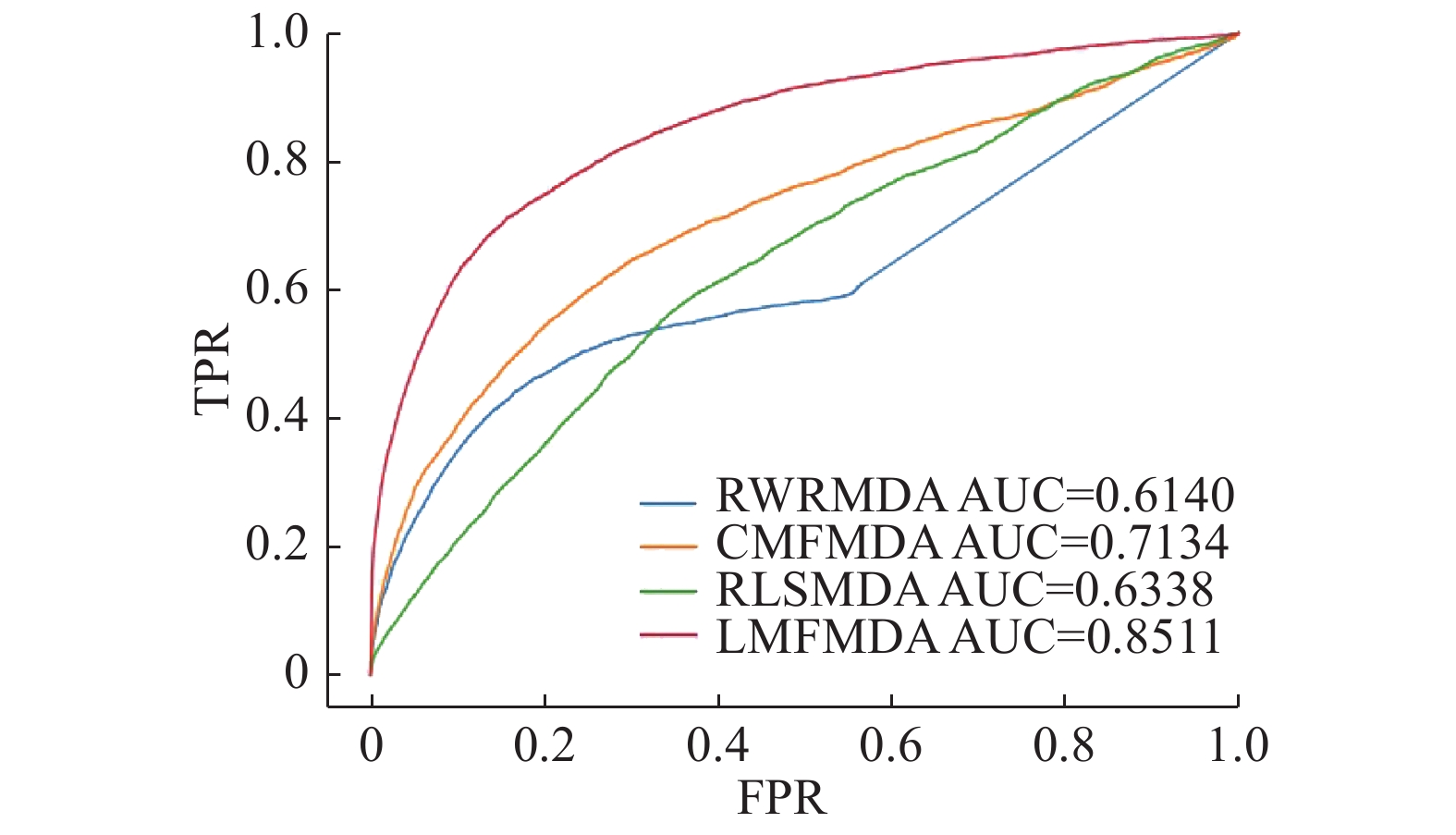
4.2 结果评价在第1节得到的446个miRNAs和322个疾病上分别实验了RWRMDA[13]、RLSMDA[22]、CMFMDA[23]以及本文提出的LMFMDA算法。实验结果如图4所示,LMFMDA的效果明显好于其他3种方法。
|
Download:
|
| 图 4 RWRMDA、CMFMDA、RLSMDA和LMFMDA的AUC结果 Fig. 4 The AUC results of RWRMDA, CMFMDA, RLSMDA and LMFMDA | |
我们分别记录了已知关联数>60的21个疾病的实验结果(见表2、表3),以及已知关联数=1的部分疾病的实验结果。已知关联数为1的疾病在进行留一法实验时,会将唯一一个已知的关联miRNA抹去,此时其已知关联数变为0,可以用于考察算法在新疾病中的应用效果。
| 表 2 高关联疾病在不同算法下的AUC结果 Tab.2 The AUC results of high association diseases on different algorithm |
| 表 3 新疾病在不同算法下的AUC结果 Tab.3 The AUC results of new diseases on different algorithm |
可以看到,不论是在关联数较多的疾病或关联数极少的疾病上,LMFMDA均表现出了优异的效果。
5 讨论在提出LMFMDA的损失函数前,曾试图对每个miRNA和疾病标注一个先验关联值,作为第k+1维,也是不参与运算的常数维。即:
| ${{{R}}'} = {{{M}}^{\rm{T}}}{{D}} - { em} - {{e}}{{{d}}^{\rm{T}}}$ |
然而其k值和AUC关联关系如图5所示。

|
Download:
|
| 图 5 带常数维模型中k与AUC关系图 Fig. 5 The relation diagram of k and AUC in a model with constant dimensional | |
可以看到,在k>100时,AUC值基本趋于稳定。而对k=100维这样的子空间来说,单独的常数维并不会对结果有很大的影响,于是删除了假设的先验关联值,最终确定了预测模型。
6 结论本文基于矩阵分解和迭代最小二乘的方法(LMFMDA)对miRNAs和疾病的关联关系进行预测。首先对miRNAs相似度矩阵、疾病相似度矩阵和miRNAs-疾病关联关系进行数据融合,采用迭代最小二乘法求解miRNAs和疾病的表达向量,最后利用miRNAs和疾病的表达向量完成对miRNA与疾病关联关系的预测。同时,通过引入辅助miRNAs和疾病变量的方法,解决了收敛结果的最优问题。实验显示,LMFMDA在高关联疾病和新疾病预测中相对于其他方法均取了较优的结果。
综上,本文提出的miRNA与疾病关联预测算法LMFMDA,一方面可以处理未知相关miRNAs的疾病、或者未知相关疾病的miRNAs;另一方面,实验结果也表明,LMFMDA算法在miRNAs和疾病的关联关系预测上相较其他算法有更好的效果。
| [1] |
WANG Qianghu, SUN Jie, ZHOU Meng, et al. A novel network-based method for measuring the functional relationship between gene sets[J]. Bioinformatics, 2011, 27(11): 1521-1528. DOI:10.1093/bioinformatics/btr154 ( 0) 0)
|
| [2] |
LV Sali, LI Yan, WANG Qianghu, et al. A novel method to quantify gene set functional association based on gene ontology[J]. Journal of the royal society interface, 2012, 9(70): 1063-1072. DOI:10.1098/rsif.2011.0551 ( 0) 0)
|
| [3] |
HRISTOVSKI D, FRIEDMAN C, RINDFLESCH T C, et al. Exploiting semantic relations for literature-based discovery[J]. AMIA annual symposium proceedings, 2006, 2006: 349-353. ( 0) 0)
|
| [4] |
KARP X, AMBROS V. Encountering microRNAs in cell fate signaling[J]. Science, 2005, 310(5752): 1288-1289. DOI:10.1126/science.1121566 ( 0) 0)
|
| [5] |
CHENG A M, BYROM M W, SHELTON J, et al. Antisense inhibition of human miRNAs and indications for an involvement of miRNA in cell growth and apoptosis[J]. Nucleic acids research, 2005, 33(4): 1290-1297. DOI:10.1093/nar/gki200 ( 0) 0)
|
| [6] |
MISKA E A. How microRNAs control cell division, differentiation and death[J]. Current opinion in genetics and development, 2005, 15(5): 563-568. DOI:10.1016/j.gde.2005.08.005 ( 0) 0)
|
| [7] |
XU Peizhang, GUO Ming, HAY B A. MicroRNAs and the regulation of cell death[J]. Trends in genetics, 2004, 20(12): 617-624. DOI:10.1016/j.tig.2004.09.010 ( 0) 0)
|
| [8] |
YOU Zhuhong, HUANG Zhian, ZHU Zexuan, et al. PBMDA: a novel and effective path-based computational model for miRNA-disease association prediction[J]. PLoS computational biology, 2017, 13(3): e1005455. DOI:10.1371/journal.pcbi.1005455 ( 0) 0)
|
| [9] |
SHI Hongbo, ZHANG Guangde, ZHOU Meng, et al. Integration of multiple genomic and phenotype data to infer novel miRNA-disease associations[J]. PLoS one, 2016, 11(2): e0148521. DOI:10.1371/journal.pone.0148521 ( 0) 0)
|
| [10] |
JIANG Qinghua, HAO Yangyang, WANG Guohua, et al. Prioritization of disease microRNAs through a human phenome-microRNAome network[J]. BMC systems biology, 2010, 4(S1): S2. ( 0) 0)
|
| [11] |
JIANG Qinghua, WANG Guohua, WANG Yadong. An approach for prioritizing disease-related microRNAs based on genomic data integration[C]//Proceedings of the 3rd International Conference on Biomedical Engineering and Informatics. Yantai, China, 2010: 2270–2274.
( 0) 0)
|
| [12] |
CHEN Xing, LIU Mingxi, YAN Guiying. RWRMDA: predicting novel human microRNA–disease associations[J]. Molecular biosystems, 2012, 8(10): 2792-2798. DOI:10.1039/c2mb25180a ( 0) 0)
|
| [13] |
CHEN Hailin, ZHANG Zuping. Similarity-based methods for potential human microRNA-disease association prediction[J]. BMC medical genomics, 2013, 6: 12. DOI:10.1186/1755-8794-6-12 ( 0) 0)
|
| [14] |
SHI Hongbo, XU Juan, ZHANG Guangde, et al. Walking the interactome to identify human miRNA-disease associations through the functional link between miRNA targets and disease genes[J]. BMC systems biology, 2013, 7: 101. DOI:10.1186/1752-0509-7-101 ( 0) 0)
|
| [15] |
XUAN Ping, HAN Ke, GUO Maozu, et al. Prediction of microRNAs associated with human diseases based on weighted k most similar neighbors[J]. PLoS one, 2013, 8(8): e70204. DOI:10.1371/journal.pone.0070204 ( 0) 0)
|
| [16] |
XU Chaohan, PING Yanyan, LI Xiang, et al. Prioritizing candidate disease miRNAs by integrating phenotype associations of multiple diseases with matched miRNA and mRNA expression profiles[J]. Molecular biosystems, 2014, 10(11): 2800-2809. DOI:10.1039/C4MB00353E ( 0) 0)
|
| [17] |
MØRK S, PLETSCHER-FRANKILD S, PALLEJA CARO A, et al. Protein-driven inference of miRNA–disease associations[J]. Bioinformatics, 2014, 30(3): 392-397. ( 0) 0)
|
| [18] |
PASQUIER C, GARDÈS J. Prediction of miRNA-disease associations with a vector space model[J]. Scientific reports, 2016, 6: 27036. DOI:10.1038/srep27036 ( 0) 0)
|
| [19] |
SUN Dongdong, LI Ao, FENG Huanqing, et al. NTSMDA: prediction of miRNA–disease associations by integrating network topological similarity[J]. Molecular biosystems, 2016, 12(7): 2224-2232. DOI:10.1039/C6MB00049E ( 0) 0)
|
| [20] |
LI Xia, XU Juan, LI Yongsheng. Prioritizing candidate disease miRNAs by topological features in the miRNA-target dysregulated network[M]//AZMI A S. Systems Biology in Cancer Research and Drug Discovery. Netherlands: Springer, 2012: 289–306.
( 0) 0)
|
| [21] |
JIANG Qinghua, WANG Guohua, JIN Shuilin, et al. Predicting human microRNA-disease associations based on support vector machine[J]. International journal of data mining and bioinformatics, 2013, 8(3): 282-293. DOI:10.1504/IJDMB.2013.056078 ( 0) 0)
|
| [22] |
CHEN Xing, YAN Guiying. Semi-supervised learning for potential human microRNA-disease associations inference[J]. Scientific reports, 2014, 4: 5501. ( 0) 0)
|
| [23] |
SHEN Zhen, ZHANG Youhua, HAN K, et al. miRNA-disease association prediction with collaborative matrix factorization[J]. Complexity, 2017, 2017: 2498957. ( 0) 0)
|
| [24] |
WANG Dong, WANG Juan, LU Ming, et al. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases[J]. Bioinformatics, 2010, 26(13): 1644-1650. DOI:10.1093/bioinformatics/btq241 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


