2. 计算智能与智能系统北京市重点实验室,北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing 100124, China
污水处理过程是一个复杂的生化反应过程,伴随有物理化学反应、生化反应、相变过程及物质与能量的转化和传递过程,建模困难,导致其过程控制更加困难[1]。而在污水处理过程中,溶解氧浓度(DO)是最重要的控制参数。溶解氧浓度不足或过量都会对微生物的生存环境带来一定的影响。溶解氧浓度较低时会导致丝状菌的大规模繁殖,最终导致污泥膨胀,使得分解效果降低。相反,溶解氧浓度过高时,会破坏微生物的絮凝效果,使得悬浮固体沉降性变差,曝气能耗增加[2]。因此为了保证出水指标满足污水处理过程的标准,溶解氧的浓度必须控制在一定的范围内。
针对污水处理过程中溶解氧的控制,许多学者进行了大量研究。其中经典的PID控制由于其简单的设计而被广泛应用。Wahab等[3]提出了基于污水处理过程的多变量PID控制,实现了对溶解氧的控制,并且对PID控制器的参数进行优化;Vrecko[4]等提出了一种结合PID及前馈控制方法来溶解氧浓度进行控制。然而,PID控制器的控制参数选择需要大量的经验知识,选择过程较为繁琐,而且在实际应用中,PID控制器普遍存在控制精度较低的问题。同时,传统的PID控制器受其自身特点的限制,使得其针对污水处理过程这样一个非线性、大时变过程,并不能取得较好的控制效果[5-7]。
基于此,许多学者对非线性系统的智能控制方法进行了大量研究。其中神经网络以其强大的自学习、自适应及非线性逼近能力,而受到了广泛关注。刘等[8]将自适应模糊神经网络控制器应用到活性污泥模型中DO溶度的控制中。结果表明,该控制器具有较强的鲁棒性,获得了较好的控制效果;Huang等[9]将模糊神经网络控制方法应用到生物膜污水处理过程的曝气量控制过程中,取得了较好的控制效果;付等[10]将模糊神经网络策略应用到污水基准仿真平台BSM1中实现了对DO浓度的控制。大量研究结果表明,以神经网络为主的智能控制方法能够有效地适用于污水处理这样的非线性大滞后过程中。然而,对于一般的神经网络而言,其结构固定,使得其难以适应复杂多变的环境。基于此,如何针对特定问题自动调整神经网络结构一直是国内外研究的热点问题[11-12]。
针对以上污水处理过程中DO浓度的跟踪控制存在的问题,文中提出了一种基于自组织模糊神经网络的溶解氧浓度控制方法。该自组织模糊神经网络利用激活强度和神经元重要性来判定模糊神经网络规一化层神经元的重要程度,从而对神经元进行增加和删减,以此来自动调整模糊神经网络的结构,防止网络结构出现冗余或不足。同时为保证网络的收敛性,文中采用梯度下降算法对神经网络的中心、宽度和权值进行训练。最后将该算法应用到Mackey-Glass时间序列预测及污水处理过程基准仿真平台BSM1中,实验结果表明所提出的自组织模糊神经网络相较于其他方法,具有较好的预测和控制效果,证明了该方法的有效性。
1 BSM1模型BSM1是欧盟科学技术合作组织(COST)和国际水协会(IWAQ)合作提出的基准仿真模型[13]。其总体布局如图1所示。该模型为测试污水处理过程控制策略和方法提供了一个验证平台。BSM1模型主要由两部分组成:生化反应池和二沉池。其中生化反应池包含5个单元,前两个单元为厌氧区,其余为好氧区。在BSM1中,DO的控制主要是通过控制生化反应池第5分区KLa5来实现的。
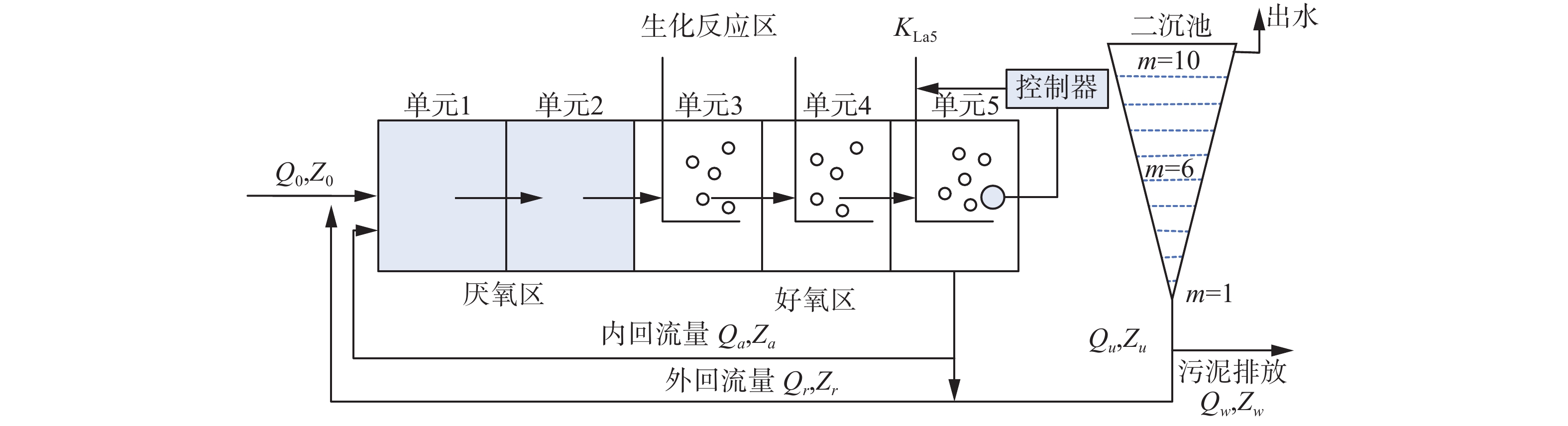
|
Download:
|
| 图 1 BSM1布局示意图 Fig. 1 The overall layout of BSM1 | |
本论文应用自组织模糊神经网络控制好氧区第5分区的DO浓度。图2为基于自组织模糊神经网络的溶解氧浓度控制器整体结构。

|
Download:
|
| 图 2 基于自组织模糊神经网络的溶解氧控制器结构框图 Fig. 2 The block diagram of the dissolved oxygen control system based on the fuzzy neural network | |
在控制系统中,控制器输入为e(k)和ec(k),其可表示为
| $e\left( k \right) = {y_d}\left( k \right) - y\left( k \right)$ |
| ${e_c}\left( k \right) = e\left( k \right) - e\left( {k - 1} \right)$ |
式中:e(k)表示溶解氧浓度的实际值与期望值的误差量;ec(k)表示误差变化量;yd(k)和y(k)分别表示控制系统中溶解氧的期望值及控制系统的实际输出值。
控制器的输出为du(k),即控制量的增量。由于在BSM1溶解氧浓度控制系统中,是通过控制生化反应池第五分区的氧传递系数KLa5来控制溶解氧浓度的,所以这里的du(k)即为KLa5的增量。
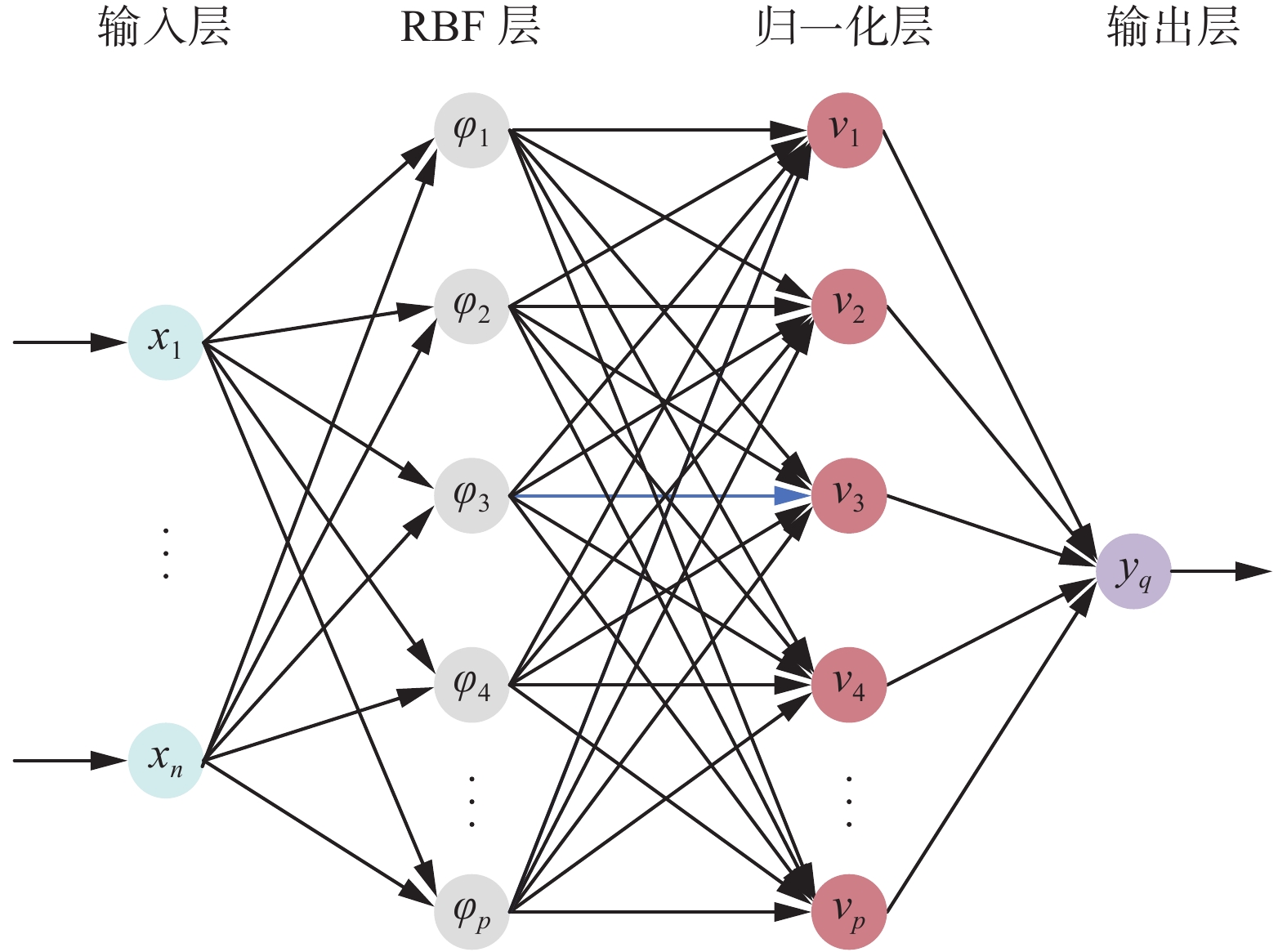
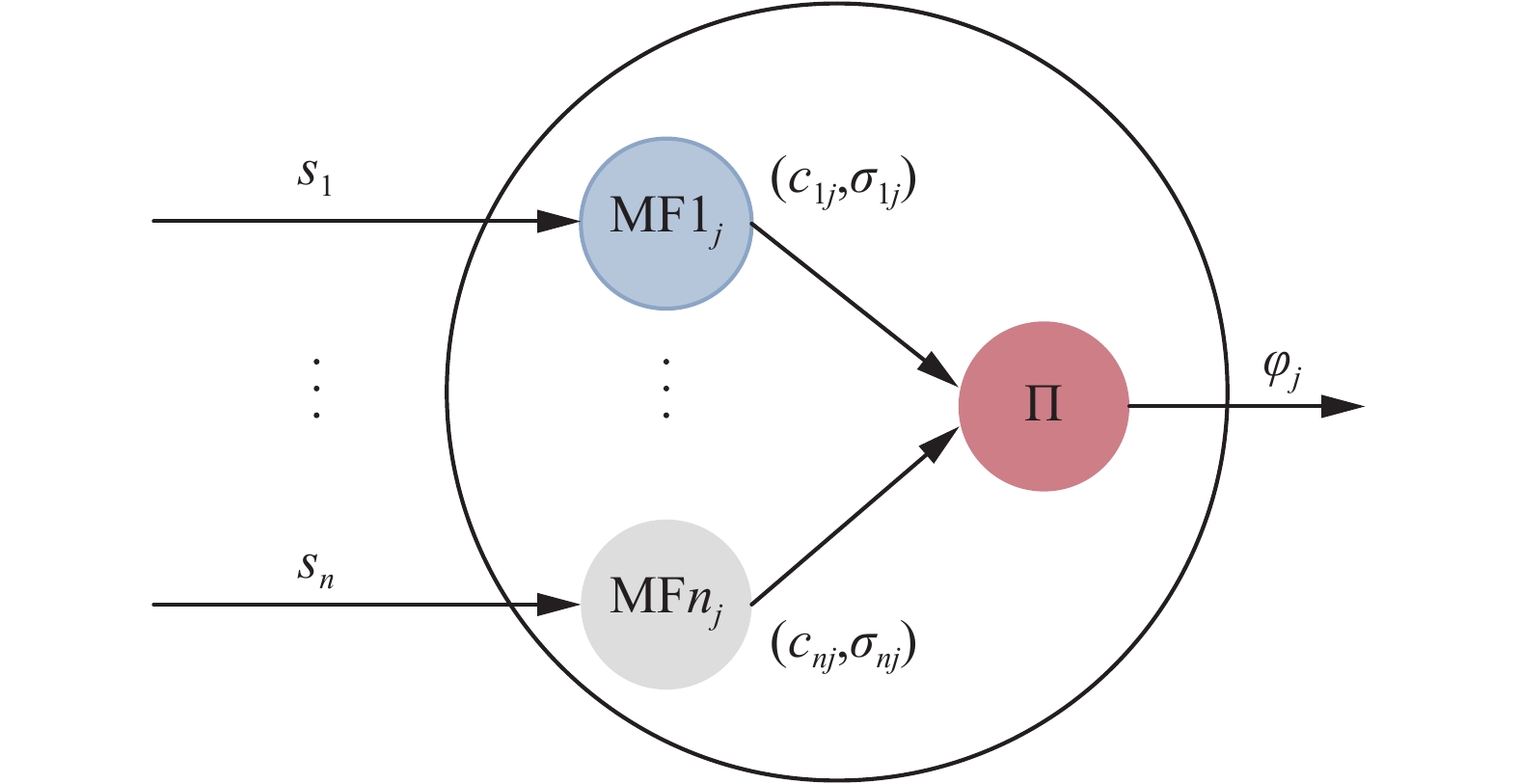
2.2 模糊神经网络结构模糊神经网是神经网络与模糊逻辑系统的结合体,它综合了两者的优点。一般而言,模糊神经网络主要由输入层、RBF层、规一化层和输出层组成,其拓扑结构如图3所示[14]。其中RBF层第j个神经元的内部结构如图4所示。
|
Download:
|
| 图 3 模糊神经网络拓扑结构 Fig. 3 The structure of fuzzy neural network | |
|
Download:
|
| 图 4 RBF层第j个神经元的结构 Fig. 4 The jth neural structure of the RBF layer | |
第1层为输入层,只起到信息传递的作用。该层共有n个神经元,代表FNN的输入变量的个数。其输出表达式为
| ${s_i} = {x_i}$ |
式中:i=1,2,···,n;si表示第i个神经元的输出;且输入变量为
第2层为RBF层,该层的功能是对输入量进行模糊化处理,在这里选取RBF神经元作为隶属函数进行模糊化,隶属函数选用为高斯函数。该层第j个神经元的输入为
| ${\varphi _j} = \exp \left( { - \sum\limits_{i = 1}^n {\left( {{{{{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{2\sigma _{ij}^2}}} \right)} } \right)$ |
式中:i=1,2,
第3层为规一化层,该层的神经元数与RBF层相同,有p个神经元。该层第l个神经元输出为
| ${v_l} = \frac{{{\varphi _l}}}{{\displaystyle\sum\limits_{j = 1}^p {{\varphi _j}} }} = \frac{{\exp \left( { - \displaystyle\sum\limits_{i = 1}^n {\left( {{{{{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{\sigma _{ij}^2}}} \right)} } \right)}}{{\displaystyle\sum\limits_{j = 1}^p {\exp \left( { - \sum\limits_{i = 1}^n {\left( {{{{{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{\sigma _{ij}^2}}} \right)} } \right)} }}$ |
式中:j=1, 2,
第4层为输出层,该层的功能是解模糊,这里采用重心法来对其进行进行归一化处理,其输出表达式为
| ${y_q} = \sum\limits_{l = 1}^p {{w_{lq}}{v_l}} = \frac{{\displaystyle\sum\limits_{l = 1}^p {{w_{lq}}\exp \left( {{{ - {{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{\sigma _{ij}^2}}} \right)} }}{{\displaystyle\sum\limits_{j = 1}^p {\exp \left( { - \displaystyle\sum\limits_{i = 1}^n {\left( {{{{{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{\sigma _{ij}^2}}} \right)} } \right)} }}$ |
式中:wl表示规一化层第l个神经元与输出层神经元之间的连接权值;y表示网络输出。
2.3 模糊神经网络在线学习模糊神经网络的在线学习主要包括结构调整和参数学习两部分。结构学习采用增长−修剪算法,参数学习采用梯度下降算法。
2.3.1 结构增长算法利用激活强度[15]作为结构增长的判断准则。激活强度定义公式如式(1)所示。激活强度大小表明该神经元对网络的贡献。激活强度越大,表明该神经元对网络的贡献越大;反之,则说明贡献较小。当输入数据对RBF层中所有神经元的激活强度的最大值仍小于设定的增长阈值时,表明当前的规则无法对新数据进行有效覆盖,需要增加神经元以满足当前控制环境的要求。
| ${\rm{AI}}_{j} = \exp \left( { - \sum\limits_{i = 1}^n {\left( {{{{{\left( {{u_i} - {c_{ij}}} \right)}^2}}/{2\sigma _{ij}^2}}} \right)} } \right)$ | (1) |
最大激活强度为
| ${I_g} = \arg \mathop {\max }\limits_{1 \leqslant j \leqslant p\left( t \right)} {\rm{AI}}_{j}$ | (2) |
式中:j=1,2,
若
| ${c_{\rm{new}}} = \frac{1}{2}\left( {{c_g} + x\left( t \right)} \right)$ | (3) |
| ${\sigma _{\rm{new}}} = {\sigma _g}$ | (4) |
| ${w_{\rm{new}}} = \frac{{{y_d} - y}}{{\exp \left( { - \displaystyle\sum\limits_{i = 1}^k {\displaystyle\frac{{{{\left( {x\left( t \right) - {c_{\rm{inew}}}} \right)}^2}}}{{2\sigma _{\rm{inew}}^2}}} } \right)}}$ | (5) |
式中:cnew、σnew和wnew分别表示新增神经元的参数;g表示距离当前样本欧式距离最小的神经元;cg、σg为神经元g的中心和宽度;yd和y分别为期望输出和网络输出。
2.3.2 结构修剪算法在实际的生物细胞中,神经元并不是总处于一个活跃状态,一直不活跃的神经元终究会走向衰亡。同时为避免网络结构过度增长,避免网络结构出现冗余的现象,本文采用了一种基于神经元重要性的网络在线修剪算法[16]。该算法的思想为:初始条件下每个神经元的重要性为1,并设置不活跃阈值ρ。每次计算每个神经元的激活强度,若激活强度小于设定的不活跃阈值ρ时,说明该神经元对输出的贡献较小,可以忽略并将该神经元进行一次重要性衰减,其计算公式由式(6)表达。当t时刻满足删减条件(7)时,则删除该神经元。
| ${I_k}\left( {t + 1} \right) = \left\{ \begin{array}{l} {I_k}\left( t \right)\exp \left( { - \tau } \right),\,\,\,\,\quad A{I_k} < \rho \\ {I_k}\left( t \right),\,\,\,\,\quad A{I_k} \geqslant \rho \\ \end{array} \right.$ | (6) |
| ${I_k} \leqslant {I_{\rm{cth}}}$ | (7) |
式中:Ik表示第k个神经元的重要性,初始条件下为1;
为保证神经网络输出稳定,减少删除神经元后对网络的影响,这里参照文献[14]对神经网络参数进行补偿,具体参数设置如下:
| $c_h' = {c_h}$ | (8) |
| $\sigma _h' = {\sigma _h}$ | (9) |
| $w_h' = \frac{{{w_h}\exp \left( { - \displaystyle\sum\limits_{i = 1}^k {\frac{{{{\left( {x\left( t \right) - {c_{ih}}} \right)}^2}}}{{2\sigma _{iq}^2}}} } \right) + {w_s}\exp \left( { - \displaystyle\sum\limits_{i = 1}^k {\frac{{{{\left( {x\left( t \right) - {c_{is}}} \right)}^2}}}{{2\sigma _{is}^2}}} } \right)}}{{\exp \left( { - \displaystyle\sum\limits_{i = 1}^k {\left( {\frac{{{{\left( {x\left( t \right) - {c_{\rm{ih}}}} \right)}^2}}}{{2\sigma _{\rm{ih}}^2}}} \right)} } \right)}}$ | (10) |
| $c_s' = 0$ | (11) |
| $\sigma _s' = 0$ | (12) |
| $w_s' = 0$ | (13) |
式中:s表示被修剪的神经元;h表示距离神经元s欧式距离较小的神经元;
在模糊神经网络参数训练中,采用梯度下降算法,通过该算法对网络的中心值、宽度值和权值进行更新。
在参数训练过程中,首先定义一个目标函数:
| $J\left( k \right) = \frac{1}{2}{\left( {{y_d}\left( k \right) - y\left( k \right)} \right)^2} = \frac{1}{2}e_{}^2\left( k \right)$ | (14) |
式中:yd(k)和y(k)分别表示系统期望输出和实际的神经网络输出。参数学习的目的是使得期望目标函数J(k)达到最小。
在梯度下降算法中,各个参数更新公式如式(15)~(20)所示:
| ${c_{ij}}\left( {k + 1} \right) = {c_{ij}}\left( k \right) - \eta \frac{{\partial J\left( k \right)}}{{\partial {c_{ij}}\left( k \right)}}$ | (15) |
| ${\sigma _{ij}}\left( {k + 1} \right) = {\sigma _{ij}}\left( k \right) - \eta \frac{{\partial J\left( k \right)}}{{\partial {\sigma _{ij}}\left( k \right)}}$ | (16) |
| ${w_l}\left( {k + 1} \right) = {w_l}\left( k \right) - \eta \frac{{\partial J\left( k \right)}}{{\partial {w_l}\left( k \right)}}$ | (17) |
式中:
| $\frac{{\partial J\left( k \right)}}{{\partial {c_{ij}}\left( k \right)}} = - \frac{{e\left( k \right){w_l}\left( k \right){v_l}\left( k \right)\left( {{u_i}\left( k \right) - {c_{ij}}\left( k \right)} \right)}}{{\sigma _{ij}^2\left( k \right)}}$ | (18) |
| $\frac{{\partial J\left( k \right)}}{{\partial {\sigma _{ij}}\left( k \right)}} = - \frac{{e\left( k \right){w_l}\left( k \right){v_l}\left( k \right){{\left( {{u_i}\left( k \right) - {c_{ij}}\left( k \right)} \right)}^2}}}{{\sigma _{ij}^3\left( k \right)}}$ | (19) |
| $\frac{{\partial J\left( k \right)}}{{\partial {w_l}\left( k \right)}} = - e\left( k \right){v_l}\left( k \right)$ | (20) |
式中:η表示参数学习率。
基于以上分析,SOFNN算法具体流程如下:
1)初始条件下模糊神经网络归一化层神经元数为3,并对模糊神经网络的中心、宽度和权值参数进行随机初始化;设置增长阈值Igth、神经元不活跃阈值ρ及修剪阈值Icth;
2)根据式(2)计算最大激活强度,并判断该神经元是否满足增长条件,若满足,则需要增长,并利用式(3)~(5)对新增神经元的中心、宽度和权值进行初始值化设定;否则转向步骤3);
3)根据修剪条件对网络隐含层神经元进行分析,若满足式(6),则对相应的模糊规则重要性进行一次衰减。当满足删减条件式(7)时,则对该模糊规则进行删除。并且神经元参数调整如式(8)~(13);
4)利用式(14)~(20)对神经网络的参数进行修改;
5)直到所有样本都学习完毕或满足停止条件,否则,转向步骤5)(结构调整已完成)或步骤2)(结构还需调整)进行重复训练。
3 仿真实验为了验证所提出的自组织模糊神经网络方法的可行性和有效性,文中通过Mackey-Glass时间序列和污水处理过程溶解氧浓度跟踪控制进行仿真实验。
3.1 Mackey-Glass时间序列预测Mackey-Glass时间序列可由式(15)描述:
| $x\left( {t + 1} \right) = \left( {1 - a} \right)x\left( t \right) + \frac{{bx\left( {t - \tau } \right)}}{{1 + {x^{10}}\left( {t - \tau } \right)}}$ | (21) |
式中:a=0.1,b=0.2,τ=17,x(0)=1.2
根据式(21)产生1 000个样本,其中前500个样本用于训练,剩余500个样本用于测试。
性能评价指标分别采用最终规一化层神经元数、均方根误差RMSE和平均百分比误差APE,其中RMSE和APE计算公式如式(22)~(23)所示:
| $\rm{RMSE} = \sqrt {\frac{1}{P}\sum\limits_{p = 1}^P {{{\left( {{y_d}\left( t \right) - y\left( t \right)} \right)}^2}} } $ | (22) |
| ${\rm{APE}} = \frac{1}{P}\sum\limits_{p = 1}^P {\frac{{\left| {{y_d}\left( t \right) - y\left( t \right)} \right|}}{{\left| {{y_d}\left( t \right)} \right|}}} \times 100\text{%} $ | (23) |
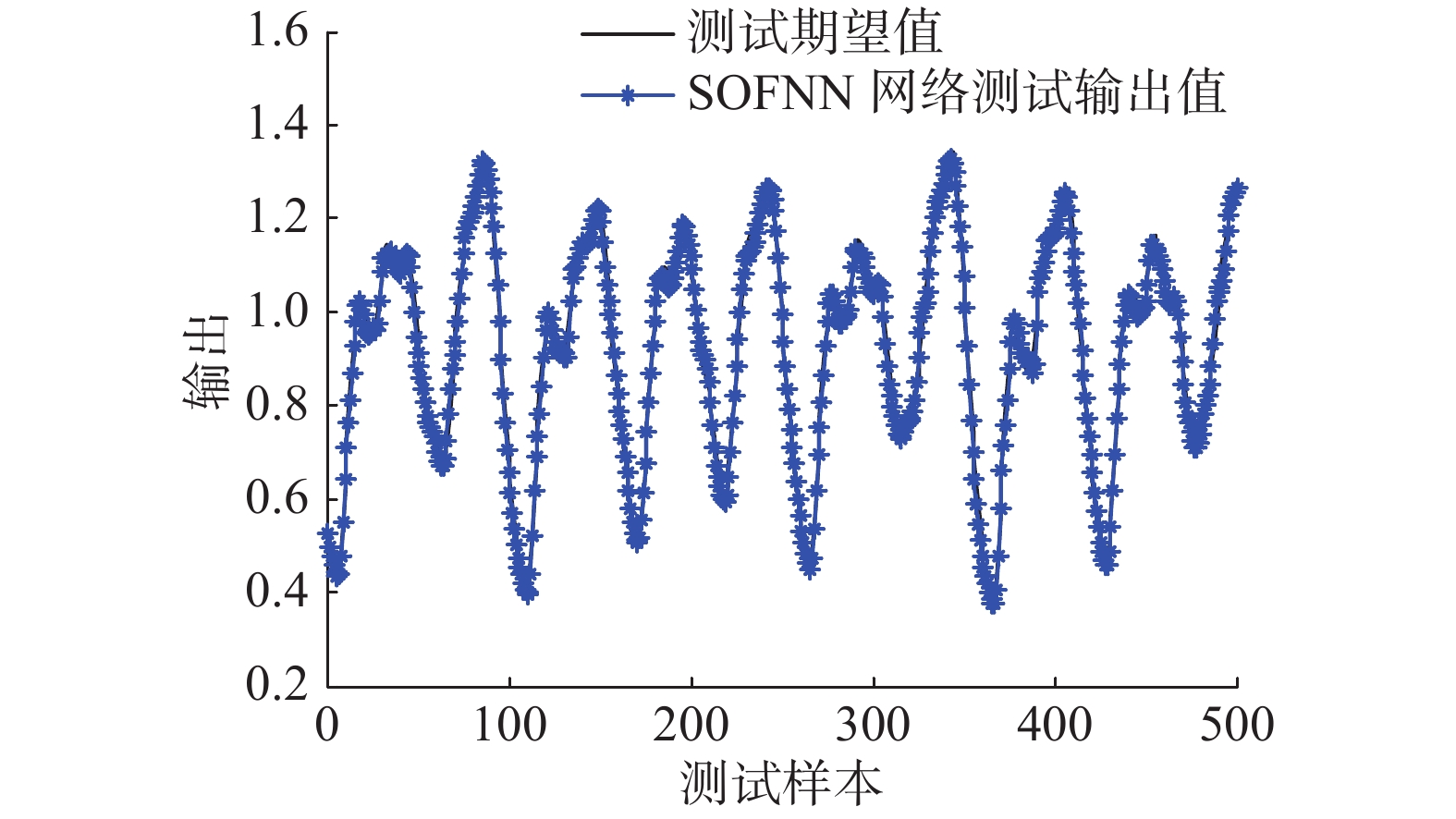
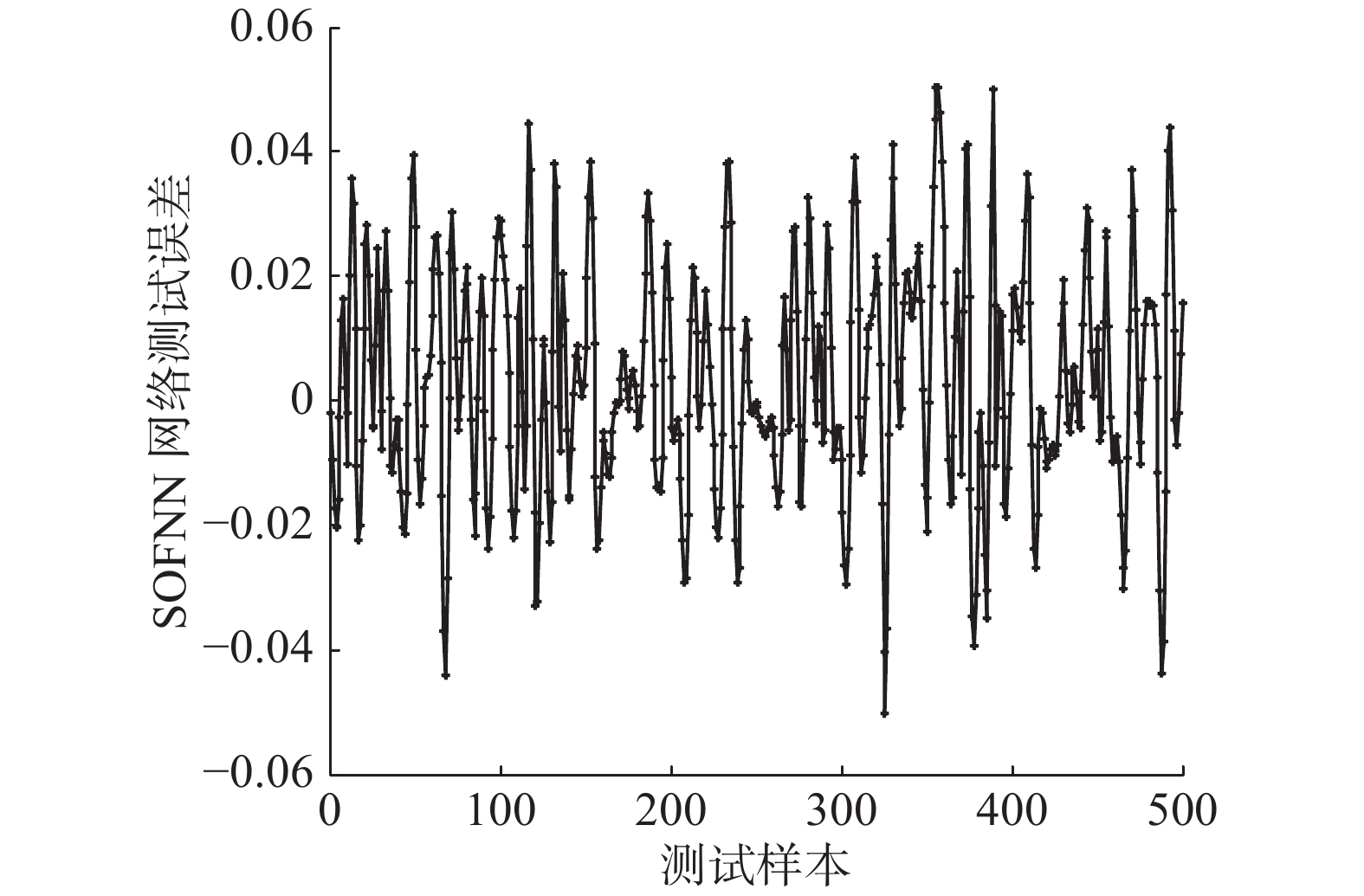
图5给出了训练过程归一化层神经元数的变化情况,可以看出最终神经元数稳定在7个左右。网络预测结果及预测误差分别如图6和图7所示,从图6中可以看出,所提出的SOFNN网络输出与期望输出曲线基本吻合,表明该方法能够对非线性时间序列进行较好地逼近。从图7可以看出网络的测试误差值保持在[−0.05,0.05]较小的范围内,表现出良好的泛化性能。

|
Download:
|
| 图 5 规一化层神经元变化曲线 Fig. 5 The neural number variation of normalized layer | |
|
Download:
|
| 图 6 预测结果 Fig. 6 The prediction error | |
|
Download:
|
| 图 7 预测误差 Fig. 7 Prediction errors | |
表1给出了不同算法的性能比较。从表1中可以看出,SOFNN算法的最终神经元数为7,各项指标都优于其他算法。结果表明该方法能够使得网络的结构得到最大化的精简,网络的泛化能力得到提高。
| 表 1 不同算法性能比较 Tab.1 Performance comparison of different algorithms |
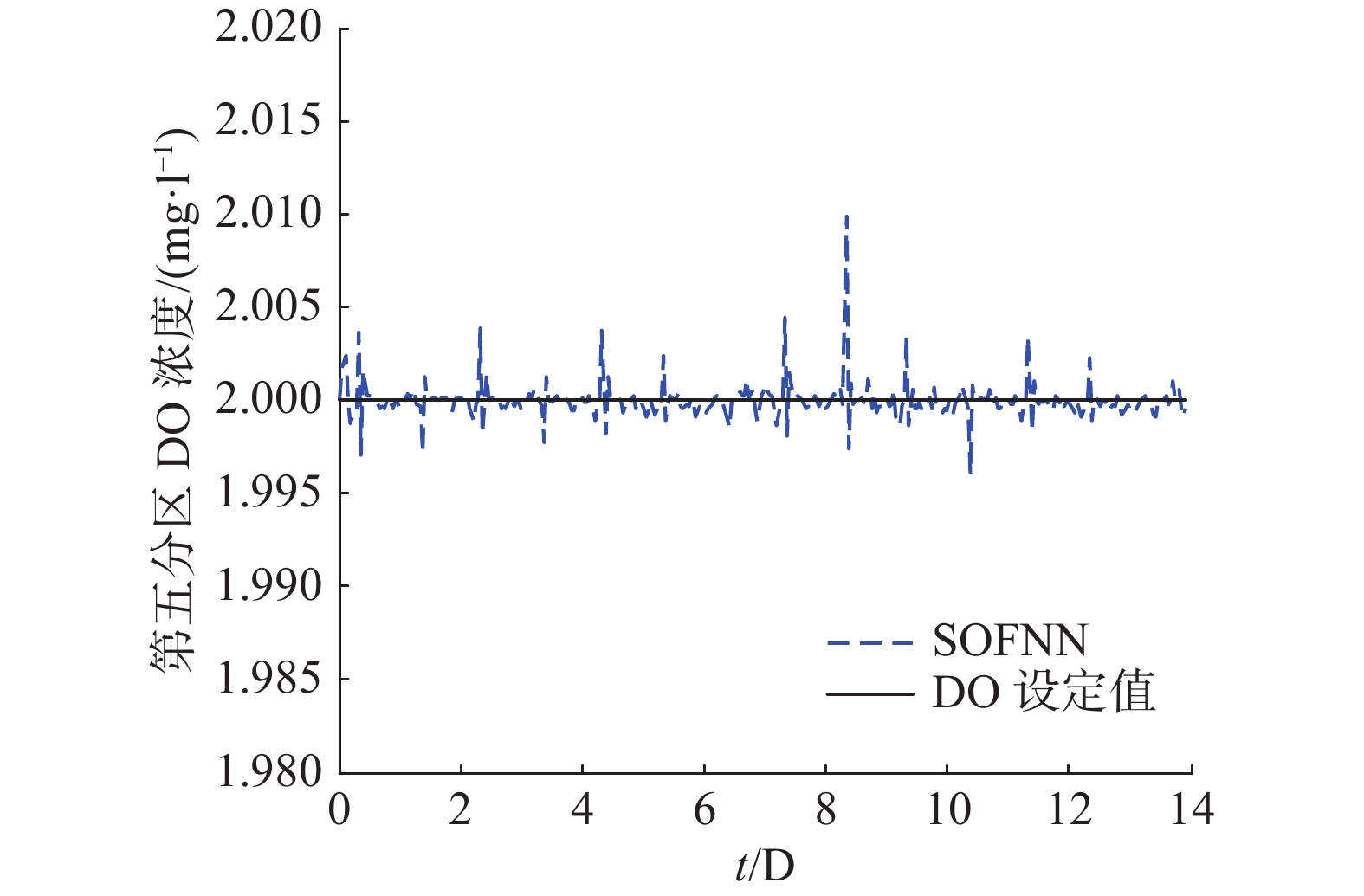
首先,设计对溶解氧浓度的恒定设定值(2 mg/l)的跟踪控制试验。在阴雨天气工况下,对生化反应池第五分区溶解氧浓度进行控制。并将该方法与其他3种控制策略进行比较。
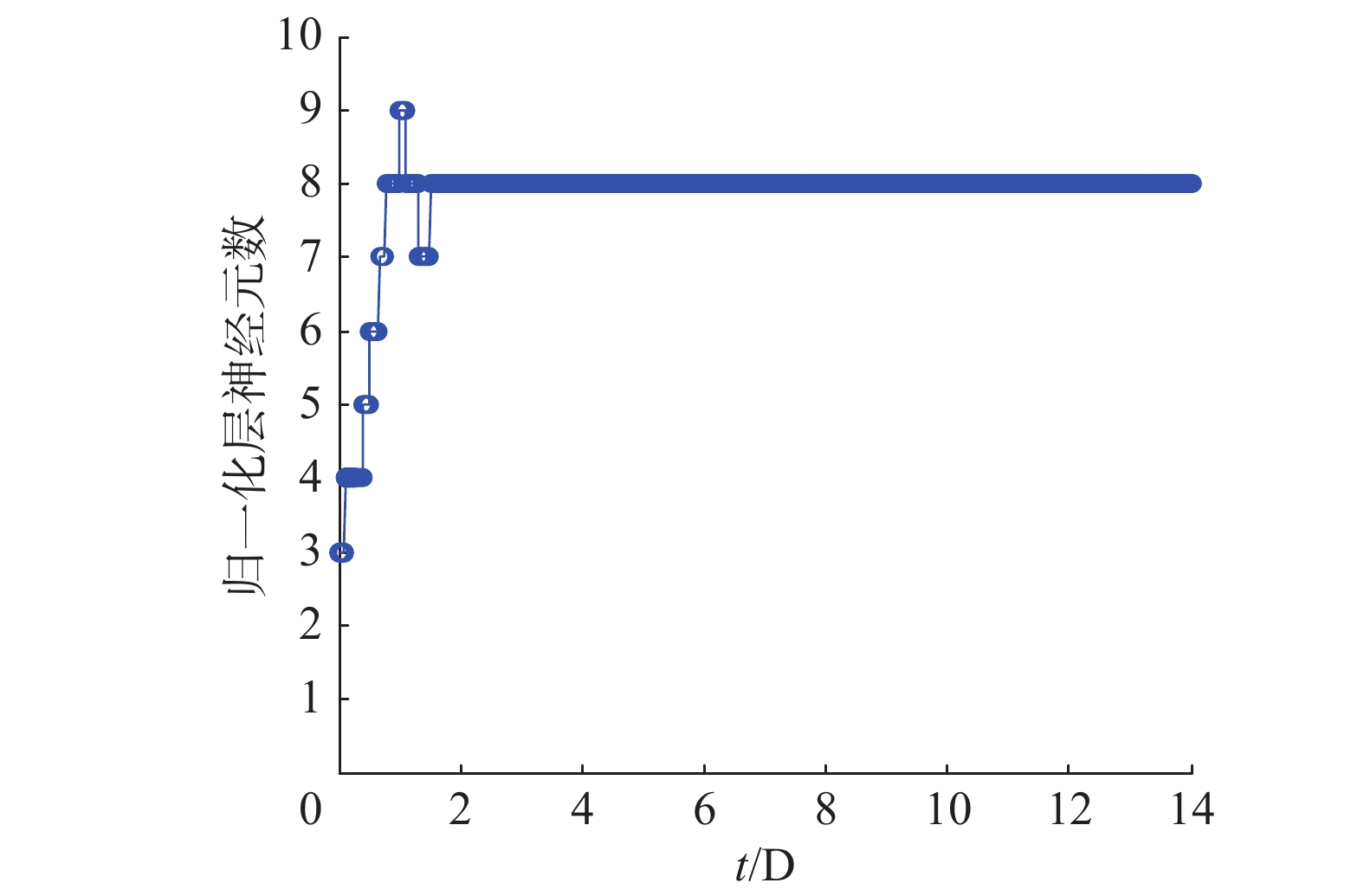
图8给出了该方法对溶解氧浓度的控制效果。图9给出了在控制过程中规一化层神经元数的变化情况。从图8可以看出,所提出的SOFNN控制器能够对DO设定值进行较好的跟踪,具有较好的控制精度。从图9可以看出,通过激活强度和神经元重要性的在线结构调整机制,使得控制器的网络结构最终稳定在8个左右,表明在控制过程中通过在线增长和修剪算法,能够获得一个较为精简的网络结构。
|
Download:
|
| 图 8 恒设定值溶解氧的控制效果 Fig. 8 The control effect of constant DO set-point | |
|
Download:
|
| 图 9 规一化层神经元数变化 Fig. 9 The neural number variation of normalized layer | |
表2给出了不同控制器的性能比较。通过与其他3种控制器的性能指标比较,可以看出基于SOFNN的DO控制系统相较于PID、FNN及BP控制算法,具有更好的控制效果。
| 表 2 不同控制器性能比较 Tab.2 Performance comparison of different controllers |
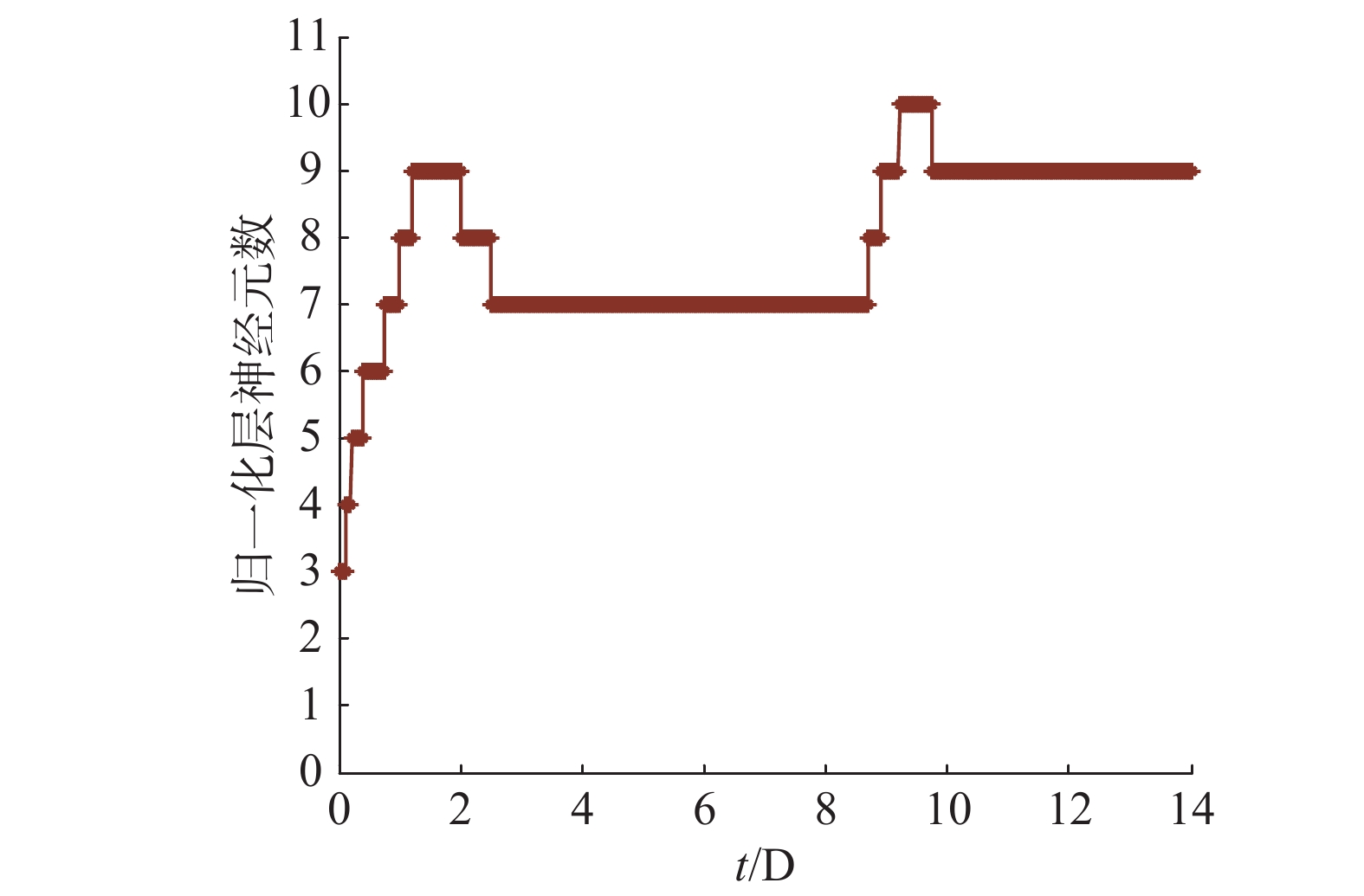
为了更好地验证SOFNN控制器的稳定性和鲁棒性,文中将溶解氧浓度的设定值1.8 mg/l~2.2 mg/l范围内阶跃变化,并考察SOFNN控制器在阴雨天气条件下的溶解氧浓度跟踪控制性能。图10给出了SOFNN控制效果图,图11给出了规一化层神经元数变化曲线。

|
Download:
|
| 图 10 变设定值溶解氧的控制效果 Fig. 10 The control effect of step change DO set-point | |
|
Download:
|
| 图 11 规一化层神经元数变化 Fig. 11 The neural number variation of normalized layer | |
从图10可以看出,当DO期望设定值发生变化后,控制器能够及时地根据当期那状况对DO进行良好跟踪控制,使其稳定在期望值附近。并且从图11可以看出,当环境发生变化时,所提出的SOFNN控制器能够根据当前环境情况变化自组织的调整控制器结构。通过性能指标比较可以看出,所提出的SOFNN控制器具有较小的IAE、ISE和MaxDev,表明该SOFNN控制器性能优于其他3种控制器,具有较好的控制效果、稳定性及控制精度。并且,通过比较隐含层神经元数可以看出,该SOFNN控制方法具有较少的神经元数,网络结构更加紧凑,如表3。
| 表 3 不同控制器性能比较 Tab.3 Performance comparison of different controllers |
针对污水处理过程中溶解氧浓度难以控制的问题,提出了一种基于自组织模糊神经网络(SOFNN)的控制方法。该自组织方法考虑到实际生物神经网络中的特性及神经元对网络输出的贡献程度,采用了一种基于神经元重要性的删减方法和基于神经元激活强度的增加方法。在删减阶段,采用基于重要性衰减的方法,这种策略虽然未能及时将“冗余”神经元进行删除,但是能够保证神经网络的稳定性,降低误删重要神经元的可能性。并通过梯度下降算法对网络的参数进行调整。然后通过两个实验来证明该方法的有效性。最后将该算法应用到Mackey-Glass时间序列预测及污水处理过程基准仿真平台BSM1中,实验结果表明所提出的自组织模糊神经网络相较于其他方法,具有较好的预测和控制效果,证明了该方法的有效性。
| [1] |
SANTÍN I, PEDRET C, VILANOVA R, et al. Advanced decision control system for effluent violations removal in wastewater treatment plants[J]. Control engineering practice, 2016, 49: 60-75. DOI:10.1016/j.conengprac.2016.01.005 ( 0) 0)
|
| [2] |
( 0) 0)
|
| [3] |
WAHAB N A, KATEBI R, BALDERUD J. Multivariable PID control design for activated sludge process with nitrification and denitrification[J]. Biochemical engineering journal, 2009, 45(3): 239-248. DOI:10.1016/j.bej.2009.04.016 ( 0) 0)
|
| [4] |
VRECKO D, HVALA N, KOCIJAN J. Wastewater treatment benchmark: what can be achieved with simple control?[J]. Water science and technology, 2002, 45(4/5): 127-134. ( 0) 0)
|
| [5] |
AYESA E, DE LA SOTA A, GRAU P, et al. Supervisory control strategies for the new WWTP of Galindo-Bilbao: the long run from the conceptual design to the full-scale experimental validation[J]. Water science and technology, 2006, 53(4/5): 193-201. ( 0) 0)
|
| [6] |
潘海鹏, 徐玉颖. 基于BP网络的流浆箱双变量PID解耦控制[J]. 化工学报, 2010, 61(8): 2154-2158. PAN Haipeng, XU Yuying. Double variable PID decoupling control of headbox based on BP neural network[J]. CIESC journal, 2010, 61(8): 2154-2158. (  0) 0)
|
| [7] |
KOTZAPETROS A D, PARASKEVAS P A, STASINAKIS A S. Design of a modern automatic control system for the activated sludge process in wastewater treatment[J]. Chinese journal of chemical engineering, 2015, 23(8): 1340-1349. DOI:10.1016/j.cjche.2014.09.053 ( 0) 0)
|
| [8] |
刘超彬, 乔俊飞, 张芳芳. 污水处理过程中溶解氧的模糊神经网络控制[J]. 山东大学学报: 工学版, 2005, 35(3): 83-87. LIU Chaobin, QIAO Junfei, ZHANG Fangfang. Fuzzy neural network controls of dissolved oxygen in the wastewater treatment processes[J]. Journal of Shandong university: engineering science, 2005, 35(3): 83-87. (  0) 0)
|
| [9] |
HUANG Mingzhi, WAN Jinquan, MA Yongwen, et al. Control rules of aeration in a submerged biofilm wastewater treatment process using fuzzy neural networks[J]. Expert systems with applications, 2009, 36(7): 10428-10437. DOI:10.1016/j.eswa.2009.01.035 ( 0) 0)
|
| [10] |
FU Wentao, QIAO Junfei, HAN Gaitang, et al. Dissolved oxygen control system based on the T-S fuzzy neural network[C]//Proceedings of 2015 International Joint Conference on Neural Networks. Killarney, Ireland, 2015: 1–7.
( 0) 0)
|
| [11] |
张伟, 乔俊飞, 李凡军. 溶解氧浓度的直接自适应动态神经网络控制方法[J]. 控制理论与应用, 2015, 32(1): 115-121. ZHANG Wei, QIAO Junfei, LI Fanjun. Direct adaptive dynamic neural network control for dissolved oxygen concentration[J]. Control theory and applications, 2015, 32(1): 115-121. (  0) 0)
|
| [12] |
HABBI H, BOUDOUAOUI Y, KARABOGA D, et al. Self-generated fuzzy systems design using artificial bee colony optimization[J]. Information sciences, 2015, 295: 145-159. DOI:10.1016/j.ins.2014.10.008 ( 0) 0)
|
| [13] |
JEPPSSON U, PONS M N. The COST benchmark simulation model—current state and future perspective[J]. Control engineering practice, 2004, 12(3): 299-304. DOI:10.1016/j.conengprac.2003.07.001 ( 0) 0)
|
| [14] |
HAN Honggui, QIAO Junfei. A self-organizing fuzzy neural network based on a growing-and-pruning algorithm[J]. IEEE transactions on fuzzy systems, 2010, 18(6): 1129-1143. DOI:10.1109/TFUZZ.2010.2070841 ( 0) 0)
|
| [15] |
FIGUEROA-GARCÍA J C, OCHOA-REY C M, AVELLANEDA-GONZÁLEZ J A. Rule generation of fuzzy logic systems using a self-organized fuzzy neural network[J]. Neurocomputing, 2015, 151: 955-962. DOI:10.1016/j.neucom.2014.09.079 ( 0) 0)
|
| [16] |
HSU Chunfei. Self-organizing adaptive fuzzy neural control for a class of nonlinear systems[J]. IEEE transactions on neural networks, 2007, 18(4): 1232-1241. DOI:10.1109/TNN.2007.899178 ( 0) 0)
|
| [17] |
WU Shiqian, ER M J, CAO Yang. A fast approach for automatic generation of fuzzy rules by generalized dynamic fuzzy neural networks[J]. IEEE transactions on fuzzy systems, 2001, 9(4): 578-594. DOI:10.1109/91.940970 ( 0) 0)
|
| [18] |
DE JESÚS RUBIO J. SOFMLS: online self-organizing fuzzy modified least-squares network[J]. IEEE transactions on fuzzy systems, 2009, 17(6): 1296-1309. DOI:10.1109/TFUZZ.2009.2029569 ( 0) 0)
|
| [19] |
WANG Ning, ER M J, MENG Xianyao. A fast and accurate online self-organizing scheme for parsimonious fuzzy neural networks[J]. Neurocomputing, 2009, 72(16/17/18): 3818-3829. ( 0) 0)
|
| [20] |
LENG Gang, MCGINNITY T M, PRASAD G. Design for self-organizing fuzzy neural networks based on genetic algorithms[J]. IEEE transactions on fuzzy systems, 2006, 14(6): 755-766. DOI:10.1109/TFUZZ.2006.877361 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


