双目视觉测距技术是计算机视觉技术的一种应用。它具有通过对人类双眼处理景物方式的模拟感知周围环境空间深度的功能[1]。在一些领域,机器视觉正在代替人眼成为有效的新工具。双目视觉在机器人导航与避障、机械臂的引导、三维成像、汽车导航等诸多领域都极具应用价值[2-3]。与目前其他测距方法相比,双目测距具有成本低、精度高、方便快捷等优点[4-5]。作为计算机视觉的分支,双目视觉技术在近些年来得到了长足的发展[6]。
双目视觉测距技术的基本原理是基于物体在左右相机像平面成像的相差,利用相似三角形的几何关系,得到物体距相机的距离[7]。其中的关键部分则是对左右视图进行匹配得到特征点的相差。而surf算法的特征点匹配具有稳定性高,实时性高的特点[8]。本文在对视图进行显著性检测的基础上,用surf算子对提取出的目标区域进行特征点匹配。准确地得到了目标的距离,并提高了测距过程的实时性。
1 双目视觉测距系统本文设计的双目视觉测距系统旨在为旋翼飞行器机械臂系统提供目标物体的距离信息,如图1所示,双目相机安装在旋翼飞行器机械臂系统的机械臂末端,通过双目相机对目标物体的实时测距并反馈距离信息,来控制旋翼飞行器机械臂系统操作实现抓取功能。双目视觉系统的原理图如图2所示。

|
Download:
|
| 图 1 双目视觉系统实物 Fig. 1 Real object drawing of binocular vision system | |

|
Download:
|
| 图 2 双目视觉结构原理 Fig. 2 The principle diagram of the binocular vision | |
假设左右相机的焦距和其他相关参数均相等,且平行放置。镜头基线均垂直于成像平面,左右相机满足
| $\left\{ \begin{array}{c}{x_l} =\displaystyle\frac{{{F_x}}}{Z}X\\ y =\displaystyle \frac{{{F_x}}}{Z}Y\\ {x_r} = -\displaystyle \frac{{{F_x}}}{Z}(T - X)\\ \displaystyle\frac{Z}{T} = \displaystyle\frac{{Z - {F_x}}}{{T - ({x_l} - {x_r})}}\end{array} \right.$ | (1) |
推导可得:
| $\left\{ \begin{array}{c}X = \displaystyle\frac{{{x_l}}}{{{x_l} - {x_r}}}T\\ Y = \displaystyle\frac{y}{{{x_l} - {x_r}}}T\\ Z = \displaystyle\frac{{{F_x}}}{{{x_l} - {x_r}}}T\end{array} \right.$ | (2) |
式中
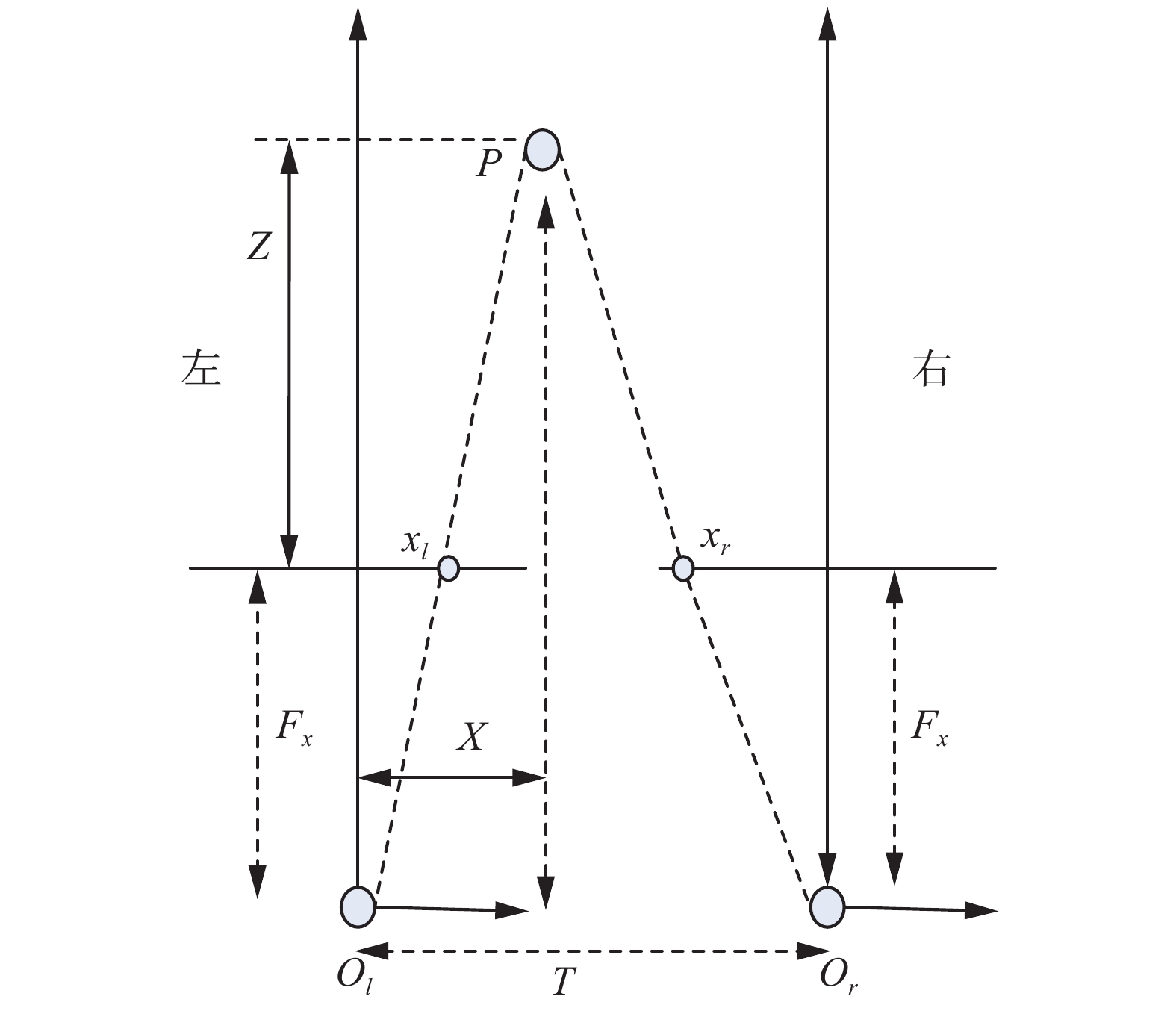
|
Download:
|
|
图 3 |
|
为了提高双目测距过程的实时性,本文设计了一种双目视觉成像测距模型,并重点研究了目标检测识别与左右视图特征匹配的问题,提出了一种基于显著性检测的双目视觉测距方法。根据目标物体在视图中颜色对比度比较明显的特征,采用基于直方图对比度(histogram contrast, HC)的显著性值检测方法[11]提取检测目标区域。针对相机焦距会随距离变化产生误差的特点,提出了一种用多组实验数据拟合相机焦距的方法,随后对检测到的目标物体应用surf算子[8]进行匹配,得到目标物体的距离信息,算法流程如图4所示。
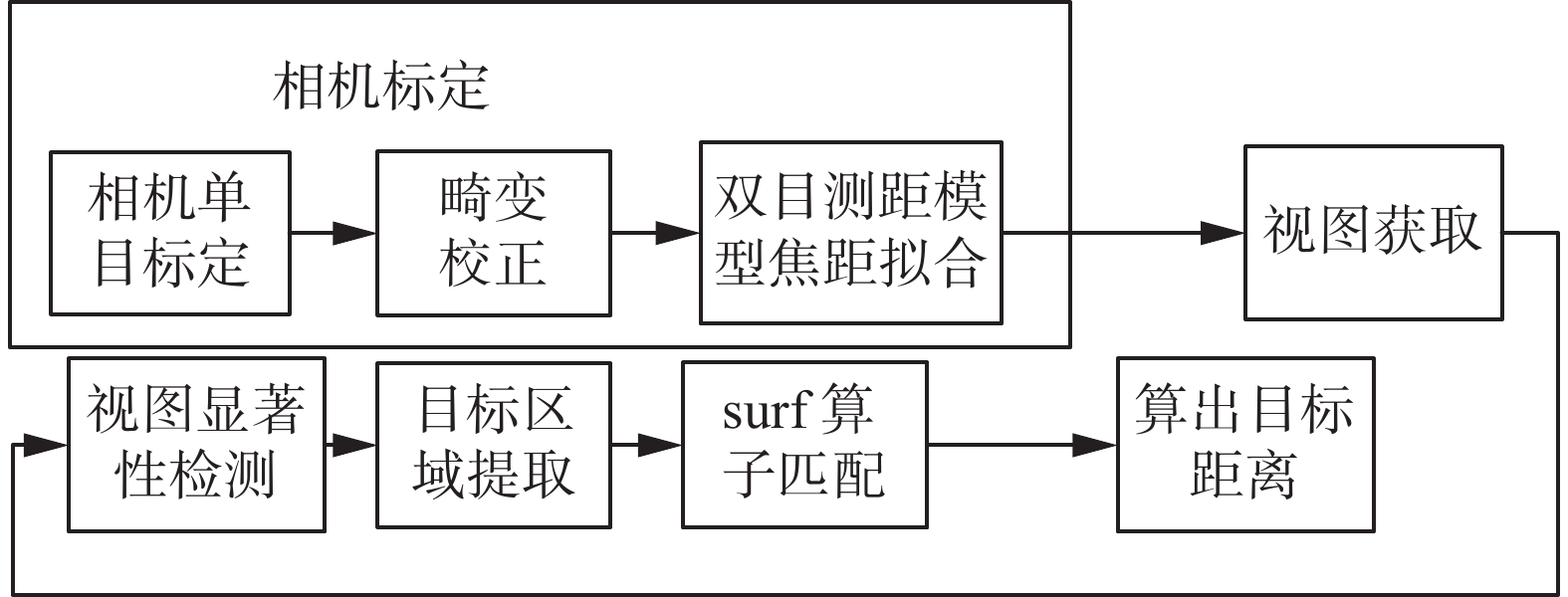
|
Download:
|
| 图 4 本文算法流程图 Fig. 4 The flowchart of the proposed method | |
在本文模型中主要考虑相机的径向畸变问题[12]。由图5可以看出,由于径向畸变的存在,在远离图像中心的区域a与区域b,现实当中的直线已经出现明显的弯曲。设不考虑畸变的图像坐标为
| $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} = x + x({k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2})$ | (3) |
| $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} = y + y({k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2})$ | (4) |
式中
假设在图像像素坐标系下,不考虑畸变的坐标为
| $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} = u + (u - {u_0})({k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2})$ | (5) |
| $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} = v + (v - {v_0})({k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2})$ | (6) |
式中
| $\left[ {\begin{array}{*{20}{c}} {(u - {u_0})({x^2} + {y^2})}&{(u - {u_0}){{({x^2} + {y^2})}^2}} \\ {(v - {v_0})({x^2} + {y^2})}&{(v - {v_0}){{({x^2} + {y^2})}^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{k_1}} \\ {{k_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} - u} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} - v} \end{array}} \right]$ |
假设有
| ${{k}} = {({{{D}}^{\rm{T}}}{{D}})^{ - 1}}{{{D}}^{\rm{T}}}{{d}}$ | (7) |
在考虑到畸变参数之后把世界坐标系下的点反投影到图像坐标系下,并与理想无畸变的参数进行最大似然估计,得到式(8),可以采用LM算法进行计算求取最优解。
| $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left\| {{u_{ij}} - f(M,{R_i},{t_i},{k_1},{k_2},{U_{ij}})} \right\|}^2}} } $ | (8) |
然后由式(9)与式(10),
| $u = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} + (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} - {u_0})[{k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2}]$ | (9) |
| $v = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} + (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} - {v_0})[{k_1}({x^2} + {y^2}) + {k_2}{({x^2} + {y^2})^2}]$ | (10) |
即完成了相机畸变校正的过程,其中

|
Download:
|
| 图 5 畸变矫正前图像 Fig. 5 Image before distortion correction | |

|
Download:
|
| 图 6 畸变矫正后图像 Fig. 6 Image after distortion correction | |
在双目视觉的测距过程中,由于误差存在的原因,随着距离的变大,测量的焦距逐渐增大[13],焦距与距离近似满足线性关系如式(11)。于是本文采用测量多组数据进行线性回归拟合以得到焦距的方法。其中,求取焦距与实际距离的拟合公式为
| ${F_x} = G\left( D \right)$ | (11) |
测量的焦距
| ${F_x}T = kD + b$ | (12) |
式中
由方程组
| ${F_x}T = kD + b$ | (13) |
| $D = {F_x}T/\left( {{x_l} - {x_r}} \right)$ | (14) |
可以得到实际距离
| $D({x_l} - {x_r} - k) + b = 0$ | (15) |
得到D与
| $Q = \sum\limits_{i = 1}^n {{{(k{x_i} + b - {y_i})}^2}} $ | (16) |
最小,先求出
| $Q = \sum\limits_{i = 1}^n {{{\left[ {\left( {b + k\bar x - \bar y} \right) - \left( {{y_i} - \bar y} \right) + k\left( {{x_i} - \bar x} \right)} \right]}^2}} $ | (17) |
将平方开出,并整理得
| $\begin{split} Q =& {k^2}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2} - 2k\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} } + \\ & n{\left( {b + k \cdot \bar x - \bar y} \right)^2} + \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} \end{split}$ | (18) |
此为关于
| $\left\{ \begin{array}{c}k =\displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {({x_i} - \bar x\bar y)({y_i} - \bar y)} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} }} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{x_i}{y_i} - n\bar x\bar y} }}{{\displaystyle\sum\limits_{i = 1}^n {x_i^2 - n{{\bar x}^2}} }}\\b = \bar y - k \cdot \bar x\end{array} \right.$ | (19) |
时,误差
| 表 1 拟合焦距所测得的数据 Tab.1 Measured data by fitting the focal length |
实验所得线性回归方程拟合所得图像如图7所示。
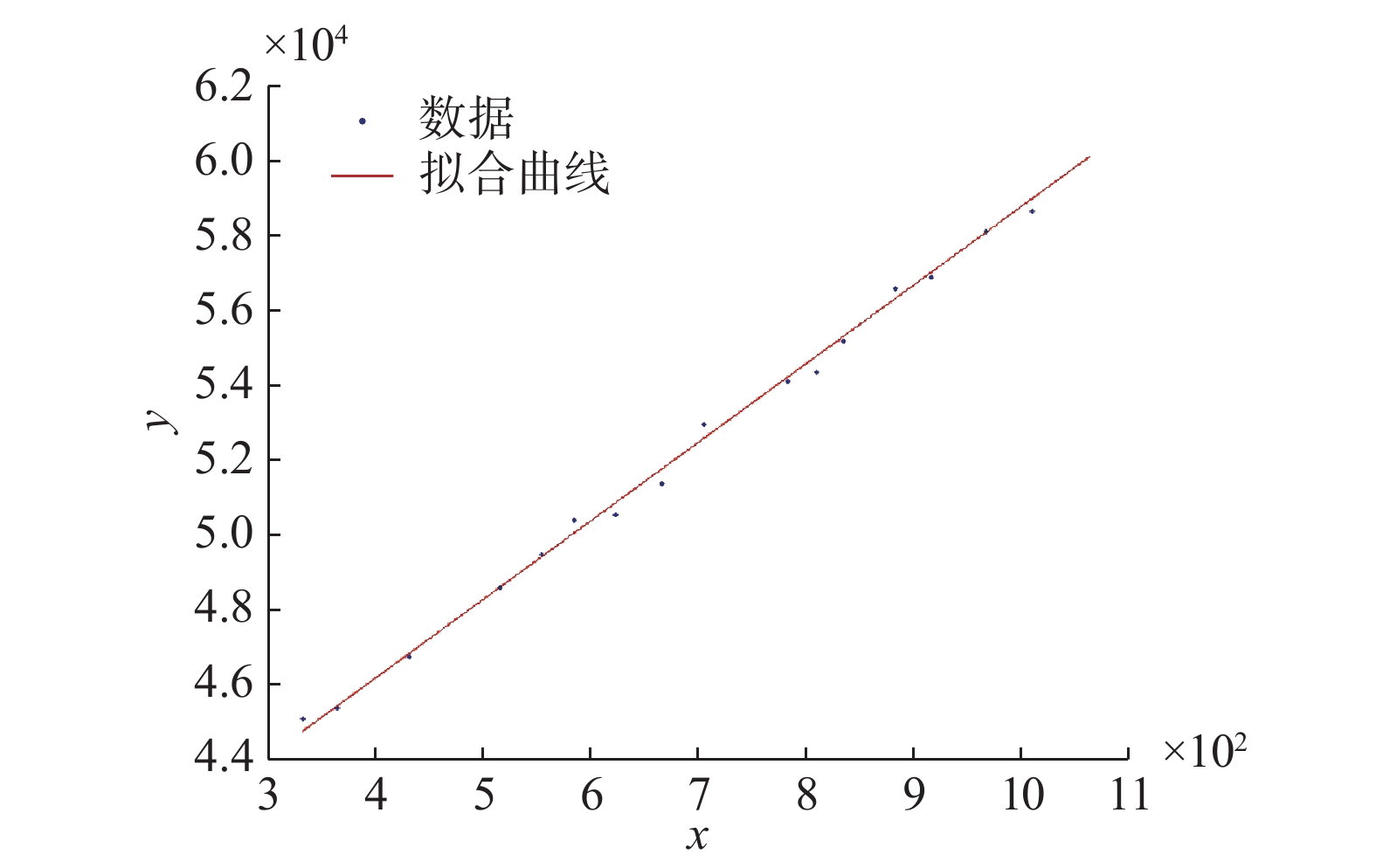
|
Download:
|
| 图 7 线性拟合图像 Fig. 7 Linear fitting image | |
图像的显著性区域检测是近年来计算机视觉和图像预处理领域的研究热点之一,其本质是模拟人眼观察自然界图像时的视觉选择性注意机制,是一种视觉注意模型[14]。显著区域检测在图像检索、图像分割、目标识别[15-17]等诸多领域有广泛的应用。
本文采用CHENG的基于直方图对比度(histogram contrast, HC)的图像像素显著性值检测方法[11]。该方法利用人的视觉系统对高对比度的视觉信号比较敏感的特点,首先定义一个像素的显著性值
| $S({I_k}) = \sum\limits_{\forall {I_i} \in I} {D({I_k},{I_i})} $ | (20) |
式中
将式(20)按照像素顺序展开得到:
| $S({I_k}) = D({I_k},{I_1}) + D({I_k},{I_2}) + \cdots +D({I_k},{I_n})$ | (21) |
可以看出,由于没有考虑空间的关系,在这种定义下,具有相同颜色值的像素会具有相同的显著性值,因此把具有相同颜色值
| $S({I_k}) = S({c_l}) = \sum\limits_{j = 1}^n {{f_j}D({c_l},{c_j})} $ | (22) |
式中:为

|
Download:
|
| 图 8 显著性检测前效果图 Fig. 8 Renderings before significance detection | |

|
Download:
|
| 图 9 显著性检测后效果图 Fig. 9 Renderings after significance detection | |
在得到目标物体的显著图后,首先对显著图进行腐蚀与膨胀操作,去除显著图中的噪点干扰,如图10所示。随后根据显著图中得到的目标区域信息对原图做与运算,则目标区域内像素值不变,目标区域外像素值置零,将目标区域从原图中提取出来,如图11所示。在此基础在上,对所得到的图像信息进行判断,只对像素不为零的值进行特征点匹配,处理流程如图12所示。

|
Download:
|
| 图 10 对显著图先腐蚀后膨胀效果图 Fig. 10 Renderings after erosion and dilate | |

|
Download:
|
| 图 11 目标区域从原图中提取出后效果图 Fig. 11 Renderings after extracted the target area from original image | |

|
Download:
|
| 图 12 目标区域处理流程图 Fig. 12 The flowchart of target area processing | |
由于SIFT算子在检测的过程中存在计算数据大,耗时长的问题,Bay等[8]提出了一种对尺度和旋转具有鲁棒性的快速鲁棒的特征描述方法(speed up robust features,surf)。surf检测算子与sift检测算子类似,首先构建尺度空间,初步检测极值点,在确定特征点主方向后确定特征点描述子。与sift对图像构造金字塔图不同,surf是通过改变滤波器的大小构造金字塔图层构建尺度空间,在此基础之上采用Hessian矩阵检测极值点,对检测的速度有很大提高。
2.5.1 Hessian矩阵确定特征点在surf算子检测特征点的过程中Hessian矩阵判别式尤为关键,在构建尺度空间后,当Hessian矩阵判别式的局部值最大时所检测出的即为待选的特征点。在图像I中,点
| ${ H}(x,y,\sigma ) = \left[ {\begin{array}{*{20}{c}} {{L_{xx}}(x,y,\sigma )}&{{L_{xy}}(x,y,\sigma )} \\ {{L_{xy}}(x,y,\sigma )}&{{L_{yy}}(x,y,\sigma )} \end{array}} \right]$ |
式中:
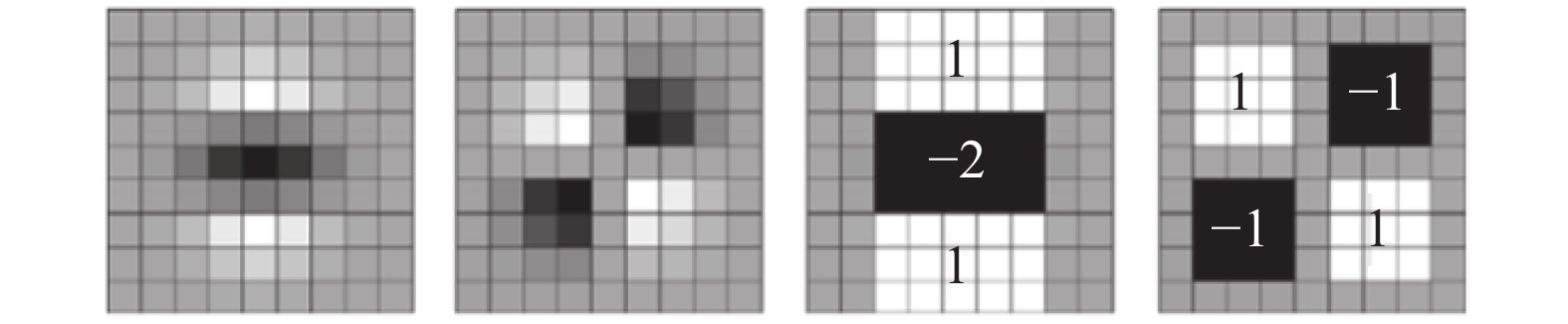
|
Download:
|
| 图 13 框状滤波模板代替高斯二阶偏导滤波 Fig. 13 Frame filter template instead of Gaussian second-order partial derivative filter | |
在模板中用
| $\det {{H}} = {D_{xx}}{D_{yy}} - {(\omega {D_{xy}})^2}$ | (23) |
由于高斯滤波与近似高斯滤波的差异性,用滤波响应的相对权重系数
为了保证surf特征点的描述子具有旋转不变的特性,需要确定特征点的主方向。以某个特征点为圆心,在半径为6
在此基础之上,构造一个带方向(前面计算的主方向)的正方形区域,边长设定为20
双目立体视觉系统中最关键且最重要的一步是立体特征匹配[18]。在双目立体视觉系统中的立体匹配通常是通过寻找两幅图像中能够检测到的具有明显特征的元素如角点,边缘或者区域进行匹配。由双目立体视觉测距原理可知图像匹配的准确度决定了测量距离的精度[19]。
surf特征匹配采用近邻欧氏距离比例法,通过对图像中特征向量属性进行判断,来达到两幅图像匹配成功的目的[20]。在本文算法过程中,首先计算左图中局部特征点的特征向量
| $D = \sqrt {\sum\limits_{i = 1}^n {{{(x_i^l - x_i^r)}^2}} } $ | (24) |
| $\eta = \frac{{{D_{{\rm near}}}}}{{{D_{{\rm sub\_near}}}}}$ | (25) |
为了降低双目视觉测距的误差,降低特征匹配的错误率,本文首先对使用的相机进行了单目标定,用标定后的参数对原始图像进行了畸变校正。在此基础之上本文采取了10组目标与角度不同的图片,图为应用显著性检测方法前后surf算子匹配时间对比,可以看出在应用本文算法之后,匹配时间缩短,实时性提高,如表2所示。
| 表 2 算法处理前后时间对比 Tab.2 The time comparison before and after the algorithm processing ms |
为了测量距离更加准确,本文对相机的焦距进行了焦距拟合。并与未进行焦距拟合的实验结果进行对比。表中拟合前的测量值为将目标1与目标2实验数据计算所得焦距代入测距模型所得到的实验结果。拟合后测量值为进行线性拟合后所得焦距代入测距模型中,所得到的实验结果,如表3、表4所示。
可以看出,在该测距模型中,与拟合实验中目标1、目标2比较接近的距离误差较小,随着测量距离与目标1、目标2的距离的差距的增大,测量误差增大较快。使用进行线性拟合后的焦距测量的实验结果,相对于未进行线性拟合算出的焦距测量的实验结果,随着距离的增加误差增大较慢,测量的距离准确性增高明显。
| 表 3 焦距拟合前测距实验结果对比 Tab.3 Distance measurement results before fitting of focal length |
| 表 4 焦距拟合后测距实验结果对比 Tab.4 Distance measurement results after fitting of focal length |
本文主要提出了一种在双目视觉测距系统中通过显著性检测方法识别出目标物体,在应用特征点来进行双目视觉中左右视图的匹配,来准确获得物体距离信息的方法。本文在对相机畸变校正后,对相机进行了焦距拟合,与相机拟合前的实验结果进行对比,得到了误差更小的实验结果。本文方法旨在为旋翼飞行器中机械臂系统提供待抓取物体的深度信息。通过实验可得,本文方法得到的目标物体的深度信息准确可靠,为旋翼飞行器机载机械臂的任务抓取提供了可靠准确的数据支持。
| [1] |
杨景豪, 刘巍, 刘阳, 等. 双目立体视觉测量系统的标定[J]. 光学精密工程, 2016, 24(2): 300-308. YANG Jinghao, LIU Wei, LIU Yang, et al. Calibration of binocular vision measurement system[J]. Optics and precision engineering, 2016, 24(2): 300-308. (  0) 0)
|
| [2] |
邱雪娜, 刘士荣. 基于序贯检测机制的双目视觉运动目标跟踪与定位方法[J]. 机器人, 2011, 33(1): 181-190. QIU Xuena, LIU Shirong. Moving objects tracking and localization with binocular vision based on sequential detection mechanism[J]. Robot, 2011, 33(1): 181-190. (  0) 0)
|
| [3] |
赵振庆, 叶东, 陈刚, 等. 垂直直线特征的双目视觉位姿测量方法[J]. 光学学报, 2014, 34(10): 1015003. ZHAO Zhenqing, YE Dong, CHEN Gang, et al. Binocular vision method of measuring pose based on perpendicular lines[J]. Acta optica sinica, 2014, 34(10): 1015003. (  0) 0)
|
| [4] |
刘俸材, 谢明红, 王伟. 双目视觉的立体标定方法[J]. 计算机工程与设计, 2011, 32(4): 1508-1512. LIU Fengcai, XIE Minghong, WANG Wei. Stereo calibration method of binocular vision[J]. Computer engineering and design, 2011, 32(4): 1508-1512. (  0) 0)
|
| [5] |
郭慧, 刘亚菲, 王勇, 等. 大型齿轮工件焊接的双目视觉测量标定[J]. 东华大学学报: 自然科学版, 2013, 39(4): 455-459. GUO Hui, LIU Yafei, WANG Yong, et al. Calibration of binocular vision measurement of large gear workpiece welding[J]. Journal of Donghua university: natural science, 2013, 39(4): 455-459. (  0) 0)
|
| [6] |
历艳琨, 毛建旭, 刘仁明. 基于特征点的3D人脸姿态跟踪[J]. 电子测量与仪器学报, 2016, 30(4): 605-612. LI Yankun, MAO Jianxu, LIU Renming. 3D face pose tracking based on feature matching[J]. Journal of electronic measurement and instrument, 2016, 30(4): 605-612. (  0) 0)
|
| [7] |
张国刚, 徐向辉. 基于加权纹理特征的SAR图像目标识别算法[J]. 国外电子测量技术, 2015, 34(9): 22-25. ZHANG Guogang, XU Xianghui. SAR image target recognition algorithms based on weighted texture features[J]. Foreign electronic measurement technology, 2015, 34(9): 22-25. DOI:10.3969/j.issn.1002-8978.2015.09.005 (  0) 0)
|
| [8] |
BAY H, TUYTELAARS T, VAN GOOl L. SURF: speeded Up robust features[C]//Proceedings of the 9th European conference on Computer Vision. Graz, Austria, 2006: 404–417.
( 0) 0)
|
| [9] |
余小欢, 韩波, 张宇, 等. 基于双目视觉的微型无人机室内3维地图构建[J]. 信息与控制, 2014, 43(4): 392-397. YU Xiaohuan, HAN Bo, ZHANG Yu, et al. Binocular stereo vision based 3D mapping for micro aerial vehicles in an indoor environment[J]. Information and control, 2014, 43(4): 392-397. (  0) 0)
|
| [10] |
公衍超, 万帅, 杨楷芳, 等. 利用双目视觉视频的实时三维裸手手势识别[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(4): 130-136. GONG Yanchao, WAN Shuai, YANG Kaifang, et al. Real-time 3D bare-hand gesture recognition using binocular vision videos[J]. Journal of Xidian university, 2014, 41(4): 130-136. (  0) 0)
|
| [11] |
CHENG Mingming, ZHANG Guoxin, MITRA N J, et al. Global contrast based salient region detection[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA, 2011: 409–416.
( 0) 0)
|
| [12] |
ZHANG Zhengyou. Flexible camera calibration by viewing a plane from unknown orientations[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra, Greece, 2002, 1: 666–673.
( 0) 0)
|
| [13] |
丁莹, 范静涛, 宋天喻. 双目立体视觉检测系统正向最优化设计方法研究[J]. 仪器仪表学报, 2016, 37(3): 650-657. DING Ying, FAN Jingtao, SONG Tianyu. Optimal forward design method for the binocular stereo vision inspection system[J]. Chinese journal of scientific instrument, 2016, 37(3): 650-657. DOI:10.3969/j.issn.0254-3087.2016.03.023 (  0) 0)
|
| [14] |
HOU Xiaodi, ZHANG Liqing. Saliency detection: a spectral residual approach[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA, 2007: 1–8.
( 0) 0)
|
| [15] |
YAN Qiong, XU Li, SHI Jianping, et al. Hierarchical saliency detection[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA, 2013: 1155–1162.
( 0) 0)
|
| [16] |
GOFERMAN S, ZELNIK-MANOR L, TAL A. Context-aware saliency detection[C]//Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA, 2010: 2376–2383.
( 0) 0)
|
| [17] |
KANAN C, COTTRELL G. Robust classification of objects, faces, and flowers using natural image statistics[C]//Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA, 2010: 2472–2479.
( 0) 0)
|
| [18] |
VALLERAND S, KANBARA M, YOKOYA N. Binocular vision-based augmented reality system with an increased registration depth using dynamic correction of feature positions[C]//Proceedings of 2003 IEEE Virtual Reality. Los Angeles, USA, 2003: 271–272.
( 0) 0)
|
| [19] |
BANKS J, CORKE P. Quantitative evaluation of matching methods and validity measures for stereo Vision[J]. The international journal of robotics research, 2001, 20(7): 512-532. DOI:10.1177/02783640122067525 ( 0) 0)
|
| [20] |
BAY H, ESS A, TUYTELAARS T, et al. Speeded-Up robust features (SURF)[J]. Computer vision and image understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


