智能车辆的研究内容十分多样，例如它的结构设计，控制理论^[1-2]，路径规划。对于智能车的路径规划，设计最优的曲线是此问题的核心。智能车的路径规划按照范围可分为宏观与微观2类，按照状态可分为动态规划和静态规划2类。对于智能车的宏观路径规划，Dijkstra算法、Floyd-Warshall算法，支持向量机算法^[3]，A*算法^[4-5]等均有文献进行应用和改进。而对于智能车的动态路径规划，人工势场算法^[6]、神经网络算法、遗传算法等智能算法也被广泛的应用。上述算法大多是对宏观的道路网络节点进行路径规划，然而对于微观的道路上的轨迹规划问题，目前国内外文献较少从最优性这一角度进行考量，还需要进行进一步的探索与研究。对于轨迹规划问题，基于Dubins路径^[7]的轨迹生成方法是一种可行的方法。此外还有三角函数曲线、圆弧曲线等轨迹生成方法。考虑到曲率连续问题，文献[7]给出了基于五次多项式的轨迹规划方法。此外还有文献采用模糊逻辑控制^[8-10]、粒子群算法、蚁群算法等智能算法进行优化与控制。上述文献给出了十分有价值的理论成果，但大多是对首末位置以及障碍物信息已知情况下的轨迹规划，不少文献采用GPS定位方式确定信息，鉴于目前GPS装置的精度和性能，可能会和实际路况存在较大误差。因此，在实际道路中目标点的确定依然是一个难题，而邻域系统理论是一种可行的解决方式。

本文主要以邻域系统^[8-12]理论为基础，研究智能车在邻域系统内的最优轨迹，是微观道路上的轨迹规划问题。邻域系统是一个数学上的常用概念，是对事物及其关联事物体系的抽象描述。本文一方面将数学中的邻域系统应用于智能车辆具体的控制过程，这里涉及到了设计具体控制规则，实现数学抽象到具体应用的转变；另一方面将具体的智能车控制过程抽象成一般的数学模型，并通过具体的求解算法，进行数学模型的求解。通过分层决策思想，将动态的车辆运动规划中近乎无限多的信息缩小至车辆的邻域系统内，继而缩小至有限个标准可行邻域内，从而将复杂道路中的运动简化为车辆在一系列简单的邻域内的静态决策过程的叠加。因此只需考虑某一个单一邻域内的最优轨迹规划问题，这为问题求解带来了极大地简化。

对于单一邻域内的最优轨迹规划问题。首先根据乘车者的需求对标准可行邻域内的轨迹曲线寻求泛函极值。具体做法是应用泛函的思想确立轨迹曲线的弯阻指数与长度指数等指标，其中采用曲线曲率的积分定义了曲线的弯阻指数。上述指标的建立是为了模拟乘车者的感受，以弯阻指数为例，若道路曲率越小，则弯阻指数越小，车辆行驶越顺畅。按照上述指标的要求，本文建立了最优轨迹曲线的多目标优化模型，并给出了一种实用的和可操作的求解方案，构造了一种采用Hermite插值法的轨迹曲线，并和其他几类常用的轨迹曲线进行了对比，结果表明本文构造的曲线是一种比较好的满意轨迹曲线，更接近人工经验轨迹。

1 智能车辆的邻域系统

智能车辆会因人们的各类需求而装配有各类传感器，例如距离传感器、红外线传感器、超声波传感器、图像传感器等。当智能车辆在道路上运动时，这些传感器会给出当前道路包括障碍物的各种信息，用以确定车辆的一个安全行走范围，这就是车辆的一个可行邻域，可行邻域的定义如下。

定义1　可行邻域^[8]

假设状态论域X的一个有界区域Q(x₀, T)满足： $\forall $ z∈Q(x₀, T)， $\exists$ {x(t); x₀, T}∈Γ(x₀)，使得z∈{x(t); x₀, T}且{x(t); x₀, T} $ \subseteq $ Q(x₀, T)，则称Q(x₀, T)是初态x₀的一个可行邻域，其中T称可行区域的保持时间，Γ(x₀)为初始状态为x₀的轨迹集合。

由初始状态x₀的所有可行邻域构成的集合称为该状态的可行邻域系统，记为FNS(x₀)。状态x₀的一个可行邻域包括了从x₀出发的一段时间T内状态轨迹的集合，在一个确定的可行邻域内可能含多条轨迹。

要实现智能车等智能轮式机器人的自主移动，首先需要模仿智能生物的行为决策过程。智能生物在面对复杂的动态环境时，通常先寻找一个短时间不变或保持相对稳定的环境作为其下一步活动的决策范围，然后再进行行为决策。这一决策范围即可行邻域，一系列的可行邻域构成邻域系统。基于邻域系统的动态决策模型^[8]就是描述这样一个基于邻域系统的控制决策过程。其控制过程由以下几个步骤组成：

1)根据控制过程中观测变量的特点选择合适的邻域系统；

2)通过一些优化方法，在当前状态下确定一个满意的可行邻域；

3)在满意的邻域中，根据一些规划方法给予满意的决策，实施新的决策行为；

4)在可行邻域的持续时间内保持相同的行为，直到产生下一个决策；

5)上述过程是一个完整的决策循环。当一个周期完成后，一个新的循环开始依次执行步骤2)～4)。

可以看到，各个邻域的控制过程不断重复叠加，从而构成了整个控制过程。模型将复杂的宏观环境下的动态决策过程分解为一系列简单的邻域内的静态决策过程的组合，简化了整个决策过程，使得面对的是一个有限的、局部的简单环境，而不是无限的、复杂的整个世界。由此可见，车辆在道路上的运动轨迹问题被转化为在每一个可行邻域里的运动规划问题的叠加。

如图1所示，为智能车某一时刻在道路上行驶的示意图。其中上下两侧的平行线为仿真道路的边界，道路内部的虚线所围成的不规则多边形是传感器能够确立的车辆行驶的一个可行邻域。注意到可行邻域的形状与数学表达都很难描述，因此需要建立车辆的标准可行邻域，其中图1内虚线围成的矩形框就是一个标准可行邻域。鉴于标准可行邻域没有一个统一的定义，本文的标准可行邻域含义如下。

标准可行邻域：可行邻域中数量有限的特定邻域。

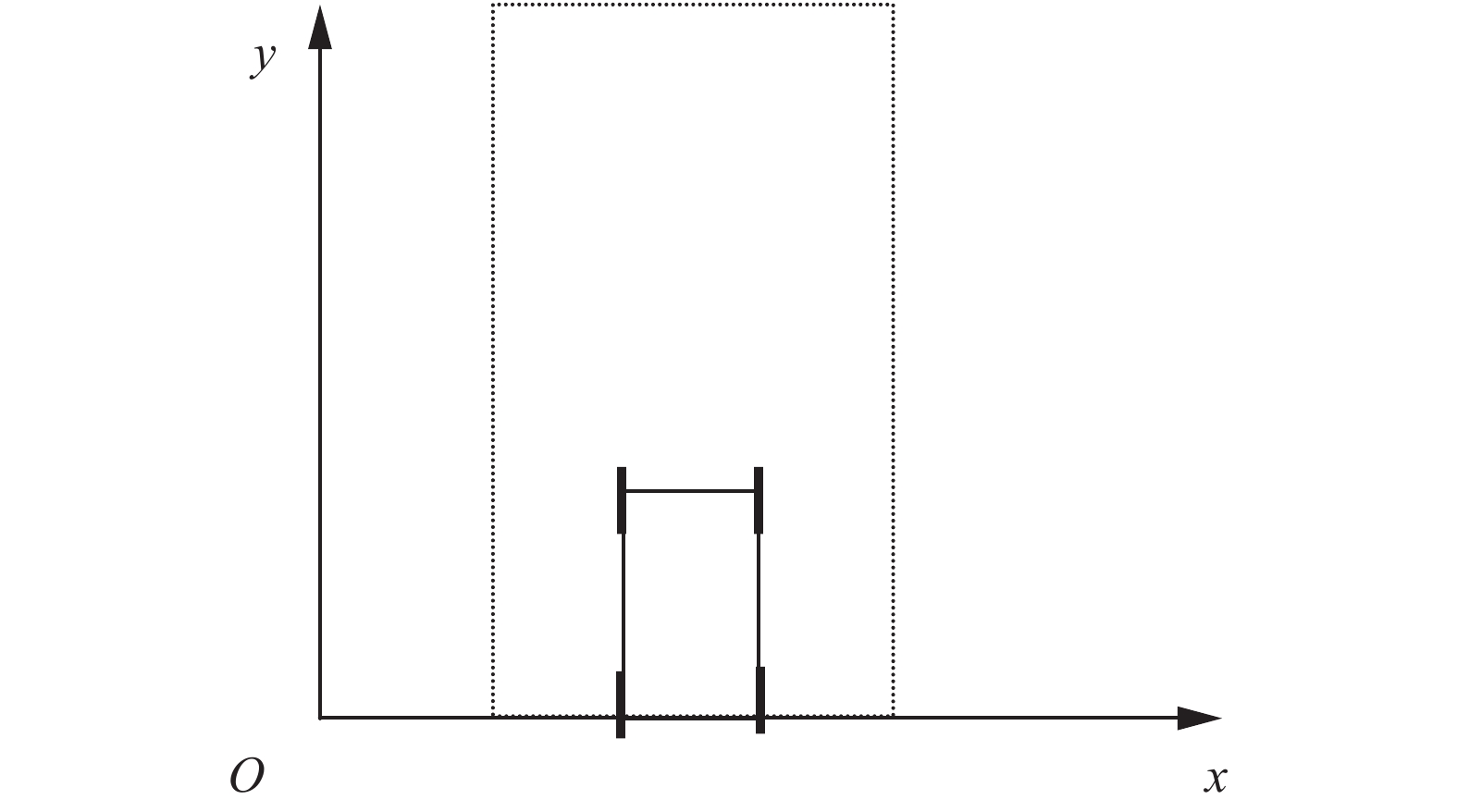
标准可行邻域的提出是为了在计算机仿真的过程易于进行模型的建立和数学描述，根据目的的不同可以建立不同形状、不同大小的标准可行邻域。如图2所示，为智能车的标准矩形邻域。要求标准矩形邻域的底边与车体的底边是重合的。智能车的邻域系统控制思想可以将复杂的动态控制转化为简单的静态控制。主要包括2个步骤，第一步是将控制范围缩小至一个局部的可行邻域，第二步是将局部可行邻域内的控制简化至有限个标准的可行邻域内的控制。

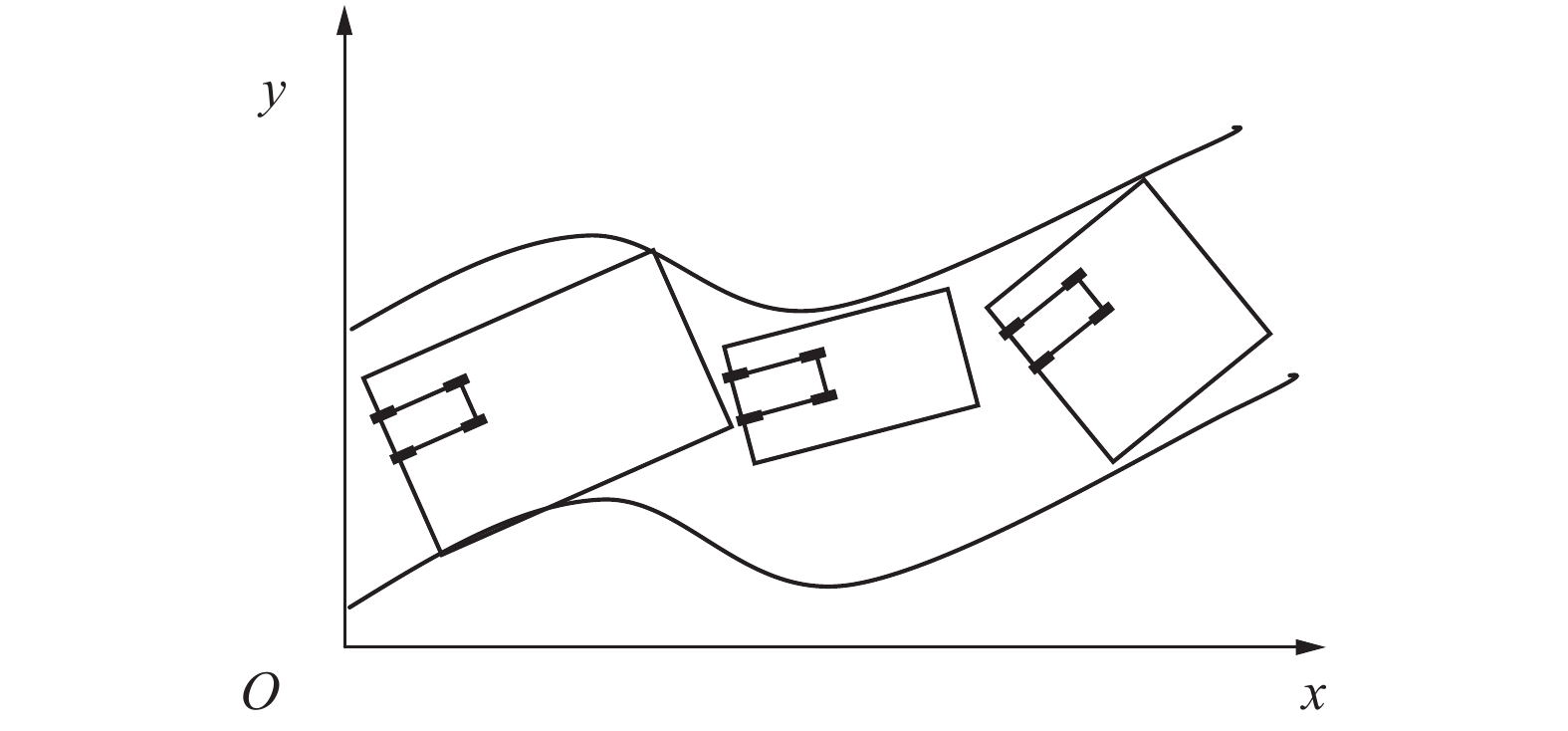
如图3所示，给出了智能车在3个不同时刻的行驶状态，其中每一个矩形框为智能车此时确立的标准可行邻域。智能车在道路上的轨迹规划就是在一个个局部的标准可行邻域内的轨迹规划的累积过程。

2 最优轨迹曲线的评判指标 2.1 基于邻域系统的最优轨迹曲线

在本文的智能车控制系统中，设Q为标准可行邻域系统，则寻求最优轨迹曲线可以抽象为对标准可行邻域内的信息寻求泛函极值的过程。

$J\left[ {x\left( t \right)} \right] = \int_0^T {F\left( {t,x\left( t \right),x'\left( t \right)} \right){\rm{d}}t} $

(1)

式中：方括号为泛函记号；时间t是自变量，满足 ${\rm{0}} \leqslant t \leqslant T$ ，T为控制总时间； $\left\{ {x\left( t \right);{x_0},T} \right\}$ 为过x₀的轨迹集合；F为被积函数，随不同乘车者的需求而取不同的形式，例如可取轨迹的长度。

对最优轨迹曲线的选取进一步细分，可根据不同的需求划分如下：

1)用时较短；

2)行走路径较短；

3)乘客感到舒适。

这是一个多目标优化问题，上述问题的最优解是车辆在标准可行邻域内的最优曲线。

2.2 最优轨迹曲线的评判指标

由上述需求，对于轨迹曲线L的轨迹方程y=y(x)。构造规则如下：

1)轨迹曲线的首尾位置是固定的，起始位置为当前邻域相对坐标系的原点，末位置为当前标准可行邻域的尾部中点向左平移一个车体长度。

2)轨迹曲线的方程为单值函数，即对于自变量x，其对应的函数值f(x)是唯一的。

3)轨迹曲线是连续的。

如图4所示，曲线A不满足构造规则2)，不是本文的轨迹曲线。这也是符合实际驾驶经验的，车辆在单行道路行驶时，不会出现反向行驶的情况。曲线B，C为车辆的轨迹曲线。

对于轨迹曲线，如何在轨迹曲线族中选取最优的轨迹曲线是整个轨迹规划理论的关键。考虑多目标优化条件，本文给出下述2个指标。

定义2　长度指数

$ J = J\left[ {y\left(x \right)} \right]{\rm{ = }}\int_{{x_0}}^{{x_1}} {\sqrt {1{\rm{ + }}{{\left( {y'\left( x \right)} \right)}^2}} } {\rm{d}}x $

(2)

称之为曲线L的长度指数。

定义3　弯阻指数

$ K = K\left[ {y\left( x \right)} \right] = \int_{{x_0}}^{{x_1}} {\frac{{\left| {y''\left( x \right)} \right|}}{{\sqrt {{{\left( {1{\rm{ + }}y'\left( x \right)} \right)}^3}} }}} {\rm{d}}x $

(3)

称之为曲线L的弯阻指数。

长度指数是衡量首末位置等同的不同轨迹的驾驶长度。一般来说，对于一固定首末点的曲线，轨迹长度越短，可以认为沿此曲线行驶的驾驶效率越好。

车辆行驶的弯阻指数主要取决于行驶轨迹的顺畅，不同于轨迹曲率这一局部概念，是一个整体性的概念。对于行驶轨迹的平稳，易知曲率越小，轨迹越顺畅，乘客越舒适。其次由定义式可知，弯阻指数取决于轨迹的固有特征，与其他因素无关，是描述轨迹性质的常数。

对于定义3，可给出推论1：

推论1　对于A、B两条首末位置相同的曲线，若A曲线每一点的曲率的绝对值都小于B曲线，则A曲线的弯阻指数小于B曲线。

由推论1显然可以得出，对于2条定长曲线，曲率越小的曲线越令人感到顺畅。

2.3 评判指标的标准化

为了便于进行指标的评判和比较，本文的指标标准化方法如下：

定义4　距离优度

$ J^* = 1{\rm{ - }}\displaystyle\frac{{\displaystyle\frac{{\int_{{x_0}}^{{x_1}} {\sqrt {1{\rm{ + }}{{\left( {y'\left( x \right)} \right)}^2}} } dx}}{{{\rm{1 + }}\int_{{x_0}}^{{x_1}} {\sqrt {1{\rm{ + }}{{\left( {y'\left( x \right)} \right)}^2}} } dx}} - \displaystyle\frac{{\left( {{x_1} - {x_0}} \right)}}{{{\rm{1 + }}\left( {{x_1} - {x_0}} \right)}}}}{{1 - \displaystyle\frac{{\left( {{x_1} - {x_0}} \right)}}{{{\rm{1 + }}\left( {{x_1} - {x_0}} \right)}}}} $

(4)

称之为曲线L的距离优度。

对式(4)进行化简，令

$ J_{\min }^*{\rm{ = }}\frac{{\left( {{x_1} - {x_0}} \right)}}{{{\rm{1 + }}\left( {{x_1} - {x_0}} \right)}} $

(5)

结合定义2，有

$ J^*=1{\rm{ - }}\frac{{\frac{J}{{{\rm{1 + }}J}} - J_{\min }^*}}{{1 - J_{\min }^*}} = \frac{1}{{\left( {{\rm{1 + }}J} \right)\left( {1 - J_{\min }^*} \right)}} $

(6)

曲线L的距离优度就是对长度指数的标准化。其中区间 $\left[ {{x_0},{x_1}} \right]$ 代表智能车轨迹曲线首末位置所在的区间。因此最短距离为直线距离 $d = {x_1} - {x_0}$ ， $J_{\min }^*$ 为最短距离d的标准化形式。考虑到无限长的连续曲线可以围住一块有限的面积这一事实，标准化过程就是将长度指数的范围从 $\left[ {d, + \infty } \right]$ 映射到[0,1]区间上。当长度指数J为最短距离d时，代入式(6)， $J^*$ 取1；当长度指数为 $ + \infty $ 时， $J^*$ 取0。因此 $J^*$ 的取值越接近1越令人满意。

定义5　顺畅度

$ K^* = 1{\rm{ - }}\displaystyle\frac{{\int_{{x_0}}^{{x_1}} {\displaystyle\frac{{\left| {y''\left( x \right)} \right|}}{{\sqrt {{{\left( {1{\rm{ + }}y'\left( x \right)} \right)}^3}} }}} {\rm{d}}x}}{{1{\rm{ + }}\int_{{x_0}}^{{x_1}} {\displaystyle\frac{{\left| {y''\left( x \right)} \right|}}{{\sqrt {{{\left( {1{\rm{ + }}y'\left( x \right)} \right)}^3}} }}} {\rm{d}}x}} $

(7)

称之为曲线L的顺畅度。

结合定义3对式(7)进行化简，则有

$ K^* = 1{\rm{ - }}\frac{K}{{1 + K}} = \frac{1}{{1 + K}} $

(8)

曲线L的顺畅度是弯阻指数的标准化过程，考虑到直线的曲率为0，因此标准化的过程就是将弯阻指数的范围从 $\left[ {0, + \infty } \right]$ 映射到[0,1]区间上。当弯阻指数K为0时，代入式(8)， $K^*$ 取1；当弯阻指数为 $ + \infty $ 时， $K^*$ 取0。因此 $K^*$ 的取值越接近1越令人感到顺畅。

在实际应用时，可根据不同需求选用指数型指标或标准化指标。对于不同驾驶风格的驾驶员，可初步划分为驾驶平稳型和追求速度型，他们对于上述2个指标是有着不同偏好的。为了综合评判不同驾驶员对于最优轨迹曲线的要求，现引入对于最优轨迹曲线的综合评判指标。

定义6　综合评判指标

$ C^* = {w_1} \cdot J^*{\rm{ + }}{w_2} \cdot K^* $

(9)

称之为曲线L的综合评判指标，其中w₁、w₂为不同驾驶风格的驾驶员对于J*、K*指标的权重，可由专家评判给出。

综上可知，在众多轨迹曲线中选取一个最优曲线，只需比较不同轨迹曲线的综合评判指标的值，数值最大的曲线即为所求。

3 最优轨迹曲线模型及其求解方法 3.1 最优轨迹曲线模型及其满意条件

首先建立最优轨迹曲线的多目标优化模型—最优轨迹曲线模型　对于标准可行领域Q内的轨迹集合Γ(x₀)，寻求最优轨迹曲线 $y^*\left( {{x_0}} \right)$ , 使得下列目标函数可取得极值

$ \left\{ \begin{array}{l} \min T \\ \min J\left[ {y\left( x \right)} \right] \\ \min K\left[ {y\left( x \right)} \right] \\ \end{array} \right. $

(10)

限制条件为

$ \left\{ \begin{array}{l} y\left( {{x_0}} \right) \subset \varGamma \left( {{x_0}} \right) \subset Q \\ T \leqslant {T_{\max }} \\ \end{array} \right. $

(11)

式中：T为智能车在标准可行邻域内完成规划的轨迹所用的总时间； ${T_{\max }}$ 完成规划的轨迹能够接受的最长时间；J、K分别为轨迹曲线的长度指数和弯阻指数。目标函数的最优解 $y^*\left( x \right)$ 为最优轨迹曲线，此模型可简写为OTC模型。

尽管式(10)给出了最优轨迹曲线模型，但该模型的一般求解是困难的。在实际问题中只需给出一种实用的、可操作的构造方法即可。因此需要给出满意曲线的满意条件。寻求满意曲线的过程是一个筛选与尝试的过程，需要建立合理的限定规则，提高筛选与尝试的效率。参考图4的3条曲线，其中曲线B是一条符合生活经验的满意曲线，考虑到曲线B的特征，本文的规则如下：

规则1：车体轨迹应较为光滑。

规则2：车体的末位置应尽可能满足底边中点到邻域两边是等距的要求，即在邻域中部运动。

基于上述规则，满意条件如下：

定义7　 p-水平满意集

$ B = \left\{ {y\left( x \right){\rm{|}}{w_1} \cdot J^*\left[ {y\left( x \right)} \right]{\rm{ + }}{w_2} \cdot K^*\left[ {y\left( x \right)} \right] \geqslant p} \right\} $

(12)

为曲线y(x)的p-水平满意集。

由式(12)可知，根据目标阈值p，可求出满意曲线的集合B，若最优曲线的集合为C，易知 $C \subseteq B$ ，因此可通过逐步迭代法来寻找满意曲线。

3.2 满意曲线的求解算法

如图5所示，为智能车的邻域坐标系，其中车体与可行邻域底部的中点距离为s，邻域长为H，车体长为l。假设轨迹曲线二阶光滑，其中初始位置坐标为o(0，0)，末位置坐标为 (H-l，s)，且二者一阶导数皆为0；Hermite插值法可以将函数值和导数值完全利用，根据插值节点的个数不同，可求出不同的轨迹曲线，兼顾满意度和复杂性，本文将插值节点的个数定为3个。则满意轨迹曲线的迭代算法如下：

1)确定初始值。

设在节点 $0 \leqslant x < {x_2} < \cdots < {x_n} \leqslant H - l$ 上，取n=3，对于初始点满足

$ \left\{ {\begin{array}{*{20}{l}} {y\left( {{x_1}} \right){\rm{ = }}0,}&{{x_1}{\rm{ = }}0}\\ {y\left( {{x_2}} \right){\rm{ = }}{y_2},}&{{x_1} < {x_2} < {x_3}}\\ {y\left( {{x_3}} \right) = s,}&{{x_3}{\rm{ = }}H - l} \end{array}} \right. $

(13)

导数值满足

$ \left\{ \begin{array}{l} y'\left( {{x_1}} \right){\rm{ = }}0\\ y'\left( {{x_2}} \right) = y_2'\\ y'\left( {{x_3}} \right){\rm{ = }}0 \end{array} \right. $

(14)

式中O₁(x₁, y₁)、O₃(x₃, y₃)为已知节点，因此需要确定节点O₂的坐标值和导数值。假设满意轨迹曲线对称，则节点O₂的坐标值为曲线中点，导数值k是一个和邻域大小相关的量，可设初始值为

$ {k_0} = s/h - l $

(15)

2)计算轨迹曲线指标。

将上述数据代入，函数f(x)在节点处的插值多项式为

$ {H_{2n + 1}}\left( x \right){\rm{ = }}\sum\limits_{i = 1}^n {{H_i}\left( x \right)} \cdot {y_i}{\rm{ + }}\sum\limits_{k = 1}^n {{h_k}\left( x \right)} \cdot {y_k}' $

(16)

根据多项式计算长度指数和逆舒指数，并选择合适的权重，计算式(9)的综合评判指标 $C_{i}^*$ ，执行3)。

3)计算导数值。

对于导数初值k₀，确定搜索区间[αk₀,βk₀],其中α<1,β>1，设步长为t，对于每次迭代i，导数值为

$ {k_i} = \left( {\alpha + ti} \right){k_0} $

(17)

合理调整步长，转2)，使得每次迭代的结果 $C_{i}^*$ > $C_{{i - 1}}^*$ ，直到 $C_{i}^*$ 的值达到p，则迭代终止。

按照上述算法，本文以满意度指数p=0.8，权重w₁₌0.4、w₂₌0.6，所计算出的节点O₂的坐标值和一阶导数如下：

1)节点坐标为 $\left( {\displaystyle\frac{{H - l}}{2},\frac{s}{2}} \right)$ ，为曲线的中点。

2)节点一阶导数为 $\displaystyle\frac{{3s}}{{2\left( {H{\rm{ - l}}} \right)}}$ 。

3.3 满意曲线的理论分析

对于上述操作算法，首先证明最优轨迹曲线的存在性。

由算法的构造过程可知，曲线首末位置已知，斜率均为零；插值点为曲线中点，斜率可连续变动。因此对于斜率搜索区间[αk₀,βk₀]，由闭区间有界性定理， $J\left[ {y\left( x \right)} \right]$ 与 $K\left[ {y\left( x \right)} \right]$ 在[αk₀,βk₀]上有上界。又由连续函数的四则运算以及最值定理可知，存在最优值

$\zeta = \sup C^*\left[ {y\left( x \right)} \right]$

(18)

这就证明了最优轨迹曲线的存在性。其次由满意曲线的求解过程可知，每次迭代产生的 $C_{i}^*$ 子列，有

$C_{1}^* \leqslant C_{2}^* \leqslant \cdots \leqslant C_{{i - 1}}^* \leqslant C_{i}^*$

(19)

继续这样做下去， $C_{i}^*$ 是有界数列，所以由Bolzano-Weierstrass定理可知，存在

$\mathop {\lim}\limits_{i \to \infty } {\rm{ }}C_{i}^* = \zeta $

(20)

因此本文给出的求解算法是可行的。

4 仿真结果以及同其他文献的对比

目前利用邻域系统的思想进行智能车研究的国内外文献较少，因此同其他文献研究成果的对比主要在于叙述各文献的研究思路和解决问题的思想与本文的异同点。

本文的研究区别于一些文献所研究的静态规划^[3]问题, 适用于智能车在道路上的动态规划。

对于此动态规划问题目前可分为3个不同层次。第1个层次是对于宏观的道路网络节点进行路径规划，文献[4]主要研究这一问题，是对整个交通信息网的统筹规划。

第2个层次是在宏观路径规划的基础上，对于微观的行驶轨迹进行研究。这个层次又可细化成2种研究方式，一种是行驶轨迹直接默认；例如文献[5]采用激光雷达进行定位，对于障碍物的规避轨迹直接默认了Dubins路径。另一种研究方式是根据实时信息进行轨迹自主规划；例如文献[6]运用人工势场算法对路径进行搜索；例如文献[7]给出了一种基于三角函数的轨迹搜索方法。

第3个层次是根据目前规划出的运动轨迹，控制智能车进行轨迹的跟踪。

本文研究上述分类中的第2个层次，并且研究方式是对于已知的道路信息以及障碍物，根据智能车的传感器对周边的道路信息进行实时的采样分析，从而进行轨迹的规划与搜索。本文采用了邻域系统的相关理论，目前对于在邻域系统的路径规划的文献[8]−[12]大多还需要进一步的改进，其中文献[8]虽奠定了邻域系统控制的基础理论，但仅用于智能车实施可行邻域的选取，对邻域内的路径规划未做深入研究。文献[9]给出了倒车环境下的轨迹规划，对于复杂道路上的轨迹规划还需要进一步研究；文献[10-11]利用邻域系统理论，给出了很多初步的研究结果。其中文献[11]给出的满意解的论述是一种可行的研究方法，本文满意曲线的建立沿用了此思想；文献[12]建立了障碍物的避障规则和邻域内的移动规则，但未考虑轨迹的顺畅和效率问题。综上所述，上述文献做出了很多有建设性和启发性的工作，但是首先从运动轨迹入手，以构造轨迹的平稳光滑为首要目标，来解决轨迹规划问题，目前还是邻域系统的一个欠缺部分，本文主要完善了这一问题。

如图6所示，为智能车在某一时刻的邻域相对坐标系。为便于进行数据的比较，对其中一些数据进行了放缩。其中标准可行邻域长为45 m，宽为14 m；智能车长为5 m，距离邻域底部中心3 m。A、B、C为3条轨迹曲线，其中A曲线为多项式曲线, 由图形“--”表示；B曲线为本文所构造的5次Hermite插值曲线，与C曲线十分接近，在图7表示为一条连续的曲线；C曲线为文献[7]提到的三角函数曲线，由图形“*”表示。3条轨迹曲线的方程如下：

$\begin{array}{l} {y_{\rm{A}}}\left( x \right){\rm{ = }} - 1.21 \cdot {10^{ - 8}} \cdot {x^7} + 2.08 \cdot {10^{ - 6}} \cdot {x^6} - 1.40 \cdot {10^{ - 4}} \cdot {x^5} {\rm{ + }} \\ \qquad\qquad 4.65 \cdot {10^{ - 3}} \cdot {x^4} - 7.63 \cdot {10^{ - 2}} \cdot {x^3} + 5.09 \cdot {10^{ - 1}} \cdot {x^2} \\ \end{array} $

$\begin{array}{l} {y_{\rm{B}}}\left( x \right){\rm{ = }} 3.13 \cdot {10^{ - 7}} \cdot {x^5} - 3.13 \cdot {10^{ - 5}} \cdot {x^4} + {\rm{ }} \\\quad\qquad 8.75 \cdot {10^{ - 4}} \cdot {x^3} - 2.50 \cdot {10^{ - 3}} \cdot {x^2} \\ \end{array} $

${y_{\rm{C}}}\left( x \right){\rm{ = }}\frac{3}{2} \cdot \sin \left( {\frac{{{\text{π}} \cdot x}}{{40}} - \frac{\pi }{2}} \right) + \frac{3}{2}$

现计算长度指数J[y(x)]，则有

$ J\left[ {{y_A}\left( x \right)} \right] = 44.832\text{、}J\left[ {{y_B}\left( x \right)} \right] = 40.304\text{、}J\left[ {{y_C}\left( x \right)} \right] = 40.138 $

其中有 $J\left[ {{y_C}\left( x \right)} \right] < J\left[ {{y_B}\left( x \right)} \right] < J\left[ {{y_A}\left( x \right)} \right]$ ，因此曲线C的路程最短。

现分别求出轨迹曲线弯阻指数K，则有

$ K\left[y_{A}(x)\right]\!=\!333\;18\text{、}\!K\left[y_{B}(x)\right]\!=\!0.402\;2\text{、}\!K\left[y_{C}(x)\right]\!=\!0.993\;1 $

其中有 $K\left[y_{B}(x)\right]<K\left[y_{C}(x)\right]<K\left[y_{A}(x)\right]$ ，因此曲线B的弯阻指数最低。

进行标准化处理，可求得

$ J^{*}\left[y_{A}(x)\right]=0.903\text{、}J^{*}\left[y_{B}(x)\right]=0.992\text{、}J^{*}\left[y_{C}(x)\right]=0.996 $

$ K^{*}\left[y_{A}(x)\right]=0.231\text{、}K^{*}\left[y_{B}(x)\right]=0.713\text{、}K^{*}\left[y_{C}(x)\right]=0.501 $

最后进行综合评判。以驾驶稳定型驾驶员为例，设驾驶员对于J*、K*指标所取权重为w₁=0.3、w₂=0.7，代入计算可得

$ C^*\left[y_{A}(x)\right]=0.433\text{、}C^*\left[y_{B}(x)\right]=0.797\text{、}C^{*}\left[y_{C}(x)\right]=0.649 $

考虑权重的变化，对于驾驶稳定型驾驶员而言，只需保证弯阻指数所占的权重大于长度指数所占权重。因此，若取J*、K*指标所取权重为w₁=0.4、w₂=0.6，可求得

$ C^{*}\left[y_{A}(x)\right]=0.499\text{、}C^{*}\left[y_{B}(x)\right]=0.824\text{、}C^{*}\left[y_{C}(x)\right]=0.699 $

若取J*、K*指标所取权重为w₁=0.45、w₂=0.55，可求得

$ C^{*}\left[y_{A}(x)\right]=0.533\text{、}C^{*}\left[y_{B}(x)\right]=0.838\text{、}C^{*}\left[y_{C}(x)\right]=0.723 $

对上述结果进行整理，可发现虽然权系数的取值发生了改变，不等式 $C^{*}\left[y_{A}(x)\right]<C^{*}\left[y_{C}(x)\right]<C^{*}\left[y_{B}(x)\right]$ 始终成立。因此应用本文方法所求出的插值曲线B为这3条曲线中的最优轨迹曲线。在后续控制中可以选取本文给出的构造B曲线的方法作为一种满意控制的方法。从上述过程可知。本文的评判模型对于智能车轨迹曲线的选取提供了一种方法。

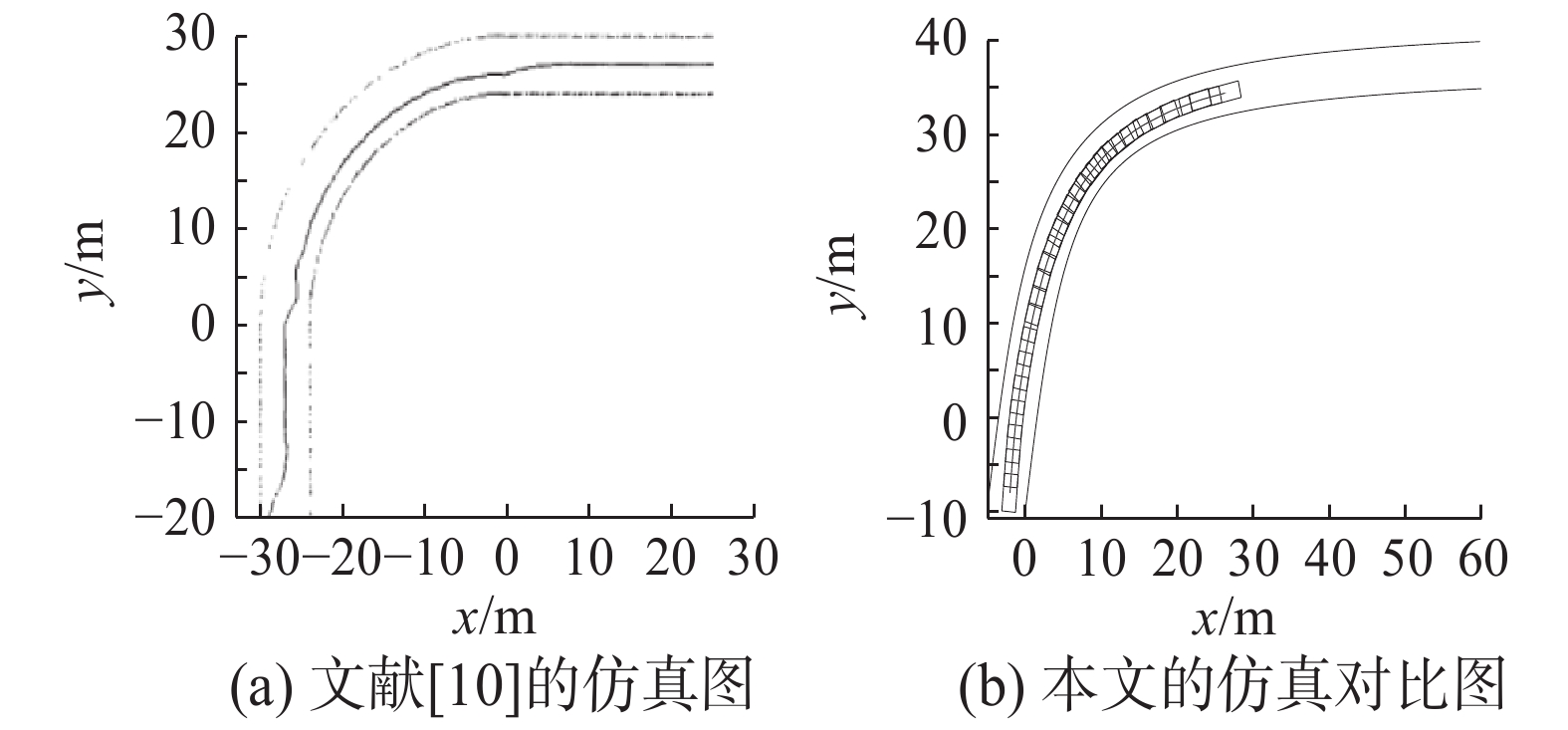
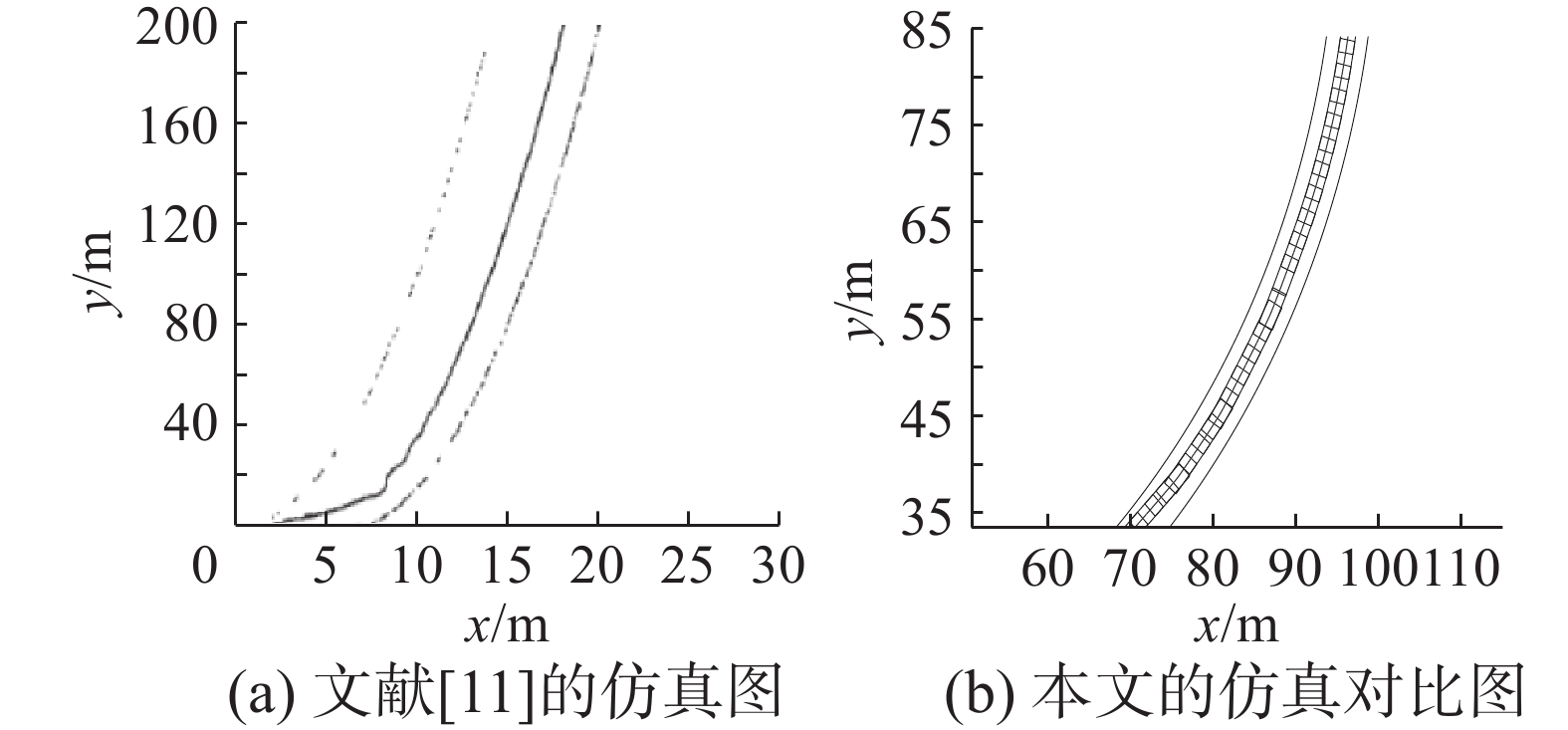
如图7所示，为本文的轨迹曲线在道路上的仿真图。本文从邻域系统入手，重点搜索标准可行邻域内的满意路径。在现有的邻域系统相关文献中，很少有文献从控制轨迹的平稳光滑角度去搜寻满意控制规则，忽略了控制轨迹的顺畅度和效率。下图为文献[10]−[11]的控制仿真图，同本文仿真图对比可以看出，本文的控制理论在轨迹的平稳光滑性上具有一定的优越性。

5 结束语

对于微观的道路上的最优轨迹的规划问题，邻域系统理论可以将复杂动态过程转化为简单静态过程，简化了问题的复杂性。本文定义了曲线的弯阻指数和长度指数，并以此为基础给出了邻域内最优轨迹的综合评判求解模型，给出了一种满意的轨迹曲线算法。仿真结果说明了本文的规划理论在轨迹的平稳光滑性上具有一定的优越性。