通过模拟人类的概念认知思维，Wille^[1]教授于1982年在格论基础上发展了面向概念建模的概念格理论。作为格论的重要应用分支，概念格具有坚实的数学理论基础，其中概念、格代数结构、对偶伽罗瓦连接等是核心要素。近年来，伴随着概念格自身理论发展以及与粗糙集^[2-3]、模糊集等的深度融合，其理论体系日趋成熟，应用范围也得到了极大的拓展。

粗糙集无需借助先验知识，且符合人类的近似思维，易于理解，因此受到了国内外学者的广泛关注^[4]。近年来，对于不完备信息的处理，粗糙集已经取得了大量的研究成果。把缺失值理解为任何可能值，Kryszkiewicz^[5-6]提出了基于容差关系的拓展粗糙集模型，其中容差关系满足自反性和对称性，随后，将缺失值视为不存在或是不允许比较的未知值，Stefanowski^[7]提出了基于不对称相似关系(满足自反性和传递性)的粗糙集拓展模型，结合上述2种模型的优点，王国胤^[4]进一步提出了基于限制容差关系(满足自反性和对称性)的扩充模型，该模型相对以往模型更加符合实际，Leung等^[8]将极大相容类视为一个粒，探讨了不完备信息系统中的知识获取，张文修^[9]将不完备信息系统理解为一个集值信息系统，并探讨了面向集值的相容关系。

目前，关于不完备信息系统已有大量的研究成果，然而对于不完备形式背景的分析处理尚处于起步阶段^[10-16]。从研究对象来讲，形式背景本质上是一种特殊的信息系统，它们之间存在着天然联系，具有较强的相容性，这也意味着面向不完备信息系统的知识获取方法对于不完备形式背景的处理具有一定的借鉴作用。事实上，将不完备信息系统中的方法推广到不完备形式背景中，也是一项非常有意义的研究工作，其不仅能为不完备形式背景的分析处理提供必要的支撑，而且也有助于概念格与粗糙集的理论融合。

考虑到不完备形式背景的普遍性以及经典概念格的局限性，在概念格框架体系中，本文融入了粗糙集中的粒化思维，探讨了概念格视角下的信息粒化，提出了基于等价类和基于极大相容类的知识获取方法。这些方法一方面有助于概念格与粗糙集的融合，另一方面也为探索不完备形式背景的分析处理机制提供了有益思路。

1 概念格基本知识

通常，称 $({{G}}, \;{{M}}, \;{{I}}\, )$ 是一个形式背景，若 ${{G}}$ 是对象集，M是属性集，I表示G和M之间的二元关系。在此意义下， $(x, m) \in {{I}}$ 或 $m(x) = {\rm{1}}$ 表示对象 $x \in {{G}}$ 拥有属性 $m \in {{M}}$ ，相反， $(x, m) \notin {{I}}$ 或 $m(x) = {\rm{0}}$ 表示对象 $x$ 不拥有属性 $m$ 。

定义1　在 $K = ({{G}}, \;{{M}}, \;{{I}}\, )$ 中，对于任意 ${{X}} \in {{\rm{2}}^{{G}}}$ 和 ${{B}} \in {{\rm{2}}^{{M}}}$ ，相应的经典内涵算子与外延算子定义为

${{{X}}^ * } = \{ \, m \in {{M}}|\;(x, m) \in {{I}}, \;\forall x \in {{X}}\, \} $

(1)

${{{B}}^ * } = \{ \, x \in {{G}}|\;(x, m) \in {{I}}, \;\forall m \in {{B}}\, \} $

(2)

式中 ${{\rm{2}}^{\cal{X}}}$ 是集合 ${\cal{{{X}}}}$ 的幂集。若 ${{B}} = {{{X}}^ * }$ 且 ${{X}} = {{{B}}^ * }$ ，称 $({{X}}, {{B}})$ 是一个概念，其中X和B分别称为概念的外延和内涵。在此意义下，任意概念 $({{{X}}_1}, {{{B}}_1})$ 和 $({{{X}}_2}, {{{B}}_2})$ 之间的序关系定义为

$({{{X}}_1}, {{{B}}_1}) \leqslant ({{{X}}_2}, {{{B}}_2}) \Leftrightarrow {{{X}}_1} \subseteq {{{X}}_2} \Leftrightarrow {{{B}}_2} \subseteq {{{B}}_1}$

基于上述认识和理解，一个格代数结构 $\left( {{\cal{{{B}}}}({{K}}), \; \leqslant } \right)$ 可以从K中推导出来，其中 ${\cal{{{B}}}}({{K}})$ 是K中所有概念的集合。关于概念格详细资料请查阅文献[17]。

对象和属性之间的关系如果存在缺失，则称 $({{G}}, \;{{M}}, \;{{I}}\, )$ 是一个不完备形式背景。一个典型的不完备形式背景如表1所示，其中，若 $x \in {{G}}$ 和 $m \in {{M}}$ 之间的关系是缺失的(即无法确定是 $(x, m) \in {{I}}$ 还是 $(x, m) \notin {{I}}$ )，则记为 $m(x) = * $ 。

2 概念格与粒化分析

等价类、极大相容类等是粗糙集中的基本粒。在粒内部，不同对象往往拥有相同的特征和相近的特征值，这就意味着粒内部不同对象之间的特征值是可以相互借鉴的。据此，本文尝试在概念格理论框架内探讨基于二元关系的信息粒化。

二元关系与形式背景存在着天然联系，它们之间可以相互表示。通常，二元关系有2种不同的类型，即内部二元关系和外部二元关系。其中，内部二元关系存在于单个集合的内部，例如，偏序集 $({{V}}, \leqslant )$ 中的序关系“ $ \leqslant $ ”即是一种内部二元关系；外部二元关系是指存在于集合之间的关系，例如， $({{V}}, {{W}}, \leqslant )$ 中的序关系“ $ \leqslant $ ”即是一种外部二元关系。

推论1　内部二元关系是一种特殊的外部二元关系。例如，虽然 $({{V}}, \leqslant )$ 与 $({{V}}, {{V}}, \leqslant )$ 在形式上存在一定差异，但本质上却是相同的。

推论2　内部二元关系与外部二元关系均可以表示为形式背景。在下文中，无论是内部还是外部二元关系均统一表示为形式背景。

在粒化思维下，对于数据集的分析和处理，人们通常注重的是集合，而非单个元素；注重的是集合之间的关系，而非单个元素之间的关系。

定义2　设 ${\cal{{{R}}}}$ 是非空集合 ${\cal{{{X}}}}$ 中的一个二元关系。若 ${{X}} \subseteq {\cal{{{X}}}}$ 和 ${{Y}} \subseteq {\cal{{{X}}}}$ 之间满足下述条件：

对于任意 $x \in {{X}}$ 和任意 $y \in {{Y}}$ ，均有 $(x, y) \in {\cal{{{R}}}}$ ，即 ${{X}} \times {{Y}} \subseteq {\cal{{{R}}}}$ ，称 ${{X}}$ 和 ${{Y}}$ 是关联的。设 ${{X}}$ 和 ${{Y}}$ 是关联的，即 ${{X}} \times {{Y}} \subseteq {\cal{{{R}}}}$ 。若不存在 ${{{X}}_1} \times {{{Y}}_1} \subseteq {\cal{R}}$ 满足 ${{X}} \times {{Y}} \subset {{{X}}_1} \times {{{Y}}_1}$ ，称 ${{X}}$ 和 ${{Y}}$ 是极大关联的。

定义3　称 ${{K}} = ({\cal{{{X}}}}, {\cal{{{X}}}}, {\cal{{{R}}}})$ 是一个关系背景，其中 ${\cal{{{R}}}}$ 是非空集合 ${\cal{{{X}}}}$ 中的一个二元关系。

定理1　在关系背景 ${{K}} = ({\cal{{{X}}}}, {\cal{{{X}}}}, {\cal{{{R}}}})$ 中，下列论述是等价的：

1) $({{X}}, {{Y}}) \in {\cal{{{B}}}}({{K}})$ ；

2) ${{X}}$ 和 ${{Y}}$ 是极大关联的。

证明　当 $({{X}}, {{Y}}) \in {\cal{{{B}}}}({{K}})$ 时，由定义1可知，对于任意 $x \in {{X}}$ 和任意 $y \in {{Y}}$ ，有 $(x, y) \in {\cal{{{R}}}}$ 成立，这就意味着 ${{X}}$ 和 ${{Y}}$ 是关联的。假设 ${{X}}$ 和 ${{Y}}$ 不是极大关联的，即存在 ${{{X}}_1} \times {{{Y}}_1} \subseteq {\cal{R}}$ 满足 ${{X}} \times {{Y}} \subset {{{X}}_1} \times {{{Y}}_1}$ 。在此情形下，必然有 ${{Y}} \subset {{{X}}^ * }$ 且 ${{X}} \subseteq {{{Y}}^ * }$ 成立，或 ${{Y}} \subseteq {{{X}}^ * }$ 且 ${{X}} \subset {{{Y}}^ * }$ 成立，而非 ${{Y}} = {{{X}}^ * }$ 且 ${{X}} = {{{Y}}^ * }$ 成立，由此即得 $({{X}}, {{Y}}) \notin {\cal{{{B}}}}({{K}})$ ，显然，该结论与已知条件 $({{X}}, {{Y}}) \in {\cal{{{B}}}}({{K}})$ 是相互矛盾的。故当 $({{X}}, {{Y}}) \in {\cal{{{B}}}}({{K}})$ 时， ${{X}}$ 和 ${{Y}}$ 是极大关联的。证毕。

定义4　设 ${\cal{{{R}}}}$ 是非空集合 ${\cal{{{X}}}}$ 中的一个二元关系。若 ${\cal{{{D}}}}$ 是满足下述条件的 ${\cal{{{X}}}}$ 中的最大子集，对于任意 $x, y \in {\cal{{{D}}}}$ ，均有 $(x, y) \in {\cal{{{R}}}}$ ，即 X $ \times {{X}} \subseteq {\cal{{{R}}}}$ ；则称 ${{{\cal{D}}}}$ 是 ${\cal{{{X}}}}$ 中的一个信息粒。

定理2　在关系背景 ${{K}} = ({\cal{{{X}}}}, {\cal{{{X}}}}, {\cal{{{R}}}})$ 中，下述结论成立：

$({\cal{{{D}}}}, {\cal{{{D}}}}) \in {\cal{{{B}}}}({{K}})$ ，当且仅当 ${\cal{{{D}}}}$ 是一个信息粒

证明　当 $({{{\cal{D}}}}, {\cal{D}}) \in {\cal{B}}({{K}})$ 成立时，由定理1得 ${\cal{D}}$ 和 ${\cal{D}}$ 是极大关联的，这也意味着 ${\cal{D}}$ 将满足下述条件：

对于任意 $x, y \in {\cal{D}}$ ，均有 $(x, y) \in {\cal{R}}$ ，即 ${\cal{D}} \times {\cal{D}} \subseteq {\cal{R}}$

假设 ${{\cal{D}}_{\rm{1}}}$ 是满足上述条件的最大集合，其中 ${\cal{D}} \subset {{\cal{D}}_{\rm{1}}}$ 。在此情形下， ${{\cal{D}}_{\rm{1}}} \times {{\cal{D}}_{\rm{1}}} \subseteq {\cal{R}}$ 是成立的，进而判定 $({\cal{D}}, {\cal{D}}) \notin {\cal{B}}({{K}})$ 。显然，该结论与 $({\cal{D}}, {\cal{D}}) \in {\cal{B}}({{K}})$ 是矛盾的。故当 $({\cal{D}}, {\cal{D}}) \in {\cal{B}}({{K}})$ 成立时， ${\cal{D}}$ 是满足上述条件的最大集合，即 ${\cal{D}}$ 是一个信息粒。

反过来，当 ${\cal{D}}$ 是信息粒时，由定义4即得 ${\cal{D}} \times {\cal{D}} \subseteq {\cal{R}}$ ，且不存在 ${{\cal{D}}_{\rm{1}}} \times {{\cal{D}}_{\rm{1}}} \subseteq {\cal{R}}$ 满足 ${\cal{D}} \subset {{\cal{D}}_{\rm{1}}}$ 。在此情形下，由定义2可知 ${\cal{D}}$ 和 ${\cal{D}}$ 是极大关联的，进而由定理1得 $({\cal{D}}, {\cal{D}}) \in {\cal{B}}({{K}})$ 。故当 ${\cal{D}}$ 是一个信息粒，有 $({\cal{D}}, {\cal{D}}) \in {\cal{B}}({{K}})$ 成立。证毕。

在定理2中，对于任意 $({\cal{D}}, {\cal{D}}) \in {\cal{B}}({{K}})$ ，当 ${\cal{R}}$ 是一个满足自反性和对称性的相容关系时，粒 ${\cal{D}}$ 本质上是一个相容类；当 ${\cal{R}}$ 是一个满足自反性、对称性和传递性的等价关系时，粒 ${\cal{D}}$ 是一个等价类。

3 基于等价类的数据分析模型

定义5　设 $({{G}}, \;{{M}}, \;{{I}})$ 是一个不完备形式背景， ${\rm{0}} \leqslant \delta \leqslant {\rm{1}}$ ， ${\rm{1}} \leqslant \kappa \leqslant {\rm{2}}$ 。对于任意 $x \in {{G}}$ 和 $y \in {{G}}$ ，它们之间的相似度定义为

${\bf{Sim}}(x, y) = \frac{{|{\bf{Sa}}{{\bf{m}}_ - }(x, y)| + \, \delta \times \, \, |{\bf{La}}{{\bf{c}}_ - }(x, y)|}}{{|{\bf{Sa}}{{\bf{m}}_ - }(x, y)| + \;\delta \, \times |{\bf{La}}{{\bf{c}}_ - }(x, y)| + \;\kappa \; \times |{\bf{Di}}{{\bf{f}}_ - }(x, y)|}}$

(3)

式中：

${\bf{Sa}}{{\bf{m}}_ - }(x, y) = \left\{ {\, a \in {{M}}|m(x) = m(y) = 1\;\, {\rm{or}}\, \;m(x) = m(y) = 0\, } \right\}$

(4)

${\bf{La}}{{\bf{c}}_ - }(x, y) = \left\{ {\, m \in {{M}}|\;m(x) = * \;\, {\rm{or}}\, \;m(y) = * \, } \right\}$

(5)

$ \begin{split} & \qquad\qquad\qquad\qquad\quad{\bf{Di}}{{\bf{f}}_ - }(x, y) =\\ & \left\{ {\, m \in {{M}}|m(x) = 0\;{\rm{and}}\;m(y) = 1, \;\, {\rm{or}}\;m(x) = {\rm{1}}\;{\rm{and}}\;m(y) = {\rm{0}}\, } \right\} \end{split} $

(6)

参数 $\delta < 1$ 意味着 ${\bf{La}}{{\bf{c}}_ - }$ 对 ${\bf{Sim}}$ 的影响力要小于 ${\bf{Sa}}{{\bf{m}}_ - }$ 和 ${\bf{Di}}{{\bf{f}}_ - }$ ；参数 ${\rm{1 < }}\kappa \leqslant {\rm{2}}$ 意味着 ${\bf{Di}}{{\bf{f}}_ - }$ 对 ${\bf{Sim}}$ 的影响力大于 ${\bf{Sa}}{{\bf{m}}_ - }$ 和 ${\bf{La}}{{\bf{c}}_ - }$ 。从相似度 ${\bf{Sim}}$ 出发，首先会生成一个模糊相似关系矩阵 $\tilde {{R}}$ ，进而借助传递闭包算法将 $\tilde {{R}}$ 转化为模糊等价关系矩阵 $\bar {{R}}$ 。在此基础上，用户设置阈值参数 ${\rm{0}} \leqslant \lambda \leqslant {\rm{1}}$ ，可最终得到一个 $\lambda $ -阶等价关系矩阵 ${{{R}}_\lambda }$ 。 ${{{R}}_\lambda }$ 本质上是一个等价关系。此时，用户可依据定理2从 ${{{R}}_\lambda }$ 推导出若干个等价类，其中 $x \in {{G}}$ 决定的等价类记为 ${[x]_\lambda }$ 。

当 $\delta = \kappa = {\rm{1}}$ 时，用户从表1能推导出如表2、表3所示的模糊相似关系矩阵和模糊等价关系矩阵。当 $\lambda = {\rm{1}}$ 时，{1}、{2}、{3, 4}、{5, 6}、{7, 8}、{9}是等价类；当 $\lambda = {\rm{0}}{\rm{.8}}$ 时，{1, 2}、{3, 4}、{5, 6}、{7, 8, 9}是等价类；当 $\lambda = {\rm{0}}{\rm{.6}}$ 时， $\{1, 2, \cdots, 9\}$ 是唯一的等价类。

为避免单一粒度认知的片面性，对于任意缺失值的估计，用户可以设置多个阈值参数 ${\textit{λ}}_1{\text{，}}{\textit{λ}}_2 {\text{，}} \cdots {\text{，}}{\textit{λ}}_N$ ， ${\rm{0}} \leqslant {\textit{λ}}_i \leqslant {\rm{1}}$ ，进而结合多个粒度下的分类结果去分析和求解问题。

定义6　设 ${{{R}}_{{\textit{λ}}_i}}$ 是 ${\textit{λ}}_i$ -阶模糊等价关系矩阵，称 ${\textit{λ}}_i$ 是边界值，若不存在 ${\textit{λ}}_k$ 满足 ${\textit{λ}}_i < {\textit{λ}}_k$ 且 ${R_{{\textit{λ}}_i}} = {R_{\lambda _k}}$ 。

准则1　在不完备形式背景 $({{G}}, \;{{M}}, \;{{I}}\, )$ 中，设 $m(x) = * $ ， ${\textit{λ}}_i$ 是边界值， $i = 1, 2, \cdots , N$ 。

若 $\alpha \geqslant \beta $ ，则 $m(x) = {\rm{1}}$ ；若 $\alpha < \beta $ ，则 $m(x) = {\rm{0}}$ 。

其中

$(\alpha \;\beta ) = \left( {\begin{array}{*{20}{c}} {{\textit{λ}}_{\rm{1}}}&{{\textit{λ}}_{\rm{2}}}& \cdots &{{\textit{λ}}_N} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {{\rho _{{\textit{λ}}_1}}(x, m, 1)}&{{\phi _{{\textit{λ}}_1}}(x, m, 0)} \\ \vdots & \vdots \\ {{\rho _{{\textit{λ}}_N}}(x, m, 1)}&{{\phi _{{\textit{λ}}_N}}(x, m, 0)} \end{array}} \right)$

$ \begin{aligned} & {\rho _{\lambda_i}}(x, m, 1) = \frac{{\, \left| {\, \{ \, y \in {{[x]}_{\lambda_i}} \, |\, \, m(y) = 1\, \} \, } \right|}}{{|{{[x]}_{\lambda_i}}|}}\, \, \\ & {\phi _{\lambda_i}}(x, m, 0) = \frac{{\, \left| {\, \, \{ y \in {{[x]}_{\lambda_i}} \, |\, \, m(y) = 0\, \} \, } \right|}}{{|{{[x]}_{\lambda_i}}|}}\, \, \end{aligned} $

基于上述判定准则，用户可以对不完备形式背景进行预处理，从而得到一个完备的形式背景。接上例，对于 $d(7) = * $ ，依据准则1及下述计算结果，即得 $d(7) = {\rm{0}}$ 。

$\left( \!\!{\begin{array}{*{20}{c}} {\rm{1}}&{{\rm{0}}{\rm{.8}}}&{{\rm{0}}{\rm{.6}}} \end{array}}\!\! \right) \times \left( \!\!{\begin{array}{*{20}{c}} {{\rm{0}}{\rm{.00}}}&{{\rm{0}}{\rm{.50}}} \\ {{\rm{0}}{\rm{.33}}}&{{\rm{0}}{\rm{.33}}} \\ {{\rm{0}}{\rm{.44}}}&{{\rm{0}}{\rm{.33}}} \end{array}}\!\! \right) = \left(\!\! {\begin{array}{*{20}{c}} {{\rm{0}}{\rm{.53}}}&{{\rm{0}}{\rm{.97}}} \end{array}}\!\! \right)$

其中 $({\textit{λ}}_{\rm{1}}\;\, {\textit{λ}}_{\rm{2}}\;\, {\textit{λ}}_{\rm{3}}) = ({\rm{1}}\;\, 0.8\;\, 0.6)$

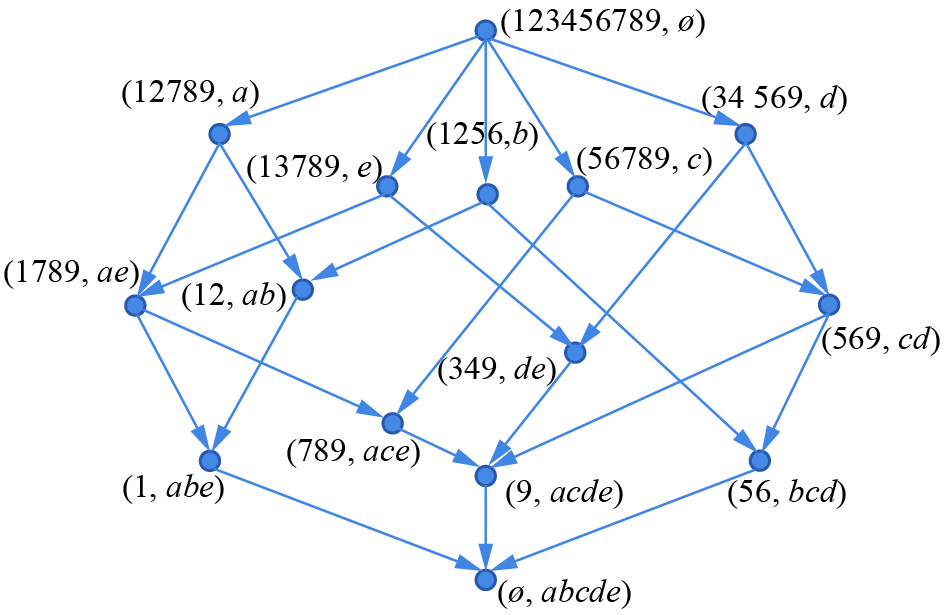
类似地，用户也可以判定其它缺失值，相应的判定结果如表4所示。在此基础上，复用经典概念格生成算法，用户可以从表4生成一个格代数结构，如图1所示。

4 基于极大相容类的数据分析模型

在不完备形式背景 $\left( {{{G}}, \;{{M}}, \;{{I}}} \right)$ 中，一个相容关系 ${{{R}}_\sigma }$ 可以描述为

$\begin{array}{l} {{{R}}_\sigma } = \{ \left. {\, \, (x, y) \in {{G}} \times {{G}}\, } \right|\, \, {\bf{Sim}}(x, y) \geqslant \sigma \, \} ,0 \leqslant \sigma \leqslant 1 \end{array} $

式中 ${\bf{Sim}}$ 是定义5中构造的相似度模型。从定理2和 ${{{R}}_\sigma }$ 出发，用户即可推导出若干个极大相容类，并基于准则2对缺失值进行判定。

准则2　设 $m(x) = * $ ， $x \in {{G}}$ 同时属于 $N$ 个极大相容类 ${{\cal{D}}_1},{{\cal{D}}_2}, \cdots , {{\cal{D}}_N}$ 。

若 $\overset{\frown} {\alpha } \geqslant \overset{\frown} {\beta } $ ，则 $m(x) = {\rm{1}}$ ；若 $\overset{\frown} {\alpha } < \overset{\frown} {\beta } $ ，则 $m(x) = {\rm{0}}$ 。

其中

$(\overset{\frown} {\alpha } \;\, \overset{\frown} {\beta } \, ) \!=\! (\, |{{\cal{D}}_1}|\;\,|{{\cal{D}}_2}|\; \cdots \;\, |{{\cal{D}}_N}|\, )\;\, \!\times \!\;\, \left( {\begin{array}{*{20}{c}} {{{\overset{\frown} {\rho } }_1}(x, m, 1)}&{{{\overset{\frown} {\phi } }_1}(x, m, 0)} \\ \vdots & \vdots \\ {{{\overset{\frown} {\rho } }_N}(x, m, 1)}&{{{\overset{\frown} {\phi } }_N}(x, m, 0)} \end{array}} \right)$

$ \begin{split} & {\overset{\frown} {\rho } _i}(x, m, 1) = \frac{{\, \, \left| {\, \left\{ {\, x \in {{\cal{D}}_i} \, |\, \, m(x) = 1\, } \right\}\, } \right| + {\rm{1}}\;}}{{\, \left| {\, \left\{ {\, x \in {{\cal{D}}_i} \, |\, \, m(x) = 0\, } \right\}\, } \right| + {\rm{1}}}} \\ & {\overset{\frown} {\phi } _i}(x, m, 0) = \frac{{\, \, \left| {\, \left\{ {\, x \in {{\cal{D}}_i} \, |\, \, m(x) = 0\, } \right\}\, } \right| + {\rm{1}}\;}}{{\left| {\, \left\{ {\, x \in {{\cal{D}}_i} \, |\, \, m(x) = 1\, } \right\}\, } \right| + {\rm{1}}}} \end{split} $

在表5中，当 $\delta = \kappa = {\rm{1}}$ 、 $\sigma = {\rm{0}}{\rm{.8}}$ 时，{1, 2}、{2, 3, 4}、{3, 4, 5}、{5, 6, 7}、{6, 7, 8}、{7, 8, 9}、{2, 7}是极大相容类。基于准则2，用户可以对不完备形式背景进行预处理，进而得到一个完备的形式背景。例如，对于 $d(7) = * $ ，基于准则2和下述计算结果

$(3\, \;3\, \;3\, \;{\rm{2}}) \times \left( {\begin{array}{*{20}{c}} {\rm{1}}&1 \\ {{\rm{1/3}}}&3 \\ {{\rm{1/3}}}&3 \\ 2&{{\rm{1/2}}} \end{array}} \right) = (9\;\, 22)$

即可判定 $d(7) = {\rm{0}}$ ，其中， ${{\cal{D}}_{\rm{1}}}\text{、} {{\cal{D}}_{\rm{2}}}\text{、} {{\cal{D}}_{\rm{3}}}\text{、}{{\cal{D}}_{\rm{4}}}$ 依次表示{5, 6, 7}、{6, 7, 8}、{7, 8, 9}、{2, 7}。

类似地，用户也可以判定其它缺失值，相应的判定结果如表6所示。在此基础上，复用经典概念格生成算法，用户可以从表6生成一个格代数结构，如图2所示。

基于准则1和准则2的模型本质上都属于间接处理模型，即需要对原始数据集进行预处理，给出缺失数据的估算值，进而复用经典理论对完备形式背景进行分析处理。

在不完备形式背景 $\left( {{{G}}, \;{{M}}, \;{{I}}} \right)$ 中，一个相容关系R可以描述为

$ \begin{aligned} {{R}} = & \{ \, (x, y) \in {{G}} \times {{G}}|m(x) = m(y)\;{\rm{or}}\;m(x) = \\ & * \;{\rm{or}}\;m(y) = * , \;\forall m \in {{M}}\, \} \end{aligned} $

下文中，由上述相容关系决定的极大相容类的集合记为 $\Delta $ 。

准则3　在任一极大相容类中，不同对象在同一属性下应具有相同的属性值。在此情形下，一个极大相容类 ${\cal{D}}$ 在属性 $m \in {{M}}$ 下的值域只可能有以下4种情况，即{1}、{0}、{1, *}、{0, *}，而不可能是{0, 1, ﹡}。

当 ${\cal{D}}$ 在 $m$ 下的值域为{1, *}时，若“*”代表“0”，则必然与准则3相违背，此时，“*”代表的只能是“1”；同理，若 ${\cal{D}}$ 在 $m$ 下的值域为{0, *}，则“*”代表的值只能是“0”。下文中， ${V_m}({\cal{D}}) = 1$ 表示 ${{D}}$ 在 $m$ 下的值域为{1}或{1, *}； ${V_m}({\cal{D}}) = {\rm{0}}$ 表示 ${\cal{D}}$ 在 $m$ 下的值域为{0}或{0, *}。

定义7　设 $({{G}}, \;{{M}}, \;{{I}}\, )$ 是一个不完备形式背景，对于任意集合 ${{X}} \in {2^{{G}}}$ ，记

$ \begin{aligned} {{{X}}^ + } = & \{ \, m \in {{M}}|\, \, \left( {m(x) = 1} \right)\, {\rm{or }}\\ & \left( {\, \exists {\cal{D}} \in \varDelta , \, \, x \in {\cal{D}}, \, \, {{{V}}_m}({\cal{{{D}}}}) = 1\, } \right), \;\forall x \in {{X}}\, \} \end{aligned} $

对于任意集合 ${{B}} \in {2^{{M}}}$ ，记

$ \begin{aligned} {{{B}}^ + } = & \{ \, x \in {{G}}|\;\, \left( {m(x) = 1} \right)\, {\rm{or }} \\ & \left( {\, \exists {\cal{D}} \in \varDelta , \, \, x \in {\cal{D}}, \, \, {V_m}({\cal{D}}) = 1\, } \right), \;\forall m \in {{B}} \, \} \end{aligned}$

与定义1中的经典算子相类似，从上述算子出发同样可以导出一个格代数结构，相关证明过程与经典算子类似，在此不再详述。

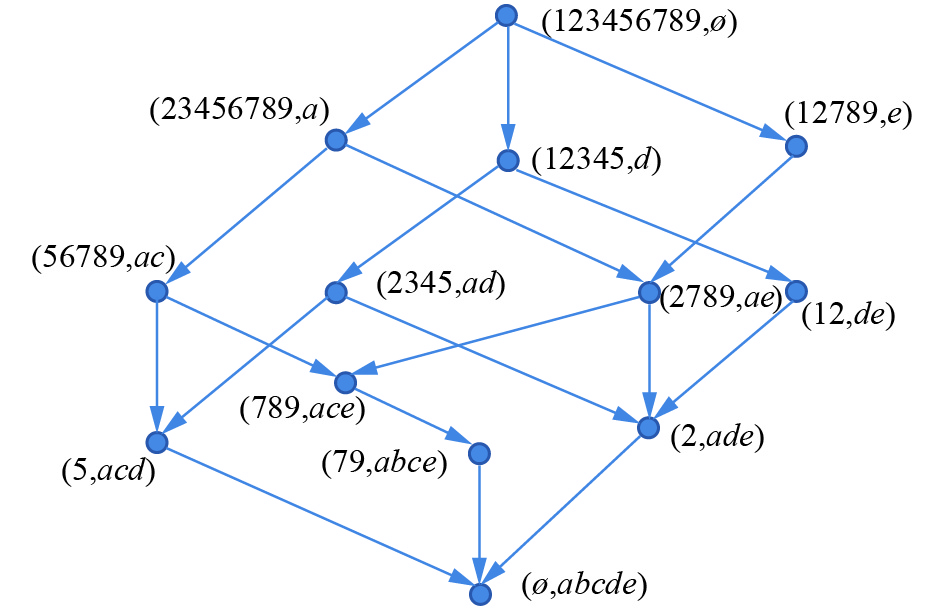
例如，在表5中，从定理2和定义7出发，可判定{1}、{2}、{3, 4}、{5}、{6}、{7, 8}、{7, 9}是极大相容类，如表7所示，进而基于定义7中的算子生成图3所示的格代数结构。除(79, abce)之外，图3、图2中的其他结点均一致，这也从侧面反映了这样一个事实，即无论是基于准则2，还是基于准则3，所构造的模型可能会得到相似的结论。

定义8　称 $\overset{\frown} {{{K}}} = ({{\varDelta}} , \;{{M}}, \;{{J}})$ 是 $K = ({{G}}, \;{{M}}, \;{{I}}\, )$ 的粒化背景，若

$({\cal{D}}, \, \, m) \in {{J}} \Leftrightarrow {{{V}}_m}({\cal{D}}) = 1$

在粒化背景 $\overset{\frown} {{{K}}} $ 中，对于任意 $\overset{\frown} {{{X}}} \in {2^\varDelta }$ ，记

$\overset{\frown} {X} ' = \{ \, m \in {{M}}|\, \, ({\cal{D}}, \, \, m) \in {{J}}, \;\forall {\cal{D}} \in \overset{\frown} {{{X}}} \, \} $

对于任意 ${{B}} \in {2^M}$ ，记

${{B}}' = \{ \, {\cal{D}} \in \Delta |\;\, ({\cal{D}}, \, \, m) \in {{J}}, \;\forall m \in {{B}} \, \} $

其中， $({\cal{D}}, \;m) \in {{J}}$ 亦可表示为 $m({\cal{D}}) = 1$ 。

基于准则3的知识获取模型，其本质是将分析尺度放大，以极大相容类为研究对象，而非单个对象。在准则3下，任意 ${\cal{D}}$ 在属性 $m$ 的取值是确定的，即要么 $m({\cal{D}}) = 1$ 成立，要么 $m({\cal{D}}) = 0$ 成立，这就意味着，不完备形式背景可以转化为一个完备的粒化形式背景。事实上，在准则3下，无论是基于定义7，还是定义8，得到的格代数结构本质上是相同的，仅仅在外延表示形式上存在略微差异。

定理3　若 $({{X}}, {{B}}) \in {\cal{B}}({{K}})$ ， $(\overset{\frown} {{{X}}} , {{B}}) \in {\cal{B}}(\overset{\frown} {{{K}}} )$ ，则

${{X}} = \bigcup\nolimits_{{\cal{D}} \in \overset{\frown} {{{X}}} } {\cal{D}} $

证明　由定义7和定义8即得。证毕。

与准则1和准则2最大的不同是，基于准则3的知识获取模型无需对缺失信息进行预判定并给出估算值，而是直接在原始不完备形式背景上建立知识获取模型。

5 实例分析

表8是一个以医院病例为原型而得到的不完备形式背景，其中P_i(i= $1, 2, \cdots, 9$ )表示患者代码；(H, yes)、(H, no)、(M, yes)等表示身体症状特征，其中H、M、T、F依次表示Headache、Muscle-pain、Temperature、Flu；若某患者具有某种症状，则在表8中用“1”来表示，反之用“0”来表示；若某诊断结论存在缺失，则用“*”来表示。

当 $\delta = \kappa = {\rm{1}}$ 时，用户基于准则1得到的预处理结果，如表9所示。其中，当 $\lambda = {\rm{1}}$ 时，{1}、{2, 5, 7, 8}、{3}、{6}、{4, 9}是等价类；当 $\lambda = {\rm{0}}{\rm{.89}}$ 时，{1, 6}、{2, 5, 7, 8}、{3}、{4, 9}是等价类；当 $\lambda = {\rm{0}}{\rm{.78}}$ 时，{1, 3, 6}、{2, 5, 7, 8}、{4, 9}是等价类；当 $\lambda = {\rm{0}}{\rm{.67}}$ 时，{1, 2, 3, 4, 5, 6, 7, 8, 9}是唯一等价类。

当 $\delta = \kappa = {\rm{1}}$ 、 $\sigma = {\rm{0}}{\rm{.78}}$ 时，用户基于准则2同样可以得到如表9所示的预处理结果，其中，{1, 6}、{2, 5, 7, 8}、{3, 6}、{4, 9}是极大相容类。

事实上，表9中的完备化结果与下述事实性规则是吻合的，这也在一定程度上反应了准则1和准则2的合理性和有效性。例如，当患者体温是“very high”时，则其体温一定也是“high”；当患者体温“normal”时，则其体温一定不是“high”和“very high”；当患者“Flu, yes”时，则一定不是“Flu, no”等。

事实性规则：(T, very high)→(T, high)、(T, normal) $\not \to $ (T, high)、(T, normal) $\not \to $ (T, very high)、(H, yes) $\not \to $ (H, no)、(H, no) $\not \to $ (H, yes)、(F, no) $\not \to $ (F, yes)、(F, yes) $\not \to $ (F, no)。

在概念格经典理论中，概念内涵和蕴涵规则都占有极其重要的地位。本文认为，无论间接处理模型，还是直接处理模型，它们都应该得到相同的内涵集和蕴涵规则集(内涵集和蕴涵规则集是相互唯一决定的)。据此，本文提出了如下有效性判定准则：

有效性判定准则对于同一个不完备形式背景，若多个不同模型得到的蕴涵规则集合或内涵集合是相同的，则本文认为这些模型在一定程度上是有效的，得到的结果在一定程度上也是可信的。

定义9　设 ${{K}} = ({{G}}, \;{{M}}, \;{{I}})$ 为一个形式背景， ${{{B}}_1}$ 、 $ {{{B}}_2} \subseteq M$ 。若 ${{{B}}'_1} \subseteq {{{B}}'_2}$ ，则称 ${{{B}}_1} \to {{{B}}_2}$ 是 ${{K}}$ 中的蕴涵规则。

准则3相对应的极大相容类有{1}、{2, 7, 8}、{3}、{4, 9}、{5, 8}、{6}。在此基础上，基于定义7或定义8，用户可得到相应的格代数结构。经验证明，基于准则3直接从表8得到的概念内涵集与基于准则1或准则2间接从表8中得到的概念内涵集是相同的。显然，在这种情形下，依据有效性判定准则给出的判定原理，可以在一定程度认为基于准则1、准则2或准则3构建的模型是合理的，相应的求解结果也是可信的。

总体来看，准则1和准则2需要引入阈值参数，属于间接处理模型；而准则3则无需引入阈值，属于直接处理模型。在实际应用中，如果数据缺失量大，本文倾向于选用直接处理模型，因为先选择间接模型可能会导致原始数据集失真；如果数据缺失量少，则无论是直接模型还是间接模型，都可以选用。

6 结束语

为消除不完备信息带来的影响，使概念格模型具有更强的数据处理能力与更广的应用领域，本文尝试将经典形式背景中的知识获取方法进一步拓展到不完备形式背景中，依次探讨了基于等价类的分析模型和基于极大相容类的分析模型。在实际应用中，用户既可以选择基于准则1或准则2的间接处理模型，也可以选择基于准则3的直接处理模型。此外，对于模型的机制有效性和结果可信性，本文也尝试性的进行了探讨，并提出了一些初步的验证方法。相信本文所做的工作能为下一步相关研究提供一些有益的思路。