联盟生成是多Agent系统(multi-agent system，MAS)研究基本问题之一^[1-2]，主要将Agent进行合作或协商，使其效用增加。Agent联盟基本上被认为在MAS的框架内的一组Agent，愿意与这组中的其他Agent合作，共同合作活动的目的是达到最佳的标准。当Agent通过组建联盟共同工作时，联盟结构生成就会发生^[3]。目标就是求一种最优的联盟结构，使得所求的社会福利最大，并返回其值^[4-5]。

Agent在联盟生成时达到最优方案不一定是全局最优解，但是应该是Nash最优解^[6-7]或者次优解，因此联盟生成主要包括以下活动：

1) 联盟结构生成：Agent之间进行协商生成联盟，但不考虑各个联盟之间的协商。

2) 解决每个联盟优化问题：将Agent的任务和资源集中在一起，共同解决问题。Agent之间进行协商使联盟的社会福利尽可能最大化，即寻找最优的方法使得联盟本身的效用最大化。

3) 划分值：在进行收益分配的时候，常用的方法有两种，即公平(每个Agent所得到的收益是Agent在博弈中的贡献的体现)和稳定(存在没有和其他Agent协商而单独形成自己的自私利益联盟)。

同样，存在很多方法寻找和创建一个最优的联盟——协商或搜索以及用于找出解决问题的几种潜在的方法，例如：遗传算法、博弈论、粒子群算法等。但是，随着研究的不断深入，在现实世界的应用中有一些联盟结构是不允许生成的^[8]。目前，联盟研究的热点问题主要是约束条件下联盟生成。在现有研究中，很多文献已经考虑将联盟进行广泛应用，例如：通过形成联盟，自主传感器可以改善某些区域的监控情况^[9]；认识无线电网络可以增加它们的吞吐量^[10]；购买者可以通过批量购买而获得较低的价格^[11]；自主连接车辆进行护航工作^[12]；形成联盟促进社交网络关系^[13-14]等。

在Agent联盟研究发展中，Sandholm等^[15]最先提出最坏情况有限界联盟结构生成；Yeh等^[16]首次使用动态规划算法联盟生成并求得精确最优解；随着研究的不断深入，Agent数量的增加，先前的算法越来越不能满足当前的需求，Dang等^[17]首次提出建立次优联盟结构并求得次优解；Greco等^[18]经过进一步研究，提出了一种新的联盟结构生成的方式——约束联盟结构，即在生成联盟的过程对联盟添加约束。

1 基本定义 1.1 主要定义

假设所有的Agent都是理性的，并使用合作博弈建模进行Agent之间的合作和协商。在博弈中，令 $N$ 是一个Agent集，其中 $n = \left| N \right|$ 表示 $N$ 中Agent的个数，则 $N = ({a_1},{a_2}, \cdot \cdot \cdot ,{a_n})$ ，联盟即 $N$ 中非空的子集。

定义1　联盟结构。对于任意联盟 $C$ ，在 $C$ 上形成的联盟结构 ${\rm CS} = \{ {C_1},{C_2}, \cdot \cdot \cdot ,{C_k}\} $ ，其中 $ \cup {\rm CS} = C$ ，并且对于任意 $i,j \in \left\{ {1,2, \cdot \cdot \cdot ,k} \right\},i \ne j$ 都需要满足 ${C_i} \cap {C_j} = \text{Ø} $ 。

例1　一个集合 $N = \{ {a_1},{a_2},{a_3}\} $ ，N上的联盟一共有7种情况，分别是 $\{ {a_1}\} $ 、 $\{ {a_2}\} $ 、 $\{ {a_3}\} $ 、 $\{ {a_1},{a_2}\} $ 、 $\{ {a_1},{a_3}\} $ 、 $\{ {a_2},{a_3}\} $ 、 $\{ {a_1},{a_2},{a_3}\} $ ，联盟结构一共存在5种情况，分别是 $\{ \{ {a_1}\} ,\{ {a_2}\} ,\{ {a_3}\} \} $ 、 $\{ \{ {a_1}\} ,\{ {a_2},{a_3}\} \} $ 、 $\{ \{ {a_2}\} ,\{ {a_1},{a_3}\} \} $ 、 $\{ \{ {a_3}\} ,\{ {a_1},{a_2}\} \} $ 和 $\{ {a_1},{a_2},{a_3}\} $ 。

定义2　社会福利。社会福利即为联盟结构CS中所有的联盟 ${C_i},i \in \{ 1,2, \cdot \cdot \cdot ,k\} $ 的收益之和，将联盟的值记为 $v({C_i})$ ，并且要求 $v({C_i}) \geqslant 0$ ，联盟结构的社会福利记为 $V({\rm CS})$ ，将具有最大的社会福利联盟结构称为最优联盟结构，记为 ${\rm C}{{\rm S}^*}$ ，其最优社会福利记为 $V({\rm C}{{\rm S}^*})$ ，则

$ V\left( {\rm CS} \right) = \sum\limits_{i = 1}^k {\nu ({C_i})} $

定义3　次加性。对于任意的不相交的联盟 $S,T \in N$ ，都存在 $v(S \cup T) \leqslant v(S) + v(T)$ 。换言之， $\{ \{ {a_1}\} ,\{ {a_2}\} , \cdot \cdot \cdot ,\{ {a_n}\} \} $ 为最大社会福利的联盟结构。

定义4　特征函数。给定一个 $n$ 个Agent的博弈， $C$ 是一个联盟， $v(C)$ 是指 $C$ 和 $N - C $ 两个Agent博弈中 $C$ 的最大效用， $v(C)$ 称为联盟 $C$ 特征函数(characteristic function)，规定 $v(\text{Ø} ) = 0$ 。

1.2 博弈类型

在常用的联盟博弈模型中，通常用货币来表示联盟的价值(或奖励^[19])。在进行博弈的过程中，假设存在一个在Agent之间可以自由流动的交换媒介(如货币)，每个Agent可以根据自己的绩效得到相应的货币，这种博弈被称为“单边支付”博弈或可转移效用(transferable utility，TU)博弈。相反，联盟的绩效是用向量表示的，直接指定每个成员的绩效，Agent只能服从这种分配方案，不能对分配方案进行修改，这种博弈被称为不可转移效用(non-transferable utility，NTU)博弈。在多Agent系统中，可转移效用博弈受到了很大的关注。

1) 特征函数博弈

特征函数博弈(characteristic function games，CFGs)是联盟的价值完全取决于它所包含的Agent的值。将特征函数博弈定义为 $(N,v)$ ，其中 $N$ 表示Agent数据集， $v$ 是一个函数，称为特征函数，对于每个联盟C映射到函数中的值 $v(C)$ 记为 $v:{2^N} \to {\bf {R}}$ 。

2) 分区博弈

在分区博弈(partition function games，PFGs)中联盟的价值不仅仅取决于所包含的Agent的值，也会受非成员分区的影响。将分区博弈定义为 $(N,w)$ ，其中 $N$ 表示Agent数据集， $w$ 是一个分区函数，每个嵌入式联盟 $(C,{\rm CS})$ 映射到函数中的值是 $w((C,{\rm CS}))$ 或 $w(C,{\rm CS})$ 。

CFGs是PFGs的子集，联盟C在CFGs中有一个精确值，但在PFGs中却存在很多值，这是因为使用PFGs有不同的方法对 $N/C$ 中的Agent进行分区。因此，在进行研究的过程中，使用CFGs更容易得到解决方案，提高算法的效率。

1.3 空间表示

在联盟结构生成问题中，通过联盟结构搜索得到最优联盟结构。

1) 联盟结构图

Sandholm等^[15]提出的联盟结构图中，每个节点代表一个联盟结构，并且将节点进行了划分，表示为 $\varPi_1^C,\varPi_2^C, \cdot \cdot \cdot ,\varPi _n^C$ ，其中 $\varPi _i^C$ 表示由i个联盟组成的所有的联盟结构的节点；边缘连接两个联盟结构，当且仅当它们属于不同的划分，如 $\varPi _i^C$ 和 $\varPi _{i - 1}^C$ ；其中 $\varPi _i^C$ 中的联盟结构是由 $\varPi _{i - 1}^C$ 中的联盟分裂成两个联盟形成的。图1所示为具有4个Agent集联盟结构图。

2) 整数分区图

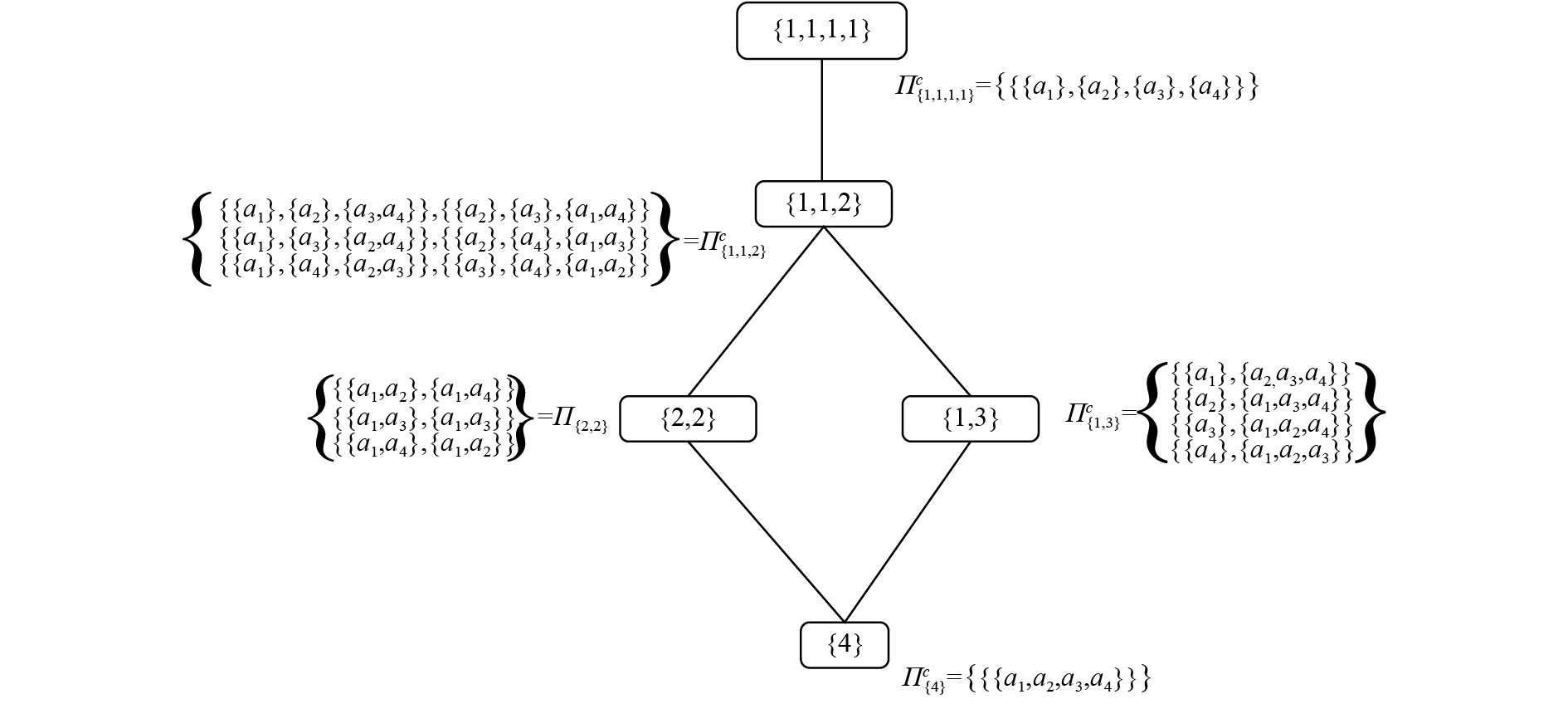
在联盟结构图中，能直接看出具有i个联盟所组成的联盟结构的情况。而Dean等^[20]提出的整数分区图中，则是基于联盟结构中所包含的联盟的数量，将联盟结构中的空间划分成不相交的子空间，每个子空间是由n个整数分割表示的。整数n的分区值可以通过递归的方法计算^[21]，用 ${P^n}$ 表示整数分区。例如： ${P^4} = \{ \{ 4\} ,\{ 1,3\} ,\{ 2,2\} ,\{ 1,1,2\} , $ $\{ 1,1,1,1\} \} $ 。

假设 $I \in P$ ，定义 $\varPi _I^C \in {\varPi ^C}$ 是所有联盟结构组成的子空间，其中联盟的大小受 $I$ 部分的影响。例如： $\varPi _{\{ 1,1,2\} }^{\{ {a_1},{a_2},{a_3},{a_4}\} }$ 表示是由2个只有1个Agent联盟和1个有2个Agent组成的联盟形成的联盟结构。对于这种表示一般用整数分区图来表示。整数分区图也是一个无向图，其中每个节点代表一个子空间。两个节点 $I,I' \in {P^n}$ 是通过边连接的，当且仅当 $i,j \in I$ 时， $I' = (I\backslash \{ i,j\} )\Xi \{ i + j\} $ ( $\Xi $ 表示多重集的结合操作)。图2给出了有4个Agent整数分区图。

2 联盟生成的复杂度 2.1 输入值的大小

对于具有n个Agent的数据集，会产生 ${2^n} - 1$ 个非空的子集，生成 ${2^n} - 1$ 个联盟，在进行运算时需要输入 ${2^n} - 1$ 个值。联盟结构生成算法的输入值和Agent的个数之间呈指数关系。

理论上，在进行输入操作时即可排除一些不合理的联盟，或者在进行联盟结构生成的时候就可以忽略一部分的输入。但是在接下来进行的操作过程中无法保证存在单一的联盟与其他的联盟进行合作之后的社会福利不是最佳社会福利，这是因为：被排除在外的联盟中可能存在比其他的联盟社会福利更大的联盟。

2.2 联盟结构的数量

随着联盟结构不断发展，Agent数量的增多，新问题也随之产生。联盟结构的个数表示为

$\sum\limits_{i = 1}^N {Z(n,i)} $

其中：n代表数据集中的Agent个数； $Z(n,i)$ 表示具有i个联盟组成的联盟结构的个数； $Z(n,i)$ 满足第2类Striling数的特征，即

$Z(n,i) = iZ(n - 1,i) + Z(n - 1,i - 1)$

式中： $Z(n,i) = Z(n,1) = 1$ ； $iZ(n - 1,i)$ 表示在现有存在的联盟中增加一个新的Agent形成的联盟结构的个数； $Z(n - 1,i - 1)$ 表示将一个新的Agent加入到已有的联盟中，因为现在的联盟结构中只有i－1个联盟被计算。有以下基本结果^[22-24]：

命题1　对于具有n个Agent的集合，具有 $\displaystyle{2^{n - 1}}$ 个联盟， $\displaystyle{{O}}({n^n})$ 和 $\displaystyle\omega ({n^{n/2}})$ 个联盟结构(即联盟结构的个数的阶介于 $\displaystyle\frac{n}{2}$ ~n之间)。

命题2　寻找最优联盟结构是NP难问题。

随着Agent数量的增加，联盟结构的数量也随之增加。经过实验的证明，当数据集中Agent个数超过15时，使用穷举法列举出所有联盟结构是不可行的。

3 最坏情况有限界联盟结构生成

Dean和Boddy在时间依赖规划(time dependent planning)的基础上提出了Anytime算法，其本质是一种反复求解使得结果更加精确的算法。在算法的运行过程中，能够很快得到一个不精确的解，然后进行若干次的重复过程，经过重复后逐步提高解的质量，Anytime算法一个最显著的优点就是能够很好地权衡计算时间和解的质量。Sandholm等^[15]使用Anytime算法开创性地提出了一种最坏情况有限界联盟结构生成。

命题1表明，在联盟结构图上找到最优的联盟结构是不可行的。所以，在进行联盟结构图的搜索的时候设定一个限界。

对联盟结构的子集N进行搜索，目的在于寻找搜索中的最优联盟结构，即局部最优联盟结构，记：

$ CS_N^* = \arg \mathop {\max }\limits_{CS \in N} V(CS) $

同时，为了保证设定的联盟结构在最佳范围内，即存在一个有限的但是尽可能小的值k，k被称为搜索的解的界限，也是衡量局部最优解 $V(CS_N^*)$ 的标准。能够建立起界限的最小的k记为

$ k = \min \{ \kappa \} ,\,\,\, \kappa \geqslant \frac{{V(C{S^{\rm{*}}})}}{{V(CS_N^*)}} $

通常，如果没有对联盟结构进行完全搜索，设定一个正确的界限是很难的。这是因为：在剪枝的过程中虽然可以减少一些联盟结构的搜索，但是很难保证没有剪掉的比剪掉的具有更优性。在进行社会福利的定义的时候，令任意一个联盟 ${C_i}$ 的值 $v({C_i}) \geqslant 0$ ，并且一个联盟结构的社会福利 $V(CS) = \sum\limits_{i = 1}^k {v({C_i})} $ ，这两点就保证了上述假设是不存在的，即在没有对联盟结构进行搜索的前提下设置一个界限来缩小搜索联盟结构的数量。

3.1 建立界限

本节主要讨论如何尽可能地减少对图的搜索的前提下，建立一个界限k。

定理1　对于界限k，可以只搜索联盟结构图的最低的两级(图1中第 $\varPi _1^C\text{、}\varPi _2^C$ 层)。在这个搜索中，界限k=n，需要搜索的联盟结构节点的数量是 ${2^{n - 1}}$ ，这也是能够建立起界限的最小的搜索，即 ${n_{\min }} = {2^{n - 1}}$ 。并且，没有其他的算法对于联盟结构的搜索的数量会比 ${2^{n - 1}}$ 少。

最底层具有1个联盟结构，第二最底层中具有 ${2^n} - 2$ 个联盟(N中的所有子集，除掉全集和空集)。在这一层中，每个联盟结构都有2个联盟，所以一共有 $\displaystyle\frac{1}{2}({2^n} - 2)$ 个联盟结构。只搜索最底下两层，一共搜索 $1 + \displaystyle\frac{1}{2}({2^n} - 2) = {2^{n - 1}}$ 个联盟结果。

3.2 算法描述

算法1　最坏情况有保证联盟结构生成算法

1) 搜索联盟结构图的最底二层；

2) 从联盟结构图的顶层(第n层)开始，作宽度优先搜索，一直搜索到时间不允许为止或搜索完整个联盟结构图；

3) 返回迄今为止所得到的最优的联盟结构。

先前使用特征函数的方式^[25-26]进行联盟结构生成，算法1是一种任意时间算法，可以在任何时间中断。如果将第1、2层搜索完成后，还存在剩余时间，则可进一步地搜索缩小界限。

定理2　如果联盟结构图的第1、2层已经被搜索完成并且第1层以及以上的层也被搜索完成( $l > 3$ )，当 $n \equiv h - l(od h)$ 且 $n \equiv l(od h)$ 时， $k = \left\lceil {\displaystyle\frac{n}{h}} \right\rceil $ 是紧的，否则 $k = \left\lfloor {\displaystyle\frac{n}{h}} \right\rfloor $ 是紧的，其中 $h = \left\lfloor {\displaystyle\frac{{n - l}}{2}} \right\rfloor + 2$ 。

在 ${2^{n - 1}}$ 个节点被搜索完之前，无法建立一个界限。当搜索到 ${2^{n - 1}} + 1$ 个节点时，可以建立界限k=n；搜索到 ${2^{n - 1}} + 1$ 个节点的时候，界限变成 $k = \displaystyle\frac{1}{2}n$ 。通过更多实验验证：当界限k变成 $\displaystyle\frac{1}{3}n$ 时，搜索的层数就会增加2层。当搜索的层数每增加2层，界限k前面的除数就会加1，若只多搜索一层时，没有明显效果。

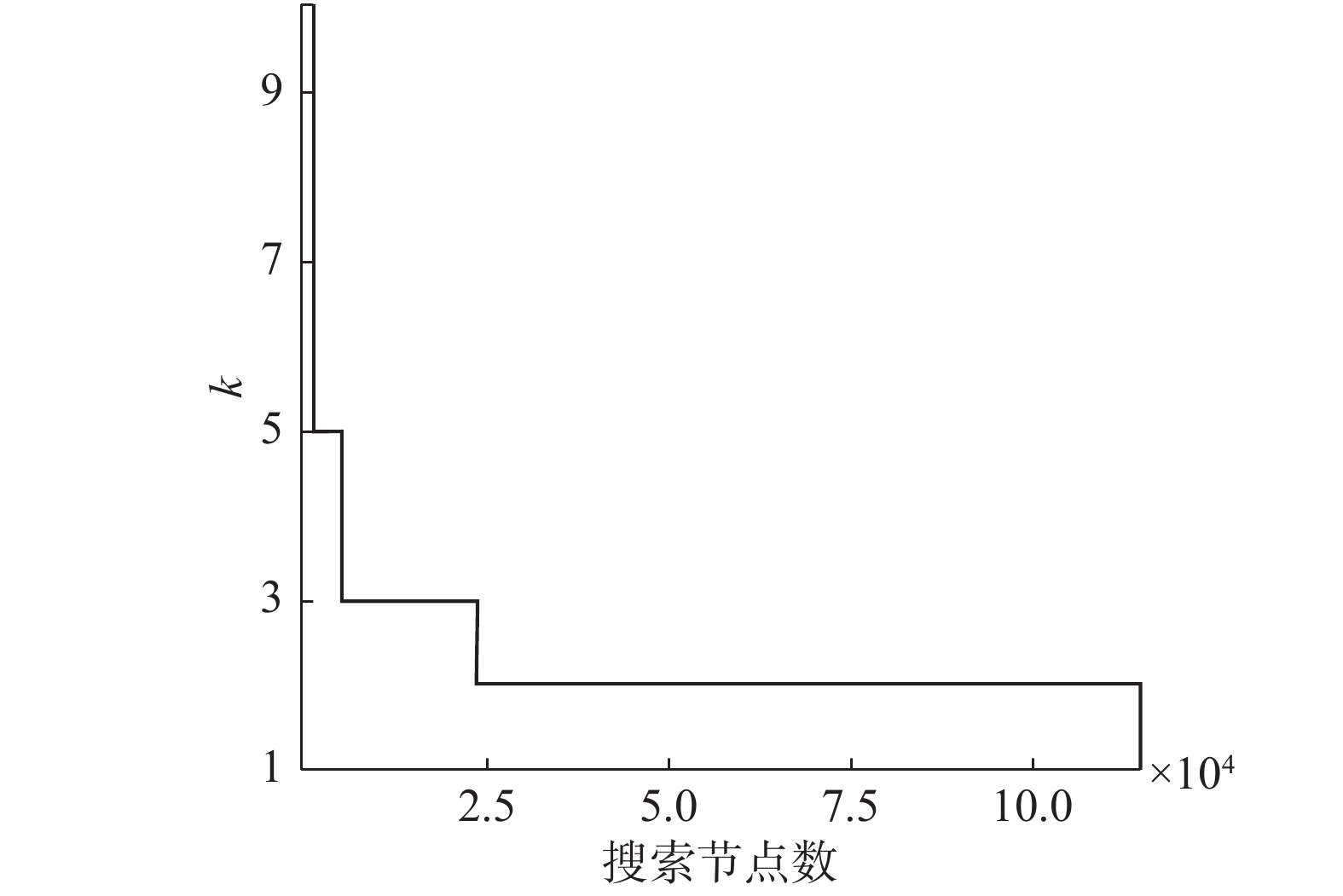
总之，最坏情况有限界联盟结构生成算法中第2步具有很强的理性，即界限k能够迅速地下降，同时该算法的收益递减，如图3所示。

界限 $k = \displaystyle\frac{1}{2}n$ 的建立与输入的Agent联盟的个数之间呈线性关系，这是因为输入 ${2^{n - 1}}$ 个数据，而当界限 $k = \displaystyle\frac{1}{2}n$ 时能够建立 ${2^{n - 1}}$ 个联盟结构，就是所说的第1、2层和第n层上面的节点。

胡山立等^[27-28]对算法1深入研究并进行改进，给出了解决问题的一种任一时间联盟结构生成算法和给定界限要求的联盟结构生成。Dang等^[29]提出不以层为单位最坏情况有限界的联盟结构生成。

4 动态规划联盟生成求精确最优解

动态规划(dynamic programming，DP)算法和分治法类似，其基本思想是将待求解的问题分解成若干个次级子问题，在求解的过程中，先求解子问题，然后从子问题的解中得到要求解的问题的答案。将动态规划算法应用于最优化的问题，一般分为4个步骤来完成：

1) 找出最优解的性质，并刻画其结构特征；

2) 递归定义的最优值；

3) 以自顶向下的方式计算出最优值；

4) 根据计算最优值所得到的信息，构造最优解。

将动态规划算法应用于联盟中的想法是Yeh在1986年首次提出的^[16]；Rothkopf^[30]及刘惊雷等^[31]使用DP算法对求解最优联盟结构的算法进行了改进，主要解决存在大量重复子问题计算的问题；Rahwan等^[32]提出了IDP(improved dynamitic programming)算法；张新良等^[33]在2007年提出了一种快速动态生成 (search of coalition structure, SCS) 算法，主要降低搜索次数。本文中，DP算法主要基于定理3。

定理3　任意给定一个联盟 $C \in N$ ， $V({\rm C}{{\rm S}^*})$ 是最优联盟结构的社会福利，即 $ V({\rm C}{{\rm S}^*}) ={\max \limits_{CS \in {\varPi ^n}}}V({\rm CS})$ ，则

$ V({\rm C}{{\rm S}^*}) = \left\{ \begin{array}{l} v(C){\rm{,}}\;\;\;\;\left| C \right| = 1\\ \max \{ v(C),{\max\limits _{\{ C',C''\} \in {\varPi ^N}}}(v(C') + v(C'')\} ,\;\;\;{\text{其他}} \end{array} \right. $

使用定理3进行动态规划，先计算只有一个Agent的联盟，接着迭代具有2个Agent的联盟，然后是具有3个Agent的联盟，一直迭代到具有n个Agent的联盟。对于每个联盟C都需要使用式(1)计算。从式(1)中易知：当 $\left| C \right| \ne 1$ 时，需要分别计算 ${\max \limits_{\{ C',C''\} \in {\varPi ^N}}}v(C') + v(C'')$ 和 $v(C)$ 的值，然后将两个值进行比较，得到具有较大社会福利的联盟。在此过程中，将所产生的暂存结果保存在变量 $t\left( C \right)$ 中。

通过上述操作，计算出来的最大 $v(C)$ 就是我们最终要求的 $V({\rm C}{{\rm S}^*})$ 。计算 ${\rm C}{{\rm S}^*}$ 的迭代过程具体操作如例2所示。

例2　令数据集 $N = \{ {a_1},{a_2},{a_3},{a_4}\} $ ，假设特征函数为

$\begin{array}{c} v(\{ {a_1}\} ) = 30,v(\{ {a_2}\} ) = 40,\\ v(\{ {a_3}\} ) = 25,v(\{ {a_4}\} ) = 45,\\ v(\{ {a_1},{a_2}\} ) = 50,v(\{ {a_1},{a_3}\} ) = 60,\\ v(\{ {a_1},{a_4}\} ) = 80,v(\{ {a_2},{a_3}\} ) = 55,\\ v(\{ {a_2},{a_4}\} ) = 70,v(\{ {a_3},{a_4}\} ) = 80,\\ v(\{ {a_1},{a_2},{a_3}\} ) = 90,v(\{ {a_1},{a_2},{a_4}\} ) = 120\\ v(\{ {a_1},{a_3},{a_4}\} ) = 100,v(\{ {a_2},{a_3},{a_4}\} ) = 115,\\ v(\{ {a_1},{a_2},{a_3},{a_4}\} ) = 140 \end{array}$

表1表示算法的具体运算过程。由表1知， $t(N) = (\{ {a_1},{a_2}\} ,\{ {a_3},{a_4}\} )$ ，能够将N分裂成 $\{ {a_1},{a_2}\} $ 和 $\{ {a_3},{a_4}\} $ ，而 $t(\{ {a_3},{a_4}\} ) = \{ \{ {a_3},{a_4}\} \} $ ，这是因为 $\{ {a_1},{a_2}\} $ 分裂成 $\{ {a_1}\}\text{、} \{ {a_2}\} $ 后的社会福利比较大， $\{ {a_3},{a_4}\} $ 不需要进行分裂。所以 ${\rm C}{{\rm S}^*} = \{ \{ {a_1}\} ,\{ {a_2}\} , \{ {a_3},{a_4}\} \} $ 。

定理4　给定一组Agent集，使用动态规划算法求得最优联盟结构的时间复杂度 $O({3^n})$ 。

DP算法在该算法的运行过程中实际做了如下几方面：

1) 评估图上的运动；

2) 在表t中存储最优结构；

3) 从底部节点开始向上运动。

5 联盟生成求近似最优解

Rahwan等^[34]将联盟配置与Anytime算法进行结合提出一种联盟结构相似最优解算法；为Albizuri等^[35]基于整数分区对联盟结构进行推广从而对联盟配置(coalition configuration)进行了定义。

5.1 基本定义

在进行求解的过程中，设 ${\rm{C{L}}_s} \in {2^n}$ ，其中 $s \in \{ 1,$ $ 2, \cdot \cdot \cdot ,k\} $ 是联盟列表， ${\rm{CL}}_i$ 是联盟列表 ${\rm{C{L}}_s}$ 的集合(见表2)。设 ${G_1},{G_2}, \cdot \cdot \cdot ,{G_{\varsigma {\rm{cs}}}} \in {\varsigma _{\rm cs}}$ 是所有的存在的唯一配置的结合(即不存在具有相同联盟大小的两个元素)，令 $F:{\varsigma _{\rm CS}} \to {2^{\rm CS}}$ 是一个函数，按照提前设定好的配置返回所有的联盟结构。 $N$ 表示一个列表，里面的每一个元素表示一组具有相同配置的联盟结构。形式上， $N$ 定义为：N = $ \{ F({G_1}),F({G_2}), \cdot \cdot \cdot ,F({G_{\left| {{\varsigma _{\rm CS}}} \right|}})\} $ ， ${N_1}, {N_2}, \cdot \cdot \cdot ,{N_{{\varsigma _{\rm CS}}}} \in N$ 表示 $N$ 中的每个元素(见表3)。

5.2 具体实现

算法实现分为3个部分：1)预处理操作；2)构造和选择合适的配置；3)搜索元素。

1) 预处理操作

预处理的主要目的是计算 ${{\rm{CL}}_s}$ 的最大值 ${\max _s}$ 和平均值 ${\rm{avg}}{_s}$ 并返回计算值，同时将当前搜索社会福利最大的联盟结构返回记为 ${\rm{CS}}'$ 。此过程中，主要进行2种操作，分别是评估互补大小和包含配置为 $\{ 1, 2,\cdot \cdot \cdot ,i\}$ 的联盟。

①评估互补大小：将 ${{\rm{CL}}_s}$ 和 ${{\rm{CL}}_{n - s}}$ 称为互补的，如 ${{\rm{CL}}_3}$ 和 ${{\rm{CL}}_1}$ 。在此过程中需要计算由互补中的联盟组成的不相交的联盟结构的值。

②包含配置为 $\{ 1,2, \cdots ,i\} $ 的联盟：计算 $G = \{ 1,2, \cdots ,i\} $ 配置的联盟结构的值。

经过上述两个操作搜索联盟结构，可以搜索空间的一部分(随着n的增加而减小)。表4表示的是8个Agent搜索结果，其中配置 $G = \{ 8\} $ ， $G = \{ 4,4\} $ ， $G = \{ 3,5\} $ ， $G = \{ 2,6\} $ ， $G = \{ 1,7\} $ ， $G = \{ 1,1,6\} $ ， $G = \{ 1,1,1,5\} $ ， $G = \{ 1,1,1,1,1,3\} $ ， $G = \{ 1,1,1,1,1,3\} $ ， $G = \{ 1,1, 1,1,1,1,2\}$ ， $ G = \{ 1,1,1,1,1,1,1,1\} $ 是在预处理操作中需要将被搜索的配置。

2) 构造和选择合适的配置

在搜索过程中，进行剪枝操作主要目的是减少搜索空间。 $G'$ 为搜索完后找到可能存在最优联盟结构的配置。

①构造独一无二的配置：保证所有的配置的集合等于所有Agent可能产生的整数分区。例如，有5个Agent，可能存在的整数分区的配置G为{5}，{4, 1}，{3, 2}，{3, 1, 1}，{2, 2, 1}，{2, 1, 1, 1}和{1, 1, 1, 1, 1}。计算每个配置G对应于F(G)的上界 ${{\rm{UB}}_G}$ 和平均值 ${{\rm{Avg}}_G}$ 。将 $V({\rm{CS}}')$ 和 ${{\rm{UB}}_{G'}}\beta $ 进行比较，如果 $G'$ 中所有的配置都满足前者大于后者，那么该解即为最优解。否则，进行②操作。

②选择合适的配置：搜索过程中满足 $\displaystyle\frac{\rm{AVG}}{{{\rm{UB}}_G^*}} \geqslant k$ ，则选择元素中最小的一个，否则继续进行剪枝工作。

③更新上边界：进行搜索的 $CS^*$ 是可以计算本身的数值或者将其自身分裂后形成联盟的最大值。例如，在搜索配置为G={1, 1, 1, 1, 2, 3, 4}的元素时，最大值可能的组合是{1, 1, 3}。当求配置G={1, 1, 1, 3, 3, 4}的上边界时，在配置G={1, 1, 3}的上边界的基础上加上 ${\max _1} + {\max _3}{\rm{ + ma}}{{\rm{x}}_4}$ 。以该方式对配置进行拆分处理，能更好地更新上边界。

3) 搜索元素

搜索过程的关键在于构建联盟结构。在该算法中，构建联盟结构的主要问题是，在执行时会进行重复操作，从而形成冗余和无效的联盟结构。

①避免重叠的联盟结构：重叠的联盟结构是 $\{ \{ {a_1},{a_2}\} \{ {a_2},{a_3}\} \} $ 这样。使用快速索引技术^[36]进行解决。

②避免冗余的联盟结构：冗余的联盟结构是 $\{ \{ {a_1},{a_2}\} ,\{ {a_3},{a_4}\} \} $ 和 $\{ \{ {a_3},{a_4}\} ,\{ {a_1},{a_2}\} \} $ 这样。在进行组合的过程中以升序排列，并且使用联盟中最小的元素 $C_k^1$ 作为关键点，以确定已经存在的联盟。

③正确性证明：通过上述步骤可以生成唯一的和有效的解决方案。

6 约束条件下联盟生成求最优解

Frankovi等^[37]将关注点从所有Agent之间的联系转移到只关注给定Agent之间建立最优的联盟。Greco等^[18]经过进一步研究，提出了一种新的联盟结构生成方式——约束联盟结构，即在生成联盟的过程对联盟添加约束。

6.1 约束联盟的基础

在进行约束联盟结构形成的过程中，主要是定义在一对 $ < N,v > $ 上的， $ < N,v > $ 称为联盟博弈，其中N = $ ({a_1},{a_2}, \cdot \cdot \cdot ,{a_n})$ 是Agent集，v是评估函数。

例3　假设一个联盟博弈为 $ < N,v > $ ，其中 $N = ({a_1},{a_2},{a_3})$ ，评估函数为

$v(\{ {a_3}\} ) = 0$

$v(\{ {a_1}\} ) = v(\{ {a_2}\} ) = v(\{ {a_1},{a_3}\} ) = v(\{ {a_2},{a_3}\} ) = 1$

$v(\{ {a_1},{a_2}\} ) = v(\{ {a_1},{a_2},{a_3}\} ) = 3$

易知，最优联盟结构是 $\{ {a_1},{a_2},{a_3}\} $ 和 $\{ \{ {a_1},{a_2}\} ,\{ {a_3}\} \} $ ，这是因为 $v(\{ {a_1},{a_2}\} ) + v(\{ {a_3}\} ) = v(\{ {a_1},{a_2},{a_3}\} ) = 3$ 。

假设在联盟博弈 $ < N,v > $ 中，Agent集上定义一个无向图G，G称为交互图。联盟C是可行的，当且仅当C在G的子图上是连通的。

6.2 约束联盟结构生成

令 $\varGamma {\rm{ = }} < N,v > $ 是联盟博弈， $D = (N,E)$ 是联盟博弈上的一个交互图，其中图中的交点是N中的Agent，边是节点集，设 $S \in N$ 是一个可能为空的Agent集，称为枢纽Agent。规定任意一个可行联盟结构中不允许存在两个及其以上的枢纽Agent。 $\alpha ,\beta :S \mapsto {\bf{R}}$ 是两个评估函数，而 $x,y \in \bf{R}$ 是两个实数，则 $\sigma {\rm{ = }} < D,S,\alpha ,\beta ,x,y > $ 是 $ < N,v > $ 的评估结构。

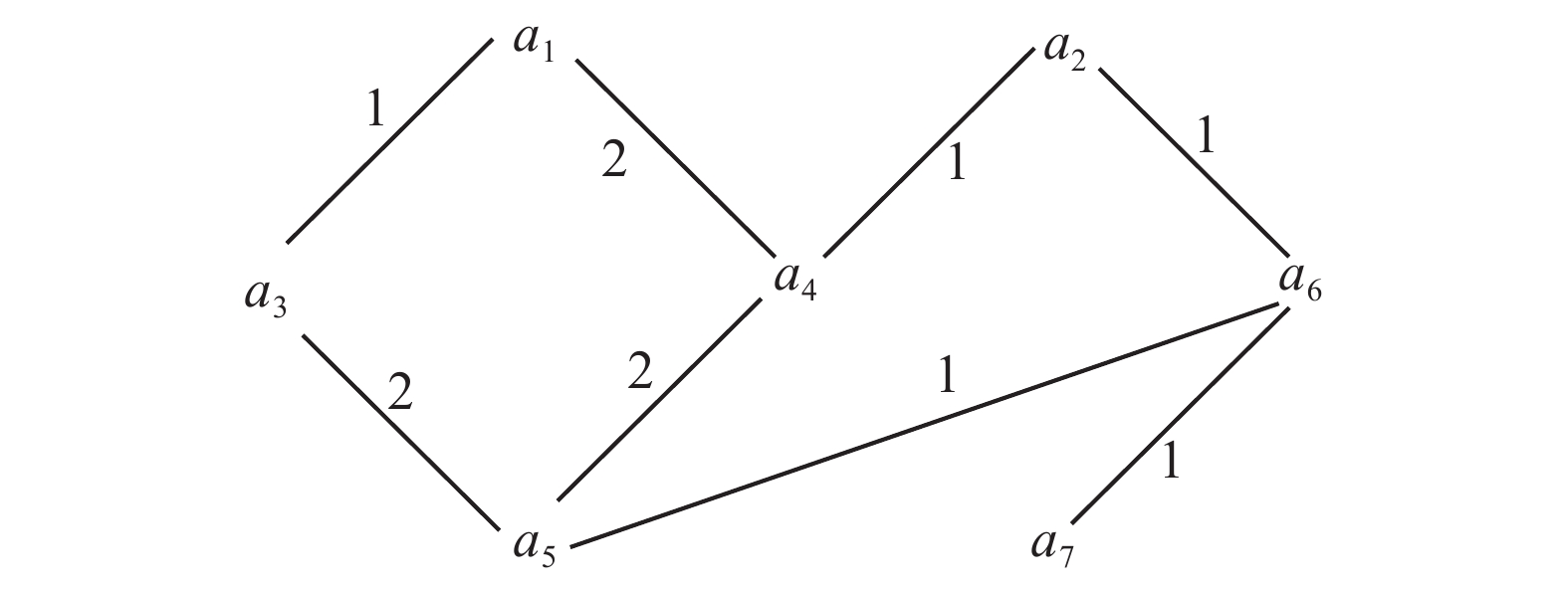
例4　给定一个联盟博弈 $\varGamma {\rm{ = }} < N,v > $ ，其中N = $\{ {a_1}, {a_2},\cdots,{a_7}\} $ 。评估结构为 $\sigma = (D,\{ {a_1},{a_2}\} ,\alpha ,\beta ,x, y)$ ，其中图D如图4所示。

图4中 ${C_1} = {\rm{\{ }}{a_1},{a_3}\} $ ， ${C_2} =$ $ \{ {a_4},{a_5},{a_6}\} $ 是2个可行联盟，而 ${\rm{\{ }}{a_1},{a_2}{\rm{\} }}$ 和 ${\rm{\{ }}{a_5},{a_7}{\rm{\} }}$ 是2个不可行联盟，前者是因为联盟中2个Agent都是枢纽Agent，后者则是因为联盟不是图4的子图。

如果C是可行联盟结构，将函数α、β和实数 x、y 通过式(2)定义成评估函数v的映射 ${{\rm{val}}_\sigma }$ 。

${{\rm{val}}_\sigma }(v,C) = \left\{ \begin{array}{l} \alpha ({a_i}) \times v(C) + \beta ({a_i}),\,\,\,\,\{ {a_i}\} = C \cap S\\ x \times v(C) + y,\,\,\,\,C \cap S = \text{Ø} \end{array} \right.$

(2)

例5　假设图4中，估值函数为v，C是一个可行联盟，则 $v(C)$ 被定义为由C所覆盖的边的权值的总和，即

$v(C) = \sum {{e \in E,\,\,e \in C}{w_e}} $

${C_1} = {\rm{\{ }}{a_1},{a_3}\} ,{C_2} = \{ {a_5},{a_6},{a_7}\} $ 的估值为

$\begin{array}{c} v({C_1}) = w({a_1},{a_3}) = 1{\rm{ }}\\ v({C_2}) = w({a_5},{a_6},{a_7}) = w({a_5},{a_6}) + w({a_6},{a_7}) = 1 + 1 = 2 \end{array}$

假设函数 $\alpha \text{、}\beta $ 分别为 $\alpha :{\rm{\{ }}{{{a}}_1},{{{a}}_2}\} \to \{ 1\} $ ， $\beta :{\rm{\{ }}{{{a}}_1}, $ ${{{a}}_2}\} \to \{ 0\} $ ，而实数x=0，y=−12，则 ${{\rm{val}}_\sigma }({C_1}) = 1 \times v({C_1})$ + $ 0 = 1,{{\rm{val}}_\sigma }({C_2}) = 0 \times v({C_2}) - 12 = - 12$ 。

6.3 边际贡献网上联盟生成

边际贡献网^[38]在过去的几年里收到了相当大的关注。边际贡献网(marginal contribution network, MC-net)是包含一系列代表Agent的布尔变量的规则，每个规则的形式为 $\{ {\rm{pattern}}\} \to {\rm{value}}$ ，其中pattern可以包含正面的连接或负面的连接，value是与此pattern相关的附加贡献。

例6　给定一个联盟博弈 $\varGamma = < N,v > $ ，其中 $N = \{ {a_1}, {a_2},\cdot \cdot \cdot ,{a_5}\} $ ， $v(\{ {a_1},{a_2}\} ) \!=\! v(\{ {a_2},{a_3}\} ) = v(\{ {a_1},{a_3}\} ) \!=\! 2$ ； $\exists i \in \{ 1, 2,\cdot \cdot \cdot ,5\} ,v(\{ {a_i}\} ) = 0\text{；}\,\,$ $\;v(\{ {a_1},{a_2},{a_3}\} ) = 5\text{；}\,\,$ $\;\exists C \subseteq \{ {a_1}, {a_2}$ , ${a_3}\} $ ， $v(C \cup \{ {a_4}\} ) = v(C \cup \{ {a_5}\} ) = v(C) = v(C \cup \{ {a_4},{a_5}\} )$ ；根据边际贡献网，给定规则为

$\begin{array}{c} \{ {a_1} \wedge {a_2} \wedge \neg {a_3}\} \to 2\\ \{ \neg {a_1} \wedge {a_2} \wedge {a_3}\} \to 2\\ \{ {a_1} \wedge \neg {a_2} \wedge {a_3}\} \to 2\\ \{ {a_1} \wedge {a_2} \wedge {a_3}\} \to 5\\ \{ {a_3} \wedge {a_5}\} \to 0\\ \{ {a_2} \wedge {a_4}\} \to 0 \end{array}$

根据给定的规则， $v(\{ {a_1},{a_1},{a_1}\} ) = 2$ 。

定理5　令 $h \geqslant 0$ 是一个固定自然数， $\varGamma = < N\text{，}v > $ 是一个博弈，其中 $v$ 是独立于不相交成员的评估函数，交互图 $D$ 所构成的树的高大于h。令 $\sigma {\rm{ = }} < D,S,\alpha ,\beta ,x,y > $ ，则 $(\varGamma ,\sigma )$ 的联盟结构生成的值可以在多项式时间内解决。

约束满足问题具有较强的灵活性，能够进行推广解决文献[32]中提到的约束问题。

7 结束语

联盟结构生成问题中如何能够更快更精确地进行优化整体性能对于研究人员一直都是挑战。本文针对这一问题进行了全面的综述：1)搜索空间的不同表示；2)动态规划算法的时候来解决这个问题；3)使用近似最优来代替最优解；4)使用评估的方法，主要是添加了约束条件。所有的这些结构都是以一种独立的方式展示出来的。

但是，在现有联盟生成的研究中，大多数是以Agent之间具有相同的协商资源和态度为前提的，只考虑了协商中的相同性，却忽略了协商中的异质性。在未来的工作中，可以考虑将协商的异质性与约束联盟中的评估结构相结合。

同时，在约束K-means聚类算法的启发下，可以将一般形式的无法连接的约束进行合理操作后有理性地加入到评估结构中。另外，可以进行扩展，将允许联盟生成的概率使用先验知识进行检验或者将Agent之间的动态相互信任添加到联盟生成的过程中。