近十年来在大数据处理、云计算和深度神经网络的推动下,人工智能从低谷走向了第三次发展高潮期,以AlphaGo为代表的研究成果创造了许多惊世骇俗的奇迹!不同于以往的两次高潮,这次世界各主要大国都纷纷制定国家战略,把AI列为未来争霸世界的国之重器:2017年7月20日国务院发布了《新一代人工智能发展规划》,计划到2030年我国AI理论、技术和应用要处于国际领先地位;紧接着2017年9月1日俄罗斯总统普京强调“未来谁率先掌握了AI,谁就能称霸世界”;2018年4月16日英国议会AI特别委员会发布报告认为,英国在AI方面有能力成为世界领导者和AI创新中心;2018年4月25日欧盟委员会计划2018—2020年在AI领域投资240亿美元,确保其世界领先地位;2018年5月10日美国白宫为在未来的AI领域“确保美国第一”成立了AI专门委员会。与此形成鲜明对照的是不少著名的AI学者纷纷指出,当今AI已陷入概率关联的泥潭,所谓深度学习的一切成就都不过是曲线拟合而已,它是在用机器擅长的关联推理代替人类擅长的因果推理,这种“大数据小任务”的智能模式并不能体现人类智能的真正含义,具有普适性的智能模式应该是“小数据大任务”。他们认为基于深度神经网络的AI是不能解释因而无法理解的AI,如果人类过度依赖它并无条件地相信它,那将是十分危险的。特别是,在司法、法律、医疗、金融、自动驾驶、自主武器等人命关天的领域,更是要慎之又慎,千万不能放任自流。基于这个大的认识和反思背景,本文拟集中讨论为什么深度神经网络会让人工智能研究丧失可解释性?我们如何才能重新找回人工智能研究的可解释性?文中所涉及的“可解释性”满足一种强定义:它要求从前提到结论的推理全过程都能用理论上成熟可靠的逻辑语言描述清楚。
1 现今的人工智能研究何以会失去可解释性 1.1 原本二值神经元与布尔逻辑算子是完全等价的人工智能学科和产业已走过整整一个甲子的成长之路,图1是这60年AI发展的整体态势示意图,其中:曲线①是主波,它说明人类社会已不可逆转地进入到信息社会,智能化是当今时代的主旋律,它必然会扶摇直上九重天,势不可挡;曲线②是叠加在主波上的次波,它说明各个时期推动AI走向发展高潮的基本原理和关键技术,虽然在一定范围内能够解决某些智能模拟问题,效果突出,但是一旦把它推广到更大范围使用时,因缺乏人类智能活动的某些重要属性,效果会立马下降,甚至闹出大笑话。这说明,人的智能活动并不是由几个确定性因素决定的简单信息处理过程,而是由众多不确定性因素参与的复杂信息处理过程,广泛存在非线性涌现效应。所以研究AI是一个由点到面、由浅入深、长期试错、不断发现、不断完善的演化过程,任何AI产品都需要在其生命周期内反复学习提高、不断演化发展,不会一成不变[1]。

|
Download:
|
| 图 1 人工智能学科和产业60年发展态势图 Fig. 1 Development trend of the AI discipline and industry in 60 years | |
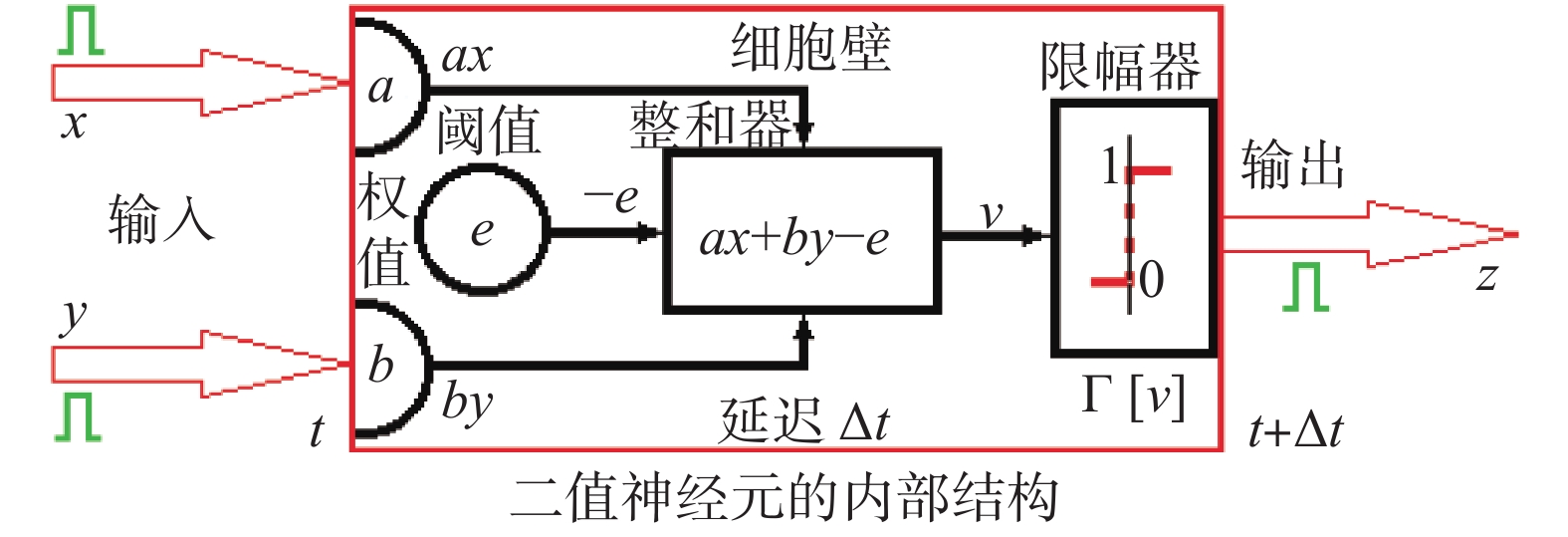
具体来看,AI学科的孕育和早期发展都是在布尔信息处理级别上完成的,当时出现了两个不同但是相互等价的视角[2]:从逻辑角度看,人类智能活动过程可用刚性逻辑(即数理形式逻辑、标准逻辑)的布尔算子组描述;从神经元角度看,人脑的智能活动过程可用二值神经元的MP模型描述。布尔逻辑算子组由英国数学家G.Boole于1854年在《思维规律》中提出:任意x, y, z∈{0, 1}, 非算子¬x=1−x, 与算子x∧y=Γ[x+y−1], 或算子x∨y=Γ[x+y], 蕴涵算子x→y=Γ[−x+y−1]。其中z=Γ[v]是0,1限幅函数,当v<0时z=0,当v>1时z=1; 否则z=v。二值神经元模型MP(又称感知机,阈元)由心理学家McCulloch和数学家W.Pitts于1943年共同提出,是一种最简单的神经元模型(见图2),依靠带阈值的0,1限幅运算z=Γ[ax+by−e]可以完成各种二值信息变换过程,其中x, y∈{0, 1}是输入变量,z∈{0, 1}是输出变量,a是输入x的连接权系数,b是输入y的连接权系数,e是神经元的激活阈值,Δt是神经元的处理延迟时间。
|
Download:
|
| 图 2 二值神经元的MP模型 Fig. 2 MP model of two valued neurons | |
对只有1个输入和1个输出的神经元z=f(x), x, z∈{0, 1}来说,只有4个可能的排列组合状态(称为信息处理模式):z=f0(x)≡0; z=f1(x)=x; z=f2(x)=1−x; z=f3(x)≡1。这4种神经元信息处理模式都有对应的刚性逻辑表达式:z≡0=x∧¬x; z=x; z=¬x;z≡1=x∨¬x。
在研究一个神经元内部信息处理模式时,没有必要考虑神经元的多输出问题,因为它只关系到一个神经元的输出z将被多少个别的神经元共享,与本神经元内部的信息处理模式毫无关系。
有2个输入和1个输出的神经元z=fi(x, y), x, y, z∈{0, 1}比较典型,是我们研究的重点,因为其他更多输入的神经元,都可以转化为2个输入神经元组成的神经网络,如:z=f(x1, x2, x3)=fj(fi(x1, x2), x3), x1, x2, x3, z∈{0, 1}; z=f(x1, x2, x3, x4)=fk(fi(x1, x2), fj(x3, x4)), x1, x2, x3, x4, z∈{0, 1}。其他以此类推,所以证明了两输入布尔信息处理的完备性就等于证明了任意多输入布尔信息处理的完备性。对2输入神经元z=fi(x, y), x, y, z∈{0, 1}来说,总共只有16种不同的信息处理模式i=0, 1, 2, 3, ···, 15,这16种信息处理模式的0,1限幅运算表达式z=Γ[ax+by−e],不论对于布尔逻辑算子还是二值神经元来说,都是完全相同的(传统的真值表表示法掩盖了这个等价关系),谁也没比对方多提供更多的信息处理能力。所以不难得出:刚性逻辑的布尔算子组和二值神经元MP模型具有相同的计算公式,两者完全等价,详细细节见图3。以后将把模式状态参数<a, b, e>作为区分不同信息处理模式的标志性参数使用,通过计算z=Γ[ax+by−e]可唯一确定一个二值神经元或者布尔算子组。

|
Download:
|
| 图 3 刚性逻辑算子和MP神经元模型等价 Fig. 3 Equivalence of the rigid logic operator and MP neuron model | |
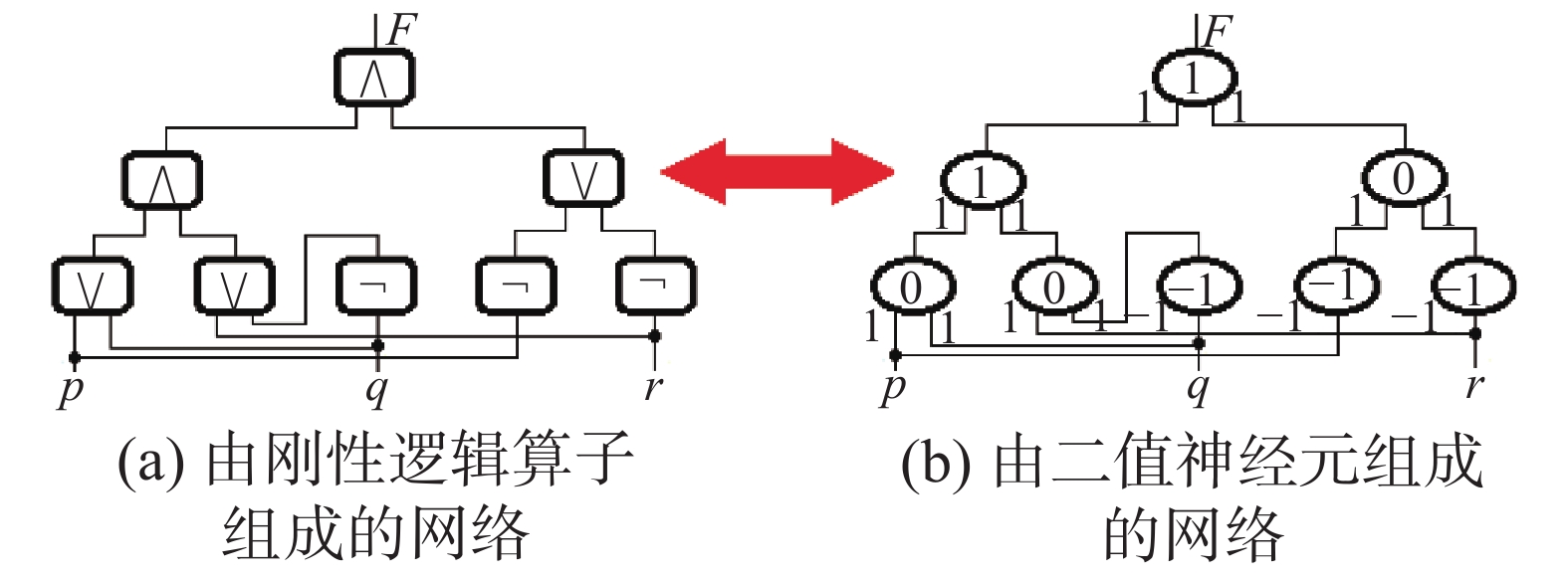
显然,上述的等价关系可推广到由任意基本单元组成的复杂网络之中,下面通过一个实例来说明:如果有一个复杂的刚性命题逻辑表达式F=((p∨q)∧(¬q∨r))∧(¬p∨¬r),它可用一些逻辑算子组成的逻辑网络来描述(见图4(a)), 一定存在一个由二值神经元组成的神经网络与之对应(见图4(b)),两者使用的0,1限幅运算公式z=Γ[ax+by−e]完全对应相同。
|
Download:
|
| 图 4 逻辑网络和神经网络等价的一个实例 Fig. 4 An example of the equivalence between logical and neural networks | |
数学理论和计算机的软硬件设计原理都是严格按照刚性逻辑建立的,不曾有半点逾越。可是人工智能学科的诞生却是因为计算机科学中出现了“算法危机”[3]而促成的!传统计算机应用都遵循“数学+计算机程序”的信息处理模式,要解决任何一个问题都必须满足3个先决条件:1)能找到该问题中输入和输出之间的数量关系,建立数学模型;2)能找到该数学模型的算法解;3)根据算法解能编制出在计算机上可实际运行的程序。上述3点都没有逾越刚性逻辑的约束,但是理论计算机科学家研究发现:1)人脑思维中的大部分智能活动无法建立数学模型;2)能找到的数学模型大部分都不存在算法解;3)能找到的算法解大部分都是指数型的,实际不可计算。为什么人脑智能可以解决的问题,数学+计算机程序的模式却解决不了?这说明计算机仅仅依靠“数学+计算机程序”的模式还不够聪明和有用,人工智能学科的创始人希望通过对人脑智能活动规律的研究和模拟,来克服上述“算法危机”,使计算机更聪明和有用。这就是狭义人工智能学科诞生的原由。由此可见,当时的科学家已经发现,仅仅依靠数学+程序是无法模拟人脑智能的。人工智能工作者最早发现的智能因素就是带有经验色彩的“启发式搜索原理”,它对刚性逻辑的有效使用具有必不可少的辅助作用。进而人们又通过专家系统的成功发现,各专门领域中通过经验归纳形成的专家知识,它们虽然不满足刚性逻辑的约束,却是“人更聪明”的重要因素,验证了“知识就是力量”的真理。
20世纪80年中期代爆发的人工智能“理论危机”无情地揭露了刚性逻辑、启发式搜索原理和经验知识推理的应用局限性:首先,刚性逻辑本身的推理效率十分低下,如果没有启发式知识的引导,单纯机械式地按照刚性逻辑的规则进行推理,算法的指数复杂度必然带来组合爆炸,计算机的时空资源迅速被吞噬殆尽;其次,在启发式搜索和经验知识推理中,客观存在的各种不确定性和演化过程都超出了刚性逻辑的有效适用范围,尽管出现了一些非标准逻辑(如模糊逻辑、概率逻辑和有界逻辑等)能解决某些实际问题,但有时会出现违反常识的异常结果,这说明非标准逻辑在理论上并不成熟可靠,无法在人工智能中安全可靠地使用。要有效解决包含各种不确定性和演化的现实问题,只能寄希望于尽快建立数理辩证逻辑理论体系,可是在当时的情况下,学术界的思想和理论准备都严重不足,建立数理辩证逻辑谈何容易!
在这种数理辩证逻辑严重缺位的背景下,人工智能研究的主流不得不偏离刚性逻辑和经验性知识推理的老方向,转入到完全不依赖逻辑和经验知识支撑,仅仅依靠数据统计的神经网络、计算智能、多Agent和统计机器学习的新方向。应该说这个研究新方向的出现也是具有积极意义的,它体现了人类智能另外的某些特征,能够有效地解决一些智能模拟问题,所以曾经推动人工智能的发展进入第二次高潮。后来人们为了克服神经网络、计算智能、多Agent和统计机器学习中的“局部极值”瓶颈,又在深度学习和深度神经网络中,依靠大数据和云计算,不惜耗费巨大的计算资源,义无反顾地连续使用数据统计法来增加神经网络的中间层次,从几层、几十层增加到几百层甚至几千层来拟合海量数据,根本忘记了二值神经元和布尔逻辑算子原本具有等价关系的基本属性。深度神经网络这种不惜一切代价取得的成功,反过来鼓励一些学者产生臆想:“深度神经网络的中间层次越多,获得的结果会越精准!”,而且“神经网络是无需逻辑和知识的智能,没有发展瓶颈”。这种盲目乐观的思潮弥漫在当今的人工智能学界,似乎现在的深度神经网络能够把第三次浪潮一直推动下去,它是人工智能学科发展的最终方向!
“物极必反”是自然的一条重要发展规律,在盲目乐观思潮弥漫的今天,已有一些著名的人工智能学者在讨论现有人工智能面临的局限性[4]:1)有智能没有智慧,无意识和悟性,缺乏综合决策能力;2)有智商没有情商,机器对人的情感理解与交流还处于起步阶段;3)会计算不会“算计”,人工智能可谓有智无心,更无人类的谋略;4)有专才无通才,会下围棋的不会下象棋。归纳起来说,目前人工智能发展正面临着六大发展瓶颈:1)数据瓶颈,需要海量的有效数据支撑;2)泛化瓶颈,深度学习的结果难于推广到一般情况;3)能耗瓶颈,大数据处理和云计算的能耗巨大;4)语义鸿沟瓶颈,在自然语言处理中存在语义理解鸿沟;5)可解释性瓶颈,人类无法知道深度神经网络结果中的因果关系;6)可靠性瓶颈,无法确认人工智能结果的可靠性。由此可知,人工智能的发展正面临又一次的发展瓶颈,本文统称为“可解释性瓶颈”。这些应用局限性和发展瓶颈对于人类智能来说并不明显存在,为什么却在当今的人工智能研究中成了难以逾越的巨大困难?笔者认为这些困难是由无视逻辑和知识在智能中的重要价值,过度依赖数据统计和深度神经网络引起的。
2011年图灵奖得主Judea Pearl是曾在20世纪80年代推动机器以概率(贝叶斯网络)方式进行推理的领头人,现在他却指出:深度学习所取得的所有成就都只是根据(有效)数据进行的曲线拟合,AI已陷入概率关联泥潭,它不能完全体现智能的真正含义。跳出泥潭的关键措施是用因果推理来代替关联推理,在AI中一旦因果关系就位,机器就有可能提出反事实问题,询问因果关系在某些干预下会如何变化,这才是科学思考的基础。所以只有因果推理才能使机器具有类人智能,有效地与人类交流互动。也只有这样,机器才能获得道德实体的地位,具有自由意志和运用人类谋略的能力。
1.3 重温人类智慧的两个重要特征人类智能的第一个重要特征是:在智能活动中需要机动灵活且恰如其分地使用各种行之有效的方法,相互配合起来才能取得事半功倍的效果。例如:人在识别汉字的过程中,会合理使用数据统计法和结构分析法(逻辑关系)于不同场合,以便获得最佳识别效果。又如:在认识汉字的基本笔划(如︑、ー、〡、ノ、ヽ)阶段,最有效的方法是图像数据统计法,而在此基础上进一步有效区分不同的汉字(如一、二、三、十、土、王、玉、五、八、人、入、大、太、天、夫等)阶段,最有效的方法则是结构分析法(逻辑关系),如果一味使用图像数据统计法一竿子插到底,在区分复杂结构的汉字(如逼、逋、迥、遒)时,速度和识别率会严重下降,事倍功半。
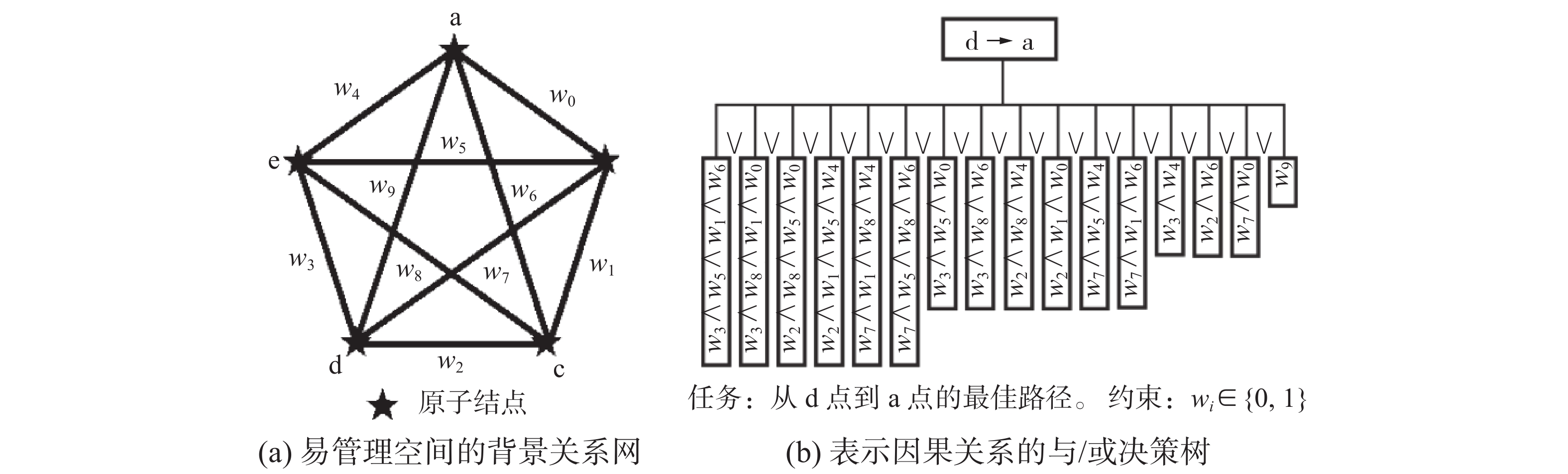
人类智能的第二个重要特征是:为有效管理和使用已知的各种知识,必须把它们分门别类地一层一层向上分类、归纳、抽象,形成由不同粒度知识组成的多层次网状结构。比如大家熟悉的地图知识,在范围最小的村落里,每户人家可是一个原子结点,它们通过原子道路相互连通。图5是一个高度简化了的村落级地图,图中用5个原子结点代表有限n户人家,用全互连图代表原子道路的分布状况(wi=1表示此路通畅,wi=0表示此路不通),形成了一个村落内部的刚性关系网络。利用这个关系网络可以解决村落内部的各种交通路径规划问题,图5中画出来的因果决策树就是为规划“从d家到a家”去做客的最佳路径规划,它可根据任务从刚性关系网络中诱导出来,并按照道路的实时通畅情况,选择完成任务的最佳路径。
|
Download:
|
| 图 5 村落地图和与/或决策树 Fig. 5 Village map and AND/OR decision tree | |
这个决策过程可用刚性逻辑或二值神经网络来实现:1)决策树中有16条不同的路径可供选择,彼此之间是“或”的关系,即只要有一条路径畅通这个问题就有解;2)如果一条路径经过的所有边都是畅通的,则这条路径是畅通的,即同一个路径中经过的不同边之间是“与”的关系;3)在多条路径都畅通时,选择经过边数最少的路径为“最佳解”。
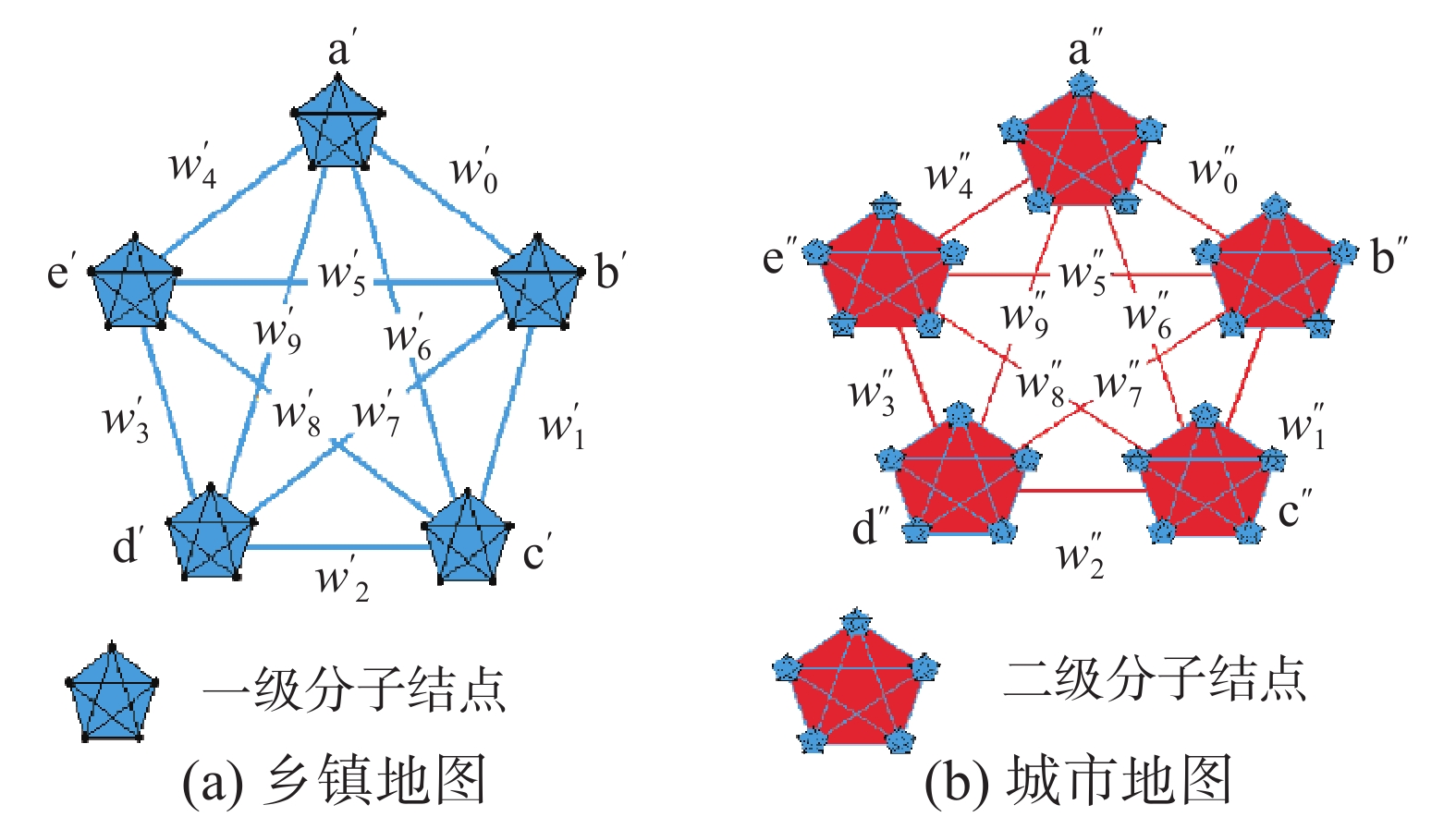
在一个自然村落范围内,上述用原子级关系网络诱导出与/或决策树来寻找最佳路径的过程是绝对有效的,并在理论上有刚性逻辑和二值神经网络的支撑。那么,是否能够无限制扩大这种绝对有效方法的应用范围呢?人类的社会实践早已做出了否定的回答,因为随着决策范围的不断扩大,涉及的原子信息(结点和边)会成几何级数地增多,其中绝大部分是与待解问题毫无关系的因素,如果把它们全部牵扯进来,不仅于事无补,反而使问题的复杂度成几何级数快速增大,成为一个实际难解、解了也无法说清楚的笨方法。人类使用的有效方法是:在有关村落级地图的基础上,进一步利用粒度更大的乡镇级地图(其中的观察粒度增大到一个村落)和地市级地图(其中的观察粒度增大到一个乡镇)来分层次地逐步解决“从d″镇d′村d家到a″镇a′村a家”的最佳路径规划问题(见图6)。
|
Download:
|
| 图 6 乡镇地图和地市地图的简化表示 Fig. 6 Simplified representation of district map and municipal map | |
图6是一个高度简化了的乡镇级地图和地市级地图,图中仍然用5个结点代表有限n个观察结点,不同的是它们都是有内部结构的分子结点,仍然用全互连图代表分子结点之间的连通状况,不同的是wi内部可能存在复杂的分子结构,不是简单的通或不通关系。这样就把一个在原子层面十分复杂的最佳路径规划问题,转化成几个相对简单得多的3个不同层面内部和层面之间的最佳路径规划子问题进行求解,整体的复杂度可以大大降低。请读者注意:图6里的分子结点“d′村”有两层含义,对内讲它包含村落里的全部内容,对外讲它是一个代表本村落与其他村落的联通结点(如村政府、公交车站、水运码头等),d″镇的含义也与此类似。利用图6来分层求解最佳路径的过程:首先在地市级地图上解决“从d″镇到a″镇”的最佳路径规划问题,然后分别去到两个乡镇级地图上解决“从d′村到d″镇”的最佳路径规划问题和“从a″镇到a′村”的最佳路径规划问题,最后再分别到两个村落级地图上解决“从d家离开d′村”的最佳路径规划问题和“从a′村进入a家”的最佳路径规划问题。
当今社会每天都在成亿次地产生制定国际国内旅游路径规划问题,对人类社会来讲这个过程已经十分轻松,没有太大的困难。这是如何做到的呢?首先是因为各国已经事先准备好了各个地区不同层面的交通路线图备客户使用,其次是因为各个业务部门都有实时更新的交通工具运行时间和价格等信息发布。有这些背景知识和信息的存在,即可快速支持任意范围内任意两点之间的旅游路径规划问题。例如:有人要从中国西安市西北工业大学去美国匹兹堡市匹兹堡大学讲学,其旅游路径规划不必从包含每家每户的世界地图上(当今世界每一个自然村落都有详细的地图,只要你不计成本和时空开销,一定可把它们全部拼接在一张世界地图上)去寻找,因为这个“最佳解”即使你用深度神经网络和云计算不计成本地找到了,它肯定是人类难以理解和解释清楚的“黑箱解”,在这个“黑箱解”的某个小环节突然出现异常时,更无法知道如何调整这个最佳路径规划。人类的做法不会如此愚钝,首先,他会根据顶层子任务“从中国到美国”在世界级地图和国际航空信息网站上找到从中国到美国的最佳航线和最佳航班信息,比如选择了某日某某航班从北京市的首都国际机场飞美国纽约市的纽瓦克机场;其次,根据两个中层子任务“从西安市到北京市首都国际机场”和“从纽瓦克机场到匹兹堡市”,分别在两个国家级地图和国内航空信息网站上找到最佳航线和最佳航班信息;最后,根据两个底层子任务“从西北工业大学到西安市咸阳机场”和“从匹兹堡机场到匹兹堡大学”,分别在两个城市级地图上根据当地实时发布的道路交通状况找到最佳的开车路线。
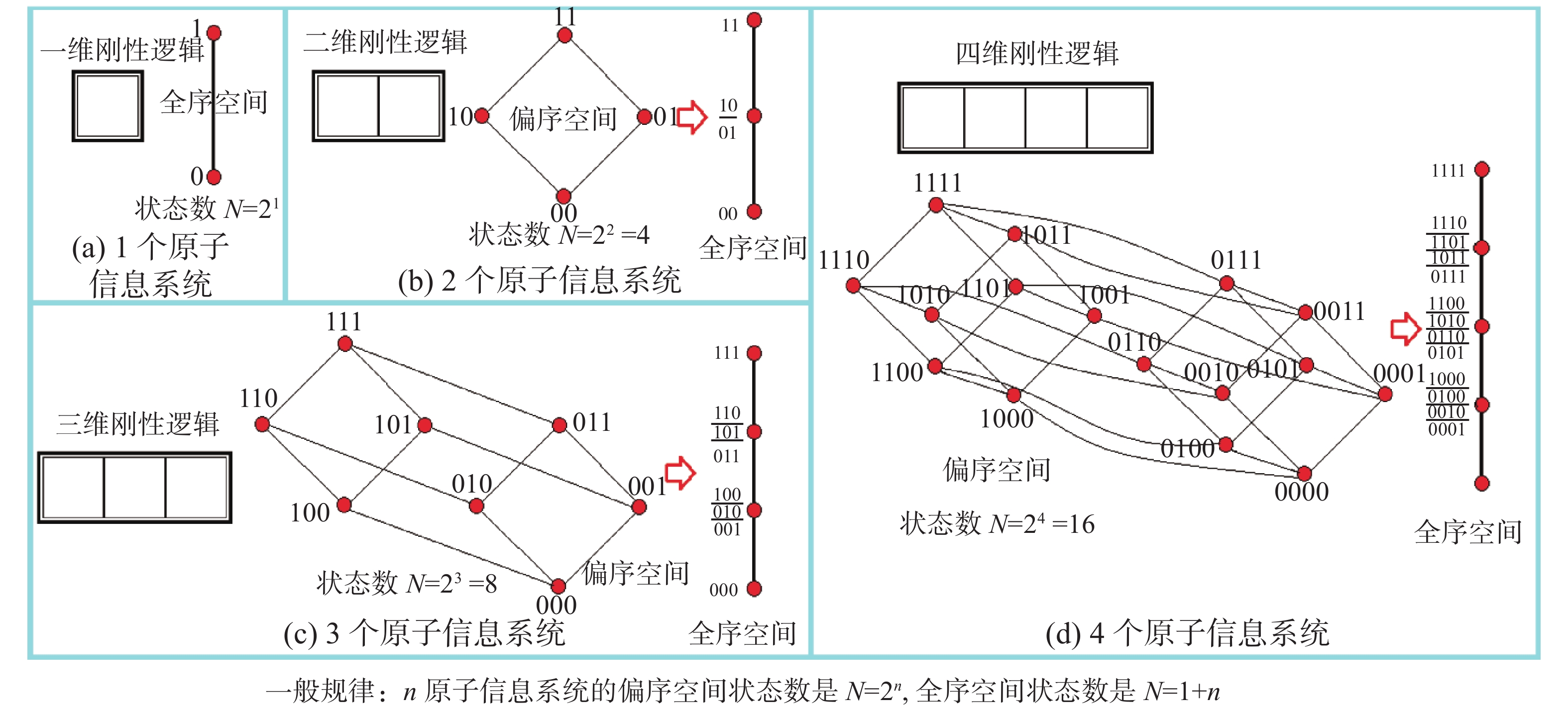
这种通过多层规划来解决复杂问题的聪明做法本质上是一种主动引入和合理利用不确定性的方法,它突破了传统问题求解观念的约束。传统问题求解观念认为,在解决问题时应努力消除各种不确定性,实在不能消除也要尽可能地避免不确定性推理,以便使用有可靠数学基础的刚性逻辑或二值神经网络解决。但是随着问题复杂度的不断增长,其时空开销会迅速达到无法实际操作的程度,人们不得不适时地进行分类、归纳和抽象,主动离开具有最细粒度和确定性的原子信息状态,果断进入具有较粗粒度和不确定性的分子信息状态。图7从时空开销(即易操作性)的角度给出了详细解释。通过归纳不难发现,n原子信息系统会形成由N=2n个不同状态组成的偏序空间,其复杂度会迅速增加到天文数字。如果忽略这些精确的偏序关系,用统计原子信息出现数目的方法把它映射到全序空间,其状态数可立即降低为N=1+n的线性复杂度(信息压缩了2n/(1+n)倍)。所以,在众多原子信息组成的系统中,除了特殊需要外,人们会主动离开过度精细的偏序空间,大胆进入到比较实用的全序空间,而不在乎它带来的不确定性, 这是人类智慧的高度体现,深度神经网络忽略了这个重要的人类智慧。
|
Download:
|
| 图 7 从确定的原子状态进入不确定性的分子状态 Fig. 7 From the determined atomic state to the molecular state of uncertainty | |
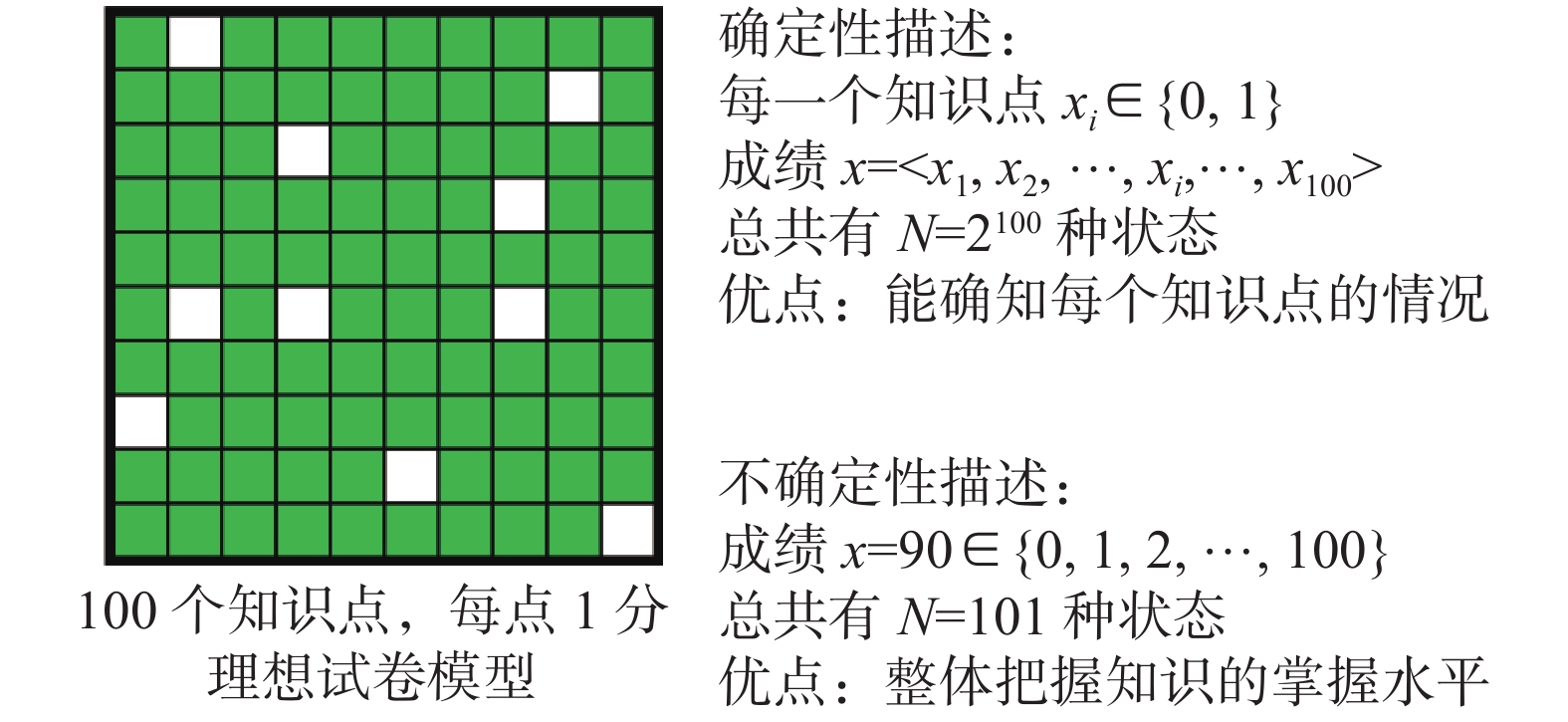
为让读者增强对主动引入和合理利用不确定性意义的认识,图8给出了学生们十分熟悉的“理想试卷模型”。设卷中有100道原子状态的是/非题(答对一道题得1分,否则得0分,没有中间过渡分数存在),用具有确定性的刚性逻辑来描述这个试卷,它是一个100维的二值逻辑,可精确描述到每一道题的得分情况,排列组合共有2100=126 7650 6002 2822 9401 4967 0320 5376≈1.267 65×1030种不同的答题状态,它们组成了一个100维的偏序空间。在现实生活中需要知道如此精准状态描述的只有阅卷老师和学生本人,其他人只需要知道他在101种不同状态组成的全序空间中的某个分数状态(图中是90分)即可,信息压缩比是(1.267 65×1030)/101=1.255 099×1028倍。而且就是这个90分本身也包含不确定性,因为尽管你确切知道他有10道题答错了,但仍然不知道错的是哪10道题,只知道它是210=1 024种不同错误状态中的一种。可见,在人类智能活动中,不仅客观上无法避免不确定性,而且为了提高决策效率需要忽略大量无关信息,主动引入不确定性。不难理解:决策的抽象层次越高,涉及的知识粒度越大,其中忽略的无关信息就越多,引入的不确定性就越大。由此可见,在深度神经网络中,有意无视逻辑和知识的作用是一种方向性错误。
|
Download:
|
| 图 8 从试卷模型看确定性和不确定性的关系 Fig. 8 A test paper model is used to illustrate the relationship between certainty and uncertainty | |
从更广泛的应用背景看,图8给出的“理想试卷模型”还可以嵌套升级成为“超级试卷模型”,即试卷中的每一道题可不是是/非题(原子题),而是具有中间过渡分数的复杂题(分子题),相当于每一道1分的题都是一个像图8一样的“理想试卷模型”,由100个原子题目组成,其得分可在0, 0.01, 0.02, ···, 0.99, 1分之间变化。这种“超级试卷模型”有什么用?用处太广泛着呢,它几乎无处不在!如我国教育部正在考虑从幼升小到高考都要全面改革,把综合素质教育和评价纳入其中。在高考录取中对学生综合素质评价的规定如下:1)学业水平。重点是学业水平考试成绩、选修课程内容和学习成绩、研究性学习与创新成果等,特别是具有优势的学科学习情况。2)艺术素养。重点是在音乐、美术、舞蹈、戏剧、戏曲、影视、书法等方面表现出来的兴趣特长,参加艺术活动的成果等。3)思想品德。重点是学生参与党团活动、有关社团活动、公益劳动、志愿服务等的次数、持续时间。4)身心健康。重点是《国家学生体质健康标准》测试主要结果,体育运动特长项目,参加体育运动的效果,应对困难和挫折的表现等。5)社会实践。重点是学生参加实践活动的次数、持续时间,形成的作品、调查报告等。这个评价模型就是“超级试卷模型”,它需要考察学生的5个关键信息,如果每个关键信息又分20方面,一共是100个方面(相当于100个1分题)。而这100个方面又是根据学生过去在学校学习各种课程的历次成绩、在社会实践和公益活动中的历次表现、在科研活动中的创新性表现、本人的团队精神、在经受挫折时表现出坚韧性、面试中获得的各种印象等组成(其中的每一个原子事件都相当于0.01分题)。所以这个“超级试卷模型”也是从原子信息开始评分的,不同的是评分者不是一个人,而是由不同时期的负责人或任课老师一级一级不断抽象上来的,大部分的中间分数已经反映在学生的档案材料之中,招生录取老师只是完成最后的分数汇总,一般不需要深入到原子信息层面去了解详细细节。
当然,要解决比原子信息处理层次更高的分子信息处理问题,就需要抽象层次更高的柔性逻辑和柔性神经元的参与,这是重新找回人工智能可解释性的理论关键。
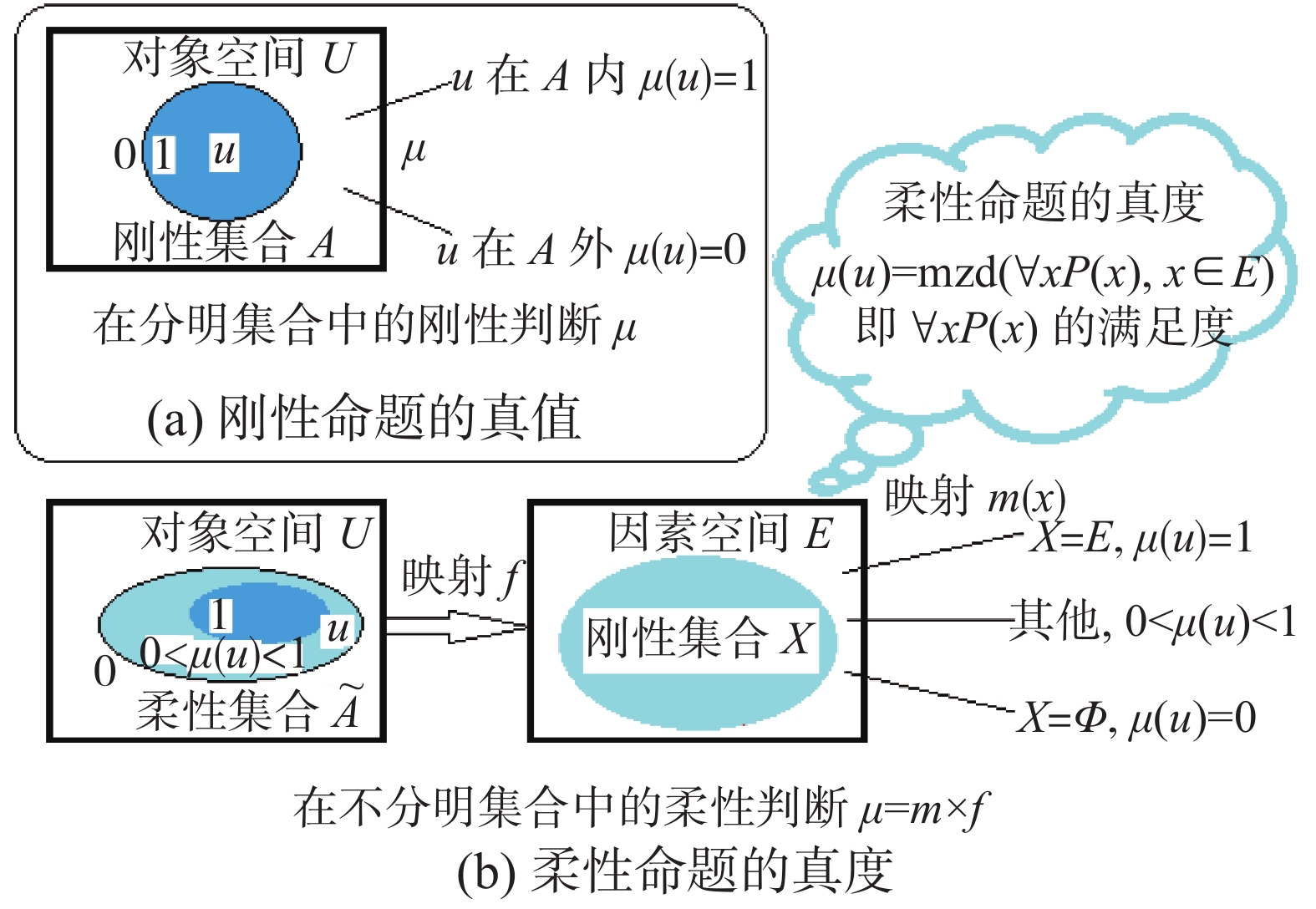
2 从刚性信息处理到柔性信息处理的扩张过程和已有结果 2.1 柔性命题真度的确定方法要妥善解决好不确定性的描述和信息处理过程,首先需要把建立在刚性集合(即分明集合、经典集合)基础上的刚性命题的真值x∈{0, 1},扩张到建立在柔性集合(即不分明集合、模糊集合)基础上的柔性命题的真度x∈[0, 1]。在逻辑上应该如何来实现这种扩张呢?本文使用的方法就是从“理想试卷模型”中抽象出来的(见图9)。
|
Download:
|
| 图 9 柔性命题真度的逻辑意义 Fig. 9 Logical meaning of the truth degree of the flexible proposition | |
在对象空间U内, Ã是边界不清晰的柔性集合(类似于一个班级的数学成绩单),任意元素(类似于一个学生)u∈Ã的隶属度(类似于这个学生的数学成绩,可在0%~100%之间变化)μ(u),需要在因素空间(类似于“理想试卷模型”)E中去找到与对象u对应的刚性集合(即学生u的数学答卷)X,求出X的概率测度m(X)来(类似于评出学生u答对试题所占的百分比)。用逻辑语言描述是:U中柔性命题的真度为
| $ \mu (u) = {\rm{mzd}}(\forall xP(x),\;x \in E) $ |
即E中谓词公式
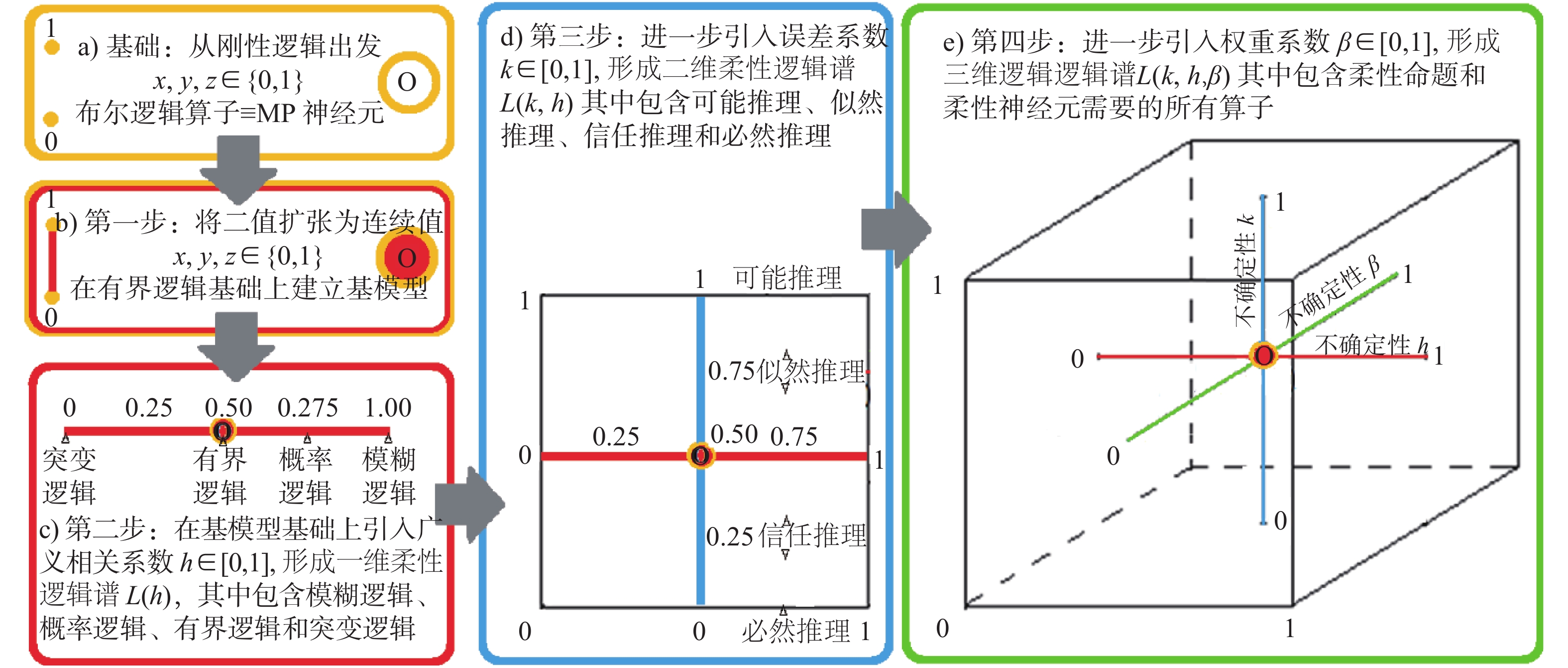
回过头来总结我们团队20余年来的探索经历,完成刚性逻辑到柔性逻辑扩张的总路线图(见图10),其起点是完全承认刚性信息处理理论在柔性信息处理理论中基础平台的核心地位,根本不需另起炉灶,推倒重来。
|
Download:
|
| 图 10 从刚性逻辑到柔性逻辑的扩张总路线图 Fig. 10 General line map from rigid logic to flexible logic | |
扩张的第一步是把刚性命题的真值x∈{0, 1}扩张为柔性命题的真度x∈[0, 1],而各种算子的计算公式z=Γ[ax+by−e]仍然保持不变。这样就把刚性信息处理的16种模式(见图3)直接扩张为柔性信息处理基模型中的16种信息处理模式(见图11)。在图11中另外增加了4种新的信息处理模式,它们都是由于中间过渡值的参与而形成的,其中包括平均运算z=Γ[0.5x+0.5y]和非平均运算z=1−Γ[0.5x+0.5y],组合运算z=Γ[x+y−e]和非组合运算z=1−Γ[x+y−e],这里的决策阈值可连续变化e∈[0, 1],不再是固定的整数。这20种基模型的信息处理模式在图11中有详细描述,以后还会重点讲解。

|
Download:
|
| 图 11 柔性信息处理中的20种基本模式 Fig. 11 The 20 basic modes in flexible information processing | |
后面的3步是在这20种基模型信息处理模式基础上,逐步引入误差系数k∈[0, 1], 广义相关系数h∈[0, 1]和权系数β∈[0, 1]的影响,利用三角范数理论和有关的公理,证明这些不确定性参数对基模型的调整程度和方式(见图12),它们是[5-7]:

|
Download:
|
| 图 12 3种不确定性参数及其调整函数 Fig. 12 Three kinds of uncertainty parameters and their adjustment functions | |
1)命题真度的误差系数k∈[0, 1],其中k=1表示最大正误差,k=0.5表示无误差,k=0表示最大负误差。k对基模型的影响完全反映在N性生成元完整簇Φ(x, k)=xn,n∈(0, ∞)上,其中n=−1/log2k。当n→0时,Φ(x, 0)=ite{0|x=0; 1}; 当n=1时,Φ(x, 0.5)=x; 当n→∞时,Φ(x, 1)=ite{1|x=1; 0}。Φ(x, k)对一元运算基模型N(x)的作用方式是N(x, k)=Φ−1(N(Φ(x, k)), k),对二元运算基模型L(x, y)的作用方式是L(x, y, k)=Φ−1(L(Φ(x, k), Φ(y, k)), k)。
2)广义相关系数h∈[0, 1],其中:h=1是最大的相吸关系或者最大的相容关系;h=0.75是独立相关关系;h=0.5是最大的相斥关系或者最小的相容关系,也就是最弱的敌我关系或者最小相克关系;h=0.25是敌我僵持关系;h=0是最强的敌我关系或者最大的相克关系。广义相关系数h对基模型的影响全部反映在T性生成元完整簇F(x, h)=xm, m∈(−∞, ∞)上,其中:m=(3−4h)/(4h(1−h))。当m→−∞时,F(x, 1)=ite{1|x=1; ±∞}; 当m→0−时,F(x, 0.75−)=1+lgx; 当m→0+时,F(x, 0.75+)=ite{0|x=0; 1}; 当m=1时,F(x, 0.5)=x; 当m→∞时,F(x, 0)=ite{1|x=1; 0}。
F(x, h)对6种二元运算基模型L(x, y)的影响是
| $ L(x,y,h) = F{^{ - 1}}(L(F(x,h),F(y,h)),h) $ |
3)权系数β∈[0, 1],其中:β=1表示最大偏x;β=0.5表示等权;β=0表示最小偏x。权系数β对基模型的影响完全反映在二元运算模型上,其对基模型L(x, y)的作用方式是:
| $ L(x,y,\beta )=L(2\beta x,2(1-\beta )y) $ |
k, h, β三者对二元运算模型L(x, y)共同的影响方式是:
| $ \begin{split} L(x,y,k,h,\beta ) = & \varPhi{^{ - 1}}(F{^{ - 1}}(L(2\beta F(\varPhi (x,k),h),2(1 - \beta )\cdot \\ & F(\varPhi (y,k),h),h),k) \end{split} $ |
如此就获得了20种柔性信息处理算子的完整簇,它包含了柔性信息处理所需要的全部算子,可根据应用需要(反映在模式参数<a, b, e>和模式内部的调整参数<k, h, β>上)有针对性地选用。
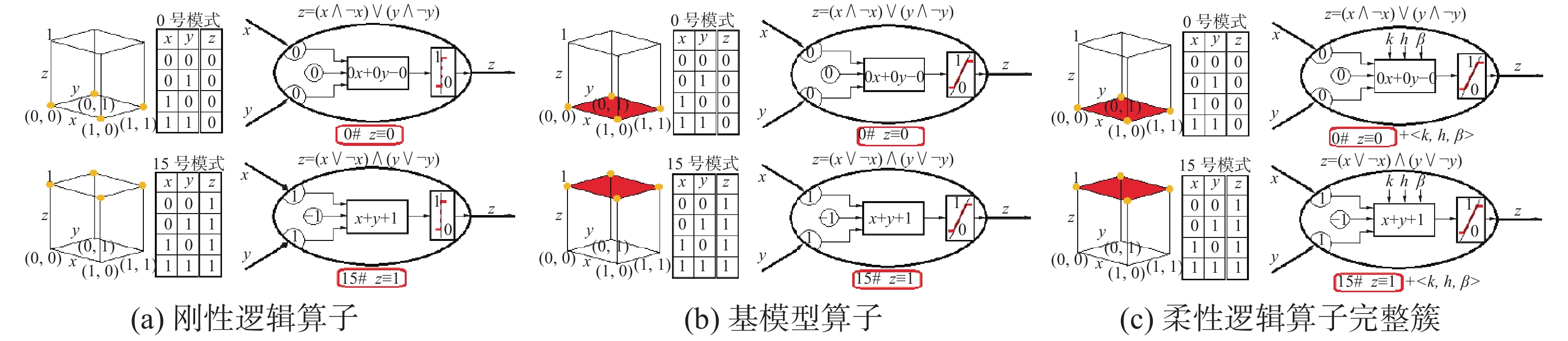
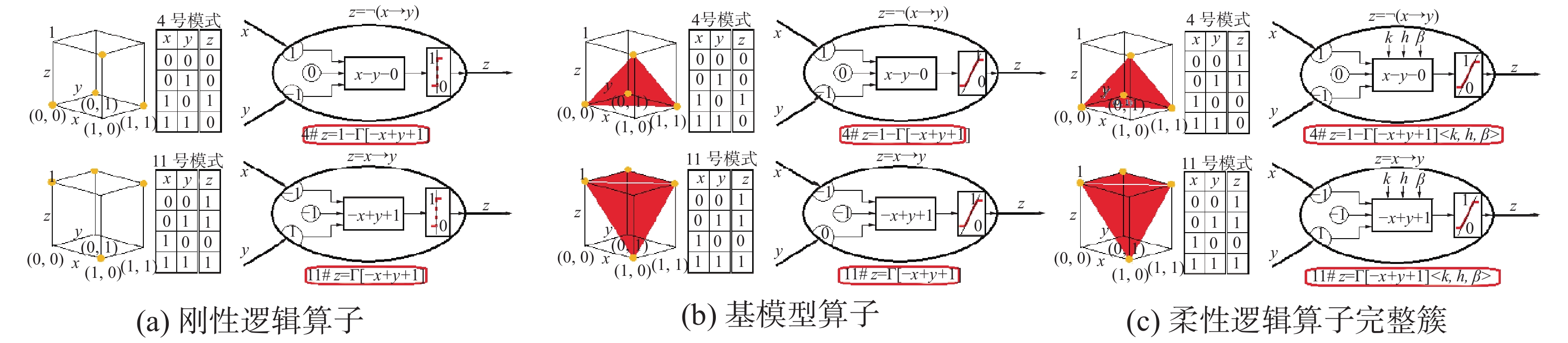
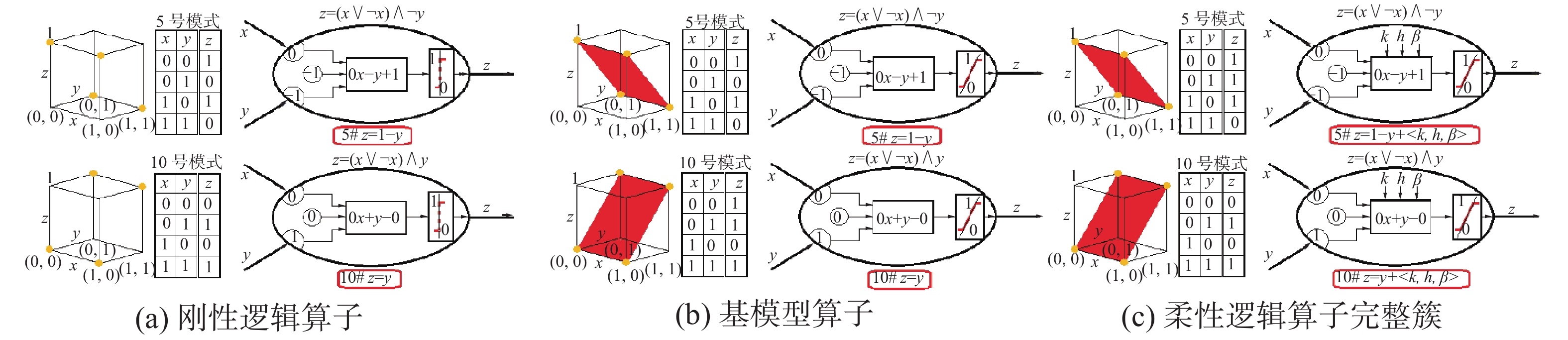
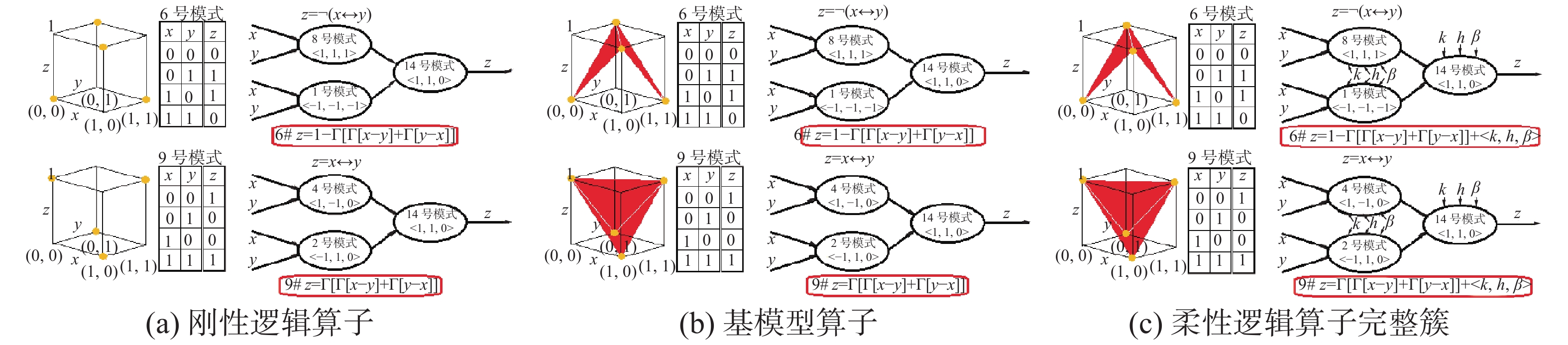
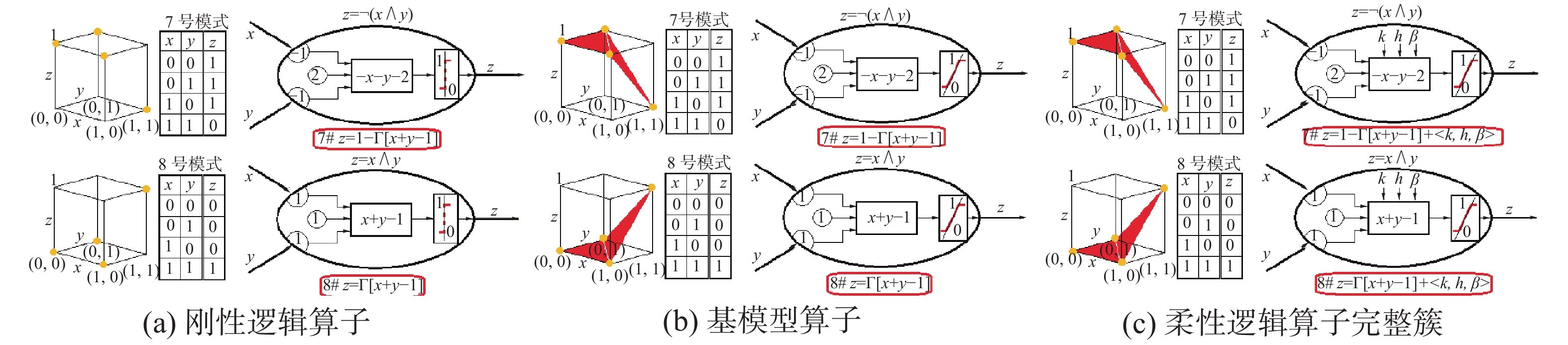
2.3 柔性信息处理扩张的过程和结果图13~22是这20种柔性信息处理模式的扩张过程和结果图,下面重点介绍几个模式。
|
Download:
|
| 图 13 恒0模式和恒1模式 Fig. 13 Constant 0 pattern and constant 1 pattern | |
|
Download:
|
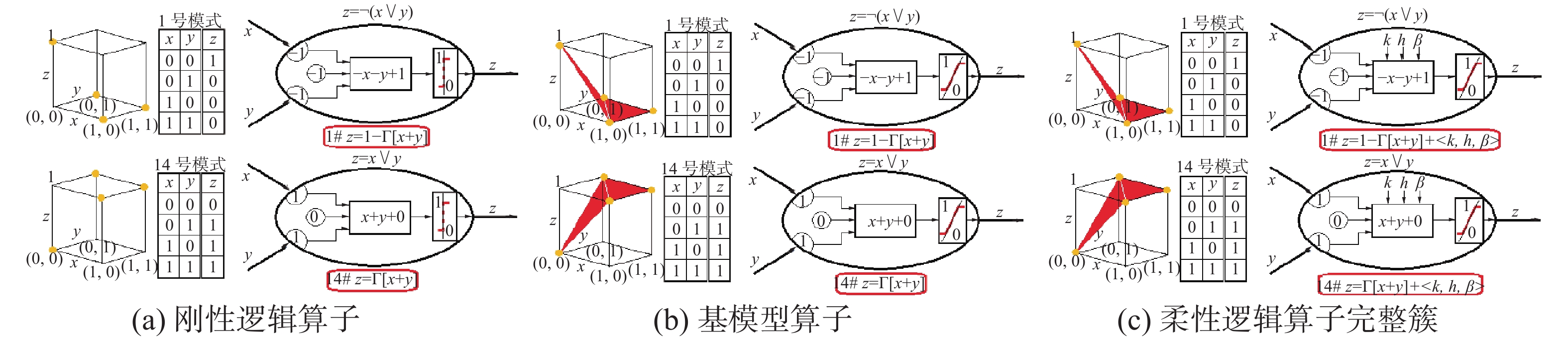
| 图 14 非或模式和或模式 Fig. 14 N-OR pattern and OR pattern | |
|
Download:
|
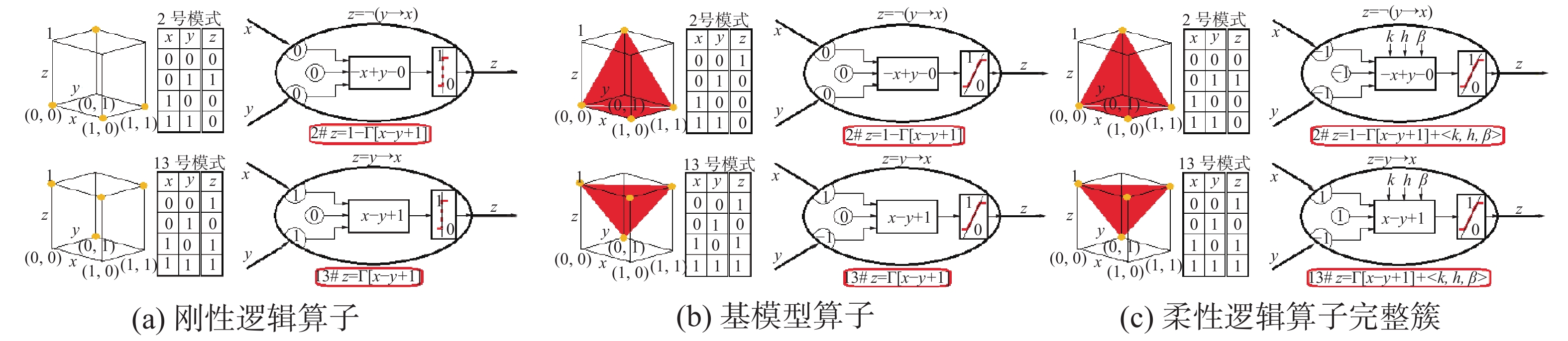
| 图 15 非蕴涵2模式和蕴涵2模式 Fig. 15 N-IMP-2 pattern and IMP-2 pattern | |
|
Download:
|
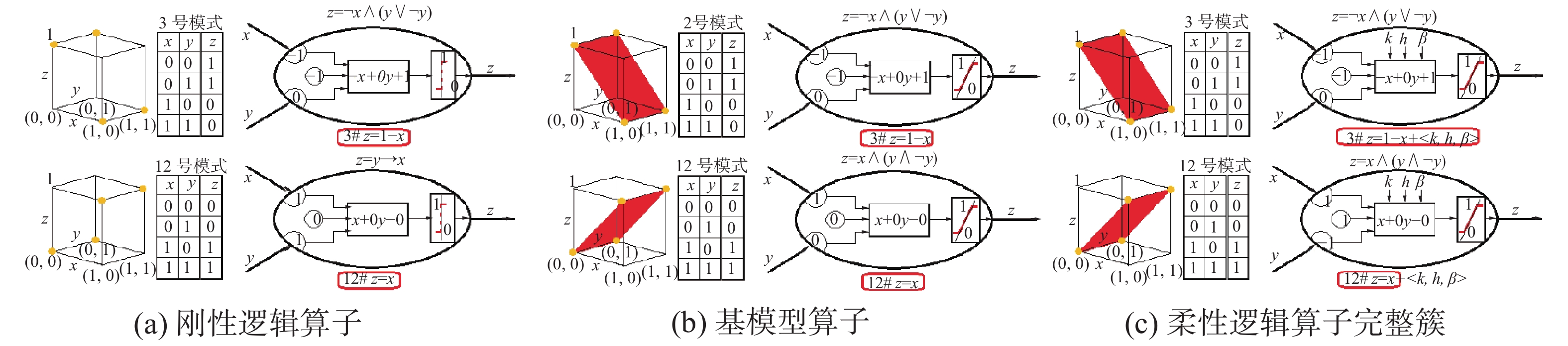
| 图 16 非x模式和指x模式 Fig. 16 NOT -x pattern and IND -x pattern | |
|
Download:
|
| 图 17 非蕴涵1模式和蕴涵1模式 Fig. 17 N-IMP-1 pattern and IMP-1 pattern | |
|
Download:
|
| 图 18 非y模式和指y模式 Fig. 18 NOT-y pattern and IND-y pattern | |
|
Download:
|
| 图 19 非等价模式和等价模式 Fig. 19 N-EQU pattern and EQU pattern | |
|
Download:
|
| 图 20 非与模式和与模式 Fig. 20 N-AND pattern and AND pattern | |

|
Download:
|
| 图 21 非平均模式和平均模式 Fig. 21 N-AVE pattern and AVE pattern | |
|
Download:
|
| 图 22 非组合模式和组合模式 Fig. 22 N-COM pattern and COM pattern | |
图13中的2种模式的共同特点是不管输入如何变化,输出是恒定不变的,也就是平常理解的“输出的结果与输入的变化没有关系”。
图14中的或运算是最常用的逻辑运算之一,可受k、h、β的联合影响,是一个运算模型完整簇:
| $ \begin{split} S(x,y,k,h,\beta ) = & \Bigl( {1 - \left( {\max \left( {0,2\beta {{\left( {1 - {x^n}} \right)}^m} + } \right.} \right.} \\ & {\left. {{{\left. {\left. {2(1 - \beta ){{\left( {1 - {y^n}} \right)}^m} - 1} \right)} \right)}^{1/m}}} \right)^{1/n}} \end{split} $ |
当β=0.5时权系数的影响消失,S(x, y, k, h)=(1−(max(0, (1−xn)m+(1−yn)m−1))1/m)1/n;
当k=0.5时误差系数的影响消失,S(x, y, h)=(1−(max(0, (1−x)m+(1−y)m−1))1/m。
S(x, y, h)有4个特殊算子: Zadeh或算子S(x, y, 1)=max(x, y) ;概率或算子S(x, y, 0.75)=x+y−xy;有界或算子S(x, y, 0.5)=min(1, x+y);突变或算子S(x, y, 0)=ite{max(x, y)|min(x, y)=0;1}。
图15中的非运算是常用的逻辑运算之一,它只受误差系数k的影响,是一个N范数完整簇:
| $ N(x, k)=\left(1-x^{n}\right)^{1 / n} $ |
其中:N(x, 1)=ite{0|x=1; 1}是最大非算子,N(x, 0.5)=1−x是中心非算子, N(x, 0)=ite{1|x=0; 0}是最小非算子。
图17中的蕴涵运算是常用逻辑运算之一,它可受k、h、β的联合影响,是一个运算模型完整簇:
| $ I(x,y,k,h,\beta ) = {(\min (1,\;1 - 2\beta {x^{nm}} + 2(1 - \beta ){y^{nm}}))^{1/mn}} $ |
当β=0.5时权系数的影响消失,I(x, y, k, h)=(min(1, 1−xnm+ynm))1/mn;
当k=0.5时误差系数的影响消失,I(x, y, h)=(min(1, 1−xm+ym))1/m。
I(x, y, h)有4个特殊算子: Zadeh蕴涵I(x, y, 1)=ite{1|x≤y; y};概率蕴涵I(x, y, 0.75)=min(1, y/x) ;有界蕴涵I(x, y, 0.5)=min(1, 1−x+y);突变蕴涵I(x, y, 0)=ite{y|x=1; 1}。
图19中的等价运算是常用的逻辑运算之一,它可受k、h、β的联合影响,是一个运算模型完整簇:
| $ \begin{split} Q(x, y, k, h, \beta )= & \text { ite }\left\{\left(1+\left|2 \beta x^{n m}-2(1-\beta) y^{n m}\right|\right)^{1 / m n} | m \leqslant 0\right.;\\ & \left(1-\left|2 \beta x^{n m}-2(1-\beta) y^{n m}\right|\right)^{1 / m n} \} \end{split} $ |
当β=0.5时权系数的影响消失,Q(x, y, k, h)=ite{(1+|xnm−ynm|)1/mn|m≤0; (1−|xnm−ynm|)1/mn};
当k=0.5时误差系数的影响消失,Q(x, y, h)=ite{(1+|xm−ym|)1/m|m≤0; (1−|xm−ym|)1/m}。
Q(x, y, h)有4个特殊算子: Zadeh等价Q(x, y, 1)=ite{1|x=y;min(x, y)};概率等价Q(x, y, 0.75)= min(x/y, y/x);有界等价Q(x, y, 0.5)=1−|x−y|;突变等价Q(x, y, 0)=ite{x|y=1;y|x=1;1}。
图20中的与运算是常用的逻辑运算之一,它可受k、h、β的联合影响,是一个运算模型完整簇:
| $ T\left( {x,y,k,h,\beta } \right) = {\left( {\max \left( {0,2\beta {x^{nm}} + 2(1 - \beta ){y^{nm}} - 1} \right)} \right)^{1/mn}} $ |
当β=0.5时权系数的影响消失,T(x, y, k, h)=(max(0, xnm+ynm−1))1/mn;
当k=0.5时误差系数的影响消失,T(x, y, h)= (max(0, xm+ym−1))1/m。
T(x, y, h)有4个特殊算子: Zadeh与算子T(x, y, 1) =min(x, y);概率与算子T(x, y, 0.75)=xy;有界与算子T(x, y, 0.5)=max(0, x+y−1);突变与算子T(x, y, 0)=ite{min(x, y)|max(x, y)=1; 0}。
图21中的平均运算是常用的逻辑运算之一,它可受k、h、β的联合影响,是一个运算模型完整簇:
| $ M(x,y,k,h,\beta ) = {(1 - {(\beta (1 - {x^n}){^m} + (1 - \beta)(1 - {y^n}){^m})^{1/m}})^{1/n}} $ |
当β=0.5时权系数的影响消失,M(x, y, k, h) =(1−((1−xn)m+(1−yn)m)1/m)1/n;
当k=0.5时误差系数的影响消失,M(x, y, ···, h)=1−((1−x)m+(1−y)m)1/m。
M(x, y, h)有4个特殊算子: Zadeh平均M(x, y, 1) =max(x, y);概率平均M(x, y, 0.75)= 1−((1−x)(1−y))1/2 ;有界平均M(x, y, 0.5)=(x+y)/2;突变平均M(x, y, 0)=min(x, y)。
常见的平均算子还有:几何平均1−M(1−x, 1−y, 0.75)=(xy)1/2;调和平均1−M(1−x, 1−y, 0.866)=2xy/(x+y)。可见柔性命题逻辑的平均运算完整簇能够包容各种平均算子。
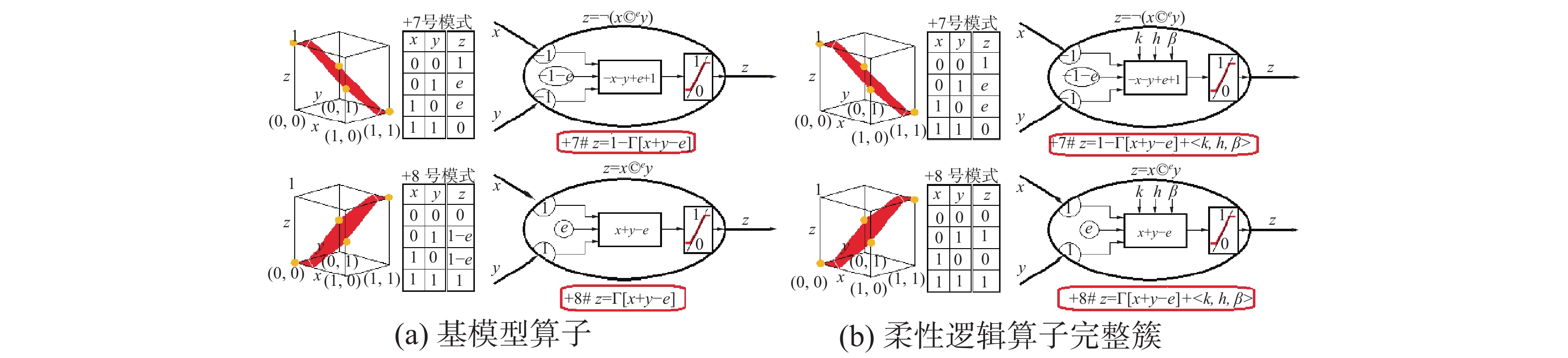
图22中的组合运算是常用的逻辑运算之一,它可受k、h、β的联合影响,是一个运算模型完整簇:
| $ \begin{aligned} & {C^e}(x,y,k,h,\beta ) = {\rm{ite}}\{ \min (e,\;(\max (0,\;2\beta {x^{nm}} + \\ & 2(1 - \beta ){y^{nm}} - {e^{nm}}){)^{1/mn}}|2\beta x + 2(1 - \beta )y2e;\\ & (1 - (\min (1 - {e^n},\;(\max (0,\;2\beta {(1 - {x^n})^m} + \\ & 2(1 - \beta ){(1 - {y^n})^m} - {(1 - {e^n})^m}){)^{1/m}}){)^{1/n}})|\\ & 2\beta x + 2(1 - \beta )y > 2e;e\} ; \end{aligned} $ |
当β=0.5时权系数的影响消失,Ce(x, y, k, h)= ite{min(e, (max(0, xnm+ynm−enm))1/mn|x+y<2e; (1−(min (1−en, (max(0, (1−xn)m+(1−yn)m−(1−en)m))1/m))1/n))|x+y>2e;e};
当k=0.5时误差系数的影响消失,Ce(x, y, h)=ite{min(e, (max(0, xm+ym−em))1/m|x+y<2e; (1−(min(1−e, (max(0, (1−x)m+(1−y)m−(1−e)m))1/m)|x+y>2e; e}。
Ce(x, y, h)有4个特殊算子: Zadeh组合Ce(x, y, 1)=ite{min(x, y)|x+y<2e; max(x, y)|x+y>2e;e};概率组合Ce(x, y, 0.75)=ite{xy/e|x+y<2e;(x+y−xy−e)/(1−e)|x+y>2e;e};有界组合Ce(x, y, 0.5)=Γ[x+y−e];突变组合Ce(x, y, 0)=ite{0|x, y<e; 1|x, y>e; e}。
图23是阈值参数e∈[0, 1]对有界组合Ce(x, y, 0.5)=Γ[x+y-e]的影响图。

|
Download:
|
| 图 23 在组合运算中决策阈值e的影响 Fig. 23 Influence of decision threshold e on the combinatorial operation | |
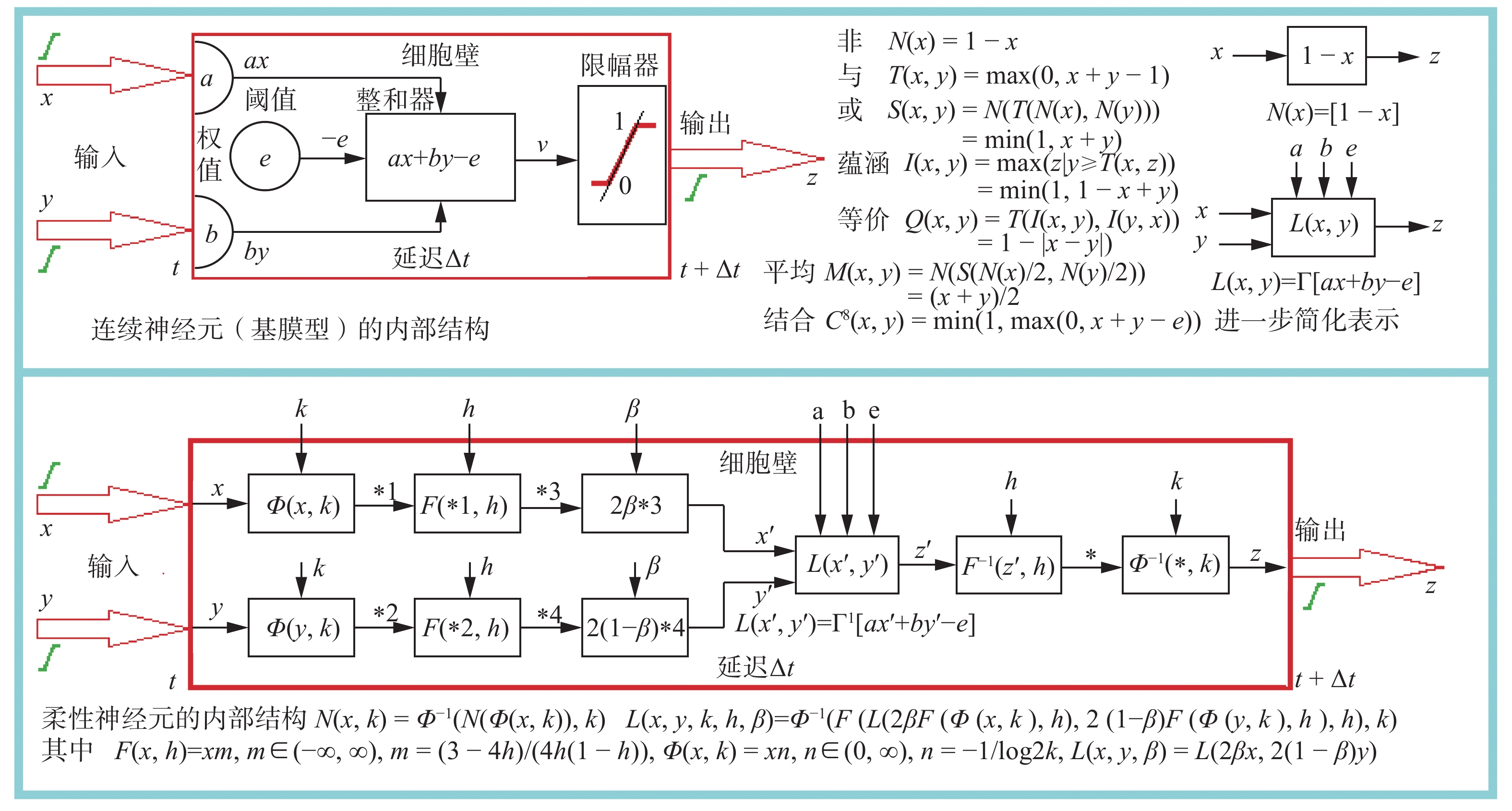
由于上述扩张过程都是在逻辑算子和神经元共同的0,1限幅函数z=Γ[ax+by-e]基础上完成的,所以它不仅是对刚性逻辑算子的柔性扩张,而且是对二值神经元的柔性扩张,两者完全一一对应,具有等价关系,详见图24。
|
Download:
|
| 图 24 柔性神经元的信息处理全过程 Fig. 24 Entire process of information processing of flexible neurons | |
下面通过两个典型的柔性命题逻辑谱来了解其包容性:在一维命题逻辑谱L(x, y, h)中(见图25),不仅包含了已知的非标准逻辑模糊逻辑、概率逻辑、有界逻辑、僵持逻辑和突变逻辑,而且还包含了分布在这些逻辑之间的无穷多个未知的非标准逻辑(在概率论中它们只能用条件概率描述,不能构成逻辑形态)。整个逻辑谱按照基本属性分成两大类:朋友之间的相生相关(1≥h≥0.5), 它满足相容律,即T(x, y, h)+S(x, y, h)=x+y;敌我之间的相克相关(0.5≥h≥0), 它满足相克律,即在x+y>1时,因为有相互杀伤,推迟出现下饱和效应,T(x, y, h)=0;在x+y<1时,因为扩军备战,提前出现上饱和效应S(x, y, h)=1。再细分有4小类:相吸关系(1≥h>0.75), 它满足T(x, y, h)>xy;相斥关系(0.75>h≥0.5), 它满足T(x, y, h)<xy;冷战关系(0.5>h>0.25), 它在少一半情况下满足相克律;热战关系(0.25>h≥0), 它在多一半情况下满足相克律。

|
Download:
|
| 图 25 一维命题逻辑谱L(x, y, h)的包容性 Fig. 25 Inclusiveness of the one-dimensional propositional logic spectrum L(x, y, h) | |
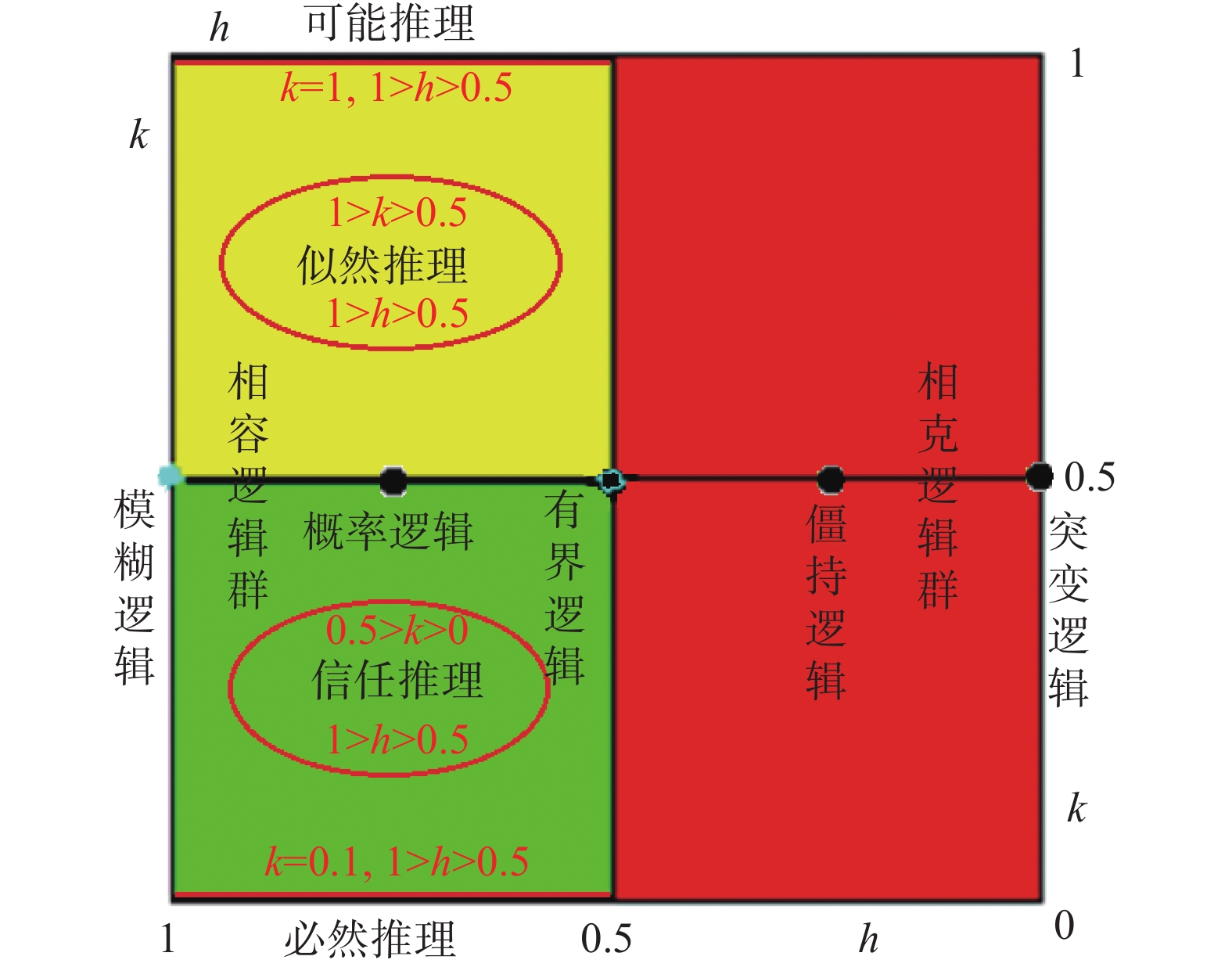
在二维命题逻辑谱L(x, y, k, h)中(见图26),不仅包含了一维命题逻辑谱L(x, y, h)中的全部逻辑算子簇L(x, y, 0.5, h),而且进一步包含了分布于k∈[0, 1]范围内其他的无穷多个已知和未知的各种非标准逻辑,如图26左边已知的可能推理逻辑、似然推理逻辑、信任推理逻辑和必然推理逻辑等[8],而图右边尚未开垦的处女地是相克逻辑群,它在研究对抗性行为中将大有可为。
|
Download:
|
| 图 26 二维命题逻辑谱L(x, y, k, h)的包容性 Fig. 26 Inclusiveness of the two-dimensional propositional logic spectrum L(x, y, k, h) | |
从上述扩张全过程不难证明柔性命题逻辑算子簇具有完备性,它包含了所有命题级的柔性信息处理算子,理由有3条(见图27)。

|
Download:
|
| 图 27 使用柔性逻辑算子如同查三角函数表一样方便 Fig. 27 Using flexible logic operators is as convenient as looking at trigonometric functions | |
1)二元布尔信息处理只有16种信息处理模式,二元柔性基模型信息处理只有20种信息处理模式,三元以上的信息处理可以用多个二元信息处理来表示,所以这20种模式是完备的,它们由信息处理模式的状态参数<a, b, e>唯一确定。
2)在基模型中已经包含了命题真度的不确定性x∈[0, 1],它可以从最大值1连续变化到最小值0,中间没有遗漏,具有完备性。
3)能够对各种基模型产生调控作用的不确定性参数只有3个,它们是k∈[0, 1],h∈[0, 1],β∈[0, 1],另外能对组合运算基模型产生调控作用的不确定性还有一个e∈[0, 1],它们形成的算子完整簇都能够从最大可能的算子连续变化到最小可能的算子,中间没有遗漏,具有完备性,它们可由模式内的不确定性调整参数<k, h, β>唯一确定,(另一个不确定性调整参数e是两边共用的参数)。
所以,这个完备的命题级柔性信息处理算子库可以事先由软件或者硬件实现后,封闭起来放在后台让应用程序直接调用计算结果,如同查三角函数表一样方便(见图27)。
请读者注意:为了帮助有兴趣深入理解命题泛逻辑各个算子完整簇的变化细节,包括20种柔性信息处理模式<a, b, e>(常用的7种柔性逻辑算子完整簇)、各种算子完整簇内部受不确定性调整参数<k, h, β>和e影响的具体变化情况,以及宏观把握数理辩证逻辑和数理形式逻辑的关系、逻辑和神经网络的关系等,我们将《泛逻辑仿真系统软件》放置在百度云盘中供大家下载使用,没有时限,提取密码为gs56,链接地址为https://pan.baidu.com/s/1YutRNQTtB1ULQteETqVYwA。
2.4.2 柔性命题逻辑算子的应用针对性在刚性逻辑中,只有16种信息处理模式,用不同的模式特征参数<a, b, e>区分,分别对应16种不同的逻辑算子,它们共同组成了二元刚性逻辑的算子组来完成逻辑推理的职能,在一个信息处理模式内是“一把钥匙开所有锁”的关系。在柔性逻辑中由于包含了5种命题级不确定性,情况完全变了,它不仅有20种信息处理模式,用不同的模式特征参数<a, b, e>区分,分别对应20种不同的逻辑算子完整簇,其中包含无穷多个算子,用不确定性调整参数<k, h, β>来区分(在组合运算中还有不确定性参数e∈[0, 1]是决策阈值,具有特征参数和调整参数的双重身份),它们共同组成了二元柔性逻辑的算子完整簇来完成柔性信息处理模式的职能,在一个信息处理模式内是“一把钥匙开一把锁”的关系。
图28是一个示意图,它用“钥匙”来比喻算子,用“锁孔型”来比喻算子要完成的信息变换模式。在刚性逻辑中只有16种不同的“锁孔型”<a, b, e>,对应有16种不同的“钥匙”<a, b, e>,没有进一步的齿形变化。所以,只要知道了“锁孔型”的<a, b, e>(信息处理模式),就可以根据<a, b, e>选择合适的“钥匙”去完成信息变换过程。这是古代老式锁的设计原理,一种“锁孔型”只用一种“钥匙”即可打开,“一把钥匙开万把锁”。在现代锁的设计原理中,不仅保留了“锁孔型”的变化<a, b, e>(信息处理模式),还进一步增加了“钥匙齿形”的变化<k, h, β>(各种不确定性调整参数),这就是柔性逻辑能够一个信息处理模式内部生成无穷多个算子,实现辨证论治、对症下药、“一把钥匙开一把锁”的机理所在。

|
Download:
|
| 图 28 在柔性逻辑中需要一把钥匙开一把锁 Fig. 28 A key needed to open a lock in the flexible logic | |
这就是说,我们不仅要像刚性逻辑那样严格根据信息处理模式<a, b, e>的不同选择不同的逻辑算子(已扩张成一个算子完整簇),更需要根据不确定性调整参数<k, h, β>的不同来精确地选择簇中合适的算子使用。如与刚性逻辑不同,幂等律只能在同一个柔性命题之间成立T(x, x, k, 1)=x,S(x, x, k, 1)=x,矛盾律只能在同一个柔性命题和它的非命题之间成立T(x, N(x, k), k, 0.5)=0,排中律只能在同一个柔性命题和它的非命题之间成立S(x, N(x, k), k, 0.5)=1,对合律只能在同一个柔性命题的两次相同误差否定的情况下成立N(N(x, k), k)=x,在一般情况下满足否定之否定律N(N(x, k1), k2)=1−N(x, k12),k12=k1(1−k2)/(k1+k2−2k1k2),分离律只在相同的k, h条件下成立T(x, I(x, y, k, h), k, h)=x等。如果不根据不确定性调整参数<k, h, β>和e来精确地选择合适的算子使用,就不能达到辨证论治对症下药的智能化需求。由此可见,不看<k, h, β>和e的变化盲目使用柔性逻辑算子是应用非标准逻辑时出现违反常识的异常结果的根源。
3 确保智能信息处理过程和结果的可解释性在人工智能研究中这个问题很重要,可从必要性和可能性两方面来论述。
3.1 智能信息处理必须正视各种不确定性和演化过程必要性可从客观规律和主观需要两方面来认识。在几千年漫长的机械工具时代和最近几百年的动力工具时代,人们面对的工具都是简单的机械系统,这类系统的共同特征是它的确定性:在工具的生命周期内,它面对的应用需求和工作职能都是确定不变的,其工作原理、内部结构和行为方式也是确定不变的。所以在设计、生产、使用和维护工具的过程中,可用决定论的科学观去完全把握它,用还原论的方法论去有效处理它,整个过程都可用“非真即假”的语言来严格地描述,用刚性逻辑予以求解,不会出现例外。这种形而上学的思维方式与数学思维高度一致,以至于这种决定论科学观和还原论方法论已完全与所谓“现代科学理念”和“标准逻辑思维”紧密融合在一起,渗透到科研活动的方方面面成为铁律。
现在,人类已进入信息时代,智能机器已成为推动时代发展的主要工具形式。由于“智能”是人类认识世界和改造世界的核心能力,它本质上不可能是终生确定不变的东西,随着人类对客观世界规律的认识越来越广泛和深入,人类的智能也会变得越来越强大,不会永远停留在原始状态而一成不变。所以,演化必然是智能工具的核心特征,如同宇宙的演化、生物的演化、人类社会的演化、语言的演化、市场的演化、气候的演化等一样的自然而然,这是智能工具不同于机械工具和动力工具的基本特征。按照现代复杂性系统的研究,各种复杂性系统之所以能够不断演化发展,是因为其中包含了众多的辩证矛盾,系统中每个基本事物的内部都是一个“亦真亦假”的矛盾对立统一体,无处不在的各种不确定性是这种矛盾对立统一关系的外在表现。成千上万种辩证矛盾集中在一个系统内相互作用、此消彼长,必然会涌现出某些原来没有的新事物(如恒星系的形成、生命的诞生、人类的诞生、市场的形成、互联网的形成等都是非线性系统涌现效应的结果,它们在原有系统中都是“非真非假”的新事物),通过优胜劣汰的环境选择就能保留或淘汰一些新、老事物,不断推动复杂性系统的演化发展。
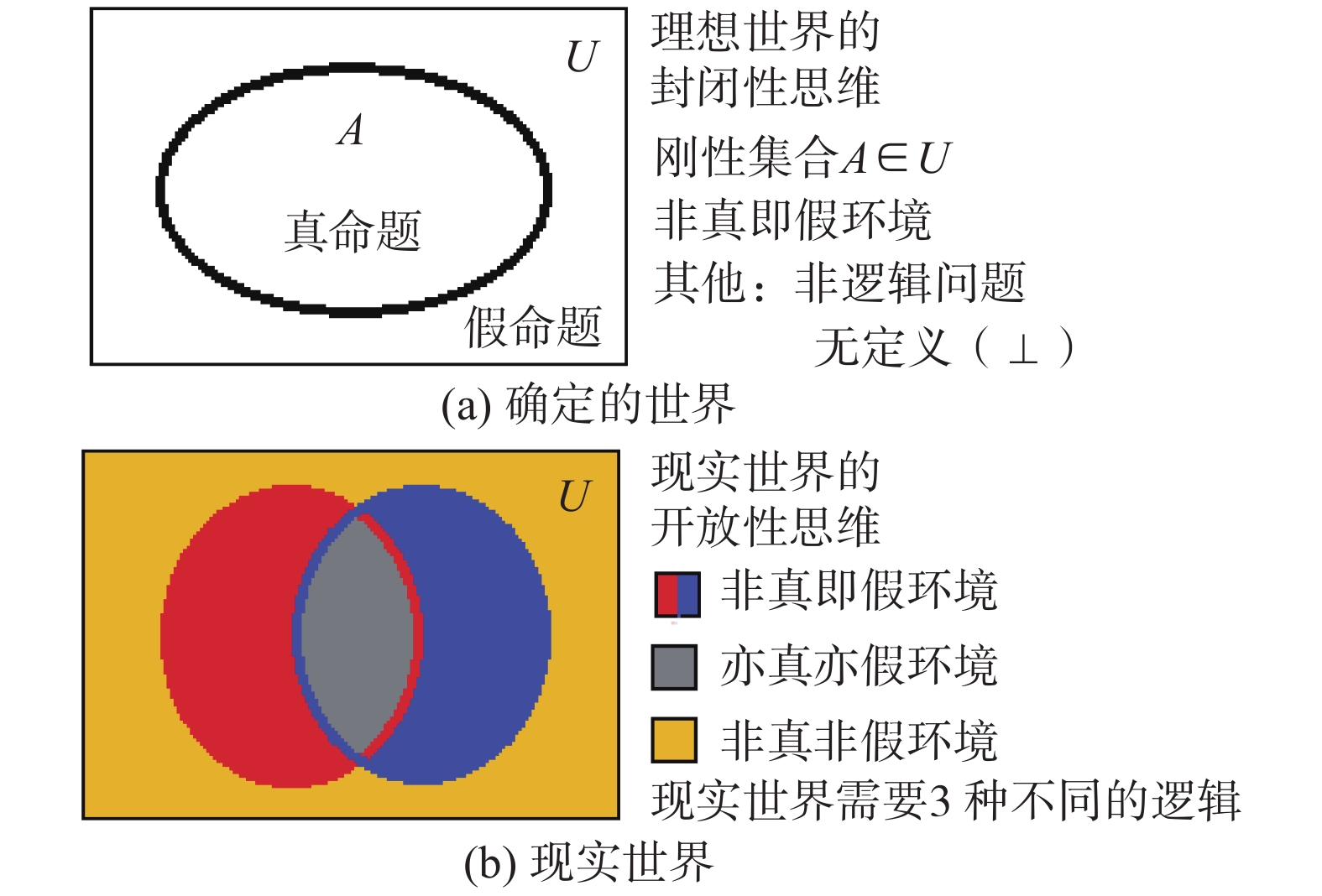
图29对比分析了两种不同科学观和方法论对逻辑推理范式的内在需求。
|
Download:
|
| 图 29 不同世界有不同的逻辑环境 Fig. 29 Different worlds have different logical environments | |
在确定性世界假设中,构造的是一个单一封闭的逻辑环境,其中只存在理想化的“非真即假性问题”,其他的问题都属于“非逻辑问题”或者“无定义(⊥)问题”被排斥在环境外。所以,在这个世界中只有真命题和假命题两种研究对象,可用论域U中的分明集合A来刻画,U中任意元素u∈A是真命题,当且仅当u是A的元素,否则u∈A是假命题,可见在确定性世界中有刚性推理范式即可解决全部问题。如数学之所以能用刚性推理范式求解问题,是因为它事先已将现实问题中所有不确定性全部忽略,抽象为规律确定不变、状态真假分明、已知条件齐全的理想化问题,可机械式求解。又如在科学问题中,可假设在太阳系的范围内,在上下一万年的时期中,系统的各个组成部分(太阳、地球等各大行星、月亮等各个卫星)的质量、体积、运动轨道、物体的客观运动规律等都是确定不变的,于是万年历、潮汐表、一年四季的交替循环、二十四节气等结果都可以计算出来,它们如同钟表运动一样准确无误,利用它们可以精准地追溯过去,预测未来。人们之所以相信决定论科学观和还原论方法论,其更深层的哲学信念是:人们相信世间万物都受确定不变的客观规律控制,时间是标量,不确定性是人对客观规律和问题的状态掌握不完全引起的近似性。所以人类认知的前进方向是不断消除这些认知不确定性,实现对客观规律和状态参数的全部掌握,最后实现绝对的确定性。这种信念的终极结果就是让人们坚信,依靠刚性逻辑推理范式一定可实现所谓“数学的终结”和“科学的终结”。
然而,耗散结构理论创立者伊利亚·普里戈金的《确定性的终结》(1996年问世,1998年出中文版)宣告了确定论哲学信念的终结[9],因为它不符合客观实际情况,犯了认知的方向性误判。如现代人都知道,上述的万年历、潮汐表、一年四季的交替循环,二十四节气等所谓精准结果,仅仅是在太阳系范围内、在上下一万年的时间内有效的近似结果,因为只有在如此短暂的时空范围内,各种变化才十分微小,可忽略不计。而在更大的时空范围内看,所有天体都处在持续不断地演化发展过程之中,太阳系从“无”到今天的“有”也只不过150亿年左右,在未来100多亿年之后,它一定会塌陷到黑洞之中而回归于“无”,如同“人生一世,草木一秋”一样有发生、发展和消亡的过程,来去匆匆,没有永恒。
其实,人类之所以有智能,也是因为他不是用固定的眼光一成不变地看待周围的一切,他可根据眼前问题的真实状况和变化趋势,在已有经验启发下选择辨证施治对症下药的方式解决问题。如失败可从头再来反复试探下去,并能通过历史的经验教训进行学习,不断完善自身发现问题和解决问题的能力(这就是演化)。人们之所以会相信演化论科学观和涌现论方法论,其更深层哲学信念是:相信世间万事万物都处在由辩证矛盾不断推动的演化发展过程中,时间是矢量,过去、现在和未来扮演着不同的角色,不确定性是客观世界的本质属性,确定性是人在局部时空环境内产生的近似性认知。人类认知的前进方向是不断消除这些近似性认知,精准把握各种不确定性(辩证矛盾)在生态平衡中的演化发展规律和各种影响,理想化只是权宜之计。
所以,人工智能面对的逻辑环境是一个现实开放的复杂逻辑环境,其中除了具有“非真即假性”的确定性问题,可用刚性逻辑描述外;更多的是具有“亦真亦假性”的不确定性问题,需要用柔性逻辑描述;特别是具有“非真非假性”的演化问题,需要用S−型超协调逻辑描述[10-12]。图30给出了智能信息处理需要的完整逻辑谱,其中:左极限是刚性逻辑(数理形式逻辑),它针对的是全部逻辑要素都受“非真即假性”约束的确定性问题;右极限是完整的数理辩证逻辑,它针对的是全部逻辑要素都具有不确定性的问题。在一般情况下,只有部分逻辑要素具有“亦真亦假性”或者“非真非假性”(涌现出新的对象),需要用柔性逻辑或者S−型超协调逻辑描述。

|
Download:
|
| 图 30 智能信息处理需要的完整逻辑谱 Fig. 30 Complete logic spectrum required for intelligent information processing | |
下面再从人类认识世界和改造世界的主观需求来论述主动引入不确定性的重要意义。众所周知,人类认识世界通常有两个不同的前进方向:一个方向是自顶向下地逐步深入,逐步具象化;另一个方向是自底向上地逐步扩大,逐步抽象化。这两种研究方向相互结合交替进行,当获得的各种有效知识足够丰富完整之后,自然就形成了一幅完整的多层次、多粒度的知识结构图(见图31):选择其中任意大中小3层来看,中粒度知识子空间中的一个结点,必然对应着一个小粒度知识子空间;若干中粒度知识结点组成的子空间,必然对应着大粒度知识子空间中的一个结点;如此层层累加,就组成了整个知识空间的n层树形子空间结构。由于每一个知识子空间的结点数目都比较合适,属于易操作的知识子空间,所以在利用知识空间来解决问题时,这种知识结构十分有利于快速有效地进行求解(如前面讨论的制定国际国内旅游路径规划问题)。

|
Download:
|
| 图 31 多层次多粒度的知识结构图 Fig. 31 Multilevel and multigranularity knowledge structure diagrams | |
一般来说,最底层知识子空间包含的是原子级的知识,它受“非真即假性”约束,只有真、假两种可能的状态,不可能再进一步向下分割成为更小粒度的知识了,其中的因果关系可以用刚性逻辑进行描述,求解起来比较简单快捷。但是这个最底层知识子空间能有效管辖的范围不应该太大,否则,它包含的原子级的知识太多,会出现因果关系复杂度的几何级数增长,影响问题求解的效率(如在理想试卷模型中,100个原子信息组成的系统就有2100≈1.267 65×1030种不同的状态组合,绝大多数情况下不需要知道这些细节)。在这个问题上“人更聪明”表现在他能够适时地利用聚类、归纳和抽象等手段,把数目恰当的若干原子信息变换成粒度更大的分子信息(知识),在这些分子级信息(知识)基础上建立新的相对抽象的因果关系。一般来讲,分子级信息(知识)已是具有“亦真亦假性”的不确定性知识,需要用柔性逻辑描述。所以,在许多基于二值信息处理的复杂问题中,为了减少问题的复杂度,提高处理效率,人们需要适时地主动引入不确定性,这是人类智能的一种重要属性。同样,当由分子级知识组成的知识空间管辖的范围太大,包含的分子级知识结点数目太多,影响到问题求解效率时,还可以进一步适时地利用聚类、归纳和抽象等手段,把数目恰当的若干粒度较小的分子级知识变换成粒度较大的分子级知识,在这些较大分子级知识基础上建立新的更加抽象的因果关系,仍然可用柔性逻辑描述。这种逐级抽象的过程可以不断进行下去,没有最高层限制。
3.2 如何精确确定各种柔性逻辑算子的有关参数下面具体讨论本文的核心论题:如何实现智能信息处理过程和结果的强可解释性?这个问题的本质就是我们在用神经网络进行数据挖掘和机器学习时,如何适时地把神经网络参数准确翻译成可靠的逻辑表达式,这里的所谓可靠逻辑就是指有可靠数学基础理论证明的刚性逻辑(数理形式逻辑)及其扩张——柔性逻辑(命题级数理辩证逻辑)。
先来讨论最简单的情况——二值信息处理。假设我们需要处理的数据都是“非真即假”的原子信息,且正好是二元信息处理的情况,其中x, y∈{0, 1}是输入信息,z∈{0, 1}是输出信息。根据图3它只有16种不同的信息处理模式,通过统计识别具体的函数关系z=fi(x, y), i∈{0, 1, 2, 3, ···, 15}可把它们准确无误地用模式状态参数<a, b, e>区分开来,利用z=Γ[ax+by−e]公式计算出输出和输入的关系,也就是说,可直接获得每种模式的神经元参数和逻辑表达式,实现强可解释性。由于图3已经十分详尽,这里不再重述。
如果出现多元信息处理的情况,可以参照z=
| $ f\left( {{x_1},{x_2},{x_3}} \right) = {f_j}\left( {{f_i}\left( {{x_1},{x_2}} \right),{x_3}} \right),i,j \in \{ 0,1,2,3, \cdots ,15\} \text{。} $ |
1)当i=j时
z=fi(fi(x1, x2), x3)=fi(x1, x2, x3), i∈{0, 1, 2, 3, ···, 15}
| $ \begin{aligned} {\textit{z}} = & f\left( {{x_1},{x_2},{x_3},{x_4}} \right) = {f_k}\left( {{f_i}\left( {{x_1},{x_2}} \right),{f_j}\left( {{x_3},{x_4}} \right)} \right), \\ & i,j,k \in \{ 0,1,2,3, \cdots ,15\} \end{aligned} $ |
2)当i=j=k时
z=fi(fi(x1, x2), fi(x3, x4))=fi(x1, x2, x3, x4), i∈{0, 1, 2, 3, ···, 15}
的方式进行处理(由于在柔性信息处理中也只有20种模式,所以也与只有16种模式的二值信息处理类同)。
在多数情况下,原始数据库K0中需要处理的数据量非常巨大,如果全部都停留在原子级粒度上进行处理,其复杂度会快速上升到需要消耗计算机的巨大时空资源的程度,得不偿失,更会对信息处理过程和结果的可解释性提出严重挑战。所以人工智能需要学习人类的聪明做法,适时通过聚类、归纳和抽象,把属于一类原子信息抽象成一个分子结点,把几个类之间的因果关系抽象为几个分子结点之间的柔性因果关系,重新建立粒度较大的抽象知识库K1,在K1中就可以应用柔性逻辑来描述和求解这类柔性的因果关系。
设在K0中我们已经通过某种数据处理手段获得了一个完整的类E, 它是决定K1中某个柔性命题x真度的因素空间,令柔性命题x在E中的投影是集合X,当X=E时真度x=1;X=Φ时真度x=0;否则真度x=mzd(
有了柔性命题x真度的因素空间定义,就可以根据X在E中的实际变化情况,计算出x真度的变化轨迹,一般用离散点刻画,如x=0, 0.1, 0.2, 0.3, ···, 0.9, 1的11点方案,或者x=0, 0.05, 0.1, 0.15, ···, 0.9, 0.95, 1的21点方案等。当有因果关系的各个柔性命题的真度都在K1中刻画好后,就可以像二值信息处理一样,首先按照端点值x, y, z∈{0, 1}之间的关系,确定柔性因果关系的信息处理模式是否属于16种共有的模式之一,如果它不在16种模式之中,再根据中间过渡值的变化情况来确定,是4种柔性信息处理专有的模式中哪一个,具体的确定方法是:当0=(0, 0), 1>(0, 1)>0, 1>(1, 0)>0, 1=(1, 1)时,是平均模式或组合模式中的一个;当1=(0, 0), 1>(0, 1)>0, 1>(1, 0)>0, 0=(1, 1)时,是非平均模式或非组合模式中的一个。进一步区分是平均模式还是组合模式的基本特征是:组合模式有一定程度的上下平台0=(0+Δ, 0+Δ), 1=(1−Δ, 1−Δ)出现,而平均模式根本没有上下平台0<(0+Δ, 0+Δ), 1>(1−Δ, 1−Δ)存在。完成上述柔性信息处理模式的识别非常重要,它可以把柔性信息处理的基本模式严格确定下来,准确获得它的模式状态参数<a, b, e>和基模型计算公式:
| $ z = \Gamma [{{a}}x + {{b}}y - {{e}}],\quad x,y,z \in [0,1] $ |
接下来就可以在模式之内根据在K1中的数据确定可能存在的不确定性调整参数<k, h, β>。
1)误差系数k的确定。在柔性非运算N(x, k)中,k是不动点N(k, k)=k,所以在K1中非模式的因果关系数据中,如果发现有输入和输出相等的情况x=z=k,这个k就是误差系数,k=0.5表示没有误差。如果没有发现完全相等的数据,可以寻找尽可能接近的数据对<x; z>,这时的k≈(x+z)/2。
2)广义相关系数h的确定。根据K1中柔性与运算T(x, y, h)的因果关系数据,确定广义相关系数h的方法主要有两种:与算子体积法和x=y主平面上的标准尺测量法。
①与算子体积法:
| $ \begin{array}{c} h = 3\int_0^1 {\int_0^1 T } (x,y,h){\rm{d}}x{\rm{d}}y \approx 3{\Sigma _i}{\Sigma _j}T\left( {{x_i},{y_j},h} \right)/mn,\\ i = 1,2,3, \cdots ,m,j = 1,2,3, \cdots ,n \end{array} $ |
一般m =n=11或者21。只要统计计算出与算子的体积来,乘上3倍,就是h。
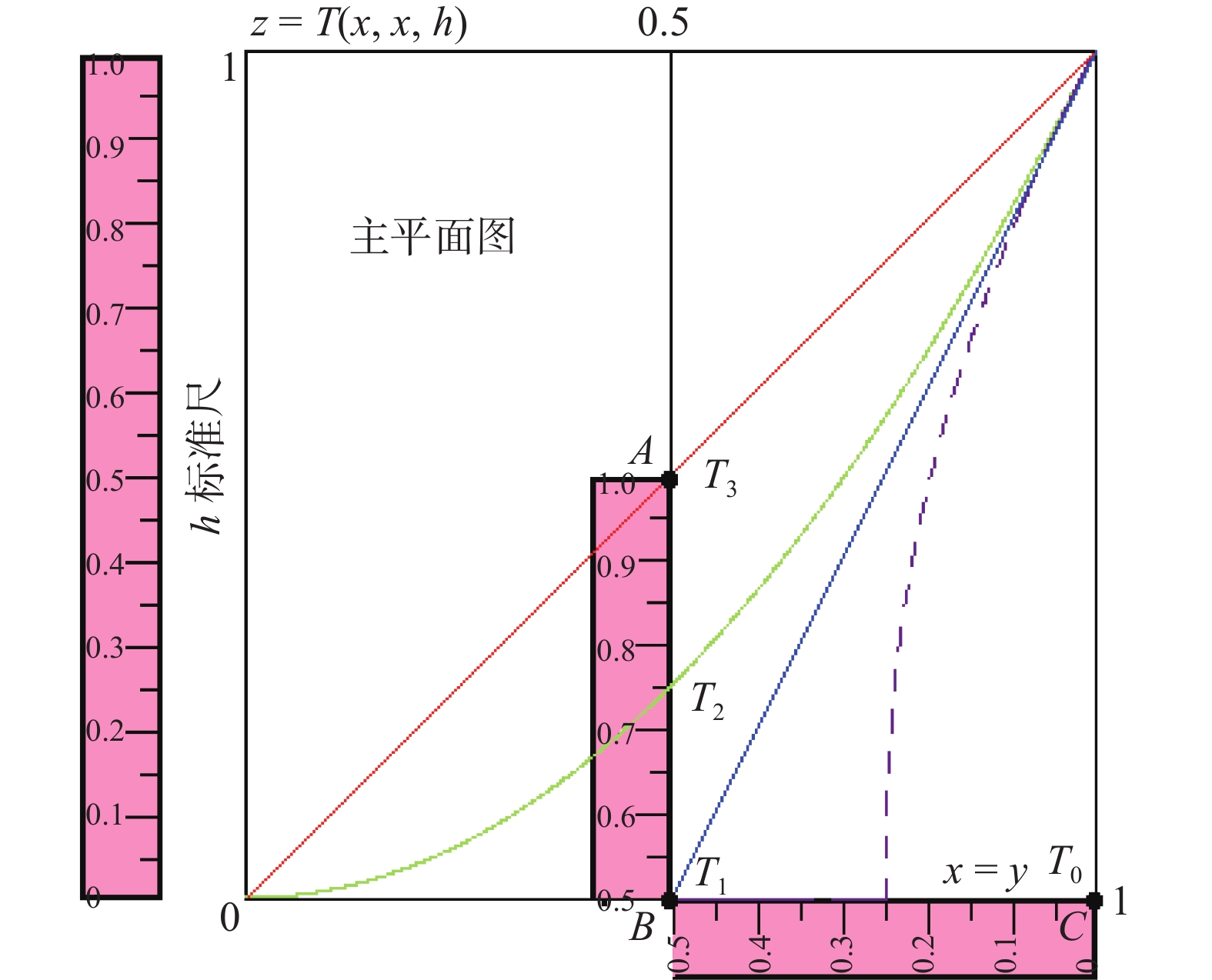
② x=y主平面上的标准尺测量法:
在x=y平面上绘制z=T(x, x, h)曲线,这个曲线与x=0.5的垂直线或者z=0的水平线的交点位置(相对于图32中垂直分布的h标准尺来说),就是这个与算子的广义相关系数h。
|
Download:
|
| 图 32 h的标准尺测量法 Fig. 32 The standard measurement of h | |
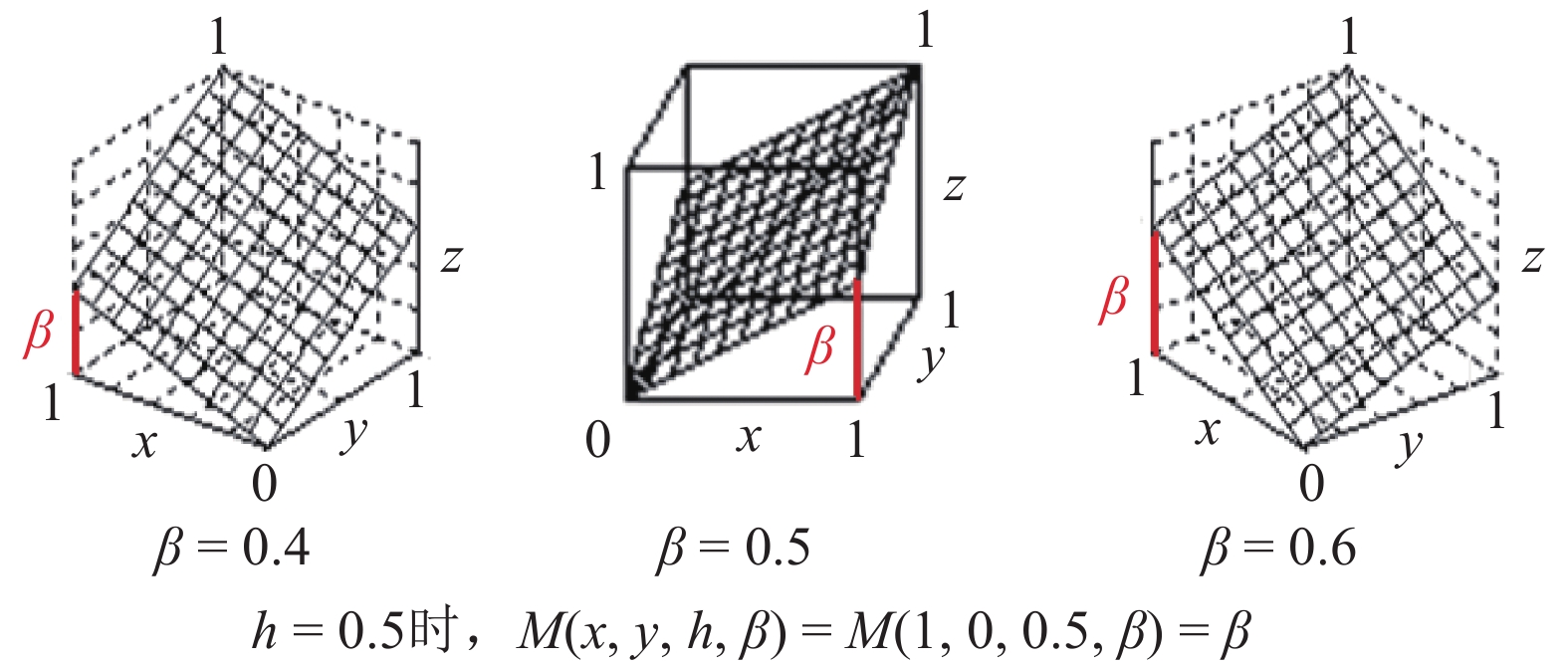
3)相对权重系数β的确定。根据K1中柔性平均运算M(x, y, h, β)的因果关系数据,确定相对权重系数β的方法在M(x, y, 0.5, β)时比较方便,因为这时的M(1, 0, 0.5, β)=β(见图33),而在K1中寻找这样的特殊数据是不困难的。
|
Download:
|
| 图 33 相对权重系数β的确定 Fig. 33 Determination of coefficient β of the relative weight | |
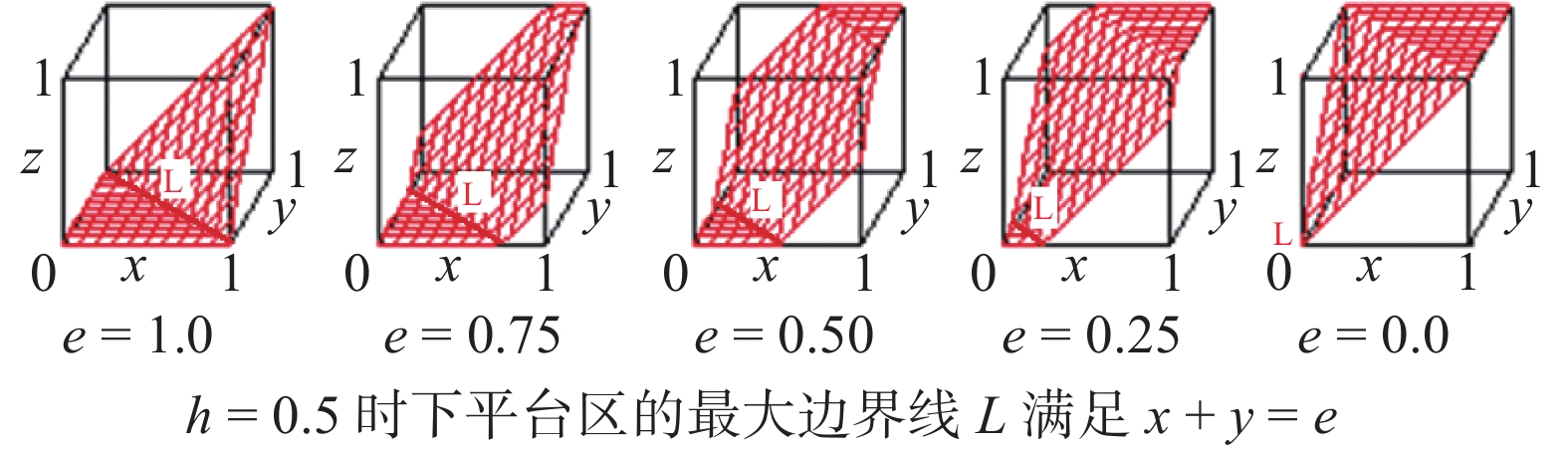
4)组合运算中决策阈值系数e的确定。根据K1中柔性组合运算Ce(x, y, h)的因果关系数据,确定决策阈值系数e的方法在Ce(x, y, 0.5)中比较方便,因为这时组合运算的下平台区最大边界线L正好是满足x+y=e的一条直线(见图34),这样的数据在K1中很容易找到。
|
Download:
|
| 图 34 组合运算中决策阈值系数e的确定 Fig. 34 Determination of decision threshold coefficient e in the combinatorial operation | |
最后应该指出,上述不确定性参数确定的方法都是在孤立的理想情况下给出的,它们之所以基本可用,是因为在通常情况下各个不确定性参数都偏离0.5不远,而且同时出现的概率不大。但是,严格地说不确定性参数接近上下极限的可能性还是存在,特别是广义相关系数h,它除了在基模型中h=0.5外,还经常出现在上极限h=1和中极限h=0.75处。而且其他的不确定性参数k、β、e等一旦同时出现,会对上述不确定性参数确定的结果带来误差。所以,在实际系统中,上述确定的不确定性参数只是一个近似值,需要利用某种误差消除算法来不断地逼近客观数据,获得精确结果。
当然,逻辑和知识信息处理只是智能机制中的一个环节,他只有与钟义信的机制主义人工智能通用理论[13]和汪培庄的因素空间理论[14]深度融合,才能共同建立人工智能的通用基础理论,这是未来人工智能发展的重中之重。
4 结束语数学面对的是“非真即假”的理想环境,可依靠数理形式逻辑(标准逻辑、刚性逻辑)来解决所有的问题。人工智能研究面对的现实环境要复杂得多,不仅有“非真即假”的理想问题,更多的是具有“亦真亦假性”的不确定性问题,在发生涌现效应的场合还会出现“非真非假”的域外项问题。依靠柔性逻辑(命题级数理辩证逻辑)可有效解决“亦真亦假”的不确定性问题,依靠S型超协调逻辑(另有专文介绍),可有效解决“非真非假”的演化问题。人工智能研究的强可解释性需要上述3种逻辑来保证。进一步的研究方向是建立广义概率论和全方位的数理辩证逻辑。
| [1] |
何华灿. 人工智能导论[M]. 西安: 西北工业大学出版社, 1988. 11-15
( 0) 0)
|
| [2] |
何华灿. 泛逻辑学理论: 机制主义人工智能理论的逻辑基础[J]. 智能系统学报, 2018, 13(1): 19-36. HE Huacan. Universal logic theory: logical foundation of mechanism-based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 19-36. (  0) 0)
|
| [3] |
何华灿, 何智涛. 从逻辑学的观点看人工智能学科的发展[M]//. 涂序彦. 人工智能: 回顾与展望. 北京: 科学出版社, 2006: 77-111.
( 0) 0)
|
| [4] |
谭铁牛. 人工智能: 天使还是魔鬼?[EB/OL]. (2018-06-13)[2019-04-10]. http://www.sohu.com/a/235446077_453160.
( 0) 0)
|
| [5] |
何华灿, 王华, 刘永怀, 等. 泛逻辑学原理[M]. 北京: 科学出版社, 2001.
( 0) 0)
|
| [6] |
HE Huacan, WANG Hua, LIU Yonghuai, et al. Principle of universal logics[M]. Beijing: Science Press, 2006.
( 0) 0)
|
| [7] |
HE Huacan. The outline on continuous-valued logic algebra[J]. International journal of advanced intelligence, 2012, 4(1): 1-30. ( 0) 0)
|
| [8] |
张文修. 不确定性推理原理[M]. 西安: 西安交通大学出版社, 1996.
( 0) 0)
|
| [9] |
伊利亚·普里高津. 确定性的终结: 时间、混沌与新自然法则[M]. 湛敏, 译. 上海: 上海科技教育出版社, 1998: 1–12
( 0) 0)
|
| [10] |
张金成. 逻辑及数学演算中的不动项与不可判定命题(I)[J]. 智能系统学报, 2014, 9(4): 499-510. ZHANG Jincheng. Fixed terms and undecidable propositions in logical and mathematical calculus (I)[J]. CAAI transactions on intelligent systems, 2014, 9(4): 499-510. (  0) 0)
|
| [11] |
何华灿. S型超协调逻辑中的一项重大研究突破: 评张金成《逻辑及数学演算中的不动项与不可判定命题》[J]. 智能系统学报, 2014, 9(4): 511-514. DOI:10.3969/j.issn.1673-4785.2014.04.022 ( 0) 0)
|
| [12] |
张金成. 悖论、逻辑与非Cantor集合论[M]. 哈尔滨工业大学出版社, 2018.
( 0) 0)
|
| [13] |
钟义信. 机制主义人工智能理论: 一种通用的人工智能理论[J]. 智能系统学报, 2018, 13(1): 2-18. ZHONG Yixin. Mechanism-based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 2-18. (  0) 0)
|
| [14] |
汪培庄. 因素空间理论: 机制主义人工智能理论的数学基础[J]. 智能系统学报, 2018, 13(1): 37-54. WANG Peizhuang. Factor space-mathematical basis of mechanism based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 37-54. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


