面对多媒体信息数据量的激增和模态复杂多样化的挑战，跨模态检索因其可以处理不同模态的数据成为国内外学者研究的重要课题。跨模态检索应用得比较成熟的领域主要为计算机视觉、模式识别、文本图像检索等^[1-4]，其研究的重点依然放在图像和文本两种模态之间。但是图像反映的颜色、纹理等信息和文本对物体的描述有时不能带给我们足够的信息量，比如在网购过程中，消费者仅通过浏览购买商品的文字和图片信息，有时不能在大脑完整地构建商品的特征信息，因而会购买到与需求不符的商品；在深海和太空探索领域，由于视频和图像受环境因素影响较大，仅凭摄像机反馈回来的视频和图像不足以让人们确定未知物体的材质信息；在日常生活中，当我们购买家具或西瓜时，仅通过视觉信息并不能准确判断家具所用木材质量的好坏或西瓜是否熟透，常常通过敲击其表面产生的声音来辅助判定。

引入声音模态在某些方面可以解决文本和图像信息量不足的问题。目前关于声音的检索技术大多涉及的是与语音和音乐相关的检索技术，其中声音特征采用梅尔频率倒谱系数(Mel-frequency cepstral coefficients，MFCC)。梅尔频率倒谱系数模仿人耳的感知特性^[5]，该方法具有很好的识别性和可靠性，是应用最广泛的声音特征之一。另一方面，图像特征采取卷积神经网络(convolutional neural network，CNN)提取。卷积神经网络的出现使得图像识别领域发展迅速，国外已有研究将卷积神经网络应用于跨模态检索的图像特征提取^[6]。

1 跨模态检索

不同于相同模态之间的检索，在跨模态检索中，检索结果和查询的模态是不同的。如何在不同模态之间建立相关性成为跨模态检索的关键。目前，应用在跨模态检索中的方法有典型相关分析法^[7-9]、偏最小二乘法^[10]、耦合字典学习法^[11]等。对比其他方法，典型相关分析(canonical correlation analysis，CCA )因其简单高效的特点在跨模态检索领域应用十分广泛，文献[7]提出多标签典型相关分析，可以处理多标签信息量大的数据集的情况。文献[8]提出多视图典型相关分析方法，利用不同视图的互补和相关信息可以处理多视图数据。文献[9]提出核典型相关分析，解决了非线性情况下不同模态间相关性的问题。

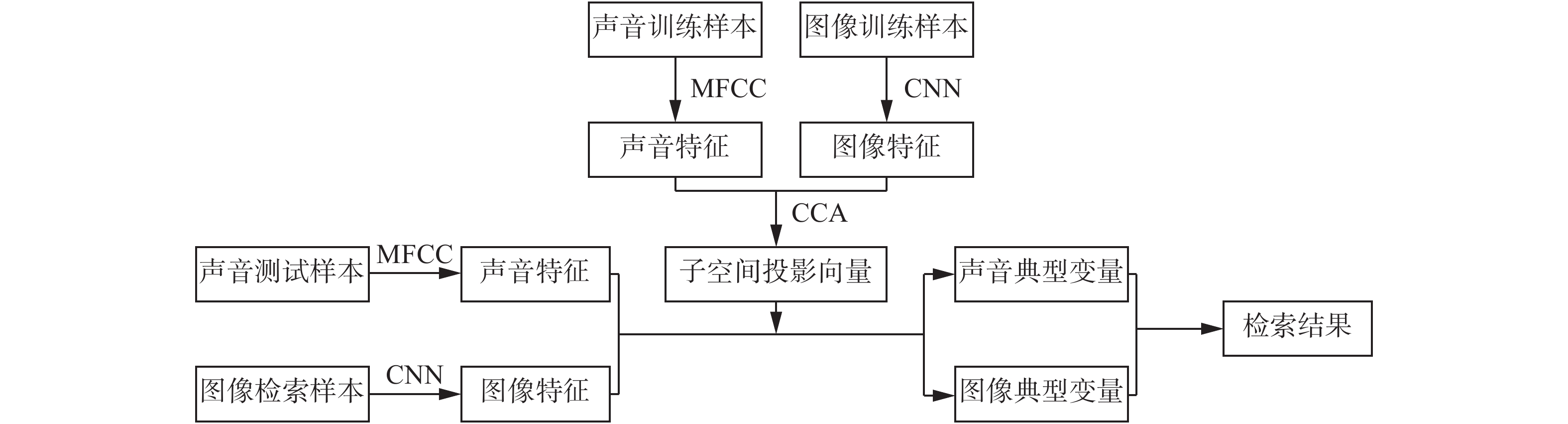
然而，传统的典型相关分析在应用时要求两组变量间符合一一配对关系。当两组变量间出现多个对应关系或配对形式为组配对时，上述方法将不再适用。针对上述情况，本文引入聚类典型相关分析方法。首先使用梅尔频率倒谱系数声音特征和卷积神经网络提取的图像特征，然后利用聚类典型相关分析将两种特征映射到子空间并用欧氏距离进行检索，最后在慕尼黑工业大学触觉纹理数据集上进行验证，实验结果表明所述方法适用于材质检索，具体流程如图1所示。

2 声音和图像特征提取

本文的声音特征使用梅尔频率倒谱系数特征，图像特征使用卷积神经网络提取得到。

2.1 梅尔频率倒谱系数

梅尔频率倒谱系数是语音处理中最常用的特征之一。文献[12]对敲击物体产生的声音提取梅尔频率倒谱系数特征，并应用于声音的分类。本文求得梅尔频率倒谱系数的一阶和二阶差分特征系数，结合标准梅尔频率倒谱系数^[13]，最终得到39维梅尔频率倒谱系数特征。图2(a) 、(b)所示为训练集中敲击竹木和红色羊毛毡的声音时域信号，图2(c)、(d)所示为经过上述过程得到的声音特征。

2.2 卷积神经网络

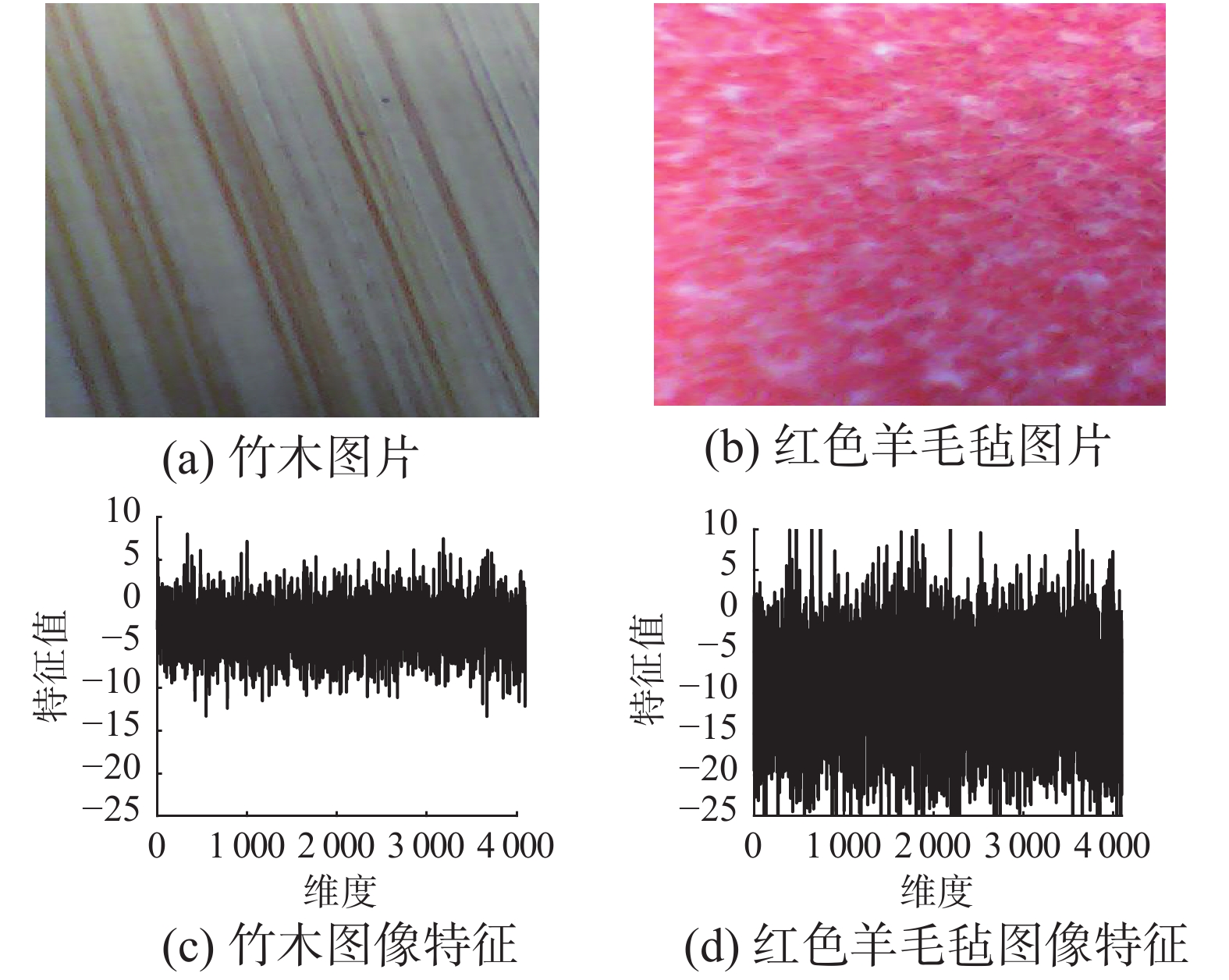
近年来，卷积神经网络已经被广泛地应用于图像的识别检测领域。本文选用的网络为预先训练好的AlexNet网络^[6]，包含5个卷积层和3个完全连接层。将图片分辨率调整为256×256输入到文献[6]所述模型之中，最终得到4 096维图像特征。图3(a)、(b)所示为训练集中敲击竹木和红色羊毛毡的图片，图3(c)、(d)所示为经过上述过程得到的图像特征。

3 典型相关分析

典型相关分析作为一种灵活有效、可扩展能力强的数据分析方法，在跨模态检索领域占据着重要地位。典型相关分析不仅可以最大化两组变量在投影空间的相关性，还能对复杂特征进行降维处理。本文使用这种方法对声音特征和图像特征进行相关性分析处理。

3.1 典型相关分析基本原理

使用典型相关分析对声音特征矩阵X=[x₁x₂ $ \cdots $ x_n] 和图像特征矩阵Y=[y₁ y₂ $ \cdots $ y_n] 进行处理。将X和Y表示为各自特征的线性组合， ${{U}} = {{{\omega}} _{{x}}}^{\rm{T}}{{X}}$ 和 ${{V}} = {{{\omega}} _{{y}}}^{\rm{T}}{{Y}}$ ，通过研究U和V的关系来代替X和Y的关系，U和V的相关系数 $\rho $ 表达式为

$ \rho = \frac{{{{{\omega}} _{{x}}}^{\rm{T}}{{{\varSigma }}_{{{XY}}}}{{{\omega}} _{{y}}}^{\rm{T}}}}{{\sqrt {({{{\omega}} _{{x}}}^{\rm{T}}{{{\varSigma }}_{{{XX}}}}{{{\omega}} _{{x}}})} \sqrt {({{{\omega}} _{{y}}}^{\rm{T}}{{{\varSigma }}_{{{YY}}}}{{{\omega}} _{{y}}})} }} $

(1)

式中： ${{{\omega}} _{{x}}}$ 和 ${{{\omega}} _{{y}}}$ 为两组变量对应的投影向量； ${{{\varSigma }}_{{{XX}}}}$ 和 ${{{\varSigma }}_{{{YY}}}}$ 分别表示特征集X和Y的协方差矩阵； ${{{\varSigma }}_{{{XY}}}}$ 表示X和Y的互协方差矩阵：

${{{\varSigma }}_{{{XY}}}}{\rm{ = }}\frac{{\rm{1}}}{n}\sum\limits_{p{\rm{ = 1}}}^n {{{{x}}_p}{{y}}_p^{\rm{T}}} $

${{{\varSigma }}_{{{XX}}}}{\rm{ = }}\frac{{\rm{1}}}{n}\sum\limits_{p = 1}^n {{{{x}}_p}{{x}}_p^{\rm{T}}} $

${{{\varSigma }}_{{{YY}}}}{\rm{ = }}\frac{{\rm{1}}}{n}\sum\limits_{p = 1}^n {{{{y}}_p}{{y}}_p^{\rm{T}}} $

通过构造拉格朗日等式，在约束条件 ${{{\omega}} _{{x}}}^{\rm{T}}{{{\varSigma }}_{{{XX}}}}{{{\omega}} _{{x}}}{\rm{ = 1}}$ 和 ${{{\omega}} _{{y}}}^{\rm{T}}{{{\varSigma }}_{{{YY}}}}{{{\omega}} _{{y}}}{\rm{ = 1}}$ 下，找到合适的投影向量 ${{{\omega}} _{{x}}}$ 和 ${{{\omega}} _{{y}}}$ ，使U和V的相关性达到最大化：

$ L = {{{\omega}} _{{x}}}^{\rm{T}}{{{\varSigma }}_{{{XY}}}}{{{\omega}} _{{y}}} - \frac{\lambda }{2}({{{\omega}} _{{x}}}^{\rm{T}}{{{\varSigma }}_{{{XX}}}}{{{\omega}} _{{x}}} - 1) - \frac{\theta }{2}({{{\omega}} _{{y}}}^{\rm{T}}{{{\varSigma }}_{{{YY}}}}{{{\omega}} _{{y}}} - 1) $

(2)

式中：L为构造的拉格朗日函数； ${\textit{λ}} $ 和 ${{\theta}} $ 为引入的系数变量。

将求解转化为常规的特征值问题， ${{{\omega}} _{{x}}}$ 和 ${{{\omega}} _{{y}}}$ 可以通过其对应最大特征值的特征向量找到：

$ {{\varSigma }}_{{{XX}}}^{ - 1}{{{\varSigma }}_{{{XY}}}}{{\varSigma }}_{{{YY}}}^{ - 1}{{{\varSigma }}_{{{YX}}}} = {\lambda ^2}{{\omega}} $

(3)

3.2 改进的典型相关分析

当样本变量不再是一一对应关系时，雅虎和微软研究院的Rasiwasia等^[14]改进典型相关分析，提出均值典型相关分析 (mean canonical correlation analysis，MCCA )和聚类典型相关分析 (cluster canonical correlation analysis，CCCA )，相应的子空间对应关系如图4所示，不同的形状代表不同的种类，相同形状代表同一种类中的不同物体。

对于本文使用的声音数据集X=[X₁ X₂ $ \cdots $ X_C]和图像数据集Y=[Y₁ Y₂ $ \cdots $ Y_C]，其中C表示数据集的总类别数， ${{{X}}_c}$ 和 ${{{Y}}_c}$ 是属于类别c对应的数据X、Y的子集。

${{{X}}_c} = [x_{\rm{1}}^{{c}}\;x_{\rm{2}}^{{c}}\cdots x_{\left| {{X_c}} \right|}^{{c}}]$

${{{Y}}_c} = [y_{\rm{1}}^{{c}}\;y_{\rm{2}}^{{c}} \cdots y_{\left| {{Y_c}} \right|}^{{c}}]$

式中： $\left| {{X_c}} \right|$ 和 $\left| {{Y_c}} \right|$ 分别为相应第c类数据个数。

3.2.1 均值典型相关分析

均值典型相关分析较为简单，首先求得每个子集的平均值，然后求得投影向量来建立子集均值之间的相关关系，最后寻找相关系数最大时的投影向量，即

$ \rho = \frac{{{{{\omega}} _{{x}}}^{\rm{T}}{{{M}}_{{{XY}}}}{{{\omega}} _{{y}}}^{\rm{T}}}}{{\sqrt {({{{\omega}} _{{x}}}^{\rm{T}}{{{M}}_{{{XX}}}}{{{\omega}} _{{x}}})} \sqrt {({{{\omega}} _{{y}}}^{\rm{T}}{{{M}}_{{{YY}}}}{{{\omega}} _{{y}}})} }} $

(4)

其中，M_XY、M_XX和M_YY定义分别为

$ {{{M}}_{{{XY}}}}{\rm{ = }}\frac{{\rm{1}}}{C}\sum\limits_{c = 1}^C {{{\mu}} _x^c(} {{\mu}} _y^c{)^{\rm{T}}} $

${{{M}}_{{{XX}}}}{\rm{ = }}\frac{{\rm{1}}}{C}\sum\limits_{c = 1}^C {{{\mu}} _x^c(} {{\mu}} _x^c{)^{\rm{T}}}$

${{{M}}_{{{YY}}}}{\rm{ = }}\frac{{\rm{1}}}{C}\sum\limits_{c = 1}^C {{{\mu}} _y^c(} {{\mu}} _y^c{)^{\rm{T}}}$

式中： ${{\mu}} _x^c$ 、 ${{\mu}} _y^c$ 为相应的第c类子集的平均值， $ {{\mu}} _x^c{\rm{ = }}$ $\displaystyle\frac{{\rm{1}}}{{\left| {{{{X}}_c}} \right|}}\sum\limits_{i = 1}^{\left| {{X_c}} \right|} {{{x}}_i^{{c}}} $ ， $\displaystyle{{\mu}} _{{y}}^c{\rm{ = }}\frac{{\rm{1}}}{{\left| {{{{Y}}_c}} \right|}}\sum\limits_{j = 1}^{\left| {{Y_c}} \right|} {{{y}}_j^{{c}}} $ 。

3.2.2 聚类典型相关分析

聚类典型相关分析不再建立子集间均值的关系，而是建立子集中每一个数据点和对应子集所有数据点的关系，此时相关系数表达式为

$ \rho = \frac{{{{{\omega}} _{{x}}}^{\rm{T}}{{{R}}_{{{XY}}}}{{{\omega}} _{{y}}}^{\rm{T}}}}{{\sqrt {({{{\omega}} _{{x}}}^{\rm{T}}{{{R}}_{{{XX}}}}{{{\omega}} _{{x}}})} \sqrt {({{{\omega}} _{{y}}}^{\rm{T}}{{{R}}_{{{YY}}}}{{{\omega}} _{{y}}})} }} $

(5)

其中，R_XY、R_XX和R_YY定义如下：

${{{R}}_{{{XY}}}}{\rm{ = }}\frac{{\rm{1}}}{T}\sum\limits_{c = 1}^C {\sum\limits_{i = 1}^{\left| {{{{X}}_c}} \right|} {\sum\limits_{j = 1}^{\left| {{{{Y}}_c}} \right|} {{{x}}_i^c{{({{y}}_j^{\rm{c}})}^{\rm{T}}}} } } $

${{{R}}_{{{XX}}}}{\rm{ = }}\frac{{\rm{1}}}{T}\sum\limits_{c = 1}^C {\sum\limits_{i = 1}^{\left| {{{{X}}_c}} \right|} {\left| {{{{Y}}_c}} \right|{{x}}_i^c{{({{x}}_i^{{c}})}^{\rm{T}}}} } $

${{{R}}_{{{YY}}}}{\rm{ = }}\frac{{\rm{1}}}{T}\sum\limits_{c = 1}^C {\sum\limits_{j = 1}^{\left| {{{{Y}}_c}} \right|} {\left| {{{{X}}_c}} \right|{{y}}_j^c{{({{y}}_j^{{c}})}^{\rm{T}}}} } $

式中：T为建立对应关系的总对数， $T{\rm{ = }}$ $\displaystyle\sum\limits_{c = 1}^C {\left| {{{{X}}_c}} \right|\left| {{{{Y}}_c}} \right|} $ 。

4 实验结果及分析

本实验所用的数据集为慕尼黑工业大学建立的触觉纹理数据集^[15]。数据集中包含108种不同的物体，按照材质和表面特征分为固体网状物、石头、玻璃陶瓷、木材、橡胶、纤维、泡沫、塑料纸片、纺织面料等九大类，具体每类物体的图像如图5所示，图5中数字表示该类材质第一个物体的起始位置。训练集包括声音集和图片集，声音集中每个声音样本由一个人敲击待测物体表面1次所得，其长度为0.2 s。将108种待测物体每种重复敲击10次，共得到1 080个声音样本。图片集每张图片分辨率为320×480，在不打开闪光灯情况下，同样由一个人重复拍摄待测物体10次所得，共得到1 080张图片样本。测试集数据数量和样本大小与训练集相同，不同之处在于采集数据的过程有所差别，测试集中声音和图片样本不是由同一个人重复10次完成，而是由10个不同的人每人采集1次所得。整个数据集的特点是采集数据的过程均为人工完成，没有施加约束条件，例如敲击物体表面时，没有限制施加力的大小。

根据第2章得到的39维声音特征和4 096维图像特征，应用于第3节所述典型相关分析方法，找到训练集中声音特征和图像特征典型相关分析子空间，然后将测试集中的声音特征和图像特征映射到典型相关分析的子空间，即可使用子空间的声音特征去检索图像特征，通过计算欧氏距离度量样本特征的相似性。

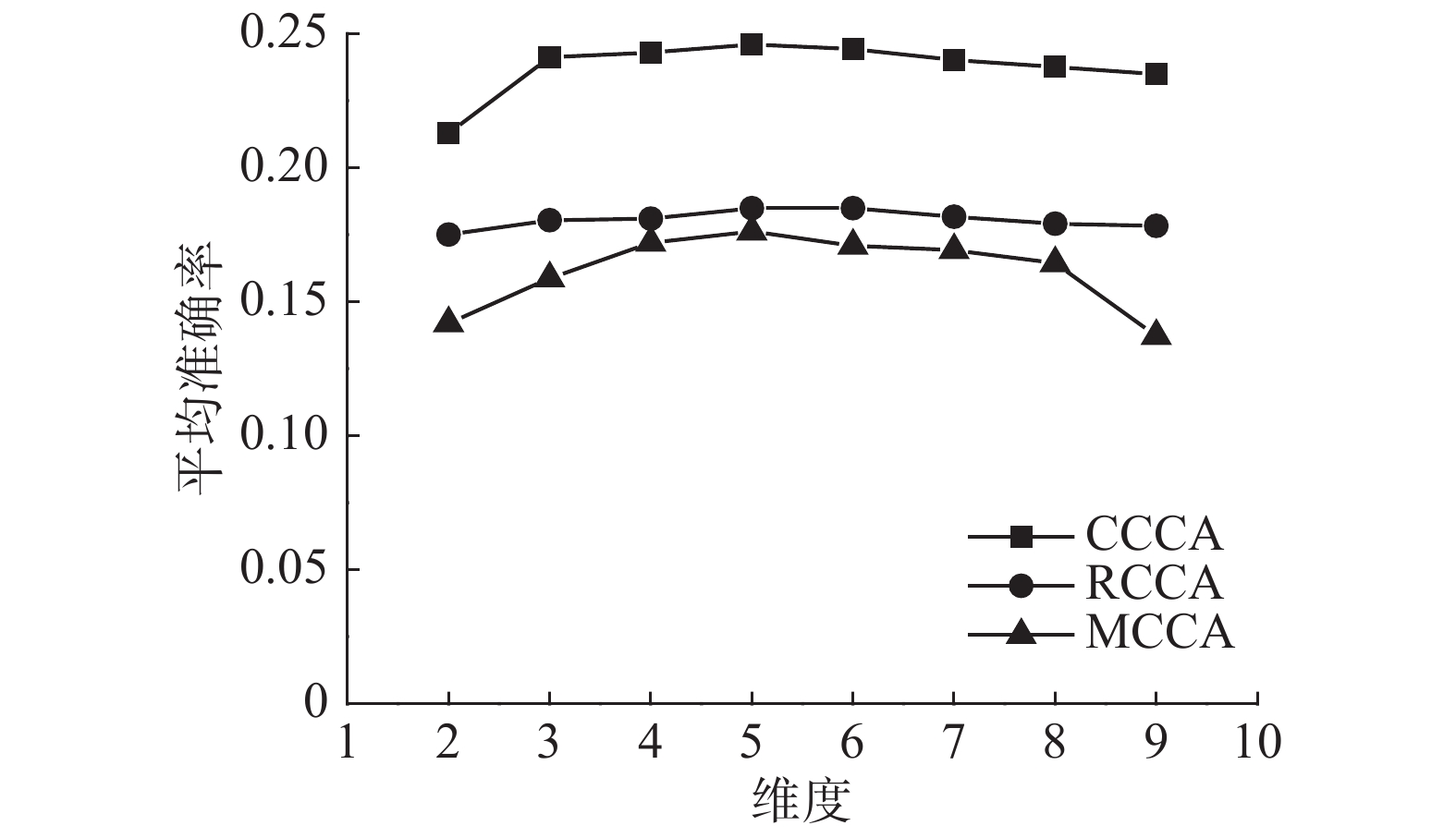
实验最终在测试集上执行从声音到图像的跨模态信息检索。常用的信息检索的评价指标有查准率P、查全率R和平均准确率 (mean average precision，MAP)等。PR曲线比较直观地显示出检索效果的好坏，MAP则考虑到检索结果的排名情况。PR曲线与坐标轴围成的面积越大，MAP值越高，则检索效果越好。本文使用MAP和PR曲线对RCCA (同种物体声音图像随机匹配)、MCCA和CCCA 3种方法的实验结果进行评价。图6所示为3种不同方法的MAP值的大小随子空间维度的变化，从图6可以得到，子空间维度为5时，3种方法效果最好，且CCCA的MAP值明显优于其他2种方法。

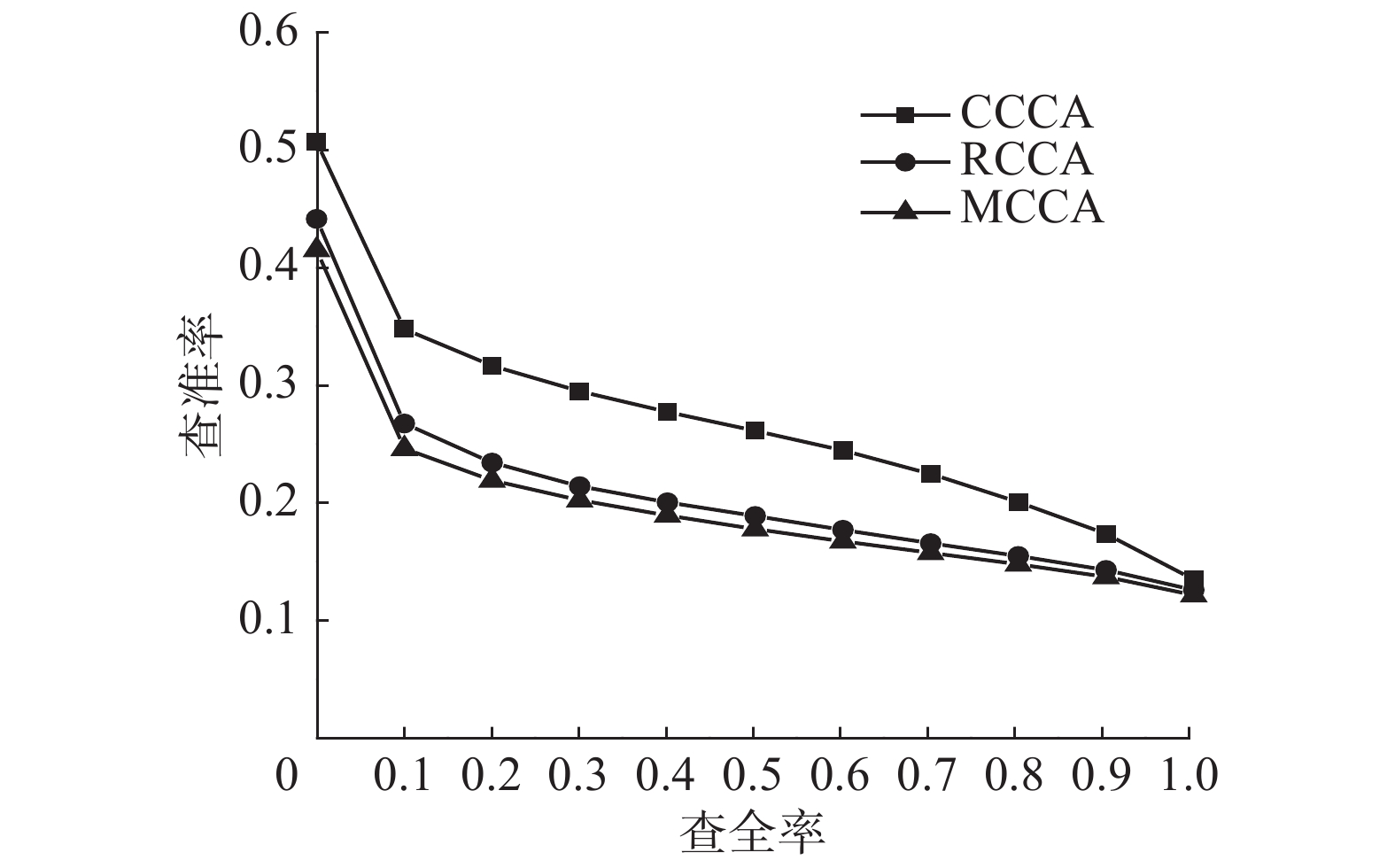
图7所示为子空间维度为5时，3种方法的PR曲线，从中可以看出，CCCA的PR曲线与坐标轴围成的面积最大，检索效果最好。由于所使用的数据集中的数据不符合传统意义上的一一配对关系，RCCA 和MCCA的检索效果不如CCCA。

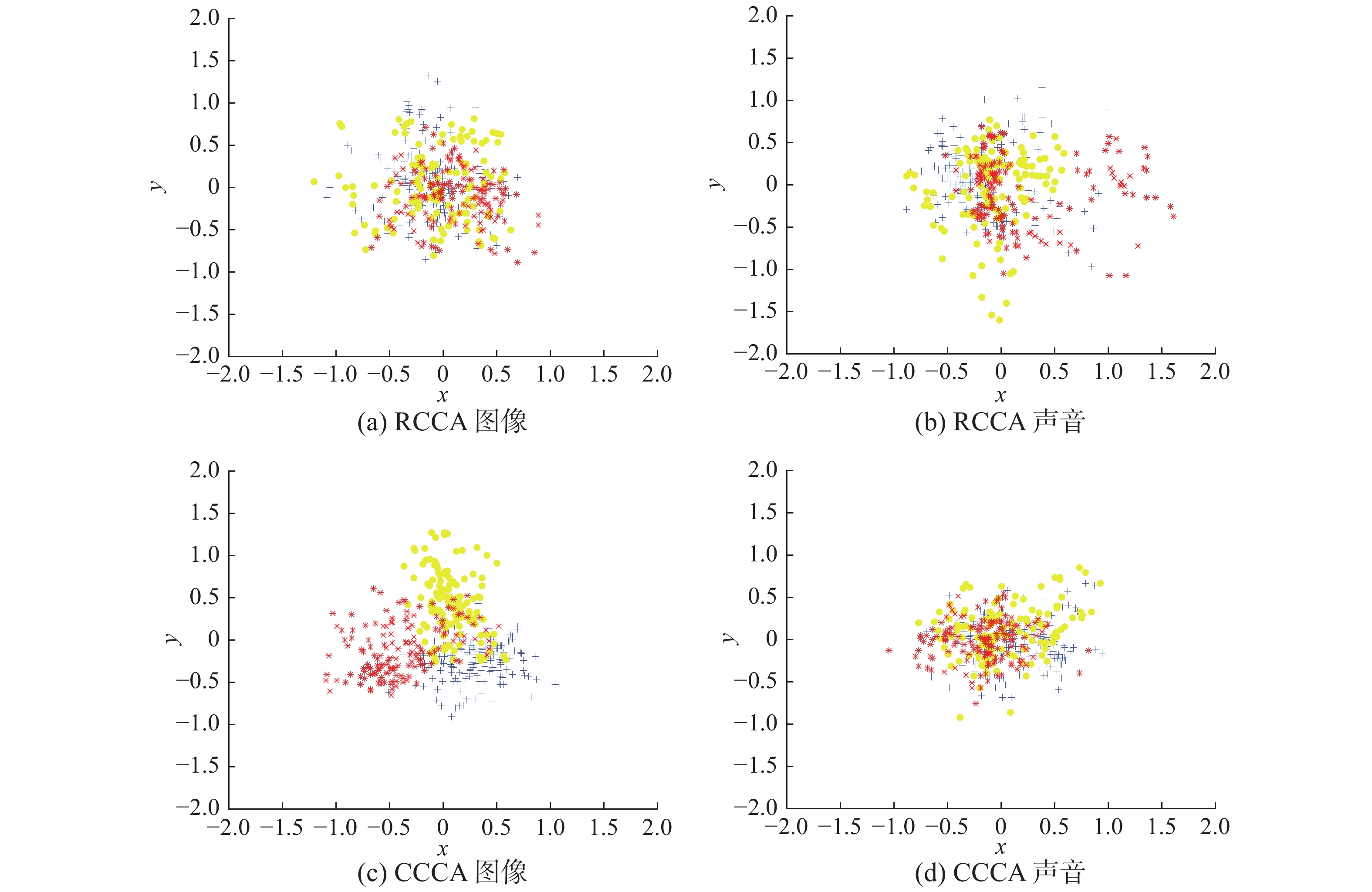
图8所示为数据集中纤维、泡沫和塑料3种材料图像和声音数据的低维映射，其中蓝色代表纤维，黄色代表泡沫，红色代表塑料。从图8中可以看出，CCCA对这3类材料的区分度要强于RCCA的效果。

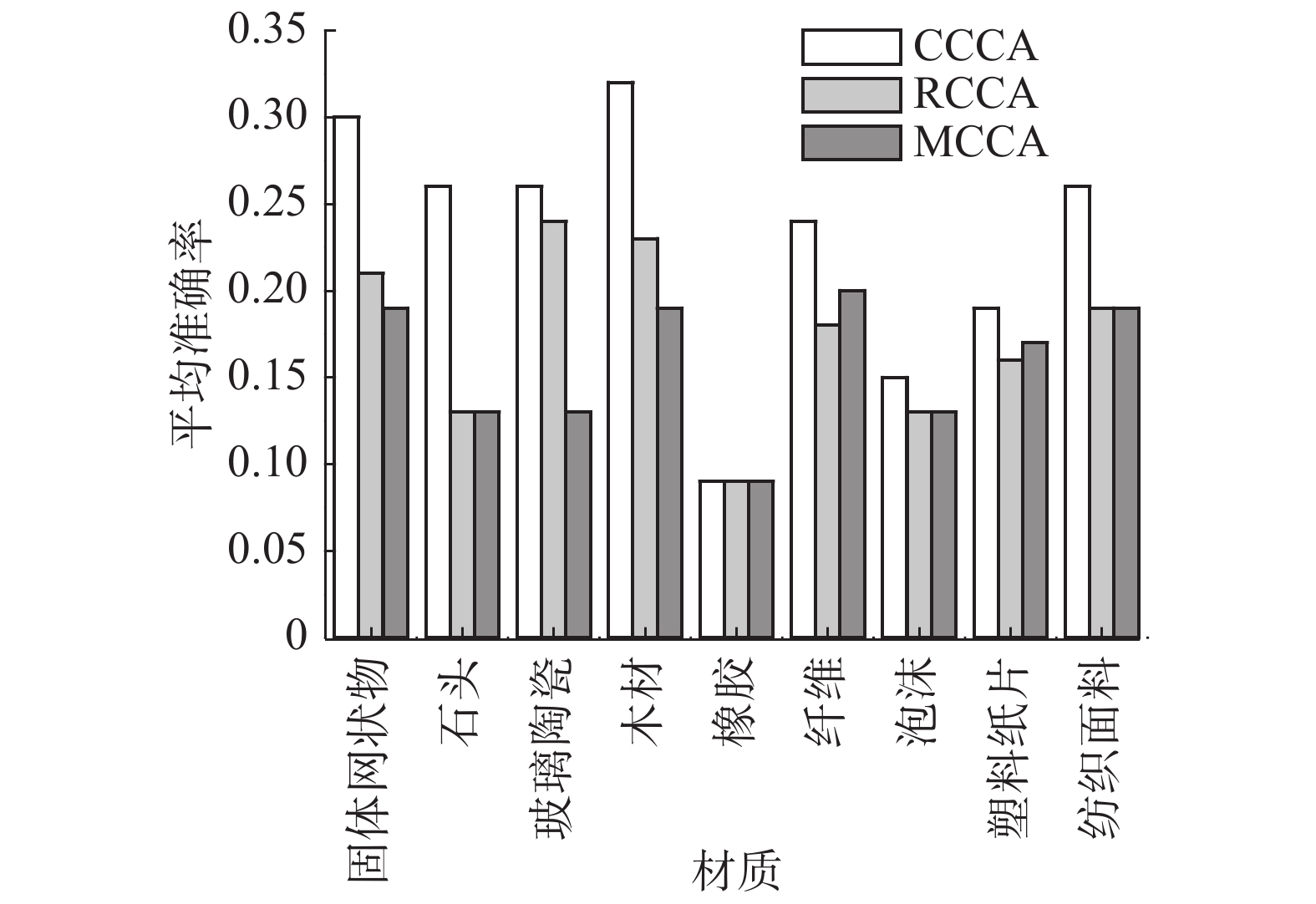
表1为3种方法下不同材质类别的MAP大小，图9为对应的柱形图。整体结果显示，本文引入的CCCA在硬质材质(固体网状物、石头、玻璃陶瓷等)的检索效果比软质材料(橡胶、纤维、泡沫等)好，这主要由于本文所使用的声音数据是由敲击物体表面所得，而实验过程中待测物体放置在实验台上，采集数据时容易受到实验台影响。特别是，CCCA在石头这类材料测试中的表现尤为出色，MAP值达到0.32，比RCCA和MCCA高50%。

图10(a)所示为测试集一个竹木图片，图10(b)为敲击这种竹木的声音样本，使用CCCA进行检索，检索得到图10(c)所示的10张图片，从左到右依次为落叶松木、纺织网、石瓦片、铝板、樱桃树木、压缩木板、落叶松木、山毛榉木、压缩木材、银橡木。从实验结果可以看出，与测试集竹木样本最相似的10个结果有7个和测试样本属于同一类别，检索正确率达到70%，可见CCCA在木材类材质识别效果较好。

5 结束语

本文跨越不同模态之间的限制，结合声音图像特征与典型相关分析方法，将跨模态检索方法应用于材质检索领域，在慕尼黑工业大学触觉纹理数据集上取得较好效果。虽然通过实验验证该方法目前的效果存在一定的局限性，但随着不同模态信息的不断加入和特征提取的方法不断改进，未来该方法的应用前景必定更加广阔。