传统的监督学习算法，如Naïve Bayes^[1]、One-R^[2]和J48^[3]等，其分类效果依赖于训练数据的有效性。通常情况下，使用已标记的样本作为训练集，学习算法以此训练出分类模型。然而，在真实的数据分析场景下，大量的无标注样本较易获取，而已标注样本数量稀少且难以获取。对海量数据进行标注是耗时、昂贵且困难的。在此情况下，半监督学习(semi-supervised learning)^[4]和主动学习(active learning)^[5]被提出并得到快速发展，已经被广泛地应用在文本分类^[6]、语音识别^[7]和图像分类^[8]等领域。

主动学习模拟一种人机交互场景，允许学习算法根据查询策略，主动获取选取样本的真实类标签，对主动标注的样本进行训练，不断修正已有分类模型，从而提高分类器的泛化能力和分类精度。因此，主动学习的主要挑战是制定有效的样本选择策略。目前，比较常见的主动学习方法有不确定抽样(sampling uncertainty, UC)^[9]，基于聚类(clustering-based approaches, CBA)^[10]和基于委员会投票采样法(query-by-committee, QBC)^[11]。其中，不确定性抽样方法选择当前分类器中不确定度最高的未标注样本进行标注，并将其添加到训练集中。由于单一分类器存在分类偏好，使得泛化能力产生定式，而QBC通过多种同质或异质分类器共同参与分类，一般选取冲突性(不一致性)最高的未标注样本进行标注。基于聚类的样本选择方法旨在通过分析样本间的内在相似性，对样本进行划簇，而后从每簇中选择代表样本进行标注。

PageRank^[12]建立在随机冲浪模型上，通过计算网页的PageRank分值，解决了互联网搜索引擎的网页排名问题。PageRank理论基于两个简单的假设：1)较重要的网页被更多的网页链接；2)PageRank分值越高的网页将传递更高的权重。本文结合PageRank理论，将PageRank分值作为样本信息量的度量指标，同时充分考虑样本的分布信息，提出一种基于PageRank的主动学习算法(PageRank-based active learning algorithm, PAL)，为主动学习算法中样本的选择问题提供一种可行的方案。

实验在8个公开数据集上进行，通过设置不同规模的训练集，测试PAL算法的分类性能。实验结果表明，PAL算法较Naïve Bayes、J48、kNN^[13]和One-R等经典分类算法，通常能得到更高的分类精度，且与QBC、KQBC^[14]和MADE^[15]等主动学习算法相比，有更好的分类性能。

1 数据模型

在本节中，主要介绍决策信息系统、PageRank理论等基本概念。

1.1 决策信息系统

定义1　决策信息系统^[16]。决策信息系统定义成一个三元组：

$S = {\rm{ (}}U,C,d)$

(1)

式中：U代表一个非空样本集合，也称论域；C代表一个非空条件属性集合；d指的是样本的决策属性。表1是1个决策信息系统， $U \!=\! \{ {x_0},{x_1},{x_2},\cdots,{x_{15}}\} $ ， $C = \{ {a_1},{a_2},{a_3},{a_4}\} $ 。

定义2　曼哈顿距离。向量 ${{x}} = [{a_1}\;{a_2}\cdots\;{a_m}]$ 与 ${{y}} = [{b_1}\;{b_2}\cdots\;{b_m}]$ 的曼哈顿距离为

${\rm{dis}} ({{x}},{{y}}) = \sum\limits_{i = 1}^m {|{a_i} - {b_i}|} $

(2)

式(2)表示在多维空间中两个点之间的距离。信息表的样本可以用向量表示。相应地，可以定义任意一组样本的相似度。

定义3　相似度。给定一个决策信息系统S = $ {\rm{(}}U,C,d)$ ，任意 $x,y \in U$ 的相似度记为

${\rm{sim}}(x,y) = \frac{1}{{1 + {\rm{dis}}(x,y)}}$

(3)

根据式(2)、式(3)，可计算表1的决策信息系统中 ${\rm{sim}}({x_0},{x_6}){\rm{ }} = {\rm{ }}0.13$ ， ${\rm{sim}}({x_3},{x_{12}}) = {\rm{ }}0.127$ 。

定义4　邻域。对于任意的样本 $x \in U$ ，可以通过设置相似度阈值θ的方式确定其邻域，样本的邻域定义为

$n(x,\theta ) = \{ y \in U|{\rm{sim}} (x,y) \geqslant \theta \} $

(4)

相似度阈值θ越小，样本的邻域越大。根据表1所示的决策信息系统可以计算出 $n({x_0},0.5) = $ $ \{ {x_1},{x_2},{x_3},{x_4}\} $ 。

1.2 PageRank模型

Web中的网页通过超链接相互链接，PageRank算法计算每个网页的PageRank分值。PageRank分值可作为网页重要程度的度量指标。图1表示一个Web超链接图。

定义5　PageRank分值。将互联网中的网页抽象成一个有向图 $G = \left( {V,E} \right)$ 。E是网页超链接集合，V是网页集合。设 $n = |V|$ ，网页i的PageRank分值point(i)定义为

${\rm{point}}(i) = \sum\limits_{(j,i) \in E} {\frac{{{\rm{point}}(j)}}{{{O_j}}}} $

(5)

式中O_j表示网页j的出度。此时，PageRank分值的n维行向量可用P表示，即

${{P}} = {\left[ {{\rm{point}}(1)\;\;{\rm{point}}(2)\;\;\; \cdots \;\;\;{\rm{point}}(n)} \right]^{\rm{T}}}$

(6)

有向图G的邻接矩阵可以用 ${{A}} = {({a_{ij}})_{n \times n}}$ 表示，其中：

${a_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{ }}1/{O_i},\;\;\;\;\;(i,j) \in E}\\ {{\rm{ }}0{\rm{,}}\;\;\;\;\;{\rm{\text{其他}}}} \end{array}} \right.$

(7)

根据式(6)、式(7)可定义n维方程组为

${{{P}}_i} = {{{A}}^{\rm{T}}}{{{P}}_{i - 1}}$

(8)

式(8)是循环定义式。迭代求得分值向量P，即P不再显著变化或者趋近收敛时，停止迭代。初始情况下，所有网页的排名是相同的，即 ${{{P}}_0} = $ $ [1\;1\cdots\;1]$ 。极小值ε是人工设定的收敛阈值，用于验证向量P是否收敛。每轮迭代结束后，若 $|{{{P}}_i} - {{{P}}_{i - 1}}| < \varepsilon $ ，则认为达到收敛条件。

在有向图G中，存在没有出度的网页v，称之为悬挂网页，如图1中的V₅。悬挂网页导致排名下沉，PageRank分值向量P在经过i次迭代后，其值均为0。将Web图用马尔可夫链^[17]进行建模可以解决上述问题。

将网页看作马尔可夫链的状态，超链接表示状态转移。这样，Web冲浪将表示成一种随机过程。状态转移矩阵T必须满足3个条件：随机矩阵、不可约、非周期。因此，将邻接矩阵A进行如下修订：

${{T}} = \gamma {{{A}}^{\rm{T}}} + (1 - \gamma )\frac{{{E}}}{n}$

(9)

式中：γ是阻尼系数，一般情况下γ∈(0, 1)；E是一个n×n阶且元素全为1的矩阵；E /n表示一网页链接其他网页的随机概率，即1/n。

2 问题与算法 2.1 问题描述

在主动学习应用场景中，算法标注最具信息量的样本来构建高精度分类器。可供查询的标签数量N是输入参数之一。

输入　决策信息系统 $S = (U,C,d)$ ；

输出　分类精度accuracy；

约束条件　 $U = {U_r} \cup {U_t}$ 。

优化目标　最大化精度accuracy，即

${\rm{accuracy}} = \frac{{|{U_t}{\rm{|}} - {\rm{error}}}}{{|{U_t}{\rm{|}}}} \times {\rm{100\text{%} }}$

(10)

式中：|U_r|是训练集大小；|U_t|是测试集大小；error是误分类样本数量。若可供查询的标签数量为N，则 $|{U_t}{\rm{|}} = {\rm{ }}n{\rm{ }} - {\rm{ }}N$ 。

2.2 PAL算法描述

PAL算法可以细分为3个子算法，分别是PageRank排名计算算法、二叉树生成算法和二叉树聚类算法。伪代码符号定义如表2。

2.2.1 PageRank排名计算算法

利用PageRank计算每个样本的分值，该分值可作为样本信息量的度量标准，即分值越大样本所含信息量越高。

给定决策信息类系统 $S = {\rm{ (}}U,C,d)$ ，对于任意的 $x,x' \in U$ ，且 $x \in n(x',\theta )$ 。根据式(4)、式(5)计算样本x在PageRank模型下所获得的分数point(x)：

${\rm{point}}(x) = \sum\limits_{x \in (x',\theta )} {\frac{{{\rm{point}}(x')}}{{|n(x',\theta )|}}} $

(11)

根据式(7)决策系统邻接矩阵可用 ${{A}}' = {({a_{ij}}^\prime )_{n \times n}}$ 表示，其中:

$ {a'_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1/|n({x_i},\theta )|,\;\;\;\;{x_j} \in n({x_i},\theta )}\\ {0,\;\;\;\;{\rm{\text{其他}}}} \end{array}} \right. $

(12)

算法1　PageRank排名计算算法

输入　决策信息系统S = (U, C, d)；

输出　排名向量Rank。

1) for (each x∈U) do

2) for (each y∈U) do

3) 根据式(2)计算dis(x y);

4) 根据式(3)计算sim(x, y);

5) end for

6) 根据式(4)计算n(x);

7) end for

8) 根据式(12)计算邻接矩阵A;

9) k = 1;

10) T = γA^T + (1 − γ)E/n;

11) ${{{P}}_0} = \left[ {1{\rm{ }}1{\rm{ }} \cdots 1} \right]_{1 \times n}^{\rm{T}}$ ;

12) while (|P_k − P_k-1| > ε) do

13) P_k = TP_k-1;

14) k++;

15) end while

16) Rank = sort(P_k);

17) return Rank;

算法1描述了样本的排名向量的计算过程。1)~7)通过计算样本间的相似度，确定每个样本的邻域；10)根据式(9)计算状态转移矩阵T；11)定义初始分值向量P₀；12)~15)计算收敛条件下分值矩阵P；16)对分值矩阵P进行降序排序。

2.2.2 二叉树生成算法

主动学习阶段在二叉树上进行，为了避免离群点对该阶段标签查询、预测的影响，保证查询到的样本均具有较高的信息量，仅利用排名前R的代表样本去构建二叉树。同时，树形结构能够充分体现数据的层次关系，便于数据分析，从而得到更好的聚类结果。

二叉树生成算法是一个典型递归算法。其构建过程分为两步：寻找孩子节点，根据孩子节点划分集合。根结点root的孩子节点是U′中最不相似的两个样本，其余节点x的左孩子是当前集合中与x最相似的样本x_l，右节点是当前集合中与x_l最不相似的节点x_r。

算法2　二叉树生成算法

输入　排名前R的代表集合U′；

输出　二叉树root。

1) while (U′ != Ø) then

2) if (root) then

3) 计算最不相似的一对样本x_l, x_r∈U′;

4) root. setChild (x_l, x_r);

5) U′ = U′ − { x_l, x_r};

6) else then

7) 计算与root最相似的样本x_l∈U′;

8) 计算与x_l最不相似的样本x_r∈U′;

9) root. setChild (x_l, x_r);

10) U′ = U′ − { x_l, x_r};

11) end if

12) U_l = Ø, U_r = Ø;

13) for (each x∈U′) do

14) if (sim(x, x_l) > sim( x, x_r)) then

15) U_l = U_l ∪ {x};

16) else then

17) U_r = U_r ∪ {x};

18) end if

19) end for

20) 对x_l，U_l继续调用算法2;

21) 对x_r，U_r继续调用算法2;

22) end while

23) return root；

3)~5)寻找root的孩子节点，即U′中最不相似的一对样本；7)~10)寻找非root节点的孩子节点；12)定义x_l和x_r的样本集合；13)~19)通过比较集合U′中样本与x_l、x相似度大小，实现集合的划分；20)~21)递归调用算法2。

2.2.3 二叉树聚类算法

一般来说，聚类簇数K与聚类质量关系密切，然而大多数聚类算法只能通过经验或者试凑指定簇数K。本文采用一种执行边缘分离的聚类策略，不需要将K作为输入，而是根据二叉树的内部结构自然地分簇。

通过计算二叉树节点间的相似度，将二叉树的边划分为分割边或者非分割边。假设两节点足够相似，可将该连边定义成非分割边，反之定义为分割边。这种边界划分方式基于一个阈值。第一轮迭代时，阈值是二叉树相连节点间相似度的最小值。

算法3　二叉树聚类算法

输入　二叉树根节点root；

输出　聚类信息块 ${\bf{bl}} = \left[ {{\rm{b}}{{\rm{l}}_1}\;{\rm{b}}{{\rm{l}}_2} \cdots \! {\rm{ b}}{{\rm{l}}_k}} \right]$ 。

1) clusterT (root.lc，count，threshold) start

2) cn[root.lc] = count;

3) if (root.lc.lc! = null) then

4) if (sim (root.lc, root.lc.lc) ≤ threshold)

5) clusterT (root.lc.lc, ++count, threshold);

6) else then

7) clusterT (root.lc.lc, count, threshold);

8) end if

9) end if

10) if (root.lc.rc! = null) then

11) 步骤4)、5)、6)、7)；

12) end if

13) end clusterT (root.lc，count，threshold)

14) for(i = 0 to count) do

15) tempNum= 0;

16) for( j = 0 to N) do

17) if(cn_j = i)then

18) bl(i, tempNum) = j; tempNum ++;

19) end if；

20) end for

21) end for

22) return bl;

算法3详细描述了基于二叉树的聚类过程。通过遍历树的节点，同时用数组cn记录节点的簇号，实现聚类。lc表示左孩子，同理rc表示右孩子。count用于记录递归过程中最大簇数。1)定义聚类函数；2)记录节点的簇号；3)~9)根据相似度关系判断簇边界，如当前节点与它的孩子节点的相似度小于阈值threshold，count自增后进行下一次递归；14)~21)整理 cn得到分块信息表bl。该方法可以解决聚类算法需要人工设定K值的问题。

2.2.4 主动学习

主动学习阶段，利用二叉树聚类算法生成的信息块bl对代表样本进行标记和预测。

1)如bl_i中存在未分类样本，则查询bl_i中PageRank值较高的一部分样本的标签。

2)如bl_i中已分类的样本数量足够大( $ {P_i} \geqslant \sqrt {{\rm{b}}{{\rm{l}}_i}} $ )且标签一致，则可预测该块中剩余样本的标签。

3)增大阈值threshold，进行下一轮聚类、标记和预测。达到标签查询上限后，对不纯的块，采取投票的方式确定剩余未标记代表样本的标签。

主动学习阶段结束时，代表样本均已获得标签。将代表样本作为训练集，采用kNN算法对其他样本进行分类。

2.3 样例分析

提供一个样例分析来进一步清楚说明PAL算法。使用表1的决策信息系统，允许查询的最大标签数N=7。设置阻尼γ=0.95，ε=0.01。图2和图3展示两次迭代聚类之后查询标签的情况。

1) 根据算法1得到排名向量

Rank=[1 2 3 7 14 13 6 8 10 11 15 0 4 12 5 9]

根据算法2生成二叉树，如图2(a)所示。由于数据集极小，设定R=100。令标记集合U₁= $ \text{Ø} $ ，预测集合U₂= $ \text{Ø} $ ，未分类集合U₃=U。

2) 选择节点间的较低相似度0.196作为当前阈值threshold，根据算法3聚类可得块信息 ${\rm{bl}} = \left[ {{\rm{b}}{{\rm{l}}_1}\;{\rm{b}}{{\rm{l}}_2} \cdots {\rm{ b}}{{\rm{l}}_4}} \right]$ ；如图2(b)所示。接着，查询bl₁、bl₂、bl₃和bl₄中样本x₉、x₁₁、x₆和x₀的标签，分别是iv、it、iv和is。在此次迭代后， ${U_1}' \!=\! \left\{ {{x_0},{x_6},{x_9},{x_{11}}} \right\}$ ， ${U_1} = \text{Ø} \cup {U_1}' = \left\{ {{x_0},{x_6},{x_9},{x_{11}}} \right\}$ ， ${U_3} = {U_3} - {U_1} = \left\{ {{x_1},{x_2},{x_3},} \right.$ $ \left. {{x_4},{x_5},{x_7},{x_8},{x_{10}},{x_{12}},{x_{13}},{x_{14}},{x_{15}}} \right\}$ ；在第一次迭代后，|U₁|≤7。增大阈值threshold进行第2次聚类。

3) 设置阈值threshold = 0.323，聚类簇信息块如图3所示。查询bl₁、bl₂、bl₃和bl₄中样本x₁₂、x₁₃和x₇的标签，分别是it、it和iv 。此时， ${U_1}' = $ $\left\{ {{x_{12}},{x_{13}},{x_7}} \right\}$ ， ${U_1} \!=\! {U_1} \cup {U_1}' \!=\! {\rm{ }}\left\{ {{x_0},{x_6},{x_7},{x_9},{x_{11}},{x_{12}},{x_{13}}} \right\}$ 。bl₂中已被标记的样本数量已经足够多，且已标记样本标签均为it，便可预测bl₂中剩余样本x₁₄和x₁₅的标签为it。同理可预测块bl₃中剩余样本x₈、x₁₀的标签均为iv。 ${U_2} \!=\! {U_2} \cup {U_2}' = \left\{ {{x_8},{x_{10}},{x_{14}},{x_{15}}} \right\}$ ， ${U_3} = {U_3} - {U_1} - {U_2} = \left\{ {{x_1},{x_2},{x_3},{x_4},{x_5}} \right\}$ 。在第2次迭代后，|U₁|≥7。不再进行第3次聚类。

4) ${U_3} = \left\{ {{x_1},{x_2},{x_3},{x_4},{x_5}} \right\}$ 通过投票给予标签；bl₄中x₀被标记为is。所以x₁、x₂、x₃、x₄和x₅被标记为is。

在本例中，查询7个样本的标签，预测4个样本的标签，5个样本通过投票获得标签。无样本被错误标记，因此，精度为100%。

3 实验及分析

在本节中，通过实验将PAL算法与传统的分类算法、主动学习算法进行比较，并回答以下问题：

1) PAL算法选择代表样本是否具有可靠性，尤其不同二叉树比例R的设置对精度的影响；

2) PAL算法是否比其他监督学习算法更精确；

3) PAL算法是否比主动学习算法的分类效果好。

3.1 实验步骤

实验结合Weka，在macOS Sierra操作系统下运行，其硬件配置为：2.6 GHz Intel Core i5处理器，8 GB 1600 MHz DDR3。

实验采用8个公开的数据集，并将PAL算法与J48、kNN、Naïve Bayes、One-R和Logistics^[18]这5种传统的监督学习算法进行比较，同时与QBC、KQBC和MADE这3种主动学习算法作对比。实验采用分类精度accuracy作为评估指标。

与传统的监督学习分类算法的比较实验中，针对每个数据集，实验设置训练集以1%为步长，规模由1%增加到10%。在训练集规模不同的情况下，观察分类精度的变化。在与主动学习算法的比较实验中，训练集规模均设置为10%。

设置二叉树比例R∈[20%, 50%]，阻尼因子γ∈[0.65, 0.95]，极小值ε=0.01。为了降低实验的随机性误差，采用相同参数设置进行10次重复实验，取得平均值作为实验结果。

实验所用数据集详细信息如表3所示。

3.2 参数R对分类效果的影响

在本节中，将回答问题1)。讨论不同的二叉树比例R对实验精度的影响。表4展现了在训练集规模是数据集的10%的情况下，所得精度随R的变化情况。

由表4可以看出，对于不同的数据集，最佳的二叉树比例取值存在差异。但从整体来看，最佳取值都集中在[20, 50]区间。

实验结果符合数据集样本的分布规律，信息量较高的样本所占的比例较小。二叉树比例取值越大时，越多的信息量低的样本参与到二叉树的构建，一些离群点、边界点影响聚类结果，而导致分类错误。同时表明，将PageRank分值作为样本信息量的度量指标具有可靠性。

Iris、Seeds、Twonorm数据集样本均匀，不存在样本倾斜问题，二叉树聚类算法能够获得很好的分簇效果，因此二叉树比例取值较小时，能够保证查询到的样本都具有高信息量，反而分类精度更高。

较大数据集，如Twonorm、Aggregation，R比例较小，所选代表样本构成的树形结构也能很好地表现样本的层次结构，因此对分类精度不会有较大影响。

在本文后续的研究讨论中，R当作经验参数参与二叉树的构建。

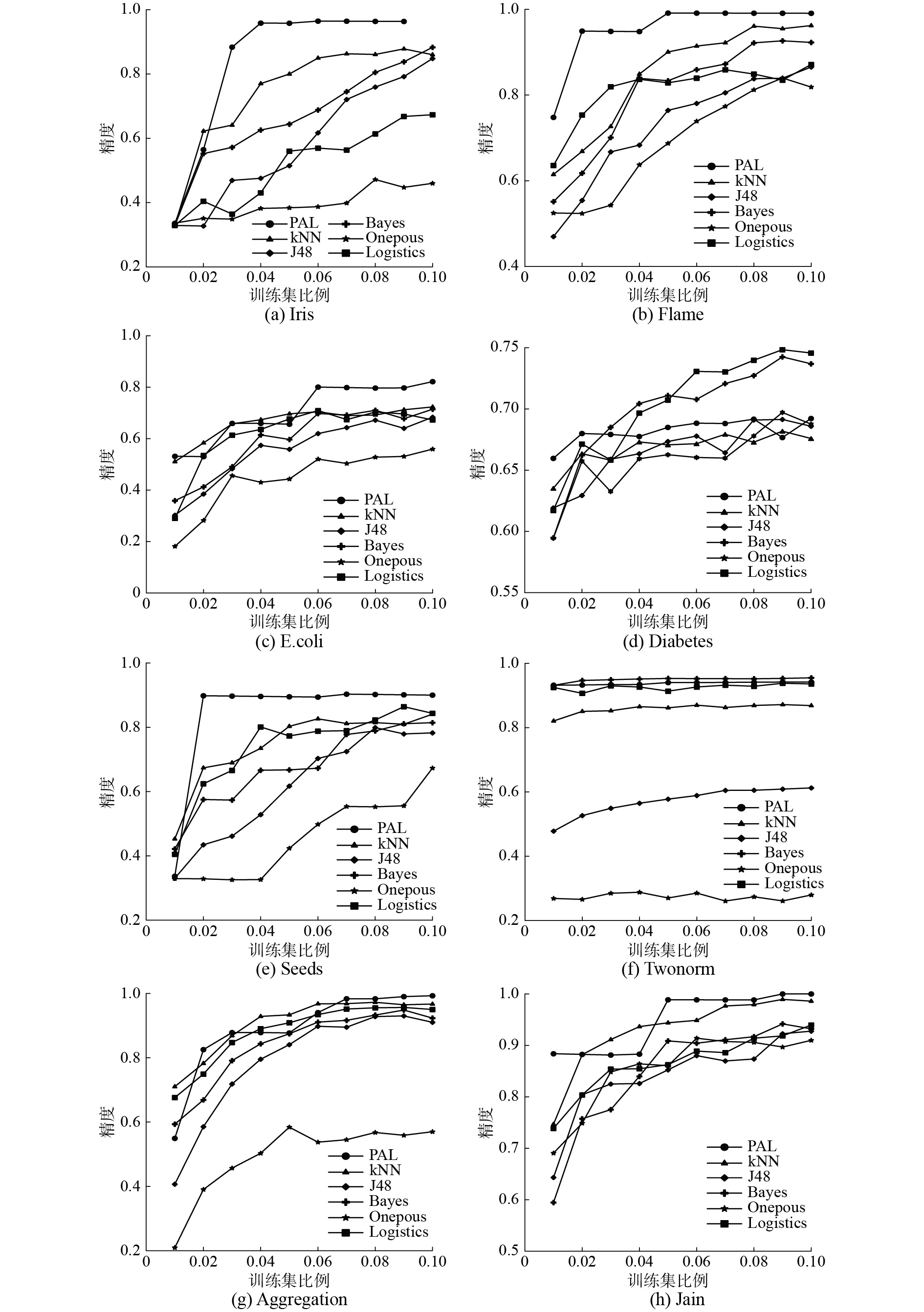
3.3 与经典算法对比

在本节中，将回答第二个问题。PAL在8个数据集上与J48、Naïve Bayes、kNN、One-R和Logistics经典算法做了对比。图4展示了PAL算法以及对比算法在不同训练集比例下的分类精度变化趋势。

实验结果表明，本文提出的PAL算法在Iris、Flame、Ecoli、Seeds、Aggregation和Jain数据集上，分类精度高于对比的经典算法，尤其是Flame数据集，在实验所选的训练集比例下，分类精度均高于经典分类算法。在Twonorm数据集上也能取得较好的分类精度，分类精度达到97%，仅略低于Naïve Bayes算法。在Diabetes数据集上优势不明显，尤其是在Diabetes数据集上，PAL算法分类精度高于kNN、J48和One-R，但是低于Naïve Bayes和Logistics。

图4(b)、(d)、(f)显示，在实验所选的所有训练集规模下，对应数据集上PAL算法分类精度均高于kNN算法；图(a)、(c)、(e)、(g)、(h)显示，在多数训练集规模下，对应数据集上PAL算法分类精度高于kNN算法。PAL对代表样本采用主动学习算法进行标记和预测，而对于剩余样本则采用kNN进行预测。因此，当二叉树比例R=0时，PAL算法将退化成KNN算法。该结果表明，PAL的样本选择策略和主动学习算法具有可行性。

图4(a)、(b)、(d)、(e)、(h)显示，在训练集规模极小的情况下，如R=10%时，PAL较其他经典算法能取得较好的分类精度；图4(a)、(b)、(e)、(g)显示，训练集规模为30%之前，PAL算法的分类精度快速地上升，逐渐趋于稳定，说明PageRank分值作为样本信息量的度量指标具有可靠性，结合聚类算法，利用样本的分布信息能够有效地进行样本选择。

图4(a)、(b)、(e)、(f)显示，在Iris、Flame、Seeds数据集上分类时，训练集的规模对PAL分类精度影响不明显，是因为数据集太小，训练集比例对分类效果影响较低。在Twonorm数据集上，训练集的规模对所有算法的分类精度影响均不明显，说明在该数据集上数据分布较为均匀。

3.4 与主动学习算法对比

将PAL算法与流行的3种主动算法进行比较。表5展现了在训练集规模是数据集的10%，R设置为40%的情况下，QBC、KQBC、MADE和PAL的分类精度。为了更清晰地展示各个算法的性能差异，设计以排名为衡量标准的评估方法。

从总体上看，本文提出的PAL算法与其他主动学习算法比较平均排名靠前。PAL算法在Iris、Flame、Seeds、Diabetes和Twonorm数据集上，分类精度高于其他对比的主动学习算法，尤其在Flame数据集上，分类精度达到98%。在Ecoli、Jain和Aggregation数据集上也有很好的分类表现。

4 结束语

本文提出了一种基于PageRank的主动学习算法，为样本的选择问题提供了一种可行的方案。利用PageRank理论发现信息量较高的代表样本，从而在该集群上构建二叉树，用来表示样本的层次结构。在二叉树上进行迭代聚类，标记和预测，能够保证查询到的样本分布均匀，同时避免离群点的影响。用代表对象训练得到分类模型，采用kNN算法处理剩余样本。实验结果表明，PAL算法相比于Naïve Bayes和J48等传统分类算法，能得到更高的分类精度，且与QBC等主动学习算法相比，分类效果更好。