置换流水车间调度问题(permutation flow-shop scheduling problem, PFSP)是广泛受到研究的一种组合优化问题，属于NP−hard问题。PFSP的搜索空间中存在诸多局部最优解，且问题复杂度越高，越容易局部最优化，因此许多学者针对PFSP特性不断对求解PFSP的算法进行优化。求解PFSP的算法可分为精确算法和近似算法，精确算法虽能求出最优解，但时间复杂性较高，随着问题的规模增大将变得不可行。近似算法对于较大规模的问题能在可行时间内求出近优解，是研究PFSP问题的重要方法。近似算法包括遗传算法^[1]、蚁群算法^[2]、模拟退火算法^[3]等。

遗传算法(genetic algorithm, GA)通过选择、交叉和变异等操作搜索解空间的最优解，已经成功应用于解决旅行商问题、车辆路径问题和车间调度问题等不同领域的组合问题。但是遗传算法的局部搜索能力较差，在实际应用中容易产生早熟收敛的问题。怎么运用遗传算法既能保留优良个体，又能维持群体的多样性，一直是遗传算法中较难解决的问题。近年来针对PFSP，不少学者为提高遗传算法的有效性，将遗传算法与其他算法相结合对该问题进行求解，取得了不错的效果。Benbouzid等^[4]针对PFSP提出VacGA(introduces vaccination into the field of GAs)，将遗传算法和免疫算法相结合，遗传算法执行全局搜索，人工免疫系统执行局部搜索，以克服演化过程中遗传算法局部搜索能力不足的问题。Chen等^[5]将遗传算法与广义邻域搜索相结合，提出一种新型混合遗传算法求解PFSP。Bessedik等^[6]提出一种基于免疫的遗传算法，这种算法分为两种形式：1）将接种引入到基于免疫理论的遗传算法；2）从免疫网络理论得到启发，并将其运用到遗传算法中。Ganguly等^[7]将贪婪局部搜索算子引入到遗传算法，有效地解决大范围的排序和调度离散优化问题。齐学梅等^[8]为求解PFSP问题，将变邻域搜索算法与遗传算法相结合，加快了收敛速度。吴秀丽等^[9]将变邻域搜索算法和遗传算法相结合提出了一种变邻域改进遗传算法求解混合流水车间调度问题，增强了遗传算法的局部搜索能力。

Chang等^[10]针对置换流水车间调度问题，提出一种基于区块的遗传算法(puzzle-based artificial chromosome genetic algorithm，p-ACGA)，将遗传算法和蚁群算法相结合，通过简单遗传算法的交叉、突变等操作产生精英群体，针对这些精英群体，利用蚁群算法的信息素浓度对工件与工件的关系进行统计分析，进而建立信息素相依矩阵并根据矩阵挖掘区块，利用区块和非区块重组形成人工染色体，然后将其注入到进化过程中。虽然p-ACGA能够避免局部最优问题，一定程度上改善了解的质量，加快了进化速度，但是算法在初始化、信息素分布统计等方面还存在一些不足。因此本文提出一种改进区块遗传算法(puzzle-based improved artificial chromosome genetic algorithm，p-IACGA)。该算法在种群初始化时引入反向学习的思想，并对其进行了改进，将其与随机机制相结合产生初始解，大大提高了初始解的多样性和质量；为进一步描述信息素在路径上的分布情况，算法考虑了信息素在节点上的分布情况，即工件与所在解序列位置的关系，并将其与p-ACGA中的统计分析工件与工件的相邻关系相结合，以全面地描述解的空间分布情况。然后，根据这两种关系建立相依信息素矩阵和位置信息素矩阵，进而挖掘区块以组合人工染色体。最后，引入染色体重组机制，进一步提高解的质量。

1 置换流水车间生产调度问题描述

PFSP生产调度问题可以描述为：有 $n$ 个作业以相同的顺序在 $m$ 台机器上加工。同时，要满足的约束条件包括：1)操作是独立的，可以在零时间开始；2)每台机器在同一时间最多加工一个工件；3)每一个工件在同一时间只能在一台机器上加工。用 $P(i,j)$ 表示工件 $i$ 在机器 $j$ 上的处理时间，用( ${{\textit{π}} _1},{{\textit{π}} _2}, \cdots ,{{\textit{π}} _n}$ )表示工件序列，用 $C({{\textit{π}} _i},j)$ 表示完成时间的计算，即

$C({{\textit{π}} _1},1) = P({{\textit{π}} _1},1)$

$C({{\textit{π}} _i},1) = C({{\textit{π}} _{i - 1}},1)P({{\textit{π}} _i},1)$

$C({{\textit{π}} _1},j) = C({{\textit{π}} _1},j - 1) + P({{\textit{π}} _1},j)$

$C({{\textit{π}} _i},j) = \max \{ C({{\textit{π}}_{i - 1}},j),C({{\textit{π}} _i},j - 1)\} + p({{\textit{π}} _i},j)$

式中： $i = 2,3, \cdots ,n;j = 2,3, \cdots ,m $ 。

最大完工时间： ${C_{\max }}({\textit{π}} ) = C({{\textit{π}} _i},m)$ 。

适应度为： $f(x) = 1/{C_{\max }}({\textit{π}} )$ 。

2 求解置换流水车间调度问题的改进区块遗传算法

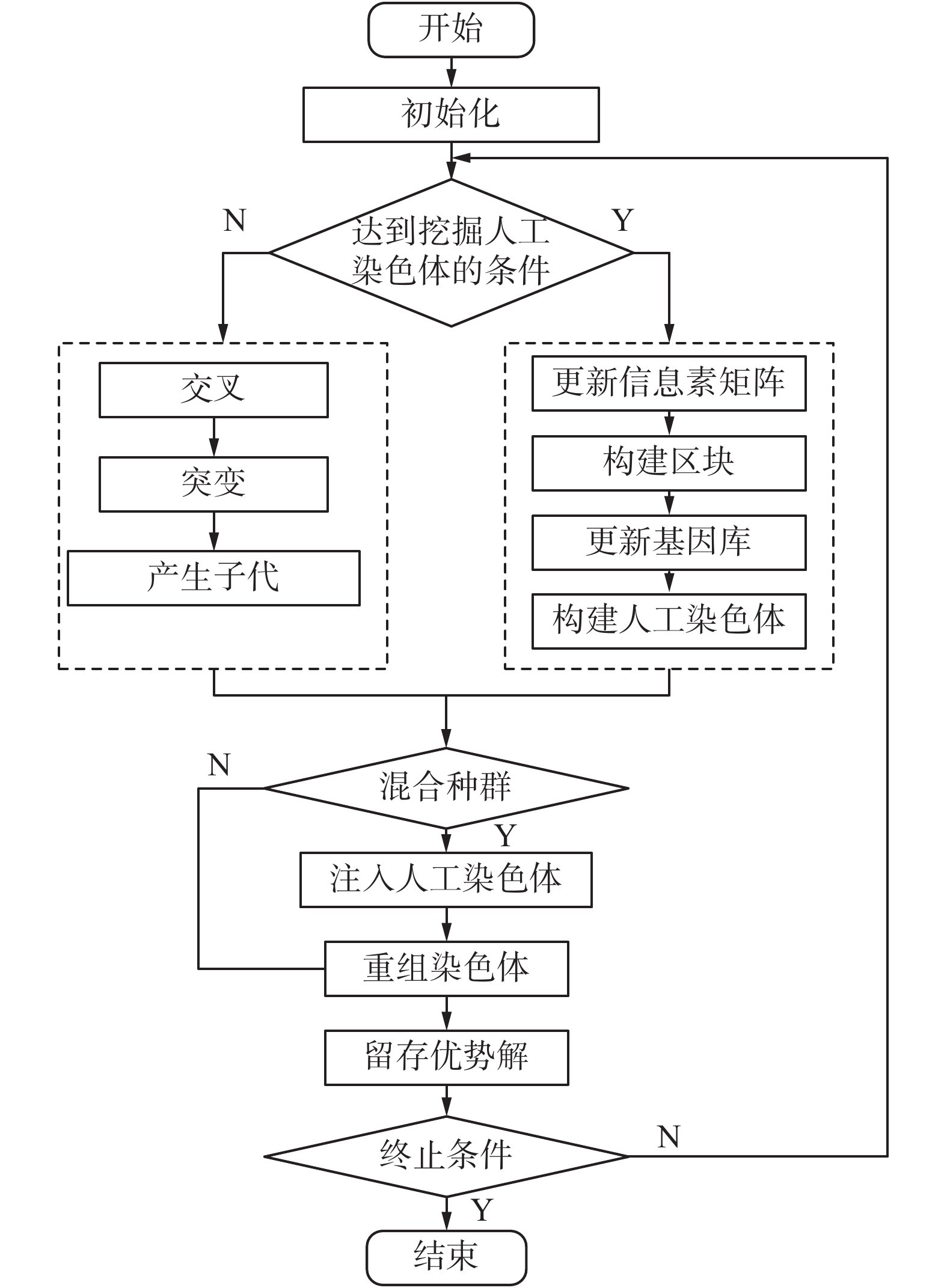
p-IACGA主要分为5部分：产生初始解、挖掘区块、构建人工染色体、染色体重组和保留优势解。p-IACGA流程如图1所示，因为染色体携带的较优信息是逐代积累的，所以为了挖掘出较优人工染色体，每执行 $n$ (给定的一个数)代遗传算法后挖掘一次区块，这样每一轮执行的总代数是 $n + 1$ 。

2.1 改进反向学习法初始化种群

1)反向学习法

反向学习法(opposition-based learning，OBL)^[11]的主要思想是同时考虑原始解序列和它的反向解序列，以获得当前候选解中的最优解。假设X = $ ({x_1},{x_2}, \cdots ,{x_n})$ 是 $n$ 维空间中的一个解，其中 ${x_i} \! \in \! {\bf{R}}$ 和 ${x_i} \! \in \! [{l_i},{u_i}]$ ， ${l_i}$ 、 ${u_i}$ 是搜索空间的上、下界。 ${\forall i} \in \{ 1,2, \cdots ,n\} $ ，那么它的反向解是 $X' = ({x'_1},{x'_2}, \cdots ,{x'_n})$ ，其中 ${x'_i} = {l_i} + {u_i} - $ ${x_i}$ 。OBL优化过程为：

①在 $n$ 维搜索空间中生成初始解 $X = ({x_1},{x_2}, \cdots ,$ ${x_n})$ 和反向解 $X' = ({x'_1},{x'_2}, \cdots ,{x'_n})$ ；

②求出初始解的适应度 $f(x)$ 和其反向解的适应度 $f(x')$ ，评估两个解的适应度；

③如果 $f(x') \geqslant f(x)$ ，用 $x'$ 替换 $x$ ；否则，继续使用 $x$ 。

通过同时评估这两个解可以获得更好的结果。

2)应用改进反向学习法进行种群初始化

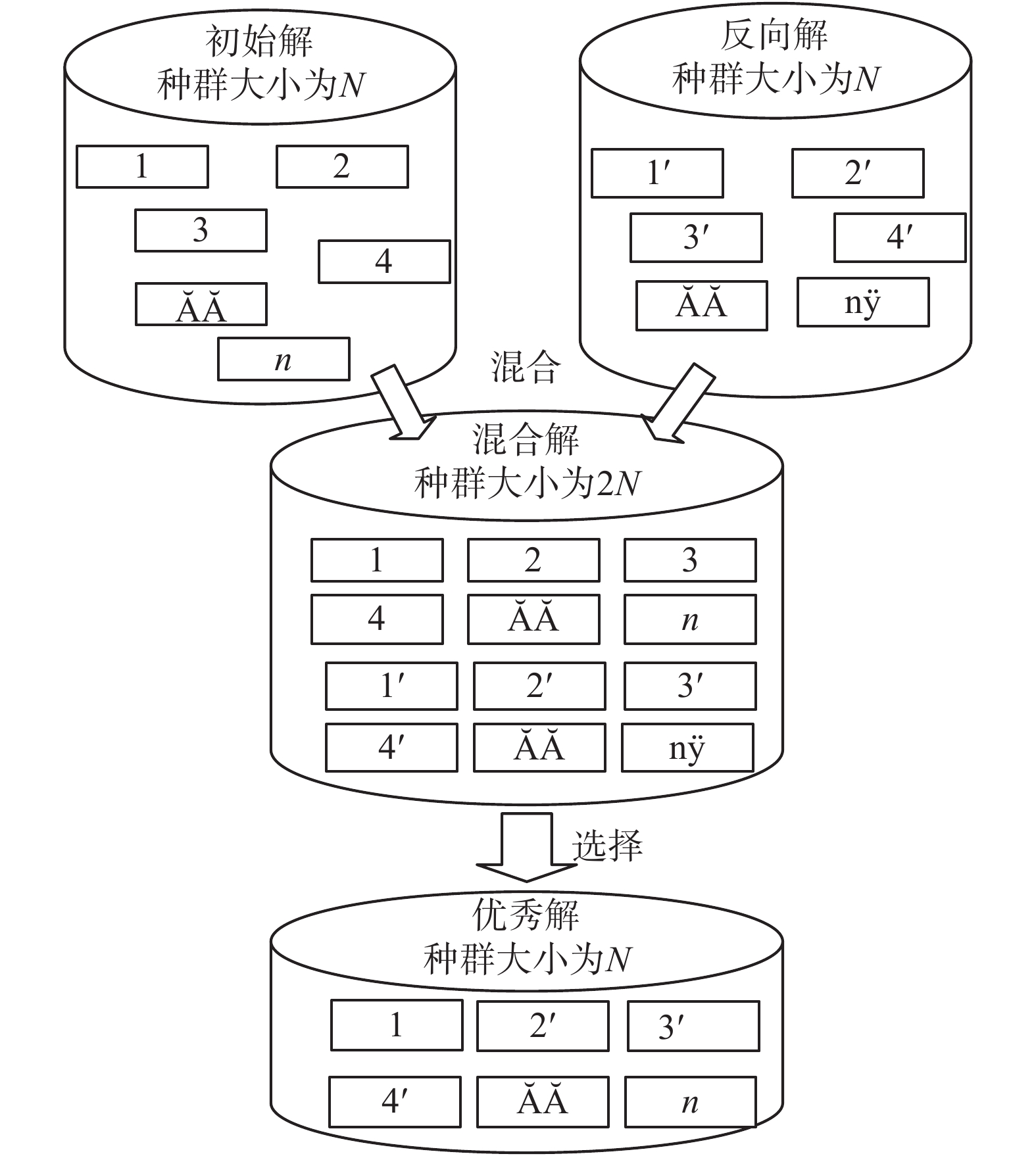
初始化过程采用随机机制和改进反向学习机制相结合的方式，以兼顾初始解的多样性和质量。本研究对反向学习法作了改进以减少优秀解的丢失，基本思路就是将所有原始解和所有反向解混合在一起形成混合群体，然后从混合群体中选出适应度较高的解，如图2所示。首先利用随机方式产生 $N$ ( $N$ 为给定的初始种群规模)条初始解并对每条初始解求出它的反向解；然后，将两种群混合在一起形成规模为2 $N$ 的种群，计算每个解的适应度，并按照适应度大小对解降序排列；最后，选择前 $N$ 条适应度较大的解作为进化的初始种群。

2.2 挖掘区块

在遗传算法中，进化若干代后，大部分染色体都会携带与较优解相似的一些信息，这些信息具有相似性并且这些相似性在大规模的种群中具有一定的可靠性^[12]。在p-IACGA中，使用蚁群优化算法(ant colony optimization，ACO)中的蚂蚁信息素浓度来识别染色体中较好的相似序列并通过区块的方式将它们挖掘出来。

1)建立信息素矩阵

本研究使用相依信息素矩阵和位置信息素矩阵来记录蚂蚁经过的路径信息，其中位置信息素矩阵记录每个节点(工件在解序列中的位置)的信息素浓度信息，相依信息素矩阵记录两节点间的路径(两工件间的相邻关系)的信息素浓度信息。矩阵建立过程如下：

①对信息素矩阵进行初始化

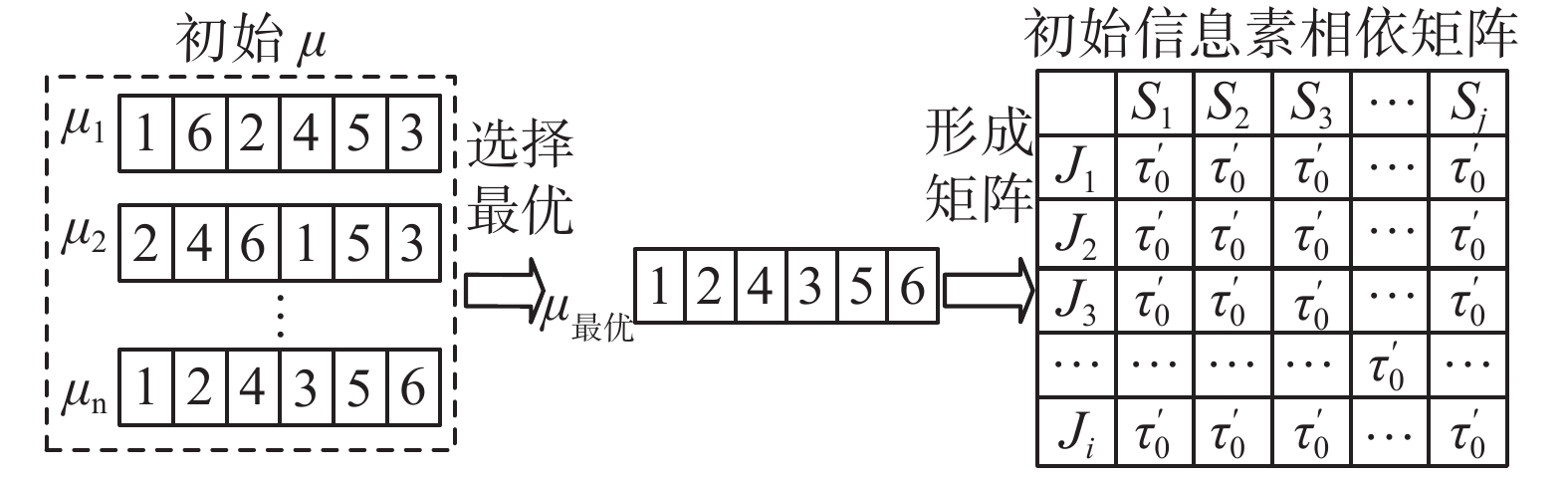
从第 $n$ 代中选择一条最优染色体进行矩阵初始化。图3为初始相依信息素矩阵生成过程，两个工件间的初始信息素表示为 ${\tau _0}$ (见式(1))。同样的方法生成初始位置信息素矩阵如图4。

${\tau _0} = \frac{1}{L}$

(1)

式中 $L$ 表示完工时间。

②更新信息素矩阵

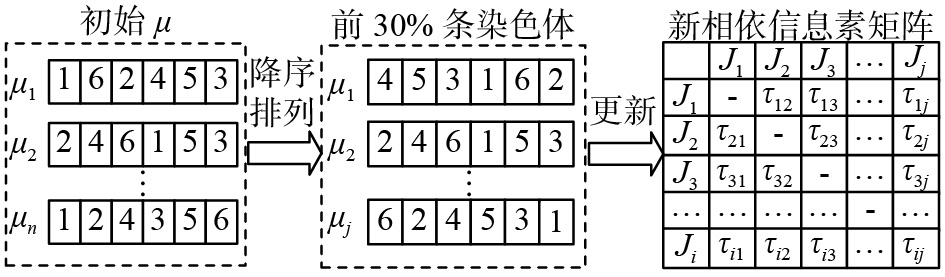
由遗传算法产生的最新一代的前30%适应度较高的染色体更新信息素矩阵，更新过程如图5，更新公式如式(2)：

$\begin{array}{c} {\tau _{ij}}(t + 1) = (1 - \rho ) \times {\tau _{ij}}(t) + \rho \Delta {\tau _{ij}}(t + 1)\\ \Delta {\tau _{ij}}(t + 1) = \left\{ {\begin{array}{*{20}{l}} {1/L{\rm{ , }\quad}\text{若蚂蚁经过路径}(i,j)}\\ {0,{\rm{ }\quad}\text{其他} } \end{array}} \right. \end{array}$

(2)

式中： ${\tau _{ij}}$ 表示每对相邻工件( $i,j$ )间的信息素浓度； ${\tau _{ij}}(t + 1)$ 表示更新的 ${\tau _{ij}}$ ； $\rho $ 表示信息素的蒸发速率^[12]。

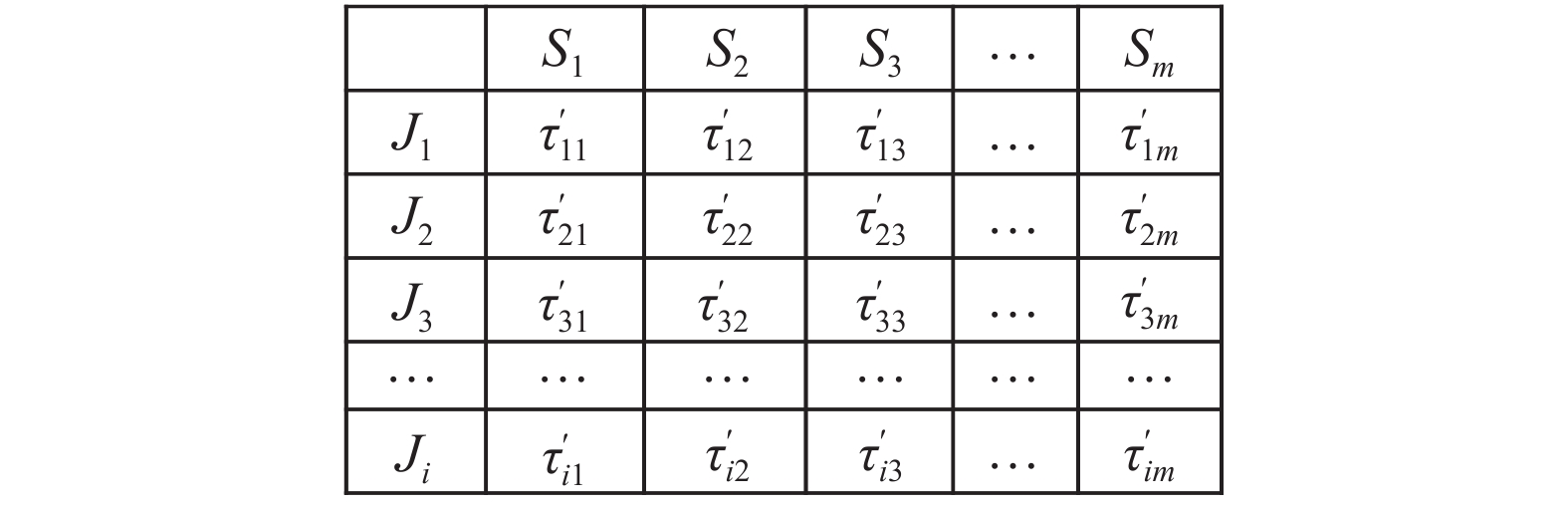
同理，得到更新的位置信息素矩阵如图6。更新公式如式(3)：

$\begin{array}{c} {\tau '_{mi}}(t + 1) = (1 - \rho ) \times {\tau '_{mi}}(t) + \rho \Delta {\tau '_{mi}}(t + 1)\\ \Delta {\tau '_{mi}}(t + 1) = \left\{ {\begin{array}{*{20}{l}} \!\!\!\!{1/L{\rm{ , }\quad}\text{若蚂蚁经过的第}m\text{个节点为节点}i}\\ \!\!\!\!{0,{\rm{ }\quad}\text{其他} } \end{array}} \right. \end{array}$

(3)

式中： ${\tau '_{mi}}$ 为蚂蚁经过的第 $m$ 个节点为节点 $i$ 时在节点 $i$ 处释放的信息素。

2)构建区块

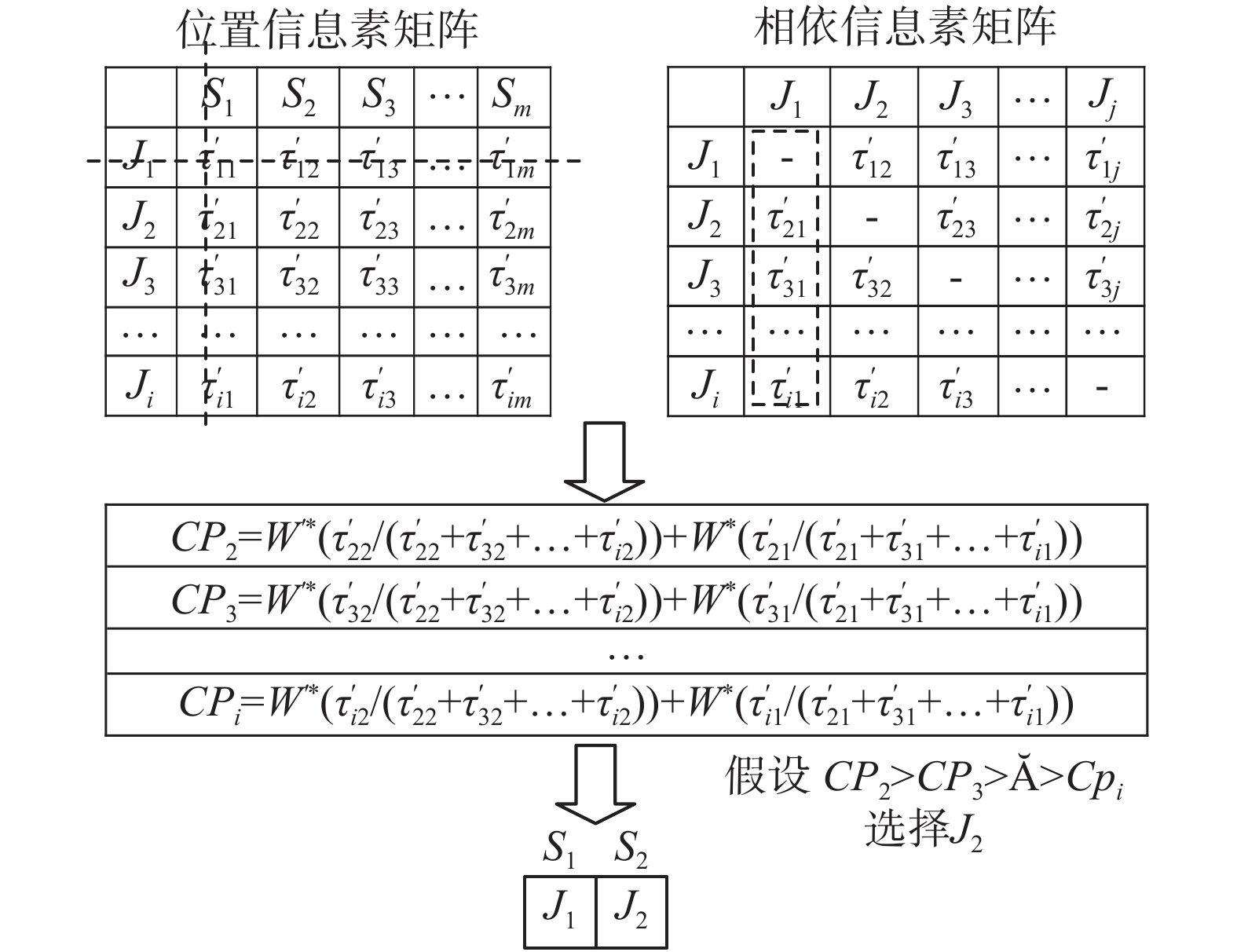
区块是简短的染色体片段，本研究通过学习链接关系^[13]构建区块。首先确定区块的最小长度，然后随机选择起始位置，最后为各位置选择工序。在区块最小长度内，起始位置采用位置信息素矩阵中的信息选择工序，如图7，假设 ${P'_{{{11}}}} > $ $ {P'_{{{21}}}} > \cdots > {P'_{i{{1}}}}$ ，选择工件 ${J_{{1}}}$ 放入起始位置 ${S_{{1}}}$ 。其他位置采用位置信息素矩阵和相依信息素矩阵的合并信息，以轮盘赌选择法(roulette wheel section，RWS)^[13]对工序进行筛选，已经入选的工件不再进行筛选，如图8，假设 $C{P_{{2}}}$ 最大，选择工件 ${J_{{2}}}$ 放入位置 ${S_{{2}}}$ 。

当出现两个或多个较大值时随机选择。位置信息素浓度概率计算公式为

${P'_{im}} = \frac{\tau '_{mi}}{{\sum\limits_{i \in uns} {\tau '_{mi}}}}i,\quad m = 1,2, \cdots ,n$

(4)

相依信息素浓度概率计算公式为

${P_{ij}} = \frac{{{\tau _{ij}}}}{{\sum\limits_{i \in uns} {{\tau _{ij}}} }},\quad i,j = 1,2, \cdots ,n$

(5)

合并概率计算公式

${{{CP}}_i} = (W \times {P_{ij}}) + (W' \times {P'_{im}}),\quad i,j,m = 1,2, \cdots ,n$

(6)

式中： $i$ 表示工件号； $j$ 表示 $i$ 所连接的上一个工件号； $m$ 表示染色体上的工件的位置； $n$ 表示染色体长度； ${P'_{im}}$ 表示工件 $i$ 与位置 $m$ 在位置矩阵的概率； ${P_{ij}}$ 表示相依矩阵中工件 $j$ 相连于工件 $i$ 之后的概率； ${{{CP}}_i}$ 表示工件 $i$ 的合并概率； $W'$ 与 $W$ 分别表示位置矩阵与相依矩阵的权重值，权重值会随着进化代数的增加不断改变^[14]。

对最小长度外的位置进行工序选择时设立合并概率最小阈值^[15]，作为筛选条件。当工件的合并概率大于最小阈值时，选择该工件，否则停止选择工件，本区块完成挖掘，如图9所示。因为当区块包含的工件越多总体概率越低，组合错误的概率越大，区块阈值将会保证区块的质量，同时也将会导致挖掘出的区块长度也有所不同。挖掘的区块均存放在区块资料库中。

3)区块竞争

区块竞争^[16]就是去除有重复信息的区块。将区块资料库中的区块的工序与位置进行比对，如果区块之间出现重复的工序或涵盖的位置重复，则通过比较平均概率的方式进行选择，平均概率较大者保留至区块资料库，较小者则删除，举例如图10。平均概率的计算公式为

$P_{{B^l}}^{\rm{AVG}} = \frac{{P_{B_l^i}^{\rm{dom}} + \sum\limits_{i = 2}^n {{{{{\rm{CP}}}}_{B_l^i}}} }}{n},\quad l = 1,2, \cdots ,n$

(7)

式中： $i$ 表示区块号； $l$ 表示区块的第 $l$ 个位置； $n$ 表示区块的长度； $P_{B_1^i}^{\rm{dow}}$ 表示第 $i$ 条区块的第 $l$ 个工件的位置概率； ${{{{\rm{CP}}}}_{B_l^i}}$ 表示第 $i$ 个区块的第 $l$ 个工件的合并概率。

2.3 组合染色体

本研究利用新建区块资料库中的区块和非区块资料库中的工件组合出较优染色体。先将区块资料库中的所有区块复制到确定长度的空白染色体对应位置，对于尚未放入工序的空位置依照其位置顺序(由左到右)，利用RWS方法根据合并概率从剩余的工件中选择合适工件放入其中。例如图11区块资料库中有2个区块，非区块资料库有2个工件，合并概率 ${{{{\rm{CP}}}}_6}$ 大于 ${{{{\rm{CP}}}}_5}$ ，选择 ${J_6}$ 放至位置5，剩下 ${J_5}$ 放至位置9。

2.4 染色体重组

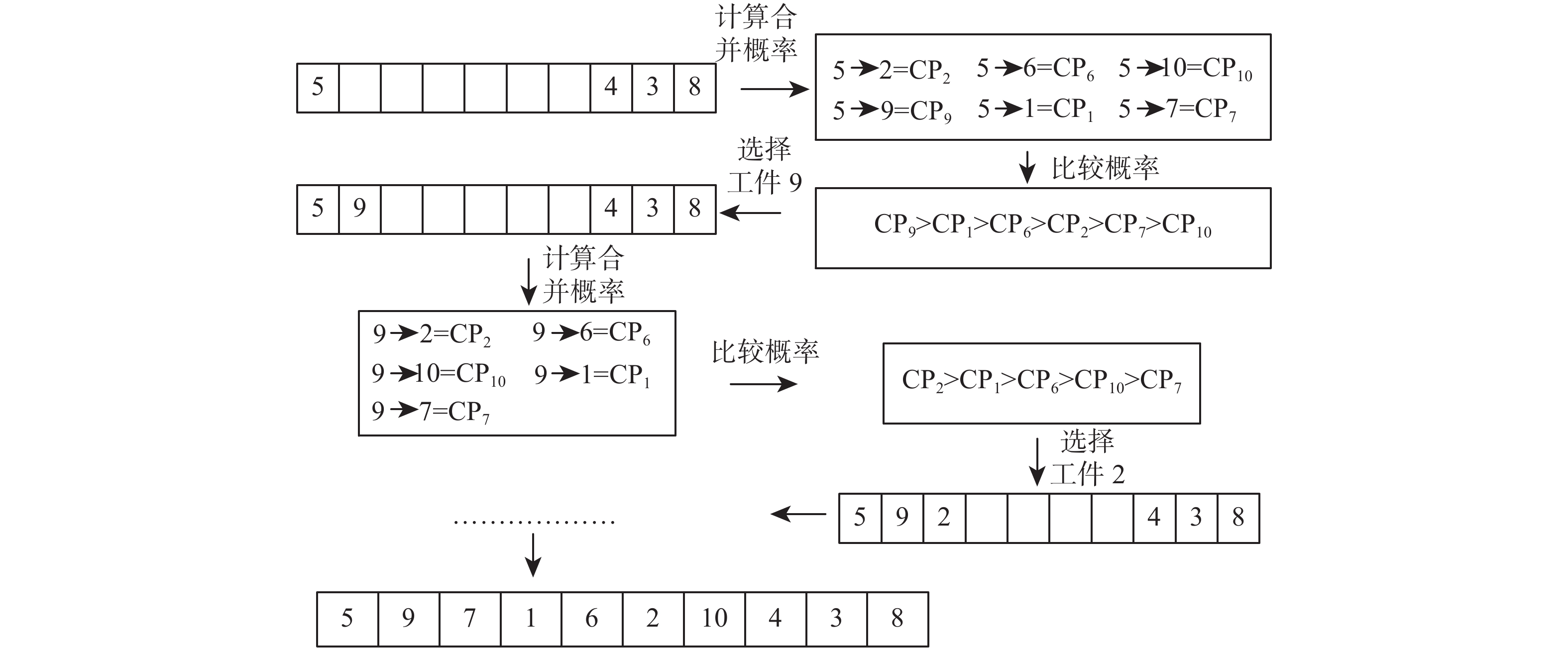
为了进一步提高算法搜索到最优解的机会，对每一代染色体进行重组。首先随机选择 $N$ 个切点，将一条完整的染色体分割成 $N + 1$ 个片段，再从这些片段中选择出长度最长的片段进行重组。以工件数为10切点数为2为例，如图12，切割完成后的段数为3段，分别为{5，2}、{2，6，10，9，1，7}及{7，4，3，8}，选择长度较长的片段进行重组，过程如图13所示。

2.5 留存优势解

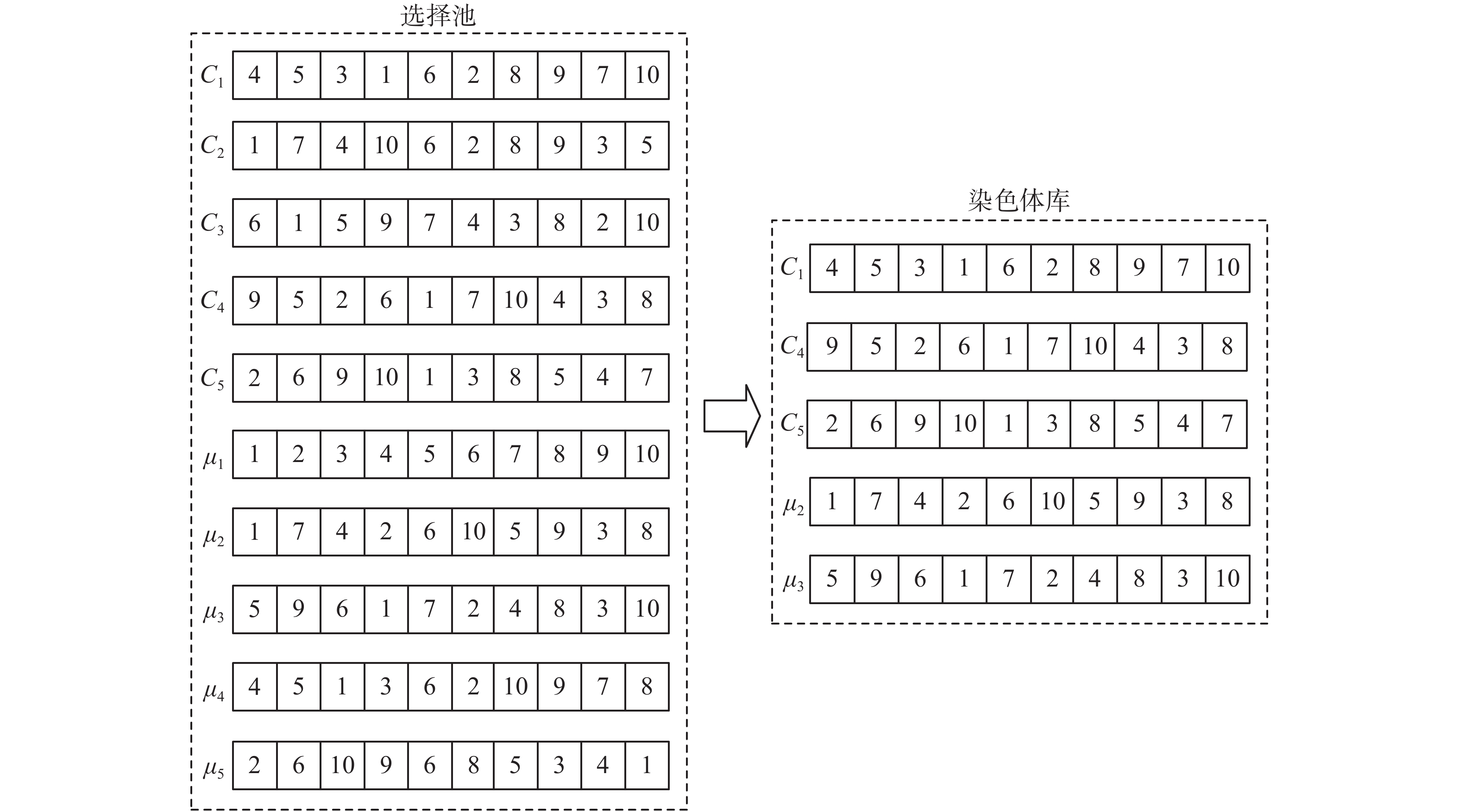
将重组后的GA最新子代 ${\mu _i}$ 和人工染色体C_i放入选择池，使用二元竞赛法^[17]选择出优秀染色体作为子代进入下一代进化。首先，从选择池中随机选择两条染色体，比较适应度，选择适应度较大的染色体放入染色体库，适应度较小的染色体放回选择池继续筛选，反复执行上述步骤，直到染色体库中染色体的数量满足设定的群体大小，如图14。

3 实验结果分析

为了评估所提出的算法的性能，本研究将通过对不同实例进行测试，使用误差率(ER)作为对比指标，与其他算法进行比较。误差率是指测试中算法所得最优解与实例已知最优解的差值占实例已知最优解的比例，ER计算公式为

${\rm{ER}}{_i} = \frac{{{C_{\max }} - {U_i}}}{{{U_i}}} \times 100{\text{%}} $

(8)

式中： ${U_i}$ 是实例的已知最优解； ${C_{\max }}$ 是测试算法的最优解。

本文所提算法由C++语言编写，程序的运行环境为：处理器Intel(R) Core(TM) i5-4005U CPU @ 3.40 GHz，内存为4.0 GB的计算机。在本文中，选择了29个调度问题进行比较，其中21个Reeves实例和8个Taillard实例，每个实例独立运行30次，并求出ER的平均值。为了达到性能评价的目的，在SGA^[18]、ACGA^[19]、p-ACGA^[10]、BBEDA^[18]、LMBBEA^[20]、p-IACGA的参数设置上选择了最佳的、相同的参数配置以保证了算法的可比性。

以SGA、ACGA、p-ACGA、BBEDA、LMBBEA和p-IACGA计算Taillard实例，结果如表1所示。从表1可以看出，ta005、ta010、ta020、ta030、ta070和 ta080这6个实例中的ER值均为0，即找到了6个与实例已知解相同的解，多于其他算法所能找到的个数。尽管在 ta050实例中，BBEDA和LMBBEA的 ER值为0.85，p-IACGA的ER值为0.97，前两者的结果优于p-IACGA，但是p-IACGA的平均值ER为0.32%，均低于其他算法，表明p-IACGA的整体求解问题的性能优于其他算法。同理，用这些算法计算Reeves实例，结果如表2。通过对Reeves的21个实例测试，发现p-IACGA在 $\rm{Re} c$ 01、 $\rm{Re} c$ 03、 $\rm{Re} c$ 09、 $\rm{Re} c$ 11和 $\rm{Re} c$ 35实例中ER的值为0，找到了5个与实例已知解相同的解，多于其他算法，且p-IACGA的平均误差率为0.46，均小于其他算法，充分表明p-IACGA求解PFSP的优良性能。

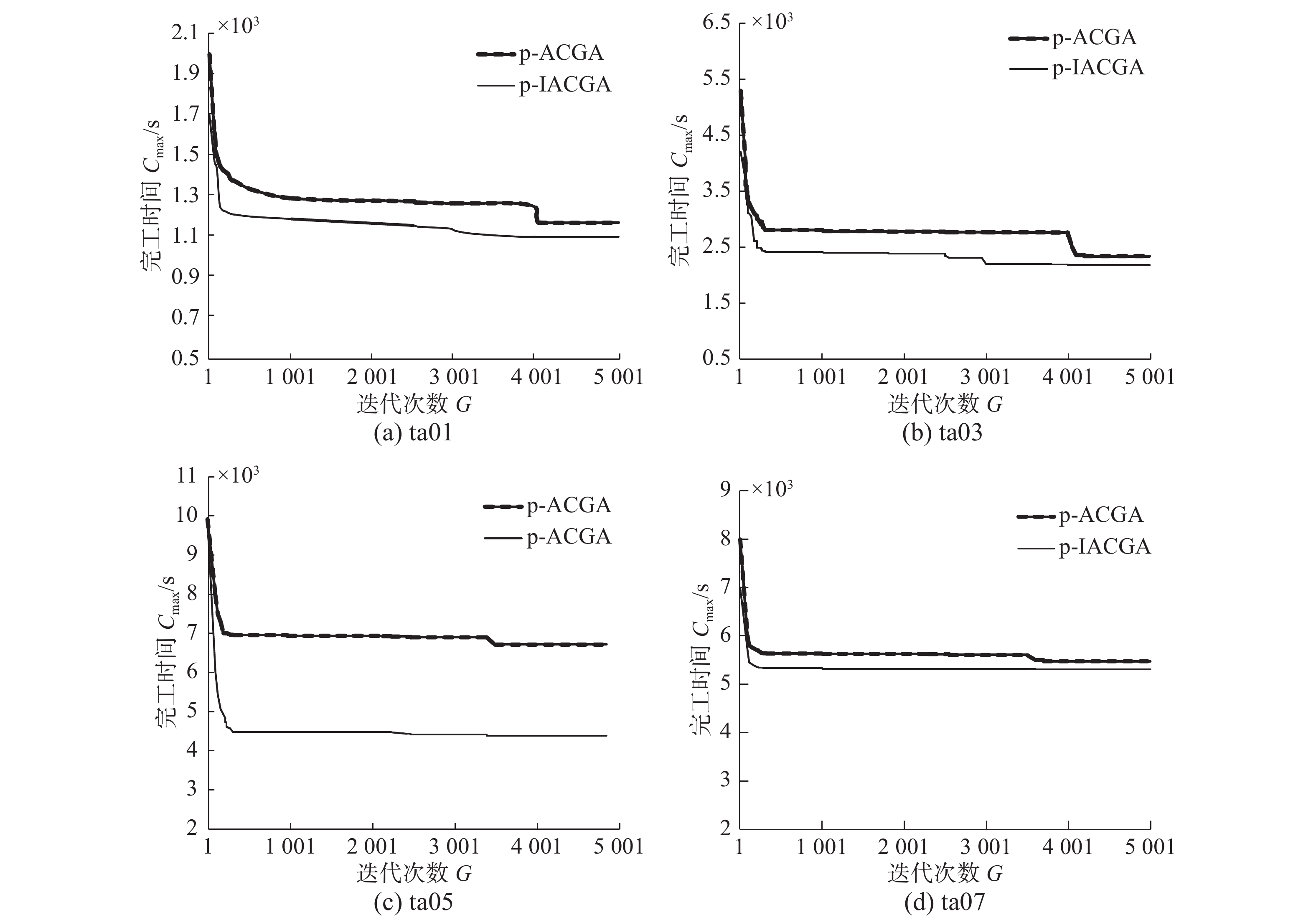
为了更直观地比较算法性能，图15给出了关于p-ACGA和p-IACGA两个算法测试部分Taillard实例的收敛图。从图15中可以看出，在相同的最大迭代次数下，p-IACGA的收敛速度比p-ACGA更快。在进化初期，算法通过优化初始方法提高初始解的质量，保证进化过程中解的质量；采用节点信息浓度和路径信息度相结合的方式生成矩阵，提高了区块质量。在进化的后期，应用二元竞赛法来寻找具有更优适应值的解，加快了进化速度。

通过实验数据分析，对于求解PFSP，本文提出的p-IACGA相较于SGA、ACGA、p-ACGA、BBEDA、LMBBEA和p-IACGA具有较优的求解性能。

4 结束语

本文针对置换流水车间调度问题，通过对p-ACGA改进，提出了p-IACGA。该算法初始化采用随机机制和改进反向学习机制相结合的方式，提高了初始种群的多样性和质量。进一步考虑了工件与所在解序列的位置关系，对节点信息素浓度进行了分析，通过位置信息素矩阵和相依信息素矩阵挖掘区块加快了收敛速度，提高了最终解的质量。该算法保留了传统GA的交叉、变异等操作，通过若干代的GA进化过程产生精英群体，不断更新区块，提高了人工染色体的质量和更新速度。实验中，通过Taillard和Reeves实例进行测试，以误差率作为比较指标，将结果与其他算法比较，验证了p-IACGA的有效性。

未来研究方向可以将所提出的p-IACGA应用于其他组合优化问题，如旅行商问题、车辆路径问题等。也可以通过改进该算法对PFSP的最小化流程时间、最小化延迟时间等其他一个或多个目标进行研究。