可拓数据挖掘[1-2]是可拓学与数据挖掘结合的产物,其把数据与基元对应起来,利用可拓集、可拓推理和关联函数等,从数据库已有的数据中,挖掘与相关领域问题有关的变换知识和规律,为决策者未来的相关决策提供理论依据。相关学者将其应用到经济、管理、营销等多个领域,获得了多项国家级基金的支持,取得了一些研究成果[3-7]。但将其运用到国防军事领域的文献还未见。
在导弹武器系统性能的分析与研究中,各参数指标会积累大量的信息、知识和实验数据,如果能从这些实验数据中挖掘出对导弹武器系统设计、定型及性能改进有价值的知识,会显得尤其重要。本文将可拓数据挖掘理论引入到导弹武器系统性能的分析与研究中。当导弹武器系统某些参数指标发生变化时,由于参数指标之间的相关性,必会导致其他参数指标及导弹性能指标发生传导变换,利用挖掘有关正质变域和正量变域的可拓分类知识,挖掘出各项参数指标对其他参数指标及各性能指标的影响规律及影响程度,可以为导弹武器系统的设计、定型及性能的改进提供重要的理论参考。
1 挖掘有关正质变域的可拓推理知识为了利用基元[1]和基元集描述信息、知识和数据,文献[2]给出了信息元和信息元集的概念。将预处理的信息和数据用信息元和信息元集[2]刻画为
| $I = \{ {I_i}{\rm{, }}\,\,i{\rm{ = 1,2,}} \cdots {\rm{,}}n \} $ | (1) |
式中
为了评价信息元符合要求的程度[8],根据专业知识和实际情况,确定评价特征
| $ \begin{array}{*{20}{c}} W = \{ D\} = \{ {D_i}\left| {{D_i}} \right. = ({I_i}, {C_D}, {U_i}) = \\ \left[ {\begin{array}{*{20}{c}} {{I_i}, }&{{d_1}, }&{{u_{i1}}} \\ {}&{{d_2}, }&{{u_{i2}}} \\ {}& \vdots & \vdots \\ {}&{{d_q}, }&{{u_{iq}}} \end{array}} \right], \, i = 1, 2, \cdots , n\} \end{array} $ | (2) |
实轴上的区间给定
| $\rho (x, Y) = \left| {x - \frac{{{y_1} + {y_2}}}{2}} \right| - \frac{{{y_2} - {y_1}}}{2}$ |
设
| $k(x) = \frac{{\rho (x, b, {X_0})}}{{D(x, {X_0}, X)}}$ | (3) |
式中
| $ \rho (x, b, {X_0}) = {a_2} - x,\,\,\,\, x < b $ |
| $ D(x, {X_0},X) = \rho (x, X) - \rho (x, {X_0}) + {a_1} - b,\,\, \,\,x \in {X_0} $ |
根据式(3)建立关于评价特征
| $ {k_{ip}} = \frac{{{k_p}({D_{ip}})}}{{\mathop {\max }\limits_{p \in \{ 1, 2, \cdots , q\} } \left| {{k_p}({D_{ip}})} \right|}} $ | (4) |
式中:
建立评价信息元
| $K({D_i}) = \sum\limits_{p = 1}^q {{\alpha _p}{k_{ip}}} $ | (5) |
由层次分析法确定权系数
| $ \begin{aligned} & {E_ + } = \{ {I_i}/{I_i} \in \{ I\} , {D_i} = ({I_i}, {C_D}, {U_i}), K({D_i}) > 0\} \\ & {E_ - } = \{ {I_i}/{I_i} \in \{ I\} , {D_i} = ({I_i}, {C_D}, {U_i}), K({D_i}) < 0\} \\ & {E_0} = \{ {I_i}/{I_i} \in \{ I\} , {D_i} = ({I_i}, {C_D}, {U_i}), K({D_i}) = 0\} \end{aligned} $ |
对任意信息元
| $\begin{gathered} \{ \varphi I\} = \{ {{I'}_i}\left| {{{I'}_i} = \varphi {I_i}} \right. = ({{O'}_i}, C, {{V'}_i}) = \\ \left[ {\begin{array}{*{20}{c}} {{{O'}_i}, }&{{c_1}, }&{{{v'}_{i1}}} \\ {}&{{c_2}, }&{{{v'}_{i2}}} \\ {}& \vdots & \vdots \\ {}&{{c_m}, }&{{{v'}_{im}}} \end{array}} \right], \;i = 1, 2, \; \cdots , n\} \\ \end{gathered} $ | (6) |
变换
| $ \begin{array}{c} \{ {}_\varphi {T_D}D\} = \{ {D'_i}\left| {{{D'}_i}} \right. = {}_\varphi {T_{{D_i}}}{D_i} = ({I'_i}, {C_D}, {U'_i}) =\\ \left[ {\begin{array}{*{20}{c}} {{{I'}_i}}&{{d_1}}&{{{u'}_{i1}}} \\ {}&{{d_2}}&{{{u'}_{i2}}} \\ {}& \vdots & \vdots \\ {}&{{d_q}}&{{{u'}_{iq}}} \end{array}} \right], \;\;i = 1, 2, \cdots , n\} \end{array}$ | (7) |
对
| $K({}_\varphi {T_{{D_i}}}{D_i}) = \sum\limits_{p = 1}^q {{\alpha _p}{{k'}_{ip}}} $ | (8) |
在变换
根据变换实施前后的
| $ \begin{array}{c} {\mathop D\limits_ {\bullet +} }({}_\varphi {T_{{D_i}}}) = \{ {D_i}\left| {{D_i}} \right. = ({I_i}, {C_D}, {U_i}), K({D_i}) \leqslant 0, \\ K({}_\varphi {T_{{D_i}}}{D_i}) > 0, i \in {J_{{{\mathop D\limits_ \bullet }_ + }}}\} \end{array}$ | (9) |
式中:
| $ \begin{array}{c} {D_ + }({}_\varphi {T_{{D_i}}}) = \{ {D_i}\left| {{D_i}} \right. = ({I_i}, {C_D}, {U_i}), K({D_i}) > 0, \\ K({}_\varphi {T_{{D_i}}}{D_i}) > 0, i \in {J_{{D_ + }}}\} \end{array} $ | (10) |
式中:
| $ {\mathop E\limits_ {\bullet +} }(\varphi ) = \{ {I_i}\left| {} \right.{I_i} = ({O_i}, C, {V_i}), {D_i} \in {\mathop D\limits_ {\bullet +} }({}_\varphi {T_{{D_i}}}), i \in {J_{{{\mathop D\limits_ \bullet }_ + }}}\} $ | (11) |
正稳定域
| $ {E_ + }(\varphi ) = \{ {I_i}\left| {} \right.{I_i} = ({O_i}, C, {V_i}), {D_i} \in {D_ + }({}_\varphi {T_{{D_i}}}), i \in {J_{{D_ + }}}\} $ | (12) |
设
若
| $L:{v_{ij}} \in {\mathop V\limits_{ \bullet {j + }}}(i \in {J_{{{\mathop D\limits_ \bullet }_ + }}}, {c_j} \in \{ c_j'\} )$ |
则可获得关于评价信息元正质变域的可拓推理知识[1, 9-13]:
| $ \begin{array}{c} \{ {I_i} \mathrel\backepsilon I\} \wedge \left\{ {K({D_i}) < 0} \right\} \wedge \{ \varphi {I_i} = I_i'\} \wedge \{ {I_i} \mathrel\backepsilon L\} \wedge\\ \left\{ {v_{ij}' \in \mathop V\limits_{ \bullet {j + }}'} \right\} \Rightarrow (\varphi{\text{为正质变换}} ) \wedge \{ {I_i} \in {\mathop E\limits_ {\bullet + }}(\varphi )\} \wedge \\ \left\{ {K({}_\varphi {T_{{D_i}}}{D_i}) > 0} \right\} \wedge \left\{ {{\beta _i} \in [{\beta _{\min }}, {\beta _{\max }}], {\beta _i} > 0} \right\} \end{array}$ | (13) |
由可拓推理知识式(13)表示如果信息元[8]
在海军某型导弹武器系统的设计、定型过程中,产生了大量的实验数据。由于篇幅所限,仅通过部分实验数据研究本文的可拓分析过程。
改进导弹的结构设计及某些电子部件(记为变换
已有的4个批次该型号导弹武器系统,用信息元和信息元集描述(如式(1)),其中
| 表 1 导弹武器系统关于参数指标的量值表 Tab.1 The value table of a missile weapon system |
为了对该型导弹武器系统的各项性能进行综合分析,引入3个新的性能指数作为评价特征。
1)杀伤指数
| ${d_1} = {c_1} \times {c_2} \times {c_3}$ | (14) |
2)探测指数
| ${d_2} = {c_9} \times \left[ {1 - ({c_{10}} + {c_{11}} - {c_{10}} \times {c_{11}})} \right]$ | (15) |
3)突防生存指数
| ${d_3} = {c_4} \times {c_5} \times {c_6} \times {c_7} \times (1 - {c_8})$ | (16) |
将各参数指标的量值代入式(14)~(16),计算出各导弹关于3个评价特征的量值,得到评价信息元集如式(2),其中,
根据实验数据和专家意见,取
根据式(3)建立评价特征
| ${k_1}(x) = \frac{{\rho (x, 0.900\;0, {X_{01}})}}{{D(x, {X_{01}}, {X_1})}}$ | (17) |
式中
| $\rho (x, 0.900\;0, {X_{01}}) = 0.450\;0 - x, \quad x \leqslant 0.900\;0 $ |
| $D(x, {X_{01}}, {X_1}) = \left\{ \begin{array}{l} - 0.550\;0, \begin{array}{*{20}{c}} {} \end{array}\;x = 0.456\;0{\text{或}} 0.450\;2 \\ - 0.1, \;\begin{array}{*{20}{c}} {} \end{array}x = 0.425\;8{\text{或}}0.420\;3 \end{array} \right.$ |
同理,类似于式(17),可定义
| ${k_2}(x) = \frac{{\rho (x, 0.1, {X_{02}})}}{{D(x, {X_{02}}, {X_2})}}$ | (18) |
式中
| $\rho (x, 0.1, {X_{02}}) = 0.05 - x, \quad x \leqslant 0.1 $ |
| $ D(x, {X_{02}}, {X_2}) = \left\{ \begin{array}{l} - 0.015,\,\,\,\,\,\, \;x = 0.038\;9{\text{或}} 0.048\;6{\text{或}} 0.041\;4 \\ - 0.065,\,\,\,\,\,\, \;x = 0.053\;4 \end{array} \right. $ |
| ${k_3}(x) = \frac{{\rho (x, 0.6, {X_{03}})}}{{D(x, {X_{03}}, {X_3})}}$ | (19) |
式中
| $\rho (x, 0.6, {X_{03}}) = 0.25 - x, \quad x \leqslant 0.6 $ |
| $ D(x, {X_{03}}, {X_3}) = \left\{ \begin{array}{l} - 0.4,\,\,\,\,\,\, \;x = 0.26 \\ - 0.05,\,\,\,\,\,\, \;x = 0.232\;4{\text{或}} 0.218\;1{\text{或}} 0.212\;6 \end{array} \right. $ |
根据层次分析法,确定权系数为 a1=0.5,a2=0.2,a3=0.3。
2.3 实施主动变换,改变参数指标的量值实施变换
| 表 2 变换 φ 后该导弹关于参数指标的量值 Tab.2 The value of the missile on the characteristics of the table after the transformation φ |
根据表2中的参数指标值及式(14)~(19),通过MATLAB计算机编程,计算出变换
|
Download:
|
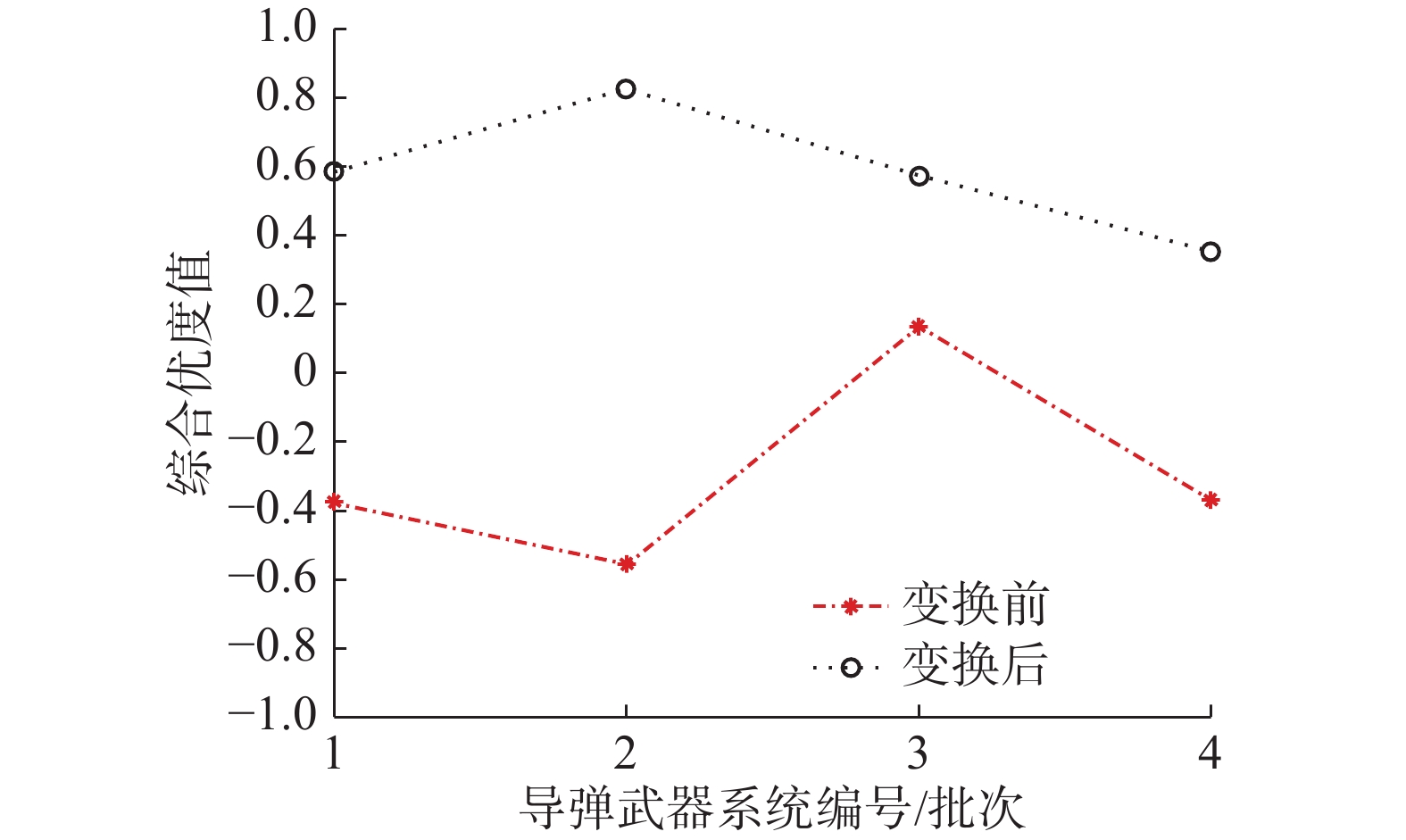
| 图 1 变换实施前后的综合优度 Fig. 1 Comprehensive advantages before and after transformation | |
从图1可见,
变换
| 表 3 变换 φ 实施前后性能的综合优度对比 Tab.3 Comparison of the performance before and after transformation φ |
发生正质变的3个批次导弹武器系统
综合,根据文献[1-2]可得到关于各性能指标提高的可拓推理知识:
1)
| $[{\beta _{\min }}, {\beta _{\max }}] = \left[ {0.768\;2, 1.428\;6} \right]$ |
2)
| $K({}_\varphi T{}_{{D_3}}{D_3}) - K({D_3}) = 0.513\;3$ |
可拓数据挖掘把可拓集理论与数据挖掘相结合,挖掘可拓分类知识、传导知识以及其他有关变换的知识。本文通过引入杀伤指数、探测指数和突防生存指数3个新的性能指数作为评价特征,改进导弹结构设计,使导弹武器系统的某些参数指标发生变化,利用挖掘正质变域和正量变域的知识,初步挖掘出某些参数指标对其他参数指标及性能指标的影响规律和程度,寻求导弹武器系统性能分析研究中的有价值的知识。通过简单的实例分析,挖掘出了某些参数指标对某型导弹武器系统各项性能的影响程度。可见,将可拓数据挖掘的理论与方法用于导弹等武器系统各性能的分析与研究,可为导弹等武器系统的设计、定型、改进提供数量化的理论依据。下一步,将结合该型导弹武器系统工厂鉴定实验及设计定型实验中产生的大量实验数据,利用计算机编程仿真,深入挖掘各项参数指标对该型战术导弹武器系统性能的影响规律及程度,为其设计、定型、改进提供理论和实践参考。
| [1] |
YANG Chunyan, CAI Wen. Extenics theory, method and application[M]. Beijing: Science Press, 2013: 107–276.
( 0) 0)
|
| [2] |
蔡文, 杨春燕, 陈文伟, 等. 可拓集与可拓数据挖掘[M]. 北京: 科学出版社, 2008: 14–95.
( 0) 0)
|
| [3] |
孙江, 张海鹰, 张新春. 基于可拓集方法的导弹毁伤评估[J]. 战术导弹技术, 2012(6): 32-37. SUN Jiang, ZHANG Haiying, ZHANG Xinchun. Damage evaluation of missile based on extensive set method[J]. Tactical missile technology, 2012(6): 32-37. (  0) 0)
|
| [4] |
张金春, 张家宾, 李超亚, 等. 基于可拓数据挖掘技术的故障诊断和预防方法[J]. 兵工自动化, 2015, 34(5): 1-4. ZHANG Jinchun, ZHANG Jiabin, LI Chaoya, et al. Methods of fault diagnosis and prevention of equipment based on extenics and data mining technology[J]. Ordnance industry automation, 2015, 34(5): 1-4. (  0) 0)
|
| [5] |
朱佳俊, 郑建国, 李金兵. 基于粗糙分类的不确定可拓群决策数据挖掘及应用[J]. 控制与决策, 2012, 27(6): 850-854. ZHU Jiajun, ZHENG Jianguo, LI Jinbing. Rough classification algorithm for uncertain extension group decisionmaking[J]. Control and decision, 2012, 27(6): 850-854. (  0) 0)
|
| [6] |
王建林, 杨印生, 王学玲. 基于可拓数据挖掘的黄河三角洲土地利用评价[J]. 吉林大学学报(工学版), 2012, 42(S1): 479-483. WANG Jianlin, YANG Yinsheng, WANG Xueling. Evaluation of land use in Yellow River delta based on extension data mining[J]. Journal of Jilin University(engineering and technology edition), 2012, 42(S1): 479-483. (  0) 0)
|
| [7] |
叶广仔, 李卫华. 可拓数据挖掘在教师科研考核评价中的应用[J]. 数学的实践与认识, 2015(12): 53-59. YE Guangzai, LI Weihua. The application of extension data mining in teachers scientific research evaluation[J]. Mathematics in practice and theory, 2015(12): 53-59. (  0) 0)
|
| [8] |
蔡文, 杨春燕. 评价信息元及其原信息元的获取方法[J]. 智能系统学报, 2009, 4(3): 234-238. CAI Wen, YANG Chunyan. A method for evaluation of information-elements and acquirement of the original information element[J]. CAAI transactions on intelligent systems, 2009, 4(3): 234-238. DOI:10.3969/j.issn.1673-4785.2009.03.007 (  0) 0)
|
| [9] |
王丰, 李日华, 尹付梅, 等. 基于优度评价方法的空袭目标威胁评估[J]. 兵工自动化, 2011, 30(7): 39-41. WANG Feng, LI Rihua, YIN Fumei, et al. Threat evaluation of air attack target based on priority degree evaluation method[J]. Ordnance industry automation, 2011, 30(7): 39-41. DOI:10.3969/j.issn.1006-1576.2011.07.012 (  0) 0)
|
| [10] |
王丰, 袁延昭, 张新春, 等. 共轭分析与传导度在导弹武器系统作战效能研究中的应用[J]. 兵工自动化, 2013, 32(11): 24-26. WANG Feng, YUAN Yanzhao, ZHANG Xinchun, et al. Application of conjugate analysis and conductivity in missile weapon system combat efficiency study[J]. Ordnance industry automation, 2013, 32(11): 24-26. DOI:10.7690/bgzdh.2013.11.006 (  0) 0)
|
| [11] |
王丰, 张磊, 胡春万. 基于多级优度评价方法的导弹武器系统效能评估[J]. 指挥控制与仿真, 2017, 39(3): 74-77. WANG Feng, ZHANG Lei, HU Chunwan. Efficiency evaluation of missile weapon system based on multi-level priority degree evaluation method[J]. Command control and simulation, 2017, 39(3): 74-77. DOI:10.3969/j.issn.1673-3819.2017.03.017 (  0) 0)
|
| [12] |
王丰, 顾佼佼, 徐宇茹. 多指标可拓预测方法在航空装备技术保障质量预测中的应用[J]. 兵器装备工程学报, 2019, 40(1): 47-50. WANG Feng, GU Jiaojiao, XU Yuru. Application of multi-index extension prediction method in quality prediction of aviation equipment technical support[J]. Journal of ordnance and equipment engineering, 2019, 40(1): 47-50. DOI:10.11809/bqzbgcxb2019.01.010 (  0) 0)
|
| [13] |
彭本红, 武柏宇, 周叶. 冷链物流断链风险的熵权可拓评价研究[J]. 北京交通大学学报(社会科学版), 2017, 16(1): 110-119. PENG Benhong, WU Baiyu, ZHOU Ye. A study on the risk assessment of cold chain scission based on entropy weight and extension decision model[J]. Journal of Beijing Jiaotong University(social sciences edition), 2017, 16(1): 110-119. (  0) 0)
|
| [14] |
赵蕾, 陈方予, 郝昀, 等. 弹道导弹突防干扰机收发隔离方法研究[J]. 现代防御技术, 2016, 44(6): 1-6. ZHAO Lei, CHEN Fangyu, HAO Yun, et al. Isolation between receiving and transmitting of BM penetration jammer[J]. Modern defense technology, 2016, 44(6): 1-6. DOI:10.3969/j.issn.1009-086x.2016.06.001 (  0) 0)
|
| [15] |
于建国, 郑咏岚. 变推力固体火箭发动机战术导弹弹道优化研究[J]. 现代防御技术, 2014, 42(4): 20-23, 38. YU Jianguo, ZHENG Yonglan. Trajectory optimization design of tactical missile with variable thrust solid rocket engine[J]. Modern defense technology, 2014, 42(4): 20-23, 38. DOI:10.3969/j.issn.1009-086x.2014.04.004 (  0) 0)
|
| [16] |
刘培毅, 刘鑫, 孙迎丰. 数据挖掘在战术导弹保障辅助决策系统中的应用[J]. 新技术新工艺, 2016(8): 36-39. LIU Peiyi, LIU Xin, SUN Yingfeng. The application of data mining in the decision support system of armament maintenance support[J]. New technology & new process, 2016(8): 36-39. DOI:10.3969/j.issn.1003-5311.2016.08.011 (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


