2. 西南交通大学 信息科学与技术学院,四川 成都 610031;
3. 电子科技大学 经济与管理学院,四川 成都 610054
2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China;
3. School of Management and Economics, University of Electronic Science and Technology of China, Chengdu 610054, China
作为粒计算理论处理不确定问题的重要方法之一,三支决策是加拿大学者Yao[1] 在近十年来提出并发展起来的一种处理不确定性决策的粒计算方法,是一种符合人类认知过程的“三分而治”模型。三支决策的主要思想是:在决策过程中将整体分为3个部分或3个粒,对于不同的部分或者粒度采取不同的决策行为或处理策略。粗糙集理论是三支决策的一种典型代表,它利用上下近似集将论域分为3个互不相交的区域。下近似集生成正域,上近似集的补集生成负域,正域和负域诱导确定性规则;上下近似集的差集形成边界域,边界域诱导可能性规则。进一步地,将三支决策思想应用到粗糙集理论中,可赋予粗糙集新的语义解释:从正域里得到的正规则可以表示接受或赞成某事物;从负域里获取的负规则可以表示拒绝或反对某事物;落在边界域上的规则具有不确定性,需要进一步观察或思考,此时需要作出“延迟决策”的判断。可以看到,粗糙集理论中的3个论域对应了决策分析中的3种决策结果(即三支决策),这与人类在处理实际决策问题的方法是一致的。三支决策通过“分而治之”和自下而上“化繁为简”的思想,按照分治法将复杂问题转化为3个规模较小的问题,从而提高决策效率、减少决策成本、降低决策时间。通过对现有文献的整理和分析,三支决策的研究主要集中在理论、方法、算法和应用4个层面上。
在理论研究上,胡宝清[2]将几类有代表性的三支决策模型统一到一个数学理论框架中,研究了三支决策空间问题。李小南等[3]提出了一种基于子集评估的一般性三支决策模型。Yao [4]给出了一种三支决策与认知计算的研究框架。Ciucci等[5]利用一个图形来探讨三支决策下的三值逻辑问题。Abd El-monsef等[6]将决策粗糙集模型中的等价关系扩展到广义二元关系,提出了一种具有5个决策划分区域的扩展决策粗糙集模型。马卫民等[7]和钱宇华等[8]分别讨论了多论域和多粒度情形下的三支决策理论模型。Deng等[9]研究了模糊集的决策三支近似,并进一步考虑了基于阴影集的三支决策模型。祁建军等[10]讨论了三支决策与概念格的理论模型。张清华等[11]探讨了三支决策过程中,两类分类错误相关问题。刘盾等[12]提出了一种4层次决策粗糙集模型。
在方法研究上,李华雄等[13]根据不同决策者的不同风险偏好,提出一种多视角三支决策模型,并分析了乐观、中性和悲观风险偏好下的决策规则。Herbert等[14] 提出了博弈三支决策模型,其主要思想是:把代价损失函数作为博弈矩阵的收益函数,并利用Nash均衡思想来求解三支决策阈值问题。杨晓平等[15]考虑了多个代理人情形下的决策粗糙集模型,进而提出一种多代理三支决策方法。刘盾等[16-18]考虑了当损失函数为几类典型的不确定性测度时,相应不确定性三支决策阈值的获取方法;进而将区间性、随机性和模糊性3种不确定测度引入到决策粗糙集中,提出了一系列不确定性三支决策模型。Yao等[19]建立了基于阴影集的不确定性三支决策模型。Li等[20]讨论了三支决策中边界域的不确定性建模问题。Zhao等[21]考虑了基于模糊概率测度的区间模糊决策粗糙集模型。Zhou[22]讨论了一种多分类决策粗糙集模型。Zhang等[23]提出了基于Gini系数的三支决策模型。梁德翠等[24]考虑了在多人决策环境下,基于群决策的三支决策问题。张楠等[25]从决策理论中的效用函数出发,讨论了基于效用函数的三支决策模型。Liu等[26]将前景理论引入到三支决策过程中,研究了行为视角下的群决策三支决策模型。郎广名等[27]分析了决策粗糙集相应决策规则的冲突问题。
在算法研究上,现有研究主要集中在属性约简和规则获取两个方面。在属性约简方面,Yao等[28]最早研究了决策粗糙集的属性约简理论。他们发现经典代数粗糙集约简理论已不再适用于决策粗糙集模型,并从性质保留性和属性独立性2个方面入手,给出了一种广义的概率粗糙集约简定义。在此基础上,Zhao等[29]利用信息表中的区分矩阵,借鉴保持决策属性不变和决策区域不变思想,给出了基于决策粗糙集的2种属性约简方法。李华雄等[30]提出决策粗糙集正域约简定义和算法,并指出:不同于Pawlak粗糙集模型,决策粗糙集模型中的正域变化具有非单调性,其大小随着属性集的减少可能会增大。基于这种思想,他们提出一种保持正域最大的启发式约简算法。贾修一等[31]考虑了由代价损失函数引起的决策风险问题。他认为最优约简应满足总体决策风险最小原则,并提出了一种基于决策风险最小的属性约简方法。闵帆等[32]提出了基于代价敏感最小化的属性约简方法。鞠恒荣等[33]将决策风险最小化的思想引入到不完备信息系统中,提出了
在实际应用上,三支决策已经在医疗诊断、石油开采、论文审稿、政策制定、环境管理、文本分类、垃圾邮件过滤、产品检验、矿床选择等领域得到了较好的应用[42]。
通过对已有文献分析发现,国内外学者主要对三支决策理论模型、数学性质、算法设计、应用背景进行研究,对于三支决策系统性整理和总结的论述还较为少见。本文在现有研究的基础上,分别从时间和空间两个维度出发,以时序性和层次性为研究脉络,提出时间三支决策和空间三支决策基本模型,并详细讨论不同模型的建模机理和应用前景。最后,进一步对三支决策的时空性作了深入探讨和分析。
1 三支决策模型与基本概念假设
| $ f:U \to \left\{ {{R_1},\;{R_2},\;{R_3}} \right\} $ | (1) |
式中:
| $ \begin{array}{l} R_1^c = {R_2} \cup {R_3}\\ R_2^c = {R_1} \cup {R_3}\\ R_3^c = {R_1} \cup {R_2} \end{array} $ | (2) |
对于3个区域
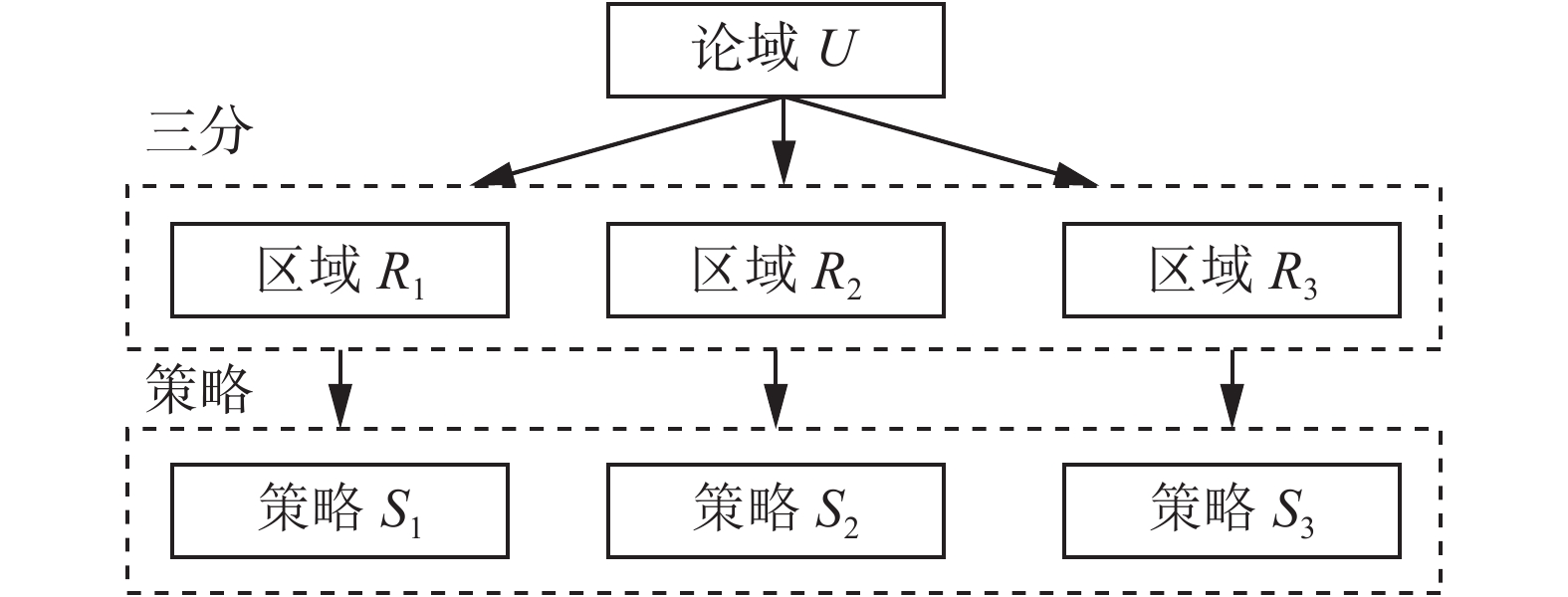
|
Download:
|
| 图 1 三支决策模型示意图 Fig. 1 Three-way decision model diagram | |
在图1中,二元关系
此外,三支决策模型在众多不确定性理论中也有不同的表示方法,文献[43]通过结合区间集、模糊集、粗糙集、阴影集和偏序集5种不确定性度量来说明三支决策的构造过程。表1给出了不同情形下的三支决策模型。
| 表 1 不同情形下的三支决策模型 Tab.1 The three-way decision models under different conditions |
以粗糙集为例,对于某个概念

|
Download:
|
| 图 2 三支决策与粗糙集理论的转换模型 Fig. 2 Transformation model between 3WD and rough sets | |
对于三支决策基本模型,提出了一种广义三支决策和狭义三支决策的模型[43]。广义三支决策主要从不同的内涵和外延去探讨不同的决策模型,主要包括三支决策空间、三支决策一般模型、三支决策与认知模型、三支决策与形式概念分析、三支决策逻辑、三支决策与商空间等。狭义三支决策侧重对模型的语义解释、方法设计和实际应用,主要包括三支决策分类与聚类、代价敏感三支决策、不确定性三支决策、三支推荐、机器学习与三支决策等。进一步地,在2009—2018年连续十届国际粗糙集联合学术会议(IJCRS),以及2011—2018年连续八届中国粒计算与知识发现学术会议(CGCKD)上都举办了与“三支决策与决策粗糙集”相关的主题研讨会。国内学者先后出版了4本专著:《三支决策理论与应用》[44]、《三支决策与粒计算》[45]、《三支决策: 复杂问题求解方法与实践》[46]、《粒计算、商空间及三支决策的回顾与发展》[47],介绍了三支决策研究的最新动态。国际著名SCI 期刊International Journal of Approximate Reasoning、Information Sciences、Knowledge-based Systems和International Journal of Machine Learning and Cybernetics等分别出版多本专辑来介绍和推动三支决策研究领域的发展。
2 基于时间维度三支决策模型在很多决策问题中,其决策过程往往呈现出实时性、多次性、序贯性的特征。决策者需要考虑过去(past)、现在(now)和将来(future),或是昨天(yesterday)、今天(today)和明天(tomorrow)这些时间维度对决策结果的影响。本文首先以北京获得的2008年奥运会举办权时的投票过程作为例子来阐述基于时间维度的三支决策思想。
2001年7月13日,国际奥委会第112次全会在俄罗斯莫斯科召开,与会全体委员将投票选举出第29届夏季奥运会的举办城市。有北京、多伦多、伊斯坦布尔、巴黎和大阪5个候选城市参加选举,一共118名国际奥委会委员进行投票。在第一轮投票中,有14名申办城市委员和时任主席萨马兰奇不参加投票,实际有104名委员投票,2票弃权,有效票102张。其中,北京获得44票,多伦多获得20票,伊斯坦布尔获得17票,巴黎获得15票,大阪获得6票。第一轮投票结束,北京占据优势,大阪得票最少被淘汰,其余3个城市作为待定城市进入下一轮竞选。在接下来的第二轮投票中,有106名委员(2名日本委员因大阪淘汰获得投票权)实际参加投票,1票弃权,有效票105张。最终,北京获得56票,超半数票成功获得举办权,多伦多、巴黎、伊斯坦布尔分别获得22票、18票和9票被淘汰。从投票过程可以看到,随着外界环境和时间的变化,中选城市(
此外,Jeffery通过Savage打鸡蛋的故事通俗易懂地描述了三支决策随时间变化的序贯决策过程。故事大意为:孩子们早餐想吃煎鸡蛋,厨房里有6个鸡蛋,丈夫Savage自告奋勇过来帮忙。在打鸡蛋的过程中,鸡蛋有可能是好鸡蛋也可能是坏鸡蛋。如果是好鸡蛋,把它直接打到碗里和前面鸡蛋合并即可;如果是坏鸡蛋,所有的鸡蛋都会被扔掉。Savage是一个决策论爱好者,他需要设计在每打一颗鸡蛋时相应的行动策略,使得总体决策代价最小。表2给出了Savage在第i次决策过程中可能采取的3种策略和后果。
| 表 2 Savage可能采取的3种策略和后果 Tab.2 Three strategies and results of Savage’s omelet problem |
对于Savage而言,在他作出每一步决策前,需要预估下一个鸡蛋是好鸡蛋的概率。他可以按照以往的经验(先验知识)来判断:若有充分把握判定是好鸡蛋则直接打到碗里,否则就扔掉。如果没有任何先验知识,Savage的最优做法是把每个鸡蛋打到另一个碗里,他将最终付出多洗5个碗的决策代价。
基于上面的例子,可以构造一种基于时间维度的三支决策模型。假设
| $ {R^{\left( t \right)}}\left( {{s_j}|x} \right) = \sum\limits_{i = 1}^m {{\lambda ^{\left( t \right)}}\left( {{s_j}|{\omega _i}} \right){P^{\left( t \right)}}\left( {{\omega _i}|x} \right)} $ | (3) |
根据式(3),对于每一个对象x可以计算其条件风险
| $ \left\{ {\begin{array}{*{20}{l}} {{R^{\left( t \right)}}\left( {{s_1}|x} \right){\rm{ = }}{\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _1}} \right){P^{\left( t \right)}}\left( {{\omega _1}|x} \right) + {\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _2}} \right){P^{\left( t \right)}}\left( {{\omega _2}|x} \right)}\\ {{R^{\left( t \right)}}\left( {{s_2}|x} \right){\rm{ = }}{\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _1}} \right){P^{\left( t \right)}}\left( {{\omega _1}|x} \right) + {\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right){P^{\left( t \right)}}\left( {{\omega _2}|x} \right)}\\ {{R^{\left( t \right)}}\left( {{s_3}|x} \right){\rm{ = }}{\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _1}} \right){P^{\left( t \right)}}\left( {{\omega _1}|x} \right) + {\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _2}} \right){P^{\left( t \right)}}\left( {{\omega _2}|x} \right)} \end{array}} \right. $ | (4) |
根据贝叶斯决策准则,需要选择期望损失最小的行动集作为最佳行动方案,于是可得到如下三条决策规则:
1)若
2)若
3)若
由于
| $ \left\{ \begin{array}{l} {\lambda ^{(t)}}({s_{\rm{1}}}|{\omega _{\rm{1}}}) \leqslant {\lambda ^{(t)}}({s_{\rm{2}}}|{\omega _{\rm{1}}}) < {\lambda ^{(t)}}({s_{\rm{3}}}|{\omega _{\rm{1}}})\\ {\lambda ^{(t)}}({s_{\rm{3}}}|{\omega _{\rm{2}}}) \leqslant {\lambda ^{(t)}}({s_{\rm{2}}}|{\omega _{\rm{2}}}) < {\lambda ^{(t)}}({s_{\rm{1}}}|{\omega _{\rm{2}}}) \end{array}\right. $ | (4) |
以状态
1) 若
2) 若
3) 若
其中:
| $\left\{ \begin{array}{l} {\alpha ^{\left( t \right)}}{\rm{ = }}\displaystyle\frac{{ {{\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right)} }}{{\left[ {{\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right)} \right] + \left[ {{\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _1}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _1}} \right)} \right]}}\\ {\beta ^{\left( t \right)}}{\rm{ = }}\displaystyle\frac{{ {{\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right)} }}{{\left[ {{\lambda ^{\left( t \right)}}\left( {{s_2}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _2}} \right)} \right] + \left[ {{\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _1}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _1}} \right)} \right]}}\\ {\gamma ^{\left( t \right)}}{\rm{ = }}\displaystyle\frac{{ {{\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _2}} \right)} }}{{\left[ {{\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _2}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _2}} \right)} \right] + \left[ {{\lambda ^{\left( t \right)}}\left( {{s_3}|{\omega _1}} \right) - {\lambda ^{\left( t \right)}}\left( {{s_1}|{\omega _1}} \right)} \right]}} \end{array}\right. $ | (6) |
特别地,若
1) 若
2) 若
类似地,可以推导以状态
三支决策对于空间维度的描述主要通过粒计算方法来实现,其核心问题主要关注粒层的构建、粒度的刻画、最优粒层和粒度的选取等。下面给出从粒计算思想解决空间三支决策问题的途径和策略。
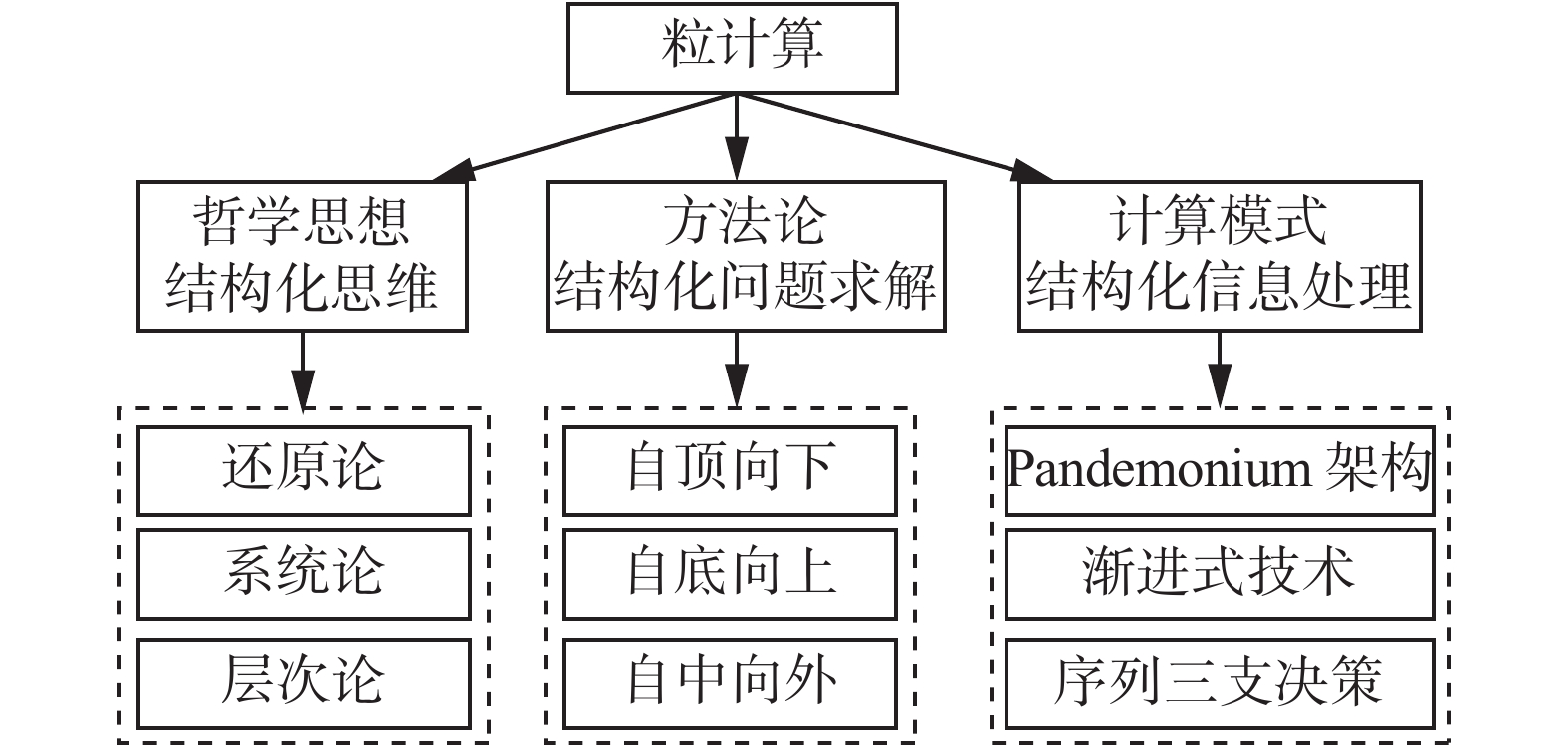
首先,Yao[48] 从粒、粒层和层次结构出发,提出一种粒计算的三元论思想,分别从哲学思想、方法论和计算模式3个层面诠释了粒计算的结构化思维、结构化问题求解和结构化信息处理的统一研究框架。他进一步指出:粒计算哲学关注不同粒度层次下的结构化理解和表示,包含还原论、系统论和层次论;粒计算方法是基于粒结构的结构化问题求解,分为自顶向下、自底向上和自中向外3种处理方法;粒计算的计算模式是运用粒结构来实现结构化粒信息处理,具体有Pandemonium架构、渐进式计算、序列三支决策等。图3给出了这种粒计算三元论的思想,这为空间三支决策理论的构建提供了思想指导。
|
Download:
|
| 图 3 粒计算的三元论 Fig. 3 Trialistic theory of granular computing | |
其次,粒计算利用粒对现实问题的抽象、粒层之间的关系、粒的分解和合成以及粒与粒之间的转换来描述复杂决策问题,通过模拟人类思维方式和行为模式来处理复杂决策问题,借鉴自上而下“分而治之”和自下而上“化繁为简”的思想,用满意近似解替代精确解,来解决复杂决策问题。正如粒计算中商空间理论的创始人张钹院士和张铃教授的观点一样,人类公认的一个特点就是,能从不同的粒度上观察和分析同一问题。人们不仅能在不同粒度的世界上进行问题求解,而且能够很快地从一个粒度世界跳到另一个粒度世界,往返自如,毫无困难[47]。在实际问题中,人们常常利用2个算子,即Zooming-in 算子和Zooming-out算子,通过粒的细化和粗化来描述上述关系。Zooming-in算子表示为

|
Download:
|
| 图 4 | |
再者,近几年来国内外学者从模糊集、粗糙集、商空间、机器学习、云计算等众多领域提出了一系列粒度表示、粒度计算、粒度优化、粒度选择的模型与方法,并从粒的“多层次”和“多视角”两个维度对粒度的内涵和外延进行了深入的分析和探讨。其中,具有代表性的研究方法有多粒度分析[49]和多尺度分析[50]等。多粒度分析主要从信息融合视角出发,通过粒化获得的信息粒集和多个粒结构进行数据分析,并从挖掘的知识中融合集成有效的决策知识。多尺度分析主要从信息粒层视角出发,通过研究不同尺度下决策规则在某种不确定性测度的一致性和不变性(如信息表协调性一致),来选取合适的决策粒层和粒度。上述相关研究从方法和策略层面为空间三支决策理论提供了有力借鉴。
最后,结合前面分析图5给出了一种基于粒度分析的空间三支决策一般性模型框图。

|
Download:
|
| 图 5 空间三支决策一般模型 Fig. 5 General model of spatial three-way decisions | |
在图5中,对于每一个层次的每个区域,在其下一层次都会生成3个子区域,并产生对应的3种子策略,直到根据实际问题搜寻到最优的(合适的)粒层或粒度为止。特别地,在粗糙集理论中,由于3个区域分别对应了正域、边界域和负域,生成的正域和负域可以直接采取接受或拒绝的策略,在每个层次里只需考虑边界域下一层的划分情况,直到边界域对象满足某种终止条件或者等于空集为止。
对于每一粒层区域的划分阈值选取,一种可行的方法为事先确定每一层划分阈值的取值。假设
在很多实际决策问题中,时间和空间2种属性往往是相生相伴、相互依存的。例如:在增量学习中,由于时间变化会导致外界决策环境变化,从而导致粒层选择(空间)的变化。在经济分析中,面板数据包含了不同地区在不同时间的变量取值,这需要设计相应的时间序列模型去解决空间随时间变化的函数关系。粒的时空性表现为:粒可以根据不同的时间,进行不同程度的自由细化或粗化。通过粒的细化或粗化,形成对不同问题粒描述结构的变化,从而对决策问题进行不同程度的描述和求解。对原始粒的细化越多,则可以从更细的层次去理解相应问题,问题也能得到更为深入的分析,但消耗的资源或代价成本也会增加;反之,粗化的层次越多,对问题的描述和理解就相应地越少,这在一定程度上会影响问题分析的细致程度,但是消耗的资源或代价成本也会相应地降低。因此,三支决策的时空模型要综合考虑目标、约束、精度、代价等不同因素。
数据仓库是体现三支决策时空观的一个典型例子。考虑到数据仓库是一个面向主题的、随时间变化的、集成的且不容易丢失的数据集合,人们可以根据用户的具体需求来开发和设计相应的数据仓库,用以支持实际管理问题和决策过程。在数据仓库设计过程中,决策者选择不同的时间维度,采取不同的数据粒层作为粒度划分标准,都将直接决定数据仓库中数据存储容量和查询质量,并进一步影响到决策结果。例如:在某一时刻,某公司的管理者若按照国家、区域、分区域和分区域内,具体到销售员层次关系来查看公司的销售情况,他就需要集结商品维、时间维、客户维、销售事实表、销售员工表及其所在国家、地区、分区的数据库信息。若在另一时刻,公司决策者认为只需要了解各个地理区域的销售情况,而不需要了解每个销售人员的具体销售情况,则只需把地域相关的表格集结成为地理维度就足够了,而没有必要把销售员维作为一个基本粒度。
数据立方体是数据仓库一种重要的表现形式。在数据立方体中,在最低抽象层创建的基本粒层对应了感兴趣的个体实体,如产品销售额或顾客等;在最低抽象层创建的顶点方体给出一个汇总值,如所有商品类型、所有分店一年销售总额等。数据立方体利用切片、切块、旋转、上卷、下钻5种操作,并通过联机事务处理技术(OLTP)对实际需求进行数据粒度选取与数据分析,为数据仓库设计者和管理者提供了技术支持。数据立方体思想也赋予了三支决策时空性研究新的启发:上卷和下钻操作分别对应了三支决策粗化和细化过程,而切片、切块和旋转等操作为三支决策和粒计算提供了一系列新的粒化思考途径和问题解决方法。相对于三支决策时间“时序性”或空间“层次性”研究,三支决策的时空性更具一般性和代表性。通过时间和空间两个维度对决策空间进行“三分而治”的划分策略,对复杂性决策和大数据分析有很好的借鉴和启示作用。
5 结束语本文系统地回顾、梳理和总结了三支决策近年来在理论、方法、算法和应用的发展踪迹,从时间和空间两个维度,对三支决策的时空性进行深入的探讨和分析。本文分别提出了基于时间和空间视角的三支决策基本模型,并讨论了其相应的应用背景。时间三支决策模型主要考虑时间变化下,实时性、多次性、序贯性的决策问题;空间三支决策模型主要考虑在信息粒化过程中,最优粒层和粒度的选择问题。此外,本文从粒计算理论出发,探讨了粒度分析与三支决策的融合机理,以及它们在解决时空决策问题时潜在的可行的理论和方法,这为三支决策后续研究提供了新的思路,并从思想层面上给予人们一种简单、直观的决策认知和行为方式。然而,三支决策的研究才刚刚起步,方兴未艾,其一般化理论还需进一步探索。后续研究工作:1)三支决策如何在复杂信息系统和不确定性环境下进行理论建模;2)三支决策如何在大数据决策环境下进行快速数据分析和增量算法改进;3)如何将三支决策的时空性观点与实际应用背景相结合,更为有效地处理现实决策过程中遇到的具体问题。
| [1] |
YAO Yiyu. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341-353. DOI:10.1016/j.ins.2009.09.021 ( 0) 0)
|
| [2] |
HU Baoqing. Three-way decisions space and three-way decisions[J]. Information sciences, 2014, 281: 21-52. DOI:10.1016/j.ins.2014.05.015 ( 0) 0)
|
| [3] |
LI Xiaonan, YI Huangjian, SHE Yanhong, et al. Generalized three-way decision models based on subset evaluation[J]. International journal of approximate reasoning, 2017, 83: 142-159. DOI:10.1016/j.ijar.2017.01.005 ( 0) 0)
|
| [4] |
YAO Yiyu. Three-way decisions and cognitive computing[J]. Cognitive computation, 2016, 8(4): 543-554. DOI:10.1007/s12559-016-9397-5 ( 0) 0)
|
| [5] |
CIUCCI D, DUBOIS D. A map of dependencies among three-valued logics[J]. Information science, 2013, 250: 162-177. DOI:10.1016/j.ins.2013.06.040 ( 0) 0)
|
| [6] |
ABD EL-MONSEF M M E, KILANY N M. Decision analysis via granulation based on general binary relation[J]. International journal of mathematics and mathematical sciences, 2007: 12714. ( 0) 0)
|
| [7] |
MA Weimin, SUN Bingzhen. On relationship between probabilistic rough set and Bayesian risk decision over two universes[J]. International journal of general systems, 2012, 41(3): 225-245. DOI:10.1080/03081079.2011.634067 ( 0) 0)
|
| [8] |
QIAN Yuhua, ZHANG Hu, SANG Yanli, et al. Multigranulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 225-237. DOI:10.1016/j.ijar.2013.03.004 ( 0) 0)
|
| [9] |
DENG Xiaofei, YAO Yiyu. Decision-theoretic three-way approximations of fuzzy sets[J]. Information sciences, 2014, 279: 702-715. DOI:10.1016/j.ins.2014.04.022 ( 0) 0)
|
| [10] |
QI Jianjun, QIAN Ting, WEI Ling. The connections between three-way and classical concept lattices[J]. Knowledge-based systems, 2016, 91: 143-151. DOI:10.1016/j.knosys.2015.08.006 ( 0) 0)
|
| [11] |
ZHANG Qinghua, XIA Deyou, WANG Guoyin. Three-way decision model with two types of classification errors[J]. Information sciences, 2017, 420: 431-453. DOI:10.1016/j.ins.2017.08.066 ( 0) 0)
|
| [12] |
LIU Dun, LI Tianrui, RUAN Da. Probabilistic model criteria with decision-theoretic rough sets[J]. Information sciences, 2011, 181(17): 3709-3722. DOI:10.1016/j.ins.2011.04.039 ( 0) 0)
|
| [13] |
LI Huaxiong, ZHOU Xianzhong. Risk decision making based on decision-theoretic rough set: a three-way view decision model[J]. International journal of computational intelligence systems, 2011, 4(1): 1-11. DOI:10.1080/18756891.2011.9727759 ( 0) 0)
|
| [14] |
HERBERT J P, YAO Jingtao. Game-theoretic rough sets[J]. Fundamenta informaticae, 2011, 108(3/4): 267-286. ( 0) 0)
|
| [15] |
YANG Xiaoping, YAO Jingtao. Modeling multi-agent three-way decisions with decision-theoretic rough sets[J]. Fundamenta informaticae, 2012, 115(2/3): 157-171. ( 0) 0)
|
| [16] |
LIANG Decui, LIU Dun, PEDRYCZ W, et al. Triangular fuzzy decision-theoretic rough sets[J]. International journal of approximate reasoning, 2013, 54(8): 1087-1106. DOI:10.1016/j.ijar.2013.03.014 ( 0) 0)
|
| [17] |
LIANG Decui, LIU Dun. Systematic studies on three-way decisions with interval-valued decision-theoretic rough sets[J]. Information sciences, 2014, 276: 186-203. DOI:10.1016/j.ins.2014.02.054 ( 0) 0)
|
| [18] |
LIANG Decui, LIU Dun. Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets[J]. Information sciences, 2015, 300: 28-48. DOI:10.1016/j.ins.2014.12.036 ( 0) 0)
|
| [19] |
YAO Yiyu, DENG Xiaofei. Sequential three-way decisions with probabilistic rough sets[C]//Proceeding of 10th International Conference on Cognitive Informatics and Cognitive Computing. Banff, AB, Canada, 2011, 120–125.
( 0) 0)
|
| [20] |
LI Yuefeng, ZHANG Libiao, XU Yue, et al. Enhancing binary classification by modeling uncertain boundary in three-way decisions[J]. IEEE transactions on knowledge and data engineering, 2017, 29(7): 1438-1451. DOI:10.1109/TKDE.2017.2681671 ( 0) 0)
|
| [21] |
ZHAO Xuerong, HU Baoqing. Fuzzy and interval-valued fuzzy decision-theoretic rough set approaches based on fuzzy probability measure[J]. Information sciences, 2015, 298: 534-554. DOI:10.1016/j.ins.2014.12.008 ( 0) 0)
|
| [22] |
ZHOU Bing. Multi-class decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 211-224. DOI:10.1016/j.ijar.2013.04.006 ( 0) 0)
|
| [23] |
ZHANG Yan, YAO Jingtao. Gini objective functions for three-way classifications[J]. International journal of approximate reasoning, 2017, 81: 103-114. DOI:10.1016/j.ijar.2016.11.005 ( 0) 0)
|
| [24] |
LIANG Decui, LIU Dun, KOBINA A. Three-way group decisions with decision-theoretic rough sets[J]. Information sciences, 2016, 345: 46-64. DOI:10.1016/j.ins.2016.01.065 ( 0) 0)
|
| [25] |
张楠, 姜丽丽, 岳晓东, 等. 效用三支决策模型[J]. 智能系统学报, 2016, 11(4): 459-468. ZHANG Nan, JIANG Lili, YUE Xiaodong, et al. Utility-based three-way decisions model[J]. CAAI transactions on intelligent systems, 2016, 11(4): 459-468. (  0) 0)
|
| [26] |
LIU Shuli, LIU Xinwang, QIN Jindong. Three-way group decisions based on prospect theory[J/OL]. Journal of the operational research society, 2017. https://doi.org/ 10.1057/s41274-016-0159-2.
( 0) 0)
|
| [27] |
LANG Guangming, MIAO Duoqian, CAI Mingjie. Three-way decision approaches to conflict analysis using decision-theoretic rough set theory[J]. Information sciences, 2017(406/407): 185-207. DOI:10.1016/j.ins.2017.04.030 ( 0) 0)
|
| [28] |
YAO Yiyu, ZHAO Yan. Attribute reduction in decision-theoretic rough set models[J]. Information sciences, 2008, 178(17): 3356-3373. DOI:10.1016/j.ins.2008.05.010 ( 0) 0)
|
| [29] |
ZHAO Yan, WONG S K M, YAO Yiyu. A note on attribute reduction in the decision-theoretic rough set model[M]//PETERS J F, SKOWRON A, CHAN C C, et al. Transactions on Rough Sets. Berlin, Heidelberg: Springer, 2011: 61–70.
( 0) 0)
|
| [30] |
LI Huaxiong, ZHOU Xianzhong, ZHAO Jiabao, et al. Non-monotonic attribute reduction in decision-theoretic rough sets[J]. Fundamenta informaticae, 2013, 126(4): 415-432. ( 0) 0)
|
| [31] |
JIA Xiuyi, LIAO Wenhe, TANG Zhenmin, et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information sciences, 2012, 219: 151-167. ( 0) 0)
|
| [32] |
MIN Fan, HE Huaping, QIAN Yuhua, et al. Test-cost-sensitive attribute reduction[J]. Information sciences, 2011, 181(22): 4928-4942. DOI:10.1016/j.ins.2011.07.010 ( 0) 0)
|
| [33] |
JU Hengrong, DOU Huili, QI Yong, et al. δ-cut decision-theoretic rough set approach: model and attribute reductions
[J]. The scientific world journal, 2014, 2014: 382439. ( 0) 0)
|
| [34] |
MA Xi’ao, WANG Guoyin, YU Hong, et al. Decision region distribution preservation reduction in decision-theoretic rough set model[J]. Information sciences, 2014, 278: 614-640. DOI:10.1016/j.ins.2014.03.078 ( 0) 0)
|
| [35] |
REN Ruisi, WEI Ling. The attribute reductions of three-way concept lattices[J]. Knowledge-based systems, 2016, 99: 92-102. DOI:10.1016/j.knosys.2016.01.045 ( 0) 0)
|
| [36] |
ZHANG Xianyong, MIAO Duoqian. Three-layer granular structures and three-way informational measures of a decision table[J]. Information sciences, 2017, 412/413: 67-86. DOI:10.1016/j.ins.2017.05.032 ( 0) 0)
|
| [37] |
HUANG Jiajin, WANG Jian, YAO Yiyu, et al. Cost-sensitive three-way recommendations by learning pair-wise preferences[J]. International journal of approximate reasoning, 2017, 86: 28-40. DOI:10.1016/j.ijar.2017.03.005 ( 0) 0)
|
| [38] |
ZHANG Hengru, MIN Fan, SHI Bing. Regression-based three-way recommendation[J]. Information sciences, 2017, 378: 444-461. DOI:10.1016/j.ins.2016.03.019 ( 0) 0)
|
| [39] |
WANG Min, MIN Fan, ZHANG Zhiheng, et al. Active learning through density clustering[J]. Expert systems with applications, 2017, 85: 305-317. DOI:10.1016/j.eswa.2017.05.046 ( 0) 0)
|
| [40] |
YU Hong, LIU Zhanguo, WANG Guoyin. An automatic method to determine the number of clusters using decision-theoretic rough set[J]. International journal of approximate reasoning, 2014, 55(1): 101-115. DOI:10.1016/j.ijar.2013.03.018 ( 0) 0)
|
| [41] |
LIU Dun, LI Tianrui, LIANG Decui. Incorporating logistic regression to decision-theoretic rough sets for classifications[J]. International journal of approximate reasoning, 2014, 55(1): 197-210. DOI:10.1016/j.ijar.2013.02.013 ( 0) 0)
|
| [42] |
刘盾, 李天瑞, 李华雄. 粗糙集理论: 基于三支决策视角[J]. 南京大学学报 (自然科学), 2013, 49(5): 574-581. LIU Dun, LI Tianrui, LI Huaxiong. Rough set theory: a three-way decisions perspective[J]. Journal of Nanjing university (natural sciences), 2013, 49(5): 574-581. (  0) 0)
|
| [43] |
刘盾, 梁德翠. 广义三支决策与狭义三支决策[J]. 计算机科学与探索, 2017, 11(3): 502-510. LIU Dun, LIANG Decui. Generalized three-way decisions and special three-way decisions[J]. Journal of frontiers of computer science and technology, 2017, 11(3): 502-510. (  0) 0)
|
| [44] |
贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M]. 南京: 南京大学出版社, 2012.
( 0) 0)
|
| [45] |
刘盾, 李天瑞, 苗夺谦, 等. 三支决策与粒计算[M]. 北京: 科学出版社, 2013.
( 0) 0)
|
| [46] |
于洪, 王国胤, 李天瑞, 等. 三支决策: 复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015. YU Hong, WANG Guoyin, LI Tianrui, et al. Three-way decisions: methods and practices for complex problem solving[M]. Beijing: Science Press, 2015. (  0) 0)
|
| [47] |
张燕平, 姚一豫, 苗夺谦, 等. 粒计算、商空间及三支决策的回顾与发展[M]. 北京: 科学出版社, 2017.
( 0) 0)
|
| [48] |
YAO Yiyu. A triarchic theory of granular computing[J]. Granular computing, 2016, 1(2): 145-157. DOI:10.1007/s41066-015-0011-0 ( 0) 0)
|
| [49] |
QIAN Yuhua, LIANG Jiye, YAO Yiyu, et al. MGRS: a multi-granulation rough set[J]. Information sciences, 2010, 180(6): 949-970. DOI:10.1016/j.ins.2009.11.023 ( 0) 0)
|
| [50] |
WU Weizhi, LEUNG Y. Optimal scale selection for multi-scale decision tables[J]. International journal of approximate reasoning, 2013, 54(8): 1107-1129. DOI:10.1016/j.ijar.2013.03.017 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


