随着电网的不断发展,电力设备的安全性、可靠性受到了越来越多的关注,电力设备的损坏大部分是由绝缘损坏所引起的。因此有效地将绝缘存在的缺陷检测出来对电网的安全运行具有重要意义[1]。电容器在电力系统无功补偿中有着广泛的应用,电力电容器的介质损耗因数是表征其质量的重要参数[2]。目前,电力电容器进行维护的方式主要有定期检修和在线监测2种[3-7]。然而,定期检修存在检修周期长、试验条件与运行状态不一致等问题,无法反映出电力电容器的真实运行状态[6]。在线监测的方式可以及时发现电容器的早期故障,具有更好的监测效果。正向计算和解空间搜索是计算电力电容器介损角的2种方式。正向计算方法主要有谐波分析法[8-11]、异频电源法[12-14]、正交分解法[14-16]和自由矢量法等[17-19]。其中,谐波分析法使用离散傅里叶变换对电容器的电流、电压信号进行谐波分析,进而得到二者的基波,然后求出介损角。BP神经网络具有较好的非线性映射能力并且适用于处理大规模的数据。支持向量机模型结构简单,可以在少量样本情况取得较好的分类效果,并且模型不易过拟合。因此,本文提出了BP神经网络和SVM相结合的方法(BP-SVM方法)进行电力电容器介损角的在线辨识,通过BP神经网络提取信号Dδ(t)特征,将原本线性不可分的信号通过提取特征向量的方式趋向于线性可分,同时通过提取特征向量的方式降低信号Dδ(t)的维度,压缩训练样本规模,然后使用模型结构更加简单的SVM进行介损角辨识。
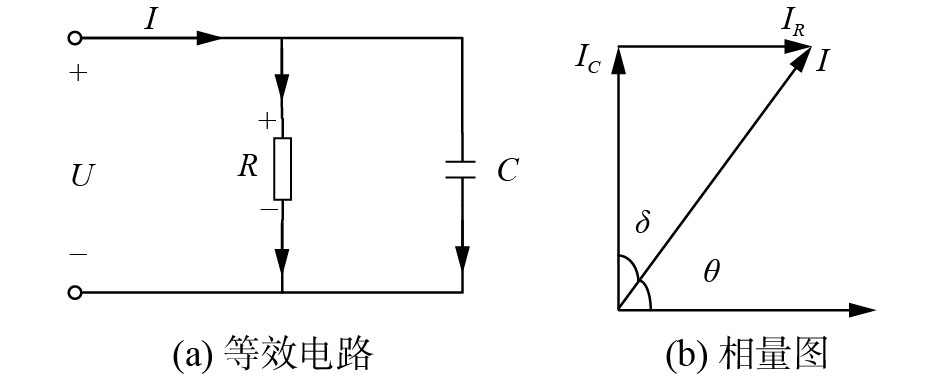
1 介损角Dδ(t)信号的表示在交流电压的作用下,电容设备的等效电路和相量图如图1所示。其中,介质等效电阻为R,介质等效电容为C,介质损耗角为δ,电压U和电流I的相位差为θ。通常情况下,介损角δ的测量可以转换为计算绝缘介质损耗因数tan δ的值。
本文将监测到的电压、电流的信号转换为可表示介损角δ信号Dδ(t)的方法:
| $U\left( t \right) = {A_U}{\rm{sin}}\left( {\omega t + {\varphi _U}} \right)$ | (1) |
| $I\left( t \right) = {A_I}{\rm{sin}}\left( {\omega t + {\varphi _I}} \right)$ | (2) |
式中:U(t)为电容器的工作电压;I(t)为电容器的工作电流;AU为电压幅值;ω为角频率;φU为电压的初始相位;AI为电流幅值;φI为电流的初始相位。
在电流、电压同步采样的方式下,可忽略电流、电压的幅值,依据U(t)和I(t)的相位差计算介损角δ。采样信号的电流、电压幅值归一化为1。此外,将采样信号I(t)移相φI使其初始相角为0,则U(t)和I(t)退化为无量纲的信号
| $\tilde I\left( t \right) = {\rm{sin}}\left( {\omega t} \right)$ | (3) |
| $\tilde U\left( t \right) = {\rm{sin}}\left[ {\omega t + \left( {{\varphi _U} + {\varphi _I}} \right)} \right]$ | (4) |
将采样信号
| $\begin{split} {{\tilde U}_s}\left( t \right) = \sin \left[ {\omega t + \left( {{\varphi _U} - {\varphi _I}} \right) - \frac{{\text{π}}}{2}} \right] = {\rm{sin}}\left( {\omega t - \delta } \right) \end{split}$ | (5) |
介损角δ可由
|
Download:
|
| 图 1 电容设备的等效电路和相量图 Fig. 1 Capacitance equipment equivalent circuit and phasor diagram | |
定义信号Dδ(t)为
| $\begin{split} {D_\delta }\left( t \right) = & {{\tilde U}_s}\left( t \right) - \tilde I\left( t \right) = - 2{\rm{sin}}\left( {\frac{\delta }{2}} \right){\rm{cos}}\left( {\omega t - \frac{{{\text{π} }}}{2}} \right) \end{split}$ | (6) |
由式(6)可以看出,信号Dδ(t)与电容器电流和电容器电压的角频率有关。此外,信号Dδ(t)的幅值与被测的介损角δ有关。
定义信号Dδ(t)幅值的绝对值为Aδ,则Aδ=2sin(δ/2),设R(δ)为Aδ与δ的比值,即
| $R\left( \delta \right) = \frac{{{A_\delta }}}{\delta } = \frac{{2{\rm{sin}}\left( {\delta /2} \right)}}{\delta } = \frac{{{\rm{sin}}\left( {\delta /2} \right)}}{{\delta /2}}$ | (7) |
在20 ℃时,额定电压下的高压并联电容器的介损角δ值应在下列范围内:纸膜复合介质的电容器
基于BP-SVM方法的介损角δ辨识过程是一种解空间搜索过程。辨识过程的核心思想是:首先,使用每只电容器一段时间内的Dδ(t)信号训练相应电容器的BP神经网络模型;其次,使用该模型提取Dδ(t)信号的特征,形成新的训练样本;然后,采用新的训练样本和对应的标签训练SVM模型;最后,利用BP神经网络模型和SVM模型辨识新监测到的Dδ(t)信号是否为期望的δ,或是漂移了一定量的δi,该辨识过程速度较快,可用于在线监测。本文辨识介损角δ的模型结构如图2所示。

|
Download:
|
| 图 2 BP-SVM模型 Fig. 2 BP-SVM model | |
图2中左侧虚线框是一个隐含层为3层的BP神经网络模型结构,输入为Dδ(t)信号集,输入层节点个数为采样长度1 600,隐含层神经元的个数分别为200、300、200,输出节点个数为11,将介损角δ分为11类,使用交叉熵函数作为BP神经网络训练时的损失函数。图2中右侧虚线框是本文的SVM模型,由于SVM是二分类模型,而本文需要将介损角δ分为11类,因此本文采用SVM多分类模式中的一对一模式,训练55个SVM模型用以对介损角δ进行分类。此外,本文使用BP神经网络中隐含层第3层提取的Dδ(t)信号特征(维度为200)和对应的Dδ(t)信号标签训练本文的SVM模型。
介损角δ的表示和辨识过程:
1)假设目标电容器的介损角δ为3×10−4 rad,记作δ0,使用式(6)计算该电容器正常状态下的介损角表示信号
2)当δ0每次增加1×10−5 rad时,根据式(6)计算对应
3)分别对
4)使用训练好的BP神经网络模型和SVM模型辨识被测信号属于哪一类
为了验证BP神经网络与SVM相结合的方法的有效性,本文进行了仿真实验分析,仿真过程为:
1)生成介损角δi为{3×10−4, 3.1×10−4,···, 3.9×10−4, 4×10−4} rad,频率分别为{49.50, 49.75, 50.00, 50.25,50.50}Hz条件下的介损角信号集
2)对
3)所有的训练样本加入{20, 25, 30, 35}dB的4个等级的白噪声,每个等级的白噪声等级生成10个加噪信号形成新的训练集TrainSet。
4)在构建训练集方法的基础上,按照以下3个条件构建测试集TestSet:
①对各次谐波相角增加
②介损角增加−0.5×10−6~5×10-6 rad的随机漂移;
③频率增加{−0.5, −0.25, 0, 0.25, 0.5}Hz的随机漂移;
④所有的测试样本加入{20, 25, 30, 35}dB的4个等级的白噪声,每个噪声等级生成5个加噪信号。
5)用构建好的训练样本集TrainSet训练本文的BP神经网络模型,图3为BP神经网络训练过程中的损失趋势。
|
Download:
|
| 图 3 BP神经网络的损失趋势 Fig. 3 BP neural network loss trend | |
6)基于5)中训练好的BP神经网络,将训练样本集TrainSet重新输入BP神经网络中,提取BP神经网络隐含层第3层的特征向量,将该特征向量和对应的类别标签组成新的训练样本SVMTrainSet,使用SVMTrainSet训练SVM模型。
7)使用TestSet检验本文提出的BP-SVM方法在不同δi下信号Dδi(t)的辨识能力,检验过程分为:①将TestSet输入训练好的BP神经网络中,提取隐含层第3层的特征向量;②将①中提取的特征向量作为SVM的输入,使用训练好的SVM对提取的特征向量进行分类,对介损角进行辨识。
3 实验结果与分析基于BP-SVM方法的电容器介损角辨识过程本质是信号分类的问题。首先,通过BP神经网络提取训练样本TrainSet1介损角的特征向量;然后,将提取的特征向量作为新的训练样本TrianSet2训练SVM,使用SVM辨识每个样本对应的类别。其中,训练样本TrainSet1中均混入了不同程度的谐波、频率偏移、白噪声。本文使用的BP神经网络结构为(1 600,200,300,200,11),隐含层为(200,300,200),是一种对称结构,学习率为0.000 1,激活函数为ReLU,训练800轮,隐含层第3层与输出层的神经元丢失(dropout)概率为0.5,权重w值的初始化服从均值为0、标准差为0.1的高斯分布,偏置b值均初始化为0.1。SVM的核函数为“rbf”,参数C为50,参数γ为0.005。本文共收集了1 008 300条数据,选用其中的220 000条数据组成训练样本TrianSet1训练BP神经网络,使用训练完成后的BP神经网络提取TrainSet1的特征向量(220 000条)后,随机选取其中的88 000条特征向量训练SVM,形成BP-SVM模型。在剩余的788 300条数据中分别选取220 000条数据、440 000条数据和660 000条数据组成测试样本集TestSet1、TestSet2和TestSet3。
3.1 介损角辨识结果表1为基于BP-SVM方法和BP神经网络的方法在TestSet1、TestSet2、TestSet3测试样本下的辨识结果。由表1可以看出,基于本文提出的BP-SVM方法在不同的测试样本下,电容器介损角的辨识准确率均高于BP神经网络。此外,随着测试样本数量的增加,基于BP-SVM的方法依旧保持了较高的辨识准确率,当测试样本数量是训练样本3倍时,BP-SVM方法依旧取得了93.40%的辨识准确率。
| 表 1 BP-SVM和BP神经网络在测试集上的实验结果 Tab.1 BP-SVM and BP neural network experiment results on test sets |
表2为BP-SVM方法和基于深度学习(DL)方法在TestSet1上的介损角的具体分类结果。由表2可以看出,本文提出的BP-SVM方法比DL方法的辨识准确率高了2.81%,达到了94.02%。当介损角为3.2×10−4 rad和4×10−4 rad时,DL方法有较高的辨识准确率,但是BP-SVM方法的辨识准确率也达到了94%以上。当介损角为其他值时,BP-SVM方法辨识准确率明显高于DL方法,并且辨识的稳定性也优于DL方法。其中,每一类的辨识准确率均在92.22%以上,DL方法在介损角3.5×10−4~3.7×10−4 rad时,辨识准确率均低于90%,甚至当介损角为3.9×10−4 rad时,DL方法的辨识准确率降低到了81.96%,整体的辨识准确率波动幅度较大。表3为BP-SVM方法在TestSet1测试样本下的具体辨识结果,由表3可以看出,在辨识错误的介损角样本中,BP-SVM方法易将介损角辨识为较小的值。
| 表 2 BP-SVM和深度学习方法在测试集上的实验结果 Tab.2 BP-SVM and deep learning method experiment results on test sets |
| 表 3 BP-SVM在TestSet1上的实验结果 Tab.3 BP-SVM experiment results on Test Set |
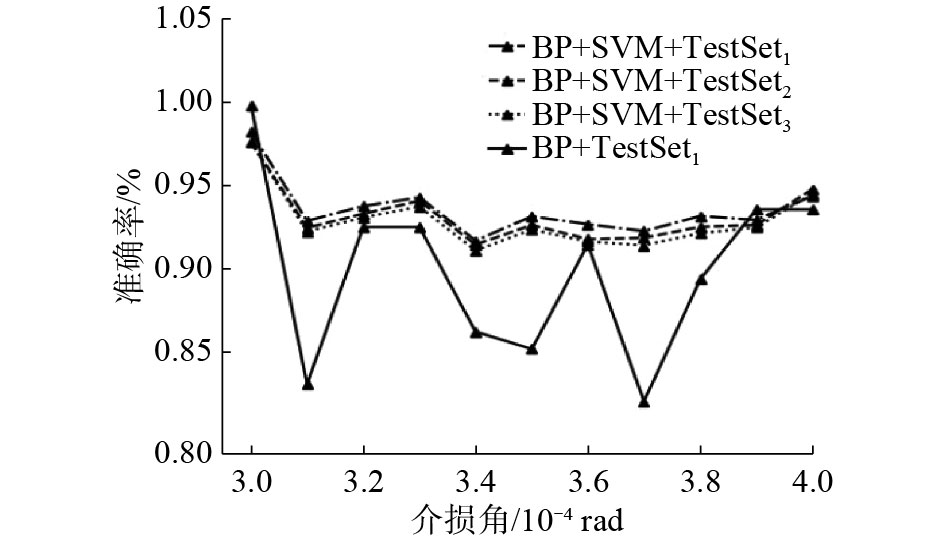
图4为基于BP-SVM的方法在不同测试样本的下的辨识结果和基于BP神经网络的方法在测试样本TestSet1下的辨识结果,从图4中可以看出,当介损角增加0% rad和0.009% rad时,BP神经网络的辨识结果要优于本文所提出的BP-SVM的方法,但是当介损角增加1×10−5~8×10−5 rad 和1×10−4 rad时,BP-SVM的方法辨识效果要明显优于BP神经网络。此外,相较于BP神经网络的辨识效果,BP-SVM方法具有更高的辨识稳定性,介损角的变化对于分类的准确率无明显影响,每一类的辨识准确率均保持在91.65%以上。
|
Download:
|
| 图 4 不同模型和不同测试样本集的测试结果 Fig. 4 Test results for different models and test sets | |
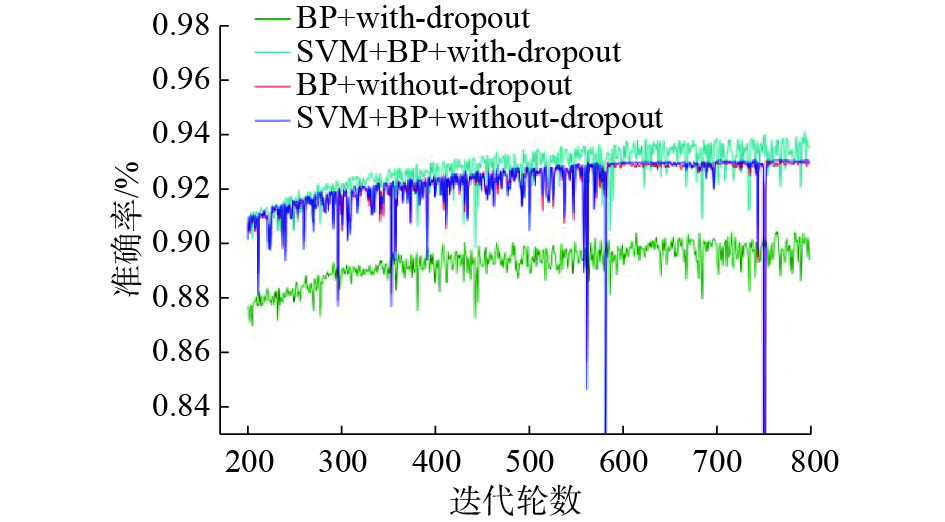
图5为基于本文提出的BP-SVM方法和BP神经网络的方法在测试样本TestSet1下的辨识准确率。此外,图5也绘制出了BP-SVM方法和BP神经网络的方法在没有引入dropout的情况下的辨识准确率。其中,测试样本TestSet1的辨识开始于BP神经网络训练200轮之后。由图5可以看出,在没有引入dropout的情况下,BP-SVM方法和BP神经网络的方法具有相近的辨识准确率,并且高于引入了dropout的BP神经网络的辨识结果。但是,这3个方法的辨识结果均低于本文提出的引入了dropout的BP-SVM方法。此外,由图5的波形可以看出,在引入了dropout的情况下,BP-SVM方法和BP神经网络方法相较于没有引入dropout的情况下,模型的辨识效果具有更好的鲁棒性,辨识准确率的波动幅度较小。同时,本文提出的BP-SVM方法相较于单一的BP神经网络的方法对于电容器介损角的辨识具有更高的准确率,平均辨识准确率提高了3.48%。
|
Download:
|
| 图 5 有无dropout的测试结果 Fig. 5 Test results with or without dropout | |
本文按照不同的噪声等级对辨识介损角的错误样本进行了统计,如图6所示,在TestSet1、TestSet2、TestSet3样本下每一等级噪声的测试样本数量分别为55 000、110 000、165 000。在3个不同的测试样本集下,当白噪声为20 dB时,对BP-SVM方法的辨识结果有较大的影响,其辨识准确率均低于90%,但是当白噪声为25、30、35 dB时,本文提出的BP-SVM的方法可以较好地辨识出介损角的变化。
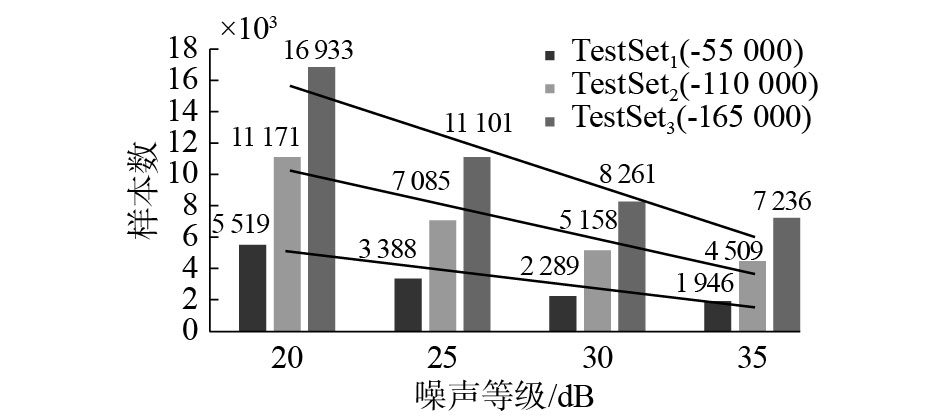
|
Download:
|
| 图 6 不同等级噪声下的测试结果 Fig. 6 Test results at different levels of noise | |
此外,本文统计了在不同频率漂移的情况下BP-SVM辨识的错误样本,如图7所示,在TestSet1、TestSet2、TestSet3样本下每一等级噪声的测试样本数量分别为44 000、88 000、132 000。相较于文献[2]提出的辨识方法,当频率减小或者增加0.25 Hz时,基于深度学习的方法对介损角的辨识结果有较大的影响。由图7可以看出,本文提出的BP-SVM方法在不同的频率漂移的情况下,依旧具有较高的辨识准确率,并且频率变化对于辨识效果没有明显影响。
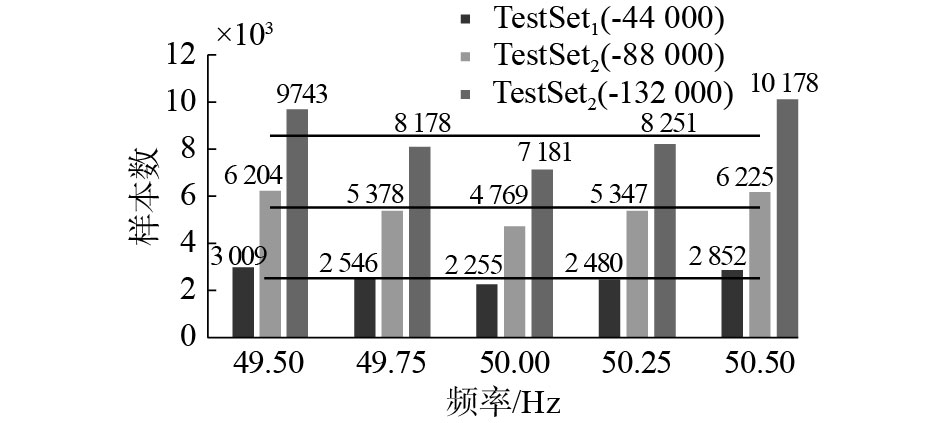
|
Download:
|
| 图 7 不同频率下的测试结果 Fig. 7 Test results at different frequencies | |
在实际监测中,谐波分析法方法在计算介损角时存在稳定性较差的问题。虽然基于深度学习的方法对于电容器介损角辨识有较好的稳定性,但是频率的波动对其辨识效果有着较大的影响,同时该方法的辨识准确率也有待提高。因此,本文提出了BP神经网络和SVM相结合(BP-SVM)的方法用以辨识电容器的介损角。实验表明:
1)本文所提出的BP-SVM方法具有更高的辨识准确率,并且在不同的测试样本集下均保持了较高的辨识准确率,模型具有更好的泛化能力。
2)本文所提出的BP-SVM方法比基于深度学习的方法具有更强的抗频率变化能力,频率的变化对于本文算法的性能无明显影响。
3)本文所提出的模型在较少的训练样本集下取得了较高的辨识准确率,当测试样本集3倍于训练样本集时,本文方法依旧将电容器介损角的辨识准确率保持在93.40%。
| [1] |
李天云, 袁明哲, 蔡国伟, 等. 基于随机子空间和最小二乘法的介质损耗角检测方法[J]. 高电压技术, 2011, 37(4): 828-833. LI Tianyun, YUAN Mingzhe, CAI Guowei, et al. Measurement algorithm of dielectric loss angle based on SSI-LS[J]. High voltage engineering, 2011, 37(4): 828-833. (  0) 0)
|
| [2] |
王晓辉, 朱永利, 王艳, 等. 基于深度学习的电容器介损角在线辨识[J]. 电工技术学报, 2017, 32(15): 145-152. WANG Xiaohui, ZHU Yongli, WANG Yan, et al. Online Identification method of power capacitor dielectric loss angle based on deep learning[J]. Transactions of China electrotechnical society, 2017, 32(15): 145-152. (  0) 0)
|
| [3] |
董爽, 李天云, 王永, 等. 在线检测介质损耗角的矩阵束方法[J]. 电工技术学报, 2015, 30(18): 229-236. DONG Shuang, LI Tianyun, WANG Yong, et al. An On-line detection method of dielectric loss angle based on matrix pencil algorithm[J]. Transactions of China electrotechnical society, 2015, 30(18): 229-236. DOI:10.3969/j.issn.1000-6753.2015.18.028 (  0) 0)
|
| [4] |
WANG P, RGHUVEER M R, MCDERMID W, et al. A digital technique for the on-line measurement of dissipation factor and capacitance[J]. IEEE transactions on dielectrics and electrical insulation, 2001, 8(2): 228-232. DOI:10.1109/94.919938 ( 0) 0)
|
| [5] |
尚勇, 杨敏中, 王晓蓉, 等. 谐波分析法介质损耗因数测量的误差分析[J]. 电工技术学报, 2002, 17(3): 67-71, 34. SHANG Yong, YANG Minzhong, WANG Xiaorong, et al. Error analysis for the dielectric loss factor measurement based on harmonic analysis[J]. Transactions of China electrotechnical society, 2002, 17(3): 67-71, 34. DOI:10.3321/j.issn:1000-6753.2002.03.015 (  0) 0)
|
| [6] |
刘伟, 黄新波, 章云. 电容型高压设备介损在线监测系统的现场采集单元设计[J]. 计算机测量与控制, 2010, 18(1): 233-236, 242. LIU Wei, HUANG Xinbo, ZHANG Yun. Design of field sampling unit of an on-line monitoring system of dielectric loss in capacitive high-voltage apparatus[J]. Computer measurement and control, 2010, 18(1): 233-236, 242. (  0) 0)
|
| [7] |
陈晓宇, 郑建勇, 梅军. 基于LC振荡频率变化量的电容器组早期故障在线智能预警方法及其实现[J]. 电力系统保护与控制, 2015, 43(5): 144-149. CHEN Xiaoyu, ZHENG Jianyong, MEI Jun. Power capacitor banks failure warning method based online intelligence LC oscillation frequency variation and its implementation[J]. Power system protection and control, 2015, 43(5): 144-149. (  0) 0)
|
| [8] |
袁飞, 杨震男, 卢毅. 一种基于相对比较法测量容性设备介质损耗的滤波算法[J]. 电力系统保护与控制, 2015, 43(19): 95-100. YUAN Fei, YANG Zhennan, LU Yi. A filtering algorithm for measuring capacitive device dielectric loss based on relative comparison method[J]. Power system protection and control, 2015, 43(19): 95-100. DOI:10.7667/j.issn.1674-3415.2015.19.016 (  0) 0)
|
| [9] |
王楠, 律方成, 梁英, 等. 基于高精度DFT的介损数字测量方法[J]. 高电压技术, 2003, 29(4): 3-5, 8. WANG Nan, LV Fangcheng, LIANG Ying, et al. Digital measurement of dielectric loss based on high accuracy DFT algorithm[J]. High voltage engineering, 2003, 29(4): 3-5, 8. DOI:10.3969/j.issn.1003-6520.2003.04.002 (  0) 0)
|
| [10] |
王微乐, 李福祺, 谈克雄. 测量介质损耗角的高阶正弦拟合算法[J]. 清华大学学报 (自然科学版), 2001, 41(9): 5-8. WANG Weile, LI Fuqi, TAN Kexiong. Higher-order sine fitting algorithm for dielectric loss measurement[J]. Journal of Tsinghua University (science and technology), 2001, 41(9): 5-8. (  0) 0)
|
| [11] |
冯小华, 张承学. 修正的谐波分析法可提高介损在线测量准确度[J]. 高电压技术, 2004, 30(8): 36-37. FENG Xiaohua, ZHANG Chengxue. Modified harmonics analysis approach for increasing precision in on-line measuring tan δ [J]. High voltage engineering, 2004, 30(8): 36-37. DOI:10.3969/j.issn.1003-6520.2004.08.014 (  0) 0)
|
| [12] |
LI Q, ZHAO T, SIEW W H. Definition and digital algorithms of dielectric loss factor for condition monitoring of high-voltage power equipment with harmonics emphasis[J]. IEE proceedings-generation, transmission and distribution, 2005, 152(3): 309-312. DOI:10.1049/ip-gtd:20045043 ( 0) 0)
|
| [13] |
张忠蕾, 李庆民, 陈鹏. 谐波条件下高压电气设备介质损耗因数的定义和数字化算法[J]. 高压电器, 2004, 40(5): 327-329, 332. ZHANG Zhonglei, LI Qingmin, CHEN Peng. Definition and digital algorithms for dielectric loss factor of high voltage power apparatus under harmonics condition[J]. High voltage apparatus, 2004, 40(5): 327-329, 332. DOI:10.3969/j.issn.1001-1609.2004.05.003 (  0) 0)
|
| [14] |
张介秋, 梁昌洪, 韩峰岩, 等. 介质损耗因数的卷积窗加权算法[J]. 电工技术学报, 2005, 20(3): 100-104. ZHANG Jieqiu, LIANG Changhong, HAN Fengyan, et al. Convolution window weighted algorithm for dielectric loss Factor[J]. Transactions of China electrotechnical society, 2005, 20(3): 100-104. DOI:10.3321/j.issn:1000-6753.2005.03.019 (  0) 0)
|
| [15] |
徐志钮, 律方成, 赵丽娟. 基于加汉宁窗插值的谐波分析法用于介损角测量的分析[J]. 电力系统自动化, 2006, 30(2): 81-85. XU Zhiniu, LÜ Fangcheng, ZHAO Lijuan, et al. Analysis of dielectric loss angle measurement by Hanning windowing interpolation algorithm based on FFT[J]. Automation of electric power systems, 2006, 30(2): 81-85. DOI:10.3321/j.issn:1000-1026.2006.02.015 (  0) 0)
|
| [16] |
段大鹏, 江秀臣, 孙才新, 等. 基于正交分解的介质损耗因数数字测量算法[J]. 中国电机工程学报, 2008, 28(7): 127-133. DUAN Dapeng, JIANG Xiuchen, SUN Caixin, et al. A novel algorithm of dielectric loss measurement based on orthogonal decomposition[J]. Proceedings of the CSEE, 2008, 28(7): 127-133. DOI:10.3321/j.issn:0258-8013.2008.07.021 (  0) 0)
|
| [17] |
陈楷, 胡志坚, 王卉, 等. 介损角的非同步采样算法及其应用[J]. 电网技术, 2004, 28(18): 58-61. CHEN Kai, HU Zhijian, WANG Hui, et al. Algorithm and application of dielectric loss angle based on asynchronous sampling[J]. Power system technology, 2004, 28(18): 58-61. DOI:10.3321/j.issn:1000-3673.2004.18.013 (  0) 0)
|
| [18] |
WANG Kang, TENG Zhaosheng, WEN He, et al. Fast measurement of dielectric loss angle with time-domain quasi-synchronous algorithm[J]. IEEE transactions on instrumentation and measurement, 2015, 64(4): 935-942. DOI:10.1109/TIM.2014.2362839 ( 0) 0)
|
| [19] |
王永, 滕召胜, 李建闽, 等. 基于采样序列重构的高精度介损角测量方法[J/OL]. 电工技术学报, [2018-04-24]. https://doi.org/ 10.19595/j.cnki.1000-6753.tces.171699. WANG Yong, TENG Zhaosheng, LI Jianmin, et al. High accuracy dielectric loss angle measurement method based on sampling sequence reconstruction[J/OL]. Transactions of China electrotechnical society, [2018-04-24]. https://doi.org/10.19595/j.cnki.1000-6753.tces.171699. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


