现实世界中数据信息是以包括图像、文本、声音、纹理等多种模态形式存在的。信息和科技智能化发展为机器学习方法提供了硬件条件。近年来，以多模态为研究对象的机器学习算法不断涌现，使得多模态机器学习成为科研人员广泛关注的研究热点。以机器人为例，越来越多的研究定位于机器人感知系统的设计，仅靠单模态中典型的视觉图像分割^[1]、物体检测^[2]等任务已经不能完全满足机器人的识别与感知需求。在机器人手势交互领域，视觉手势与其他模态(表情、方向、声音、触觉等)相结合能够增强交互的高效性和互补性^[3]。将不同隐含层局部模态信息融合得到的全局特征用于人脸识别，可以多元化检测人脸并解决遮挡问题^[4]。在机器人情感分析方面，有效结合文本和图像特征并对融合语义进行训练，会得到优于单一模态的情感分类效果^[5]。此外，对多模态异构数据进行相关性度量有助于提高视频检索效率^[6]。实现基于道路场景理解的多模态信息(RGB-D、超声、激光雷达等)融合可以提高复杂环境下环境感知和道路识别的准确性与可靠性，有助于机器人实时路径规划和自主定位与导航^[7-10]。

以上研究大多基于时下流行的深度学习算法。考虑到深度结构运行时间长、难以收敛等性质，本文旨在寻求一种简单、高效的机器学习技术，在降低模型训练时间、节约成本的基础上对不同模态信息进行融合学习，提高系统识别的准确率。宽度学习系统(broad learning system, BLS)方法以其强大的数学理论支撑、简单的平层网络结构、快速的增量建模过程等优点，成功地应用于各种分类和回归任务中，尤其在图像分类问题上表现出优越的性能^[11]。因此，本文基于宽度学习方法提出了一种用于解决多模态数据特征融合问题的模型框架，通过对各个模态并行学习、联合映射、串联融合后根据得到的特征实现分类输出。实验结果表明，本文提出的融合方法能有效提高系统的分类性能。

1 相关知识 1.1 多模态机器学习

一般而言，模态是指事件发生或客观物体存在的形态。为了更好地利用人工智能来帮助我们感知和理解世界，就需要解释和推理出多模态数据中有用的信息和特征。多模态机器学习旨在建立一个可以处理和关联多种模态之间交互信息的模型框架，从早期基于视听语音识别的研究到近期新兴的语义和视觉领域应用，多模态机器学习逐渐发展成一个有巨大挖掘潜力和研究价值的交叉学科。

多模态机器学习虽然能够学习不同模态数据的深层特征表达，但是由于模态间的差异大小和影响因子的不同，目前多模态技术还存在以下3个方面的挑战。

1)特征表达：对于同一种物体来说，不同的模态形式可能包含了同样的信息，因此，如何去除冗余属性，更好地总结和表示出不同模态的互补信息，仍是值得深入研究和探讨的问题。

2)关联和转换：如何将两个不同模态的信息关联起来，或者怎样把一种模态映射到另一种模态空间中去，是一个巨大的挑战。

3)融合与共同学习：在同一个特征映射空间中，将两种模态相互融合，使每个模态对最终的输出都产生相应的影响，即共同学习。

1.2 宽度学习方法

传统的神经网络如BP网络，因其反向传播计算的运行时间长、容易陷入局部最优等缺陷，网络的分类性能往往受初始化区域的影响较大。为了有效解决这些问题，不少研究者致力于寻求简单的单层网络模型，利用广义逆直接求解全局最优来优化网络的效率，因此基于宽度的网络结构逐渐发展起来。典型的方法有单层前馈神经网络(single layer feedforward neural networks, SLFN)^[12]、随机向量功能连接网络(random vector functional link neural network, RVFL)^[13-15]、极限学习机(extreme learning machine, ELM)^[16-18]等。

宽度学习方法^[11]是由澳门大学陈俊龙教授提出的一种基于RVFL平面网络结构的增量学习算法，模型结构如图1所示。与传统RVFL结构不同的是，宽度学习系统的输入权值矩阵不是随机生成，而是通过稀疏自编码方式经编码后，在解码过程中选取了最优权值。宽度学习方法的输入样本经过一次线性变换后将特征表达映射在特征平面上形成特征节点，得到的特征节点再经过激活函数非线性变换生成增强节点。特征节点和增强节点共同连接作为系统的实际输入信号，经由连接矩阵线性输出。与RVFL相同，考虑到经典BP算法的高时间成本和容易陷入局部最优等缺点，宽度学习方法采用岭回归广义逆直接求取输出连接矩阵。

给定输入数据 ${X} \in {{\bf{R}}^{N \times M}}$ ，其中N表示输入样本个数，M表示每个样本向量的特征维数。假设特征节点的个数为b，则根据宽度结构可以得到特征平面上的特征如式(1)：

${{Z}^{N \times b}} = {{X}^{N \times M}} \cdot {W}_{{e}}^{M \times b}$

(1)

式中 ${{W}_{{e}}}$ 是由稀疏自编码求得的最优输入权值矩阵。若生成d个增强节点，高层特征可表示为

${{H}^{N \times d}} = \phi ({{Z}^{N \times b}} \cdot {W}_{{h}}^{b \times d} + {\beta }_{{h}}^{N \times d})$

(2)

式中： ${{W}_{{h}}}$ 和 ${{\beta }_{{h}}}$ 分别代表随机矩阵和偏置； $\phi ( \cdot )$ 是一个可选择的非线性激活函数。将特征节点和增强节点相连得到的合并矩阵作为系统的实际输入，并假设输出矩阵为 ${Y} \in {{\bf{R}}^{N \times Q}}$ ，则宽度模型可以由式(3)求出：

${{Y}^{N \times Q}} = {{A}^{N \times (b + d)}} \cdot {{W}^{(b + d) \times Q}} = [{{Z}^{N \times b}}|{{H}^{N \times d}}] \cdot {{W}^{(b + d) \times Q}}$

(3)

式中：A代表BLS的实际输入矩阵; W代表输出连接权值矩阵，且W是通过对 ${{A}^ + }$ 的岭回归近似根据式(4)计算得到的：

${{A}^ + } = \mathop {\lim }\limits_{\lambda \to 0} {(\lambda {I} + {A}{{A}^{\rm{T}}})^{ - 1}}{{A}^{\rm{T}}}$

(4)

为了直观地展示出宽度学习系统，图2给出了BLS平面结构的立体模型，详细描述了一个输入样本X通过BLS网络进行学习的全过程。其中，Z表示特征节点层，H表示增强节点层，输出层为Y，网络仅需要学习输出矩阵W即可。

1.3 典型相关性分析

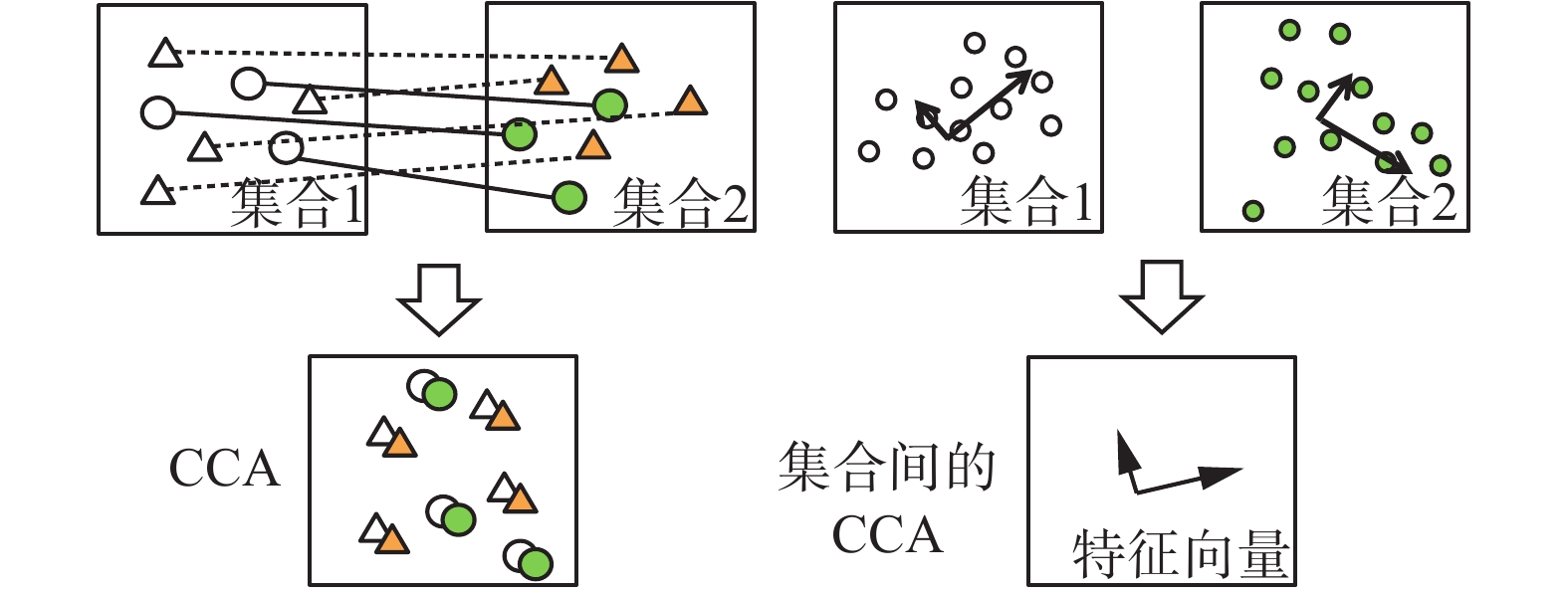
典型相关性分析(CCA)^[19]是对两个数据集合进行联合与降维的经典算法。对于两个没有显性关联的数据集，CCA可以把不同模态的数据点映射到同一个特征空间来构造关联规则。图3为CCA的基本匹配过程，通过将两种模态的数据样本进行连接，就可以得到相关特征子空间内一一对应的特征表达。

根据CCA的关联方式，假设两个分别属于不同模态，样本个数一一对应的n维数据集合X和Y，其中 ${X} = \{ {{x}_1},{{x}_2}, \cdots ,{{x}_n}\} ,{Y} = \{ {{y}_1},{{y}_2}, \cdot \cdot \cdot ,{{y}_n}\} $ 。通过映射基向量u和v进行线性变换，重新为每个集合中的数据点寻找一个新的坐标空间，并得到度量模态间相关性的参数 ${\rho }$ ，即

${\rho } = \mathop {\max }\limits_{{u,v}} \frac{{{{u}^{\rm{T}}}{{\varSigma}_{{xy}}}{v}}}{{\sqrt {{{u}^{\rm{T}}}{{\varSigma}_{{xx}}}{u}} \sqrt {{{v}^{\rm{T}}}{{\varSigma}_{{yy}}}{v}} }}$

(5)

式中Σ_xy、Σ_xx和Σ_yy代表类间和类内协方差矩阵，即

$\begin{gathered} {{\varSigma}_{{xy}}} = {\rm{E}}[{x}{{y}^{\rm{T}}}] = \frac{1}{n}\sum\limits_{i = 1}^n {{{x}_{{i}}}{{y}_{{i}}}^{\rm{T}}} \\ {{\varSigma}_{{xx}}} = {\rm{E}}[{x}{{x}^{\rm{T}}}] = \frac{1}{n}\sum\limits_{i = 1}^n {{{x}_{{i}}}{{x}_{{i}}}^{\rm{T}}} \\ {{\varSigma}_{{yy}}} = {\rm{E}}[{y}{{y}^{\rm{T}}}] = \frac{1}{n}\sum\limits_{i = 1}^n {{{y}_{{i}}}{{y}_{{i}}}^{\rm{T}}} \\ \end{gathered} $

(6)

实际应用中，式(5)表示的优化问题可以转化为特征值求解问题进行相关计算。

2 基于双宽度学习的典型相关性分析

为了实现多模态信息的融合问题，本文对宽度学习方法进行了一定程度的创新和改进，并提出了一个可以有效学习两种模态特征的融合算法框架。

2.1 双宽度学习结构

双宽度学习结构是一个以BLS为基本单元的双宽度学习(double broad learning, DBL)框架，如图4所示，此结构主要由两个BLS 单元组成，用于处理不同模态的融合问题。图中Z和H分别表示特征节点和增强节点，下标C、D、R代表彩色通道、深度通道和融合节点层。当两种模态数据输入系统时，模型训练的过程可分为以下3个部分：

1)利用宽度学习单元分别提取每个模态的高维特征，主要包括特征节点映射特征和增强节点映射特征；

2)在融合节点层将两个模态的特征映射经过一个非线性变换抽象融合起来；

3)通过学习输出权值矩阵，利用岭回归广义逆直接求取全局最优解得到输出类别属性。

2.1.1 特征提取

假设DBL模型的输入样本个数为N，设DBL的特征节点和增强节点个数分别为N₁和N₂，则彩色图像的特征表达式为

${{A}_{{C}}} = [{{Z}_1}\left| {{{H}_1}} \right.]$

(7)

式中由一个BLS单元生成、代表彩色图像的特征节点和增强节点分别可以表示为

$\begin{gathered} {{Z}_1} = \{ {{z}_{{i}}}\left| {{{z}_{{i}}} \in {{\bf{R}}^{{N_1}}}} \right.\} _{i = 1}^N \\ {{H}_1} = \{ {{h}_{{j}}}\left| {{{h}_{{j}}} \in {{\bf{R}}^{{N_2}}}} \right.\} _{j = 1}^N \\ \end{gathered} $

(8)

同理，另一个BLS单元生成的深度图像总特征以及特征节点、增强节点分别为

$\begin{gathered} {{A}_{{D}}} = [{{Z}_2}{\left| {H} \right._2}] \\ {{Z}_2} = \{ {{z}_{{i}}}\left| {{{z}_{{i}}} \in {{\bf{R}}^{{N_1}}}} \right.\} _{i = 1}^N \\ {{H}_2} = \{ {{h}_{{j}}}\left| {{{h}_{{j}}} \in {{\bf{R}}^{{N_2}}}} \right.\} _{j = 1}^N \\ \end{gathered} $

(9)

由于BLS生成特征节点过程中采用了稀疏编码，在特征提取过程中自动去除了冗余信息，减小了训练的计算复杂度，根据多模态机器学习概念，仅需要考虑后期不同模态融合过程中的信息互补即可。为了更好地学习彩色和深度这两种模态的共同特征，在输入融合节点层之前，需要将彩色图像和深度图像进行混合，使得两种模态的图像映射到同一个样本空间。考虑到神经网络的学习特性，DBL仅简单地将两种模态的特征并联起来，作为最后提取的总特征和融合空间的净输入：

${{F}^{N \times 2({N_1} + {N_2})}} = [{{A}_{{C}}}^{N \times ({N_1} + {N_2})}|{{A}_{{D}}}^{N \times ({N_1} + {N_2})}]$

(10)

2.1.2 特征的融合与分类

对于特征融合部分，由2.1.1节的介绍和图5所示立体模型可知，彩色图像模态和深度图像模态混合的总特征F就是DBL融合节点层的新输入。值得注意的是，为了更好地将两种图像模态的信息结合起来，本文引入融合节点映射层，借鉴传统神经网络的非线性拟合特点将不同的模态特征抽象融合，最后利用输出矩阵进行快速有效地学习，以提高系统的分类性能。假设融合节点个数为N₃，则融合节点层输出为

${{ T}^{N \times {N_3}}} = \phi ({{ F}^{N \times 2({N_1} + {N_2})}} \cdot { W_{ t}}^{2({N_1} + {N_2}) \times {N_3}} + { {b_t}}^N \times {N_3})$

(11)

式中选取的 $\phi ( \cdot )$ 是一个S型非线性激活函数。

基于1.2节对BLS的描述，真正意义上的宽度学习应该是将特征节点、增强节点、融合节点作为共同的特征，按照不同的权值共同作用于输出的网络。因此，DBL模型结构的输出连接矩阵W包含了两种模态的特征节点层、增强节点层和最后一层融合节点层的总权值，可以很容易地由式(12)所示的岭回归广义逆求得：

${{W}^{{[2({N_1} + {N_2}) + {N_3]}} \times O}} = {[{{F}^{N \times 2({N_1} + {N_2})}}|{{T}^{N \times {N_3}}}]^ + }{{Y}^{N \times O}}$

(12)

式中Y是由样本标签组成的O维one-hot形式的期望输出矩阵。

2.2 基于双宽度学习的典型相关性分析

图6表示基于双宽度学习的典型相关性分析(DBL-CCA)结构的多模态信息融合和学习过程。以DBL为基础，把2种模态经过特征节点和增强节点粗提取的样本特征统一映射到CCA生成的特征子空间上进行学习、匹配和降维，然后再由融合节点直接非线性化融合，连接到输出层进行分类输出。

因此，CCA在整个融合体系中承担着实现多模态机器学习关联和转换任务的作用，同时CCA的降维特性为简化模型提供了便利。由DBL结构可知，CCA层的净输入为式(10)求出的特征F，其前L个最大主成分输出 ${{P}^{N \times 2L}}$ 即为融合节点层的实际输入。因此，式(11)变为

${{T}^{N \times {N_3}}} = \phi ({{P}^{N \times 2L}} \cdot {{W}_{{t}}}^{2L \times {N_3}} + {{b}_{{t}}}^{N \times {N_3}})$

(13)

3 实验分析 3.1 康奈尔大学抓取数据集

康奈尔大学抓取数据集^[20]是判断给定物体是否可被机器人抓取的开源数据集，包含240个待判断的物体，共885幅图像。每个图像划分为若干个抓取矩形框，分别代表不同的抓取位置。根据给定标签(正表示可抓取，负表示不可抓取)可知，这是一个二分类的任务。已知矩形框共有8 019个，按照8∶2的随机划分方式可得到6 415个训练样本和1 604个测试样本，每个样本均包含尺寸为24×24的3通道彩色图像和单通道深度图像2种模态。

图7为抓取数据集的20个简单样例。图8展示了实验采用的4种分类模型，每个模型中的矩形框均代表机器人夹板的抓取操作矩形，矩形框的宽边为夹板的初始位置，矩形框的长边表示机器人夹板的运行轨迹。

DBL-CCA算法先通过特征提取及融合处理彩色图像和深度图像，之后输入分类器对物体是否可被机器人抓取作出分类判别。为了检验本文模型的融合效果，对比模型采用BLS分别对彩色图像、深度图像这两种单一模态以及两种图像的简单混合模态进行学习和分类。

对于上述提出的4种模型结构，为了提高各种模型性能的可比性，实验均设置了相同的特征节点(100)和增强节点(400)个数、收敛因子(0.5)和正则化因子( ${2^{ - 30}}$ )大小等参数，并将DBL-CCA中CCA层的输出特征维度固定在200。重复5次随机试验得到的平均测试精度、训练时间和测试时间如表1所示。从表中可以看出，只用BLS对彩色图像进行学习比只用深度图像学习得到的分类精度高、时间长；混合两种模态能够提升分类性能，但特征维度的增加消耗了一些训练时间。DBL-CCA融合算法的分类精度比以上3种方法都要高，运行时间也非常迅速，整体而言占有相当大的优势。

在融合彩色图像和深度图像的过程中，CCA层的输出特征维度会对融合结果产生一定程度的影响，图9比较了DBL-CCA与CCA、Cluster-CCA^[21]等算法在不同输出维度下的测试精度。可以看出，在CCA层输出特征维度为25时，DBL-CCA和Cluster-CCA的拐点比CCA相对明显。随着维度的增加，DBL-CCA呈上升趋势，在200维处达到最大值(95.01%)；Cluster-CCA曲线有小幅度下降趋势；CCA精度曲线在100~200维之间有小范围的波动。总体来说，DBL-CCA和Cluster-CCA算法相较于CCA而言曲线略平缓。因此，实验结果可以证明DBL-CCA无论是从收敛速度、上升趋势还是从分类精度上来看都占有极大的优势，选取该结构作为多模态图像特征的融合方法具备充分的高效性和稳定性。

为了比较不同参数对模型性能的作用和影响，实验还对DBL-CCA的节点数目和相关因子进行了参数敏感度分析。图10(a)中的N₂和N₃分别代表在 $\{ 100,200,300,400,500,600,700,800\} $ 中变化的增强节点和融合节点数目。增强节点和融合节点对图像识别精度产生的影响并不显著，说明DBL-CCA融合框架具有很好的鲁棒性，能够过滤噪声干扰。图10(b)为不同相关因子(r₁和r₂)对模型分类性能的影响程度，实验选取的参数范围为 ${10^{ - 6}} \sim {10^6}$ 。从图10可以观察到，相比于节点数目而言，相关因子对于识别率的影响较大，有更加明显的局部极大值和极小值区域。

3.2 华盛顿大学RGB-D数据集

为了验证本文提出方法的泛化性能，采用华盛顿大学RGB-D数据集^[22]作进一步的拓展实验。华盛顿大学RGB-D数据集由41 877个RGB-D(彩色和深度)图像组成，包含了具有51种不同类别的共300个实例物体。图11(a)表示“苹果”这种类别的3个具体不同实例的彩色图像及其对应的深度图像，图11(b)为部分样本的彩色图像。该数据集的采集方法是：将每个物体放置在一个转盘上，并使用Kinect的3D相机对转盘的一个完整旋转周期进行录制。每个物体均包含3个视频序列，分别记录在不同高度的摄像机上。实验按照文献[22]的划分方式选取45°角拍摄的图像生成测试集，由此可以得到用于物体识别的28 009个训练样本和13 868个测试样本。

在训练模型之前，将彩色模态和深度模态的图像分别调整成大小为24×24的3通道图像和单通道图像，然后拉伸成1 728维和576维的行向量。在此基础上根据划分标签类型的不同，可以得到300个实例分类和50个类别分类的2种实验结果。

表2说明了DBL-CCA融合算法能够有效学习彩色与深度图像的高维非线性特征，其分类识别的最优准确率明显高于单模态和线性混合模型。表3为DBL-CCA模型在2种分类方式下5次随机试验的平均训练和测试时间，相比于一般的深度结构，此方法可以有效缩短模型的时间成本，降低空间的计算复杂度。

综上所述，本文提出的DBL-CCA能够有效提取不同模态图像的丰富信息，完成融合学习和分类任务，并在训练时间、测试精度以及参数影响等方面表现出非常大的优势，使系统保持良好识别性能的同时，兼备了较高的快速性、准确性和鲁棒性。

4 结束语

为了解决实际生活经常遇到的多模态融合问题，本文提出一种新颖的DBL-CCA融合方法，通过融合学习各个输入模态的丰富特征对物体属性进行识别。考虑到训练时间、分类精度等方面的制约，DBL-CCA算法采用了宽度学习方法这种基于平层网络的架构，并在康奈尔大学和华盛顿大学的多模态图像公开数据集上验证了算法的高效性。在具体的研究与应用中，此方法能够帮助机器人完成快速准确的抓取操作；对于复杂环境下可能存在的不同噪声干扰，算法能否持续保有良好的泛化性能，是一个值得深入研究的问题。