2. 同济大学 中德学院,上海 201804
2. College of China and German, Tongji University, Shanghai 201804, China
音乐生成是使用算法将音乐创作过程的部分或全部自动化的研究。使用数学的方式研究音乐的生成虽然在一千年前就已出现,但受限于其他相关学科的发展,一直没有较大的进步。而近年来,随着深度学习的不断发展,音乐生成问题重新回到研究者们的视野中,与之相关的多种算法模型也都被应用于音乐生成问题的研究。特别是Char RNN模型的提出,以序列预测的方式训练生成网络的研究变得火热。Eck等[1]首次将LSTM引入音乐生成领域,基于前序音符生成后序音符的思想,搭建了蓝调旋律的生成系统。Sturm等[2]使用音乐的ABC格式文本作为训练数据,率先将Char RNN模型引入音乐生成领域,对音符文本进行one hot编码,使用当前音符的编码向量,预测下一个音符的概率分布,然后采样生成下一个字符,最终生成质量较好的音乐旋律。区别于ABC格式的旋律文本数据,Choi等[3]通过将旋律与和弦一起编码成文本数据,然后使用Char RNN模型生成了拥有和弦的多声部音乐。王程等[4]通过将音乐的音频数据编码成与文本类似的one hot向量,然后使用Char RNN进行音乐的生成。Lackner[5]则通过将音乐中的和弦和旋律分离的形式,使用和弦去预测旋律对Char RNN进行训练,通过输入人工创作的和弦来生成相应的旋律[5]。Chu等[6]提出了分层RNN结构的音乐生成系统,在系统底层生成音符,在更高层生成和弦及鼓节奏,通过将更多乐理知识引入神经网络的训练中,生成了结构良好的音乐作品。Makris等[7]提出了使用RNN生成节奏序列,用于生成变节奏的音乐作品。Oord等[8]提出的WaveNet用于生成原始的音频格式音乐,该网络使用音频压缩后的数据进行训练,表述为16位的整数值序列,与前人不同的是,他们使用卷积神经网络来搭建系统。Mogren[9]使用两个RNN作为生成对抗网络的生成器和判别器,音乐数据模型则采用了类似MIDI数据Event事件的编码方式。
综上所述,可以看出目前音乐生成的研究成果主要集中在旋律的生成研究上,考虑旋律与和弦搭配的多声部音乐生成的研究并不是很多,本文将从多声部音乐数据的建模方式以及生成模型的训练策略两个方向进行研究,尝试搭建多声部音乐的生成系统。
1 多声部音乐数据建模音乐数据是一种结构非常复杂的时序数据。要使用算法的方式进行音乐数据的生成,首先要理解音乐数据的结构特征和音乐信息的表达方式。本文基于现代音乐常用的表达方式,即采用MIDI格式和Piano Roll格式分析多声部音乐的特点,建立音乐数据模型。
1.1 MIDI格式与Piano Roll格式MIDI(音乐数字接口)是一种描述计算机数字接口与各种乐器连接协议的技术标准。与ABC等文本格式相比,MIDI所携带的信息量更大,现代音乐基本都是用MIDI制作合成。它的基本思想是将不同音高和音长组合的音符信息表示成一个个的事件(Event),同时还携带音符的音量和起始时间等信息,量化了音乐的基本特征,并将音乐演奏中的每种乐器表示为一个通道(channel),记录每种乐器的音符弹奏的方式。MIDI的事件信息有很多类型,由于本文主要聚焦于音乐本身的表达,所以此处只介绍与音乐生成系统相关的基本事件。MIDI的基本音符事件有2种:Note on事件和Note off事件。Note on事件表示一个具有某种音高、音长的音符在某个通道开始被特定乐器弹奏,如<Note on, 0, 60, 50>表示在通道1,在50个单位时间后开始演奏middle C音。Note off事件表示在某个通道的特定乐器停止演奏具有某种音高、音长的音符,如<Note off, 0, 60, 20>表示在通道1,在20个单位时间后停止演奏middle C音。
Piano Roll表示方法是受自动钢琴的启发,它的实质是一个连续的纸卷,通过在上面进行穿孔来记录信息。每个穿孔代表一个音符控制信息,用于触发给定的音符。穿孔的长度对应音符的持续时间,穿孔的定位与其间隔相对应,每一列的穿孔表示钢琴中的每一个琴键。
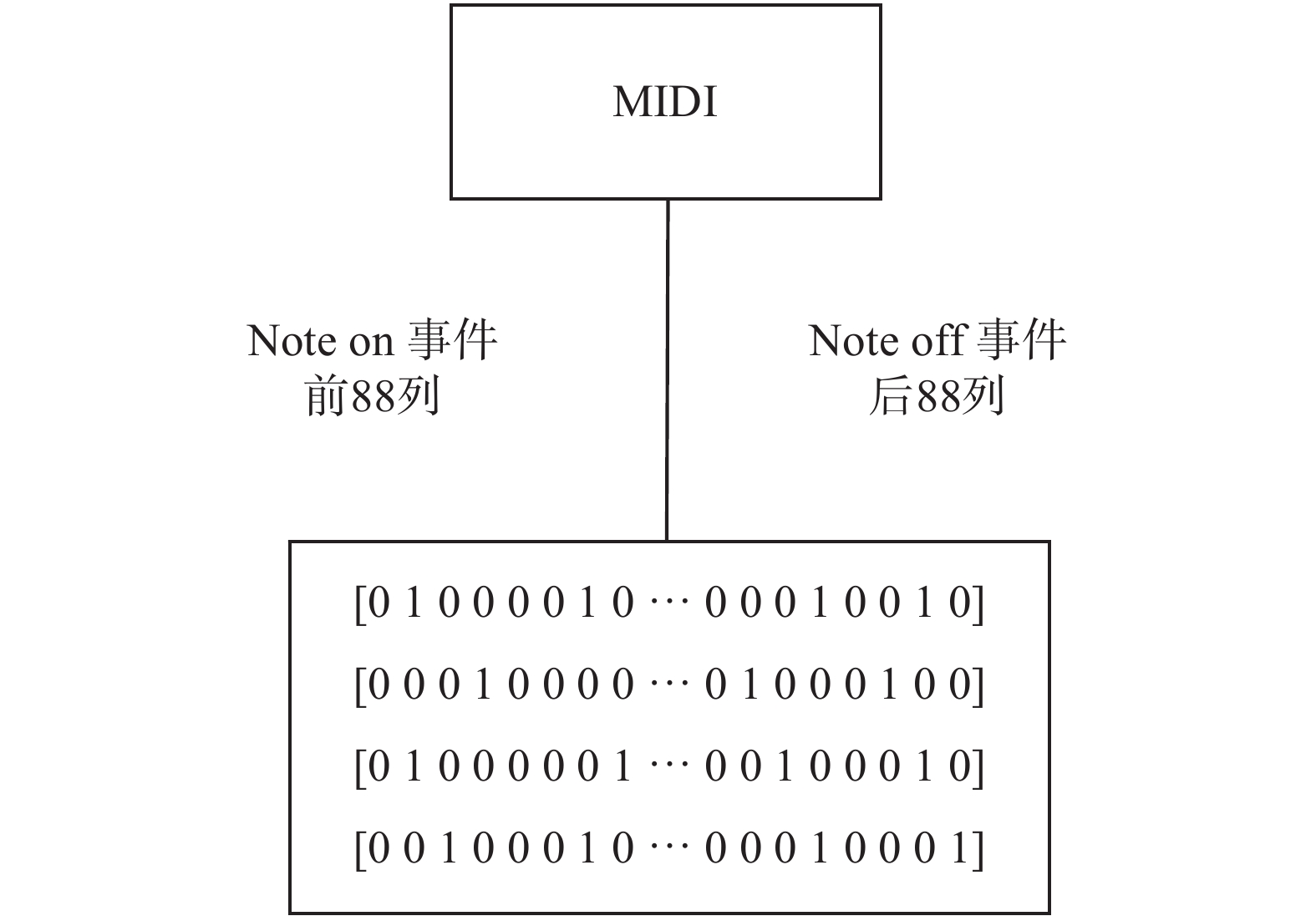
1.2 基于MIDI与Piano Roll的音乐数据建模本文所研究的是多声部音乐的生成问题,因此多声部音乐数据的表示方式至关重要。根据上文对MIDI格式和Piano Roll格式的介绍,可以较为容易地设计一种多声部音乐的表达方式,即使用0和1组成的矩阵表示多声部音乐中每个音符的状态信息,其中行表示钢琴中的88个键,也是钢琴所能表示的音高范围,列则表示时间序列。1表示琴键被按下,0表示琴键被弹起。但这种方式有1个缺陷,即在出现一连串的1时,无法分辨出是被多次弹奏还是一个持续较长的音。所以可以结合MIDI格式的Note on和Note off事件思想,将原有的钢琴键维度88扩展成176。使用前88维的1表示琴键被按下,也就是Note on事件,使用后88维的1表示琴键被弹起,也就是Note off事件,如图1所示。
|
Download:
|
| 图 1 MIDI与Piano Roll相互转化 Fig. 1 Translation between MIDI and Piano Roll | |
这种方式不仅可以有效区分长音和多次弹奏,且方便MIDI音乐数据与Piano Roll矩阵的相互转化。但通过实践发现这种多声部音乐的建模方式虽然可以用同一时刻钢琴键状态向量表示旋律与和弦的弹奏状态,但无法表征旋律与和弦在时间维度上的匹配信息,即各音符之间是独立表达的。
1.3 基于栈式自编码器的音乐隐式特征建模设计根据前文的研究分析,本文认为使用原始Piano Roll格式进行多声部音乐数据的表达方式,并不能表现旋律与和弦更高维度的组合特征。基于此,本文提出使用对同一时间步音符状态压缩的方式,提取各音符状态之间的关系作为音乐的隐式特征,并以此作为多声部音乐的数据模型。
自编码器(autoencoder)是一种具有一层隐藏层的神经网络,其特殊的结构在于:网络的输入层与输出层的神经元节点数目相同,且隐藏层的节点数要小于输入与输出层。在训练自编码器时,可以使用传统的神经网络训练方式。唯一不同的是,训练自编码器的输入数据就是要输出的目标数据。因此自编码器学习的是一种数据的表示功能。因为隐藏层的节点要比输入层的节点少,所以编码器部分必须对信息进行有损压缩,而解码器部分则需要根据压缩后的特征信息尽可能地重构原始的信息。这就迫使自编码器去发现数据中重要的区分点,所以自编码器通常用于提取数据中更高维度的特征。
随着深度学习的出现,栈式自编码器(stacked autoencoder)得到了更广泛的应用。栈式自编码器是由多个自编码器嵌套组成,且隐藏层的神经元数目依次递减。在这种结构中,编码器会不断地压缩数据以提取出更高级别的特征。因此这种类似深度神经网络的结构,是现在常用的特征提取手段之一。
通过对现有特征提取方法的比较,本文决定采用栈式自编码器对多声部音乐的Piano Roll格式数据进行隐式特征提取。
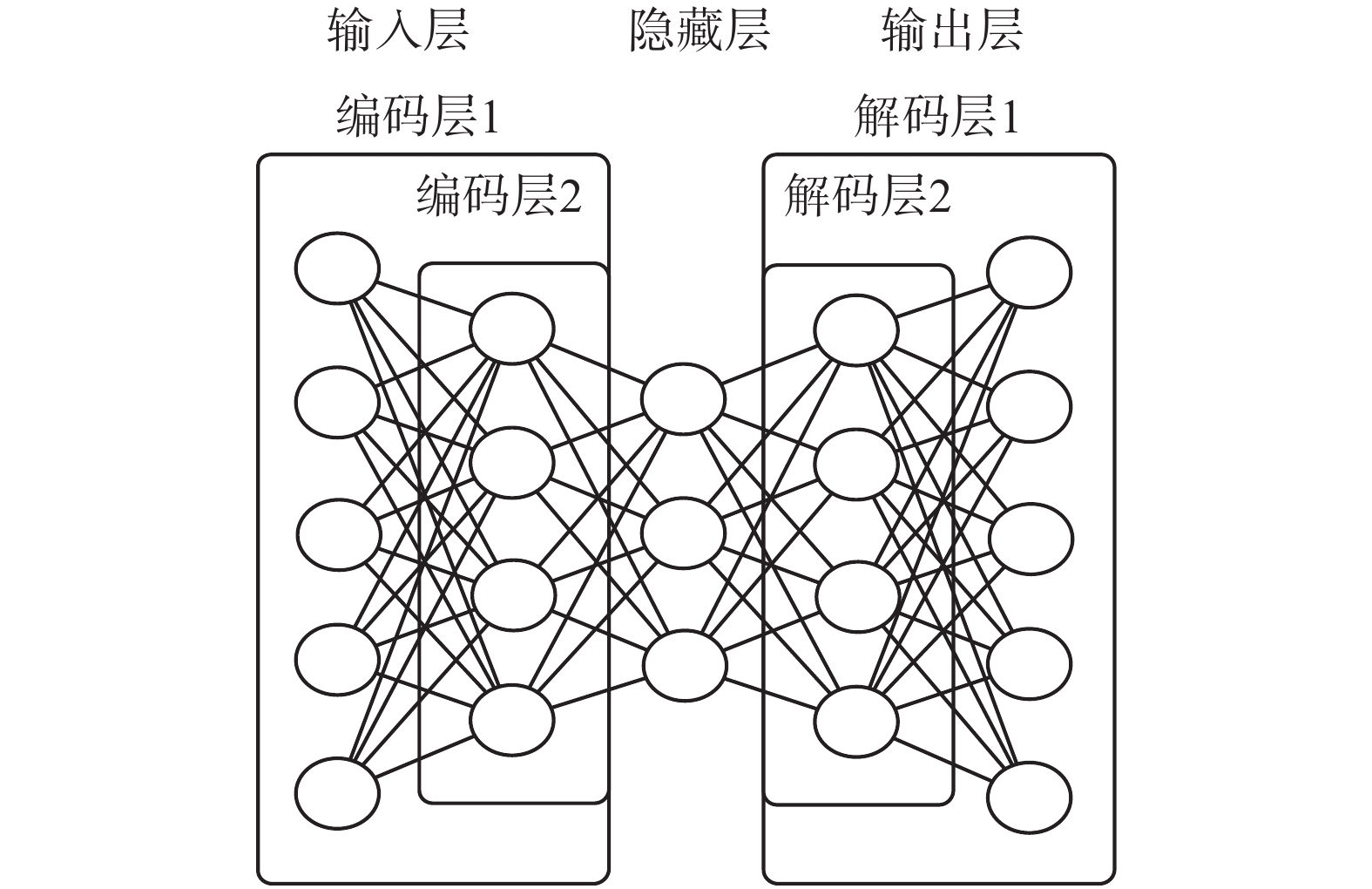
1.4 搭建用于隐式音乐特征提取的栈式自编码器本文使用从freemidi.org采集的50首MIDI格式的音乐数据进行栈式自编码器训练。通过1.2节介绍的Piano Roll格式与MIDI数据的转化关系,提取50首音乐的Piano Roll矩阵。在实验中发现,由于提取的音乐数据风格相似,音乐的音高都在24~102。通俗地讲,钢琴的88个键中只被用到了中间的78个键。为了降低计算复杂度,本文将原有的176维的Piano Roll矩阵减少到156维,根据此格式的音乐数据搭建栈式自编码器,如图2所示。
|
Download:
|
| 图 2 自编码器结构 Fig. 2 Structure of the autoencoder | |
栈式自编码器的输入层和输出层的神经元节点均为Piano Roll的钢琴键维度156。而对于隐藏层,则需先设计一个比输入输出层节点数目小的节点数,通过后续训练实践,逐一调整。
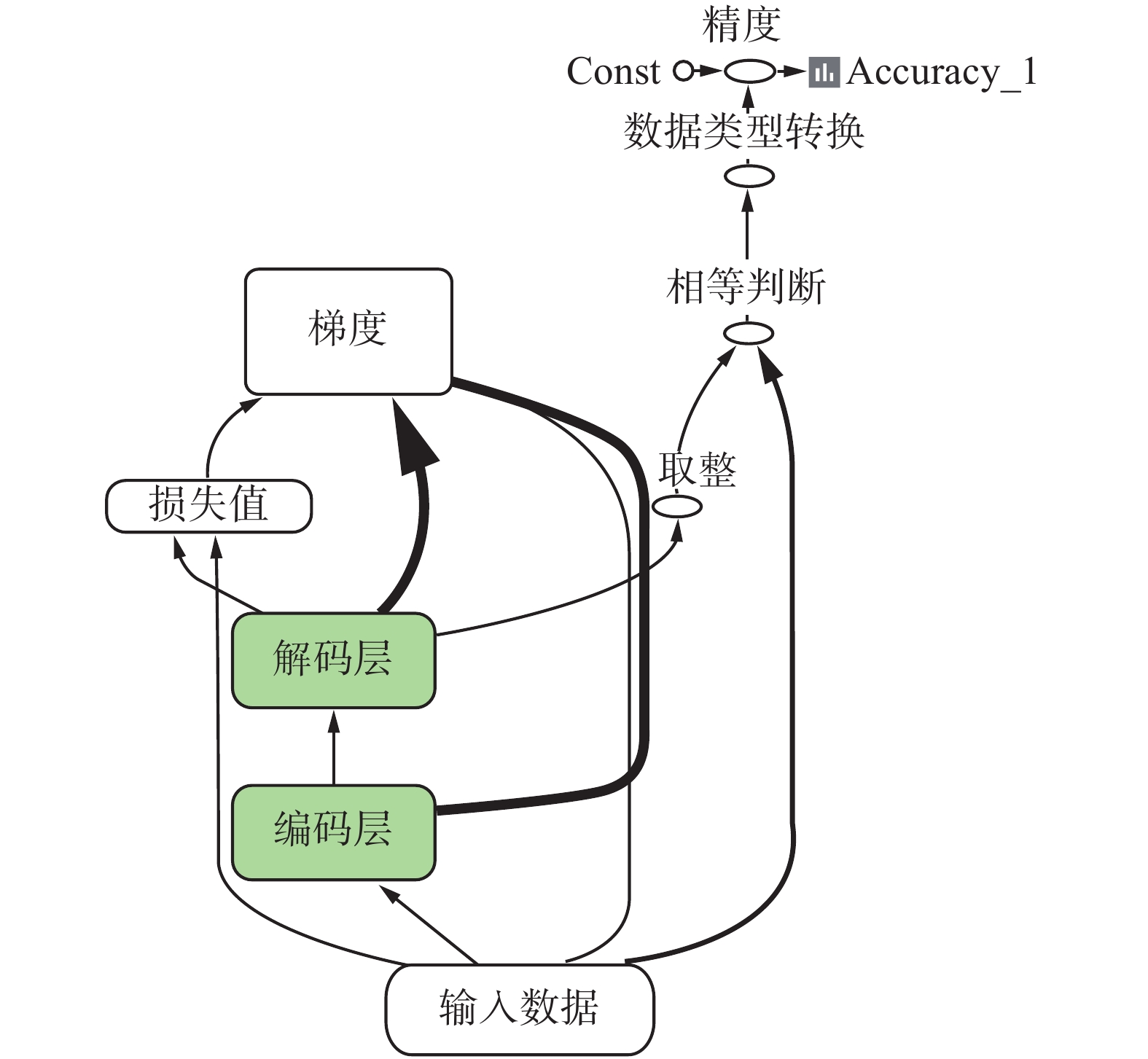
根据前文分析,本文所要搭建的栈式自编码器是对Piano Roll矩阵的每个156维的0、1向量进行特征提取。经过解码器后,应生成与输入向量相同的输出结果。所以本文采用训练网络的代价函数为均方差代价函数,即
| $\cos t = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{({a_i} - {y_i})}^2}} $ | (1) |
式中:
|
Download:
|
| 图 3 栈式自编码器计算图 Fig. 3 Computational graph of the stacked autoencoder | |
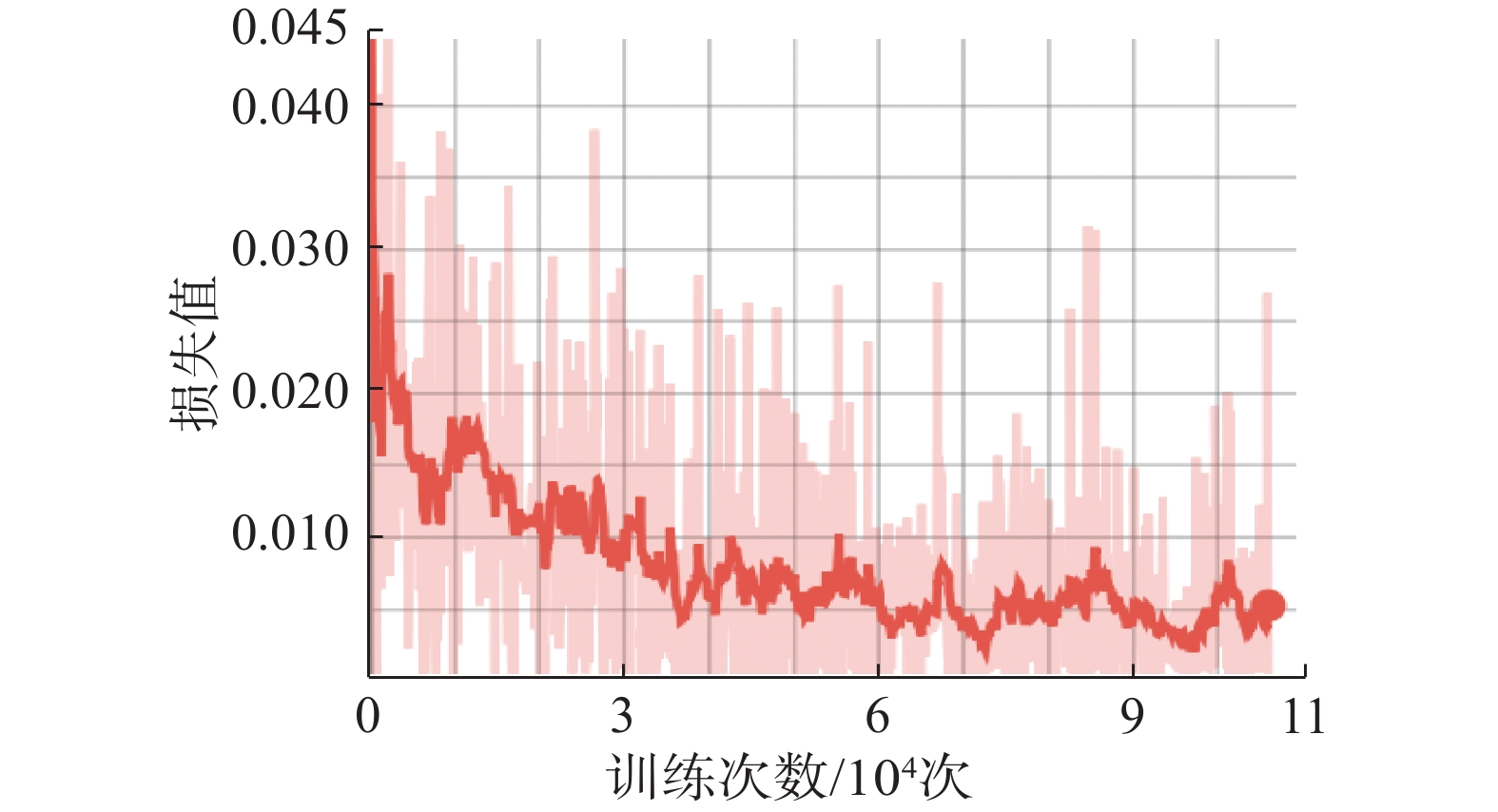
使用freemidi.org的50首MIDI音乐提取的Piano Roll矩阵对网络进行训练,通过调整网络超参数得到训练结果如图4所示,其中横坐标为训练数据分批后的迭代次数,纵坐标为根据式(1)计算的损失值。
|
Download:
|
| 图 4 训练结果 Fig. 4 Training results | |
为测试该自编码器在训练数据集以外的音乐数据中的特征提取效果,使用另外4首相同风格的MIDI音乐对网络进行测试。将音乐的音符状态数据进行编解码,比较网络的输出值与真实值,准确度如表1所示。
| 表 1 栈式自编码器的泛化结果 Tab.1 Generalization results of the stacked autoencoder |
从表1可以看出,本小节训练的栈式自编码器在这一风格的音乐数据中,编码后解码的准确率较高,可以理解为编码器提取到了较好的隐式音乐特征。通过使用栈式自编码器的编码器部分,对音乐数据的Piano Roll矩阵进行隐式特征提取,即得到了本文所要使用的多声部音乐数据模型。
2 基于隐式音乐特征和RNN的音乐生成模型 2.1 RNNRNN是全连接神经网络的扩展,在全连接神经网络的基础上,将隐藏层的节点进行连接[10],即每一个隐藏层节点的输入不再只是前一层节点的输出,同时还包括本节点在上个时刻的隐藏状态
| ${f_t} = \sigma \left( {{W_f}\left[ {{x_t},{h_{t - 1}}} \right]} \right)$ | (2) |
| ${i_t} = \sigma \left( {{W_i}\left[ {{x_t},{h_{t - 1}}} \right]} \right)$ | (3) |
| ${\tilde C_t} = \tanh \left( {{W_c}\left[ {{x_t},{h_{t - 1}}} \right]} \right)$ | (4) |
| ${C_t} = {f_t} \cdot {C_{t - 1}} + {i_t} \cdot {\tilde C_t}$ | (5) |
| ${o_t} = \tanh \left( {{W_o}\left[ {{x_t},{h_{t - 1}}} \right]} \right)$ | (6) |
| ${h_t} = {o_t} \cdot \tanh \left( {{C_t}} \right)$ | (7) |
3个门的结果都由输入
本文采用与Char RNN模型类似的训练方式对音乐生成系统进行训练。其主要训练思想可以概括为
| ${a_2},{a_3},{a_4}, \cdots ,{a_t} = f({x_1},{x_2},{x_3}, \cdots ,{x_{t - 1}})$ | (8) |
式中:
基于上文对音乐生成网络训练思路的分析,得到训练数据结构如图5所示。

|
Download:
|
| 图 5 训练数据集结构 Fig. 5 Structure of training data | |
根据BPTT的后向传播方式,每次都输入固定时间步的数据对网络进行训练,训练目标即向后推一个时间步的输入数据。
本文使用从freemidi.org采集的50首经典风格的MIDI音乐作为原始训练数据。按照第1章的建模方式,将MIDI数据转化成Piano Roll矩阵,然后使用栈式自编码器的编码器部分,将Piano Roll矩阵的音符状态数据转化成隐式特征数据。最后将数据使用图5的格式建立数据集,完成生成系统的训练数据预处理工作。
2.3 训练生成系统根据式(9)和对音乐隐式特征数据的结构分析,音乐生成网络的训练可以被认为是一个高维度时序特征的回归预测问题。因此采用回归问题常用的均方差代价函数为
| $\cos t = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{({a_i} - {y_i})}^2}} $ | (9) |
式中:
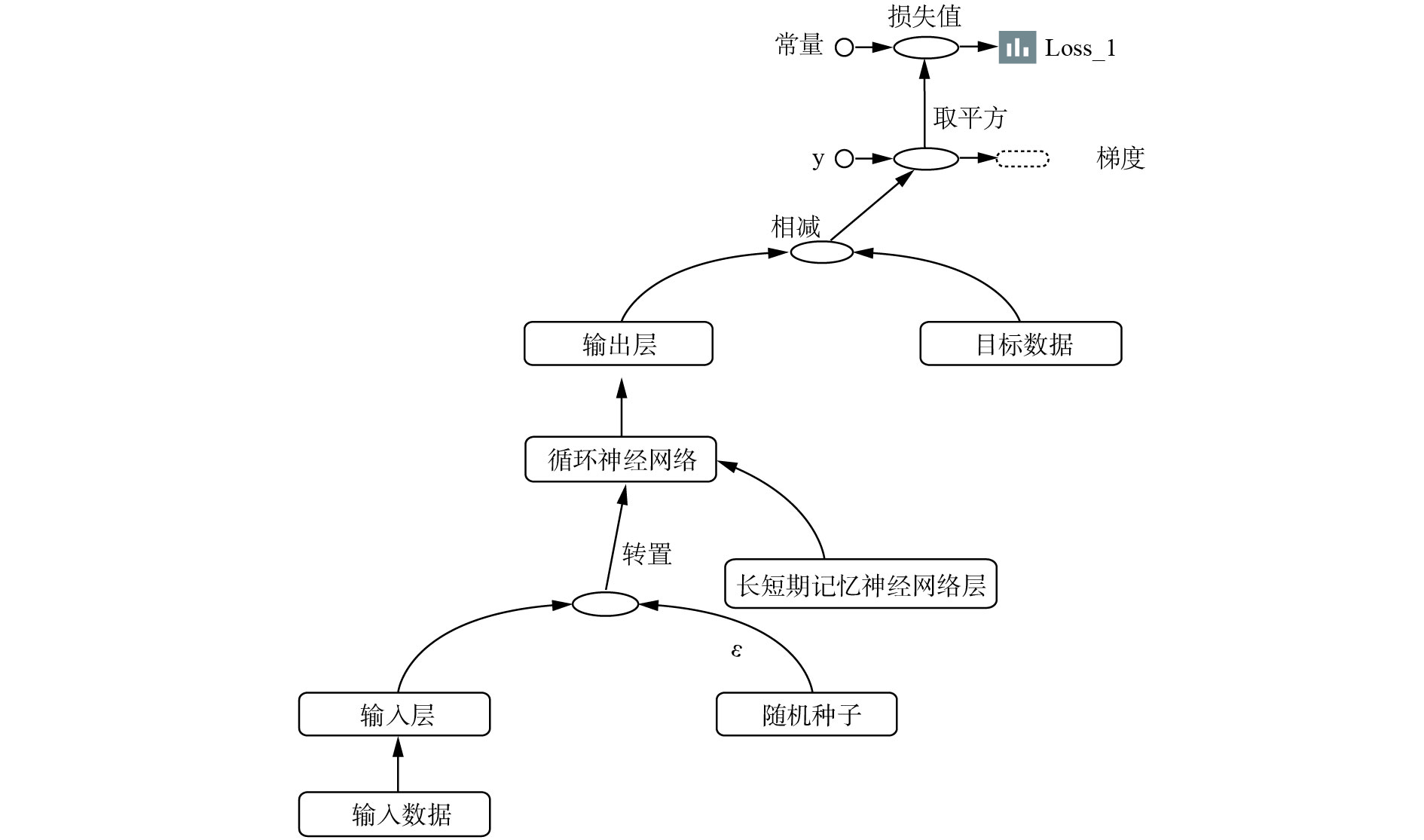
|
Download:
|
| 图 6 隐式特征的LSTM生成网络 Fig. 6 Hidden feature-based LSTM generation network | |
通过调节网络中的超参数,得到训练损失值结果如图7所示,其中横坐标为训练数据分批后的迭代次数;纵坐标为根据式(9)计算的损失值。

|
Download:
|
| 图 7 训练结果 Fig. 7 Training results | |
由图7可以看出,生成网络的损失值也有较好的收敛。
2.4 完整音乐生成系统的搭建完整音乐生成过程如图8所示。根据训练好的栈式自编码器的编码器部分,可以得到Piano Roll数据的隐式音乐特征矩阵。然后传入LSTM音乐特征生成网络生成下一个时间步的音乐特征,将新的特征序列和LSTM输出状态作为输入进行下一次的迭代生成,最后再通过解码器部分,得到最终的音符状态向量Piano Roll,完成整个音乐生成系统的生成过程。生成完成后,将Piano Roll矩阵转化成MIDI音乐。

|
Download:
|
| 图 8 完整音乐生成过程 Fig. 8 Process of music composition | |
为了更好地说明加入隐式特征后的音乐生成效果,本文使用同样的音乐数据,在不转换成隐式特征的情况下,直接使用Piano Roll矩阵训练RNN,得到用于对比的音乐生成模型。评估模型则选择使用人工选取的被标注为好与不好的音乐数据训练出的二分类模型作为评价。评价方法为:生成同样的随机种子,分别使用基于Piano Roll的多声部音乐生成模型与基于音乐隐式特征的多声部音乐生成模型进行音乐片段的生成。得到生成样本各200首,最后使用训练好的音乐评价模型对音乐样本进行评价。将标签为好的样本数的占比作为音乐生成系统的评价标准。最终得到的评价结果如表2所示。
| 表 2 评估结果 Tab.2 Evaluation results |
本文基于隐式特征,通过训练一个循环神经网络,搭建针对相同风格音乐的特征提取和音乐创作模型。在一定程度上解决了传统作曲算法,难以提取音乐中旋律与和弦之间的隐式特征生成的声部音乐的问题。仿真结果表明,通过对音乐的Piano Roll数据进行压缩编码,得到各时间步音符状态的隐式特征,然后以序列预测的方式进行多声部音乐的生成,在解决旋律与和弦的搭配问题上有较好的效果。下一步工作将着重于使用深度学习算法,基于大数据建立音乐特征深度提取模型,从而使得系统可以更好地提取并学习音乐样本特征,提升系统的创作能力。
| [1] |
ECK D, SCHMIDHUBER J. A first look at music composition using LSTM recurrent neural networks. Technical Report No. IDSIA-07-02[R]. Manno, Switzerland: Istituto Dalle Molle Di Studi Sull Intelligenza Artificiale, 2002: 1–11.
( 0) 0)
|
| [2] |
STURM B L, SANTOS J F, BENTAL O, et al. Music transcription modelling and composition using deep learning[EB/OL]. (2016-04-29)[2018-03-23]. https://arxiv.org/abs/1604.08723.
( 0) 0)
|
| [3] |
CHOI K, FAZEKAS G, SANDLER M. Text-based LSTM networks for Automatic Music Composition[EB/OL].(2016-04-18)[2018-03-23].https://arxiv.org/abs/1604.05358.
( 0) 0)
|
| [4] |
王程, 周婉, 何军. 面向自动音乐生成的深度递归神经网络方法[J]. 小型微型计算机系统, 2017, 38(10): 2412-2416. WANG Cheng, ZHOU Wan, HE Jun. Recurrent neural network method for automatic generation of music[J]. Journal of Chinese computer systems, 2017, 38(10): 2412-2416. DOI:10.3969/j.issn.1000-1220.2017.10.045 (  0) 0)
|
| [5] |
LACKNER K. Composing a melody with long-short term memory (LSTM) recurrent neural networks[D]. Munich, Germany: Technische Universität München, 2016.
( 0) 0)
|
| [6] |
CHU H, URTASUN R, FILDER S. Song from PI: a musically plausible network for Pop music generation[EB/OL].(2016-11-10)[2018-03-23].https://arxiv.org/abs/1611.03477.
( 0) 0)
|
| [7] |
MAKRIS D, KALIAKATSOS-PAPAKOSTAS M, KARYDIS I, et al. Combining LSTM and feed forward neural networks for conditional rhythm composition[C]//18th International Conference on Engineering Applications of Neural Networks. Athens, Greece, 2017: 570–582.
( 0) 0)
|
| [8] |
OORD A V D, DIELEMAN S, ZEN H, et al. WaveNet:a generative model for raw audio[EB/OL].(2016-09-19)[2018-03-23].https://arxiv.org/abs/1609.03499.
( 0) 0)
|
| [9] |
MOGREN O. C-RNN-GAN: continuous recurrent neural networks with adversarial training[C]//Constructive Machine Learning Workshop (NIPS 2016). Barcelona, Spain, 2016: 1–6.
( 0) 0)
|
| [10] |
SHEN Yan, XIE Meiping. Ship motion extreme short time prediction of ship pitch based on diagonal recurrent neural network[J]. Journal of marine science and application, 2005, 4(2): 56-60. DOI:10.1007/s11804-005-0034-z ( 0) 0)
|
| [11] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


