机器人逆运动学求解就是已知机器人末端位姿参数来计算各个关节角度值的过程[1]。其常用的方法包括封闭解法和数值解法,但这2种方法均不具备通用性且求解精度无法保证[2-3]。遗传算法是根据生物进化现象演化而来的一种智能算法,搜索能力强,能够实现全局收敛[4-5]。近年来,一些研究人员将其应用到机器人的逆运动学求解中,并取得了一定的成果。林明等[6]提出了一种改进的遗传算法,采用自适应的交叉和变异算子,改进了排序方法,并在求解过程中使用了罚函数,对多解问题进行了优化,改善了收敛速度和收敛精度。Ayyildiz等[7]采用遗传算法与其他4种不同的启发式优化算法在4R机械臂上求逆运动学解进行对比,并通过2种不同的场景来测试机器人末端执行器的运动,结果表明遗传算法可以有效地降低末端执行器的误差。Starke等[8]提出了把遗传算法和粒子群优化算法的优点进行混合,找到全姿态目标的解,结合共同的约束条件,设计一个多目标适应度函数,利用局部极值获得精确的解。然而遗传算法对非线性问题的解决并不理想,求解精度无法得到保证。
RBFNN是一种高效的前馈式神经网络[9-10],具有较好的非线性拟合能力,能够很好地逼近任意复杂的非线性系统,处理多输入多输出问题。故Zubizarreta等[11]提出了使用人工神经网络对3PRS机器人实时逆运动学问题进行计算,并实现其实时性能。Toshani等[12]采用RBFNN求解机器人逆运动学解,保证了网络权重和约束条件的收敛性,并获得了较小的误差值。Köker[13]通过结合遗传算法和神经网络的方法求解机器人运动学逆解,并成功地使用遗传算法将神经网络求解结果的浮点数部分提高了10位有效数字。尽管RBFNN在求解机器人逆运动学解上取得了一定的成果,但其仍然存在网络结构不完善、连接权值无法取得最优的缺陷,而且采用遗传算法优化RBFNN存在易陷入局部极值导致输出误差偏大的缺陷[14]。
本文采用RBFNN来求解一般机器人逆运动学解,结合一般机器人的正运动学模型,采用MPGA优化RBFNN的网络结构和连接权值的方法,并应用混合编码和同时演化的方式,实现了从机器人工作空间位姿到关节角度的非线性映射,从而避免了复杂的公式推导,提高了求解速度。最后,通过实验证明了该算法有效解决了机器人的逆运动学问题,并提高了求解速度和计算精度。
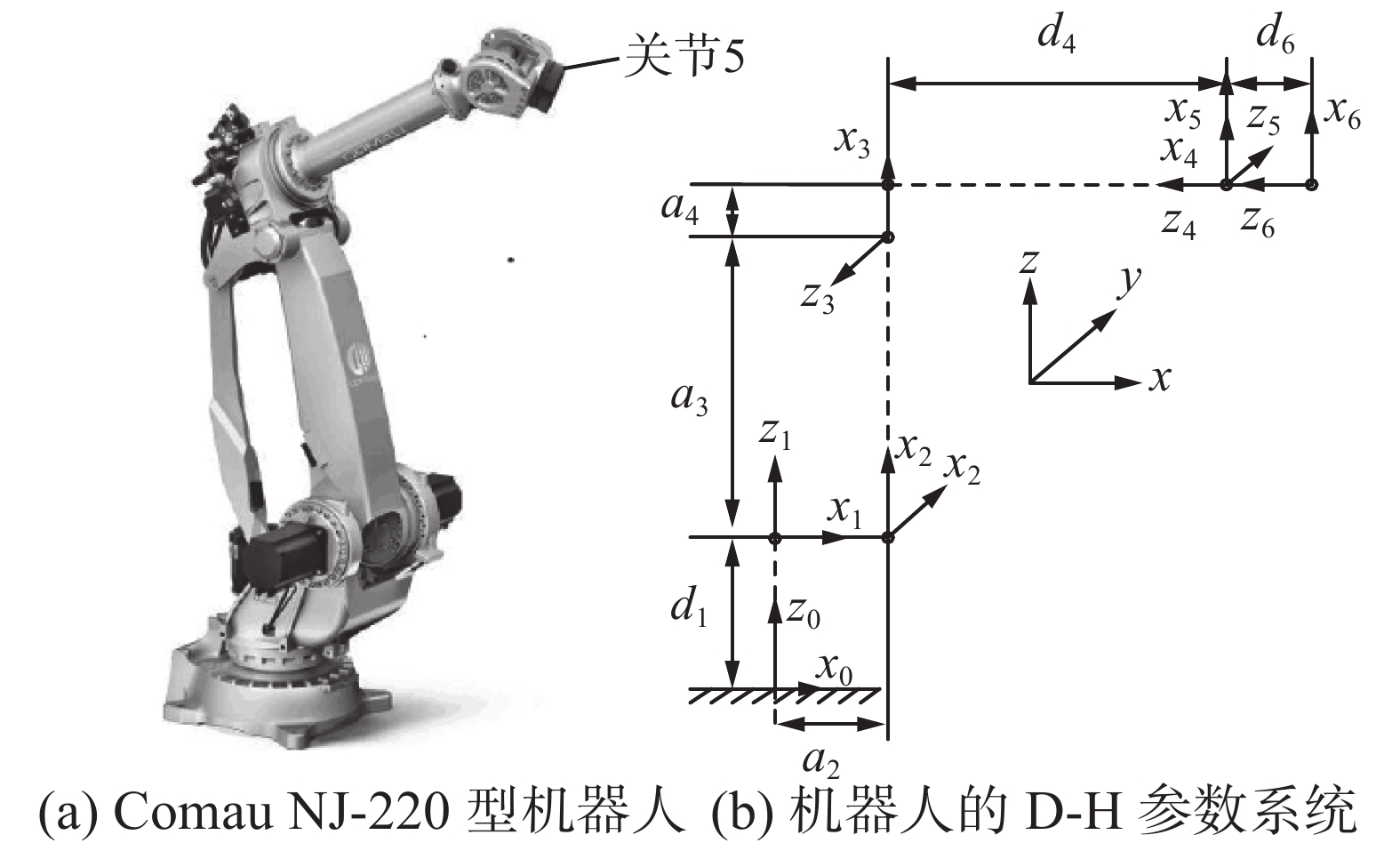
1 运动学分析本文采用改进的D-H算法[15]对Comau NJ-220型机器人[2]进行运动学建模,得到如图1所示的机器人D-H模型。在关节5处,该机器人存在沿
|
Download:
|
| 图 1 Comau NJ-220型机器人及其D-H参数 Fig. 1 The Comau NJ-220 robot and the D-H parameters | |
| 表 1 Comau NJ-220型机器人的关节参数 Tab.1 Joint parameters of the Comau NJ-220 robot |
根据表1的D-H参数,相邻坐标系间的变换矩阵为
| $\begin{gathered} _i^{i - 1}{{T}} = {\bf{Scre}}{{\bf{w}}_{{X}}}({a_{i - 1}}, {\alpha _{i - 1}}){\bf{Scre}}{{\bf{w}}_{{Z}}}({d_i}, {\theta _i}) = \\ \left[ {\begin{array}{*{20}{c}} \!\!\! {\cos {\theta _i}}&{ - \sin {\theta _i}}&0&{{{{a}}_{i - 1}}} \!\!\! \\ \!\!\! {\sin {\theta _i}\cos {\alpha _{i - 1}}}&{\cos {\theta _i}\cos {\alpha _{i - 1}}}&{ - \sin {\alpha _{i - 1}}}&{ - {{{d}}_i}\sin {\alpha _{i - 1}}} \!\!\! \\ \!\!\! {\sin {\theta _i}\sin {\alpha _{i - 1}}}&{\cos {\theta _i}\sin {\alpha _{i - 1}}}&{\cos {\alpha _{i - 1}}}&{{{{d}}_i}\cos {\alpha _{i - 1}}} \!\!\! \\ \!\!\! 0&0&0&1 \!\!\! \end{array}} \right] \\ \end{gathered} $ | (1) |
依次连乘变换矩阵,即可得到末端执行器坐标系到机器人基坐标系的变换关系:
| $\begin{gathered} {}_6^0{{T}} = \prod\limits_{i = 1}^6 {{}_i^{i - 1}} {{T}} = \left( {\begin{array}{*{20}{c}} {{{{n}}_x}}&{{{{o}}_x}}&{{{{a}}_x}}&{{{{p}}_x}} \\ {{{{n}}_y}}&{{{{o}}_y}}&{{{{a}}_y}}&{{{{p}}_y}} \\ {{{{n}}_z}}&{{{{o}}_z}}&{{{{a}}_z}}&{{{{p}}_z}} \\ 0&0&0&1 \end{array}} \right) = \\ {{p}}({\theta _1}, {\theta _2}, {\theta _3}, {\theta _4}, {\theta _5}, {\theta _6}) \\ \end{gathered} $ | (2) |
根据式(2)可以求出机器人运动学正解,即末端执行器的姿态
| $\beta = \arctan 2( - {{{n}}_z}, \sqrt {{{n}}_x^2 + {{n}}_y^2} )$ | (3) |
| $\alpha = \arctan 2({{{n}}_y}, {{{n}}_x})$ | (4) |
| $\gamma = \arctan 2({{{o}}_z}, {{{a}}_z})$ | (5) |
在运动学求逆解过程中,将
为了解决一般机器人逆运动学求解过程中存在的求解速度慢、求解精度低的问题,本文提出了采用MPGA来优化RBFNN网络结构和连接权值的方法,并应用混合编码和同时演化的方式,实现从机器人工作空间位姿到关节角度的非线性映射,从而避免了复杂的公式推导及计算量大的问题。MPGA优化RBFNN的过程如图2所示。

|
Download:
|
| 图 2 MPGA-RBFNN算法流程 Fig. 2 Algorithm flow chart of MPGA-RBFNN | |
在图2中,为了达到搜索要求,MPGA根据种群的差异,设置不同的控制参数,并将多个种群进行同时优化搜索;为了实现多个种群之间的协同进化,MPGA在不同的种群之间通过移民算子进行联系。
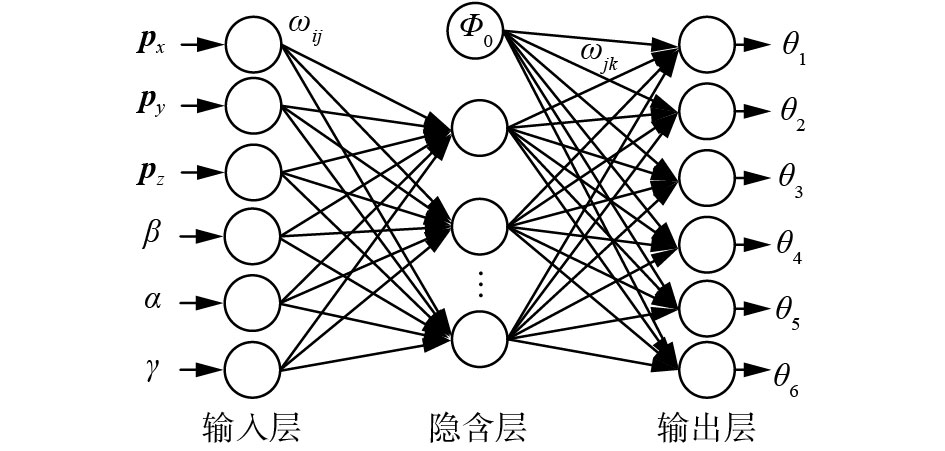
2.1 RBFNN结构RBFNN具有较好的非线性拟合能力,能够很好地逼近任意复杂的非线性系统,处理多输入多输出问题[17]。在本文的网络结构中,将末端执行器的空间位姿
|
Download:
|
| 图 3 RBFNN求逆解网络结构 Fig. 3 RBFNN structure in solving inverse kinematics | |
在隐含层的选择中,本文采用RBFNN中常用的高斯函数作为基函数:
| $\phi ({{x}}, {{{x}}_i}) = {{G}}({{x}}, {{{x}}_i}) = {{G}}(\left\| {{{x}} - {{{x}}_i}} \right\|) = \exp ( - \frac{1}{{2{{{b}}_i}^2}}\left\| {{{x}} - {{{x}}_i}} \right\|)$ | (6) |
式中:
| ${{{y}}_{{n}}}({{k}}) = \sum\limits_{i = 1}^n {{\omega _i} \times \phi ({{x}}, {{{x}}_i}} ) = \sum\limits_{i = 1}^n {{\omega _i} \times \exp ( - \frac{1}{{2{{b}}_{{i}}^2}}} \left\| {{{x}} - {{{x}}_i}} \right\|)$ | (7) |
定义在时刻
| ${{e}}({{k}}) = \sum\limits_{k = 1}^n {\left[ {{{t}}({{k}}) - {{{y}}_{{n}}}({{k}})} \right]} $ | (8) |
式中
假设RBFNN的隐含层神经元的最大个数为
| ${{{c}}_1}{{{c}}_2} \cdots {{{c}}_{{l}}}{\omega _{11}}{\omega _{21}} \cdots {\omega _{l1}}{\omega _{12}}{\omega _{22}} \cdots {\omega _{{{l}}2}}{\omega _{1{{m}}}}{\omega _{2{{m}}}} \cdots {\omega _{lm}}{{{b}}_1}{{{b}}_2} \cdots {{{b}}_{{m}}}$ | (9) |
式中:
适应度函数是评价算法的重要指标,而在神经网络中包括实际输出误差和期望输出误差,因此本文引入适应度函数为
| ${{F}} = \frac{1}{{{{e}}({{k}})}} = \frac{1}{{\sum\limits_{k = 1}^n {\left[ {{{t}}({{k}}) - {{{y}}_{{n}}}({{k}})} \right]} }}$ | (10) |
式中
选择算子采用基于轮盘赌法的非线性排名策略,即每个个体进入下一代的概率等于其适应度值与整个种群个体适应度值的总和,并且适应度值大的个体,进入下一代的可能性就越大。交叉算子采用多点交叉与均匀交叉相结合的方式,促进解空间进行稳定、高效的搜索,避免早熟现象发生。交叉概率为
| ${{{P}}_c}({{i}}) = {{{P}}_{c\min }}({{i}}) \times (1 - {\rm{rand}}({{N}}, 1)) + {{{P}}_{c\max }}({{i}}) \times {\rm{rand}}({{N}}, 1)$ | (11) |
式中:
变异算子采用基于动态变异率的变异算子。常用的变异概率值为
| ${{{P}}_b}({{i}}) = {{{P}}_{b\min }}({{i}}) \times (1 - {\rm{rand}}({{N}}, 1)) + {{{P}}_{b\max }}({{i}}) \times {\rm{rand}}({{N}}, 1)$ | (12) |
式中:
引入动态变异率后,在每代算法运行后调整概率值为
| $ {{{P}}_b}({{i}} + 1) = \frac{{{{{P}}_c}({{i}})}}{3} - \left( {\frac{{{\rm{GEN - gen}}}}{{{\rm{GEN}}}}} \right) \times (\frac{{{{{P}}_c}({{i}})}}{3} - {{{P}}_b}({{i}})) $ | (13) |
式中:
为了验证MPGA-RBFNN在逆运动学求解上的有效性,分别采用MPGA、RBFNN和MPGA-RBFNN对Comau NJ-220型一般机器人进行逆运动学求解。
3.1 算法的求解精度分析采用不重复的随机抽样法从训练样本

|
Download:
|
| 图 4 3种算法输出误差图 Fig. 4 The output error of three kinds of algorithm | |
由图4可得,3种算法都完成了求解过程,MPGA求解时的输出误差数量级维持在
为了进一步对比3种算法的差异,根据机器人各关节角的变化范围以及机器人实际工作的要求,确定各关节角的取值范围为:
对比表2中的数据,MPGA的输出误差范围为[−0.004 031,0.003 115],RBFNN的输出误差范围为[−0.001 094,0.000 918],而MPGA-RBFNN算法的输出误差范围为[−0.000 001,0.000 292]。通过第1组数据中关节角
得到训练样本后,应用MATLAB中神经网络工具箱的网络训练newrb函数进行RBFNN的创建与训练,其调用格式为net=newrb(P,T,goal,spread,MN,DF),P为网络输入,T为网络输出,goal为网络输出目标值,spread为RBFNN的扩展速度,MN为训练次数,DF为两次显示之间所添加的神经元数目。根据多次实验,得到其参数的设置为:goal=
| 表 2 逆解结果 Tab.2 Inverse kinematics solution results |
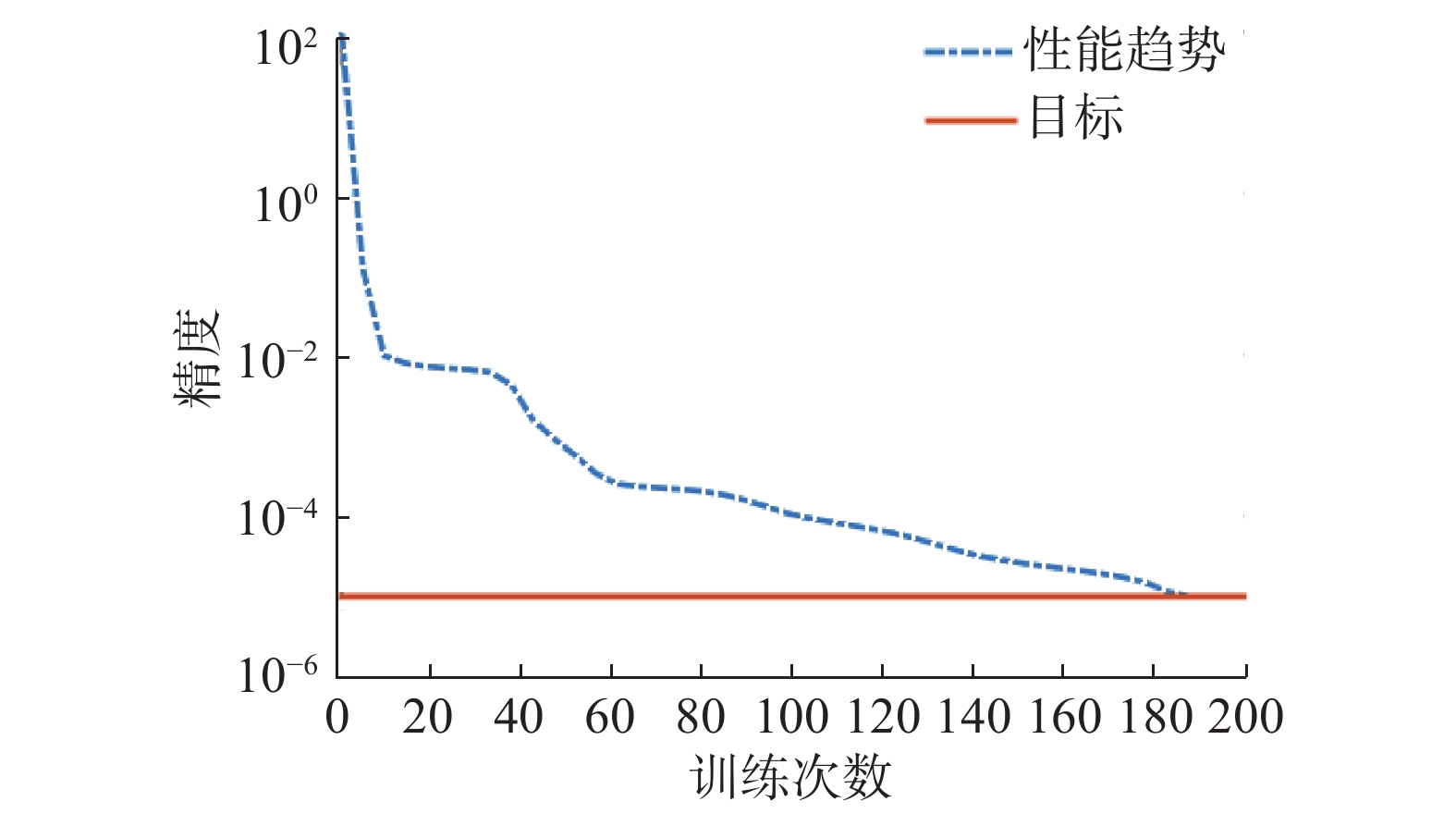
|
Download:
|
| 图 5 MPGA-RBFNN网络性能训练 Fig. 5 Performance training of MPGA-RBFNN | |
从图5可以看出,经过183次训练后,网络的训练精度为
| 表 3 算法性能对比 Tab.3 Contrasts in algorithm performance |
本文结合MPGA和RBFNN的思想,提出了适用于一般机器人逆运动学求解的MPGA-RBFNN算法。该算法结合一般机器人的正运动学模型,采用MPGA优化RBFNN的网络结构和连接权值的方法,并应用混合编码和同时演化的方式,实现从机器人工作空间位姿到关节变量的非线性映射,从而避免了复杂的公式推导及计算量大的问题。最后,在Comau NJ-220型机器人上展开对比实验,实验结果表明:MPGA-RBFNN算法不仅提高了一般机器人在逆运动学求解时的稳定性,而且该算法的训练成功率和逆解的计算准确率也得到了提高。
| [1] |
FARIA C, FERREIRA F, ERLHAGEN W, et al. Position-based kinematics for 7-DoF serial manipulators with global configuration control, joint limit and singularity avoidance[J]. Mechanism and machine theory, 2018, 121: 317-334. DOI:10.1016/j.mechmachtheory.2017.10.025 ( 0) 0)
|
| [2] |
林阳, 赵欢, 丁汉. 基于多种群遗传算法的一般机器人逆运动学求解[J]. 机械工程学报, 2017, 53(3): 1-8. LIN Yang, ZHAO Huan, DING Han. Solution of inverse kinematics for general robot manipulators based on multiple population genetic algorithm[J]. Journal of mechanical engineering, 2017, 53(3): 1-8. (  0) 0)
|
| [3] |
LIU Yuan , WANG Daqing , SUN Jian , et al. Geometric approach for inverse kinematics analysis of 6-Dof serial robot[C]// IEEE International Conference on Information and Automation. Lijiang, China: IEEE, 2015: 852–855.
( 0) 0)
|
| [4] |
ZANG Wenke, REN Liyan, ZHANG Wenqian, et al. A cloud model based DNA genetic algorithm for numerical optimization problems[J]. Future generation computer systems, 2018, 81: 465-477. DOI:10.1016/j.future.2017.07.036 ( 0) 0)
|
| [5] |
ALSHRAIDEH M A. Multiple-population genetic algorithm for solving min-max optimization problems[J]. International review on computers and software, 2015, 10(1): 9-19. ( 0) 0)
|
| [6] |
林明, 王冠, 林永才. 改进的遗传算法在机器人逆解中的应用[J]. 江苏科技大学学报(自然科学版), 2012, 26(4): 370-375. LIN Ming, WANG Guan, LIN Yongcai. Robot inverse kinematics based on improved genetic algorithm[J]. Journal of Jiangsu university of science and technology (natural science edition), 2012, 26(4): 370-375. DOI:10.3969/j.issn.1673-4807.2012.04.012 (  0) 0)
|
| [7] |
AYYILDIZ M, ÇETINKAYA K. Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator[J]. Neural computing and applications, 2016, 27(4): 825-836. DOI:10.1007/s00521-015-1898-8 ( 0) 0)
|
| [8] |
STARKE S, HENDRICH N, MAGG S, et al. An efficient hybridization of Genetic Algorithms and Particle Swarm Optimization for inverse kinematics[C]//Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics. Qingdao, China: IEEE, 2017: 1782–1789.
( 0) 0)
|
| [9] |
HALALI M A, AZARI V, ARABLOO M, et al. Application of a radial basis function neural network to estimate pressure gradient in water-oil pipelines[J]. Journal of the Taiwan institute of chemical engineers, 2016, 58: 189-202. DOI:10.1016/j.jtice.2015.06.042 ( 0) 0)
|
| [10] |
CHIDDARWAR S S, BABU N R. Comparison of RBF and MLP neural networks to solve inverse kinematic problem for 6R serial robot by a fusion approach[J]. Engineering applications of artificial intelligence, 2010, 23(7): 1083-1092. DOI:10.1016/j.engappai.2010.01.028 ( 0) 0)
|
| [11] |
ZUBIZARRETA A, LARREA M, IRIGOYEN E, et al. Real time direct kinematic problem computation of the 3PRS robot using neural networks[J]. Neurocomputing, 2017, 271: 104-114. ( 0) 0)
|
| [12] |
TOSHANI H, FARROKHI M. Real-time inverse kinematics of redundant manipulators using neural networks and quadratic programming: a Lyapunov-based approach[J]. Robotics and autonomous systems, 2014, 62(6): 766-781. DOI:10.1016/j.robot.2014.02.005 ( 0) 0)
|
| [13] |
KÖKER R. A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization[J]. Information sciences, 2013, 222: 528-543. DOI:10.1016/j.ins.2012.07.051 ( 0) 0)
|
| [14] |
JIA Weikuan, ZHAO Dean, DING Ling. An optimized RBF neural network algorithm based on partial least squares and genetic algorithm for classification of small sample[J]. Applied soft computing, 2016, 48: 373-384. DOI:10.1016/j.asoc.2016.07.037 ( 0) 0)
|
| [15] |
ZAPLANA I, BASANEZ L. A novel closed-form solution for the inverse kinematics of redundant manipulators through workspace analysis[J]. Mechanism and machine theory, 2018, 121: 829-843. DOI:10.1016/j.mechmachtheory.2017.12.005 ( 0) 0)
|
| [16] |
赵建强, 刘满禄, 王姮. 基于PSO优化BP神经网络的逆运动学求解研究[J]. 自动化与仪表, 2016, 31(11): 1-6. ZHAO Jianqiang, LIU Manlu, WANG Heng. Research on inverse kinematics solution of BP neural network based on PSO optimization[J]. Automation and instrumentation, 2016, 31(11): 1-6. DOI:10.3969/j.issn.1001-9944.2016.11.001 (  0) 0)
|
| [17] |
乔俊飞, 安茹, 韩红桂. 基于相对贡献指标的自组织RBF神经网络的设计[J]. 智能系统学报, 2018, 13(2): 159-167. QIAO Junfei, AN Ru, HAN Honggui. Design of self-organizing RBF neural network based on relative contribution index[J]. CAAI transactions on intelligent systems, 2018, 13(2): 159-167. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


