在人工智能算法设计与自动控制的相关研究中，无人机路径规划^[1]，弹道分析^[2]，公路线性设计^[3]，路径约束下的车辆行为研究^[4]，几何处理^[5]和机器视觉研究^[6]，以及植物生长模拟^[7]、结构工程分析^[8]等问题的解决都可以基于离散曲线的曲率和挠率的分析。曲率和挠率是空间曲线在固有运动下的不变量^[9]，直接描述了曲线在一点邻近的形状。其中，曲率揭示曲线在所在平面的弯曲程度，挠率则刻画曲线离开既定平面的扭曲程度。也就是说，三维空间中的曲线是可以通过一根直线弯曲(曲率)和扭曲(挠率)得到的。显然，曲率和挠率能完全刻画曲线的局部行为^[10]。因此，有研究者根据曲线的曲率挠率特性，对空间中的曲线进行分析^[11-13]、分类^[14]或判断轨迹线的形状^[15]。对于有解析或者参数方程的曲线，经典微分几何中有成熟方法计算曲线上任意一点的曲率和挠率。

因为近些年应用日益广泛的离散空间曲线没有解析方程，经典微分几何中的求解方法不能直接应用于离散曲线的情形，所以三维空间中离散曲线的曲率和挠率计算成为近些年的热点研究问题。此外，在实际应用中，受人工、仪器、环境等诸多因素影响，得到的离散曲线的数据(一个序列的三维坐标点)常常存在一定的偏差或者噪声，因此如何使算法更加准确和鲁棒，成为三维空间离散曲线的曲率和挠率计算的难点。

近些年提出的关于三维空间离散曲线的曲率和挠率计算方法大致可以分为2类。1) 基于曲线拟合的方法，这类算法主要是对给定点及其近邻点拟合一段光滑曲线，然后根据这段解析曲线的微分几何公式计算给定点的曲率和挠率。其本质就是用拟合曲线的曲率和挠率来估算离散曲线的曲率和挠率。这类算法的典型算法有多项式拟合法(polynomial curve fitting)^[16]和B样条曲线拟合法(B-spline curve fitting)^[17-19]。2) 基于离散结构的方法，这类算法无需对离散曲线进行光滑曲线的拟合，直接利用离散点之间的距离和内接多边形等离散结构，运用差分形式或者离散逼近等策略估算出离散曲线上各个点的曲率和挠率。基于离散结构的方法中比较典型的有投影法(projection)^[20]、单侧差分法(one-sided difference)^[21]和离散几何法(discrete geometry)^[22]。本文根据导数定义以及单侧差分法的设计思路，融合差商平滑策略，提出了微中心差分(microcentral difference)算法。

1 离散曲线的曲率挠率算法

经典微分几何中，设曲线 $C$ 的参数方程为 ${ r} = { r}\left( t \right) = \left( {x\left( t \right), y\left( t \right), z\left( t \right)} \right){\rm{ }}\left( {\alpha \leqslant t \leqslant \beta } \right)$ ，若一阶导函数 ${ r}'(t)$ 在区间 $\left[ {\alpha , \beta } \right]$ 上恒不为零，即参数化曲线 ${ r}(t)$ 是正则的，则曲率 $\kappa (t)$ 的计算公式^[23]为

$\kappa (t) = \;\frac{{\left| {{ r}'(t) \times { r}''(t)} \right|}}{{{{\left| {{ r}'(t)} \right|}^3}}}\;$

(1)

挠率 $\tau (t)$ 的计算公式^[16]为

$\tau (t) = \frac{{({ r}'(t), { r}''(t), { r}'''(t))}}{{{\rm{|}}{ r}{\rm{'(}}t{\rm{)}} \times { r}''(t){{\rm{|}}^2}}}$

(2)

式(1)、式(2)中的符号“×”表示叉积；式(2)中的分子表示3个微分向量的混合积。r(t)=(x(t)，y(t)，z(t))中要求3个函数x(t)、y(t)、z(t)都是连续函数，且都3阶可导。

但是对于没有方程的三维离散曲线的曲率挠率计算，研究人员提出的各种方法中有代表性的方法有：多项式曲线拟合法、B样条曲线拟合法、投影法、单侧差分法、离散几何法5种。本文在分析这5种算法的基础上，提出了微中心差分法。

1.1 多项式曲线拟合法

2005年，Cazals等^[16]提出了一种基于二次多项式曲线拟合(polynomial curve fitting，PCF)的方法来计算离散平面曲线在给定点 ${P_i}$ 的曲率、挠率。该方法对点 ${P_i}$ 及其邻域 $\{ {P_k}|i - n \leqslant k \leqslant i + n\} $ ( $n$ 为点 ${P_i}$ 一侧选取的邻近点个数)，在以 ${P_i}$ 为原点的局部坐标系中拟合一个二次多项式曲线。二次多项式曲线的数学模型为

$f(x) = {A_0} + {A_1}x + {A_2}{x^2}$

通过最小二乘拟合，可求解该二次多项式曲线及其系数 ${A_i}\left( {i = 0, 1, 2} \right)$ ，利用多项式系数 ${A_i}$ 可计算出点 ${P_i}$ 的曲率 $\kappa ({P_i})$ 。类似的可推广拟合三次或三次以上的多项式曲线，从而利用式(1)、式(2)计算出三维空间离散曲线的曲率、挠率。

1.2 B样条曲线拟合法

2017年，赵夫群等^[17]用4次B样条曲线拟合(B-spline curve fitting，BSCF)方法将空间离散曲线拟合成光滑的空间曲线，从而以此来计算离散曲线的曲率和挠率。B样条曲线的定义为：给定 $n = m + k + 1$ 个顶点，则可以定义 $m + 1$ 段 $k$ 次参数曲线第 $i$ 段B样条曲线函数可表示为

$Q(t) = \displaystyle\sum\limits_{l = 0}^k {{P_{i + l}}{N_{l, k}}(t)} $

式中： $i = 0, 1, \cdots , n$ ； $\{ {P_{i + 0}}, {P_{i + 1}}, \cdots , {P_{i + k}}\} $ 为定义第 $i$ 段曲线特征多边形的 $k + 1$ 个顶点； ${N_{l, k}}(t)$ 为B样条基底函数，表示为

${N_{l, k}}(t) = \displaystyle\frac{1}{{k!}}\sum\limits_{j = 0}^{k - l} {{{( - 1)}^j}C_{k + 1}^j{{(t + k - l - j)}^k}} $

对于离散曲线上的每一个离散点 ${P_i}$ ，选取点 ${P_i}$ 及其邻域 $\{ {P_k}|i - n \leqslant k \leqslant i + n\} $ ( $n$ 为点 ${P_i}$ 一侧选取的邻近点个数)内的点进行样条曲线拟合。类似的方法有：喻德生等^[18]采用的3次均匀B样条进行曲线拟合，Kehtarnavaz等^[19]采用的5次B样条进行曲线拟合，从而利用经典微分几何的式(1)、式(2)求解方法对离散曲线进行曲率、挠率的计算。

1.3 投影法

Mardia在1999年提出一种基于投影(projection)的算法^[20]，对于三维空间中的离散曲线，将点投影到单位切线方向上。对于由 $n$ 个点构成的离散曲线，其点 ${P_i}$ 处的单位切向量定义为

${{ T}_i}{\rm{ = }}\frac{{{P_i}{P_{i + 1}}}}{{\left| {{P_i}{P_{i + 1}}} \right|}}, \quad i = 3, 4, \cdots , n - 2$

容易计算点 ${P_i}$ 处的单位法向量 ${{ N}_i}$ ，利用 ${{ T}_i}$ 和 ${{ N}_i}$ 做叉积得到副法向量 ${{ B}_i}$ ，从而点 ${P_i}$ 处的局部投影平面离散曲线定义为

${Y_k} = \left( {\frac{{{{ T}_k} \cdot {{ N}_i}}}{{{{ T}_k} \cdot {{ T}_i}}}, \frac{{{{ T}_k} \cdot {{ B}_i}}}{{{{ T}_k} \cdot {{ T}_i}}}} \right),\quad k = i - 2, \cdot \cdot \cdot , i + 2$

然后以点 ${Y_i}$ 为中心，拟合平面二次曲线 $a{x^2} + bx$ ，从而三维空间离散曲线点 ${P_i}$ 的曲率 $\kappa ({P_i})$ 、挠率 $\tau ({P_i})$ 分别为

$\kappa ({P_i}) = \frac{{\left\| {{Y_i} - {Y_{i - 1}}} \right\|}}{{\left\| {{P_i} - {P_{i - 1}}} \right\|}}$

$\tau ({P_i}) = \frac{{2a}}{{{{({b^2} + 1)}^{3/2}}}}\kappa ({P_i})$

1.4 单侧差分法

2016年Blankenburg等^[21]通过利用一般参数方程的曲线导数的有限差商逼近，直接从离散点中采用单侧差分(one-sided difference，OSD)逼近计算出空间离散曲线在给定点 ${P_i}$ 的一阶差商、二阶差商和三阶差商，然后代入曲率和挠率的解析计算公式进行求解。在该方法中，定义差分为

$\Delta {f_k}(t) = f(t + k\Delta t) - f(t + (k - 1)\Delta t)\;, \;k = 1, 2, 3$

则一阶导数、二阶导数分别为

$f'(t) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{f(t{\rm{ + }}\Delta t) - f(t)}}{{\Delta t}}{\rm{ = }}\mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {f_1}(t)}}{{\Delta t}}$

$\begin{gathered} f''(t) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{f(t{\rm{ + 2}}\Delta t) - 2f(t{\rm{ + }}\Delta t){\rm{ + }}f(t)}}{{\Delta {t^2}}} {\rm{ = }}\\ \;\;\;\;\;\;\;\;\mathop {\lim }\limits_{\Delta t \to 0} (\frac{{\Delta {f_2}(t)}}{{\Delta {t^2}}} - \frac{{\Delta {f_1}(t)}}{{\Delta {t^2}}}) \\ \end{gathered} $

同理，三阶导数为

$f'''(t)\; = \;\;\mathop {\lim }\limits_{\Delta t \to 0} (\frac{{\Delta {f_3}(t)}}{{\Delta {t^3}}} - 2\frac{{\Delta {f_2}(t)}}{{\Delta {t^3}}} + \frac{{\Delta {f_1}(t)}}{{\Delta {t^3}}})$

从而根据曲线曲率、挠率的微分定义，将上述各阶导直接代入曲率、挠率的计算式(1)、式(2)即可求得各点处的曲率、挠率。

1.5 离散几何法

An等^[22]在2011年提出一种称为离散几何法(discrete geometry)的方法，该方法基于对称邻域的最小二乘的导数计算过程，可以归结为：利用离散导数的定义，采用约束最优化问题的求解方法来计算指定点在其对称邻域内的离散导数。

对于平面内的离散曲线，点 ${P_i} = ({x_i}, {y_i})$ 及其邻域 $\{ {P_k}|i - {n_1} \leqslant k \leqslant i + {n_1}\} $ ( ${n_1}$ 为点 ${P_i}$ 一侧选取的邻近点个数)，则点 ${P_i}$ 处的离散导数为

${y'_i} = \displaystyle\frac{{\displaystyle\sum\limits_{k = i - {n_1}}^{i + {n_1}} {({x_k} - {x_i})(} {y_k} - {y_i})}}{{\displaystyle\sum\limits_{k = i - {n_1}}^{i + {n_1}} {{{({x_k} - {x_i})}^2}} }}$

上述离散导数也称为点 ${P_i}$ 的一阶离散导数。类似的在点 ${P_i}$ 处的二阶离散导数为

${y_i}^{\prime \prime } = \displaystyle\frac{{\displaystyle\sum\limits_{k = i - {n_2}}^{i + {n_2}} {({x_k} - {x_i})(} {{y'}_k} - {{y'}_i})}}{{\displaystyle\sum\limits_{k = i - {n_2}}^{i + {n_2}} {{{({x_k} - {x_i})}^2}} }}$

同理，在点 ${P_i}$ 处的 $n$ 阶离散导数为

$y_i^{(n)} = \frac{{\displaystyle\sum\limits_{k = i - n}^{i + n} {({x_k} - {x_i})(} y_k^{(n - 1)} - y_i^{(n - 1)})}}{{\displaystyle\sum\limits_{k = i - n}^{i + n} {{{({x_k} - {x_i})}^2}} }}$

上述各阶离散导数是对连续可微函数在点 ${P_i}$ 处的各阶导数的逼近。对于三维空间中的离散曲线，为了计算其离散导数，首先要对离散曲线进行参数化。可采用累积弦长参数化方法^[24]来确定离散点的参数值。在该方法中，离散曲线 ${\psi _d}$ 在各点 ${P_i}{\rm{ = (}}{x_i}, {y_i}, {z_i})$ ( $1 \leqslant i \leqslant n$ )处的累积弦长参数 ${s_i}$ 可确定为

${s_i} = \frac{{\displaystyle\sum\limits_{k = 1}^{i - 1} {\left| {{p_{k + 1}} - {p_k}} \right|} }}{{\displaystyle\sum\limits_{k = 1}^{n - 1} {\left| {{p_{k + 1}} - {p_k}} \right|} }},\quad 2 \leqslant i \leqslant n$

并且 ${s_1} = 0$ ，从而离散曲线 ${\psi _d}$ 为

${\psi _d} = \{ {P_i}\, {\rm{\} = \{ }}\left( {x({s_i}), y({s_i}), z({s_i})} \right)\} $

式中： ${s_i} \in \{ {s_1}, {s_2}, \cdot \cdot \cdot , {s_n}\} $ ；坐标函数 ${x_i} = x({s_i})$ 、 ${y_i}{\rm{ = }}y({s_i})$ 和 ${z_i}{\rm{ = }}z({s_i})$ 就是弦长 ${s_i}$ 的离散函数。因此，平面上的离散导数的计算方法可以转化为用于计算三维空间中的离散曲线上各点的导数。从而，采用上述方法，对三维空间中的离散曲线 ${\psi _d}$ 上的点 ${P_i}$ ，其邻域为 $\{ {P_k}|i - {n_1} \leqslant k \leqslant i + {n_1}\} $ ( ${n_1}$ 为点 ${P_i}$ 一侧选取的邻近点个数)，则点 ${P_i}$ 处的离散导数 ${\rm{(}}x'({s_i}), y'({s_i}), z'({s_i}))$ 分别为

$\left\{ \begin{gathered} x'({s_i}) = \frac{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {({s_j} - {s_i})({x_j} - {x_i})} }}{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {{{({s_j} - {s_i})}^2}} }} \\ y'({s_i}) = \frac{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {({s_j} - {s_i})({y_j} - {y_i})} }}{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {{{({s_j} - {s_i})}^2}} }} \\ z'({s_i}) = \frac{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {({s_j} - {s_i})({z_j} - {z_i})} }}{{\displaystyle\sum\limits_{j = i - {n_1}}^{i + {n_1}} {{{({s_j} - {s_i})}^2}} }} \\ \end{gathered} \right.$

上述离散导数也称为点 ${P_i}$ 的一阶离散导数。类似的可计算点 ${P_i}$ 的二阶、三阶离散导数。从而利用式(1)、式(2)即可求得三维空间离散曲线的曲率、挠率。

1.6 微中心差分法

单侧差分法^[22]在进行离散曲线的曲率挠率计算时，会对给定的曲率挠率产生一定的偏移或者缩放，为了克服由单侧差分法引起的这种计算偏差，结合文献[22]中的思想和导数定义，把其单侧差分法修改为对目标离散点的双侧差商取平均的方法来得到目标离散点的各阶导数，并参考文献[25]中的性能度量算法思想和差分方式，将改进的方法命名为微中心差分法(microcentral difference algorithm)。

首先对微中心差分法名称中的“微”和“中心”作简单的说明。“微”是指在局部范围的逐阶差商计算。比如，先用改进的离散导数定义计算一阶差商，如式(3)；再利用一阶差商值计算离散曲线的二阶差商，如式(4)；最后利用二阶差商值计算三阶差商，如式(5)。“中心”指在目标点邻域内，进行差分计算时，以离散曲线的目标点为中心进行差分计算。另外，方法中涉及求目标点的各阶差商，我们指定，每阶差商目标点单侧需要上一阶差商值的个数，记为 ${k_i}(i = 1, 2, 3)$ ，称为邻域半径。根据上述说明，微中心差分算法的计算方法具体如下。定义其一阶前向差商为

$f_{\rm q}'(t) = \frac{1}{{{k_1}}}\sum\limits_{i = 1}^{{k_1}} {\frac{{f(t) - f(t - i\Delta t)}}{{\Delta t}}} $

一阶后向差商为

$f_{\rm h}'(t) = \displaystyle\frac{1}{{{k_1}}}\sum\limits_{i = 1}^{{k_1}} {\frac{{f(t + i\Delta t) - f(t)}}{{\Delta t}}} $

从而其一阶差商为

$\begin{gathered} \mathop f\nolimits' (t) = \frac{1}{2}\left( {f_{\rm q}'(t) + f_{\rm h}'(t)} \right) {\rm{ = }} \frac{1}{{2{k_1}}}\sum\limits_{i = 1}^{{k_1}} {\frac{{f(t + i\Delta t) - f(t - i\Delta t)}}{{\Delta t}}} \end{gathered} $

(3)

式中 ${k_1}$ 为邻域半径。

其二阶前向差商定义为

$ f''_{\rm q}(t) = \frac{1}{{{k_2}}}\sum\limits_{i = 1}^{{k_2}} {\frac{{\mathop f\nolimits' (t) - \mathop f\nolimits' (t - i\Delta t)}}{{\Delta t}}} $

二阶后向差商定义为

$ f''_{\rm h} (t) = \frac{1}{{{k_2}}}\sum\limits_{i = 1}^{{k_2}} {\frac{{\mathop f\nolimits' (t + i\Delta t) - \mathop f\nolimits' (t)}}{{\Delta t}}} $

从而其二阶差商定义为

$ \begin{gathered} f'' (t) \!= \!\frac{1}{2}\left( {f''_{\rm q} (t) \!+\! f''_{\rm h} (t)} \right) \!= \! \frac{1}{{2{k_2}\Delta t}}\left( {\mathop f\nolimits' (t\! +\! {k_2}\Delta t) \!-\! \mathop f\nolimits' (t - {k_2}\Delta t)} \right) \\ \end{gathered} $

(4)

式中 ${k_2}$ 为邻域半径。

同理，其三阶前向差商定义为

$ f'''_{\rm q}(t) = \frac{1}{{{k_3}}}\sum\limits_{i = 1}^{{k_3}} {\frac{{ f''(t) - f'' (t - i\Delta t)}}{{\Delta t}}} $

三阶后向差商定义为

$ f'''_{\rm h}(t) = \frac{1}{{{k_3}}}\sum\limits_{i = 1}^{{k_3}} {\frac{{ f'' (t + i\Delta t) - f'' (t)}}{{\Delta t}}} $

从而其三阶差商为

$ \begin{gathered} f''' (t) \!\!=\!\! \frac{1}{2}\left( {f_{\rm q}'''(t) \!+\! f_{\rm h}'''(t)} \right) \!\!= \!\! \frac{1}{{2{k_3}\Delta t}}\left( {f'' (t \!+\! {k_2}\Delta t) - f'' (t \!-\!\!{k_2}\Delta t)} \right) \end{gathered} $

(5)

式中 ${k_3}$ 为邻域半径。

因此对于微中心差分法，为了得到离散曲线上给定的目标离散点的曲率值，根据本文的计算方法，则需要知道目标离散点邻域内的离散点数 ${N_1} = 2({k_1} + {k_2}) + 1$ ，即目标离散点两侧各需 $({k_1} + {k_2})$ 个离散点；而对于目标离散点的挠率计算，则至少需要知道目标离散点邻域内的离散点数N₂=2 $ ({k_1} + {k_2} + {k_3}) + 1$ ，其中目标离散点两侧各 $({k_1} + {k_2} + {k_3})$ 个离散点，k₁、k₂、k₃均为大于等于1的整数。根据式(3)~(5)得到其各阶差商后，则可根据曲线曲率、挠率的微分定义，将上述各阶导数式(3)~(5)代入曲率、挠率的计算式(1)、式(2)，即可求得离散曲线上各点处的曲率、挠率。这里提出的微中心差分计算方法是对单侧差分方法的一个依据导数定义进行的一个扩展，理论上是符合连续函数条件下可导的要求。

总体来看，上述6种方法分为2种思路：1)一对近邻点进行曲线拟合，它们之间的区别在于近邻点数的确定以及拟合曲线模型的假设；2)对近邻点进行离散求导，各方法之间的区别在于取点的策略以及如何利用近邻点的信息得到各阶导函数的可靠逼近，从而得到不同的曲率和挠率的计算方法。

2 实验比较

本节通过实验对上述6种算法计算的曲率和挠率的计算精度进行评估。为了便于比较，本文中实验方法的k₁、k₂、k₃均取值为1。算法评估指标参考文献[26]的评价指标，选取最大相对误差(max relative error，MRE)和均方根误差(root mean square error，RMSE)，即对于获得的离散曲线，在每一个离散点 ${P_i}$ 处的偏差定义为 $e_\varphi ^i{\rm{ = }}{\varphi _i}{\rm{ - }}\overline {{\varphi _i}} $ ，其中 $\overline {{\varphi _i}} $ 为实验方法的计算值， ${\varphi _i}$ 为对应的准确值。因此，对于给定的离散曲线，其最大相对误差为 ${E_{{\rm{MRE}}}} = $ $\max (\left| {{{({\varphi _i}\! -\! \overline {{\varphi _i}} )} / {{\varphi _i}}}} \right|)$ , 均方根误差为 ${E_{{\rm{RMSE}}}} \! \!= \!\!\! \! \sqrt {\displaystyle\frac{1}{n}\sum\limits_{i \!= \! 1}^n {{{({\varphi _i} \!- \! \overline {{\varphi _i}} )}^2}} }$ 。最大相对误差体现算法的稳定性，均方根误差反映算法的整体有效性。实验平台为个人笔记本电脑，计算机配置是Inter(R) Core(TM) i5-7300HQ CPU @2.50 GHz处理器和8 GB内存，程序运行环境是MATLAB R2014b。

2.1 实验数据

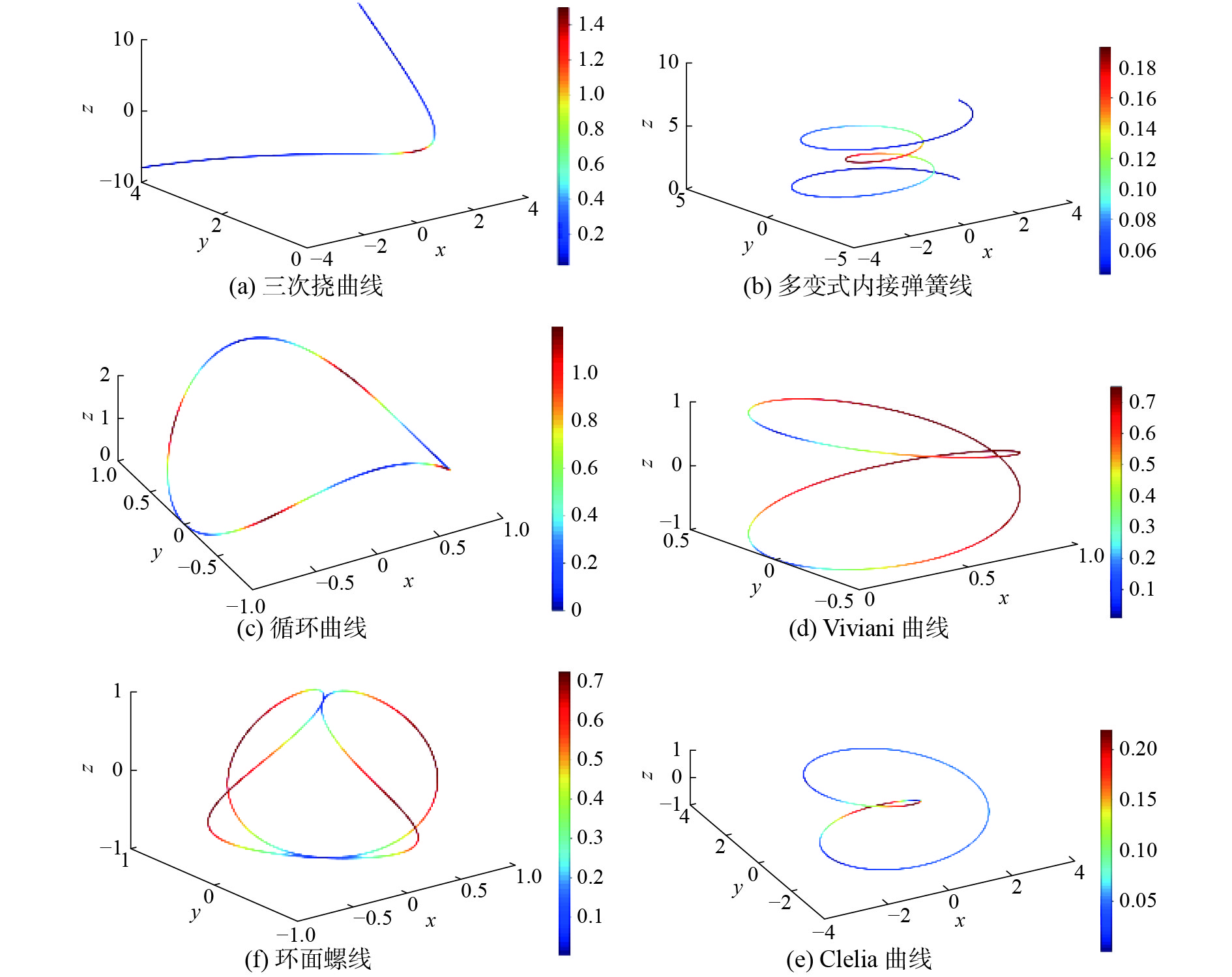
实验用如图1所示的6条连续可微参数曲线进行分析。由于有曲线方程，可以用经典微分几何的方法(式(1)、式(2))计算出曲线上任意一个点的准确曲率值和挠率值，有了准确值便于进行误差分析。实验分析用到的6条曲线参数方程如下：

1)三次挠曲线：

$r(t) = (2t, {t^2}, {t^3}), \quad t \in [ - 2, 2]$

2) 多变式内接弹簧线：

$ r(t) = (2\cos (3t) + \cos (2t), 2\sin (3t) + \sin (2t), t), \quad t \in [0, 2{\text π} ] $

3) 循环曲线：

$r(t) = (\cos (t), \sin (t), 2\sin (t)),\quad t \in [0, 2{\text π} ]$

4) Viviani曲线：

$r(t) = ({\cos ^2}(t), \cos (t)\sin (t), \sin (t)),\quad t \in [0, 2{\text π} ]$

5) Clelia曲线：

$ r(t) = (\cos (2t)\cos (t), \cos (2t)\sin (t), \sin (2t)), \quad t \in [0, 2{\text π} ] $

6) 环面螺线：

$ r(t) = ((2 + \cos (t))\cos (2t), (2 + \cos (t))\sin (2t), t),\quad t \in [0, 2{\text π} ] $

需要说明的是，解析曲线方程用于生成离散曲线，并用于计算离散曲线上每个采样点的准确的曲率值和挠率值。实验中对每条空间参数曲线通过均匀采样获得相应的离散曲线，采样点数n在定义域内从50个点变化到500个点，用于测试算法的有效性。第1章介绍的5种常用的离散曲线曲率和挠率计算方法以及本文提出的算法都采用离散曲线上的点的坐标进行计算，都用不到曲线方程。

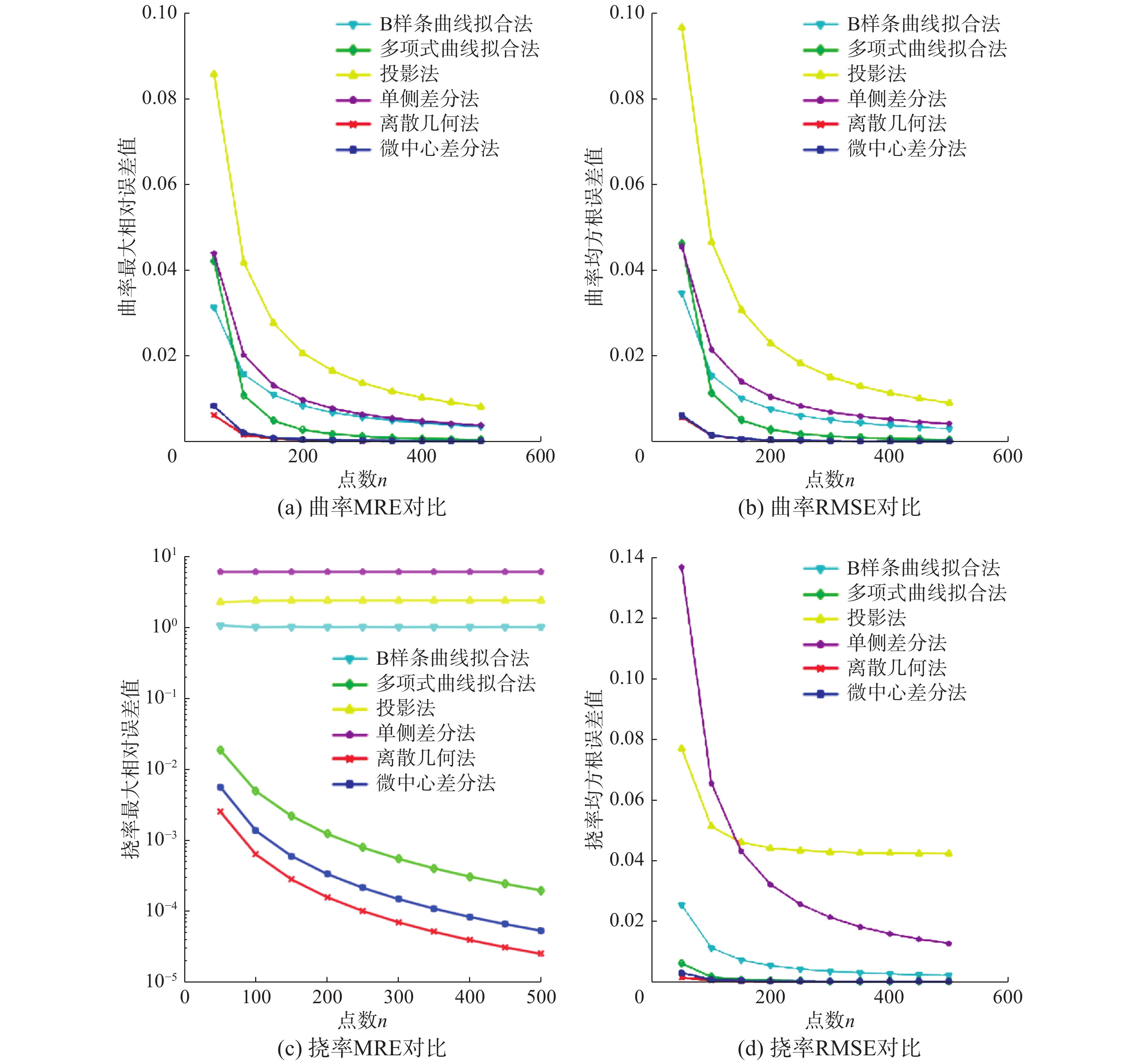
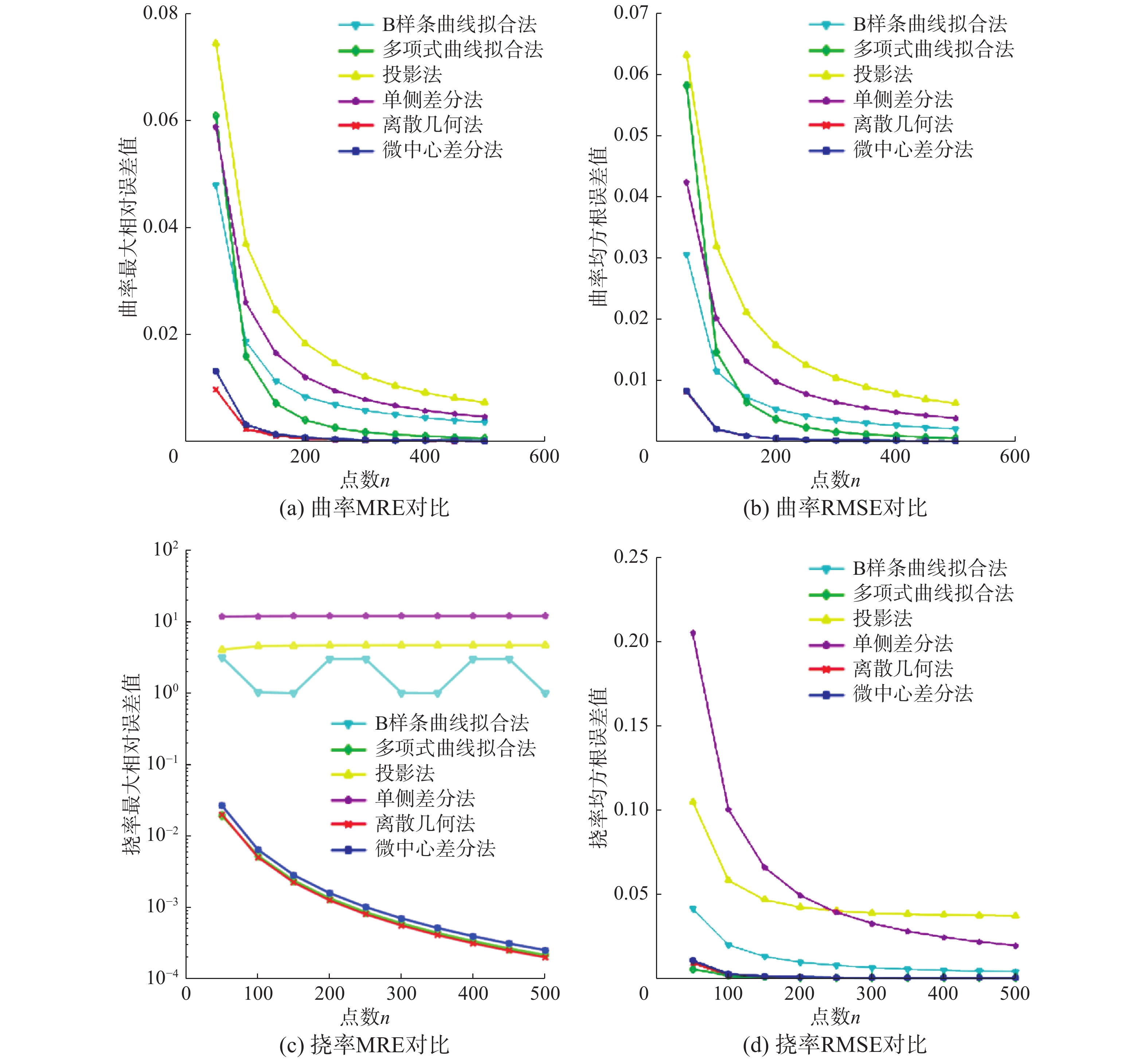
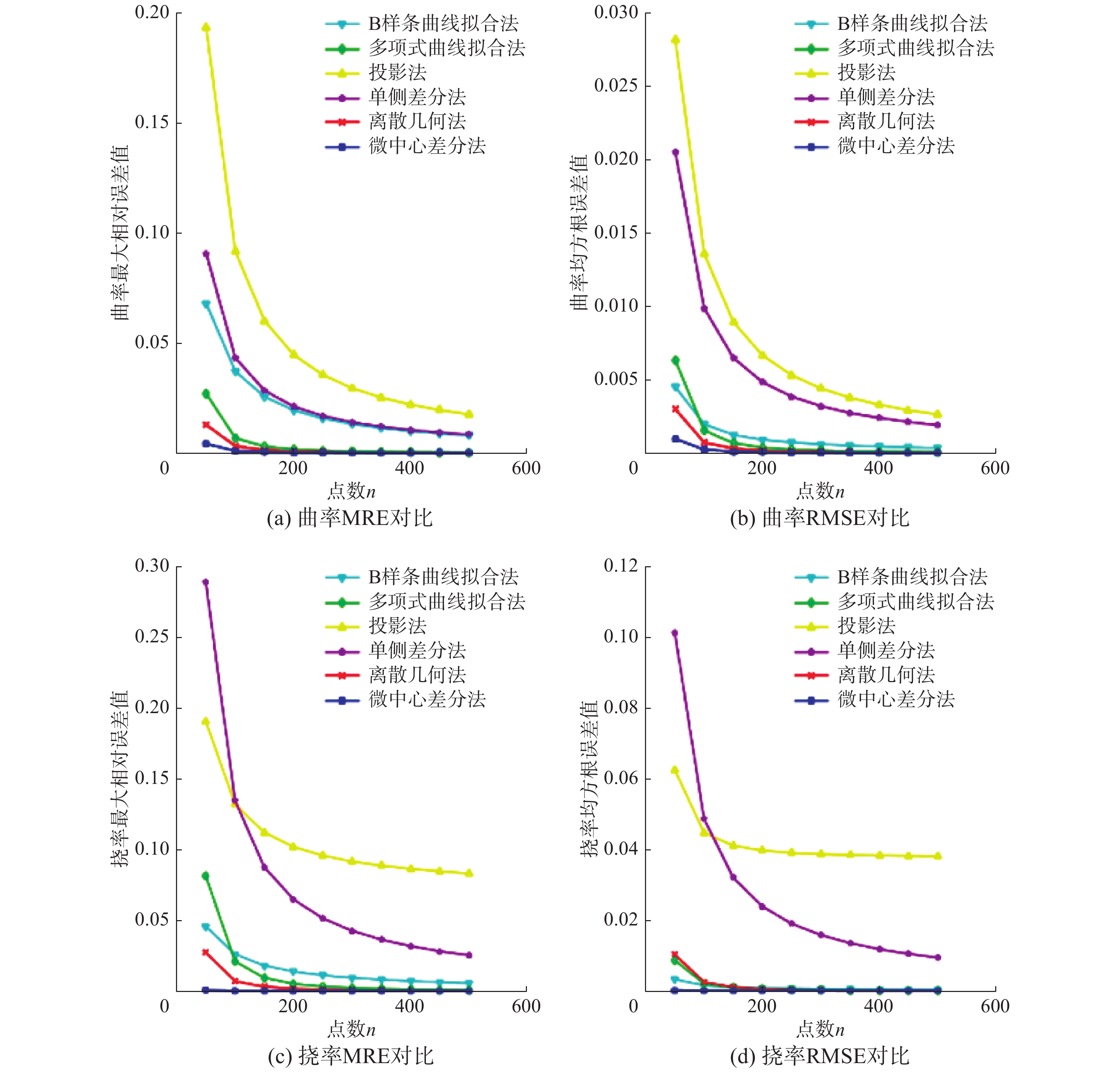
2.2 误差分析及时间效率比较

通过上述三维空间6条离散曲线来定量地评价本文提出的微中心差方法(MCD)，并将其与第1章介绍的B样条曲线拟合法(BSCF)、多项式曲线拟合法(PCF)、投影法(Proj)、单侧差分法(OSD)、离散几何法(DG)这5种算法的曲率和挠率的计算结果进行比较。图2～7分别给出了这6条离散曲线随着采样密度增加，曲率和挠率的最大相对误差(MRE)与均方根误差(RMSE)的变化。从图2~7的误差比较图可以看出，随着采样密度 $n$ 的不断增加，这6种方法计算的曲率和挠率的最大相对误差和均方根误差都逐渐地减小，并且采样密度越高，最大相对误差值和均方根误差值越接近于0，这表明这6种算法都能有效地计算出三维空间离散曲线的曲率和挠率。

当然，这6种方法在收敛速度和稳定性方面存在一些差异。从图2~7的曲率MRE对比子图可以看出：投影法和单侧差分法的最大误差最大，且随着采样密度增加，误差一直比较大；离散几何法与本文提出的微中心差分法的误差较小，特别是当采样较稀疏时，曲率估算的最大相对误差最小。从图2~7的这6个图中的每个子图(c)图的结果，也说明从均方根指标评价，也能得出同样结论。需要指出的是，从均方根误差指标看，本文提出的算法在所有离散曲线的计算结果中几乎都能取得最佳效果。

图2~7分别给出了6条离散曲线随着采样密度增加的挠率最大相对误差(MRE)。从图中可以看出，随着采样密度 $n$ 的不断增加，本文方法的挠率最大相对误差逐渐地减小，并且采样密度越大，最大相对误差值和均方根误差值就越接近于0，这表明挠率计算越准确，也表明本文方法在计算三维空间离散曲线的挠率时收敛性和稳定性较好。而单侧差分法、投影法和B样条曲线拟合法的最大相对误差有时会有较大波动。

图2~7中(c)图呈现的挠率计算的均方根误差变化结果表明，随着采样密度增大，本文方法与离散几何方法和多项式拟合方法的均方根误差能单调递减收敛于0，而单侧差分法、投影法的误差收敛速度较差。

图2～7反映了随着点的密度增加，曲率和挠率的误差的收敛性和稳定性。下面针对固定的点密度，比较一下各个方法的精度。实验中我们根据上述的密度实验，取采样点数量适中误差比较稳定的点密度，即n=200的时候进行6条曲线的曲率和挠率估计精度的比较，结果如表1所示。

从表1可以看出，本文提出的MCD方法计算的曲率和挠率平均误差分别为0.000 4和0.000 3，比另5种算法中效果最佳的DG算法的曲率和挠率平均误差(分别为0.001 4和0.000 8)，分别降低了69.74%和55.36%。可见，总体来看，本文提出的算法无论是曲率估计还是挠率估计，精度都是最高的。

关于运行效率，从算法原理可以看出，所有算法时间复杂度都是线性级的，即O(n)，因此给出平均实验时间便可以说明计算的时间效率。用6种算法分别计算6条曲线的曲率和挠率，对每条离散曲线的不同采样密度进行50次实验，总的平均运行时间如表2所示。从表2可以看出，离散结构法(Proj、OSD、DG、MCD)相比曲线拟合法(BSCF、PCF)，计算效率大幅提高；在离散结构法中，单侧差分算法(OSD)平均运行速度最快，本文提出的微中心差分法处于中间位置。

2.3 噪声数据实验

为了测试每个算法的抗噪声鲁棒性，在采样点数 $n$ 为200时，设置噪声水平为0.000 1~0.1，噪声为均值为零、标准差为离散曲线上邻近的两离散点之间的平均距离与噪声水平的乘积的高斯噪声。实验用Clelia曲线生成了不同噪声水平的离散曲线。

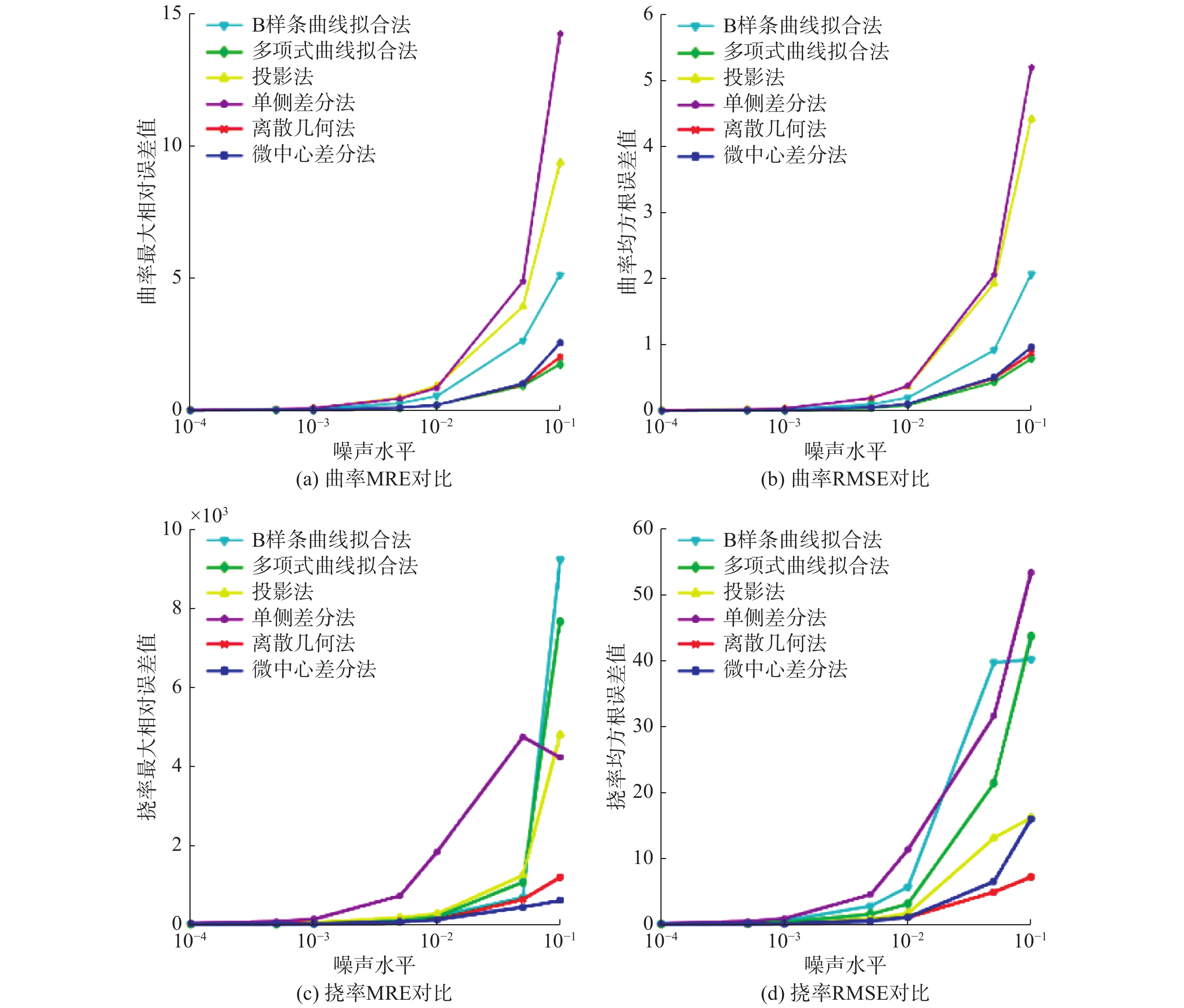
6种算法计算的曲率最大相对误差和曲率均方根误差分别如图8(a)、(b)所示，从图中可以看出：噪声水平越高，算法的误差变化越大；各算法在噪声水平不大于0.01时，均能较准确地计算离散曲线的曲率值；噪声水平大于0.01时，其误差明显变大，尤其是单侧差分法和投影法，而本文的方法误差变化浮动相对较小。

6种算法计算的挠率最大相对误差和均方根误差分别如图8(c)、(d)所示，从图中可以看出：含噪声的离散曲线在计算挠率时变得更加敏感，当噪声水平大于0.001时，6种算法得到的挠率值与真实值就已有了明显的偏差，并且随着噪声水平变大，挠率的最大相对误差和均方根误差相比曲率也会更快地增大。与其他5种算法相比，本文的方法误差变化浮动相对较小。

上述实验表明，噪声对6种算法的计算精度都有影响，尤其是当噪声水平较大时，挠率变化表现得更加明显。另外，在同样的噪声水平下，挠率的最大相对误差和均方根误差波动幅度相比曲率的最大相对误差和均方根误差波动幅度更大，这也说明离散曲线的挠率计算比曲率计算对噪声更加敏感。

3 结束语

针对三维空间离散曲线的曲率和挠率的计算方法设计问题，本文主要工作包括如下2个方面：

1)根据2016年Blankenburg等提出的单侧差分方法和导数定义，结合差商平滑策略，设计了微中心差分法，该方法能够有效计算离散曲线的曲率和挠率。从整个计算过程可以发现，本文的方法不依赖于任何曲线模型，从离散曲线中直接计算所得，从而对各类离散曲线均具有较好的普适性。

2)概述了多项式曲线拟合法、B样条曲线拟合法、投影法、单侧差分法和离散几何法5种典型算法；详细阐述了本文提出的微中心差分法的基本思想和计算公式。采用6条离散曲线数据进行了不同算法的对比实验，实验表明，本文提出的微中心差分法的平均精度最高。

从实验结果可以看出，目前的这些算法的噪声鲁棒性并不是很好，特别是在有奇异点的时候，未来的研究可以进一步研究鲁棒性更佳的算法。此外，未来也可以研究利用曲率和挠率进行特征线的分析、提取和类型识别等。