2. 信阳师范学院 计算机与信息技术学院,河南 信阳 464000
2. School of Computer and Information Technology, Xinyang Normal University, Xinyang 464000, China
近年来,随着各种网络,比如社交网络、传感器网络的不断发展,越来越多的应用在以极快的速度源源不断地产生大量数据流。与此同时,如何快速地从大量数据流中生成有用的模型或者提取有用信息吸引了大量研究者。
数据流分类是传统的有监督机器学习的一种变体,传统的有监督机器学习都是针对于由特征向量表示的未标记实例的值的预测。与传统的分类学习的不同之处在于:传统机器学习方法根据一个静态的数据集合建立模型,而在数据流环境下,实例是不断到来的,只能根据部分实例建立分类模型。因此,数据流分类器必须准备好处理大量的、快速输入的实例,而且每个实例只能在短时间内被处理或存储一次[1]。目前,数据流学习还面临很多挑战,这些挑战包括概念漂移、时间依赖关系、新类、特征漂移、类不平衡以及时间和内存受限等[1]。本文主要解决的是概念漂移问题。
解决概念漂移问题目前最流行的方法是集成学习,而现有的多数数据流集成分类方法通常只考虑精度或者只考虑多样性。这两种方法在思路上的区别就是:前者重视基分类器在最新数据上的表现,认为新数据最符合目前这个阶段的数据分布;后者考虑在以后阶段会出现各种各样的数据分布,即各种各样的“概念”。使用多样性的基分类器能使集成分类器在各种“概念”下都能取得不错的性能。但是,多样性和精度这两个方面对数据流分类来说都是重要的,所以如何综合这两个方面来提出一个更加有效的方法,是本文主要的工作。
本文的主要贡献如下:1) 提出了一种线性加权方式来计算分类器权重,将分类器在最新数据块上的精度以及该分类器在集成分类器中的多样性这两种度量分类器价值的标准以一种线性加权的方式融合成一个标准,以此作为衡量一个分类器对于当前集成分类器价值大小的依据;2)使用一种基于价值度量的集成分类器更新策略来根据最新数据对集成分类器进行更新,将对精度和多样性线性加权得到的权重作为基分类器价值的度量。当有新的分类器到来时,价值最低的基分类器将会被新建立的分类器替换。
1 相关工作由于数据流的动态性,其学习过程存在很多问题,比如,在处理大规模数据流时,经常会发生数据分布变化的情况,这种情况被称为“概念漂移”(concept drift),概念漂移的出现打破了机器学习中一个假设前提,即数据是独立同分布的。相反,也正是因为数据流不符合这个假设前提,才吸引了无数研究者。
自概念漂移问题被发现以来,研究者们提出了大量的方法和策略用于处理概念漂移问题,其中有的方法假定概念漂移存在,在学习过程中不断根据当前数据对模型进行调整,而不关心是否真的出现概念漂移;还有一些方法不断检测数据流中是否出现概念漂移,如果出现概念漂移则对模型进行相应的调整。Brzezinski等[2]提出了一种可以对多种概念漂移反应同样好的分类算法,称为精度更新集成(accuracy updated ensemble, AUE2)。该方法根据基分类器在当前数据块上的精度计算其权重并用于基分类器替换。Pietruczuk等[3]提出了一种可以动态扩展集成分类器大小的集成分类算法,其主张一个新的基分类器是否被添加进集成分类器中取决于这个添加操作是否不光提高了当前数据的精度而且也会提高整个数据流的分类精度。除了精度这种度量方式之外,多样性对于集成学习来说也是一个十分有意义的度量。Sun等[4-5]认为,应该鼓励模型之间的差异性,即多样性(diversity)提出了一种基于多样性和迁移的集成学习方法(diversity and transfer based ensemble learning, DTEL)来处理带有概念漂移的数据流分类问题。该方法使用Q统计量作为差异性度量,以基分类器之间的分类差异性作为标准来决定以前的基分类器是否保留。Rijn等[6]提出了一种结合异构模型的集成技术用于数据流分类,对集成分类器中不同基分类器的投票进行加权,重视分类器之间的差异性。也有一些研究者认为分类精度和分类多样性二者可以结合。Chandra等[7]证明了一个泛化性能好的集成分类器中,基分类器需要同时具备多样性和精确性,并且提出多样性和精度之间有一个折衷(trade-off)。Li等[8]提出了将一种结合多样性和精度的度量标准应用到遗传算法中,并通过实验结果表明了该度量方法的有效性。
2 加权多样性和精度的集成方法在正式介绍之前,先对本节所使用的符号作简单说明。令数据流S是由无数个大小相等的数据块B组成的,其中每个数据块是由数量相等的实例z={x, y}构成。集成分类器E是由n个基分类器C构成。
2.1 分类器的精度和多样性度量1) 精度度量
精度的度量通常通过计算均方误差(MSE)得到,一个分类器Ci在一个数据块Bj的均方误差MSEij可以用式(1)表示:
| ${\rm{MS}}{{\rm{E}}_{ij}} = \frac{1}{{\left| {{B_j}} \right|}}{\sum\limits_{\{ {{x}},y\} \in {B_j}} {(1 - p({f_i}({{x}}) = y))} ^2}$ | (1) |
使用MSEr表示对当前数据所有可能的类别进行随机预测所得到的均方误差,以此来反映当前数据的类分布,计算公式为
| ${\rm{MS}}{{\rm{E}}_r} = {\sum\limits_y {p(y)(1 - p(y))} ^2}$ | (2) |
精度可以使用MSEij和MSEr来表示,本文使用式(3)来表示集成分类器中已有的基分类器的精度,即
| ${\rm{Ac}}{{\rm{c}}_{ij}} = \frac{1}{{{\rm{MS}}{{\rm{E}}_{ij}} + \delta }}$ | (3) |
式中δ的存在是为了防止式(3)的分母为0。另外,新建立的分类器的精度AccC’根据式(4)来计算:
| ${\rm{Ac}}{{\rm{c}}_{C'}} = \frac{1}{{{\rm{MSE}}{}_r + \delta }}$ | (4) |
2) 集成分类器中的多样性度量
目前已有的理论和实验研究可以证明,由多个分类器组合而成的集成分类器相对于单个分类器来说泛化能力更强,并且由相互独立、互为补充且相对精确的分类器集成得到的集成分类器在泛化性能上要优于性能最好的基分类器[9]。当发生概念漂移时,所有基分类器可能全都无法处理这类新问题;而如果集成分类器中的基分类器是多样性的,那么总能找到一个最擅长处理这个新问题的基分类器,从而使集成分类器具有良好的泛化性能。
本文采用的多样性度量方法为Q统计量,计算两个分类器之间的Q统计量值的公式如式(5)所示:
| ${Q_{ij}} = \frac{{{N^{11}}{N^{00}} - {N^{01}}{N^{10}}}}{{{N^{11}}{N^{00}} + {N^{01}}{N^{10}}}}$ | (5) |
式中:Nab表示分类器i分类结果为a、分类器j分类结果为b的实例数量;1代表正确分类;0代表错误分类。比如,N11表示分类器i和分类器j同时分类正确的实例数量。
为了方便加权后的度量,所以需要将多样性转化为越大代表多样性越强,如式(6)所示:
| $Q_{ij}^* = 0.5(1 - {Q_{ij}})$ | (6) |
式中Qij表示分类器Ci与Cj的Q统计量,用这个值表示二者的差异程度,由于Qij的值域为[−1, 1],因此1 −Qij的值域为[0, 2],然后进行了归一化,归一化这一步不是必需的,是否归一化对结果影响不大。
一个分类器C与一个集成分类器E的多样性值为C与E中的每一个基分类器根据式(6)计算得到的Qij*的平均值。因此,新建立的分类器C′与集成分类器E之间的多样性值divC′可以通过式(7)计算:
| ${\rm{di}}{{\rm{v}}_{{{C}}'}} = \sum\limits_{i = C'\!\!,\;{C_j} \in E} {{{Q}}_{ij}^*} /\left| E \right|$ | (7) |
集成分类器中一个基分类器Ci与其余分类器所构成集合的多样性值可以通过式(8)计算:
| ${\rm{di}}{{\rm{v}}_i} = \sum\limits_{{C_j} \in E,i \ne j} {{{Q}}_{ij}^*} /\left| E \right|$ | (8) |
1)基于多样性和精度加权的分类器权重计算
本文提出了一种新的分类器权重计算方式,以往的集成方法在计算基分类器或者新建立分类器的权重时通常只根据精度或者多样性一个标准来计算,这难免具有片面性,所以为了同时考虑一个分类器的精度和多样性,本文采用了一种线性加权方式来计算分类器权重,将在最新数据块上分类器的精度以及该分类器与集成分类器之间的多样性这两种度量分类器价值的标准以一种线性加权的方式融合成一个标准,以此作为衡量一个分类器对于当前集成分类器价值大小的依据,并通过1个位于0~1的可调整的参数来控制精度和多样性各自在计算权重过程中的重要性。计算权重有两个目的:1)使用权重来表示一个分类器在整个集成分类器的价值,用于集成分类器更新;2)在预测阶段将每个基分类器的预测结果融合,权重高的分类器在预测时将起到更重要的作用。下面是具体的权重计算方式。
当一个新的数据块到来时,使用此数据块构建一个新的分类器C′,并根据式(4)计算C′的精度AccC′,根据式(7)计算C′的多样性divC′。C′的权重wC′根据式(9)来计算,即
| ${w_{{{C}}'}} = \alpha {\rm{Ac}}{{\rm{c}}_{C'}} + (1 - \alpha ){\rm{di}}{{\rm{v}}_{C'}}$ | (9) |
式中
已有基分类器的权重也需要根据新来的数据块调整,使用式(10)计算基分类器新的权重值wij,即
| ${w_{ij}} = \alpha {\rm{Ac}}{{\rm{c}}_{ij}} + (1 - \alpha ){\rm{di}}{{\rm{v}}_i}$ | (10) |
式中wij表示基分类器Ci在数据块Bj上的权重。
2)基于价值度量的集成分类器更新策略
本文假定集成分类器的大小是固定的,即基分类器的个数是固定的,因此在新数据块建立一个新的分类器C′后,如果基分类器的数量已经达到了规定的数目,则需要将集成分类器中的其中一个基分类器替换出,那么如何选择被替换的基分类器将至关重要。
本文采用的是一种基于价值度量的集成分类器更新策略,将式(10)计算得到的权重wij作为分类器Ci当前的价值,当有新的分类器到来时,价值最低的基分类器将会被新建立的分类器替换掉。
另外,之所以每次建立新分类器C′后都将其加入到集成分类器中,而不是先比较其是否比最弱的分类器强再决定是否加入,这里假设基分类器数量已经达到规定数量,主要因为C′是根据最新的数据块建立的分类器,因此可以说C′是最适合当前数据的。由于当前数据块的数据分布情况有很大概率与以后数据的数据分布情况类似,所以可以认为使用C′对接下来的数据分类是有效的。
3) 算法过程
本文提出的多样性精度加权集成算法DAWE2是一个基于块的方法,对于每一个新到来的数据块Bi,首先使用Bi构建一个新分类器C′,并根据式(9)计算C′的权重,然后根据式(10)计算集成分类器中基分类器的权重,分类器的权重均通过将其在最新数据块Bi上的精度与其在集成分类器中多样性值线性加权得到,使用权重值作为分类器的价值度量。当基分类器数量达到规定数目时,每产生一个新分类器C′,便选择一个权重最小的基分类器被C′替换。DAWE算法过程描述如下所示。
输入 数据流S,集成分类器中的基分类器数n。
输出 n个加权的基分类器的集成E。
1) begin
2)将E初始为空;
3)对于数据流S的每个到来的数据块Bi;
4)在数据块Bi上训练新分类器C′;
5)由式(9)计算C′的权重;
6)对于每个E中的分类器Cj;
7)计算 Cj的精度(由式(3));
8)由式(8)计算 Cj的多样性;
9)由式(10)计算Cj的权重;
10)如果E中分类器个数小于n;将C′直接添加到E中;
11)否则使用C′替换E中权重最低的分类器;
12)对于E中除去C′之外的基分类器Cj;
13)在数据块Bi上增量训练 Cj;
14) end
3 实验本文的算法在大规模数据在线分析开源平台MOA(massive online analysis)[10]下实现,在CPU为1.8 GHz、内存为8 GB、操作系统为Windows 10的PC机上进行实验,评价类使用的是MOA下的EvaluateInterleavedChunk类。
3.1 数据集在数据流挖掘中,数据集可以分为两种:真实数据集和合成数据集。人工合成的数据集可以通过设置概念漂移位置、漂移的数目和漂移的幅度等属性,实现对不同类型概念漂移的模拟,但是合成数据集无法完全代替真实数据集,因此为了评价算法的性能,除了在合成数据集上验证之外,还需要在真实数据集上验证。本文选取3个真实数据集和3个合成数据集对提出的算法性能进行验证。
3.1.1 真实数据集1)扑克牌(Poker)数据集:来源于UCI数据库,每个实例有11个属性。数据集中每个实例由52张牌中的5张组成,每张牌使用两个属性(suit和rank)来描述。
2)Covertype数据集:来自UCI数据库,该数据集包含了4个野生区域覆盖类型信息。该数据集有581 012个实例,每个实例有53个属性对应7种可能的森林覆盖类型中的1种。
3)Airlines数据集:该数据集包含根据航班的出发信息来预测此次航班是否会晚点的数据。此数据集包含539 383个实例,每个实例包含7个属性。
3.1.2 合成数据集1)SEA数据集:该数据集是Street于2001年提出的[11],因仅含有连续型属性而著名,是经典的突变式概念漂移数据集。
2)LED数据集:该数据集用来预测7段数码显示器上显示的数字。该数据集有24个属性,其中前7个属性用于显示0~9的数字。
3)随机树数据集:该数据集由5个nominal属性和5个numeric属性组成,类属性值通过随机树(random tree)确定。
3.2 实验结果对比与分析实验结果将通过3个方面展示:不同数据块大小对算法性能影响、不同方法精度的对比以及α值设置对算法性能影响。
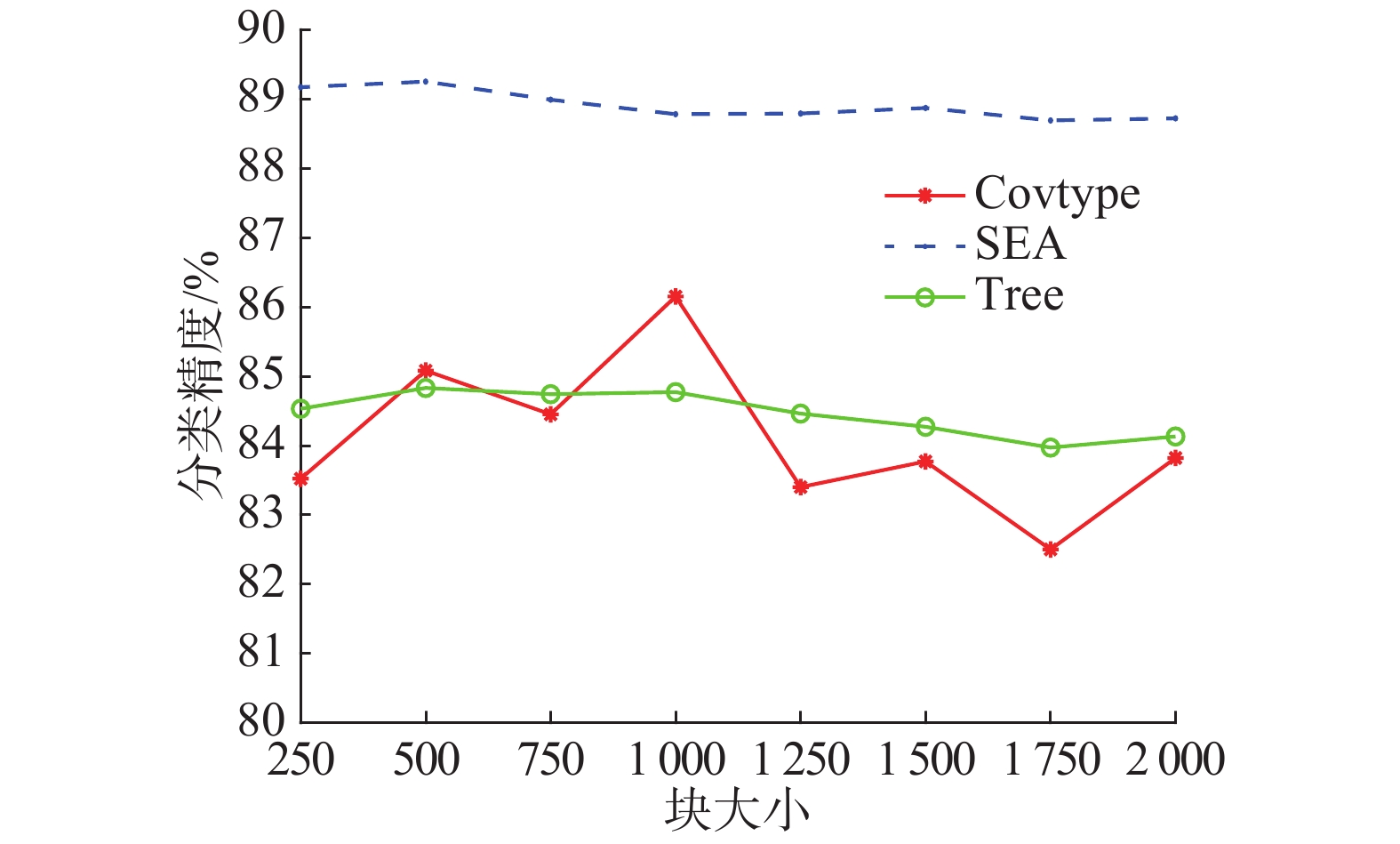
3.2.1 不同数据块大小对算法性能影响图1展示了本文提出的算法DAWE在Covertype数据集、SEA数据集以及Tree(随机树)数据集上采用不同的数据块大小时的表现。在基于块的数据流挖掘中,块大小的选取对最终的分类性能将有着重要的影响,选择较大的数据块意味着使用更多的实例建立分类器,使得当前分类器分类精度较高,缺点是对概念漂移反应不敏感;反之,选择较小的数据块虽然对概念漂移反应较敏感,但缺点是每次建立分类器时使用的实例较少,导致每个分类器的分类精度较低。因此,综合来看数据块过大或者过小都使得最终分类性能不佳。
|
Download:
|
| 图 1 不同数据块大小对算法的影响 Fig. 1 Effect of data chunk size | |
由图1可以看出,对于Covertype数据集来说数据块大小为1 000是最合适的,即每到来1 000个实例将其作为一个数据块来训练一个分类器;而数据块大小为500对于SEA数据集来说是最合适的。由此可以看出,对于不同数据集可能需要选用不同大小的数据块来达到其最佳性能。
3.2.2 不同方法对比本文选取的对比方法为MOA下的Accuracy Updated Ensemble (AUE2)、Adaptive Random Forest (ARF)[12]和Heterogeneous Ensemble Blast (Blast),分别在Poker数据集、Airlines数据集、SEA数据集和Covertype数据集上进行了对比实验。表1为几种算法在不同数据集上的平均精度对比。
| 表 1 算法平均精度对比表 Tab.1 Contrast of different algorithms |
由表1可以看出,在4个数据集上本文提出的算法DAWE的平均精度要优于其他3个算法。为了更详细地展示算法在不同数据集上的对比结果,接下来将分别展示在不同数据集上增量训练模型时各个阶段测试的精度情况。以下对比实验默认指定数据块大小为1 000。
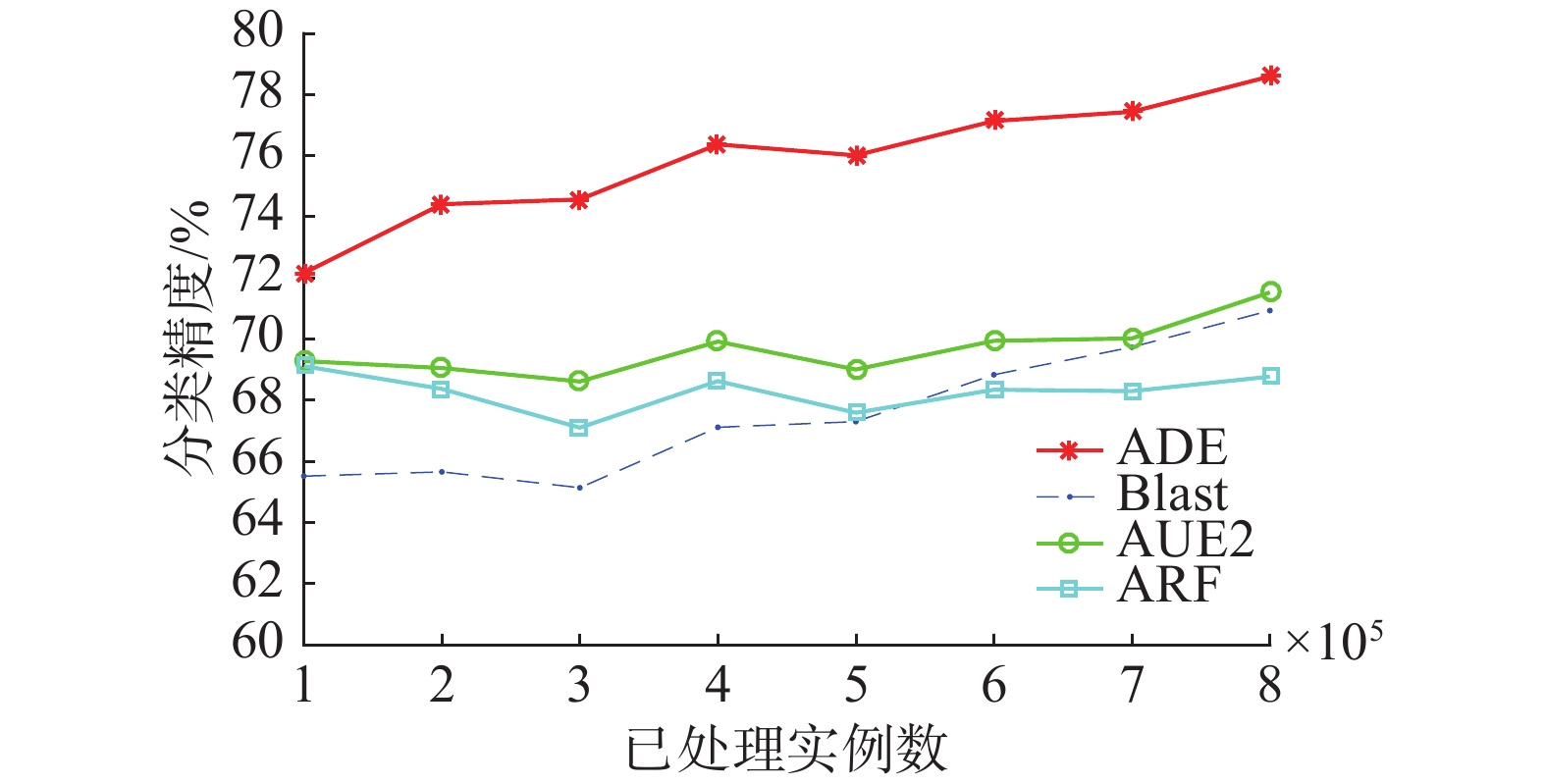
图2展示了4种算法(本文提出的算法以及3个对比算法)在Poker数据集上增量训练时各个阶段的实时精度,可以看出,本文提出的算法DAWE在Poker数据集上要远好于其他3个,在表1中也可以看出,在Poker数据集上,DAWE的平均精度相比其他3种算法分别高出6.16%、7.55%和8.30%。
|
Download:
|
| 图 2 4种算法在Poker数据集上分类精度对比 Fig. 2 Accuracy contrast of 4 algorithms on Poker | |
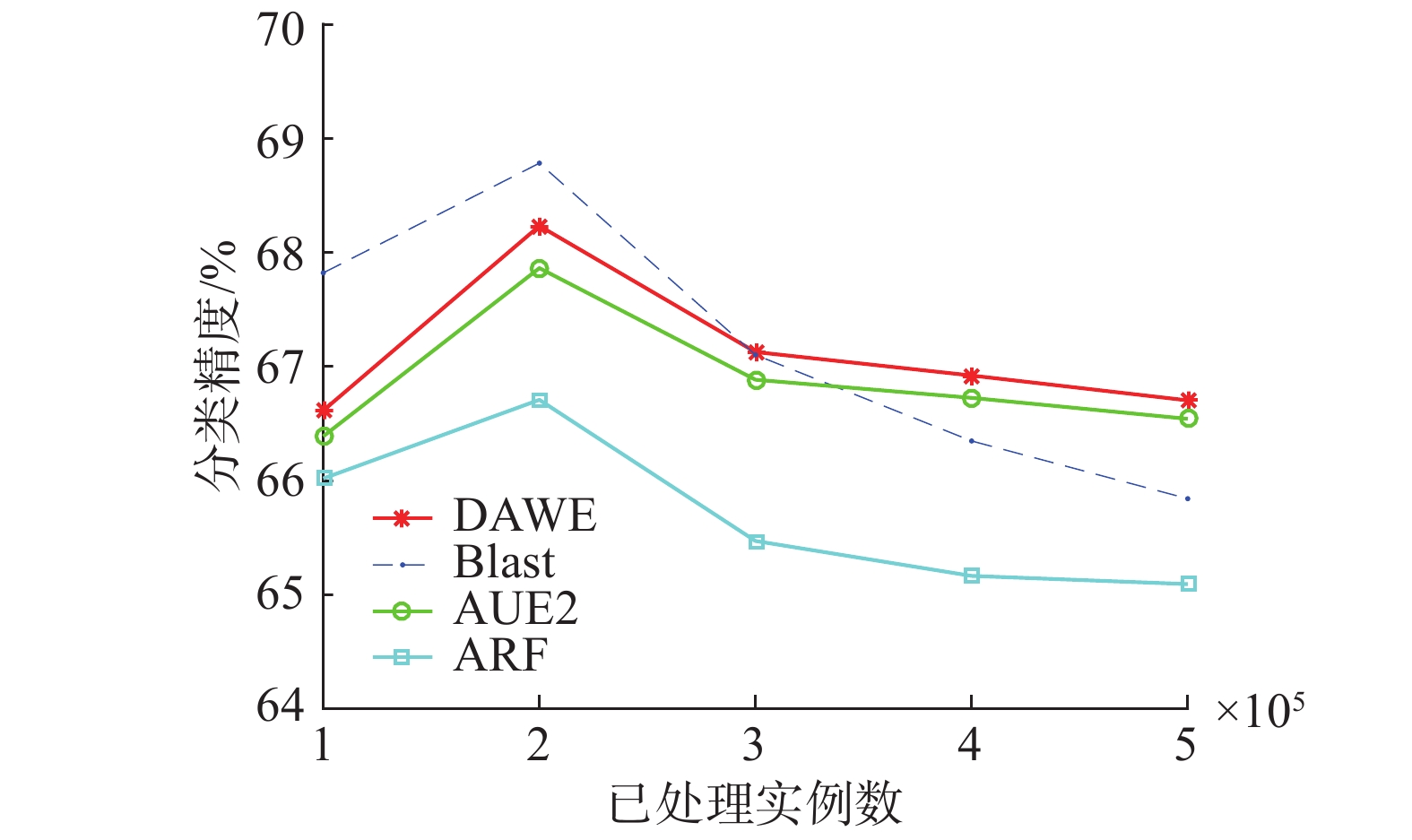
图3展示了4种算法在Airlines数据集上增量训练时各个阶段的实时精度。虽然从表1中看Blast的平均精度最高,但是从图3中可以看出,Blast之所以平均精度高是因为训练开始精度高,随着实例的不断增加,其精度呈不断下降趋势,在300 000个实例后,精度最好的算法一直是DAWE。
|
Download:
|
| 图 3 4种算法在Airlines数据集上分类精度对比 Fig. 3 Accuracy contrast of 4 algorithms on Airlines | |
图4展示了4种算法在SEA数据集上增量训练时各个阶段的实时精度。SEA是突变漂移数据集,因此为了更好检测并处理概念漂移,将数据块大小设置为500。可以看出,本文提出的算法DAWE在平均精度上仅次于APF,并且与ARF只相差0.31%。

|
Download:
|
| 图 4 4种算法在SEA数据集上分类精度对比 Fig. 4 Accuracy contrast of 4 algorithms on SEA | |
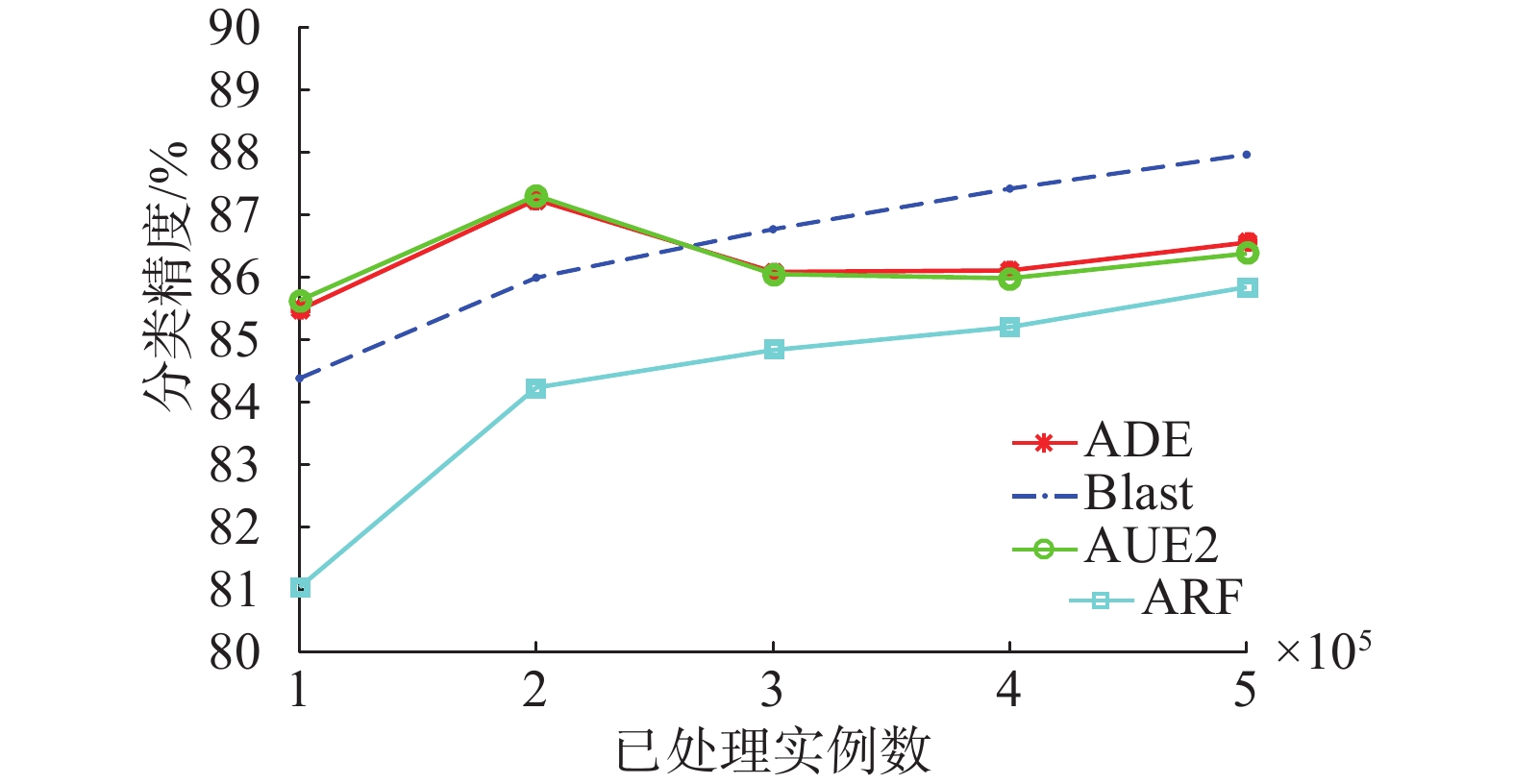
图5展示了4种算法在Covertype数据集上增量训练时各个阶段的实时精度。可以看出,DAWE和AUE2在训练前期表现较好,训练后期Blast更好,从平均精度上来看DAWE与Blast只相差0.21%。
|
Download:
|
| 图 5 4种算法在Covertype数据集上分类准确度对比 Fig. 5 Accuracy contrast of 4 algorithms on Covertype | |
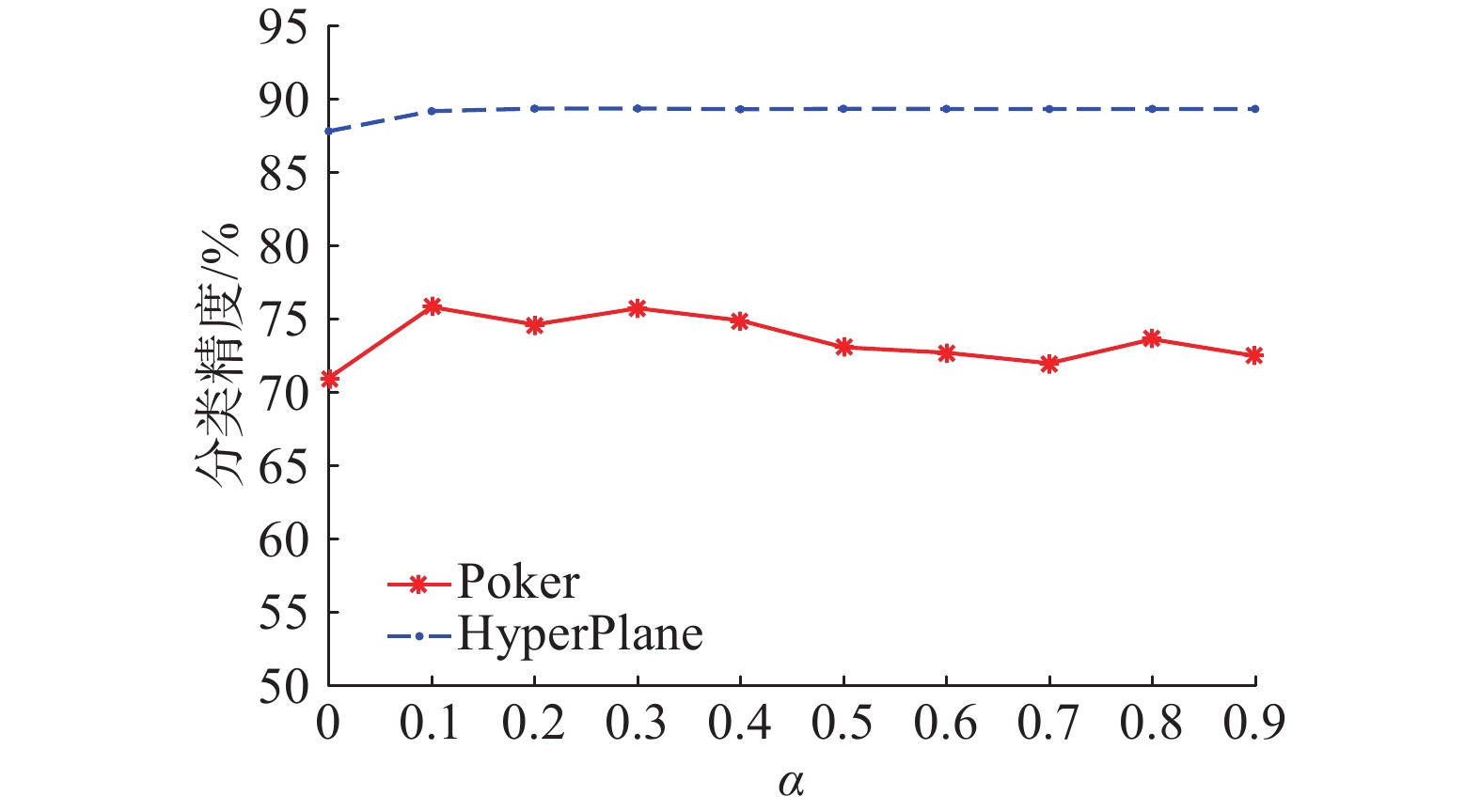
本文提出的算法通过多样性和精度的线性加权来计算分类器权重,由式(9)、式(10)可以看出,通过α来控制多样性和精度在计算权重过程中分别所占比重,所以其取值对最终的分类精度会产生影响,图6以Poker数据集以及LED数据集为例展示了不同α的取值对集成分类器的平均分类精度产生的影响。由此可以看出,对于不同数据集,需要选用不同α值以达到最佳分类性能。
|
Download:
|
| 图 6 不同α值对平均分类精度的影响 Fig. 6 Effect of different α on average accuracy | |
通过表1以及图2~5可以看出,本文提出的算法DAWE在部分数据集上优于其他算法,特别是在Poker数据集上,相较于其他算法有大幅提升;在Airlines数据集上表现也不错,在训练后半段一直占据精度第一的位置;在SEA数据集上平均精度仅次于ARF;在Covertype数据集上平均精度仅次于Blast。综合4个数据集来看,对4种算法在4个数据集上的平均精度取平均值(即表1的最后一行),通过平均值可以看出,本文提出的算法DAWE在参与对比的4种算法中是最优的。
4 结束语本文提出了一种综合考虑精度和多样性的新的集成方法用于处理数据流分类问题,使用精度与多样性的线性加权来计算一个分类器的权重,通过权重来衡量一个分类器对于整个集成分类器的重要性,权重越高表示这个分类器越重要,当有新分类器建立时需替换权重最低的基分类器。实验验证了本文所提出的算法可以有效处理数据流中的概念漂移问题。
参数α的选择会在一定程度上决定算法的性能,如何根据不同数据集选择一个合适的α值是今后研究的方向。在加权方式上,本文选择的是线性加权,在今后的研究中还可以对加权方式进一步优化。另外,将迁移学习用于数据流分类是一个值得研究的问题,迁移学习的目的是利用已有模型帮助新环境下样本的分类,与数据流挖掘中的概念漂移和特征漂移问题相符合,因此二者具备良好结合的可操作性。
| [1] |
GOMES H M, BARDDAL J P, ENEMBRECK F, et al. A survey on ensemble learning for data stream classification[J]. ACM computing surveys, 2017, 50(2): 23. ( 0) 0)
|
| [2] |
BRZEZINSKI D, STEFANOWSKI J. Reacting to different types of concept drift: the Accuracy Updated Ensemble algorithm[J]. IEEE transactions on neural networks and learning systems, 2014, 25(1): 81-94. DOI:10.1109/TNNLS.2013.2251352 ( 0) 0)
|
| [3] |
PIETRUCZUK L, RUTKOWSKI L, JAWORSKI M, et al. How to adjust an ensemble size in stream data mining[J]. Information sciences, 2017, 381: 46-54. DOI:10.1016/j.ins.2016.10.028 ( 0) 0)
|
| [4] |
孙宇. 针对含有概念漂移问题的增量学习算法研究[D]. 合肥: 中国科学技术大学, 2017. SUN Yu. Incremental learning algorithms with concept drift adaptation[D]. Hefei: University of Science and Technology of China, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10358-1017071234.htm (  0) 0)
|
| [5] |
SUN Yu, TANG Ke, ZHU Zexuan, et al. Concept drift adaptation by exploiting historical knowledge[J]. IEEE transactions on neural networks and learning systems, 2018, 29(10): 4822-4832. DOI:10.1109/TNNLS.2017.2775225 ( 0) 0)
|
| [6] |
VAN RIJN J N, HOLMES G, PFAHRINGER B, et al. Having a Blast: meta-learning and heterogeneous ensembles for data streams[C]//Proceedings of the 2015 IEEE International Conference on Data Mining. Atlantic City, USA, 2015: 1003–1008.
( 0) 0)
|
| [7] |
CHANDRA A, CHEN Huanhuan, YAO Xin. Trade-off between diversity and accuracy in ensemble generation[M]//JIN Yaochu. Multi-Objective Machine Learning. Berlin Heidelberg: Springer, 2006: 429–464.
( 0) 0)
|
| [8] |
LI Ye, XU Li, WANG Yagang, et al. A new diversity measure for classifier fusion[M]//WANG F L, LEI Jingsheng, LAU R W H, et al. Multimedia and Signal Processing. Berlin Heidelberg: Springer, 2012: 396–403.
( 0) 0)
|
| [9] |
孙博, 王建东, 陈海燕, 等. 集成学习中的多样性度量[J]. 控制与决策, 2014, 29(3): 385-395. SUN Bo, WANG Jiandong, CHEN Haiyan, et al. Diversity measures in ensemble learning[J]. Control and decision, 2014, 29(3): 385-395. (  0) 0)
|
| [10] |
BIFET A, HOLMES G, KIRKBY R, et al. MOA: massive online analysis[J]. Journal of machine learning research, 2010, 11(5): 1601-1604. ( 0) 0)
|
| [11] |
STREET W N, KIM Y S. A streaming ensemble algorithm (SEA) for large-scale classification[C]//Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, USA, 2001: 377–382.
( 0) 0)
|
| [12] |
GOMES H M, BIFET A, READ J, et al. Adaptive random forests for evolving data stream classification[J]. Machine learning, 2017, 106(9/10): 1469-1495. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


