图像分割在图像识别和计算机视觉中是关键的预处理过程,很多算法已经被提出并应用在对象分割以及特征提取中。然而,鲁棒性强和高效的图像分割算法的设计还是一个非常具有挑战性的研究课题。它的目标是将相似和邻近的像素以图像分割成相应结构连贯的元素。根据图像中像素的灰度值、纹理、颜色等将图像分为若干个互不相干的区域,每个区域内部均有其相似性,不同的区域又互有差异。图像分割可以认为是基于同质性或异质性准则将一幅图像划分为若干有意义的子区域的过程[1]。
由于待分割模型不尽相同,因此不同模型所适合的分割方法也各有优缺点。现如今,图像分割方法主要有如下几类:基于边缘检测分割法[2]、基于阈值分割法[3-4]、基于区域分割法[5]、基于形态学分水岭分割法[6]、基于聚类分割法[7-8]、基于神经网络或根据超像素[9]特定理论的分割方法。由于图像分割大多数都是在像素级基础上根据像素的灰度、颜色、纹理等特征进行分割处理,因此不可避免的对噪声敏感,容易产生很多孤立的分割点,很难找到精确的区域分割边缘,然而对医学图像[10]的处理就需要算法鲁棒性强,精准度高。
近些年,模糊聚类被广泛地应用在人工智能、模式识别、图像处理中。FCM(fuzzy C-means)在1973年被Dunn[11]提出并发展成为一种经典的模糊聚类算法,是图像分割中快速有效的方法之一,该方法将所选取样本到聚类中心误差平方与准则函数作为目标函数进行聚类,作为一个典型的无监督技术FCM已经成功地应用在模式识别和数据挖掘中,但是FCM算法进行图像分割时存在明显的缺陷,它只考虑颜色信息而没有考虑任何空间信息。为了解决这个问题,Ahmed等[12]在传统FCM的基础上引入了一个空间信息邻域项,提出了一种将空间邻域信息与模糊C均值算法相结合的算法(FCM_S),该算法对噪声有一定的抑制效果,但算法复杂度高。为了解决该问题,Chen等人[13]将邻域均值信息,以及邻域中值信息融入到算法当中,提出了FCM_S1和FCM_S2算法。这两种空间限制信息都是局部空间信息,如果图像被噪声污染严重,那么图像的局部空间信息也将受到很大的影响。然而,图像中的每个像素点都存在很多像素点与其含有相似的邻域结构,将其称之为非局部空间信息[14],当图像被噪声污染时,它的作用比局部空间信息更大。
1 融入邻域信息的多测度图像模型 1.1 多测度模型通常在使用聚类算法进行图像分割时针对的是图像本身,聚类的数据样本是单一测度的图像像素灰度值,多测度模型将原本的一种测度数据扩充为多种测度数据,如:第一测度是图像本身灰度值向量

|
Download:
|
| 图 1 多测度模型 Fig. 1 Multidimensional model | |
相似度
| ${S_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\exp (\displaystyle\frac{{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{{\sigma ^2}}})}, \,\,\,\,{i \ne j,{\sigma ^2} \ne 0}\\ 0,\,\,\,\, {i = j}\\ 1,\,\,\,\, {{\sigma ^2} = 0} \end{array}} \right.$ | (1) |
| $\sigma = \sqrt {\frac{{\sum\limits_{{x_j} \in {N_i}} {{{\left\| {{x_i} - {x_j}} \right\|}^2}} }}{{{N_R}}}} $ | (2) |
由式(1)可知,相似度Sij的取值范围为0~1,通过邻域像素点灰度值与相似度的乘积求和即可更新待考察像素点灰度值。多测度模型的提出,在不改变图像原本轮廓的基础上,将原本单一测度的图像灰度值向量扩充成了三测度,通过均值滤波与邻域像素点灰度值相似度很好地将图像局部信息与非局部信息融入到模型信息中,为聚类提供了更多的图像信息,以便获得更好的图像分割结果。
2 模糊C-均值聚类算法及应用 2.1 传统模糊C-均值聚类算法FCM(fuzzy C-means)是一种经典的模糊聚类算法,该算法根据带聚类数据的隶属度将数据划分成几类,即将相似度较高的划分到一类中。
假设
| ${u_{ij}} \in [0,1], \forall j = 1,2, \cdots ,n,\,\, \forall i = 1, 2, \cdots ,c$ |
| $ \sum\limits_{i = 1}^c {{u_{ij}}} = 1, \;\; 0 < \sum\limits_{j = 1}^n {{u_{ij}}} < n $ |
FCM算法通过最小化目标函数来得到最优隶属度矩阵及聚类中心,一般表现形式为
| $J({{U}},{{V}}) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} {{\left\| {{x_j} - {v_i}} \right\|}^2}} $ | (3) |
| ${d_{ij}} = \left\| {{x_j} - {v_i}} \right\|$ | (4) |
式中:
| ${u_{ij}} = {\left[ {\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{\frac{2}{{m - 1}}}}} } \right]^{ - 1}}$ | (5) |
| ${v_i} = \displaystyle\frac{{\sum\limits_{j = 1}^n {{u_{ij}}^m{x_j}} }}{{\sum\limits_{j = 1}^n {{u_{ij}}^m} }}$ | (6) |
在迭代过程中,设置迭代条件
图2是FCM算法对添加了0.03椒盐噪声以及0.03高斯噪声图像的处理结果,FCM算法对噪声处理效果很不理想。传统FCM算法进行图像分割,是对图像像素点灰度值进行聚类,当图像含有噪声时,算法将噪声点灰度值当成正常灰度值进行聚类,因此FCM对噪声非常敏感,这是由于算法并没有考虑像素点空间信息的原因。在图像分割中除了考虑像素点本身的数值信息外,像素点灰度值的所属聚类类别很大程度上取决于邻域像素点灰度值的所属类别。因此,像素点的空间信息对图像分割有着很重要的影响。

|
Download:
|
| 图 2 FCM算法处理结果 Fig. 2 results of FCM algorithm | |
为了解决FCM算法没有考虑空间信息的问题,FCM_S1、FCM_S2算法对FCM算法有所改进,提出了其目标函数为
| $J = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} {{\left\| {{x_j} - {v_i}} \right\|}^2}} + \alpha \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} {{\left\| {{{\overline x }_j} - {v_i}} \right\|}^2}} $ | (7) |
式中:
如果在每次聚类迭代之前提供一些先验知识作为辅助,聚类过程中再次融入空间信息,那么将能够获得更好的图像分割结果。先验概率以及邻域隶属度差异惩罚项就很好地将像素点的空间信息引入算法中,且能够有效的抑制噪声,并且能够较好地保留图像细节。
2.3.1 引入先验概率的隶属度矩阵在图像分割中邻域像素点对待分割像素点的影响至关重要,在每一次聚类迭代之前,若有先验知识作为协助,那么将会得到更好的聚类结果,也能够尽可能地减少像素点的误分割。引入先验概率的隶属度矩阵定义如下:
| ${p_{ij}} = \frac{{N_R^i}}{{{N_R}}}$ | (8) |
| $u_{ij}^ * = \frac{{{u_{ij}}{p_{ij}}}}{{\sum\limits_{k = 1}^c {{u_{kj}}{p_{kj}}} }}$ | (9) |
式中:
虽然先验概率的引入已经将空间信息引入到算法中,并且对噪声抑制效果明显,但是为了增强算法的鲁棒性,这里引入邻域隶属度差异惩罚项[16]:
| $G = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^c {\sum\limits_{k = 1}^n {{u^*}_{ij}^m{{\left( {1 - {u^*}_{ik}} \right)}^m}{Q_{jk}}} } } $ | (10) |
式中:
| ${{{Q}}_{jk}} = \left\{ {\begin{array}{*{20}{c}} {1,}\\ 0, \end{array}\begin{array}{l} { j{\text{与}}k{\text{相邻}},\;\;{\text{且}}j \ne k}\\ {j{\text{与}}k{\text{不相邻}}} \end{array}} \right.$ | (11) |
因此邻域隶属度差异惩罚项指的是像素点与邻域像素点对每一个聚类中心的隶属度差异。邻域隶属度差异度越小,则相邻的像素点越容易归为一类。
改进后的目标函数可改写为
| $J = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {{u^{*m}_{ij}}} d_{ij}^2} + \lambda \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^c {\sum\limits_{k = 1}^n {{u^{*m}_{ij}}{{\left( {1 - {u^{*}}_{ik}} \right)}^m}{{{Q}}_{jk}}} } } $ | (12) |
通过迭代获得隶属度并结合隶属度先验概率得到新的隶属度矩阵与聚类中心更新公式:
| ${u^*}_{ij} = {\left[ {\sum\limits_{r = 1}^c {{{\left( {\frac{{{d_{ij}}^2 + \lambda \sum\limits_{k = 1}^n {{{(1 - {u_{ik}})}^m}{Q_{jk}}} }}{{{d_{rj}}^2 + \lambda \sum\limits_{k = 1}^n {{{(1 - {u_{rk}})}^m}{Q_{jk}}} }}} \right)}^{\frac{1}{{m - 1}}}}} } \right]^{ - 1}}{p_{ij}}$ | (13) |
| ${v_i} = \frac{{\sum\limits_{j = 1}^n {{u^{*m}_{ij}}{x_j}} }}{{\sum\limits_{j = 1}^n {{u^{*m}_{ij}}} }}$ | (14) |
1) 算法思想
在进行图像分割时,或多或少都会受到噪声的影响,传统模糊C-均值算法对噪声敏感,究其原因是因为其没有考虑像素点的空间信息。本文算法首先使用多测度模型将图像信息从一测度扩充成三测度,将局部信息与非局部信息引入多测度模型中,为之后的聚类提供了更多的信息。其次,在原有隶属度矩阵的基础上乘以先验概率,并且为算法本身添加邻域隶属度差异惩罚项,使用改进算法对图像像素点灰度值信息进行聚类,完成图像分割。
2) 算法步骤
输入 图像
输出 隶属度矩阵
1)获取待分割图像
2)取
3)根据人工视觉预先确定聚类个数,设定聚类中心个数c,隶属度模糊参数m=2,迭代停止条件
4)初始化隶属度矩阵;
5)根据初始化得到的隶属度矩阵计算多测度模型先验概率矩阵
6)更新隶属度矩阵;
7)更新聚类中心;
8)若
9)根据最终聚类中心
为了验证本文算法的有效性,对合成图像和自然图像在添加椒盐噪声及高斯噪声情况下进行分割,对比算法为FCM、FCM_S1、FCM_S2、KWFLICM[17],编译环境为MATLABR2012a,CPU为i3_2310M,内存6GB。根据人工视觉预先确定聚类个数,设定聚类中心个数c,隶属度模糊参数m=2,迭代停止条件
对图像1和图像2添加0.05、0.08椒盐噪声,分别如图3、图4所示。

|
Download:
|
| 图 3 图像1加椒盐噪声效果对比 Fig. 3 Image 1 with pepper salt noise | |

|
Download:
|
| 图 4 图像2加椒盐噪声效果对比 Fig. 4 Image 2 with pepper salt noise | |
根据以上结果可以看出FCM_S1、FCM_S2算法对噪声处理能力一般,KWFLICM和本文算法表现良好。为了更好地分析几种算法对噪声的处理能力,将增加噪声数量,图像添加0.15椒盐噪声,以及0.15高斯噪声分析对比处理结果,见图5~7。

|
Download:
|
| 图 5 图像3加椒盐噪声效果对比 Fig. 5 Image 3 with pepper salt noise | |

|
Download:
|
| 图 6 图像4加高斯噪声效果对比 Fig. 6 Image 4 with gaussian noise | |

|
Download:
|
| 图 7 图像1加高斯噪声效果对比 Fig. 7 Image 1 with gaussian noise | |
对于添加了0.15椒盐噪声的图像,可以看出FCM_S1、FCM_S2算法对处理椒盐噪声表现一般,然而对于添加了0.15高斯噪声的图像,FCM_S1、FCM_S2算法处理效果比处理椒盐噪声效果好很多,但图像的边界处仍然有明显噪声无法去除,KWFLICM和本文算法依然表现良好。表1将根据分割精确对各算法性能进行详细比较。
| 表 1 算法分割精确率 Tab.1 Algorithm segmentation accuracy |
分割精确率SA(segmentation accuracy)定义如下:
| ${\rm{SA}} = \frac{{{\text{分割正确像素点个数}}}}{{{\text{总像素点个数}}}} \times 100{\text{% }}$ | (15) |
对于添加了0.15噪声后,图片已经变得非常模糊,FCM_S1、FCM_S2算法对于椒盐噪声效果一般,但对高斯噪声效果相对较好,KWFLICM以及本文算法对处理椒盐噪声以及高斯噪声表现良好。由表1可以看出,对于添加了0.15椒盐噪声图像,KWFLICM算法分割精度较高,但对于添加了0.15高斯噪声的图像本文算法更加优异。
3.2 自然图像去噪算法对比 3.2.1 自然图像添加椒盐噪声对自然图像11~14添加椒盐噪声,如图8~11,分析对比不同算法结果。

|
Download:
|
| 图 8 图像11加椒盐噪声效果对比 Fig. 8 Image 11 with pepper salt noise | |

|
Download:
|
| 图 9 图像12加椒盐噪声效果对比 Fig. 9 Image 12 with pepper salt noise | |
|
Download:
|
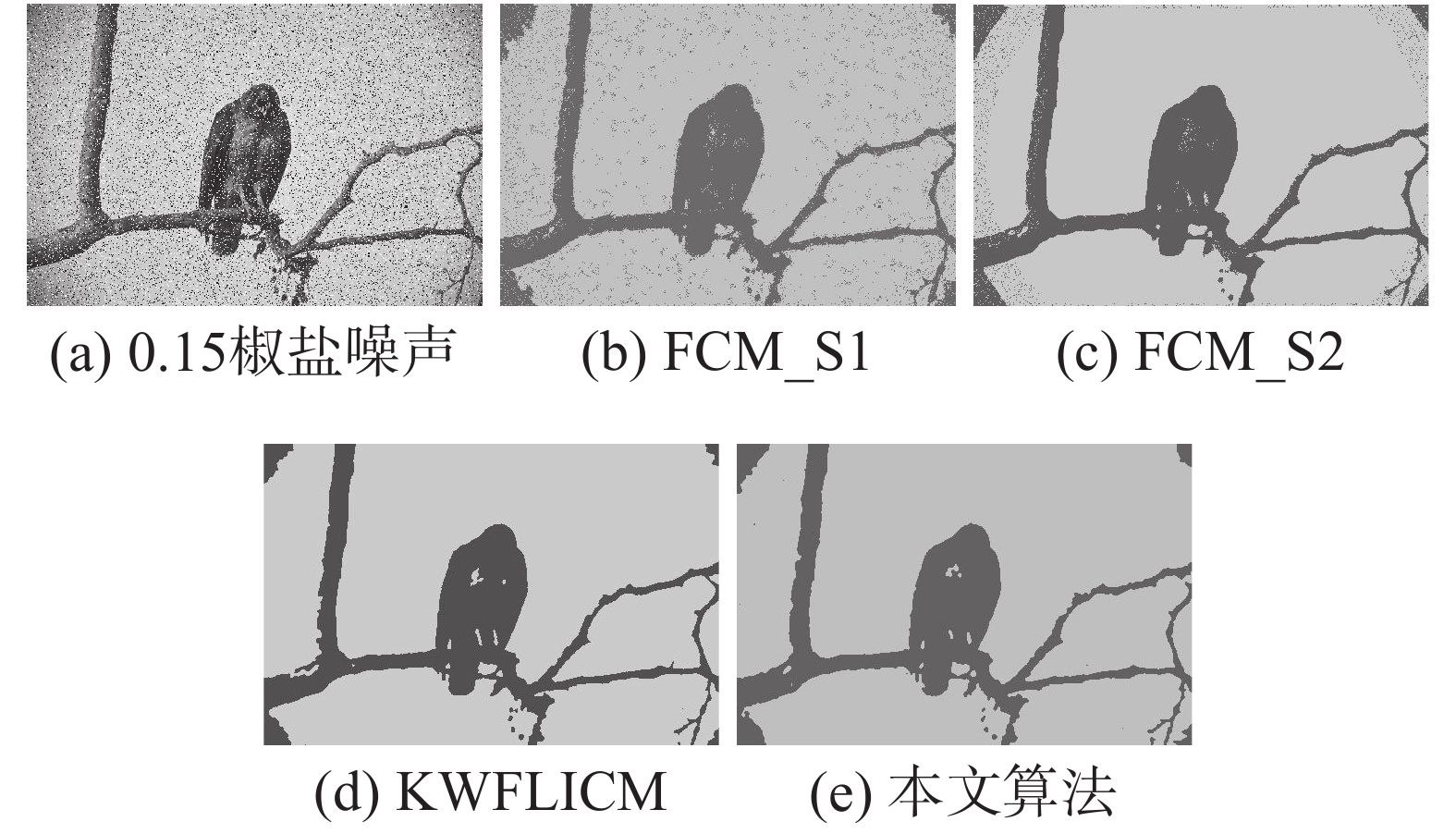
| 图 10 图像13加椒盐噪声效果对比 Fig. 10 Image 13 with pepper salt noise | |

|
Download:
|
| 图 11 图像14加椒盐噪声效果对比 Fig. 11 Image 14 with pepper salt noise | |
对自然图像添加高斯噪声,如图12~15,分析对比不同算法结果。

|
Download:
|
| 图 12 图像11加高斯噪声效果对比 Fig. 12 Image 11 with gaussian noise | |

|
Download:
|
| 图 13 图像12加高斯噪声效果对比 Fig. 13 Image 12 with gaussian noise | |

|
Download:
|
| 图 14 图像13加高斯噪声效果对比 Fig. 14 Image 13 with gaussian noise | |

|
Download:
|
| 图 15 图像14加高斯噪声效果对比 Fig. 15 Image 14 with gaussian noise | |
从自然图像添加椒盐噪声以及高斯噪声的实验中可以看出,FCM_S1、FCM_S2算法对于椒盐噪声仍然效果一般,对于高斯噪声效果较好,但依然有些许噪声颗粒无法有效剔除。KWFLICM算法以及本文算法在自然图像去除噪声方面表现良好,同时细节保留相对完好。
在自然图像的处理实验中,表2显示FCM、FCM_S1、FCM_S2在处理图像时速度有优势,但从实验结果图来看分割效果不甚理想,KWFLICM算法速度次之,本文算法速度与其相比较较慢。从合成图像实验以及自然图像实验中可以看出,FCM算法对噪声处理能力较差,FCM_S1、FCM_S2算法对于椒盐噪声处理能力一般,对高斯噪声处理效果相对较好,但图像边界处噪声无法剔除。KWFLICM算法以及本文算法对噪声处理能力较强,KWFLICM算法对椒盐噪声的处理能力优于本文算法,但本文算法处理高斯噪声能力要强于KWFLICM算法。综上所述,本文算法具有一定优势。
| 表 2 算法时间对比 Tab.2 Algorithm comparison time |
本文提出了一种融入邻域信息的多测度模糊聚类算法,将局部信息与非局部信息很好地融入到了模型中,先验概率以及邻域隶属度差异惩罚项的引入很好地修正了聚类结果。实验证明,本文算法对于含噪声图像有着很好的去噪效果,且细节保留良好。但本文算法也存在一定缺陷,从算法时间对比表可以看出,本文算法复杂度略高,虽然分割效果明显优于传统FCM算法,但是也为此消耗了时间。因此在保证图像分割效果的同时,如何减少算法时间复杂度将是本文需要解决的问题,这也将成为今后的研究方向。
| [1] |
HARALOCK R M, SHAPIRO L G. Computer and robot vision[M]. Boston: Addison-Wesley Longman Publishing Co., Inc., 1991.
( 0) 0)
|
| [2] |
LI Nan, HUO Hong, ZHAO Yuming, et al. A spatial clustering method with edge weighting for image segmentation[J]. IEEE geoscience and remote sensing letters, 2013, 10(5): 1124-1128. DOI:10.1109/LGRS.2012.2231662 ( 0) 0)
|
| [3] |
BARADEZ M O, MCGUKIN C P, FORRAZ N, et al. Robust and automated unimodal histogram thresholding and potential applications[J]. Pattern recognition, 2004, 37(6): 1131-1148. DOI:10.1016/j.patcog.2003.12.008 ( 0) 0)
|
| [4] |
赵凤, 范九伦, 潘晓英, 等. 基于灰度和非局部空间灰度特征的二维Otsu曲线阈值分割法[J]. 计算机应用研究, 2012, 29(5): 1987-1989, 2000. ZHAO Feng, FAN Jiulun, PAN Xiaoying, et al. Two-dimensional Otsu' s curve thresholding segmentation method based on gray and non local spatial gray feature[J]. Application research of computers, 2012, 29(5): 1987-1989, 2000. DOI:10.3969/j.issn.1001-3695.2012.05.103 (  0) 0)
|
| [5] |
代沁伶, 王雷光, 洪亮. 融合边缘测度的自然场景彩色图像区域分割[J]. 中国图象图形学报, 2013, 18(5): 523-528. DAI Qinling, WANG Leiguang, HONG Liang. Regional segmentation of natural scene color images by integrating edge cues[J]. Journal of image and graphics, 2013, 18(5): 523-528. (  0) 0)
|
| [6] |
VINCENT L, SOILLE P. Watersheds in digital spaces: an efficient algorithm based on immersion simulations[J]. IEEE transactions on pattern analysis and machine intelligence, 1991, 13(6): 583-598. DOI:10.1109/34.87344 ( 0) 0)
|
| [7] |
CHOUDHRY M S, KAPOOR R. Performance analysis of fuzzy C-means clustering methods for MRI image segmentation[J]. Procedia computer science, 2016, 89: 749-758. DOI:10.1016/j.procs.2016.06.052 ( 0) 0)
|
| [8] |
KRINIDIS S, CHATZIS V. A robust fuzzy local information C-means clustering algorithm[J]. IEEE transactions on image processing, 2010, 19(5): 1328-1337. DOI:10.1109/TIP.2010.2040763 ( 0) 0)
|
| [9] |
王昭, 娄昊, 范九伦. 一种基于模糊C均值的图像超像素分割方法[J]. 微电子学与计算机, 2014(10): 18–21, 27. WANG Zhao, LOU Hao, FAN Jiulun. Fuzzy C-means clustering algorithm with superpixel for image segmentation[J]. Microelectronics and computer, 2014(10): 18–21, 27. (  0) 0)
|
| [10] |
孙权森, 纪则轩. 基于模糊聚类的脑磁共振图像分割算法综述[J]. 数据采集与处理, 2016, 31(1): 28-42. SUN Quansen, JI Zexuan. Fuzzy clustering for brain MR image segmentation[J]. Journal of data acquisition & processing, 2016, 31(1): 28-42. (  0) 0)
|
| [11] |
DUNN J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of cybernetics, 1973, 3(3): 32-57. DOI:10.1080/01969727308546046 ( 0) 0)
|
| [12] |
AHMED M N, YAMANY S M, MOHAMED N, et al. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE transactions on medical imaging, 2002, 21(3): 193-199. DOI:10.1109/42.996338 ( 0) 0)
|
| [13] |
CHEN Songcan, ZHANG Daoqiang. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]. IEEE transactions on systems, man and cybernetics, part B (cybernetics), 2004, 34(4): 1907-1916. DOI:10.1109/TSMCB.2004.831165 ( 0) 0)
|
| [14] |
Do M N, VETTERLI M. Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance[J]. IEEE transactions on image processing, 2002, 11(2): 146-158. DOI:10.1109/83.982822 ( 0) 0)
|
| [15] |
CAI Weiliang, CHEN Songcan, ZHANG Daoqiang. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation[J]. Pattern recognition, 2007, 40(3): 825-838. DOI:10.1016/j.patcog.2006.07.011 ( 0) 0)
|
| [16] |
YANG Y, ZHENG C, LIN P. Fuzzy c-means clustering algorithm with a novel penalty term for image segmentation[J]. Opto-electronics review, 2005, 13(4): 309. ( 0) 0)
|
| [17] |
GONG Maoguo, LIANG Yan, SHI Jiao, et al. Fuzzy C-means clustering with local information and kernel metric for image segmentation[J]. IEEE transactions on image processing, 2013, 22(2): 573-584. DOI:10.1109/TIP.2012.2219547 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


