管路系统作为能量传递和介质传输的重要通道在各种复杂装备中起着重要的作用,对机械装备的安全性、可靠性及成本有重要影响。在机械设备工作过程中经常会因为机械振动或介质流动导致管路系统的振动故障[1],进而影响设备的正常运转。一台典型的航空发动机通常包含上百根管路,这些管路的支撑部件即卡箍的布局规划对管路振动性能有重要影响,因此针对管路卡箍布局规划展开研究对降低管路系统故障、提高机械设备工作性能等具有重要意义。
在管路卡箍布局优化方面,多年来国内外学者取得了一定的研究成果。顾文彬[2]对直管结构在自由振动、瞬态响应和随机响应下支撑的最优位置优化进行了研究,结果表明不同激励形式下直管卡箍的最优位置不同。Zhu等[3]提出通过采用伪密度技术将离散问题转化为连续体,建立了支撑布局的拓扑优化方法。尹泽勇等[4]对卡箍刚度在发动机管路系统振动特性中的影响进行了研究,分别对单管和双管卡箍进行了有限元分析计算,并进行了实验测定。Wang等[5-6]分别以基频最大化和变形最小化为优化目标,采用启发式优化算法对矩形板结构和直梁结构的支撑位置进行了优化设计。智友海等[7]基于疲劳累积损伤的破坏准则,通过 Ansys 软件中所提供的蒙特卡罗可靠性分析方法,对管路在随机振动激励下系统的可靠性进行了优化分析,得到了满足要求的可靠性优化设计方案。刘伟等[8]对发动机管路的卡箍位置进行了动力灵敏度分析,结合有限元分析法分别以结构基频最大化、随机振动响应最小化为目标,对管路系统的卡箍位置进行了优化设计,结果表明:某些卡箍位置信息对管路的性能影响更明显。李鑫等[9]针对飞机液压管路的卡箍布局问题,建立了管路的数学模型并利用传递矩阵法得到了频域特征阻抗的变化规律,以激振源的固有频率特征阻抗的加权和为单一目标函数,运用粒子群算法对管路卡箍位置进行了优化,取得了较好的效果。另外,近年来一些学者开始探索对管路卡箍多目标布局优化问题进行研究,例如:刘周[10]以调频、调幅、总轴向应力和卡箍的重量为优化目标,应用改进的多目标遗传算法对发动机管路卡箍布局进行了优化设计,但该方法的不足是算法在每次进化时都需要运用有限元分析程序计算每个个体的适应值,计算代价大且比较耗时。
在现有的管路卡箍布局方法中,主要存在如下问题:1) 多数文献只考虑单个优化目标或将多个优化目标采用线性加权的方式将其转化为单目标,并未在本质上解决管路卡箍布局问题的多目标优化属性;2) 优化效率较低,在进化过程中需要反复应用CAE分析程序对适应值函数进行评价;3) 虽然已有较多文献对管路振动性能进行了深入分析,但管路卡箍布局规划方面的研究还相对较少。本文从多目标优化的角度出发,提出一种基于Kriging模型和NSGA-II算法的航空发动机管路卡箍规划方法。该方法以管路系统的一阶和二阶固有频率为优化目标,分别对其建立Kriging代理模型,并应用NSGA-II算法对发动机管路卡箍布局的Pareto解集(非支配解集)进行求解,以避免共振并提高系统的稳定性。在算法进化过程中,应用所建多代理模型代替CAE分析程序对适应值函数进行评价。
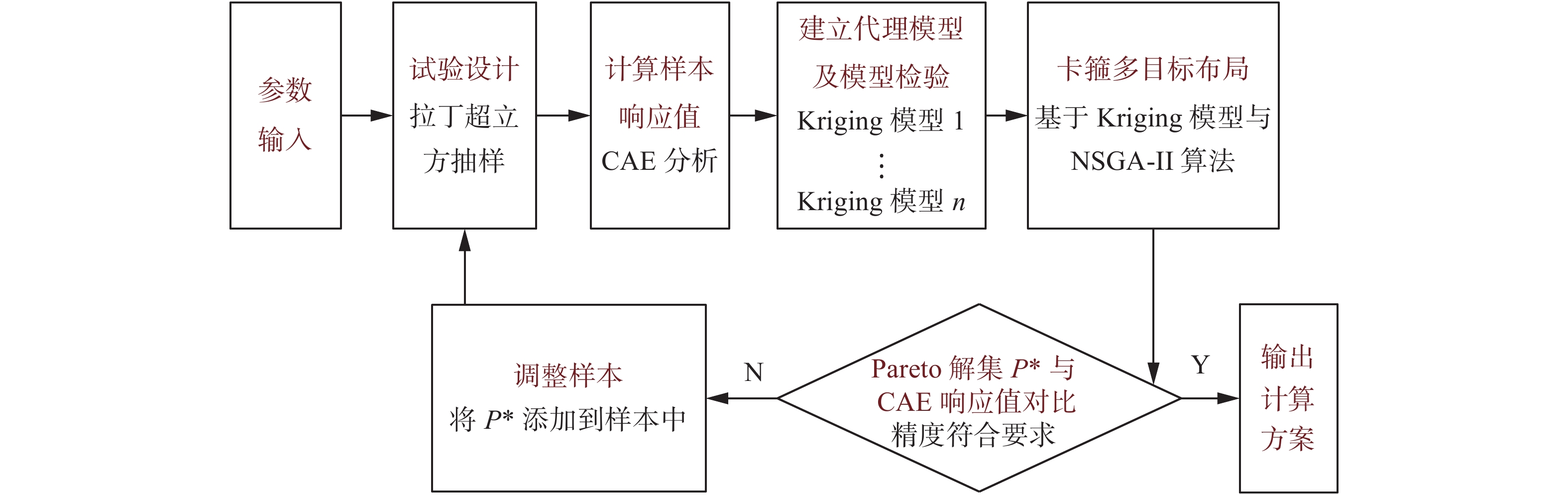
1 总体设计对于发动机管路设计而言,卡箍位置的变化对管路的动力学特性有着很大影响。因此在管路卡箍布局的优化设计中,主要目标是通过对卡箍位置的优化设计来减少管路振动并降低能量损失,从而提高管路的动力学特性,保证管路各方面性能达到最优。本文的总体设计思路如图1所示。
|
Download:
|
| 图 1 总体设计 Fig. 1 Overall design | |
总体设计主要步骤如下:
1) 建立UG模型,采用拉丁超立方抽样产生管路卡箍位置的试验样本。
2) 应用UG高级仿真模块的有限元分析计算方法,对样本点进行模态分析,得到样本响应值。
3) 根据样本及样本响应值分别建立Kriging近似模型并进行模型精度检验。
4) 基于Kriging代理模型和NSGA-II算法对管路卡箍位置进行多目标优化,最后进行验证、输出计算结果。
2 试验设计及Kriging代理模型 2.1 试验设计试验设计是数理统计学的应用方法之一,它的主要内容是讨论如何合理地安排试验、取得数据,然后进行综合的科学分析,从而达到尽快获得最优方案的目的。拉丁超立方抽样[11]是一种多维分层抽样方法,其可随机地产生尽量分布均匀的样本点,同时样本数量可以设定,因此在试验设计领域应用广泛[12]。
本文采用拉丁超立方抽样产生管路卡箍位置的试验样本。由于管路卡箍位置分布的变化性,因此将卡箍位置用每个卡箍距离管路右端点的长度来表示。假设采用双卡箍布局,卡箍位置距离管路右端点的长度分别为

|
Download:
|
| 图 2 试验样本 Fig. 2 Test sample | |
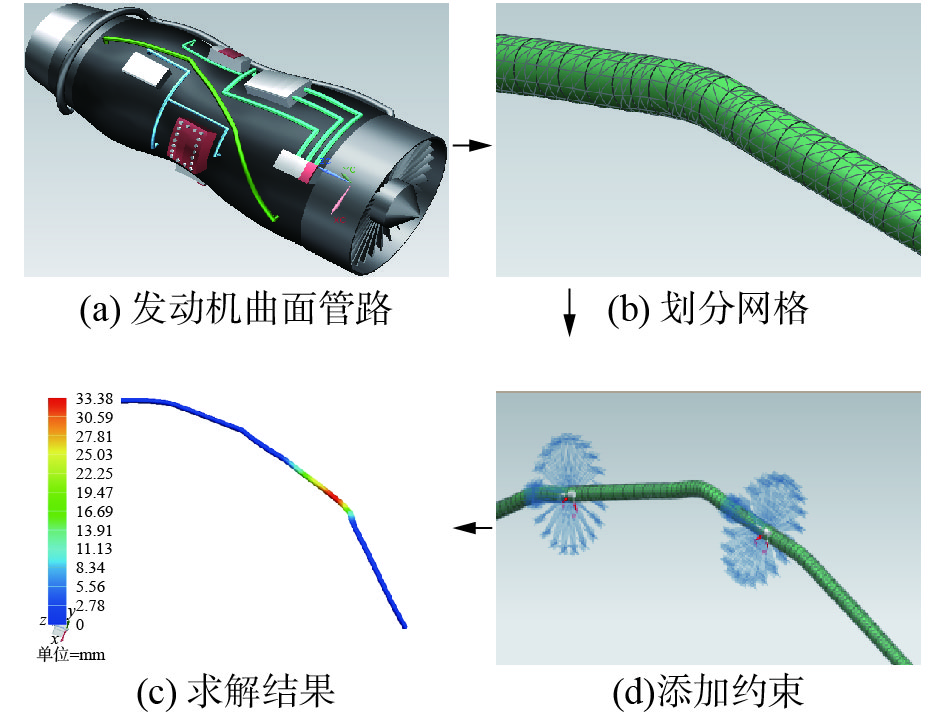
考虑到发动机管路设计领域均采用UG软件进行建模的行业惯例,为提高系统集成化程度,本文采用UG高级仿真功能进行CAE分析。此外,不同于一般的直管,本文所用的发动机曲面管路是基于B样条曲线形成的弯管,如图3(a)所示,其弯曲程度取决于发动机机匣表面的弯曲程度。根据管路卡箍位置的试验样本值建立UG模型,管路材料为Alloy steel,弹性模量为210 GPa,泊松比为0.28,密度为7 700 kg/m3。然后对所建模型进行模态分析,如图3所示,具体步骤如下:
|
Download:
|
| 图 3 模态分析示意 Fig. 3 Schematic diagram of modal analysis | |
1) 进行网格划分。选用十节点四面体单元,单元大小为1.5 mm,整个管路使用了35 470个节点, 19 976个单元,结果如图3(b)所示。
2) 添加约束。在管路两端添加固定约束,在卡箍位置处添加圆柱形约束(暂不考虑卡箍的刚度),固定其径向和轴向增长,如图3(d)所示。
3) 进行求解,记录数据。使用UG软件高级仿真的NX NASTRAN求解器,解算方案类型为SOL 103 Real Eigenvalues。求解完成后,记录管路的一阶固有频率和二阶固有频率,求解结果如图3(c)所示。
2.2 Kriging模型的基本原理近似模型是指根据样本点及其响应值构造的计算结果与仿真分析或实际试验结果相近的数学模型。它的主要优点[13-14]是效率高且计算代价小。作为一种常用的近似模型,Kriging模型最早由Sacks[15]应用于计算机试验设计与分析领域,其基本原理[16]可以简要表述如下:设近似函数为
| $y(x) = F(\beta ,x) + Z(x)$ | (1) |
式中:
此外,由于本文为多目标优化问题,因此需要分别对管路一阶固有频率和二阶固有频率建立Kriging模型,并在优化计算过程中,应用所建立的Kriging模型代替CAE分析程序对适应值函数进行评价,从而提高优化效率。
3 基于Kriging模型和NSGA-II的管路卡箍布局优化 3.1 NSGA-II简介NSGA-II是Deb等[18]在2002年对其算法NSGA的改进算法,它是目前多目标优化领域应用最广泛的算法之一。相对于NSGA而言,NSGA-II的主要特点包括:1) 使用一种新的快速非支配解排序方法,有效降低了计算的复杂度。2) 应用拥挤度的概念,克服了NSGA中需要人为指定共享参数的缺陷,从而使得个体能够扩展到整个Pareto前沿面并尽可能的均匀分布。3) 采用精英保留机制,不但扩大了采样空间,而且可以保证优良个体在进化过程中不会丢失,有效提高了种群的进化效率。
3.2 优化目标及编码设计 3.2.1 优化目标为避免管路在工作过程中与外部激励发生共振,在设计时要求卡箍安装后的管路系统工作时的固有频率在共振范围外,一般要求在发动机转速的20%以外。此外,在优化算法的设计中,约束条件和优化目标是可以相互转化的。因此本文将管路系统的一阶和二阶固有频率与发动机转动频率的差值分别作为优化目标:
| $\min \left\{ \begin{array}{l} {f_1}(x) = - |\Delta {w_1}| = - |{w_1} - {w_e}|\\ {f_2}(x) = - |\Delta {w_2}| = - |{w_2} - {w_e}| \end{array} \right.$ | (2) |
式中:
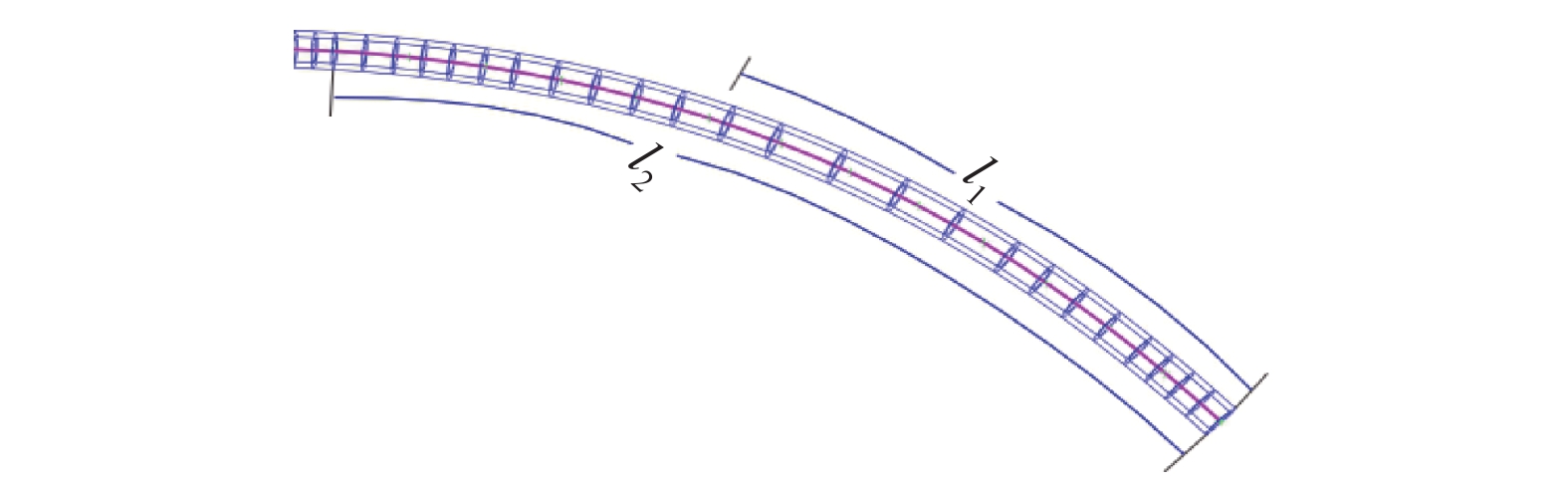
卡箍位置通常可用每个卡箍布置点距离管路右端点的长度来表示,如文献[8, 10]均采用了该编码方式。由于本文研究对象为发动机机匣表面弯管,管路中心线是一条曲线。以2.1节中所述的双卡箍为例,卡箍距离管路右端点的曲线长度可由曲线积分求得,如式(3)、(4)所示,也可通过UG软件中的求弧长的工具来求得,如图4所示。
| ${l_1} = \int_{{\varGamma _1}} {{\rm d}s} $ | (3) |
| ${l_2} = \int_{{\varGamma _2}} {{\rm d}s} $ | (4) |
式中:
| $\left[ \begin{array}{l} {l_{11}}\,\,\,\,{l_{12}}\,\,\,\, \cdots \,\,\,\,{l_{1n}}\\ \qquad\;\;\;\vdots \\ {l_{i1}}\,\,\,\,{l_{i2}}\,\,\,\, \cdots \,\,\,\,{l_{in}}\\ \qquad\;\;\;\vdots \\ {l_{M1}}\,\,\,\,{l_{M2}}\,\,\,\, \cdots \,\,\,\,{l_{Mn}} \end{array} \right]$ |
式中:
|
Download:
|
| 图 4 卡箍布置点距离管路右端点的曲线长度 Fig. 4 The curve length of clamp placement distance line right endpoint | |
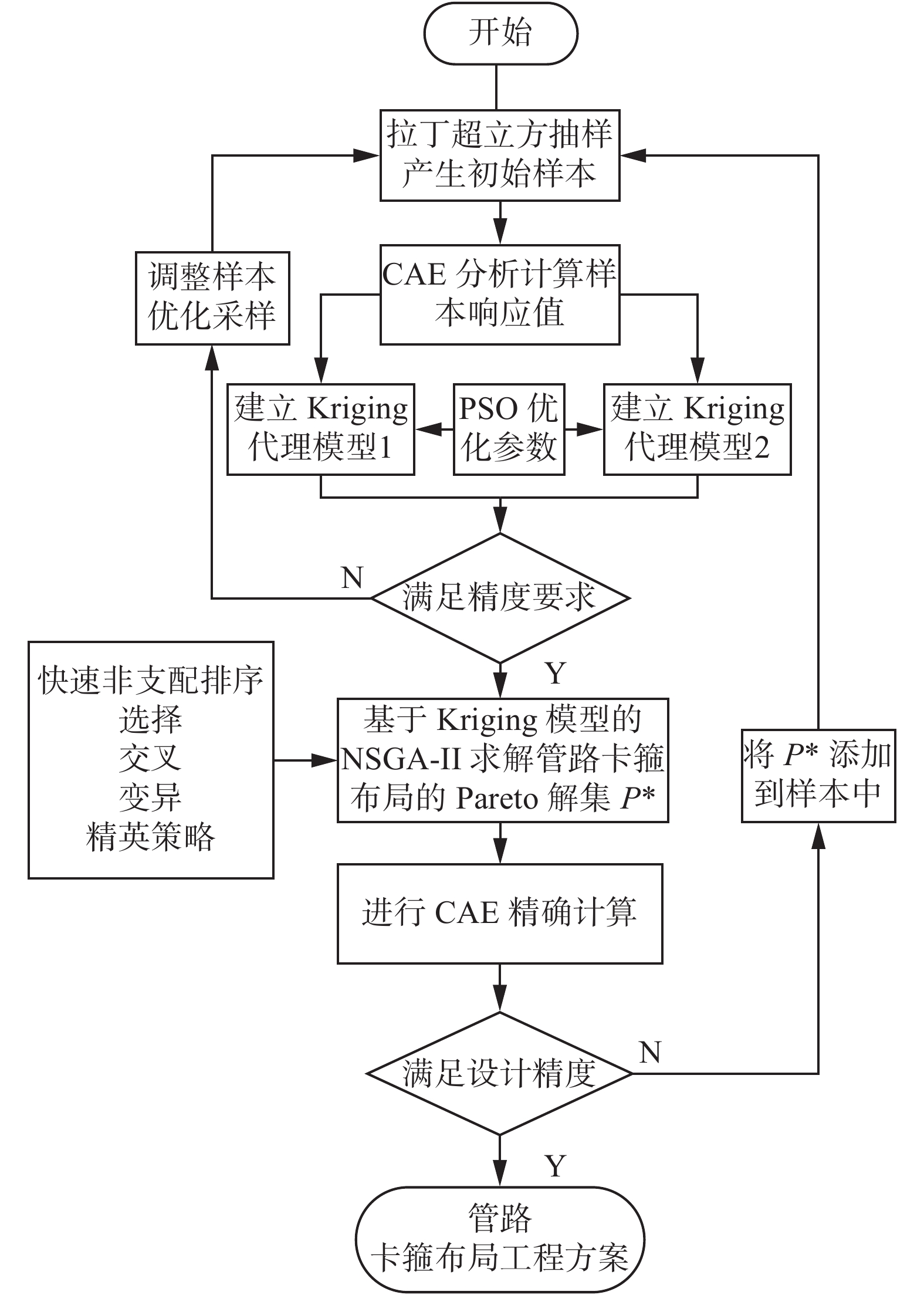
管路卡箍布局仿真实验通过MATLAB与UG联合实现,其中,UG实现三维建模及有限元分析计算,MATLAB建立Kriging模型和实现算法寻优。其总体流程如图5所示。
|
Download:
|
| 图 5 算法流程图 Fig. 5 Algorithm flow chart | |
为了验证所提方法的可行性,对所提方法进行了发动机管路卡箍多目标优化布局仿真实验。测试计算机硬件环境:CPU为 3.20 GHz Intel(R)core(TM) i5-4460,内存4 GB。仿真软件为MATLAB R2010a和UGNX10.0。
4.1 卡箍布局仿真采用双卡箍布局,管路长度为
|
Download:
|
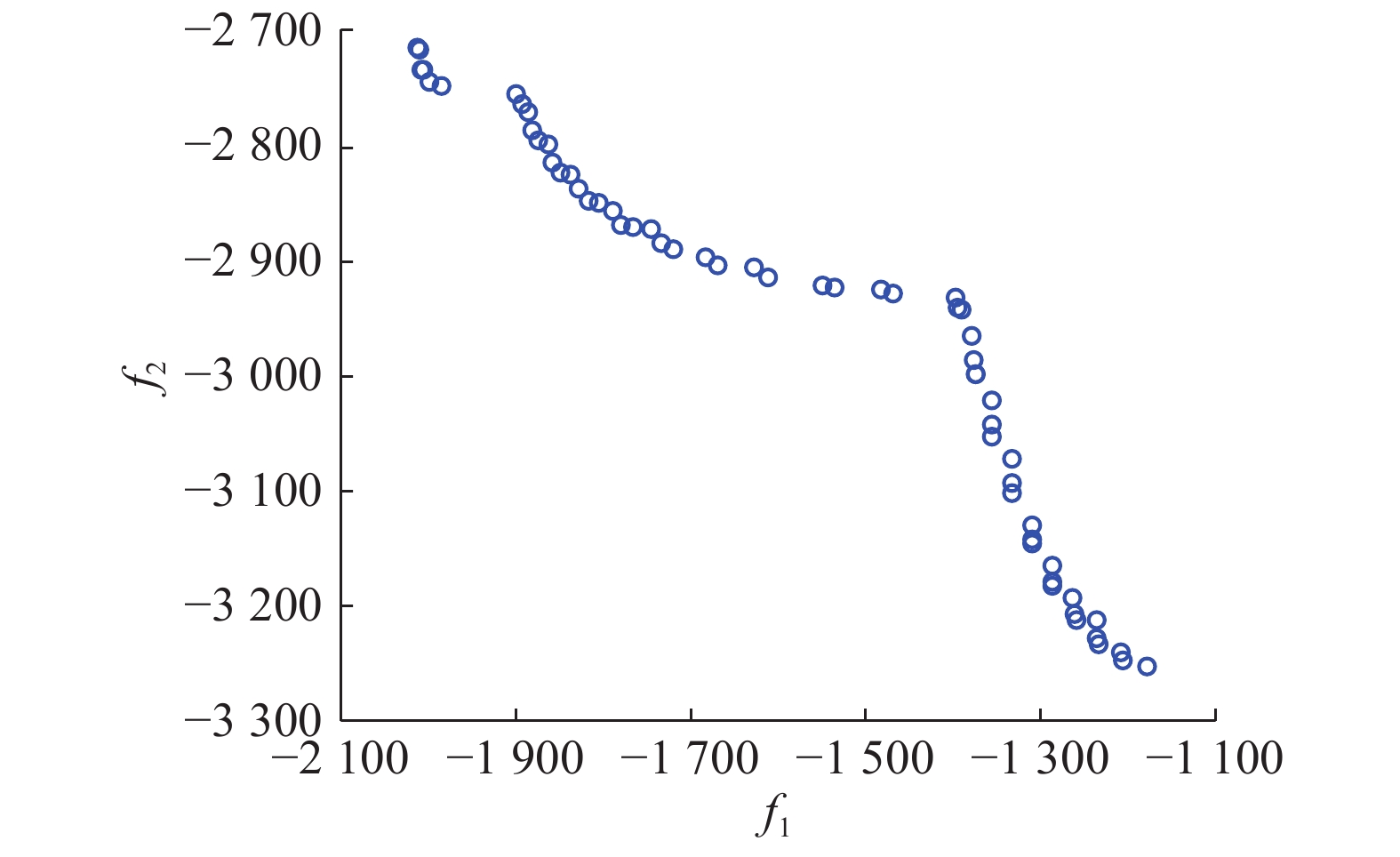
| 图 6 发动机管路卡箍布局的Pareto解集前沿面 Fig. 6 Pareto set front surface of engine pipe clamp layout | |

|
Download:
|
|
图 7 |
|
| 表 1 发动机管路卡箍布局Pareto解集部分典型个体信息 Tab.1 Typical individual information of the Pareto solution set of the engine pipe clamp layout |
|
Download:
|
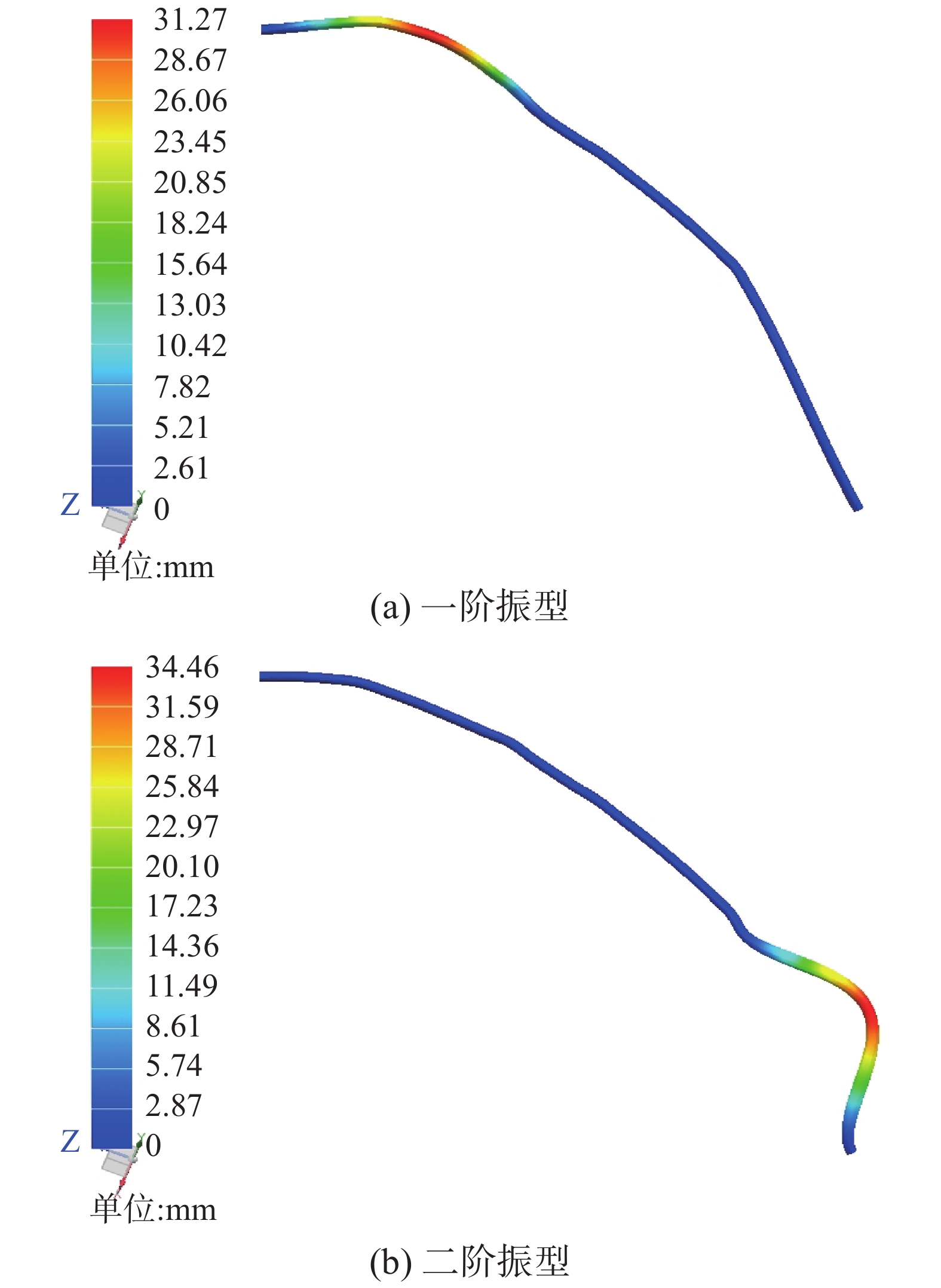
| 图 8 非支配解1 Fig. 8 Non-dominated solution 1 | |

|
Download:
|
| 图 9 非支配解2 Fig. 9 Non-dominated solution 2 | |
|
Download:
|
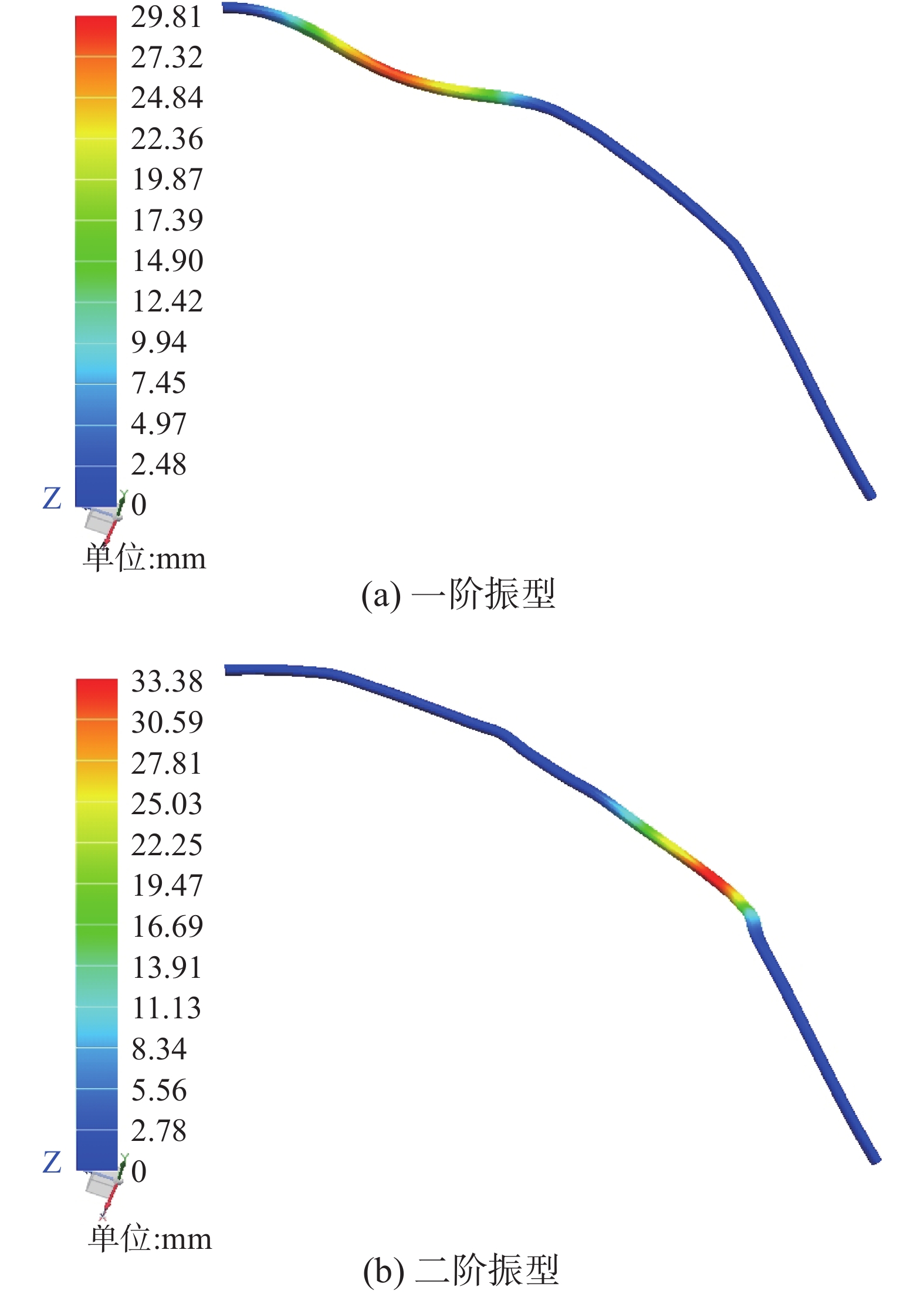
| 图 10 非支配解3 Fig. 10 Non-dominated solution 3 | |
由图7可知,所得到的最优卡箍位置分布在如表2所示的3个区间内。最终结果表明:在发动机管路卡箍多目标布局优化中,得到的一组Pareto解集不仅使管路系统工作时的固有频率在发动机转速的20%以外,而且尽可能的远离共振范围,从而提高了管路系统的稳定性,同时设计者可以根据需要选取合适的卡箍布局方案。
| 表 2 卡箍位置的最优区间 Tab.2 Optimal range of clamp position |
计算完成后,对结算结果进行误差分析,分析结果如表3所示。由Kriging模型所得到的结果和由CAE分析程序所计算得到的结果相比,一阶固有频率
| 表 3 计算结果的误差分析 Tab.3 Error analysis of calculation results |
表3中,
进一步,建立Kriging模型的样本数量为100,对管路进行一次模态分析和有限元计算所需时间大约为1 min,建立管路卡箍布局的Kriging模型需要约100 min。NSGA-II算法种群大小为100,迭代次数为100,基于Kriging模型的NSGA-II计算时间仅需0.6 min,因此基于Kriging模型和NSGA-II的优化方案总计耗时约100.6 min。若在NSGA-II进化时对每个个体都使用有限元分析计算出个体的适应值,则需要耗时
1) 本文提出了一种基于Kriging模型和NSGA-II算法的航空发动机管路卡箍多目标布局优化方法,以管路一阶固有频率和二阶固有频率为优化目标,应用NSGA-II对管路卡箍位置进行布局规划以避免共振,提高管路系统的稳定性。
2) 通过建立Kriging代理模型,避免了在优化过程中反复使用CAE分析程序对适应值函数进行评价,因此显著提高了优化效率。
3) 与传统的管路卡箍布局方法相比,本文所提方法可以得到一组非支配解集,设计人员可以根据工程经验选择适当的管路卡箍布局方案。
4) 所提方法具有很好的通用性,既适用于发动机管路卡箍布局,也适用于其他域的管路支撑部件布局问题,所用CAE软件可以根据行业特点选择Ansys、Cosmos、Pro/ENGINEER等。
| [1] |
何宇廷, 杨少华, 冯立富. 飞机地面压力加油系统导管卡箍固定间距的确定[J]. 机械科学与技术, 2000, 19(5): 726-728. HE Yuting, YANG Shaohua, FENG Lifu. On the determination of fixture intervals of pipe hoops of aircraft ground pressure refueling system[J]. Mechanical science and technology, 2000, 19(5): 726-728. DOI:10.3321/j.issn:1003-8728.2000.05.014 (  0) 0)
|
| [2] |
顾文彬. 舰船管路系统在振动环境下弹性支承的位置优化研究[D]. 上海: 同济大学, 2000. GU Wenbin. The position optimizing of ship’pipe system support under vibration excitation[D]. Shanghai: Tongji University, 2000. (  0) 0)
|
| [3] |
ZHU Jihong, ZHANG Weihong. Maximization of structural natural frequency with optimal support layout[J]. Structural and multidisciplinary optimization, 2006, 31(6): 462-469. DOI:10.1007/s00158-005-0593-2 ( 0) 0)
|
| [4] |
尹泽勇, 陈亚农. 卡箍刚度的有限元计算与实验测定[J]. 航空动力学报, 1999, 14(2): 179-182. YIN Zeyong, CHEN Yanong. Finite element analysis and experimental measurement of stiffness of hoop[J]. Journal of aerospace power, 1999, 14(2): 179-182. DOI:10.3969/j.issn.1000-8055.1999.02.015 (  0) 0)
|
| [5] |
WANG D, JIANG J S, ZHANG W H. Optimization of support positions to maximize the fundamental frequency of structures[J]. International journal for numerical methods in engineering, 2004, 61(10): 1584-1602. DOI:10.1002/(ISSN)1097-0207 ( 0) 0)
|
| [6] |
WANG D. Optimization of support positions to minimize the maximal deflection of structures[J]. International journal of solids and structures, 2004, 41(26): 7445-7458. DOI:10.1016/j.ijsolstr.2004.05.035 ( 0) 0)
|
| [7] |
智友海, 史向平. 飞机管路系统卡箍位置的可靠性优化设计[J]. 飞机设计, 2010, 30(6): 75-80. ZHI Youhai, SHI Xiangping. Reliability optimization designs of clamp's locations for airplane pipeline system[J]. Aircraft design, 2010, 30(6): 75-80. DOI:10.3969/j.issn.1673-4599.2010.06.016 (  0) 0)
|
| [8] |
刘伟, 曹刚, 翟红波, 等. 发动机管路卡箍位置动力灵敏度分析与优化设计[J]. 航空动力学报, 2012, 27(12): 2756-2762. LIU Wei, CAO Gang, ZHAI Hongbo, et al. Sensitivity analysis and dynamic optimization design of supports’ positions for engine pipelines[J]. Journal of aerospace power, 2012, 27(12): 2756-2762. (  0) 0)
|
| [9] |
李鑫, 王少萍. 基于卡箍优化布局的飞机液压管路减振分析[J]. 振动与冲击, 2013, 32(1): 14-20. LI Xin, WANG Shaoping. Vibration control analysis for hydraulic pipelines in an aircraft based on optimized clamp layout[J]. Journal of vibration and shock, 2013, 32(1): 14-20. DOI:10.3969/j.issn.1000-3835.2013.01.004 (  0) 0)
|
| [10] |
刘周. 多目标遗传算法及其在管路卡箍布局优化设计中的应用研究[D]. 武汉: 武汉理工大学, 2014. LIU Zhou. Research on multi-objective genetical algorithm and its application in optimal design of piping clamp layout[D]. Wuhan: Wuhan University of Technology, 2014. (  0) 0)
|
| [11] |
MCKAY M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 2000, 42(1): 55-61. DOI:10.1080/00401706.2000.10485979 ( 0) 0)
|
| [12] |
李耀辉. 基于Kriging模型的全局近似与仿真优化方法[D]. 武汉: 华中科技大学, 2015. LI Yaohui. The Kriging-based global approximation and simulation optimization methods[D]. Wuhan: Huazhong University of Science and Technology, 2015. (  0) 0)
|
| [13] |
韩永志, 高行山, 李立州, 等. 基于Kriging模型的涡轮叶片多学科设计优化[J]. 航空动力学报, 2007, 22(7): 1055-1059. HAN Yongzhi, GAO Hangshan, LI Lizhou, et al. Kriging model-based multidisciplinary design optimization for turbine blade[J]. Journal of aerospace power, 2007, 22(7): 1055-1059. DOI:10.3969/j.issn.1000-8055.2007.07.006 (  0) 0)
|
| [14] |
韩鼎, 郑建荣, 周骏彦. Kriging模型并行加点策略的多目标优化方法[J]. 机械科学与技术, 2016, 35(11): 1715-1720. HAN Ding, ZHENG Jianrong, ZHOU Junyan. A multi-objective optimization method using Kriging model and parallel point adding strategy[J]. Mechanical science and technology for aerospace engineering, 2016, 35(11): 1715-1720. (  0) 0)
|
| [15] |
SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical science, 1989, 4(4): 409-423. DOI:10.1214/ss/1177012413 ( 0) 0)
|
| [16] |
李小刚, 程锦, 刘振宇, 等. 基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J]. 机械工程学报, 2014, 50(3): 165-173. LI Xiaogang, CHENG Jin, LIU Zhenyu, et al. Robust optimization for dynamic characteristics of mechanical structures based on double renewal Kriging model[J]. Journal of mechanical engineering, 2014, 50(3): 165-173. (  0) 0)
|
| [17] |
柳强, 王成恩. 基于Kriging模型的复杂产品管线敷设顺序粒子群优化[J]. 机械工程学报, 2011, 47(13): 140-146. LIU Qiang, WANG Cheng’en. Kriging model-based routing sequence planning for complex products by particle swarm optimization[J]. Journal of mechanical engineering, 2011, 47(13): 140-146. (  0) 0)
|
| [18] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


