当今正处于信息智能时代,电子元器件犹如构筑起这个时代的一块块砖瓦,唯有对这些砖瓦的质量进行保证,才能坚固地铸就属于这个时代的智能大厦,贴片电阻也不例外。工厂生产出来的贴片电阻,首先需要对其进行缺陷识别、极性方向识别、正反面识别和种类识别,才能保证贴片电阻的出厂质量,因此,生产企业迫切需要一种可行的贴片电阻识别检测方法,截至目前,虽然已经有论文提出针对贴片电阻缺陷进行识别的方法,但生产企业由于其识别性能原因依旧没有广泛的使用,贴片电阻在实际生产过程中的缺陷识别、方向识别等还是依靠人工肉眼进行识别检测,不仅检测速度慢,而且长期成本高、误检率高。
针对上述问题,学者们提出的很多理论方法均可在贴片电阻识别中进行应用,比如模板匹配算法[1-2]、PCA(主成分分析)法[3-4]、Canny边缘检测算法[5]、B样条小波多尺度积边缘检测算法[6]、自适应阈值SUSAN边缘算法[7]等,通过使用这些方法首先对贴片电阻图片进行特征提取,然后将提取出的特征通过一个分类器进行识别分类,比如支持向量机[8]、决策树[9]、贝叶斯分类器[10]等进行分类。上述过程从本质上来讲,就是通过人为的方式构造专家系统和知识库对贴片电阻图片进行特征抽取,将高度相关的数据编码形式解耦成易于分类的低维数据形式,随后将提取出的低维数据向量通过一个分类器进行识别分类。上述系统的识别性能很大程度上取决于前半部分专家系统的构造,即对特定论域问题是否提取出了有用的特征和是否将高维数据转换到易于分类的低维有效空间,通常要构造出一个专家知识系统是极其困难的,而且当研究论域一旦改变或者扩展,之前构造的专家系统又不得不重新进行构造,这样的再构造过程不仅是极其枯燥和乏味的,而且通常情况下其实际效果也并不是事先所预想的那样。
然而,上述问题可以通过卷积神经网络的方法进行特征提取,从而避免繁琐的专家知识系统的构造。神经网络早在20世纪40年代就已经被提出,其作为连接主义智能实现的典范,是当今人工智能深度学习方法的重要思想源泉,也是当前类脑智能研究中的有效工具[11]。自2006年以来,Hinton等在《科学》上发表文章将神经网络推向了深度学习时代[12],指出一个训练好的多层神经网络可以将高维的数据转换成低维的数据编码形式,提出一种Pre-Training[13]的方法初始化权重,使其更加接近全局最小,随后再通过梯度下降法来Fine-Turning网络权重值,证明了采用这样的方法训练的网络比PCA方法更好;同时也证明了在参数相同的情况下,一个更深的网络结构在测试数据集上具有更低的错误识别率,但这种优势会随着权值参数的增多而逐渐消失。Hinton所证明的结论为后续网络模型设计提供了理论依据。而LeCun所提出的卷积神经网络架构,是一个真正意义上的深度网络架构[14],其不同于传统的全连接式的受限制波尔兹曼机,并在图像识别领域中取得了许多振奋人心的结果,通过端到端的训练,能够自学习出易于分类的低维特征,完全避免了人为专家知识系统的构造,与其相反所带来的代价是训练样本数据的收集。Hinton所证明的结论对于真正意义的深度网络模型是有效的,对于全连接式的深度网络模型并不适用,全连接网络总是会陷入过拟合现象,使得实际泛化效果并不理想。因此,选择识别性能更优的卷积神经网络用于贴片电阻识别,充分借鉴前人思想设计卷积神经网络,尽可能精简整个卷积神经网络的可训练参数从而保证识别速度,基于此,对比研究得出了3种不同卷积神经网络结构在贴片电阻识别任务中的实际效果。
1 贴片电阻识别任务分析从企业中调研可以发现,贴片电阻识别问题是一个复杂的多分类任务问题。图1所示贴片电阻图片来源于工厂实际拍摄,图中贴片电阻分类情况由工厂中经验丰富的工人所提供,图1(a)为50型号反面缺角缺陷,图1(c)为50型号正面涂层缺角缺陷,图1(e)为50型号反面腐蚀缺陷,图1(g)为正面字迹不清缺陷,其余4张图片为无缺陷电阻面。另一方面,假设贴片电阻已经做了外观缺陷检查,通过的合格电阻在自动编带时还需确保正反面、方向的一致性,因此需要对贴片电阻正反面和方向进行识别,由于企业生产的贴片电阻型号种类繁多,如图2所示,尺寸一样表示同一种封装形式的贴片电阻,故还需要对贴片电阻种类进行识别。

|
Download:
|
| 图 1 一种典型电阻型号需识别种类数 Fig. 1 A typical resistance type is required to identify the number of categories | |

|
Download:
|
| 图 2 需要识别的不同型号的贴片电阻示意 Fig. 2 Different types of chip resistors that need to be identified | |
因此,为了覆盖上述识别的所有情况,通过在实际工厂中拍摄大量的贴片电阻图片,再经过人工严格筛选和预处理算法处理之后,本文制作出了包含29种类别的贴片电阻数据样本集。类别标签1~13主要是电阻缺陷识别,14~29主要是方向、正反面以及种类识别,总的贴片电阻样本数量为1 044张,每一类别包含36张样本,经过预处理算法处理之后的图片,每张图片被剪切为320×320像素大小,贴片电阻居于图像正中位置,贴片电阻以外其余的像素点全部被置零为黑色背景,即清除了贴片电阻图像背景特征。在后续的实验中,每一类别均随机选取5张电阻图片用于准确率测试,其余的贴片电阻均作为训练样本,详细数据集及标签类别对应情况如图3和表1所示,图3中相邻两张图片为一个类别,以阅读的顺序与表1中的标签依次对应(如图3中第一行前两张图片对应标签为1,所属类别为50型号反面弹珠缺陷)。

|
Download:
|
| 图 3 预处理后的29种贴片电阻图片样例 Fig. 3 Samples of 29 kinds of chip resistors after preprocessing | |
| 表 1 实验详细数据表 Tab.1 Experimental detailed data sheet |
当前主流的3种用于模式识别的卷积神经网络模型——AlexNet模型[15]、GoogLeNet模型[16-17]、ResNet模型[18-19],分别在2012年、2014年、2015年的ILSVRC竞赛中取得第一名的成绩,其模型架构思想可以用图4进行概括,图中卷积层实现特征提取,全连接层实现特征分类。

|
Download:
|
| 图 4 常见卷积模型图 Fig. 4 Common convolution model diagram | |
卷积神经网络模型首先由LeCun所提出,其卷积过程类似于对图像抽取特征的各种算子,如Sobel算子、Laplace算子。算子的卷积过程:
| $\begin{array}{c} O(m,n){\rm{ = }}I(m,n)*H(m,n){\rm{ = }} \\ \displaystyle\sum\limits_{m = 0}^{M - 1} {\sum\limits_{n = 0}^{N - 1} {I(i,j)H(m - i,n - j)} }{\rm{ = }} \\ \displaystyle\sum\limits_{i = 0}^{I - 1} {\sum\limits_{j = 0}^{J - 1} {I(m - i,n - j)H(i,j)} } \\ \end{array} $ | (1) |
式中:I表示输入灰度图像;
| $\begin{gathered} {O^l}\left( {m,n} \right) = {I^k}\left( {m,n} \right) \otimes {H^{kl}}\left( {m,n} \right) = \hfill \\ \sum\limits_{k = 0}^{K - 1} {\sum\limits_{i = 0}^{I - 1} {\sum\limits_{j = 0}^{J - 1} {{I^k}\left( {m + i,n + j} \right){H^{kl}}\left( {i,j} \right)} } } \hfill \\ \end{gathered} $ | (2) |
式中:
根据神经科学的研究,存在一个阈值来控制神经元的选择性输出,从而增加整个神经系统的非线性特性和稀疏特性。数学家们将这样的阈值函数称为激活函数,早期的激活函数主要有Sigmoid函数和tanh函数两种,但二者均由于使梯度在反向传播过程中衰减过快而被人们所放弃,过快的梯度衰减与构造一个更深的卷积神经网络是矛盾的。因此人们提出了ReLU非线性激活函数[20],其表达式为
| $f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} x,&{x > 0} \\ 0,&{x \leqslant 0} \end{array}} \right.$ | (3) |
式(3)的激活函数不仅能够减少计算量,在一定程度上克服了梯度反向传播消失问题,并且增加了网络的稀疏性,因此而被广泛的使用。
2.3 Dropout(随机丢弃)层Dropout层是为了增加神经网络的稀疏性而特别设计的,其背后的理论依据是为了模仿大脑的稀疏特性。人脑的神经元大多处于抑制状态,只有不到10%的神经元处于活动状态,因此,人脑是一个典型的稀疏结构,每次训练网络通过选择性的丢弃某些神经元,使其不参与前向传播和反向传播过程,一方面可以增加网络的稀疏性,另一方面提供了正则化一大类模型的方法。
2.4 Pooling(池化)层Pooling层是为了快速降低特征图维度而设计的,从而减轻计算的负担。Pooling层通过汇总上一层特征图相邻神经元的输出,输出一个维度被降低的特征图。通过Pooling层的操作,模型计算量被减少,网络过拟合问题得到一定的缓解,网络整体性能也有所提升。常见的汇总操作有MAX和AVE,MAX操作为局部相邻神经元的最大值作为输出,AVE操作为局部相邻神经元的平均值作为输出,与图像均值滤波类似。
2.5 LRN(local response normalization)层LRN层为局部响应值归一化层,LRN层跟随在Pooling层之后,通过对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,保留关键特征,抑制非重要特征[15]。LRN层具体归一化公式如式(4)所示:
| $b_{x,y}^i = a_{x,y}^i/{\left( {k + \alpha \sum\limits_{j = \max (0,i - n/2)}^{\min (N - 1,i + n/2)} {{{\left( {a_{x,y}^j} \right)}^2}} } \right)^\beta }$ | (4) |
式中:
BatchNorm层为步长归一化层,卷积神经网络在读入训练数据和测试数据时,并不是每次只读取一张图片,而是一次读取一个Batch(步长)值的图片数据。这样就带来一个问题,深度神经网络每一层的输入分布在训练的时候会发生改变,导致卷积神经网络难以学习到数据中蕴藏的本质,这使得要训练这样的网络变得困难复杂,而这样的问题可以通过归一化每一层的输入来解决。BN的本质作用原理是强行将每一层输入分布的变化进行矫正,使得每一层输入在进行卷积之前保持零均值和单位方差[19]。使用BN层的深度网络结构,可以使用更高的学习率进行训练,而且也不用过多的关心训练权值初始化问题。实践证明加入BN层的深度网络不仅训练收敛速度极大提高,而且识别准确率也得到改善。
3 卷积模型架构设计Hinton证明了在参数相同的情况下,一个更深的网络结构在测试数据集上具有更低的错误识别率,但这种优势会随着权值参数的增多而逐渐消失,本文基于此理论依据,针对传统图像识别方法的局限性,结合AlexNet模型、GoogLeNet模型、ResNet模型思想和其突出的图像识别分类能力,设计了3种卷积神经网络模型用于识别贴片电阻图像,需同时保证设计模型的识别准确率和识别速度。
起初AlexNet模型被设计的目的是用于参加ILSVRC图像分类竞赛,同时消除人们对卷积神经网络识别性能的质疑。网络总共包含60M的可训练参数,主要是为了提升网络容量,应对包含千万张图像的ImageNet数据集,但贴片电阻识别并不需要如此巨大的可训练参数,这是因为贴片电阻数据并不像Imagenet数据集那样蕴含大量的特征,并且在实践中企业迫切希望使用少量的训练样本去达到非常理想的识别准确率,因此需要对已有模型可训练参数进行减少,防止过拟合现象。同时,贴片电阻识别既需要保证高识别准确率,也需要保证高识别速度,这就需要将卷积神经网络的深度控制在一个合理的范围之内。因此,设计的网络需从整体上进行“瘦身”,同理,另外2种模型的修改思路亦是如此,将修改后的3种模型可训练参数保持一致,可以方便比较他们的综合性能。
基于上述思想,由AlexNet模型思想修改后的网络依旧为8层深度,结构与原来保持不变,做出的改动是对原模型可训练参数进行了大量精简,可训练参数从原来的60×106降低为4×106左右,训练参数只有原来的1/15,详细参数设置如图5所示,图中参数设置含义为,比如(11×11卷积,48,/4)表示卷积核大小为11×11,输出特征图个数为48,卷积时滑动步长为4,没有写滑动步长表示默认为1,其他同理,后续网络中参数设置含义与此类似。

|
Download:
|
| 图 5 识别贴片电阻的8层经典卷积网络结构,可训练参数为4.07×106 Fig. 5 The 8-layer classical convolution network structure of identify the chip resistors with a training parameter of 4.07×106 | |
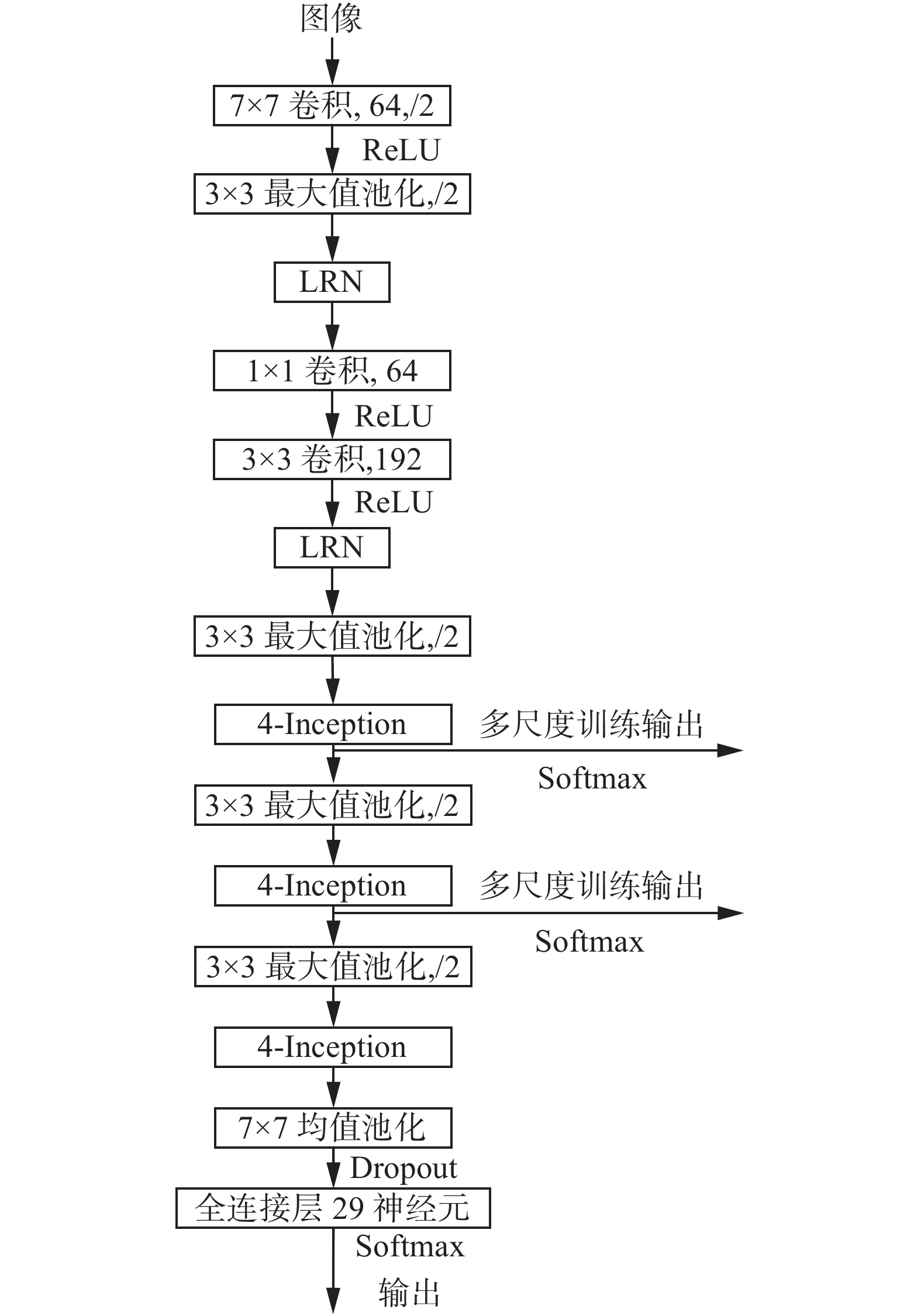
基于谷歌Inception结构思想设计的16层4-Inception网络如图6所示,模型中将两个Inception结构组合构成一个基本的结构单元,取名为4-Inception(参见图7),这样可以方便网络结构呈现。在4-Inception的卷积结构当中,卷积核大小全部使用1×1、3×3、5×5,参数设计思想是随着深度的增加,提取出的特征越来越抽象,每个特征所涉及的感受野(receptive field)越来越大。故网络越到后面,3×3、5×5卷积核比例相应增加,但卷积核的增加会带来巨大的训练参数和计算量,因此在进行卷积之前先进行1×1卷积降低特征图(通道)个数。为了克服连接器拼接特征图维度对齐问题,1×1、3×3、5×5卷积时要分别设定填充大小为0、1、2,则卷积后的尺寸保持不变,更易对齐。采用此结构设计的16层深度卷积网络,由于4-Inception基本结构单元比较复杂,需要利用多尺度的训练方法对其进行训练,从而提高网络训练收敛速度。图7中3个4-Inception结构参数详细设置见表2。
|
Download:
|
| 图 6 识别贴片电阻的16层深度4-Inception模型图,可训练参数为3.8×106 Fig. 6 The 16-layer depth 4-Inception model of identify the chip resistors with a training parameter of 3.8×106 | |
| 表 2 4-Inception详细参数设置 Tab.2 4-Inception detailed parameter settings |

|
Download:
|
| 图 7 谷歌Inception卷积结构 (4-Inception) Fig. 7 Google Inception convolution structure (4-Inception) | |
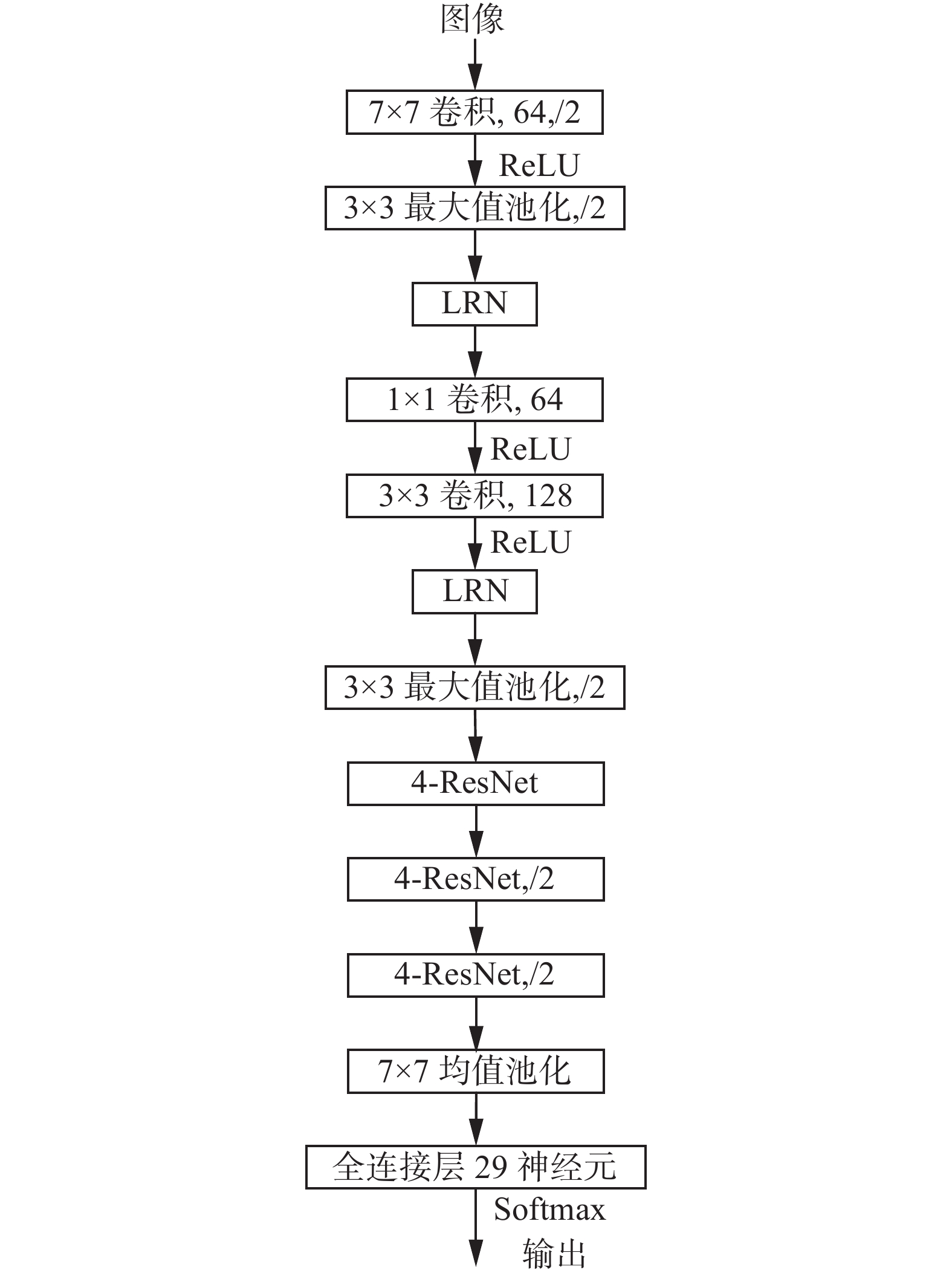
基于残差思想设计的16层4-ResNet网络如图8所示,图中4-ResNet详细结构如图9所示,该结构的主要思想是为了加深网络结构,克服梯度反向传播过程中梯度消失问题。对比本文16层深度4-Inception结构需要采用多尺度训练的方式,虽然能够很好地训练出网络模型,但同样深度的残差网络结构,直接采用端到端的训练方式,即可使网络快速收敛并取得很好的训练结果。从图9中很容易看出,梯度在反向传播的时候,求和后的函数的导数为
| $\frac{{\partial \left( {f(x) + x} \right)}}{{\partial x}} = \frac{{\partial f(x)}}{{\partial x}} + 1$ | (5) |
导数为1不会对梯度有任何的衰减,且直接跨越多个卷积层进行反向传播,和多尺度进行训练的方法有着异曲同工之妙,这就是残差网络能够快速收敛并取得良好训练结果的原因。图9中输入引出的1×1卷积可以使得第一次求和的特征图维度相同,残差结构的本质精髓就在于图9中所示的圆弧线,其能同时跨越多个(不一定是两个)卷积层。从图8中可以详细的看出模型的参数设置,4-ResNet结构中的卷积核参数全部设置成148。
|
Download:
|
| 图 8 识别贴片电阻的16层深度4-ResNet模型,可训练参数为4.0×106 Fig. 8 The 16-layer depth 4-ResNet model of identify the chip resistors with a training parameter of 4.0×106 | |
3种模型的输出神经元均被设置成29,这是由实验数据集包含29个类别所导致的,训练时均采用随机梯度下降法进行训练,选择Softmax回归模型对网络进行优化,权值更新公式为
| $\begin{array}{c} {v_{i + 1}} = 0.9 \times {v_i} - 0.000\;5 \times \varepsilon \times {w_i} - \varepsilon \times {\left\langle {{{\left. {\displaystyle\frac{{\partial L}}{{\partial w}}} \right|}_{{w_i}}}} \right\rangle _{{D_i}}} \hfill \\ {w_{i + 1}} = {w_i} + {v_{i + 1}} \hfill \end{array} $ | (6) |
式中:
假设贴片电阻存在
| $N = \sum\limits_{i = 1}^m {{n_i}} $ | (7) |
总的测试样本数为
| $T = \sum\limits_{i = 1}^m {{t_i}} $ | (8) |
总的识别错误数为
| $E = \sum\limits_{i = 1}^m {{e_i}} $ | (9) |
因此,总的贴片电阻识别准确率为
| ${\rm{acc}}\_{\rm{all}} = \left( {1 - \frac{E}{T}} \right)\times100{\text{%}} $ | (10) |
任意贴片电阻类别 的总识别错误率为
| ${\rm{err}}\_{\rm{all}} = {\frac{e_i}{T}}\times 100{\text{%}} $ | (11) |
任意贴片电阻类别
| ${\rm{acc}}\_i = \left( {1 - \frac{{{e_i}}}{{{t_i}}}} \right)\times 100{\text{%}} $ | (12) |

|
Download:
|
| 图 9 残差网络结构,取名4-ResNet Fig. 9 Residual network structure, named 4-ResNet | |
在贴片电阻姿态固定而位置随机情况下,设计的3种卷积神经网络模型对贴片电阻进行识别的准确率分析,实际中贴片电阻会被限制在一个导轨上进行运动,所拍摄的贴片电阻位置并不会都严格居于图像正中间,因此对贴片电阻随机位置的识别是与实际情况更加吻合的。
为了模拟贴片电阻在图像中位置随机的情况,每次迭代训练都进行随机截取256像素×256像素大小图片输入网络进行训练。原始数据集中每张图片为320像素×320像素大小是事先设计好的,这样总可以保证每次随机截取的256像素×256像素大小图片完全将贴片电阻信息包含在图像中。
整个实验过程基于Caffe深度学习框架,计算GPU显卡为GeForce GTX 1060 6 GB。执行训练时,训练步长(batch)为32张图片,迭代4次输出一次训练损失值,每训练20次执行一次准确率测试。测试步长(batch)为16张图片,测试迭代次数为10次。网络训练动量因子为0.9,初始学习率为0.01,权重衰减因子为0.000 5,学习率更新策略为默认方法。总的训练次数为7 200次,即训练周期约为240个(epoch)。
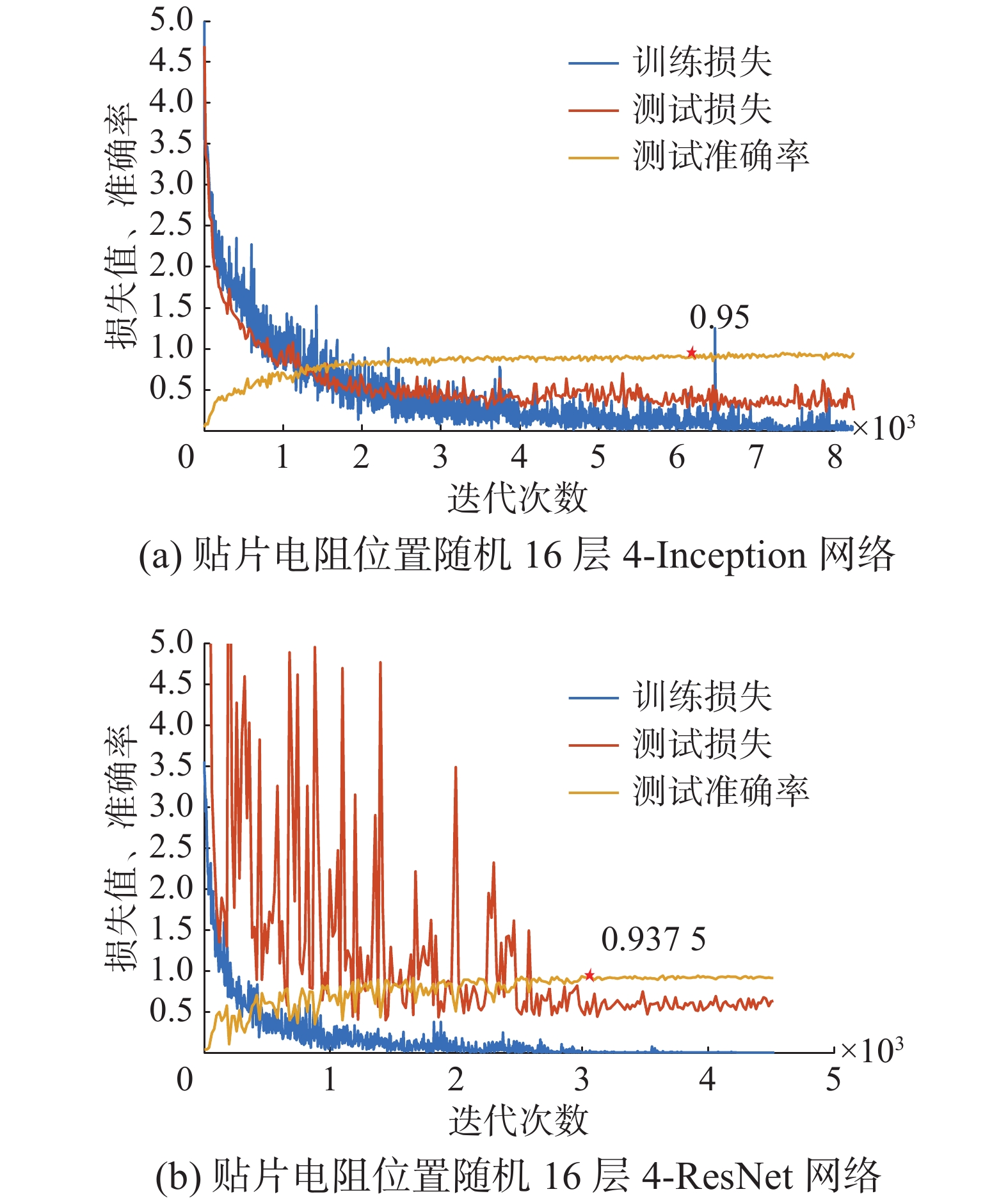
4.3 实验结果分析3种模型的训练结果分别如图10~11所示,可以看出,由于贴片电阻位置的随机性,识别准确率最高的为16层4-Inception网络,识别准确率达到95%,这说明层数更深的4-Inception网络更加擅长处理复杂情况下的图像识别,特征解耦更好,更适合贴片电阻识别分类任务。残差网络是收敛最快的网络结构,但其测试损失波动非常大并在迭代2 500次后趋于平稳,继续训练则是过拟合训练,因此实验时训练迭代次数未到7 200次则将其停止。

|
Download:
|
| 图 10 贴片电阻位置随机8层深度卷积模型训练结果 Fig. 10 Chip resistor position random 8-layer depth convolution model training results | |
|
Download:
|
| 图 11 网络训练结果 Fig. 11 Network training results | |
3种模型性能详细对比如表3所示,识别时间最快的是8层深度卷积网络,低至0.203 秒/张(256×256像素/COREI5),识别准确率最高的是16层4-Inception网络,识别准确率达95%,残差网络性能折中。
| 表 3 3种模型识别时间及准确率对比 Tab.3 Comparison of 3 model identification times and accuracy |
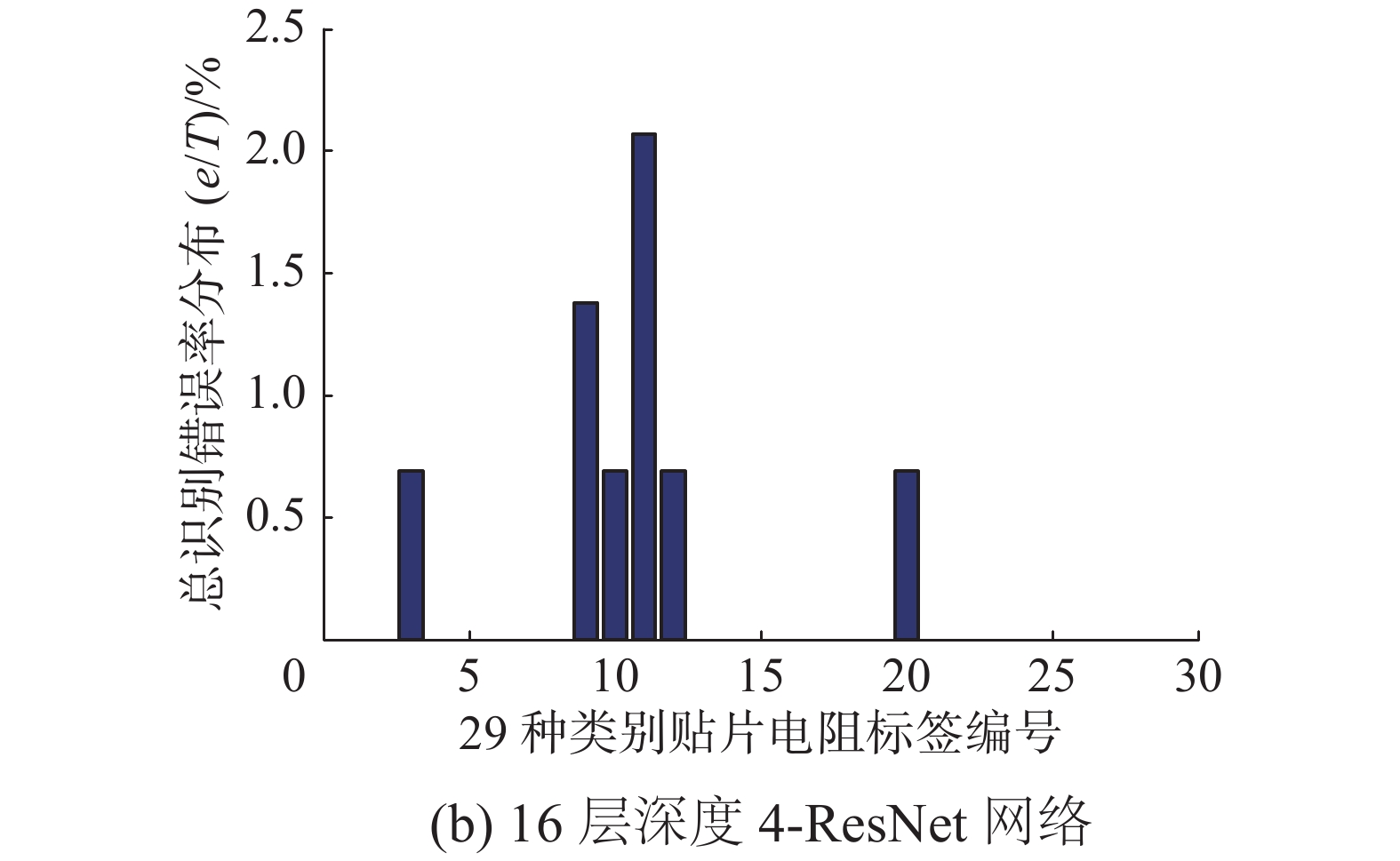
3种模型的泛化识别错误率分布如图12~13所示,可以看出,标签1~13主要属于缺陷类别识别,是识别错误率的主要来源。标签14~29主要识别正反面、方向和种类,3种模型均取得了非常理想的识别效果。图13(a)中的16层4-Inception模型,其仅在缺陷识别上存在一定的错误率,在种类、正反面和方向识别上取得了100%的识别准确率。

|
Download:
|
| 图 12 8层深度卷积网络总识别错误率分布 Fig. 12 Total error rate distribution of 8-layer deep convolutional networks | |
|
Download:
|
| 图 13 网络总识别错误分布 Fig. 13 Networks total error rate distribution | |
综上所述,当贴片电阻在图像中位置随机时,基于AlexNet思想“瘦身”后的8层深度卷积神经网络识别时间最短,16层4-Inception网络准确性更加突出,进一步提高识别准确率可适当增加缺陷样本的数量。
5 结束语本文基于AlexNet模型、GoogLeNet模型、ResNet模型思想设计了3种卷积神经网络模型,用于解决实际工业生产中贴片电阻识别问题,包括缺陷识别、方向识别、正反面识别和种类识别。实验表明,设计的3种卷积神经网络模型中,基于AlexNet模型思想“瘦身”后的卷积神经网络识别时间最短,识别时间低至0.203 秒/张(256×256像素,CORE I5),16层4-Inception网络准确性更加突出,总识别准确率达95%;16层4-ResNet网络性能折中,克服了当前主流卷积模型由于可训练参数过多、模型层数太深导致在贴片电阻识别应用中识别速度不能满足实时性要求、泛化识别准确率低的问题。上述3种卷积模型可根据具体实际需求进行选用,有望解决工业界贴片电阻分类依靠人工方式的难题。
| [1] |
GIUNCHIGLIA F, YATSKEVICH M. Element level semantic matching. Technical Report DIT-04-035[R]. Trento, Italy: Information Engineering and Computer Science, 2004.
( 0) 0)
|
| [2] |
OMACHI M, OMACHI S. Fast two-dimensional template matching with fixed aspect ratio based on polynomial approximation[C]//Proceedings of the 9th International Conference on Signal Processing. Beijing, China, 2008: 757–760.
( 0) 0)
|
| [3] |
JOLLIFFE I T. Principal component analysis[M]. New York, USA: Springer-Verlag, 1986.
( 0) 0)
|
| [4] |
ZHANG Xingfu, REN Xiangmin. Two dimensional principal component analysis based independent component analysis for face recognition[C]//Proceedings of 2011 International Conference on Multimedia Technology. Hangzhou, China, 2011: 934–936.
( 0) 0)
|
| [5] |
PELLEGRINO F A, VANZELLA W, TORRE V. Edge detection revisited[J]. IEEE transactions on systems, man, and cybernetics, part b (cybernetics), 2004, 34(3): 1500-1518. DOI:10.1109/TSMCB.2004.824147 ( 0) 0)
|
| [6] |
DUCOTTET C, FOURNEL T, BARAT C. Scale-adaptive detection and local characterization of edges based on wavelet transform[J]. Signal processing, 2004, 84(11): 2115-2137. DOI:10.1016/j.sigpro.2004.07.003 ( 0) 0)
|
| [7] |
SMITH S M, BRADY J M. SUSAN-a new approach to low level image processing[J]. International journal of computer vision, 1997, 23(1): 45-78. DOI:10.1023/A:1007963824710 ( 0) 0)
|
| [8] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [9] |
GUO H, GELFAND S B. Classification trees with neural network feature extraction[J]. IEEE transactions on neural networks, 1992, 3(6): 923-33. DOI:10.1109/72.165594 ( 0) 0)
|
| [10] |
GOLDSZMIDT M. Bayesian network classifiers[J]. Machine learning, 2011, 29(2/3): 598-605. ( 0) 0)
|
| [11] |
焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年: 回顾与展望[J]. 计算机学报, 2016, 39(8): 1697-1717. JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Seventy years beyond neural networks: retrospect and prospect[J]. Chinese journal of computers, 2016, 39(8): 1697-1717. (  0) 0)
|
| [12] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 ( 0) 0)
|
| [13] |
ERHAN D, MANZAGOL P A, BENGIO Y, et al. The difficulty of training deep architectures and the effect of unsupervised pre-training[C]//Appearing in Proceedings of the 12th International Conference on Artificial Intelligence and Statistics. Florida, USA, 2009: 153–160.
( 0) 0)
|
| [14] |
LECUN Y, BENGIO Y. Convolutional networks for images, speech, and time series[M]//ARBIB M A. The Handbook of Brain Theory and Neural Networks. Cambridge, MA, USA: MIT Press, 1998.
( 0) 0)
|
| [15] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems. Montreal, Canada, 2012: 1097–1105.
( 0) 0)
|
| [16] |
SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA, 2014: 1–9.
( 0) 0)
|
| [17] |
SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-v4, inception-resnet and the impact of residual connections on learning[J]. arXiv: 1602.07261, 2016.
( 0) 0)
|
| [18] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA, 2016: 770–778.
( 0) 0)
|
| [19] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on Machine Learning. Lille, France, 2015: 448–456.
( 0) 0)
|
| [20] |
GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]//Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, FL, USA, 2011: 315–323.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


