2. 物联网技术应用教育部工程技术研究中心,江苏 无锡 214122;
3. 江苏省模式识别与计算智能工程实验室,江苏 无锡 214122
2. Research Center of IoT Technology Application Engineering (MOE), Wuxi 214122, China;
3. Jiangsu Provincial Engineering Laboratory of Pattern Recognition and Computational Intelligence, Wuxi 214122, China
近年来,随着无线通信,计算机网络和传感器技术的巨大进步,无线传感器网络(wireless sensor networks,WSN)已成为重要的研究对象并被广泛应用于医疗、军事、环境监测等众多领域[1]。在环境监测领域,大规模的无线传感器网络通常被部署于无人监管、气候复杂的野外环境中。若长期使用,节点读数容易产生数据漂移。这对于终端用户来说是一个严重的问题,因为在无线传感器网络的大规模应用场景中必须使用精确数据,才能制定科学决策。因此,对节点数据进行漂移校准至关重要。然而,在许多大规模无线传感器网络的应用中,数百到数千个节点被分散部署到气候复杂的野外环境中,手动校准这些节点是非常困难的[2]。因此,需要自动跟踪和校准节点数据漂移的方法,现有的方法可以分为两类:盲校准和非盲校准。
非盲校准方法是基于传感器节点读数和已知的参考信息作为输入来调整参数[3]。一种简单的非盲校准方法是将已知的激励作用于传感器网络中并测量其响应,将网络响应与参考信息(网络预期值)进行比较,然后相应地调整参数。参考信息一般为出厂标准值或用户手动校准的结果。例如,Ramanathan等[4]采用额外的高精度节点读数作为参考信息。另一种类型的方法是手动校准一组节点,然后未校准节点组基于该组来调整参数[5]。非盲校准方法适用于特定空间(例如室内)小规模网络的场景下[6],然而在大规模无线传感器网络中,使用上述方法需要在每个阶段进行大量的工作,这是不切实际的且成本高昂。
鉴于非盲校准方法存在的局限性,盲校准方法得到了广泛的关注。许多盲校准方法是基于节点被密集部署的假设,因此当网络中未产生数据漂移时,节点间应具有相关的读数[7]。然而,在许多现有的大型网络中,由于环境因素和成本因素,可能无法实现节点的密集部署。Balzano等[8]首先提出了一种无需密集部署的校准方法,假定节点的测量位于测量空间的较低维信号子空间中,然后通过信号子空间投影将校准过程转换为求解线性方程。来自清华大学的杨华中等[9, 10]对这种方法进行了利用和扩充,取得了非常良好的实用价值。
基于相邻节点间具有相关测量值的假设,Takruri等[11]提出了一种分布式递归贝叶斯(distributed recursive Bayesian,DRB)盲校准算法,其使用邻居节点读数的平均值作为漂移节点的预测值。为了更好地拟合传感器节点间的时空相关性,Takruri等[12]又提出了一种基于支持向量回归(support vector regression,SVR)来预测真实值的方法。针对SVR可能存在的训练精度较低的情况,Kumar等[13]采用克里金插值作为预测方法,以避免SVR的训练阶段。这些方法基于节点间的时空相关性以预测节点数据的漂移,并都使用了卡尔曼滤波器(Kalman filter,KF)以跟踪漂移。然而,一旦预测值不精确,偏差较大的预测值也会被用来进一步校准漂移值,从而导致最终校准值的精度受累积误差的限制。
针对上述问题,本文提出了一种基于遗传算法(genetic algorithm,GA)优化的BP神经网络(BP neural network optimized by GA,GABP)与卡尔曼滤波器相结合的无线传感器网络数据漂移盲校准算法(GABP-KF)。该算法首先对节点读数进行二次采集和降噪处理。然后使用基于遗传算法优化的神经网络对目标节点和其邻居节点间的时空相关性进行数学建模,从而得到目标节点的预测值。最后将目标节点的预测值和测量值反馈入卡尔曼滤波器中以跟踪并校准其数据漂移。仿真结果表明,GABP-KF具有良好的漂移校准性能。
1 预备知识 1.1 遗传算法遗传算法是模拟自然界遗传机制的生物进化模型,是一种启发式随机搜索最优化方法。它将“物竞天择,适者生存”的进化原理和遗传变异理论引入编码串联群体中,即在每一次的进化过程中,按照所构造的适应度函数,通过选择操作、交叉操作和变异操作来对个体进行筛选,把适应度值好的个体传给下一代,反复循环,直到最终个体满足特定的条件表示进化结束[14]。遗传算法具备良好的全局搜索能力,不受求导和函数连续性的限定,能自动获取待优化的搜索空间,从而自适应地控制搜索过程[15]。
1.2 卡尔曼滤波器卡尔曼滤波器是由R.E.Kalman提出的线性最小方差递推估算的方法,是一种离散数据线性滤波问题的递归解决方案[16]。它是利用当前时刻的观测值和前一时刻的估计值来更新当前时刻的最佳估计,其所需数据存储量较小,便于实时处理[17]。
2 基于GABP-KF的WSN数据漂移校准方法 2.1 定义测量环境假设在某一区域内的传感器网络中,随机分布多个节点。其中每个节点采集该区域内的环境参数(温度、湿度或其他类型参数)。随着时间的推移,一些节点产生数据漂移,降低了数据质量,从而影响了传感器网络的可靠性。为了更好地模拟实际场景,本文对传感器网络的测量环境做了如下定义。
定义1 传感器节点的数据漂移指的是节点测量值受其内部固有偏差或外界环境影响所产生的缓慢、单向、长期的变化。在本文中,节点的数据漂移表示如下:
| $X = T + d + W$ | (1) |
式中:X表示节点的测量值;T表示所测环境的真实值;d表示漂移值;W表示测量高斯白噪声。其中,漂移d是平滑的,因为漂移通常是一个缓慢的线性或指数的变化过程,没有突变,激增或尖峰现象[18]。同时,漂移的产生是随机的,与其内部构造以及环境因素密切相关。因此,不同节点是否产生漂移以及漂移值的大小不具有相关性。由于节点在部署前都经过预先校准,以确保它们处于工作状态。因此,节点部署后的短时间内,漂移值应为零。在本文中,设定节点不会同时产生数据漂移,且产生的漂移值不同。
定义2 在以目标节点为圆心的测量区域内,该节点向其周围节点传输信号,该信号的强度会随距离的增加而减弱,当信号强度小于阈值时,接收节点无法接收到数据。因此,通信半径指的是信号衰减至阈值的距离,而邻居节点指目标节点通信半径内的其他节点。在本文中,假设目标节点i共有m−1个邻居节点,分别标号为1,2,
定义3 目标节点i与其邻居节点的时空相关性指的是同一时段内的节点测量数据的变化趋势是一致的。在本文中,假设目标节点i与其邻居节点间具有时空相关性,因此,可以用来预测目标节点的测量值,即:
| ${{\overset{\frown} x} _i} = f({\rm neighbours}\_{\rm data})$ | (2) |
式中:
GABP-KF算法的设计目标是在随机误差(噪声)和系统误差(漂移)的干扰下精确地校准目标节点i的测量值
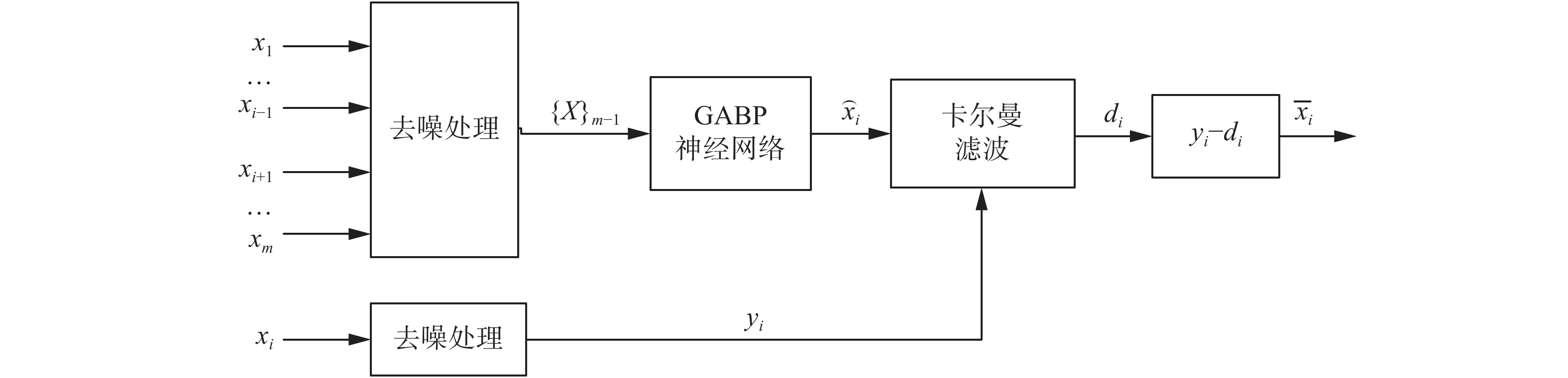
|
Download:
|
| 图 1 GABP-KF算法的数据漂移校准框架 Fig. 1 Data drift calibration framework of GABP-KF algorithm | |
在传感器网络的实际部署中,由于受到传感器节点内部固有偏差或其他环境因素,节点在测量过程中会受到噪声的干扰。在节点校准之前,必须考虑消除噪声的影响。本文采用小波去噪[19]方法来降低噪声的影响,首先使用阈值去噪法对含噪数据进行小波分解,再对小波系数进行阈值处理,最后利用处理后结果重构原信号。实验证明该方法在信号保护和噪声抑制之间达到了良好的平衡。
2.3.2 GABP神经网络的建模传统的BP神经网络具有良好的自学习、自适应能力,但同时也存在容易陷入局部最优解、收敛速度差等问题。为了克服这些缺点,本文使用遗传算法来优化BP神经网络,将遗传算法的全局搜索能力与BP神经网络的局部搜索能力有效地结合起来,从而提高了网络的预测精度和泛化能力。具体方法如下:首先,BP神经网络根据数据集的划分情况确定网络结构,从而确定遗传算法的个体长度。其次,算法通过选择操作、交叉操作和变异操作来优化BP神经网络的参数。最后,BP神经网络使用最优参数来预测目标节点的测量值。GABP神经网络的模型建立方法如图2所示。

|
Download:
|
| 图 2 GABP神经网络的建模算法 Fig. 2 Modeling algorithm of GABP neural network | |
本文使用在传感器网络部署初期(一般为前五天)所采集到的节点数据作为训练数据集,训练数据集划分为:
本文设定t时刻节点i的平滑漂移值为
| ${d_{i,t}} = {d_{i,t - 1}} + {w_{i,t}},{w_{i,t}} \sim N(0,{Q_{i,t}})$ | (3) |
式中:
式(3)表示节点数据漂移的状态跟踪方程,用来跟踪漂移值随时间的变化情况。除了状态方程,还需要建立一个观测方程来模拟节点的观测结果。假设现实中存在一种测量仪器,可以测量出节点的数据漂移值,同时一定存在与节点测量时相关联的误差,见式(4):
| ${{\textit{z}}_{i,t}} = {d_{i,t}} + {v_{i,t}},{v_{i,t}} \sim N(0,{R_{i,t}})$ | (4) |
式中:
实际上并不存在可以直接测量节点数据漂移的仪器。在这种情况下,理想的数据漂移值
| ${d_{i,t}} = {r_{i,t}} - {T_{i,t}}$ | (5) |
然而在实际场景中,实际值是无法得知的,只能使用其预测值
| ${d_{i,t}} = {r_{i,t}} - {{\overset{\frown} x} _{i,t}}$ | (6) |
综上所述,式(3)和式(4)建立了一个传感器节点的状态-观测模型,使用卡尔曼滤波器以分散迭代的方式进行跟踪漂移,具体算法参见图3。

|
Download:
|
| 图 3 针对目标节点的漂移跟踪算法 Fig. 3 Drift tracking algorithm for target node | |
如图3所示,其中
| ${\bar x_{i,t}} = {r_{i,t}} - {d_{i,t}}$ | (7) |
为了验证GABP-KF的算法性能,本文在matlab 2013b 的实验环境下针对国际通用的Intel Berkeley(LBRL)无线传感器网络数据集和LUCE无线传感器网络数据集分别实现了GABP-KF算法、未优化的BP-KF算法、Takruri提出的SVR-KF算法[12]以及DRB-KF算法[11],并进行了实验结果的比较。
3.1 数据集 3.1.1 IBRL数据集IBRL数据集来自于部署在Intel Berkeley实验室内的无线传感器网络,包含54个节点,用于监控实验室环境(参见图4)。

|
Download:
|
| 图 4 IBRL的节点分布 Fig. 4 Deployment scheme of IBRL sensor network | |
选取由IBRL部署中的两组传感器节点的数据子集进行实验。第1组数据子集(IBRL_1)包含的节点ID分别是1、2、3、4、6、7、10、33。第2组数据子集(IBRL_2)包含的节点ID分别是17、18、19、20、21、22、23。两组数据集都对应于2004-02-28~2004-03-07 9天内所收集的数据。
3.1.2 LUCE数据集LUCE数据集(洛桑城市冠层实验)来自于2006年7月以来部署在洛桑联邦理工学院内的无线传感器网络。该网络共包含97个节点,根据节点之间的时空相关性分为10组传感器节点集。
选取LUCE数据集中的两组传感器节点的数据子集作为实验对象,第1组数据子集(LUCE_1)包含的节点ID分别是10、14、15、17、18、19。第2组数据子集(LUCE_2)包含的节点ID分别是21、23、24、25、26、27、28。两组数据子集都对应于2016-10-10~2016-10-13 4天内所收集的数据。
由于上述数据集中节点的测量数据量庞大,其中存在缺漏值,且采样周期均为31 s。因此,对每个节点分别以5 min的时间间隔进行重新采样,并均使用温度作为评估数据。为了精确评估GABP-KF算法的性能,排除实验数据由于缺漏现象造成的影响,人工建立了一组具有时空相关性的测试数据集(DR_d)。表1列出了所使用的所有数据集。
| 表 1 实验所用数据集 Tab.1 Experimental data sets |
针对上述数据集中的所有节点数据,采用硬阈值去噪的方法进行处理,以减少噪声对GABP-KF算法评估所造成的影响。由于本文所采用的数据集中噪声干扰较小,为进行去噪算法的评估,故选择在数据集Ⅲ中10号节点处对节点数据手动添加高斯白噪声,去噪结果参见图5。如图5所示,原始数据与去噪后数据几近重合,这表明本方法对噪声有很好的抑制作用。

|
Download:
|
| 图 5 小波去噪实验结果 Fig. 5 Experimental results of wavelet denoising | |
为比较GABP-KF算法与其他同类算法的模型拟合程度,基于表1中的5个数据集分别随机选择其中一个节点的数据针对4种算法进行了5次对比实验,并选取平均值作为最终数据,表2给出了4种算法的模型拟合程度对比结果。本文选用均方误差(式(8))与决定系数(式(9))作为判断依据。
| ${\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - {{\hat x}_i})}^2}} $ | (8) |
| ${{\rm{R}}^2} = \frac{{{{\left( {n\sum\limits_{i = 1}^n {{{\mathord{{\hat x}} }_i}{x_i}} - \sum\limits_{i = 1}^n {{{\mathord{{\hat x}} }_i}} \sum\limits_{i = 1}^n {{x_i}} } \right)}^2}}}{{\left( {n\sum\limits_{i = 1}^n {\mathord{{\hat x}} _i^2} - {{\left( {\sum\limits_{i = 1}^n {{{\mathord{{\hat x}} }_i}} } \right)}^2}} \right)\left( {n\sum\limits_{i = 1}^n {x_i^2} - {{\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)}^2}} \right)}}$ | (9) |
式中:n表示训练样本数目,
| 表 2 4种算法的模型拟合程度对比结果 Tab.2 Comparison of the fitting degree among four algorithms |
从表2可以看出,基于本文所采用的数据集,GABP算法的均方误差比DRB算法、BP、SVR算法平均减少了0.110 8、0.121 0、0.249 5;GABP算法的决定系数比DRB、BP、SVR算法平均提高了1.74%、2.56%、4.23%。其中,4种算法在数据集V下的拟合程度均好于其余数据集,这是由于数据集V为人工建立,不受外界误差影响,其余4个数据集选自真实数据集,均受到数据缺失,数据突变等误差的影响。DRB、BP、SVR算法受这些误差的影响较大,而GABP神经网络通过GA优化有效地避免了局部误差,因此,GABP神经网络的模型拟合程度要优于其他算法。
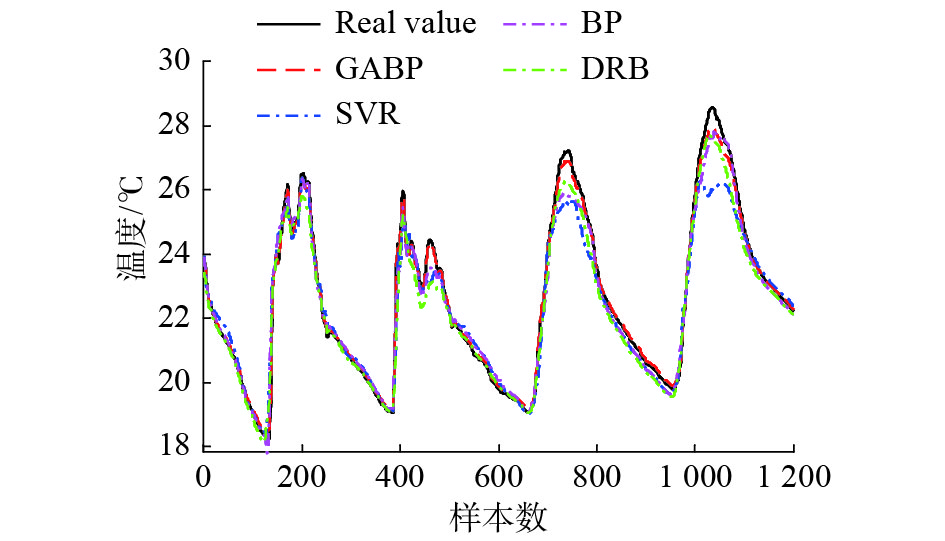
图6表示4种算法在数据集I下针对1号节点所建立的预测模型,其中real value描述的曲线表示真实值,其余4条曲线分别表示GABP、SVR、BP和DRB算法所获得的预测结果。从图6中可以直观地看出,GABP神经网络的拟合程度更好,这与表2的结果是一致的。综上所述,GABP算法具有更好的模型拟合程度,所输出的预测值与真实值的误差更小。
|
Download:
|
| 图 6 4种算法的模型对比结果 Fig. 6 Comparison among the training models of four algorithms | |
在漂移校准过程中,于不同节点测试数据的随机位置处引入不同的指数漂移值与测量噪声。其中,当观测噪声协方差R值或状态噪声协方差Q值设置过高时,预测值会产生较大误差。因此,采用试凑法对参数值进行调整,在数据集I下,基于网格搜索的原理将卡尔曼滤波器的参数Q和R分别设置为0.1和0.01。
为比较GABP-KF算法与其他同类算法的漂移校准性能,基于表1中的5个数据集分别随机选择其中一个节点的数据针对4种算法进行了3次对比实验,并选取平均值作为最终数据,表3给出了实验结果。
| 表 3 4种算法的漂移校准性能对比结果 Tab.3 Comparison of the drift calibration performance among four algorithms |
从表3中可以看出,基于本文所采用的数据集,GABP-KF算法的均方误差比DRB-KF、BP-KF、SVR-KF算法平均减少了0.295 2、0.202 0、0.370 2;GABP-KF算法的决定系数比DRB-KF、BP-KF、SVR-KF算法平均提高了1.43%、1.72%、2.40%。实验表明,基于本文所采用的数据集,GABP-KF算法具有更好的漂移校准性能。
图7表示在数据集Ⅲ下针对14号节点的数据使用GABP-KF算法进行漂移校准后的结果。从图7中可以看出,节点真实值曲线与滤波后数值曲线基本保持一致。这表明本算法成功地消除了引入的漂移值和测量噪声。

|
Download:
|
| 图 7 卡尔曼滤波后的校准示例 Fig. 7 Example of data drifts calibration after Kalman filter | |
在进行整体评估时,考虑以下两种情形。第1种情形为所有节点数据均未添加漂移值,称为N-data,第2种情形为在指定的节点数据中加入漂移值,称为D-data。两组数据N-data和D-data在经过GABP-KF算法的校准后分别称为CN-data和CD-data。其中D-data中在不同节点测试数据的随机位置处引入不同的指数漂移,即每个节点开始产生漂移的时刻不同,产生漂移的大小不同,是否产生漂移互不相关。
本文比较了5种情形下节点的平均绝对误差MAE值(见式(10))。如图8所示,情形1、2、3、4、5分别表示仅有一个节点漂移、两个节点同时漂移、3个节点同时漂移、4个节点同时漂移、5个节点同时漂移等5种情形。具体计算方法如下:在每个时刻分别计算每个节点的测量数据N-data与D-data之间的MAE值和校准后数据CN-data和CD-data之间的MAE值,然后计算网络中5种情形下的整体MAE值。本文选择在数据集IV下21号节点的数据上进行上述对比实验。
| ${\rm MAE} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{X_i} - {{{\hat X}}_i}} \right|} $ | (10) |
式中:n为训练样本数目,Xi与

|
Download:
|
| 图 8 5种情形下MAE值的变化情况 Fig. 8 Comparison of MAE among five cases | |
图8(a)表示5种情形下测量数据N-data和D-data之间的平均绝对误差。图8(b)表示5种情形下校准数据CN-data和CD-data之间的平均绝对误差。比较图8(a)与图8(b),显然,应用GABP-KF算法导致所有情形下的MAE值较小。本文假设无线传感器网络中阈值MAE值为1.2,超过阈值则表示该网络失效,阈值的选择取决于实际网络中允许的容错误差。在图8(a)中,情景2~5的曲线在第一天时就跨越了阈值线。相比之下,图8(b)中的所有情形的曲线在实验的整个周期中均未跨越阈值线。这证明使用本算法可以允许多个节点同时产生数据漂移的情况,这更符合实际情况。
4 结束语本文提出了一种使用基于遗传算法优化的BP神经网络和卡尔曼滤波器相结合的无线传感器网络数据漂移盲校准算法。仿真实验表明,与以往同类算法相比,GABP-KF算法对无线传感器网络节点数据流漂移有更好的跟踪和校准性能,使用该算法有效地提高了传感器网络数据的可靠性。在大规模无线传感器网络的应用中,节点可以同时测量多种属性的数据,本算法只考虑了单一属性(温度)下的漂移校准情况。在今后的研究将考虑节点同时采集多种属性数据时产生或未产生漂移的各种情况,以便更好地模拟实际情况。
| [1] |
WU Mou, TAN Liansheng, XIONG Naixue. Data prediction, compression, and recovery in clustered wireless sensor networks for environmental monitoring applications[J]. Information sciences, 2016, 329: 800-818. DOI:10.1016/j.ins.2015.10.004 ( 0) 0)
|
| [2] |
KUMAR D, RAJASEGARAR S, PALANISWAMI M. Geospatial estimation-based auto drift correction in wireless sensor networks[J]. ACM transactions on sensor networks, 2015, 11(3): 50. ( 0) 0)
|
| [3] |
TAN Rui, XING Guoliang, YUAN Zhaohui, et al. System-level calibration for data fusion in wireless sensor networks[J]. ACM transactions on sensor networks, 2013, 9(3): 28. ( 0) 0)
|
| [4] |
RAMANATNAN N, BALZANO L, BURT M, et al. Rapid deployment with confidence: Calibration and fault detection in environmental sensor networks[R]. Technical Report CENS TR 62, Center for Embedded Networked Sensing, 2006.
( 0) 0)
|
| [5] |
MILUZZO E, LANE N D, CAMPBELL A T, et al. CaliBree: A self-calibration system for mobile sensor networks[C]//Proceedings of the 4th IEEE International Conference on Distributed Computing in Sensor Systems. Berlin, Heidelberg, Germany: Springer-Verlag, 2008: 314–331.
( 0) 0)
|
| [6] |
TAYLOR C, RAHIMI A, BACHRACH J, et al. Simultaneous localization, calibration, and tracking in an ad hoc sensor network[C]//Proceedings of the 5th International Conference on Information Processing in Sensor Networks. Nashville, TN, USA: IEEE, 2006: 27–33.
( 0) 0)
|
| [7] |
LEE B T, SON S C, KANG K. A blind calibration scheme exploiting mutual calibration relationships for a dense mobile sensor network[J]. IEEE sensors journal, 2014, 14(5): 1518-1526. DOI:10.1109/JSEN.2013.2297714 ( 0) 0)
|
| [8] |
BALZANO L, NOWAK R. Blind calibration of sensor networks[C]//Proceedings of the 6th International Conference on Information Processing in Sensor Networks. Cambridge, MA, USA: IEEE, 2007: 79–88.
( 0) 0)
|
| [9] |
LI Zhan, WANG Yuzhi, YANG Anqi, et al. Drift detection and calibration of sensor networks[C]//Proceedings of 2015 International Conference on Wireless Communications & Signal Processing. Nanjing, China: IEEE, 2015: 1–6.
( 0) 0)
|
| [10] |
WANG Yuzhi, YANG Anqi, LI Zhan, et al. Blind drift calibration of sensor networks using signal space projection and Kalman filter[C]//Proceedings of 2015 IEEE Tenth International Conference on Intelligent Sensors, Sensor Networks and Information Processing. Singapore, Singapore: IEEE, 2015: 1–6.
( 0) 0)
|
| [11] |
TAKRURI M, ABOURA K, CHALLA S. Distributed recursive algorithm for auto calibration in drift aware wireless sensor networks[M]//ELLEITHY K. Innovations and Advanced Techniques in Systems, Computing Sciences and Software Engineering. Netherlands: Springer, 2008: 21–25.
( 0) 0)
|
| [12] |
TAKRURI M, RAJASEGARAR S, CHALLA S, et al. Online drift correction in wireless sensor networks using spatio-temporal modeling[C]//Proceedings of 200811th International Conference on Information Fusion. Cologne, Germany: IEEE, 2008: 1–8.
( 0) 0)
|
| [13] |
KUMAR D, RAJASEGARAR S, PALANISWAMI M. Automatic sensor drift detection and correction using spatial Kriging and Kalman filtering[C]//Proceedings of 2013 IEEE International Conference on Distributed Computing in Sensor Systems. Cambridge, MA, USA: IEEE, 2013: 183–190.
( 0) 0)
|
| [14] |
DING Shifei, SU Chunyang, YU Junzhao. An optimizing BP neural network algorithm based on genetic algorithm[J]. Artificial intelligence review, 2011, 36(2): 153-162. DOI:10.1007/s10462-011-9208-z ( 0) 0)
|
| [15] |
丁建立, 陈增强, 袁著祉. 遗传算法与蚂蚁算法的融合[J]. 计算机研究与发展, 2003, 40(9): 1351-1356. DING Jianli, CHEN Zhenqiang, YUAN Zhuozhi. Genetic algorithm and ant algorithm fusion[J]. Journal of computer research and development, 2003, 40(9): 1351-1356. (  0) 0)
|
| [16] |
WELCH G, BISHOP G. An introduction to the Kalman filter[R]. Chapel Hill, NC, USA: University of North Carolina at Chapel Hill, 1995.
( 0) 0)
|
| [17] |
钟伟才, 刘静, 刘芳, 等. 二阶卡尔曼滤波分布估计算法[J]. 计算机学报, 2004, 27(9): 1272-1277. ZHONG Weicai, LIU Jin, LIU Fang, et al. Second order estimation of distribution algorithms based on kalman filter[J]. Chinese journal of computers, 2004, 27(9): 1272-1277. DOI:10.3321/j.issn:0254-4164.2004.09.018 (  0) 0)
|
| [18] |
TAKRURI M, RAJASEGARAR S, CHALLA S, et al. Spatio-temporal modelling-based drift-aware wireless sensor networks[J]. IET wireless sensor systems, 2011, 1(2): 110-122. DOI:10.1049/iet-wss.2010.0091 ( 0) 0)
|
| [19] |
CHANG S G, YU Bin, VETTERLI M. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE transactions on image processing, 2002, 9(9): 1532-1546. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


