目标跟踪是计算机视觉重要研究领域之一，在智能交通、运动分析、行为识别、人机交互^[1]等方面具有广泛应用。随着可穿戴式相机的普及，基于Egocentric视频的目标跟踪引起研究人员的极大兴趣。由于单视角视野有限，当相机剧烈晃动时易造成目标丢失以至于跟踪轨迹的不连续性问题，无法进行全方位的跟踪。Multi-Egocentric视频是由多个处于同一场景中的穿戴式或手持式相机所拍摄的不同视角、不同运动轨迹的视频。多视角跟踪由于视野范围更大，视角丰富，能够根据多视角信息有效跟踪目标。相对多固定视角视频的跟踪任务，Multi-Egocentric视角随拍摄者移动，一方面带有Egocentric视频背景变化剧烈、目标尺度差异明显和视角时变性强的特点，另一方面由于继承了拍摄者的关注兴趣，能以更好的视角拍摄所关注的目标，同时多样化的视角为解决遮挡、漂移等问题提供了更为丰富的线索。

目前大多数跟踪算法致力于解决单个Egocentric视角或多个固定视角中存在的目标遮挡、跟踪漂移等问题^[2-5]。为了进行鲁棒的目标跟踪，Xu等^[4]基于目标表面模型和运动模型，提出层次轨迹关联模型构建有向无环图解决固定多视角下轨迹片段关联问题，将其应用于Multi-Egocentric视频鲁棒性较差，无法解决目标不连续性问题。Fleuret等^[6]将颜色、纹理和运动信息3个特征相结合建立目标模型，并通过目标之间的相对位置对目标进行定位，能够有效解决多固定视角下目标遮挡问题，但是将其应用于Multi-Egocentric视频跟踪任务中，背景变化剧烈情况会对跟踪结果造成很大影响，常出现轨迹误匹配问题。另外，X.Mei等^[7]提出的稀疏表示算法采用稀疏线性表示的方法使跟踪器可以应对光照变化、遮挡等问题。在线多示例学习算法^[8]使用图像块的集合表示目标，使得跟踪器在目标经历光照变化和遮挡时可以有效地跟踪目标。Yuxia Wang等^[9]采用粒子滤波方法，基于贝叶斯滤波理论，解决状态估计问题，再根据所有粒子的权重，利用蒙特卡洛序列方法确定状态的后验概率，对跟踪过程中噪声具有一定的鲁棒性。Bae等^[10]以及Dicle等^[11]跟据轨迹片段的置信度进行轨迹关联实现多目标跟踪，但由于目标轨迹不连续，容易造成短时间的目标误匹配问题。Xiang等^[12]通过构造马尔可夫决策过程求取最优策略的方法来预测目标下一刻状态。上述算法一定程度上能够解决运动视角下目标的鲁棒性跟踪问题，但对于视角时变性强的Multi-egocentric视频，容易因目标运动不连续性造成跟踪失败。近年来深度学习方法在目标跟踪领域也有广泛应用，其中MDNet算法^[13]采用共享层和特定层相结合的深度模型进行目标跟踪，该方法具有很好的鲁棒性和适应性，但对多目标跟踪具有局限性。

针对Multi-egocentric视频的特点，本文从目标空间几何关系约束的角度出发，并结合卡尔曼滤波算法，提出一种基于运动轨迹重建的多目标跟踪算法。与以上算法相比，本文算法通过轨迹重建可以有效解决Multi-egocentric视频中运动目标轨迹不连续的问题。

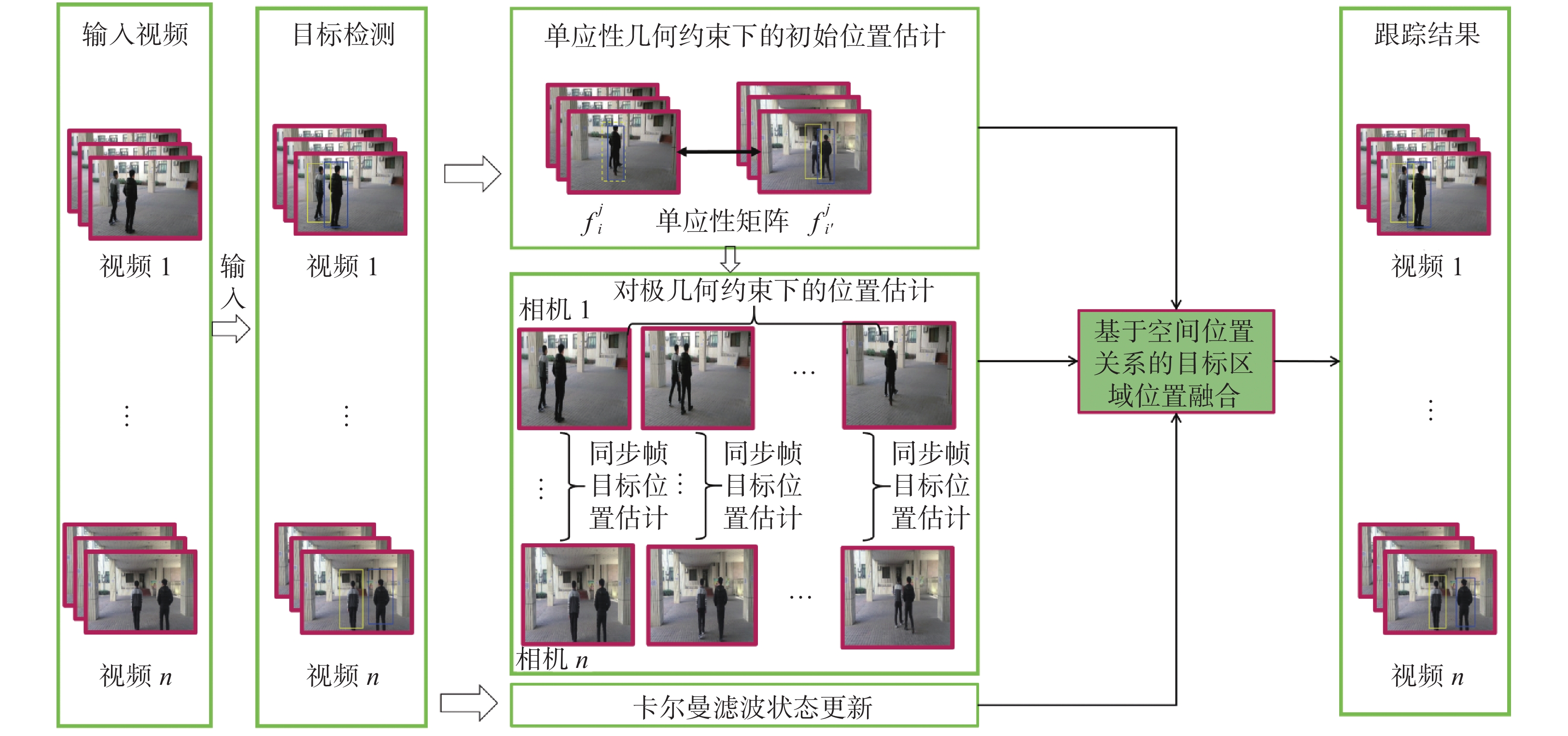
1 基于运动轨迹重建的多目标跟踪

本文针对Multi-egocentric视频的特点，提出一种基于运动轨迹重建的多目标跟踪算法，算法流程如图1所示。该算法利用多视角之间目标位置和运动轨迹的几何约束关系降低了目标定位误差、目标跟踪漂移以及轨迹不连续等对多目标跟踪造成的影响，并在Multi-Egocentric视频数据集和多固定视角数据集上验证了本文算法的有效性。

与单视角目标跟踪算法不同，多视角目标跟踪可以利用多视角之间目标位置的关联关系优化目标定位；本文提出基于运动轨迹重建的Multi-Egocentric视频多目标跟踪算法，首先在目标检测基础上，通过求解不同视角间单应性约束解决同一时刻目标的遮挡和丢失问题，然后基于多视角轨迹立体重建算法进行目标定位估计，最后结合卡尔曼滤波的状态更新实现基于空间位置关系的目标区域位置融合，得到最佳的目标跟踪结果。

1.1 多视角辅助下的目标初始位置估计

设 $f_i^j$ 为视角 $i$ ( $i$ =1,2,···,n)第 $j$ 帧图像，其中包含 $m$ 个目标 ${P_k},\text{其中}k = 1,2,\cdots ,m$ ， $B_i^j$ 表示目标检测在 $f_i^j$ 的检测框集合， $B_i^j = \{ b_{ik}^j|k = 1,2,\cdots,m\} $ ， $b_{ik}^j =\{ x_{ik}^j,y_{ik}^j, $ $ \tilde x_{ik}^j,\tilde y_{ik}^j\} $ 表示第 $k$ 个目标的Bounding Box，其中 $ x_{ik}^j{\text、}y_{ik}^j{\text、}$ $\tilde x_{ik}^j{\text、}\tilde y_{ik}^j$ 分别表示 $b_{ik}^j$ 的左上角横坐标、左上角纵坐标、右下角横坐标、右下角纵坐标，设 $t_{ik}^j$ 作为检测结果中目标 $k$ 在视角 $i$ 第 $j$ 帧的轨迹点：

$t_{ik}^j = [\tilde x_{ik}^j,(y_{ik}^j{\rm{ + }}\tilde y_{ik}^j)/2]$

(1)

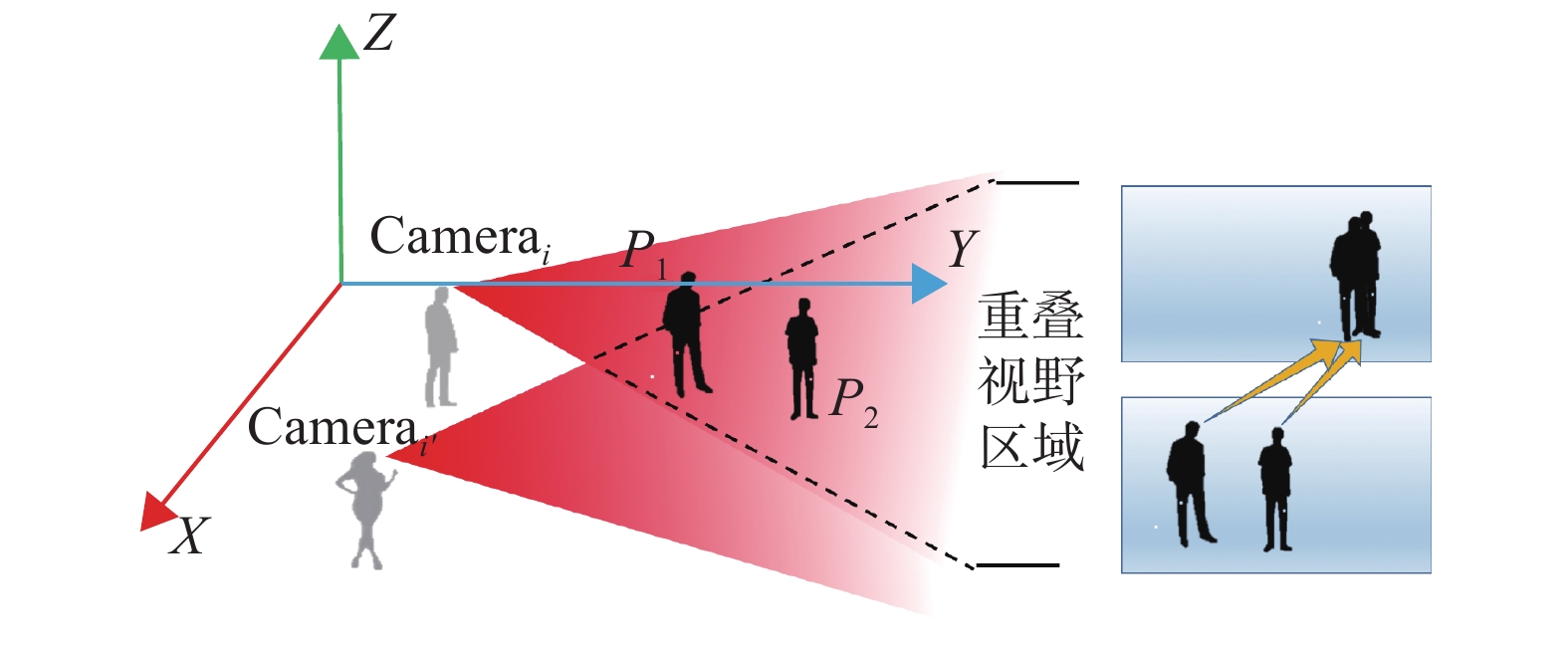
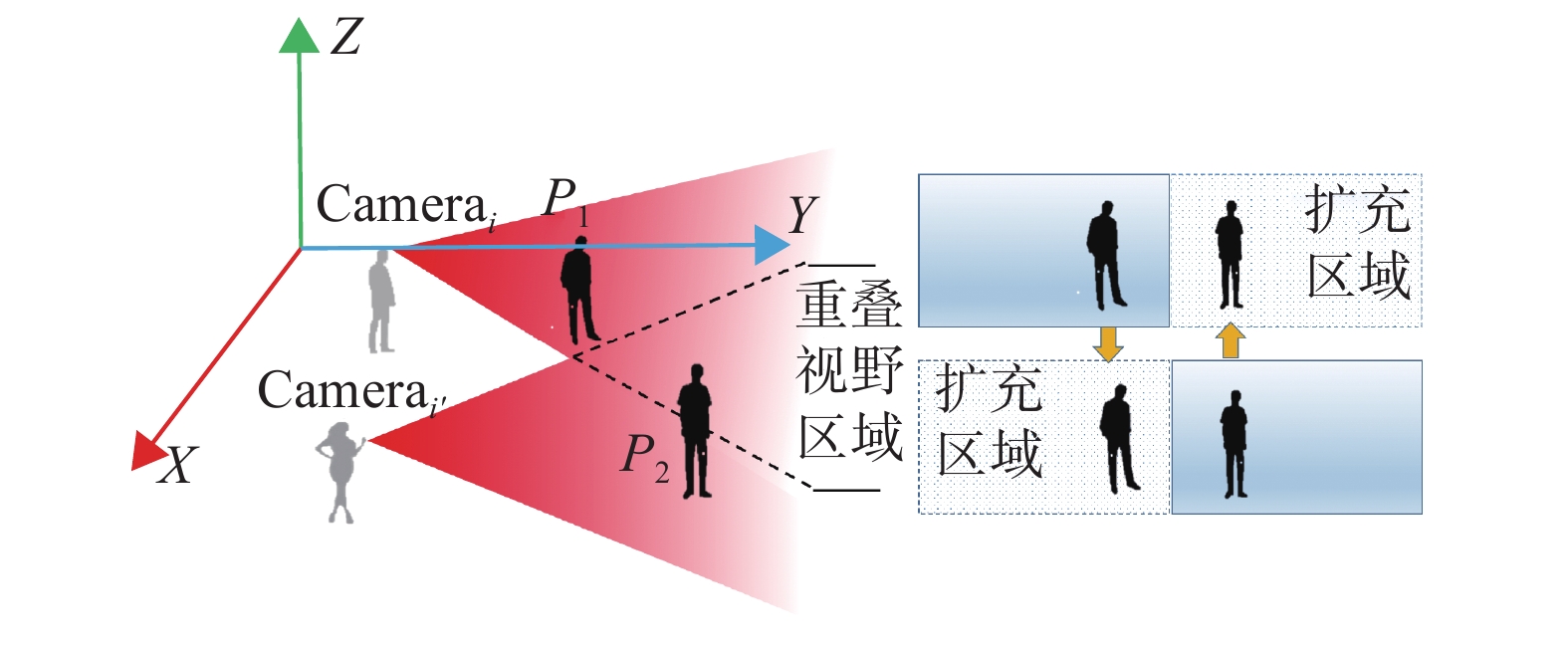
由于Egocentric视频视角时变性的特点，移动视角因剧烈晃动或平移等因素造成单个视角中目标消失等运动轨迹的不连续性问题。如图2所示，箭头指示两个视角下的相同目标所在位置。从Camera_i视角方向来看，两个目标在同一个方向造成目标遮挡，而Camera_i'的视角中各目标无遮挡问题。如图3所示，左右两视角都向两边移动时，造成单个视角只检测到部分目标，右侧扩充区域是对单个视角的视野范围的扩充，用于显示目标之间的相对位置关系。以上两种情况都会因目标丢失导致某些视角跟踪失败。

针对这种问题，本文基于具有重叠视野区域的视角之间存在平面上的单应性约束关系^[14]，利用多个视角之间目标的相对位置，根据Camera_i第 $j$ 帧 $f_i^j$ 中的目标轨迹点来估计Camera_i'第 $j$ 帧 $f_{i'}^j$ 的目标所在位置。算法具体描述和实现如算法1所示。

算法1　多视角单应性约束下的目标位置估计

输入　1) Camera_i第 $j$ 帧 $f_i^j$ 、Camera_i'第 $j$ 帧 $f_{i'}^j$ 、 $f_{i'}^j$ 中被遮挡目标k在 $f_i^j$ 中的轨迹点坐标 $t_{ik}^j$ ；

2) $f_{i'}^j$ 的目标所在位置 $t_{i'k}^j$ ；

3) 采用SIFT角点检测算法对 $f_i^j$ 和 $f_{i'}^j$ 两帧提取地面特征点，得到匹配点集合 ${ P}_i^j$ 和 ${ P}_{i'}^j$ ；

4) 利用匹配点构建方程(2)，并利用RANSAC^[15]算法剔除误匹配点求解单应性矩阵；

${ P}_i^j = {{HP}}_{i'}^j$

(2)

式中： ${{H}}$ 为3×3的单应性矩阵。

5)根据式(2)把 $t_{ik}^j$ 代入求得 $f_{i'}^j$ 中被遮挡目标 $k$ 所在位置 $t_{{i'}k}^j$ ；

输出　 $f_{i'}^j$ 的目标所在位置 $t_{i'k}^j$

通过不同视角同一时刻目标之间存在的单应性约束关系可以对遮挡和丢失目标进行重新定位，从而解决单个视角中目标的遮挡和丢失问题。同时由于特征点的检测和匹配误差使得单应性约束只能粗定位遮挡和丢失的目标，因此本文通过多视角轨迹重建进一步优化目标位置估计。

1.2 多视角轨迹重建位置估计

多视角轨迹重建位置估计是根据不同视角同一时刻帧目标的像素坐标对应位置关系做空间约束进一步对目标进行定位。根据不同视角同步帧之间重叠视野区域特征点的对应关系采用立体视觉三维重建算法实现同步帧目标位置估计。立体视觉三维算法示意图如图4所示，相机 $i$ 采用张正友标定法^[16]获得Camera_i内参矩阵 ${{{K}}_i}$ 和Camera_i'内参矩阵 ${{{K}}_{i'}}$ ，然后分别提取 $f_i^j$ 和 $f_{i'}^j$ 之间重叠区域的匹配点集合 $P_i^j$ 和 $P_{i'}^j$ ，由单应性约束得：

${({ P}_i^j)^{\rm{T}} }{{F}}_{i,i'}^j{ P}_{i'}^j = {{0}}$

(3)

${{E}}_{i,i'}^j = {({{ K}_i})^{\rm{T}} }{{F}}_{i,i'}^j{{ K}_{i'}}$

(4)

利用PnP^[17]和RANSAC算法求出基础矩阵 ${{F}}_{i,i'}^j$ 和本质矩阵 ${{E}}_{i,i'}^j$ ；当 $f_i^j$ 中目标k在Camera_i'中没有对应位置，把 $f_i^j$ 目标轨迹点 $t_{ik}^j$ 代入式(3)可以求解目标在 $f_{i'}^j$ 中的扩展匹配坐标位置 $t_{i''k}^j$ ，并把 $t_{ik}^j$ 和 $t_{i''k}^j$ 分别加入 $P_i^j$ 和 $P_{i'}^j$ 。对 ${{E}}_{i,i'}^j$ 作SVD分解，可得Camera_i'相对于Camera_i的旋转矩阵 ${{R}}_i^j$ 和平移向量 ${ T}_i^j$ 。然后计算得到目标轨迹点的三维空间坐标位置集合 $S_i^j = \{ s_{ik}^j|k = 1,2,\cdots ,m\} $ 。

由上述方法得到目标三维坐标 $S_i^j$ ，再根据像素坐标与相机坐标之间的关系，把三维跟踪轨迹转换成像素坐标系中的二维坐标 $s_i^j$ 。多视角轨迹重建利用不同视角同步帧的目标空间位置一致性对同步帧目标位置进行了优化，下一步利用同一视角的运动连续性对目标位置进行跟踪。

1.3 基于轨迹重建的多目标跟踪

设置目标的运动状态参数为某一帧目标的位置和速度。定义卡尔曼滤波^[18]第k个目标在j时刻状态是一个四维向量 ${{ r}_k}(j) = (px_k^j,vx_k^j,py_k^j,vy_k^j)$ ， $px_k^j,vx_k^j,py_k^j,vy_k^j$ 分别表示目标在x轴和y轴上的位置和速度，设单位时间T内假设目标是匀速运动、初始位置为 $s_k^j$ 、初始速度设为0、 ${{ r}_k}(0) =(x_{k,pos}^{'} $ $ 0,y_{k,pos}^{},0)^{\rm{T}} $ ；其中下一步预测方程为

$\hat u_k^{j/j - 1} = {{A}}u_k^{j - 1} + {{B}}c_k^{j - 1} + w_k^{j - 1}$

(5)

式中： $\hat u_k^{j/j - 1}$ 为目标k在第 $j - 1$ 时刻到j时刻的先验状态估计； $u_k^{j - 1}$ 为在第 $j - 1$ 时刻的后验状态估计； $c_k^{j - 1}$ 为第 $j - 1$ 时刻的控制输入； $w_k^{j - 1}$ 为第 $j - 1$ 时刻的激励噪声； ${{A}}$ 为状态转移矩阵； ${{B}}$ 为系统控制矩阵。定义状态转移矩阵 ${{A}}$ 为

${{A}} = \left[ {\begin{array}{*{20}{c}} 1&T&0&0 \\ 0&1&0&0 \\ 0&0&1&T \\ 0&0&0&1 \end{array}} \right]$

由系统方程和观测状态定义矩阵 ${{B}}$ 为

${{B}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&1&0 \end{array}} \right]$

卡尔曼滤波状态更新方程为

$u_k^j = \hat u_k^{j/j - 1} + K_k^j[z_k^j - {{H}}\hat u_k^{j/j - 1}]$

(6)

式中： $z_k^j$ 为第 $j$ 时刻的观测值， $z_k^j - {{H}}\hat u_k^{j/j - 1}$ 为观测过程残差， $K_k^j$ 为 $j$ 时刻的卡尔曼残差增益， ${{H}}$ 为观测矩阵；由既往时刻的估计值和当前时刻的观测值，利用无偏最小均方差准则，得到当前时刻的最优估计值 $u_k^j$ 。

1.4 基于空间位置关系的目标区域位置融合

由以上3个部分的结果，结合单应性约束目标位置估计结果 $t_k^j$ ，多视角轨迹重建估计结果 $s_k^j$ 和卡尔曼滤波当前时刻的最优估计值 $u_k^j$ ，求解目标 $k$ 在 $j$ 时刻的最优位置 $O_k^j$ ：

$\left\{ \begin{aligned} & O_k^j = {\omega _1}t_k^j + {\omega _2}s_k^j + {\omega _3}u_k^j \\ & {\omega _1} + {\omega _2} + {\omega _3} = 1 \end{aligned} \right.$

(7)

式中 ${\omega _1}{\text 、}{\omega _2}\text{和}{\omega _3}$ 分别表示 $b_k^j$ 、 $t_k^j$ 和 $s_k^j$ 的权重。

2 实验结果与分析

本文提出的基于Multi-Egocentric视频运动轨迹重建的多目标跟踪算法是针对Multi-Egocentric视频的，目前尚无针对此任务的公开评价数据集，为了验证算法的有效性，设计并拍摄了针对多目标跟踪任务的Multi-Egocentric视频数据集BJMOT。由于数据集采集规模所限，该视频数据集包含两个视角的视频，由两个拍摄者佩戴相同规格的运动相机拍摄，场景中有两个以上的自由运动目标，各视频经同步后，每个视频时长为45 s，帧率为每秒25帧，并从每个视频各提取220帧进行了人工标注作为ground-truth。同时为了验证本文算法的适应性，还在固定多视角的数据集EPLF-campus4进行了跟踪实验，表1为两个数据集的相关信息。

本文采用的目标检测方法为ACF算法^[19]，并将算法与MDP算法^[12]和CMOT算法^[10]进行了对比说明。实验评价指标采用中心位置误差和重叠率两种度量方式。中心位置误差是跟踪结果和实际情况中心点间的欧式距离，重叠率是PASCAL中目标检测的评分标准^[20]，即对于给定的跟踪目标框为 ${r_t}$ 和ground-truth为 ${r_g}$ ，定义中心位置误差为

${\rm Err} = \sqrt {{{({r_t}.x - {r_g}.x)}^2} + {{({r_t}.y - {r_g}.y)}^2}} $

(8)

式中： ${r_t}.x$ 和 ${r_t}.y$ 分别表示 ${r_t}$ 的中心横坐标和纵坐标， ${r_g}.x$ 和 ${r_g}.y$ 分别表示 ${r_g}$ 的中心横坐标和纵坐标，定义目标框的重叠率为

${\rm S}{\rm{core}} = \frac{{{\rm area}({r_t} \cap {r_g})}}{{{\rm area}({r_t} \cup {r_g})}}$

(9)

2.1 在BJMOT数据集上的实验结果

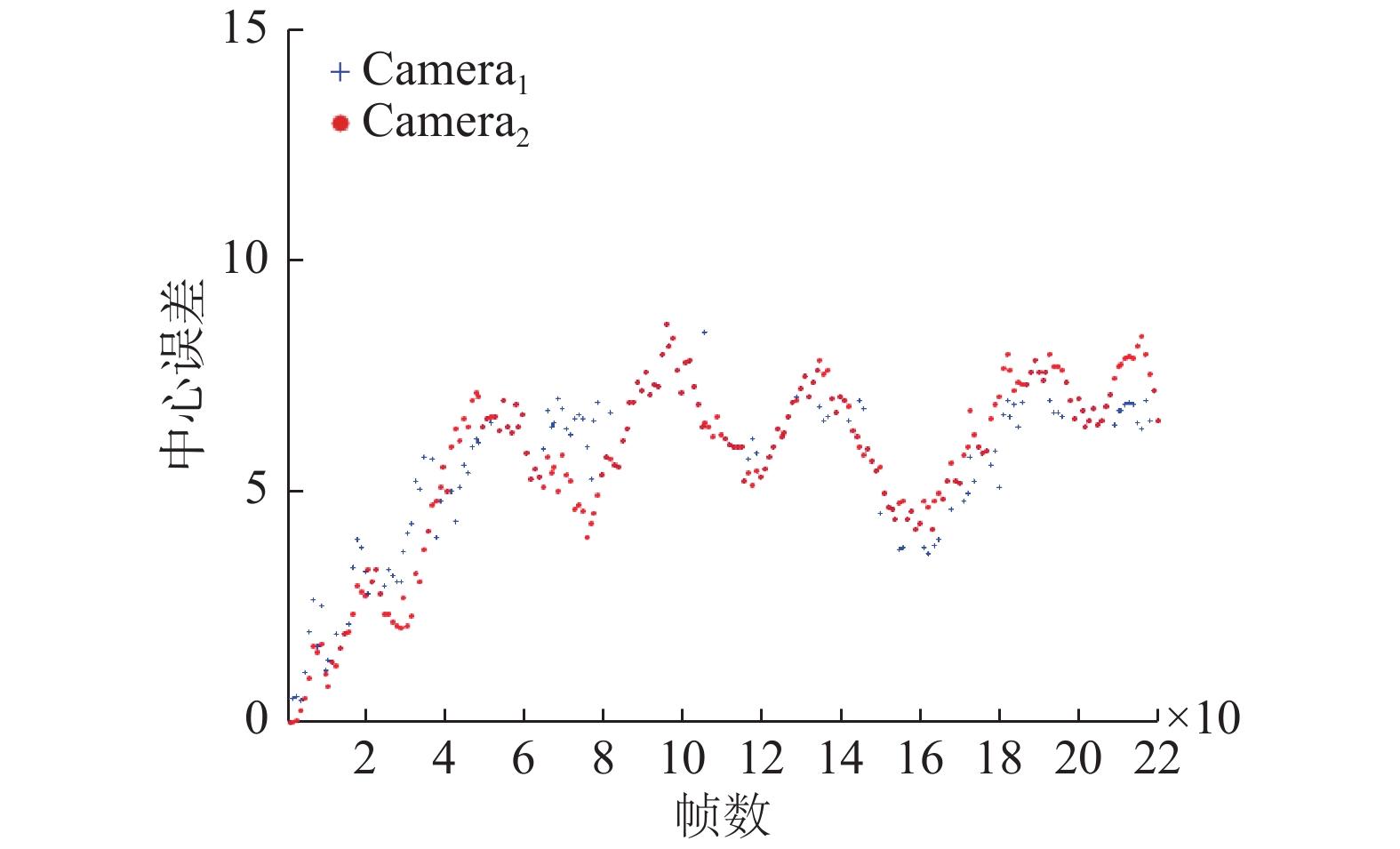
本文算法在BJMOT数据集上的平均中心误差如图5所示，表2为平均重叠率和平均中心误差的统计结果，对于部分目标丢失的情况不在计算中心误差范围之内。实验过程中，对 ${\omega _1}\text{、}{\omega _2}$ 和 ${\omega _3}$ 分别取值为 ${\omega _1} = 0.64,{\omega _2} = 0.23,{\omega _3} = 0.13$ 。相比缺少单应性约束条件的实验结果，结合单应性约束的目标初始位置估计和多视角轨迹重建的方法下，本文算法实验结果的平均重叠率在第一个视角和第二个视角分别提高了13%和9%，能够有效降低遮挡或部分丢失等因素造成的不连续因素对跟踪的影响。

部分典型帧在Camera₁和Camera₂上的实验结果分别如图6~7所示，图6~7中给出正常情况、部分遮挡情况、完全遮挡情况、部分消失和完全消失情况等5种典型情况下的目标跟踪实验结果。其中第1行表示目标检测结果或单应性约束目标位置估计结果，行中实线框表示目标检测结果，虚线框表示单应性约束计算结果；第2行中虚线框为多视角轨迹重建估计结果；第3行中虚线框为卡尔曼滤波当前时刻的最优估计值；第四行表示最终结果。第5列中由于目标缺失，在跟踪过程中通过运动一致性可以有效定位目标所在位置，算法计算出的结果在扩展视野区域；并且从图6中第2行第3列也可以看出，通过轨迹重建得到的目标位置误差较大，实验结果容易受到目标检测算法和单应性计算结果的影响；当目标检测误差较大时，该部分所产生的误差也较大，而通过融合对这类误差进行了较好的修正。

2.2 在EPLF-campus4数据集上的实验结果

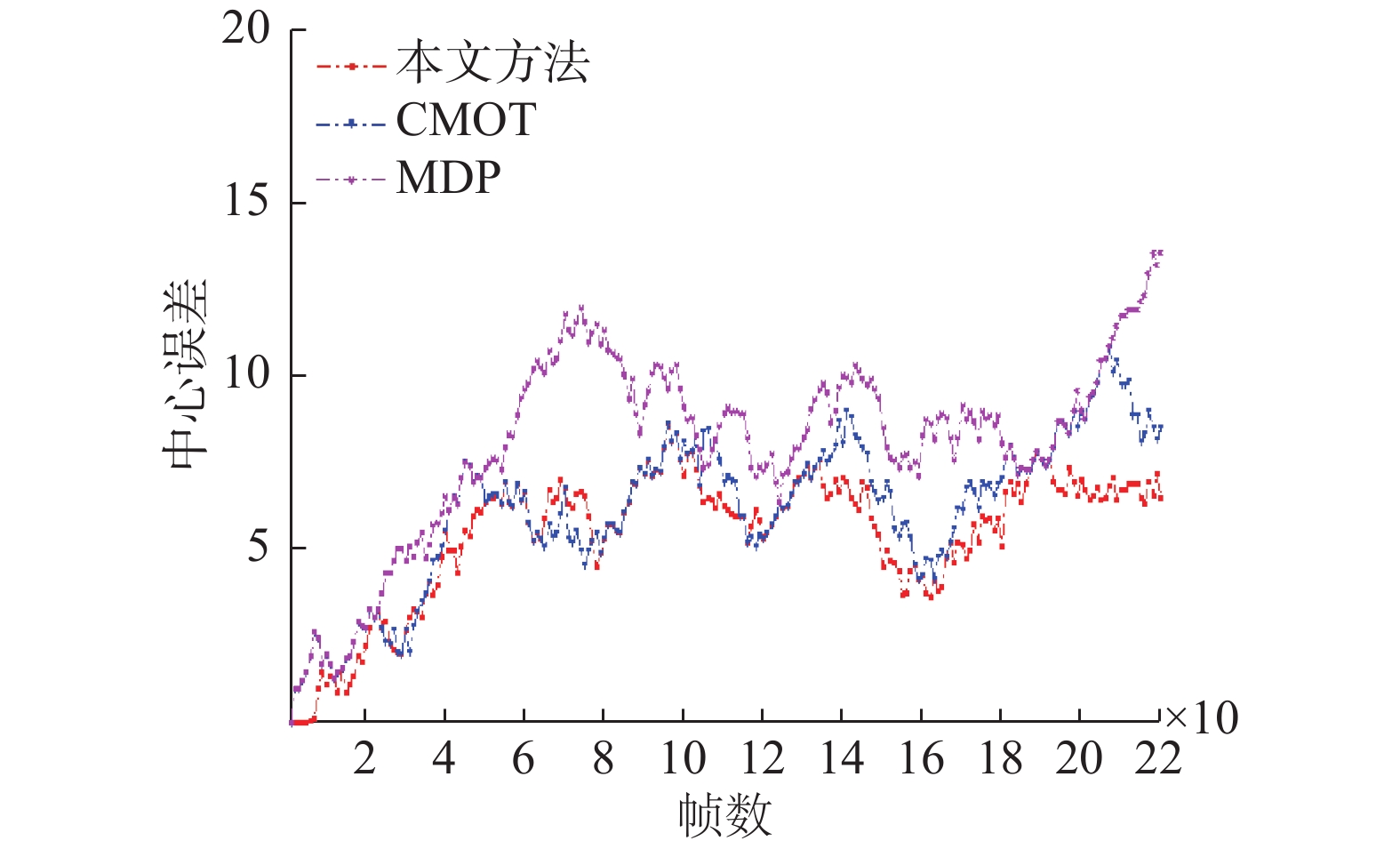
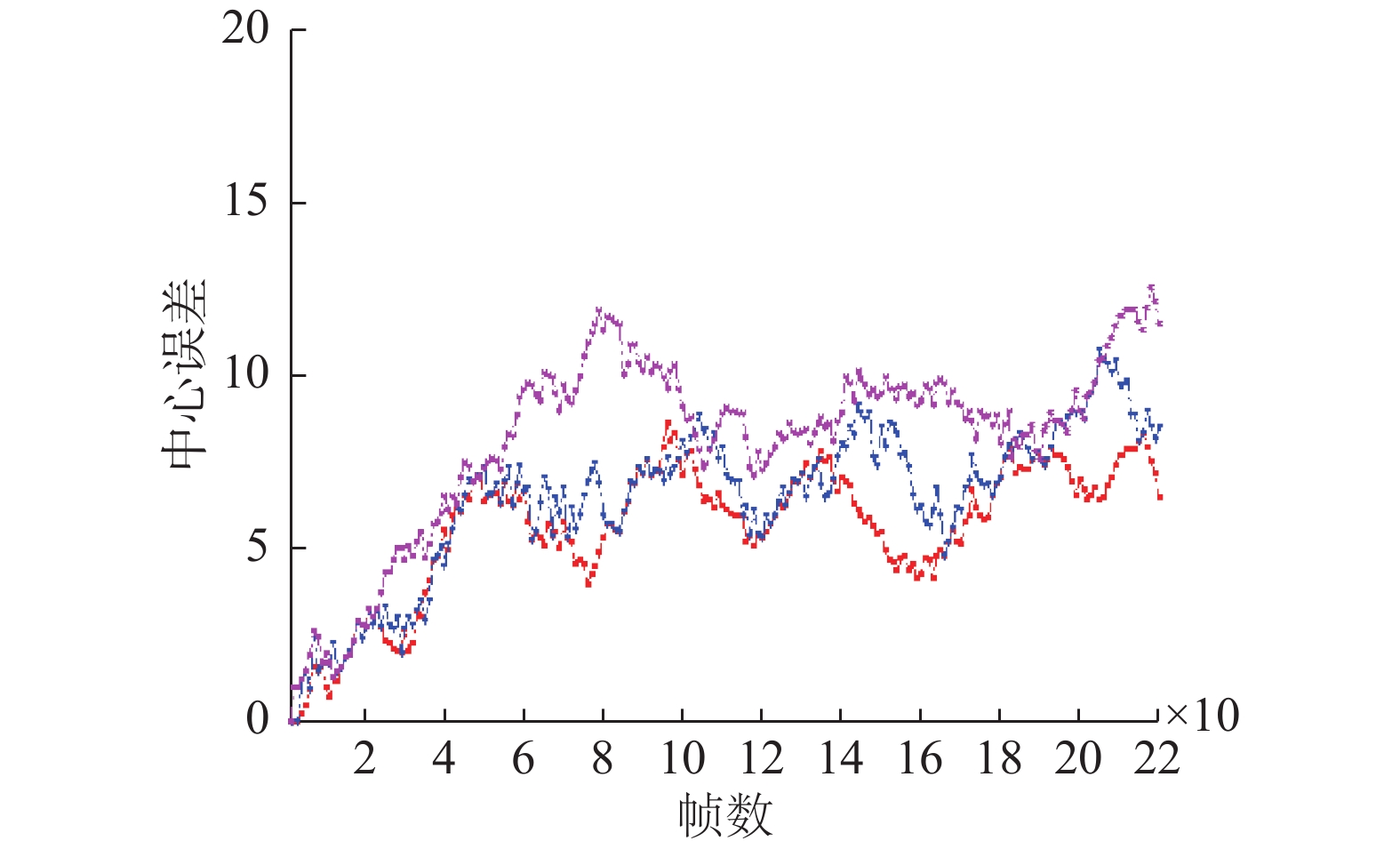
本文算法与MDP算法、CMOT算法在EPLF-campus4数据集上的平均重叠率结果对比如表3所示。表4为3个跟踪器在EPLF-campus4数据集上的平均中心位置误差。从表3中看出，相比其他两种算法，本文算法在Camera₁中的重叠率更高，而在Camera₂中的重叠率较低于CMOT算法，其原因是在CMOT算法中目标跟踪框不会随着目标大小进行变化，在目标较远时，检测框与目标真实范围重合率较大。从表4可以看出本文的算法的平均中心误差较小。因此从整体来看本文算法在该数据集上优于其他两种算法。图8~9是3种算法在EPLF-campus4数据集中两个视角的中心误差变化趋势。

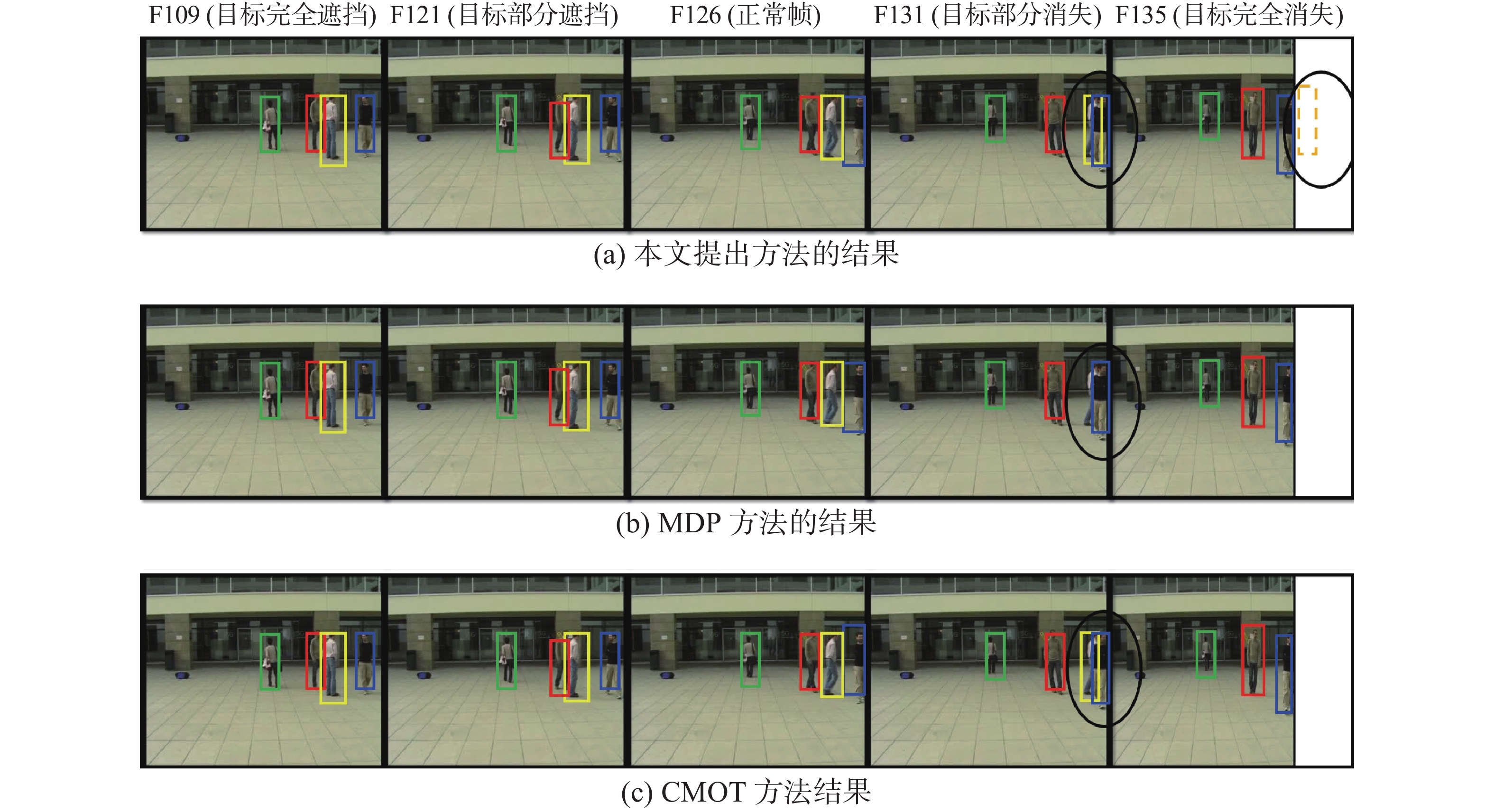
在EPLF-campus4数据集上Camera₁和Camera₂的典型帧跟踪结果分别如图10~11所示。同样选取五种典型情况下的目标跟踪实验结果进行分析。其中虚线框表示单应性约束计算结果。第五列中由于目标缺失，算法结果在扩展视野区域，椭圆区域为不同跟踪算法产生的差异性结果对比。从椭圆区域可以看出，本文算法能够根据视角之间的位置信息更好定位到目标，MDP算法在遮挡情况下出现目标丢失，CMOT虽然能跟踪到目标，但是其偏离目标中心位置，误差较大。

3 结束语

本文针对Multi-Egocentric视频中的目标遮挡和丢失问题，提出了基于多视角运动轨迹重建的多目标跟踪算法，利用多视角之间单应性约束和空间位置约束关系，结合卡尔曼滤波解决目标在不连续情况下的跟踪问题。与相关算法的对比实验结果表明，本文利用多视角的信息更加有效地解决了多目标跟踪不连续性问题。本文在单应性估计和轨迹重建方面仍然有改进空间，可以通过提高特征点匹配的准确性进一步提高本文算法的准确性。