由于分数阶算子具有许多良好的性质,如记忆性和遗传性,近年来这一领域吸引了众多学者的研究。如:Zhang等[1]为分数阶系统提出了许多简化的LMI稳定性条件,Li等[2]研究了分数阶非线性动态系统的Mittag-Leffler稳定性等。
人工神经网络的概念由McCulloch等首次提出[3]。随后Hopfield提出了一个新的名为Hopfield神经网络的循环神经网络[4],这为解决优化问题和数值计算问题做了很大的贡献。目前,神经网络被广泛应用于许多的领域,例如,模型预测[5]、自动化控制[6]以及优化[7]。但大部分结果都假设系统的动态模型是整数阶的。然而,在很多实际应用中,分数阶微分方程能够更好的描述实际系统。目前,有许多关于分数阶神经网络同步问题的研究结果,如自适应同步[8]、全局同步[9-10]、有限时间同步[11-12]、
受文献[15-16]的启发,本文用
本部分主要介绍分数阶算子的定义和相关引理,这对于我们以后的分析是非常重要的。
定义1[18] 函数
| ${}_tI_{{t_0}}^\alpha f\left( t \right) = \frac{1}{{\varGamma \left( \alpha \right)}}{\int_{{t_{\rm{0}}}}^t {\left( {t - \tau } \right)} ^{\alpha - 1}}f\left( \tau \right){\rm d}\tau$ |
式中:
定义2[18] 函数
| ${}_{{t_0}}D_t^\alpha f\left( t \right) = \frac{1}{{\varGamma \left( {n- \alpha } \right)}}\int_{{t_0}}^t {\frac{{{f^{\left( n \right)}}}}{{{{\left( {t- \tau } \right)}^{\alpha- n + 1}}}}{\rm d}\tau } $ |
式中:
特别地,当
| ${}_{{t_0}}D_t^\alpha f\left( t \right) = \frac{1}{{\varGamma \left( {{\rm{1}} - \alpha } \right)}}\int_{{t_0}}^t {\frac{{{f'}\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^\alpha }}}{\rm d}\tau } $ |
引理1[19] 设函数
| ${}_{{t_0}}D_t^\alpha {\left( {g\left( t \right) - h} \right)^2} \leqslant 2\left( {g\left( t \right) - h} \right){}_{{t_0}}D_t^\alpha g\left( t \right)$ |
其中
引理2[20] 令
| ${}_{{t_0}}I_t^\alpha {}_{{t_0}}D_t^\alpha y\left( t \right) = y\left( t \right) - \sum\limits_{k = 0}^{n - 1} {\frac{{{y^{\left( k \right)}}\left( {{t_0}} \right)}}{{k!}}} {\left( {t - {t_0}} \right)^k}$ |
特别地,当
引理3[14] 假设
引理4[21](Gronwall-Bellman 不等式) 若存在
| $x\left( t \right) \leqslant \int_0^t {a\left( t \right)} b\left( \tau \right)\exp \left( {\int_\tau ^t {a\left( s \right){\rm d}s} } \right){\rm d}\tau + b\left( t \right)$ |
如果
| $ x\left( t \right)\!\! \leqslant \!\!b\left( 0 \right)\exp \left( {\int_0^t {\!\!\!a\left( \tau \right){\rm d}\tau } } \right) \!\!+\!\! \int_0^t {\!\!\dot b\!\left( \tau \right)} \exp \left( {\int_\tau ^t {\!\!\!\!a\left( s \right){\rm d}s} } \right){\rm d}\tau $ |
如果
| $x\left( t \right) \leqslant b\left( 0 \right)\exp \left( {\int_0^t {a\left( \tau \right){\rm d}\tau } } \right)$ |
引理5[22-23] Riemann-Liouville型分数阶非线性微分方程
| $\frac{{\partial {z_i}\left( {w, t} \right)}}{{\partial t}} = - w{z_i}\left( {w, t} \right) + {f_i}\left( {{{ x}_i}\left( t \right)} \right)$ |
| ${{ x}_i}\left( t \right) = \int_0^\infty {\mu \left( w \right){z_i}} \left( {w, t} \right){\rm d}w$ |
式中:
考虑如下分数阶神经网络作为驱动系统
| ${D^\alpha }{x_i}\left( t \right) \!=\! - {c_i}{x_i}\left( t \right) \!\!+\!\! \sum\limits_{j = 1}^n {{a_{ij}}{f_j}\left( {{x_j}\left( t \right)} \right)} \!+\! {I_i},\; i \!= \!1, 2, \cdots, n $ | (1) |
式中:
| $\left| {{f_j}\left( u \right) - {f_j}\left( v \right)} \right| \leqslant {L_j}\left| {u - v} \right|$ | (2) |
式中:
考虑如下响应系统:
| $ {D^\alpha }{y_i}\left( t \right) = - {c_i}{y_i}\left( t \right) + \sum\limits_{j = 1}^n {{{\hat a}_{ij}}(t)} {f_j}\left( {{y_j}\left( t \right)} \right) + {u_i}\left( t \right) + {{ w}_i}\left( t \right) $ | (3) |
式中:
| $ D \!\!=\!\! \left\{ \!\!{{w}}\left( {{t}} \!\right) \!\! = \!\!{\left[ \!\!{{ w}_1^{\rm T}\left(\! t \!\right)\;{ w}_2^{\rm{T}}\left( \!t \!\right)\!\cdots \;{ w}_N^{\rm T}\left( \!t\! \right)}\!\! \right]^{\rm{T}}}\left| {\int_0^\infty {\sum\limits_{i \!= \!1}^N {{ w}_{{i}}^{\rm{T}}\left( t \right){{ w}_i}\left( t \right){\rm d}t \leqslant {\beta ^2}} } } \right. \!\!\right\} $ |
其中
定义3[18] 称驱动系统(式(1))与响应系统(式(3))是全局渐近同步的,如果存在控制器
| $\mathop {\lim }\limits_{t \to \infty } \left| {{y_i}\left( t \right) - {x_i}\left( t \right)} \right| = 0, \quad i = 1, 2, \cdots, n$ |
考虑闭环系统的零输入响应,即研究当外部干扰不存在时系统式(1)和式(3)的同步问题。为此,设计如下自适应控制律:
| ${u_i}\left( t \right) = - {d_i}\left( t \right){e_i}\left( t \right) + {\hat I_i}\left( t \right)$ | (4) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{D^\alpha }{d_i}\left( t \right) = {k_i}{e_i}{\left( t \right)^2} $ | (5) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{D^\alpha }{\hat I_i}\left( t \right) = - {r_i}{e_i}\left( t \right) $ | (6) |
| ${D^\alpha }{\hat a_{ij}}\left( t \right) = - {l_{ij}}{f_j}\left( {{y_j}\left( t \right)} \right){e_i}\left( t \right) $ | (7) |
式中:
利用自适应控制律式(4)~(7),动态误差闭环系统可以写成如下形式:
| $\begin{array}{c} {D^\alpha }{e_i}\left( t \right) = - {c_i}{e_i}\left( t \right) + \displaystyle\sum\limits_{j = 1}^n {{{\hat a}_{ij}}(t)} {f_j}\left( {{y_j}\left( t \right)} \right) - \\ \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}} {f_j}\left( {{x_j}\left( t \right)} \right) + {{\tilde I}_i}\left( t \right) - {d_i}\left( t \right){e_i}\left( t \right) \\ \end{array}$ | (8) |
式中:
注1 我们通常所说的控制律(控制协议)是指一系列信息传输规则,当驱动系统采取该控制律时,可以与响应系统实现同步。与传统的控制律形成对比,本文设计了新的自适应控制律(4)~(7),且控制律中
定理1 对任给的正常数
证明 定义如下类似李雅普诺夫函数:
| $\begin{split} V\left( t \right) &= \sum\limits_{i = 1}^n {\frac{1}{2}} {e_i}{\left( t \right)^2} + \sum\limits_{i = 1}^n {\frac{1}{{2{k_i}}}} {\left( {{d_i}\left( t \right) - {d_i}} \right)^2} + \\ & \sum\limits_{i = 1}^n {\frac{1}{{2{r_i}}}{{\tilde I}_i}{{\left( t \right)}^2} + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\frac{1}{{2{l_{ij}}}}} } } {{\tilde a}_{ij}}{\left( t \right)^2} \\ \end{split}$ | (9) |
式中
注意到
| $\begin{array}{c} \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{j = 1}^n {{{\hat a}_{ij}}} (t){f_j}\left( {{y_j}\left( t \right)} \right) - \sum\limits_{j = 1}^n {{a_{ij}}} {f_j}\left( {{x_j}\left( t \right)} \right)= \\ \begin{array}{*{20}{c}} {}& \end{array}\displaystyle\sum\limits_{j = 1}^n {{{\tilde a}_{ij}}} (t){f_j}\left( {{y_j}\left( t \right)} \right) + \sum\limits_{j = 1}^n {{a_{ij}}} {f_j}\left( {{y_j}\left( t \right)} \right) - \sum\limits_{j = 1}^n {{a_{ij}}} {f_j}\left( {{x_j}\left( t \right)} \right)\leqslant \\ \begin{array}{*{20}{c}} {}& \end{array}\displaystyle\sum\limits_{j = 1}^n {{{\tilde a}_{ij}}} (t){f_j}\left( {{y_j}\left( t \right)} \right) + \sum\limits_{j = {\rm{1}}`}^n {{a_{ij}}{L_j}{e_j}(t)}, \\ \end{array} $ |
其中
利用引理1,计算系统(9)的
| $\begin{array}{c} {D^\alpha }V\left( t \right) = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\frac{1}{2}{D^\alpha }} {e_i}{\left( t \right)^2} + \sum\limits_{i = 1}^n {\frac{1}{{2{k_i}}}} {D^\alpha }{\left( {{d_i}\left( t \right) - {d_i}} \right)^2} + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {\frac{1}{{2{r_i}}}{D^\alpha }{{\tilde I}_i}{{\left( t \right)}^2} + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\frac{1}{{2{l_{ij}}}}} } } {D^\alpha }{{\tilde a}_{ij}}{\left( t \right)^2} \leqslant \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {{e_i}\left( t \right){D^\alpha }} {e_i}\left( t \right) + \sum\limits_{i = 1}^n {\frac{1}{{{k_i}}}} \left( {{d_i}\left( t \right) - {d_i}} \right){D^\alpha }{d_i}\left( t \right) + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{r_i}}}{{\tilde I}_i}\left( t \right){D^\alpha }{{\tilde I}_i}\left( t \right) + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\frac{1}{{{l_{ij}}}}{{\tilde a}_{ij}}\left( t \right)} } } {D^\alpha }{{\tilde a}_{ij}}\left( t \right)= \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {{e_i}\left( t \right)} \left[{-{c_i}{e_i}\left( t \right) + \sum\limits_{j = 1}^n {{{\hat a}_{ij}}(t)} {f_j}\left( {{y_j}\left( t \right)} \right)} \right] - \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {{e_i}\left( t \right)} \left[{\sum\limits_{j = 1}^n {{a_{ij}}} {f_j}\left( {{x_j}\left( t \right)} \right) + {{\tilde I}_i}\left( t \right)-{d_i}\left( t \right){e_i}\left( t \right)} \right] + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {\left( {{d_i}\left( t \right) - {d_i}} \right)} {e_i}{\left( t \right)^2} + \sum\limits_{i = 1}^n {{{\tilde I}_i}\left( t \right){D^\alpha }\left[{-{e_i}\left( t \right)} \right]} + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left[{-{{\tilde a}_{ij}}\left( t \right){f_j}\left( {{y_j}\left( t \right)} \right){e_i}\left( t \right)} \right]} } \\ \end{array} $ |
从而
| $\begin{array}{c} \displaystyle {D^\alpha }V(t) \leqslant \sum\limits_{i = 1}^n {\left\{ { - {c_i}e_i^2(t) + {e_i}(t)\sum\limits_{j = 1}^n {{{\tilde a}_{ij}}} {f_j}({y_j}(t))} \right.} + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\displaystyle \frac{1}{{{\varepsilon _i}}}\sum\limits_{j = 1`}^n {{\mu ^2}L_{_{_{jj}}^j}^2{e_j}{{(t)}^2}} + {\varepsilon _i}{e_i}{(t)^2} + {{\tilde I}_i}(t){e_i}(t) - \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}{d_i}(t){e_i}{(t)^2} + ({d_i}(t) - {d_i}){e_i}{(t)^2} - \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\displaystyle {{\tilde I}_i}(t){e_i}(t) - \left. {\sum\limits_{j = 1}^n {{{\tilde a}_{ij}}(t){f_j}({y_j}(t)){e_i}(t)} } \right\} = - \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\displaystyle \sum\limits_{i = 1}^n {{q_i}} {e_i}{(t)^2} \leqslant - \underline q \sum\limits_{i = 1}^n {{e_i}{{(t)}^2}} \\ \end{array} $ |
式中:
事实上,我们可以通过取足够大的
由引理2和3可得
| $V\left( t \right) - V\left( 0 \right) \leqslant - \frac{{{\rm{2}}\underline {\rm{q}} }}{{\varGamma \left( \alpha \right)}}{\int_0^t {\left( {t - \tau } \right)} ^{\alpha - 1}}U\left( \tau \right){\rm d}\tau $ |
其中
| $U\left( t \right) \leqslant V\left( t \right) \leqslant V\left( 0 \right) - \frac{{{\rm{2}}\underline q }}{{\varGamma \left( \alpha \right)}}{\int_0^t {\left( {t - \tau } \right)} ^{\alpha - 1}}U\left( \tau \right){\rm d}\tau $ |
利用引理4,可以得到
| $\begin{array}{c} U\left( t \right) \leqslant V\left( 0 \right)\exp \left( { - \displaystyle\frac{{{\rm{2}}\underline q }}{{\varGamma \left( \alpha \right)}}{{\int_0^t {\left( {t - \tau } \right)} ^{\alpha - 1}}}{\rm d}\tau } \right) = \\ \begin{array}{*{20}{c}} {}&{} \end{array}V\left( 0 \right)\exp \left( { - \displaystyle\frac{{{\rm{2}}\underline q }}{{\varGamma \left( {\alpha + {\rm{1}}} \right)}}{t^\alpha }} \right) \\ \end{array} $ |
所以
综上,利用控制律(4)~(7),响应系统与驱动系统可以实现自适应同步。
注2 在定理1中,我们只能保证驱动系统和响应系统可以实现同步。为了对所有的未知参数进行辨识,需要对激励函数
| ${D^\alpha }{e_i}\left( t \right) = \sum\limits_{j = 1}^n {\left( {{{\hat a}_{ij}}\left( t \right){\rm{ - }}{a_{ij}}} \right)} {f_j}\left( {{x_j}\left( t \right)} \right) = {\rm{0}}, j = 1, 2, \cdots, n$ |
根据函数线性无关的条件,当
注3 与其他相关文献中设计的控制协议相比,如文献[14],我们所考虑的是带有未知参数和未知外部输入的系统。因此,文献[14]中所考虑的模型是本文的特例。
3.2 自适应利用
定理 2 考虑驱动系统(式(1))和响应系统(式(3))。利用控制律式(4)和估计器即式(5)~(7),则对于给定
证明 由于在零初始条件下,Caputo型导数与Riemann-Liouville型导数等价,利用引理5,误差系统(8)和估计(5)~(7)可以用以下分布表示:
| $ \left\{ \begin{aligned} &\! \frac{{\partial {z_i}\left( {w, t} \right)}}{{\partial t}} \!\!=\!\! - w{z_i}\left( {w, t} \right) \!- \!{c_i}{e_i}\left( t \right) \!+\! \sum\limits_{j = 1}^n {{{\hat a}_{ij}}\left( t \right){f_j}\left( {{y_j}\left( t \right)} \right)} - \\ &\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{} \end{array}}\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle{\!\sum\limits_{j = 1}^n {{a_{ij}}{f_j}\left( {{x_j}\left( t \right)} \right)} \!\!+\!\! {{\tilde I}_i}\left( t \right) \!-\! {d_i}\left( t \right){e_i}\left( t \right) \!\!+\!\! {w_i}\left( t \right)} \end{array} \\ &\! {e_i}\left( t \right) = \int_0^\infty {\mu \left( w \right){z_i}\left( {w, t} \right){\rm d}w} \\ \end{aligned} \right.$ | (10) |
| $ \left\{ \begin{array}{c} \displaystyle\frac{{\partial {D_i}\left( {w, t} \right)}}{{\partial t}} = - w{D_i}\left( {w, t} \right) + {k_i}{e_i}{\left( t \right)^2} \\ {{\tilde d}_i}\left( t \right) = {\displaystyle\int}_0^{\infty} {\mu \left( w \right){D_i}\left( {w, t} \right){\rm d}w} \\ \end{array} \right.$ | (11) |
| $\quad \left\{ \begin{gathered} \frac{{\partial {A_{ij}}\left( {w, t} \right)}}{{\partial t}} = - w{A_{ij}}\left( {w, t} \right) - {l_{ij}}{f_j}\left( {{y_j}\left( t \right)} \right){e_i}\left( t \right) \\ {{\tilde a}_{ij}}\left( t \right) = \int_0^\infty {\mu \left( w \right){A_{ij}}\left( {w, t} \right){\rm d}w} \\ \end{gathered} \right.$ | (12) |
| $\left\{ \begin{array}{c} \displaystyle\frac{{\partial {B_i}\left( {w, t} \right)}}{{\partial t}} = - w{B_i}\left( {w, t} \right) - {r_i}{e_i}\left( t \right) \\ {{\tilde I}_i}\left( t \right) = \displaystyle\int_0^\infty {\mu \left( w \right){B_i}\left( {w, t} \right){\rm d}w} \\ \end{array} \right.$ | (13) |
式中:
| $\begin{array}{c} V\left( t \right) = \displaystyle\frac{1}{2}\sum\limits_{i = 1}^n {\int_0^\infty {\mu \left( w \right){z_i}{{\left( {w, t} \right)}^2}{\rm d}w} } + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\frac{1}{{2{l_{ij}}}}} } \int_0^\infty {\mu \left( w \right){A_{ij}}{{\left( {w, t} \right)}^2}{\rm d}w} + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{2{r_i}}}} \int_0^\infty {\mu \left( w \right)} {B_i}{\left( {w, t} \right)^2}{\rm d}w + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{2{k_i}}}} \int_0^\infty {\mu \left( w \right)} {D_i}{\left( {w, t} \right)^2}{\rm d}w \\ \end{array} $ |
从而
| $\begin{array}{c} \dot V\left( t \right) = \displaystyle\sum\limits_{i = 1}^n {\int_0^\infty {\mu \left( w \right){z_i}\left( {w, t} \right)\frac{{\partial {z_i}}}{{\partial t}}{\rm d}w} } + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\frac{1}{{{l_{ij}}}}} } \int_0^\infty {\mu \left( w \right){A_{ij}}\left( {w, t} \right)\frac{{\partial {A_{ij}}}}{{\partial t}}{\rm d}w} + \\ \begin{array}{*{20}{c}} {}&{} \end{array} \displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{r_i}}}\int_0^\infty {\mu \left( w \right)} {B_i}\left( {w, t} \right)\frac{{\partial {B_i}}}{{\partial t}}{\rm d}w} + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{k_i}}}} \int_0^\infty {\mu \left( w \right)} {D_i}\left( {w, t} \right)\frac{{\partial {D_i}}}{{\partial t}}{\rm d}w \\ \end{array} $ |
利用不等式
| $\begin{array}{c} \dot V\left( t \right) \leqslant \displaystyle\sum\limits_{i = 1}^n {\left\{ {{\rm{ - }}\left( {{{{d}}_{\rm{i}}} + {c_i} - \left( {\sum\limits_{j = 1}^n {\frac{1}{{{\varepsilon _j}}}} } \right)L_i^2{\mu ^2} - {\varepsilon _i}} \right){e_i}{{\left( t \right)}^2}} \right\}} + \\ \begin{aligned} {}&{} \end{aligned}\displaystyle\sum\limits_{i = 1}^n {\left\{ {{e_i}\left( t \right){w_i}\left( t \right)} \right\}} \leqslant \\ \begin{aligned} {}&{} \end{aligned} \displaystyle\sum\limits_{i = 1}^n {\left\{ { - \left( {{{{d}}_{\rm{i}}} + {c_i} - \left( {\sum\limits_{j = 1}^n {\frac{1}{{{\varepsilon _j}}}} } \right)L_i^2{\mu ^2} - {\varepsilon _i} - \frac{1}{\gamma }} \right){e_i}{{\left( t \right)}^2}} \right\}} + \\ \begin{aligned} {}&{} \end{aligned}\displaystyle\sum\limits_{i = 1}^n {\left\{ {\gamma {w_i}{{\left( t \right)}^2}} \right\}} \end{array} \\$ |
| $\begin{gathered} \dot V\left( t \right) + \sum\limits_{i = 1}^n {{e_i}{{\left( t \right)}^2}} - \gamma \sum\limits_{i = 1}^n {{w_i}{{\left( t \right)}^2}} \leqslant \\ \sum\limits_{i = 1}^n {\left\{ { - \left( {{{{d}}_{{i}}} + {c_i} - \left( {\sum\limits_{j = 1}^n {\frac{1}{{{\varepsilon _j}}}} } \right)L_i^2{\mu ^2} - {\varepsilon _i} - \frac{1}{\gamma } - 1} \right)} \right\}} {e_i}{\left( t \right)^2} \\ \end{gathered} $ |
可以通过取足够大的
| $ {{{{d}}_{{i}}} + {c_i} - \left( {\sum\limits_{j = 1}^n {\frac{1}{{{\varepsilon _j}}}} } \right)L_i^2{\mu ^2} - {\varepsilon _i} - \frac{1}{\gamma } - 1} > 0 $ |
从而有
注4 目前,关于
通过给出的仿真实例来验证我们所提出的控制器在实现自适应同步和
例:对于驱动系统(式(1)),响应系统(式(3))以及控制协议即式(4)~(7),令
以及
| ${{A}} = { \left( {{{{a}}_{{{ij}}}}} \right)_{{{3}} \times {{3}}}} = \left[ {\begin{array}{*{20}{c}} 2&{ - 1.2}&0 \\ {1.8}&{1.71}&{1.15} \\ { - 4.75}&0&{1.1} \end{array}} \right]$ |
选取初始条件为
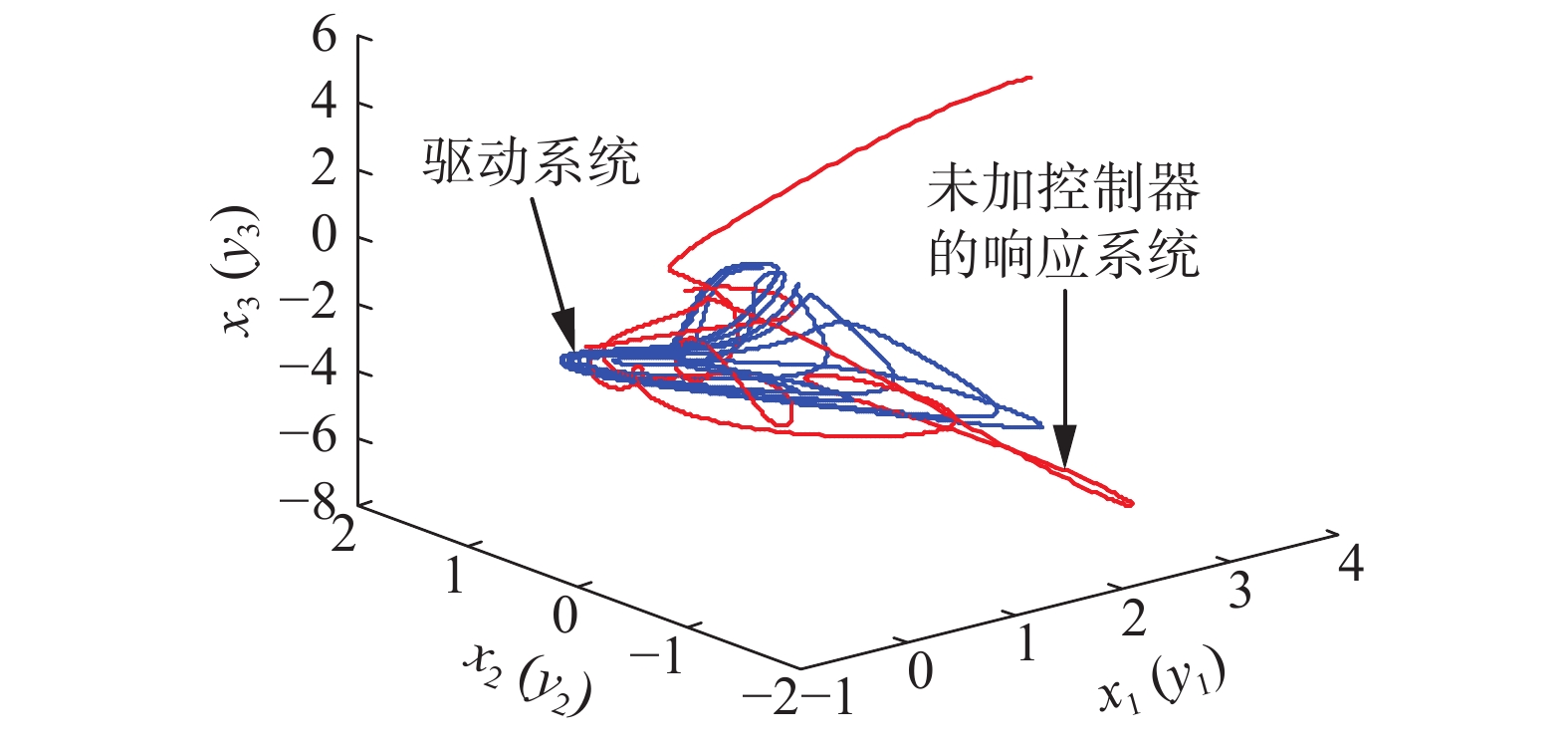
图1为驱动系统(1)和未加控制器的响应系统(3)的状态轨迹图,显然两个系统并没有实现同步。
|
Download:
|
| 图 1 驱动系统(1)与未加控制器的响应系统(3)状态图 Fig. 1 States of drive system (1) and response system (3) without controller | |
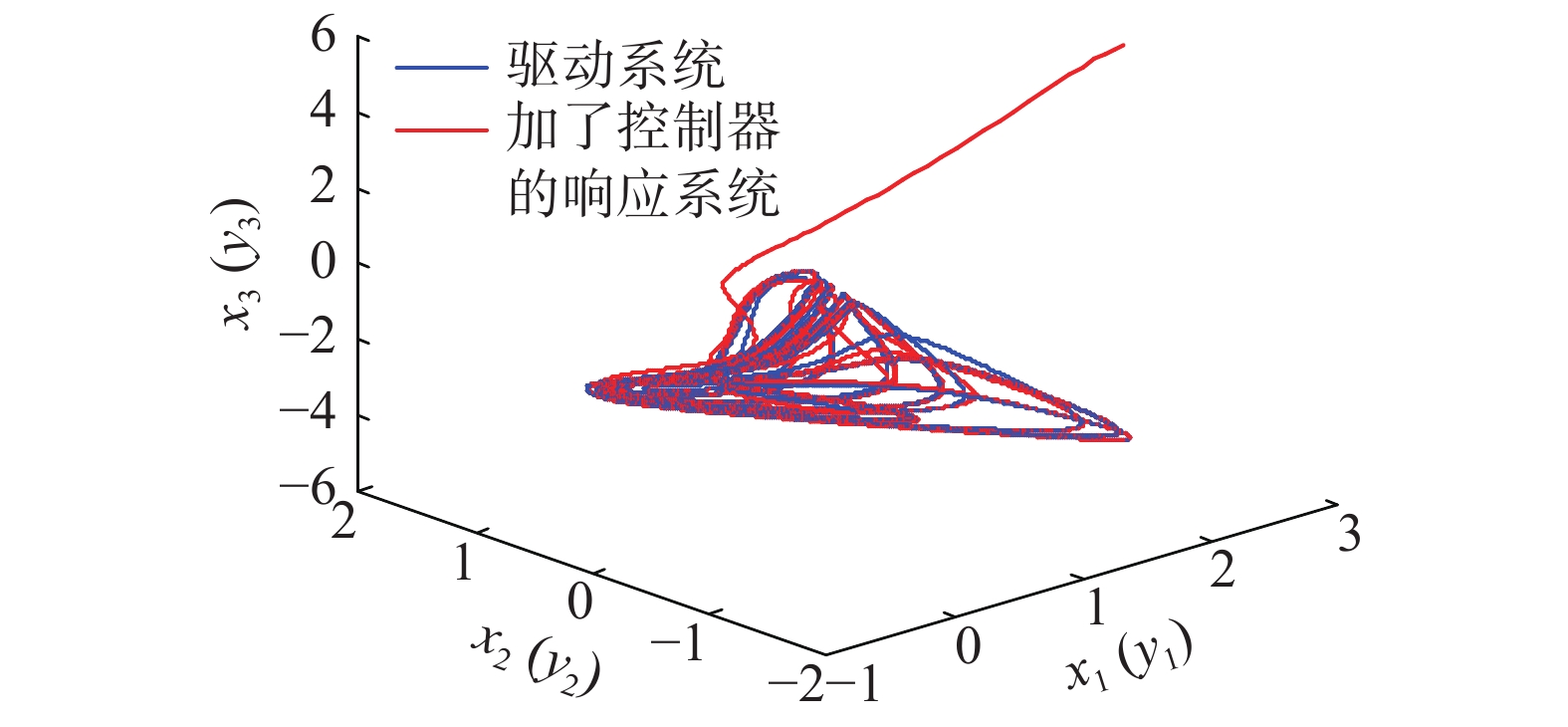
图2为驱动系统(1)和加了控制律(4)~(7)的响应系统(3)的状态轨迹图,该图显示利用控制律(4)~(7)这两个系统实现了同步。
|
Download:
|
| 图 2 驱动系统(1)与加控制律响应系统(3)状态图 Fig. 2 States of drive system (1) and response system (3) with controller | |
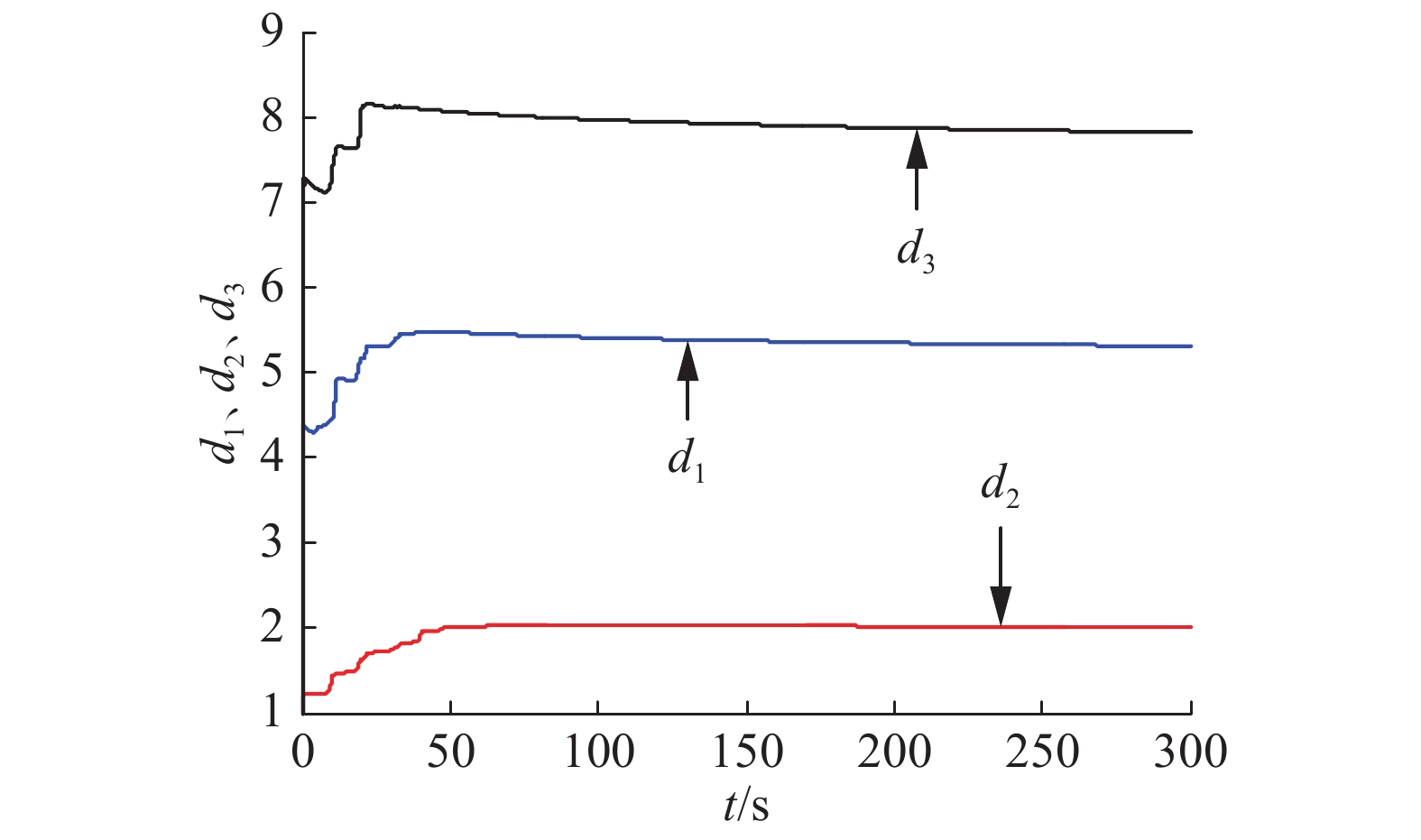
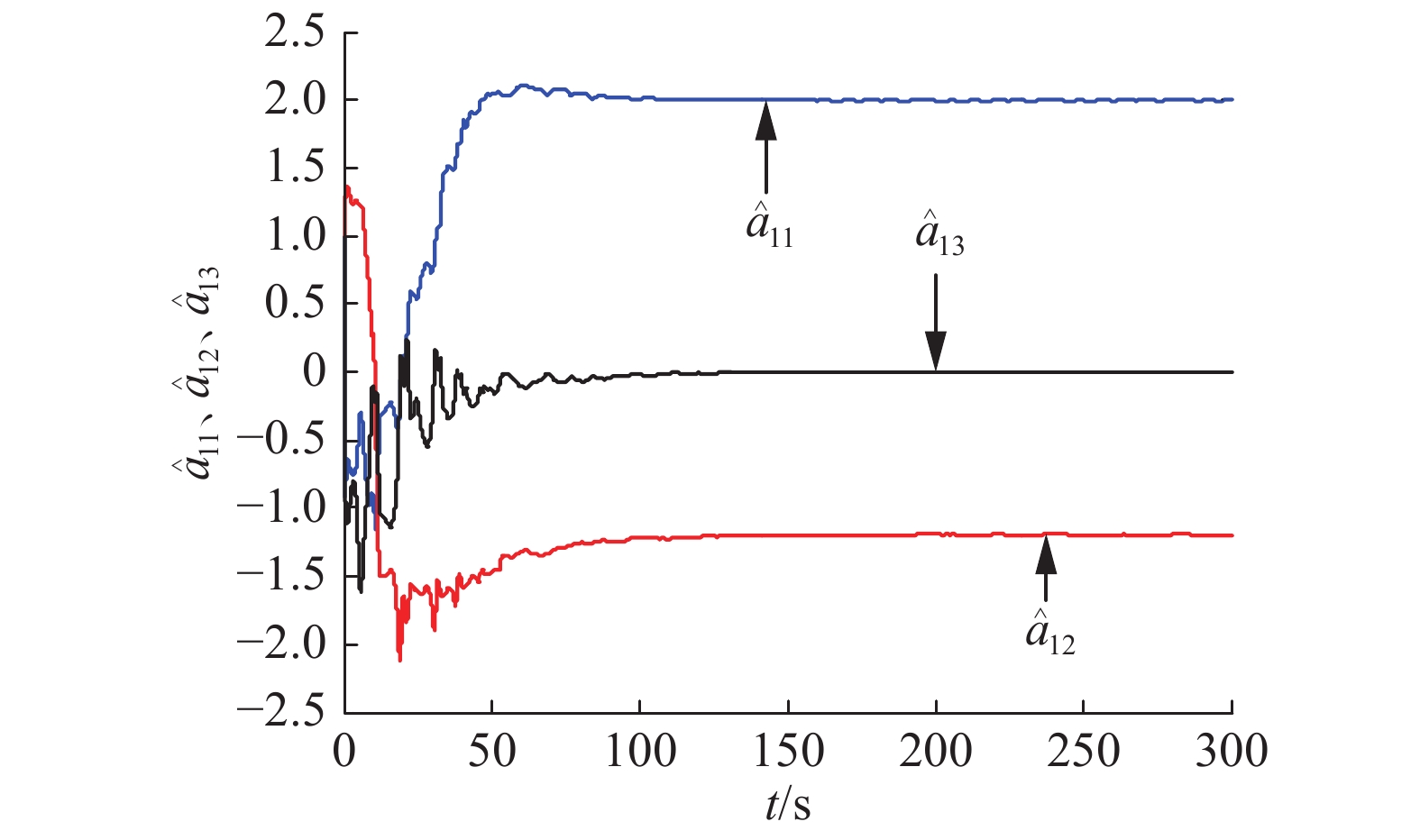
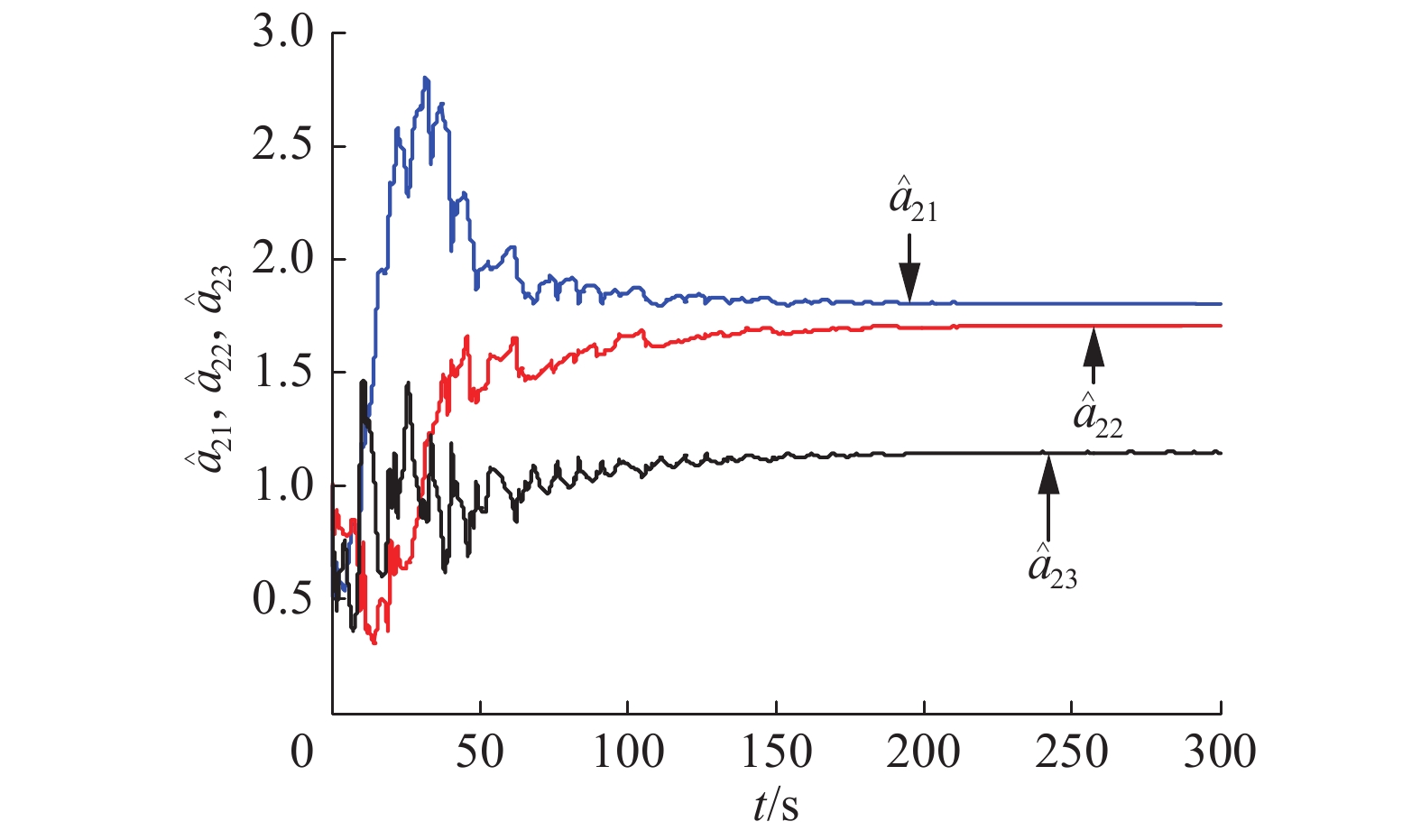
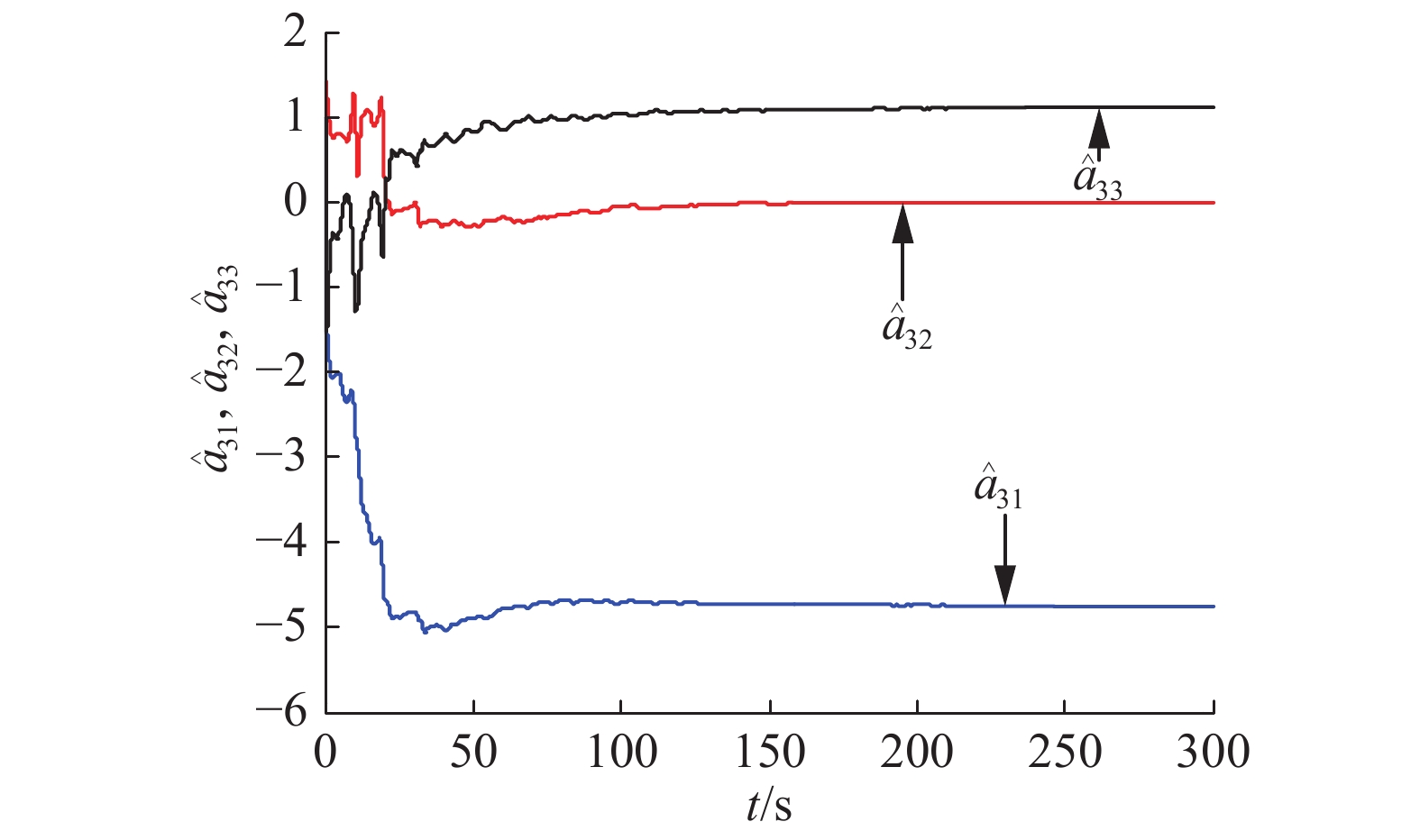
图3为控制强度,当时间趋于无穷时它们都收敛到一个确定的常数。从图4~6可以看出响应系统中(3)中所有的未知参数可以很好地辨识出来,辨识值为
|
Download:
|
|
图 3 |
|
|
Download:
|
|
图 4 |
|
|
Download:
|
|
图 5 |
|
|
Download:
|
|
图 6 |
|
| $\begin{gathered} {{\hat a}_{11}} = 1.99, {{\hat a}_{12}} = - 1.2, {{\hat a}_{13}} = 0, {{\hat a}_{21}} = 1.8, {{\hat a}_{22}} = 1.7, \\ {{\hat a}_{23}} = 1.15, {{\hat a}_{31}} = - 4.75, {{\hat a}_{32}} = 0, {{\hat a}_{33}} = 1.1 \\ \end{gathered} $ |
与权重矩阵
若将初始值改变为
| $\begin{aligned} &{{{x}}^{\rm{T}}}\left( {{0}} \right) = {\left[ {\begin{array}{*{20}{c}} {0.3}&{ - 0.4}&{\!0.9} \end{array}} \right]^{\rm{T}}},\\ &{{{y}}^{\rm{T}}}\left( {{0}} \right) = {\left[ {\begin{array}{*{20}{c}} \! {0.3}&{ - 0.4}&{\!0.9} \end{array}} \right]^{\rm{T}}} \end{aligned}$ |
并且添加条件:
| $ {w_i}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} 1,&{0 < t < 1} \\ 0,&{\text{其他}} \end{array}} \right. $ |
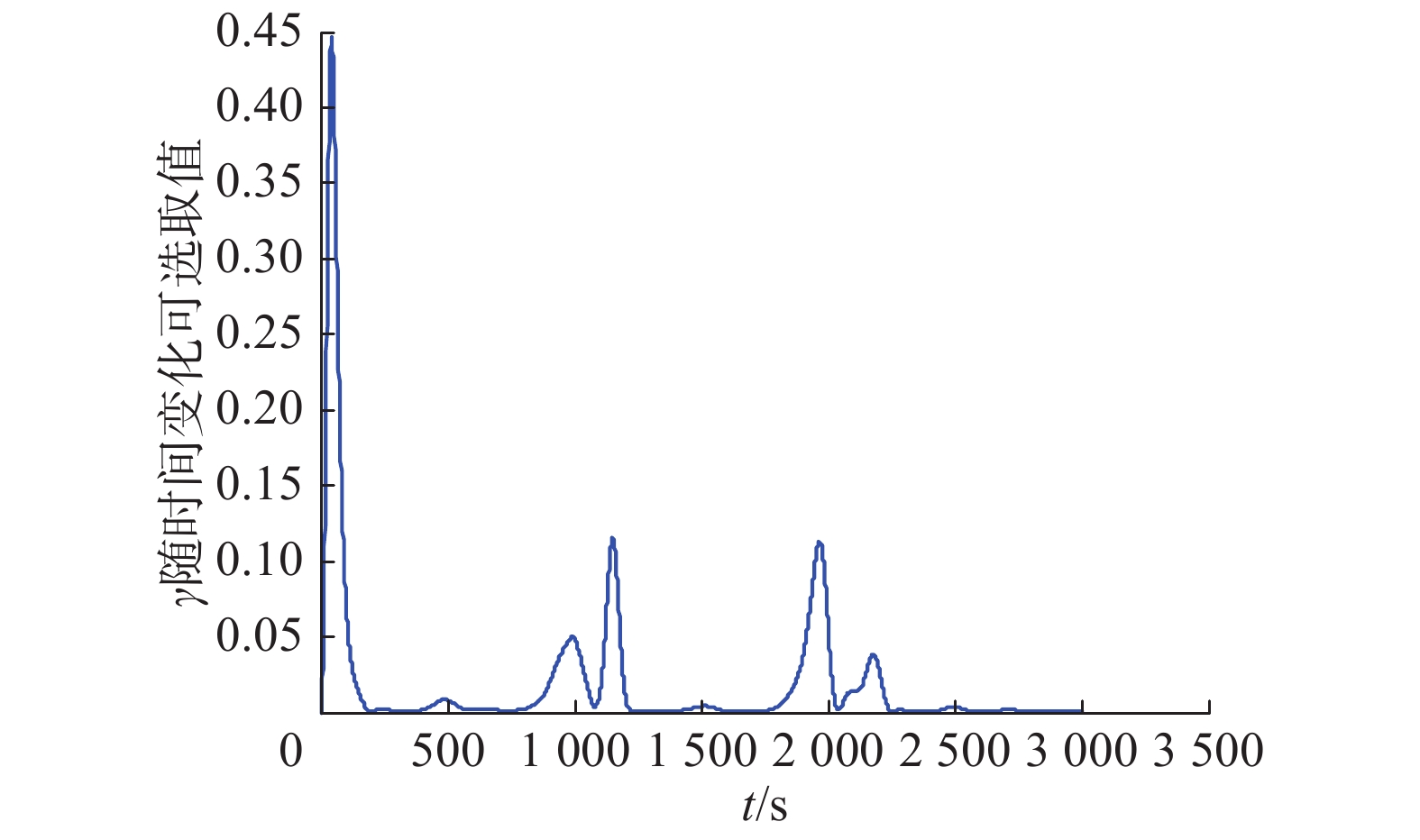
式中i = 1,2,3。通过图7可以读出
|
Download:
|
|
图 7 |
|
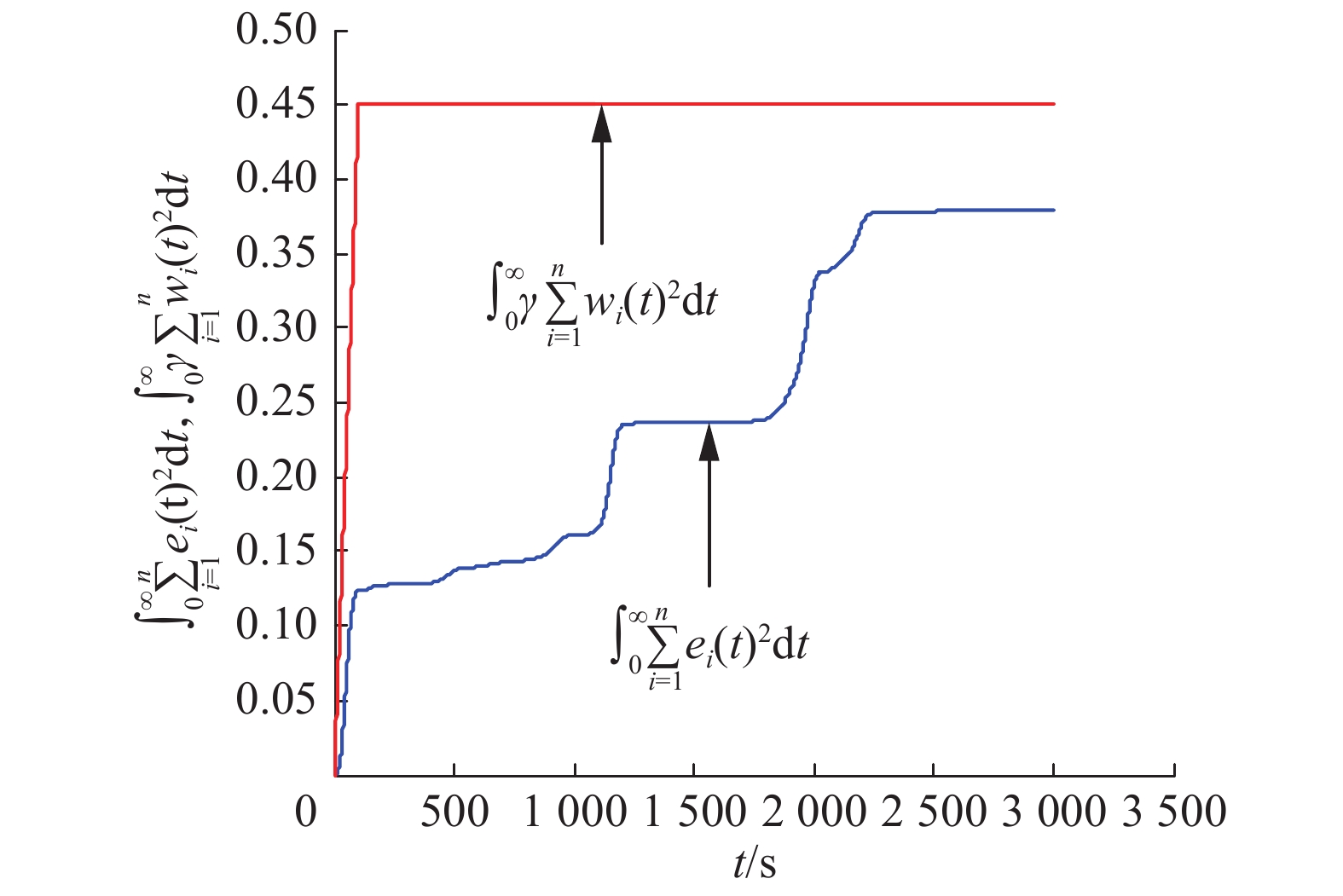
图8显示当
| $\int_{\rm{0}}^\infty {\sum\limits_{i = 1}^n {{e_i}{{\left( t \right)}^2}} {\rm d}t} < \int_{\rm{0}}^\infty {\gamma \sum\limits_{i = 1}^n {{w_i}{{\left( t \right)}^2}} } {\rm d}t$ |
即满足
|
Download:
|
|
图 8 |
|
本文针对一类不确定分数阶神经网络系统,本文研究了其自适应
然而,本文所考虑的是理想化的网络模型,在实际应用中,时滞总是存在于神经元之间的通讯过程中,并对系统的稳定性产生严重的影响,进而影响对未知参数的辨识精度。注意到,目前还没有关于此方面比较好的研究结果,因此,有必要设计相关的控制协议来抵消时滞对系统稳定性造成的影响。在未来的研究中,我们将进一步针对带有时滞的不确定分数阶神经网络,设计相关的控制协议,从而对系统中的未知参数进行精确地辨识,同时使系统实现同步。
| [1] |
ZHANG Shou, YU Yongguang, YU Junzhi. LMI conditions for global stability of fractional-order neural networks[J]. IEEE transactions on neural networks and learning systems, 2017, 28(10): 2423-2433. DOI:10.1109/TNNLS.2016.2574842 ( 0) 0)
|
| [2] |
LI Yan, CHEN Yangquan, PODLUBNY I. Mittag-Leffler stability of fractional order nonlinear dynamic systems[J]. Automatica, 2009, 45(8): 1965-1969. DOI:10.1016/j.automatica.2009.04.003 ( 0) 0)
|
| [3] |
HAYMAN S. The McCulloch-pitts model[C]//International Joint Conference on Neural Networks. Washington, USA, 1999: 4438–4439.
( 0) 0)
|
| [4] |
HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the national academy of sciences of the United States of America, 1982, 79(8): 2554-2558. DOI:10.1073/pnas.79.8.2554 ( 0) 0)
|
| [5] |
YAN Zheng, WANG Jun. Robust model predictive control of nonlinear systems with unmodeled dynamics and bounded uncertainties based on neural networks[J]. IEEE transactions on neural networks and learning systems, 2014, 25(3): 457-469. DOI:10.1109/TNNLS.2013.2275948 ( 0) 0)
|
| [6] |
PAN Yunpeng, WANG Jun. Robust model predictive control using a discrete-time recurrent neural network[C]// International Symposium on Neural Networks: advances in Neural Networks. Berlin, Heidelberg, Germany: , 2008: 883–892.
( 0) 0)
|
| [7] |
KASLIK E, SIVASUNDARAM S. Multistability in impulsive hybrid Hopfield neural networks with distributed delays[J]. Nonlinear analysis: real world applications, 2011, 12(3): 1640-1649. DOI:10.1016/j.nonrwa.2010.10.018 ( 0) 0)
|
| [8] |
BAO Haibo, PARK J H, CAO Jinde. Adaptive synchronization of fractional-order memristor-based neural networks with time delay[J]. Nonlinear dynamics, 2015, 82(3): 1343-1354. DOI:10.1007/s11071-015-2242-7 ( 0) 0)
|
| [9] |
CHEN Jiejie, ZENG Zhigang, JIANG Ping. Global mittag-leffler stability and synchronization of memristor-based fractional-order neural networks[J]. Neural networks, 2014, 51: 1-8. DOI:10.1016/j.neunet.2013.11.016 ( 0) 0)
|
| [10] |
WU Wei, CHEN Tianping. Global synchronization criteria of linearly coupled neural network systems with time-varying coupling[J]. IEEE transactions on neural networks, 2008, 19(2): 319-332. DOI:10.1109/TNN.2007.908639 ( 0) 0)
|
| [11] |
VELMURUGAN G, RAKKIYAPPAN R, CAO Jinde. Finite-time synchronization of fractional-order memristor-based neural networks with time delays[J]. Neural networks, 2016, 73: 36-46. DOI:10.1016/j.neunet.2015.09.012 ( 0) 0)
|
| [12] |
ABDURAHMAN A, JIANG Haijun, TENG Zhidong. Finite-time synchronization for memristor-based neural networks with time-varying delays[J]. Neural networks, 2015, 69: 20-28. DOI:10.1016/j.neunet.2015.04.015 ( 0) 0)
|
| [13] |
YU Juan, HU Cheng, JIANG Haijun. α-stability and α-synchronization for fractional-order neural networks
[J]. Neural networks, 2012, 35: 82-87. DOI:10.1016/j.neunet.2012.07.009 ( 0) 0)
|
| [14] |
MA Weiyuan, LI Changpin, WU Yujiang, et al. Adaptive synchronization of fractional neural networks with unknown parameters and time delays[J]. Entropy, 2014, 16(12): 6286-6299. DOI:10.3390/e16126286 ( 0) 0)
|
| [15] |
LIN Peng, JIA Yingmin, LI Lin. Distributed robust H∞ consensus control in directed networks of agents with time-delay
[J]. Systems and control letters, 2008, 57(8): 643-653. DOI:10.1016/j.sysconle.2008.01.002 ( 0) 0)
|
| [16] |
MO L, JIA Y. H∞ consensus control of a class of high-order multi-agent systems
[J]. IET control theory and application, 2011, 5(1): 247-253. DOI:10.1049/iet-cta.2009.0365 ( 0) 0)
|
| [17] |
MATHIYALAGAN K, ANBUVITHYA R, SAKTHIVEL R, et al. Non-fragile H∞ synchronization of memristor-based neural networks using passivity theory
[J]. Neural networks, 2016, 74: 85-100. DOI:10.1016/j.neunet.2015.11.005 ( 0) 0)
|
| [18] |
PODLUBNY I. Fractional differential equations: mathematics in science and engineering[M]. San Diego, Calif, USA: Academic Press, 1999.
( 0) 0)
|
| [19] |
AGUILA-CAMACHO N, DUARTE-MERMOUD M A, GALLEGOS J A. Lyapunov functions for fractional order systems[J]. Communications in nonlinear science and numerical simulation, 2014, 19(9): 2951-2957. DOI:10.1016/j.cnsns.2014.01.022 ( 0) 0)
|
| [20] |
KILBAS A A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equations[M]. Boston: Elsevier, 2006.
( 0) 0)
|
| [21] |
SLOTINE J J E, LI Weiping. Applied nonlinear control[M]. Beijing, China Machine Press, 2004.
( 0) 0)
|
| [22] |
TRIGEASSOU J C, MAAMRI N, SABATIER J, et al. A lyapunov approach to the stability of fractional differential equations[J]. Signal processing, 2011, 91(3): 437-445. DOI:10.1016/j.sigpro.2010.04.024 ( 0) 0)
|
| [23] |
TRIGEASSOU J C, MAAMRI N. State space modeling of fractional differential equations and the initial condition problem[C]//Proceedings of the 6th International Multi-Conference on Systems, Signals and Devices. Djerba, Tunisia, 2009: 1–7.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


