风的间歇性和随机性,增加了风电机组的控制难度,尤其是在额定风速以上,对于主动变桨型风力发电机组需要更加安全可靠的变桨控制策略。变桨系统作为变速恒频风电机组的重要一部分,通常用在中、大型的风力发电系统中,其主要的控制目标是保持额定风速以上的功率恒定,限制风电机组的气动转矩和额外的功率吸收,减轻机组各部件的疲劳载荷[1-3]。目前变桨控制器广泛使用的仍然是PI(D)控制器,此类控制器存在一些明显的缺陷,如参数不能自动调整、参数依赖程度强、鲁棒性低等[4-5]。国内、外专家学者在变桨控制中使用了一些更加先进的控制方法,如蜂群算法、滑模变结构、神经网络等。蜂群算法取得了良好的鲁棒性,但其稳定性差,当风电系统出现随机干扰时,系统易出现不稳定[6];滑模变结构控制取得了良好的快速性和较强的鲁棒性,但其存在高频抖振问题,与神经网络和模糊控制等相结合的改进算法设计变桨控制器,达到了一定的控制效果,也无法从根本消除这一问题[7-8];RBF神经网络变桨控制器取得了较强的适应性,较好的鲁棒性和动态性能,但其结构和参数确定较为复杂[9-10];这些控制方法较为复杂且难以硬件实现。模糊控制器拥有优良快速性与鲁棒性,模糊自适应控制器可自动地在线调整参数,二者都是依据专家经验设计而成,已相对成熟且已硬件实现;多模态控制比单一控制有更好的抗干扰性能;本文将以上两种智能控制方式与传统的PI控制相结合于多模态控制中,提出了基于T-S型模糊加权的多模软切换变桨控制策略。将检测到的发电机的转速与其额定转速进行比较,大偏差时利用模糊控制的快速性优势迅速减小偏差、抑制偏差的快速变化;中等偏差时切换到模糊自适应PID控制,进行在线时时调整;小偏差时切换到PI控制,提高稳态精度。切换时根据发电机的转速与其额定转速的偏差大小及其变化率,利用T-S型模糊推理,使用加权平均法进行清晰化,输出3种模态的权值,使用加权求和法合成输出控制量。
1 风电系统数学模型 1.1 风速模型风在流动的过程中具有很强的随机性和突变性,为了准确描述风速的变化特性,本文采用风速的四分量模型[11-12],即将风速分解为基本风vb、阵风vg、渐变风vr和随机风vn。其组合风vw可表示为
| ${v_{{w}}} = {v_{{b}}} + {v_{{g}}} + {v_{{r}}} + {v_{{n}}}$ | (1) |
| ${v_{{b}}} = l \cdot \varGamma (1 + 1/s)$ | (2) |
| ${v_{\rm{r}}} = \left\{ \begin{array}{l} {\rm{ }}0,\quad{\rm{ 0 < }}t{\rm{ < }}{t_{{\rm{1r}}}},{\rm{ }}t \geqslant {t_{{{2r}}}} + {t_{{r}}} \\ {v_{{\rm{rmax}}}}(1 -\displaystyle \frac{{t - {t_{{{2r}}}}}}{{{t_{{{1r}}}} - {t_{2r}}}}){\rm{ }},\quad{t_{{{1r}}}} \leqslant t < {t_{{{2r}}}} \\ {v_{{\rm{rmax}}}},\quad{\rm{ }}{t_{2{{r}}}} \leqslant t < {t_{{{2r}}}} + {t_{{r}}} \\ \end{array} \right.$ | (3) |
| ${v_{{g}}} = \left\{ \begin{array}{l} 0,\quad{\rm{ 0 < }}t{\rm{ < }}{t_{{{1g}}}}{\rm{, }}t \geqslant {t_{{{1g}}}} + {t_{{g}}} \\ \displaystyle\frac{{{v_{{\rm{gmax}}}}}}{2}[1 - {\rm{cos}}(2{\text{π}}\frac{{t - {t_{1g}}}}{{{t_{1g}} - {t_{{g}}}}})],\quad{\rm{ }}{t_{1g}} \leqslant t < {t_{1g}} + {t_{g}} \\ \end{array} \right.$ | (4) |
| ${v_{{n}}} = 2\sum\limits_{i = 1}^n {\sqrt {{S_{\rm{r}}}({\omega _{{i}}})\Delta {\omega _{\rm{0}}}} } \cos ({\omega _{{i}}}t + {\phi _{{i}}})$ | (5) |
式中:
| $\left\{ \begin{array}{l} {P_{{m}}}{\rm{ = }} \displaystyle\frac{1}{2}{\text{π}} \rho {R^2}{C_{\rm{P}}}(\beta ,\lambda ){v^3} \\ {T_{{m}}} = {P_{{m}}}/{\omega _{{f}}} = \displaystyle\frac{1}{2}{\text{π}}{C_{\rm{P}}}(\beta ,\lambda ){v^2}/\lambda \\ \lambda = R{\omega _{{f}}}/v \\ {C_{{P}}} = 0.517\;6(116{\lambda _1} - 0.4\beta - 5){{\rm{e}}^{ - 21/{\lambda _1}}} + 0.006\;8{\lambda _1} \\ \end{array} \right.$ | (6) |
式中:
变桨的精度与灵敏度对功率有着很大的影响。其执行机构由伺服电机或液压装置驱动,可等效为一个一阶惯性环节:
| ${G_{{\rm{pitch}}}}(s) = \frac{{\beta (s)}}{{{\beta _{{\rm{ref}}}}(s)}} = \frac{1}{{{\tau _{{b}}}s + 1}}$ | (7) |
式中:
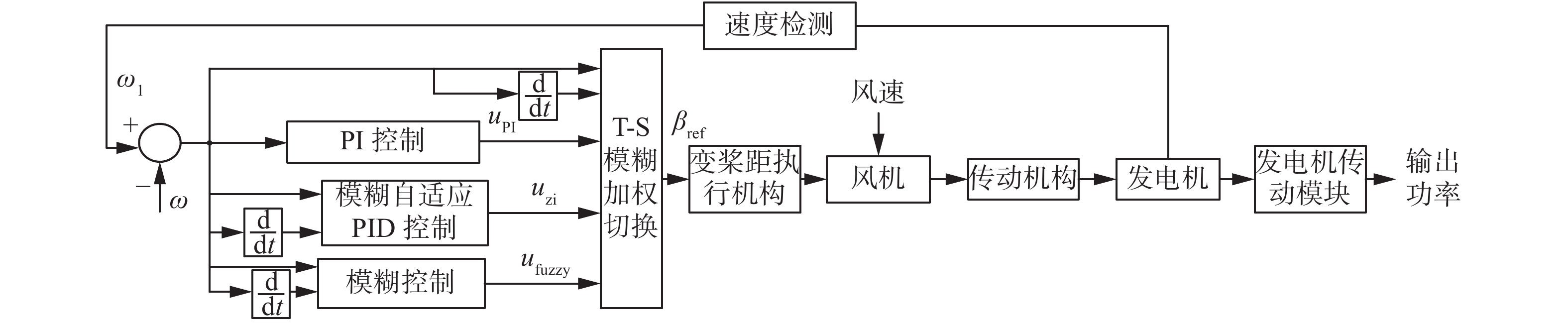
变桨控制是一种确保风电机组恒功率输出的有效方法,减小额定风速以上风力发电机机组的过载,确保风电机组的最高效运行。通过控制桨距角限制风机的气动转矩,从而限制了额外功率的吸收,减轻了机组的疲劳载荷,使风电机组的机械功率保持恒定。在很多控制方案中,桨叶的转速根据测量的风速实时修正,由于风在桨叶表面的每一点是不同的,故这种控制方案是不精确的。转速与功率结合控制会造成转速在最优运行点的输出振荡,降低了风电机组运行的可靠性[15-17]。本文通过测量发电机的转速来对桨距角进行控制,限制风轮吸收的功率,以此来稳定机组的输出功率。整体的控制框图如图1所示,ω为发电机的额定转速,ω1为实测转速。发电机的转速与其额定转速的偏差及其变化率经过T-S型模糊推理输出3种控制模态的权值,将3种权值加权到对应的模态控制来实现多模软切换,多模软切换控制的控制策略就是在大偏差时利用模糊控制的快速性优势迅速减小偏差、抑制偏差的快速变化,中等偏差时利用模糊自适应PID控制在线实时调整,在小偏差时切换为PI控制,提高控制的稳态精度。为了保证3种控制器之间的切换不会造成输出量的振荡,三者的切换采用基于T-S型模糊推理环节来实现,模糊推理采用加权平均法输出各模态的权值,合成输出采用加权求和法输出控制量,确保3种控制之间的平滑过渡。合理的设置偏差的论域和模糊论域,能兼顾3种控制方法的优势。
|
Download:
|
| 图 1 T-S模糊加权变桨距控制框图 Fig. 1 Block diagram of T-S fuzzy weighted variable pitch control | |
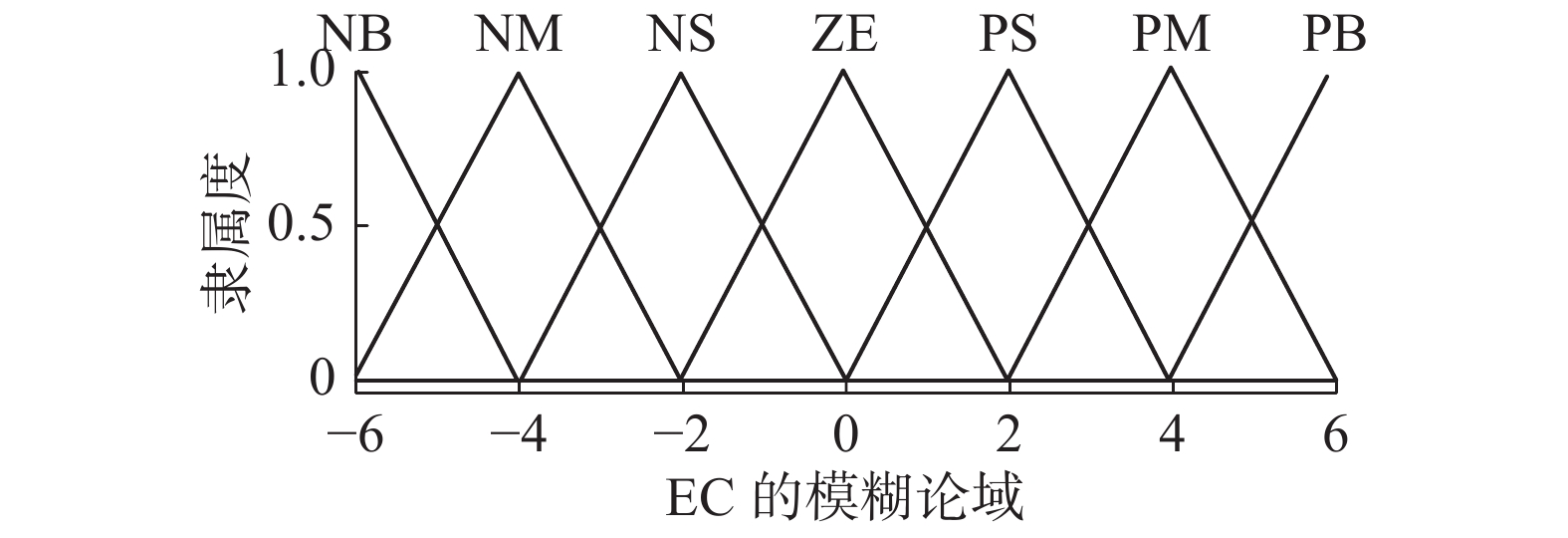
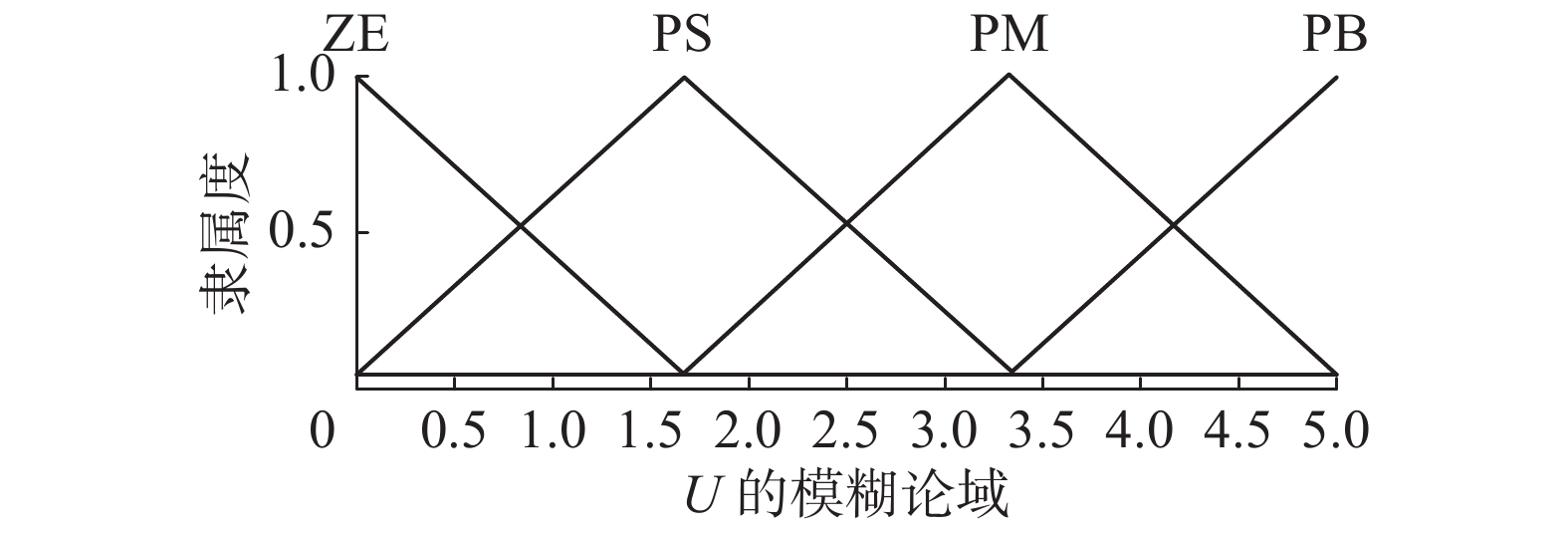
模糊控制器采用二维模糊控制器。设发电机的转速与其额定转速的偏差为E,其变化率为EC。额定风速以上时,此时发电机的转速高于额定转速,偏差为正,采用单边模糊控制。又知发电机的额定转速为27.8 r/min=2.91 rad/s,E的基本论域为[0,8],EC的基本论域为[–10,10],故设E的模糊论域为[0,4],EC的模糊论域为[–6,6]。工程应用中要求桨距角在0°~25°之间变化,且不考虑负值,设控制量U的基本论域为[0,30],其模糊论域为[0,5]。E、EC和U的隶属函数类型均取为三角型,分别如图2~4所示。设E的模糊子集

|
Download:
|
| 图 2 E的隶属函数 Fig. 2 The membership of E | |
|
Download:
|
| 图 3 EC的隶属函数 Fig. 3 The membership of EC | |
|
Download:
|
| 图 4 U的隶属函数 Fig. 4 The membership of U | |
| 表 1 |
发电机的转速与其额定转速的偏差E及其变化率EC作为模糊自适应PID控制器的两个输入,利用模糊规则在线实时地调整PID的3个参数,实现对ΔkP、ΔkI、ΔkD参数的自整定。E和EC的基本论域与模糊论域同模糊控制的设置一样。ΔkP、ΔkI、ΔkD的模糊论域分别设置为[–6,6],[–3,3],[–6,6],设E的模糊子集{PB,PM,PS},EC模糊子集为{NB,NM,NS,ZE,PS,PM,PB},ΔkP、ΔkI、ΔkD的模糊子集分别设置为{NM,NS,ZE,PS,PM,PB},{NM,NS,ZE,PS,PM,PB},{NB,NM,NS,ZE,PS,PM,PB},E、EC、ΔkP、ΔkI、ΔkD的隶属函数均为三角型,ΔkP、ΔkI、ΔkD的模糊控制规则表,如表2~4所示。
| 表 2 |
| 表 3 |
| 表 4 |
PI控制是PID控制的一种特例,当系统的偏差较小时,采用PI控制可以使控制系统具有较好的稳态性能。
3 基于T-S型模糊加权的多模软切换设计 3.1 设计原理T-S型是一种适于表达复杂系统的动态特性,其输出的隶属函数可以是线性的或者是单点常数[18]。本文主要利用T-S型模糊推理的隶属函数为单点常数使得其输出为单点常数这一特点来实现软过渡。区别于传统的切换方法只在某一阈值进行切换,本文引入了偏差及其导数,在到达阈值的前几个时刻,此时偏差小于设定的阈值,若偏差的变化率较大,本文使用的方法就进行了模态切换;同样,在到达偏差的后几个时刻,此时偏差大于设定的阈值,若偏差的变化率较小,本文使用的方法就不进行模态切换;具体的切换时刻由T-S型模糊推理实现,这也充分利用了模糊控制智能化的优势。T-S型模糊加权多模切换设计的目的是利用T-S型模糊推理平滑多种控制模态的输出,T-S型模糊加权切换的输出为模态的权值。其基本思想是根据系统的转速误差信息,需要在3个模态之间进行切换时,引入转速偏差和其导数进行模态切换判断,应用T-S型模糊推理方法,清晰化采用加权平均法,得到切换过程中3个模态的权值,使用加权求和法将3个模态的权值加权到3个模态的输出,从而平滑控制器的输出,实现T-S型模糊加权多模软切换。
令
T-S型模糊加权算法的模态划分取决于发电机的转速与其额定转速的偏差E及其变化率EC,利用这两个量来确定T-S型模糊推理各模态的权值。由于风速处于额定风速以上,此时转速高于额定转速,偏差为正,故采用单边模糊控制。选取发电机的转速与其额定转速的偏差E和偏差变化率EC的论域和模糊论域同前文模糊控制一样,E的模糊子集为
为了准确描述模糊推理的逻辑,用
| 表 5 模态模糊规则描述 Tab.5 The description of modal fuzzy rule |
T-S型模糊控制的去模糊化采用加权平均法,设第
| $U = \frac{{\displaystyle\sum\limits_{i = 1}^m {{w_{i}}{u_i}} }}{{\displaystyle\sum\limits_{i = 1}^m {{w_{{i}}}} }}{\rm{ = }}\frac{{{w_1}{u_1} + {w_2}{u_2} + \cdots {w_{{m}}}{u_{{m}}}}}{{{w_1} + {w_2} + \cdots {w_{{m}}}}}$ | (8) |
3种模态的权值
| ${w_a} + {w_b} + {w_c} = 1$ | (9) |
在控制过程中,把
| ${U_{{\rm{sum}}}} = {w_{{a}}} \times {U_{{\rm{fuzzy}}}} + {w_{{b}}} \times {U_{{\rm{zi}}}} + {w_{{c}}} \times {U_{{\rm{PI}}}}$ | (10) |
为了验证所提方法的正确性及其控制性能,在SIMULINK下搭建了直驱永磁同步发电系统在单独模糊控制、单独模糊自适应PID控制、单独PI控制以及基于T-S型模糊加权的多模软切换控制的4种变桨控制模型,以阶跃风速和组合风速分别作为系统的输入,并将4种控制方法的仿真结果进行对比。风机的额定风速为
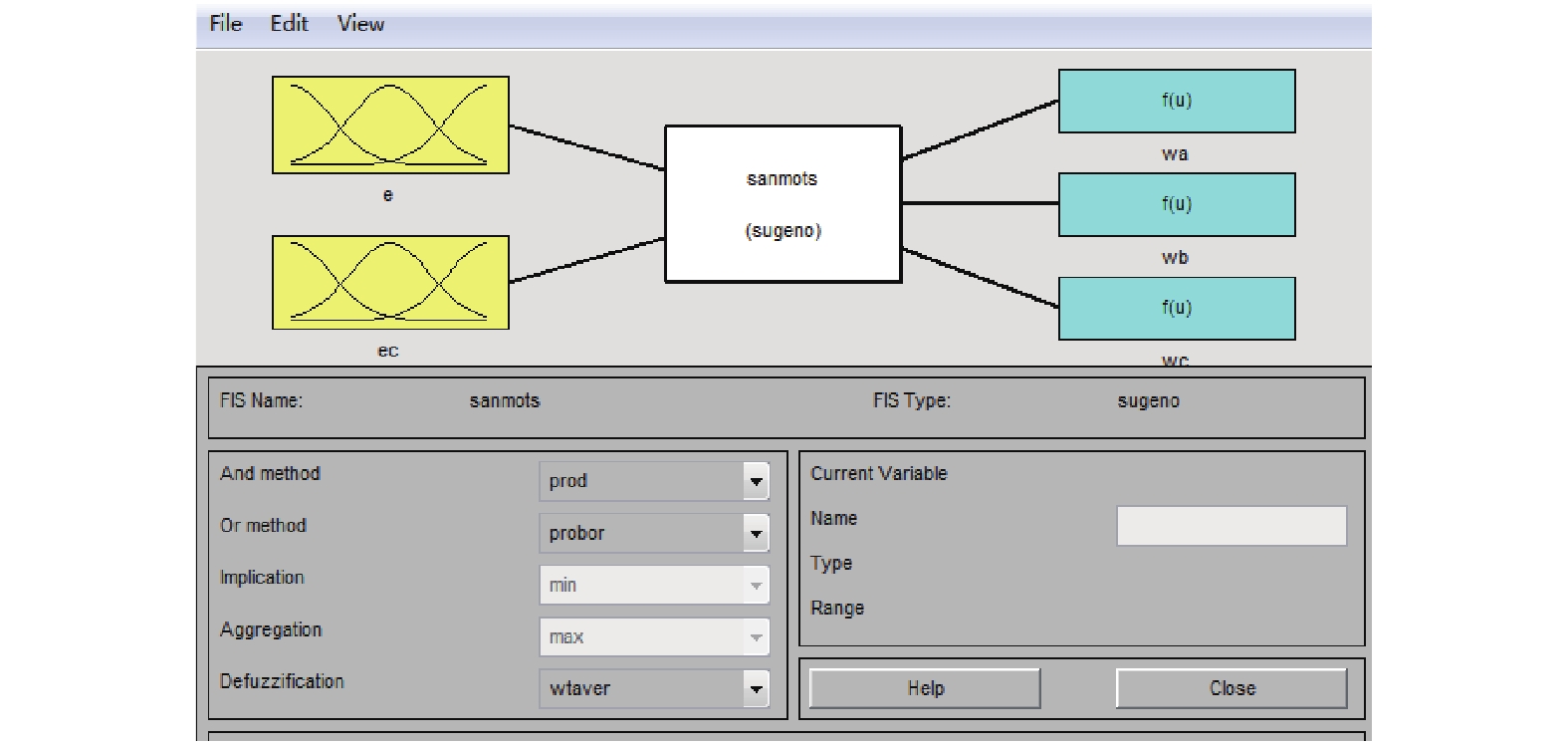
利用SIMULINK中的模糊控制工具箱建立T-S型的模糊推理系统如图5所示。
|
Download:
|
| 图 5 T-S型模糊推理系统 Fig. 5 The T-S fuzzy inference system | |
经过模糊规则设定,得到其输出权值在ruler viewer如图6所示。

|
Download:
|
| 图 6 ruler viewer中的权值输出 Fig. 6 The weight outputs in ruler viewer | |
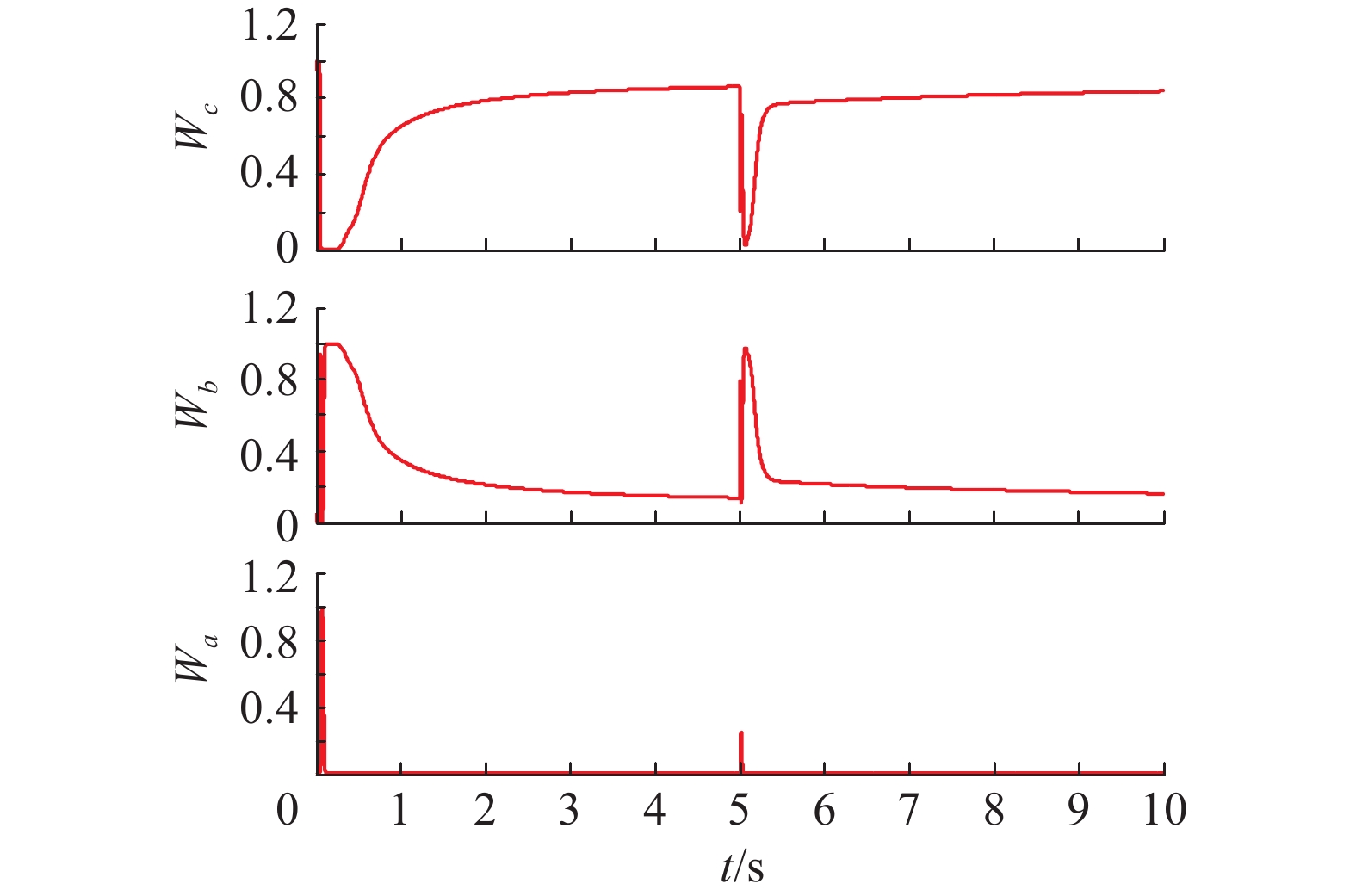
由图6可知,其权值输出满足式(9)。此时为中等偏差,偏差的变化率也中等,故模糊自适应PID控制的权值较大,模糊控制和PI控制的权值较小。
1) 阶跃风速
0~5 s风速为

|
Download:
|
| 图 7 风速 Fig. 7 The curve of wind speed | |
|
Download:
|
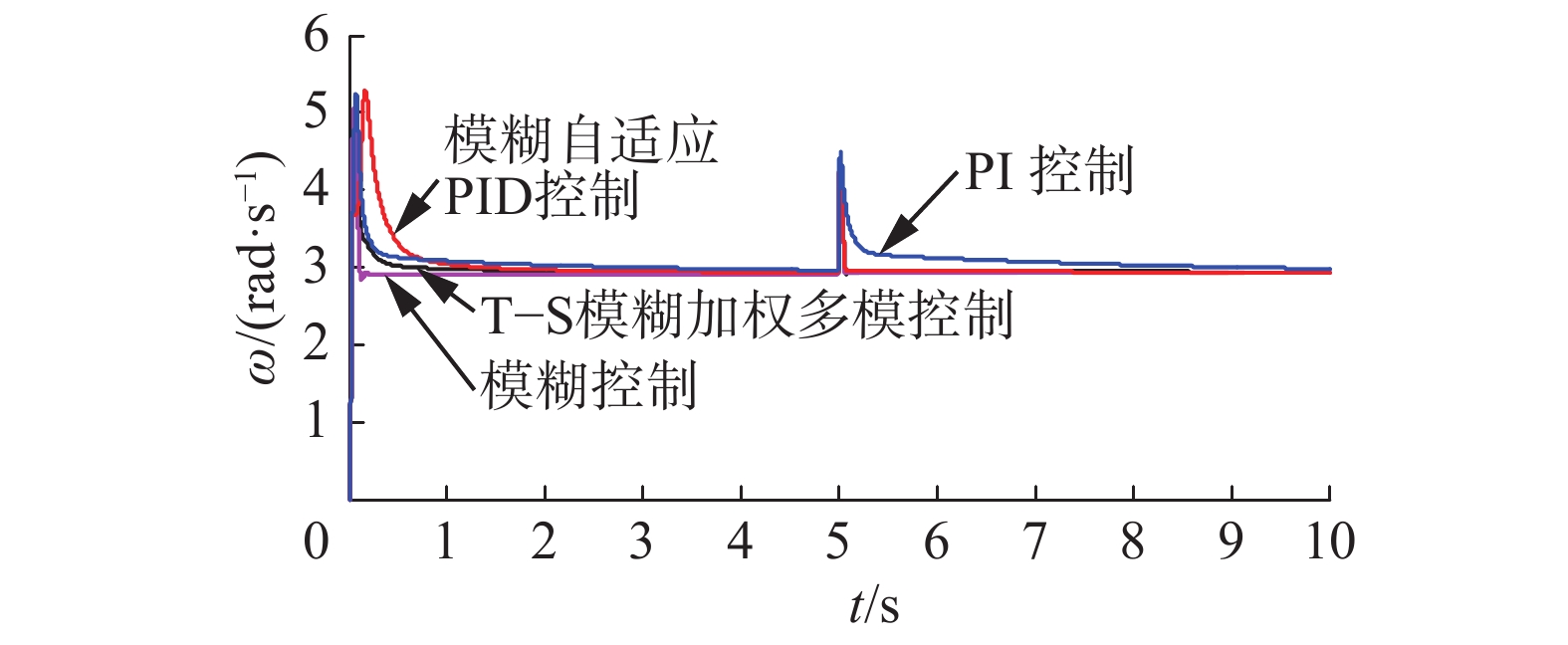
| 图 8 转速对比 Fig. 8 The comparison of rotor speed | |
|
Download:
|
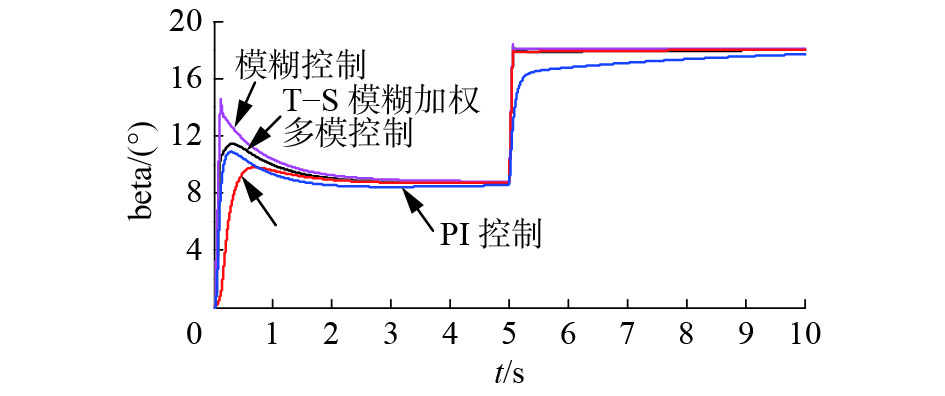
| 图 9 桨距角对比图 Fig. 9 The comparison of pitch angle | |

|
Download:
|
| 图 10 输出功率对比 Fig. 10 The comparison of generator output power | |
|
Download:
|
| 图 11 T-S型模糊推理的权值输出 Fig. 11 The weight output of T-S fuzzy inference | |
2)组合风速
采用组合风速模型时,vn用式(11)代替:
| ${v_{{n}}} = {v_{n{\rm{max}}}} \cdot {R_{{\rm{am}}}} \cdot \cos ({\omega _{{i}}} + {\phi _{{i}}})$ | (11) |
式中:
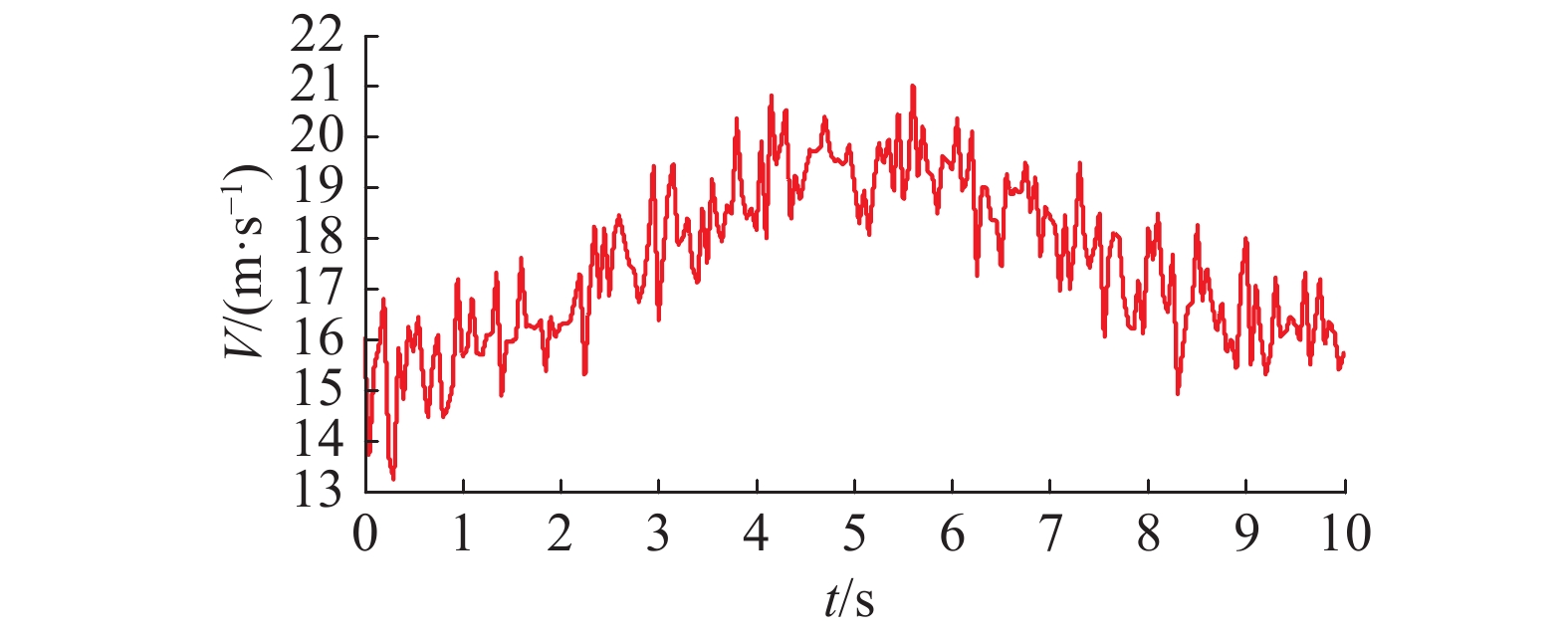
仿真时,组合风速的参数取
|
Download:
|
| 图 12 风速 Fig. 12 The curve of wind speed | |
|
Download:
|
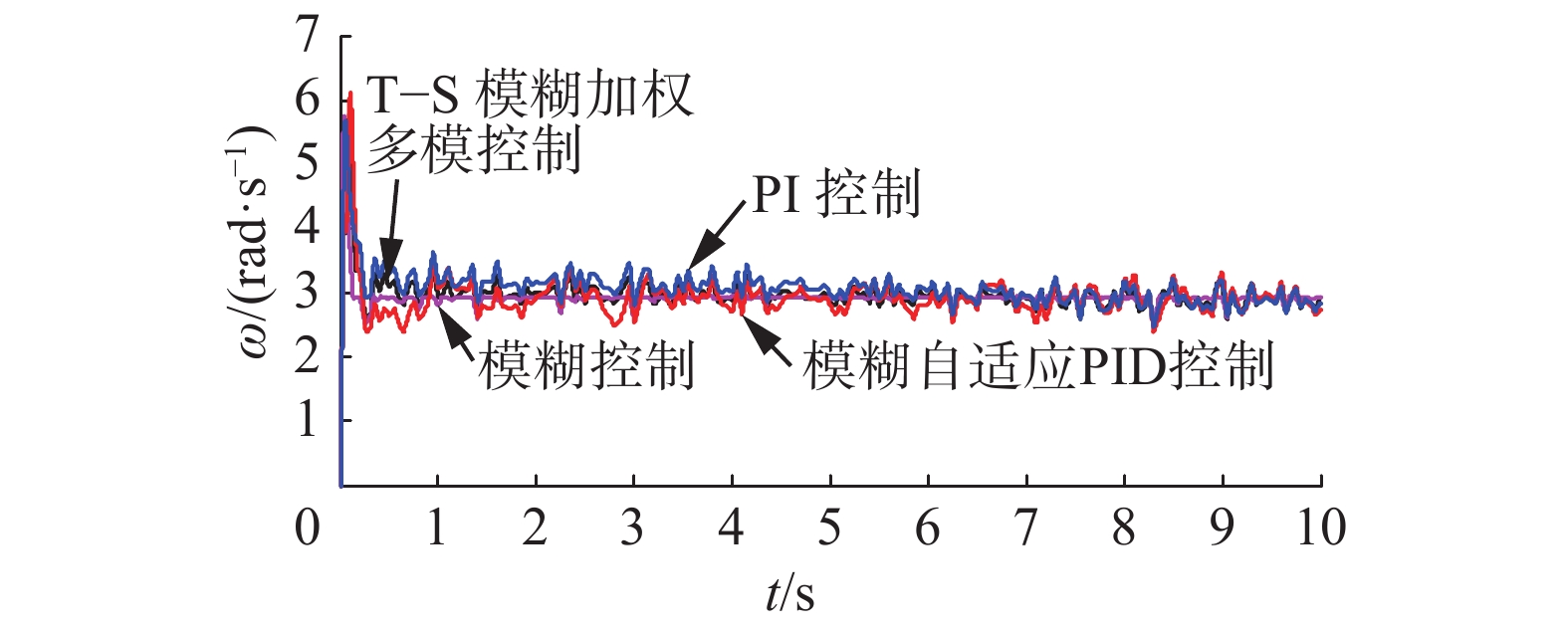
| 图 13 转速对比 Fig. 13 The comparison of rotor speed | |

|
Download:
|
| 图 14 桨距角对比 Fig. 14 The comparison of pitch angle | |

|
Download:
|
| 图 15 输出功率对比 Fig. 15 The comparison of generator output power | |
|
Download:
|
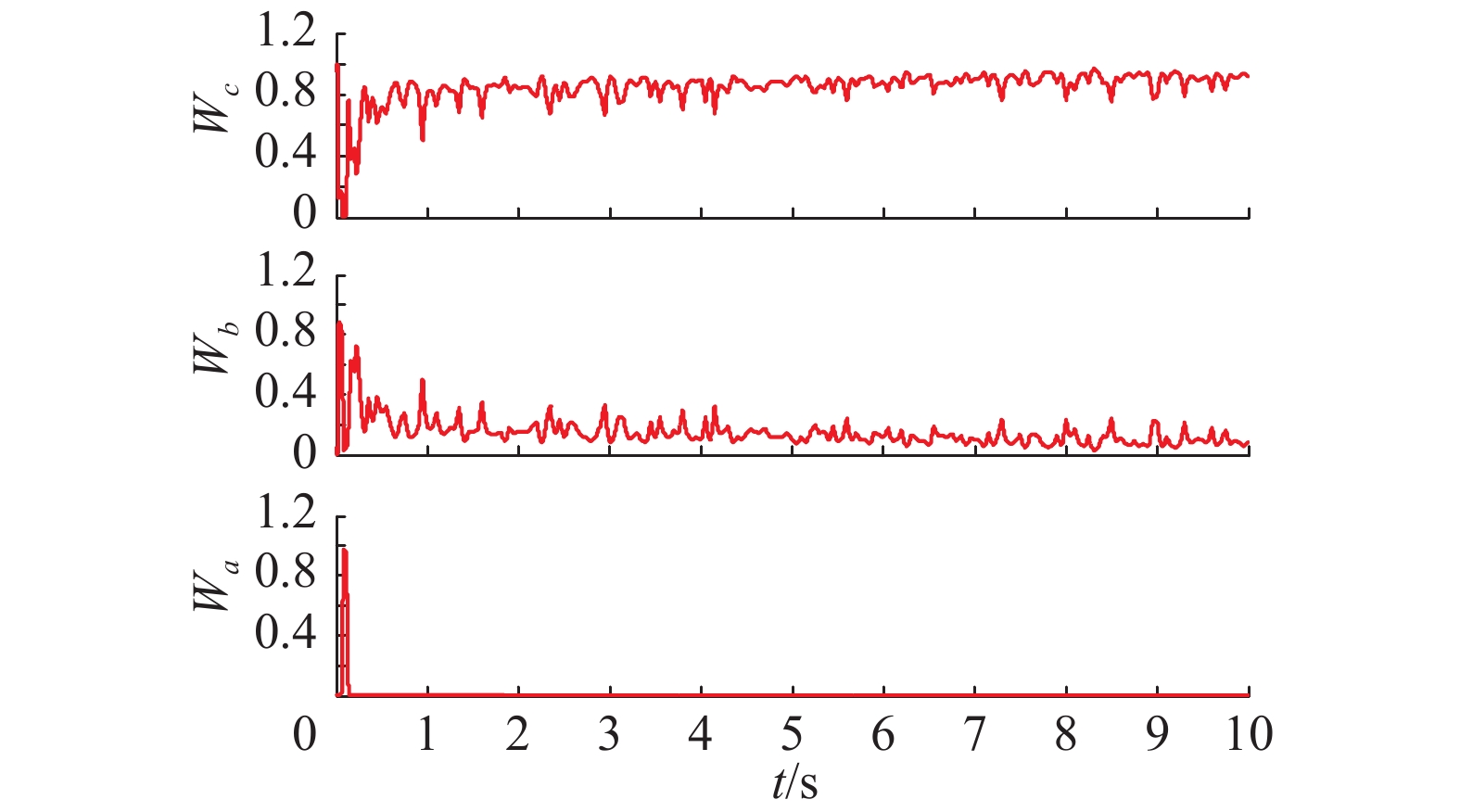
| 图 16 T-S模糊推理的权值输出 Fig. 16 The weight output of T-S fuzzy inference | |
仿真结果表明:阶跃风速和组合风速下,4种控制方法都能使发电机的输出功率稳定在额定值附近。使用模糊控制时,输出的功率与转速波动更小,更加平稳,但当风速改变时,其桨距角响应过于迅速,超调量大且波动较大,导致桨距角执行机构的频繁动作,增加了桨距角执行机构及风电机组各部件的机械疲劳载荷。所提出方法的综合控制性能优于其他3种方法,通过改变桨距角可以使转速较快地趋于稳定,即可以快速跟踪发电机的额定转速,功率也能稳定在发电机输出的额定功率附近。与其他3种方法相比,调节桨距角更加地平滑、动作频率更低,幅度更小;与模糊自适应PID与PI控制相比,减小了转速的峰值,转速与功率的脉动更小。阶跃风速下,进入稳态后,在5 s突加扰动时,又表现出良好的抗干扰性能。
5 结束语本文针对现有的变桨控制策略存在风电机阻额定风速以上恒功率运行时,桨距角执行机构的频繁动作增加了风机各部分的机械疲劳载荷,影响发电机的输出电能质量和机组的使用寿命等问题,研究了基于T-S型模糊加权的多模软切换变桨控制方法。该方法兼顾了模糊控制、模糊自适应PID控制和PI控制各自的控制优势,并利用T-S型模糊推理来进行平滑过渡,实现了软切换,克服了切换振荡。仿真结果表明,所提出的方法具有更加优良的综合控制性能,具有良好的动态性能、稳态性能和鲁棒性。在两种风速下,调节桨距角更加平滑,减缓了执行机构的频繁动作,桨距角执行机构的疲劳载荷有效的减小了,从而降低了机组其他部分的机械载荷,延长了机组的使用寿命。从对比研究易知,4种方法都能跟踪上发电机的转速并维持在额定转速,都能使发电机的输出功率稳定在额定值(2MW)附近,但所提出的方法转速的峰值更低,脉动更小,功率更加靠近额定值,功率脉动更小,更平稳。对于输出功率的脉动,风电机组在并网时加入背靠背变频器可以解决这一问题。此方法对于直驱变桨永磁同步风力发电系统,在额定风速以上的恒功率运行有一定的借鉴参考价值。
| [1] |
YIN Xiuxing, LIN Yonggang, LI Wei, et al. Adaptive sliding mode back-stepping pitch angle control of a variable-displacement pump controlled pitch system for wind turbines[J]. ISA transactions, 2015, 58: 629-634. DOI:10.1016/j.isatra.2015.07.006 ( 0) 0)
|
| [2] |
YUAN Yuan, TANG J. Adaptive pitch control of wind turbine for load mitigation under structural uncertainties[J]. Renewable energy, 2017, 105: 483-494. DOI:10.1016/j.renene.2016.12.068 ( 0) 0)
|
| [3] |
SONG Dongran, YANG Jian, DONG Mi, et al. Model predictive control with finite control set for variable-speed wind turbines[J]. Energy, 2017, 126: 564-572. DOI:10.1016/j.energy.2017.02.149 ( 0) 0)
|
| [4] |
吴洁, 孟克其劳, 贾大江, 等. 1.5MW永磁直驱风力发电机组变桨控制系统的改进[J]. 太阳能学报, 2016, 37(8): 2074-2079. WU Jie, MENG Keqilao, JIA Dajiang, et al. Improved pitch control system of 1.5 MW permanent magnet direct drive wind turbine[J]. Atct energiae solaris sinica, 2016, 37(8): 2074-2079. (  0) 0)
|
| [5] |
MORADI H, VOSSOUGHI G. Robust control of the variable speed wind turbines in the presence of uncertainties: a comparison between H∞, and PID controllers
[J]. Energy, 2015, 90: 1508-1521. DOI:10.1016/j.energy.2015.06.100 ( 0) 0)
|
| [6] |
任丽娜, 吕明月, 王振臣. 改进蜂群算法在风机变桨距控制中的应用[J]. 机械设计与制造, 2015, 36(3): 43-46. REN Lina, LV Mingyue, WANG Zhenchen. Improved bee colony algorithm on the wind turbine pitch control[J]. Machinery design and manufacture, 2015, 36(3): 43-46. (  0) 0)
|
| [7] |
Yin Xiuxing, Lin Yonggang, Li Wei, et al. A novel fuzzy integral sliding mode current control strategy for maximizing wind power extraction and eliminating voltage harmonics[J]. Energy, 2015, 85: 677-686. DOI:10.1016/j.energy.2015.04.005 ( 0) 0)
|
| [8] |
WANG Baohua, Qin Shengsheng. Backstepping sliding mode control of variable pitch wind power system[C]//2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC). Chengdu, China, 2010: 1–3.
( 0) 0)
|
| [9] |
MEDJBER A, GUESSOUM A, BELMILI H, et al. New neural network and fuzzy logic controllers to monitor maximum power for wind energy conversion system[J]. Energy, 2016, 106: 137-146. DOI:10.1016/j.energy.2016.03.026 ( 0) 0)
|
| [10] |
QIN Bin, ZHOU Hao, DU Kang, et al. Sliding mode control of pitch angle based on RBF neural-network[J]. Transactions of China electrotechnical society, 2013, 28(5): 37-41. ( 0) 0)
|
| [11] |
周飞航, 刘军. 基于状态反馈的直驱风电系统模糊控制策略[J]. 电网技术, 2016, 40(9): 2758-2763. ZHOU Feihang, LIU Jun. Fuzzy control strategy of direct-drive wind power system based on state feedback[J]. Power system technology, 2016, 40(9): 2758-2763. (  0) 0)
|
| [12] |
ANDERSON P M, BOSE A. Stability simulation of wind turbine systems[J]. IEEE transactions on power apparatus and systems, 1983, PAS-102(12): 3791-3795. DOI:10.1109/TPAS.1983.317873 ( 0) 0)
|
| [13] |
BOUKHEZZAR B, LUPU L, SIGUERDIDJANE H, et al. Multivariable control strategy for variable speed, variable pitch wind turbines[J]. Renewable energy, 2007, 32(8): 1273-1287. DOI:10.1016/j.renene.2006.06.010 ( 0) 0)
|
| [14] |
HUI J, BAKHSHAI A. A new adaptive control algorithm for maximum power point tracking for wind energy conversion systems[C]//2008 PESC Proceedings of the Power Electronics Specialist Conference. Rhodes, Greece, 2008: 4003–4007.
( 0) 0)
|
| [15] |
DAHBI A, NAIT-SAID N, NAIT-SAID M-S. A novel combined MPPT-pitch angle control for wide range variable speed wind turbine based on neural network[J]. International journal of hydrogen energy, 2016, 41(22): 9427-9442. DOI:10.1016/j.ijhydene.2016.03.105 ( 0) 0)
|
| [16] |
ZHANG Xinfang, XU Daping. Adaptive fuzzy control for variable speed variable pitch wind turbines[J]. IFAC power plants and power systems control, 2003, 36(20): 1031-1036. ( 0) 0)
|
| [17] |
BAGHERI P, Sun Qiao. Adaptive robust control of a class of non-affine variable-speed variable-pitch wind turbines with unmodeled dynamics[J]. ISA transactions, 2016, 63: 233-241. DOI:10.1016/j.isatra.2016.04.008 ( 0) 0)
|
| [18] |
唐酿, 肖湘宁, 陈众. 基于Sugeno模糊推理的静止无功补偿器多模态切换方法[J]. 电网技术, 2011, 35(8): 140-143. TANG Niang, XIAO Xiangning, CHEN Zhong. A method of multi-mode switching for SVC based on sugeno fuzzy inference[J]. Power system technology, 2011, 35(8): 140-143. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


