典型相关分析(canonical correlation analysis，CCA)^[1]是一种经典统计方法，旨在研究两组随机变量之间的相关性。通过极大化两组变量在线性投影空间中的相关性而达到特征融合的目的。CCA可用于对多模态数据的特征提取和融合^[2-4]，减小预测或识别问题中的样本复杂度^[5]，已成功应用于字符与人脸图像识别及多模态检索等任务中^[6]。核典型相关分析(kernel CCA，KCCA)^[7] 是对CCA的扩展，解决了CCA只能进行线性映射的问题。通过隐性的非线性映射将两组特征分别映射到高维特征空间，借助于核技巧，以线性的方式提取变量的非线性特征。尽管KCCA可以通过核来学习变量之间的非线性关系，但其需要通过人工选择核函数，并且当训练集规模较大时，会造成巨大的计算消耗。

为了解决KCCA存在的问题，文献[8]提出深度典型相关分析 (deep CCA，DCCA)，即用深度神经网络学习灵活的非线性相关表示，使得到的特征具有更高的相关度。文献[9]提出基于神经网络和自编码(auto encoder，AE)的深度典型相关自编码(deep canonically correlated autoencoders，DCCAE)，用于无标签多视图特征学习。但是这些方法在参数训练过程中，需要根据梯度下降法多次迭代至误差收敛，容易陷入局部最优，且计算消耗大。

另一方面，超限学习机(extreme learning machine，ELM)以结构简单、学习速度快和泛化能力好等优点^[10]，近年来已广泛应用于分类、回归等任务中。伴随着大数据时代的到来，关于数据潜在信息的挖掘引起了大量关注。然而ELM是一种单隐含层前馈神经网络，其浅层的网络结构难以发现数据深层抽象特征，因此基于ELM进行深度学习的算法相继提出。文献[11]提出了ELM-AE，首次将ELM用于数据的特征表示；文献[12]提出了基于ELM堆栈构成的深度表示模型；文献[13]将流行正则引入原始ELM-AE中，并提出一种新的深度神经网络；文献[14]使用深度ELM学习图像的非线性结构，用于图像分类中，并且在速度和准确率上表现出优越的性能；文献[15]将深度ELM模型用于多模态融合中，表明了ELM在多模态数据应用中的有效性。

为了解决基于传统深度神经网络的非线性CCA训练速度缓慢、无法快速收敛等问题，本文将ELM-AE引入CCA框架，用于多模态数据的特征提取。首先利用ELM-AE分别对每个模态进行多层无监督特征提取，然后极大化深层特征的相关性。实验结果表明，相比于线性CCA和DCCA，本文方法在取得高相关度的同时，还显著提升了算法的快速性。将该算法在康奈尔大学机器抓取数据集上进行验证，实验结果表明该方法有效提高了抓取点识别率。

1 相关工作 1.1 典型相关分析

给定N对已中心化的样本 ${{X}} = [{{{x}}_1}\,\,{{{x}}_2}\,\, \cdots \, {{{x}}_N}]$ 与 ${{Y}} = [{{{y}}_1}\,\,{{{y}}_2}\,\, \cdots \,{{{y}}_N}]$ ，CCA的基本思想是找到一对投影向量a和b，满足 ${{u}} = {{{a}}^{\rm{T}}}{{X}}$ 和 ${{v}} = {{{b}}^{\rm{T}}}{{Y}}$ 之间具有最大的相关系数。然后通过对典型相关变量u和v的相关关系研究，代替原来两组变量之间的相关关系研究。

u和v的相关系数为

$\rho = {\rm{corr}}({{{a}}^{\rm{T}}}{{X}},{{{b}}^{\rm{T}}}{{Y}}) = \frac{{{{{a}}^{\rm{T}}}{{{\Sigma }}_{{{XY}}}}{{b}}}}{{\sqrt {({{{a}}^{\rm{T}}}{{{\Sigma }}_{{{XX}}}}{{a}})({{{b}}^{\rm{T}}}{{{\Sigma }}_{{{YY}}}}{{b}})} }}$

(1)

式中： ${{{\Sigma }}_{{{XX}}}}$ 和 ${{{\Sigma }}_{{{YY}}}}$ 分别表示特征集X和Y的协方差矩阵， ${{{\Sigma }}_{{{XY}}}}$ 表示X和Y的互协方差矩阵。

典型相关分析就是在约束条件 ${{{a}}^{\rm{T}}}{{{\Sigma }}_{{{XX}}}}{{a}} = 1$ ， ${{{b}}^{\rm{T}}}{{{\Sigma }}_{{{YY}}}}{{b}} = 1$ 下求a和b的值，使 $\rho $ 达到最大，此时目标函数为 $\max \rho = {{{a}}^{\rm{T}}}{{{\Sigma }}_{{{XY}}}}{{b}}$ 。

定义矩阵 ${{T}} = {{\Sigma }}_{{{XX}}}^{ - 1/2}{{{\Sigma }}_{{{XY}}}}{{\Sigma }}_{{{YY}}}^{ - 1/2}$ ，对T进行奇异值分解，得到矩阵T的前k个左奇异向量 ${{{\alpha }}_k}$ 和右奇异向量 ${{{\eta }}_k}$ ，则最终优化目标值为 $({\mathop a \limits^ \frown},{\mathop b \limits^ \frown}) = ({{{\alpha }}_k}{{\Sigma }}^{ - 1/2}_{{XX}},{{{\eta }}_k}{{\Sigma }}^{ - 1/2}_{{YY}})$ 。

为了防止训练过拟合，在协方差计算中加入正则项 $\gamma > 0$ ：

${{{\Sigma }}_{{{XX}}}} = \frac{1}{{N - 1}}{{X}}{{{X}}^{\rm{T}}} + \gamma {{I}}$

(2)

1.2 深度典型相关分析

Andrew等^[8]对CCA进行扩展改进，提出基于深度神经网络的CCA，即DCCA。给定模态X和Y，两个深度神经网络模型 $f = f({{X}};{{{W}}_f})$ 和 $g = g({{Y}};{{{W}}_g})$ 分别用来学习X和Y的非线性结构，其中W= $ [{{{W}}_f};{{{W}}_g}]$ 为神经网络模型参数。然后通过CCA将提取的特征 $f$ 和 $g$ 相关性极大化：

$\begin{array}{c}\mathop {\max }\limits_{{{{W}}_f},{{{W}}_g},{{U}},{{V}}} \displaystyle\frac{1}{N}{\rm{tr}}({{{U}}^{\rm{T}}}f({{X}};{{{W}}_f})g{({{Y}};{{{W}}_g})^{\rm{T}}}{{V}})\\{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{{{U}}^{\rm{T}}}\left( {\displaystyle\frac{1}{N}f({{X}})f{{({{X}})}^{\rm{T}}} + {r_x}{{I}}} \right){{U}} = {{I}}\\{{{V}}^{\rm{T}}}\left( {\displaystyle\frac{1}{N}g({{Y}})g{{({{Y}})}^{\rm{T}}} + {r_y}{{I}}} \right){{V}} = {{I}}\\{{u}}_i^{\rm{T}}f({{X}})g{({{Y}})^{\rm{T}}}{{{v}}_j} = 0,\;\;\;\;\;i \ne j\end{array}$

(3)

式中： ${{U}} \!=\! [{{{u}}_1}\,\,{{{u}}_2}\,\, \cdots \,{{{u}}_L}]$ ， ${{V}} = [{{{v}}_1}\,\, {{{v}}_2}\,\,\cdots \,{{{v}}_L}]$ 是CCA对DNN输出特征的映射矩阵， ${r_x} > 0,{r_y} > 0$ 是样本协方差估计的正则化参数。

令 ${{H}}_{{X}}$ 和 ${{H}}_Y$ 分别为通过深度模型 $f$ 和 $g$ 得到的最终特征表示，中心化后得到 ${{\bar{ H}}_{{X}}} = {{{H}}_{{X}}} - {{{H}}_{{X}}}/N$ ，同理得到 ${{\bar{ H}}_{{Y}}}$ ，并且计算两者的协方差矩阵 ${{\mathop {\Sigma } \limits^ \frown}_{{XY}}}\text{、}{{\mathop { \Sigma } \limits^ \frown}_{{XX}}}$ 、 ${{\mathop { \Sigma } \limits^ \frown}_{{YY}}}$ 。根据1.1节中对CCA的描述，对 ${{H}}_{{X}}$ 和 ${{H}}_Y$ 进行相关分析，得到映射矩阵U和V。假设 ${{T}}$ 的奇异值分解矩阵为 ${{T = UD}}{{{V}}^{\rm{T}}}$ ，则目标函数对 ${{H}}_{{X}}$ 和 ${{H}}_Y$ 的梯度计算为

$\frac{{\text{∂} {\rm{corr}}({{H}}_{{X}},{{H}}_{{Y}})}}{{\text{∂} {{H}}_{{X}}}} = \frac{1}{{N - 1}}(2{\nabla _{{{XX}}}}{{H}}_{{X}} + {\nabla _{{{XY}}}}{{H}}_{{Y}})$

(4)

式中： ${\nabla _{{XY}}} \!=\! {{\mathop {\Sigma} \limits^ \frown}_{{XX}}}^{ - 1/2}{{U}}{{{V}}^{\rm{T}}}{{\mathop {\Sigma} \limits^ \frown}_{{YY}}}^{ - 1/2}$ ， ${\nabla _{{{XX}}}} \!= \! - \displaystyle\frac{1}{2}{\mathop {\Sigma} \limits^ \frown}_{{{XX}}}^{ - 1/2}{{UD}}{{{U}}^{\rm{T}}}{\mathop {\Sigma} \limits^ \frown}_{{{XX}}}^{ - 1/2}$

根据梯度下降法对网络参数 ${{W}} = [{{{W}}_f};{{{W}}_g}]$ 进行优化。 $\tilde f({{X}}) = {{{U}}^{\rm{T}}}f({{X}})$ 和 $\tilde g({{Y}}) = {{{V}}^{\rm{T}}}g({{Y}})$ 即为最终X和Y的投影矩阵，用于测试样本的映射。

与CCA不同，DCCA没有固定的解，其参数需要通过梯度下降法优化，Andrew等采用批处理算法L-BFGS对参数进行调整。王等^[16]随后提出采用随机梯度下降(stochastic gradient descent，SGD)对DCCA的权值进行优化。本文选择与后者提出的方法进行比较。

1.3 超限学习机

超限学习机是一类针对单隐含层前馈神经网络的学习算法。典型的单隐层前馈神经网络结构如图1所示，由输入层、隐含层和输出层组成。

给定N个训练样本， ${{X}} \in {\operatorname{R}^{N \times n}},{{t}} \in {\operatorname{R}^{N \times 1}}$ ，n为输入的维度。第i个样本的网络输出可表示为

${y_i} = \sum\limits_{j = 1}^h {g({{{x}}_i}{{w}}_j^{\rm{T}} + {b_j})} {\beta _j}$

(5)

式中： ${y_i}$ 是网络的实际输出，h是隐含层节点数， ${{{w}}_j} \in {\operatorname{R} ^n}$ 是输入权值， ${b_j}$ 是隐含层神经元的偏置， ${\beta _j}$ 和是输出层的权值，g(x)为隐含层的激活函数，取正切sigmoid函数。式(5)可表示为矩阵形式：

${{H\beta }} = {{T}}$

(6)

式中：H为神经网络的隐含层输出矩阵，T是网络期望输出值。

在训练过程中，对w和b随机初始化，且保持不变，而隐含层与输出层的连接权值β可以通过求解以下方程组获得：

${\mathop {\beta} \limits^ \frown}={{{H}}^{{ + }}}{{T}}$

(7)

式中：H⁺为隐含层输出矩阵H的Moore-Penrose广义逆。

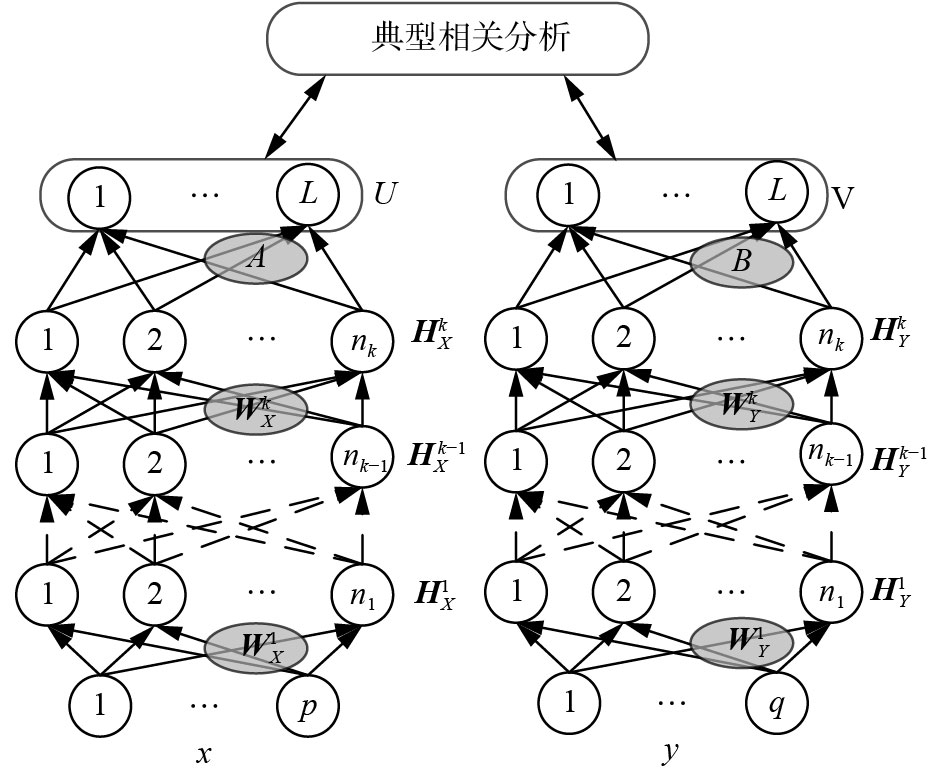
2 基于超限学习机的非线性典型相关分析

本文提出基于ELM的非线性典型相关分析(ELM-CCA)，通过对两个模态分别进行复杂的非线性转换，最终使学习到的特征最大相关，其模型结构如图2所示。给定样本 $\{ ({{{x}}_1},{{{y}}_1}), ({{{x}}_2},{{{y}}_2}), \cdots , $ $({{{x}}_N},{{{y}}_N})\} $ ，N为样本个数， ${{{x}}_i} \in {\operatorname{R} ^p},{{{y}}_i} \in {\operatorname{R} ^q}$ ，因此可以得到两个模态的样本矩阵，分别为 ${{X}} \in {\operatorname{R} ^{N \times p}}$ 和 ${{Y}} \in {\operatorname{R} ^{N \times q}}$ ，传统的CCA对X和Y进行线性变换，使变换后的两组数据相关性最大。实际中很多问题需要非线性变换来挖掘事物间潜在的非线性关系。而ELM-CCA算法可以实现非线性相关学习。

ELM-CCA结构分为两部分：分别对每个模态进行多层非线性转换；极大化对两个模态多层非线性映射后特征的相关性。对于 ${{X}} \in {\operatorname{R} ^{N \times p}}$ 中的其中一个样本 ${{x}} \in {\operatorname{R} ^p}$ ，设有k个隐含层，则第1个隐含层的输出为

${{H}}_{{X}}^1 = f({{W}}_{{X}}^1{{x}} + {{b}}_{{X}}^1)$

(8)

式中： ${{W}}_{{X}}^1 \in {\operatorname{R} ^{{n_1} \times p}}$ 是连接输入与第1个隐含层的权值， ${{b}}_{{X}}^1 \in {\operatorname{R} ^{{n_1}}}$ 是第1层隐含层的偏置向量，f是隐含层的激活函数。将上一层的输出作为输入，依次可得到第k层的输出：

${{H}}_{{X}}^k = f({{W}}_{{X}}^k{{{H}}_{{X}}^{k - 1}} + {{b}}_{{X}}^k)$

(9)

将模态X最终得到的隐含层输出简记为 ${{{H}}_{{X}}}$ ，对于模态Y，通过相同的方式，得到最后一层隐含层的输出 ${{{H}}_{{Y}}}$ 。

对 ${{{H}}_{{X}}}$ 和 ${{{H}}_{{Y}}}$ 进行典型相关分析，分别得到对应的线性转换矩阵 ${{A}} \in {\operatorname{R} ^{L \times {n_k}}}$ 和 ${{B}} \in {\operatorname{R} ^{L \times {n_k}}}$ ，最后的输出层分别为

${{U = A}}{{{H}}_{{X}}}$

(10)

${{V = B}}{{{H}}_{{Y}}}$

(11)

通过深度ELM-CCA的训练，得到X和Y的非线性映射表示U和V，并且U和V的相关度最大。

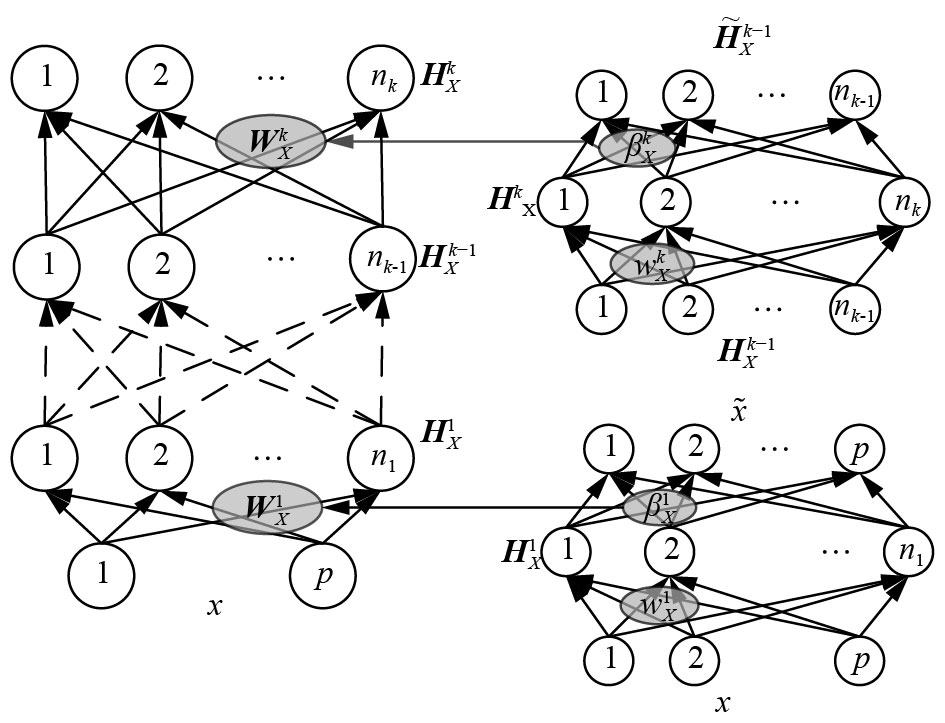
2.1 无监督非线性映射

采用ELM-AE逐层训练得到每层之间的连接权值，即每层权值的训练都作为一个独立的ELM。在独立组件ELM-AE中，令其输出y=x，通过最小化输出的重构误差来训练权值。

对于第k层权值 ${{W}}_{{X}}^k$ ，构造ELM-AE模型，如图3所示。随机给定正交化输入权值 ${{w}}_{{X}}^k$ 和隐含层偏置 ${{b}}_{{X}}^k$ ，则其隐含层输出为

$\begin{array}{l}{{H}}_{{X}}^k = f({{w}}_{{X}}^k{{{H}}_{k - 1}} + {{b}}_{{X}}^k){({{w}}_{{X}}^k)^{\rm{T}}}{{w}}_{{X}}^k = {{I}}{\rm{,}}{{b}}_{{X}}^{k{\rm{T}}}{{b}}_{{X}}^k{\rm{ = 1}}\end{array}$

(12)

式中： ${{w}}_{{X}}^k \in {\operatorname{R} ^{{n_{k - 1}} \times {n_k}}}$ 是在输入层和隐含层节点之间正交的随机权值， ${{b}}_{{X}}^k \in {\operatorname{R} ^{{n_k} \times 1}}$ 是正交的随机偏置。

ELM-AE的输出权值 ${{\beta }}$ 负责从特征空间到输入数据的学习转换。可以根据以下式子计算输出权值 $\,{{\beta }}$ ：

${{\beta }}_{{X}}^k = {\left( {\frac{{{I}}}{C} + {{({{H}}_{{X}}^k)}^{\rm{T}}}{{H}}_{{X}}^k} \right)^{ - 1}}{({{H}}_{{X}}^k)^{\rm{T}}}{{H}}_{{X}}^{k - 1}$

(13)

式中：C是正则项参数， ${{H}}_{{X}}^k$ 是ELM-AE的隐含层输出， ${{H}}_{{X}}^{k - 1}$ 是它的输入数据。

因此，第k–1层到第k层的连接权值 ${{W}}_{{X}}^k$ 为 ${{W}}_{{X}}^k = {({{\beta }}_{{X}}^k)^{\rm{T}}}$ 。

2.2 极大化非线性映射的相关性

X和Y分别经过多层非线性映射，得到特征 ${{{H}}_{{X}}} \in {\operatorname{R} ^{{n_k} \times N}}$ 和 ${{{H}}_{{Y}}} \in {\operatorname{R} ^{{n_k} \times N}}$ ，对 ${{{H}}_{{X}}}$ 和 ${{{H}}_{{Y}}}$ 执行线性CCA：

$({{A}},{{B}}) = \mathop {\arg \max }\limits_{{{A,B}}} \frac{{{{{A}}^{\rm{T}}}{{{\Sigma }}_{{{XX}}}}{{B}}}}{{\sqrt {{{{A}}^{\rm{T}}}{{{\Sigma }}_{{{XY}}}}{{A}}} \sqrt {{{{B}}^{\rm{T}}}{{{\Sigma }}_{{{YY}}}}{{B}}} }}$

(14)

由于式(14)中A或B等比例变化时，目标函数的值不变，因此CCA定义了下式约束条件 ${{{A}}^{\rm{T}}}{\Sigma _{{{XY}}}}{{A}} = {{I}},{\rm{ }}{{{B}}^{\rm{T}}}{\Sigma _{{{YY}}}}{{B}} = {{I}}$ ，此时，目标函数等价于：

$({{A}},{{B}}) = \max {{{A}}^{\rm{T}}}{\Sigma _{{{XY}}}}{{B}}$

(15)

上述优化的具体过程如下，将 ${{{H}}_{{X}}} \in {\operatorname{R} ^{{n_k} \times N}}$ 中心化： ${{\mathop {{H}} \limits^ \frown}_{{X}}} = {{{H}}_{{X}}} - {{{H}}_{{X}}}/N$ 。

计算 ${{\mathop {{H}} \limits^ \frown}_{{X}}}$ 的协方差矩阵：

${{{\Sigma}}_{{{XX}}}} = \frac{1}{{N - 1}}{{\mathop {{H}} \limits^ \frown}_{{X}}}{\mathop {{H}} \limits^ \frown}_{{X}}^{\rm{T}} + {\gamma _{{X}}}{{I}}$

(16)

式中： ${\gamma _{{X}}}$ 为正则项，I为单位矩阵。同样的方式中心化 ${{{H}}_{{Y}}} \in {\operatorname{R} ^{{n_k} \times N}}$ ，并计算协方差矩阵 ${{{\Sigma }}_{{{YY}}}}$ 。

计算 ${{{H}}_{{X}}}$ 和 ${{{H}}_{{Y}}}$ 的交叉协方差矩阵：

${{{\Sigma}}_{{{XY}}}} = \frac{1}{{N - 1}}{{\mathop {{H}} \limits^ \frown}_{{X}}}{{{\mathop {{H}} \limits^ \frown} }}_{{Y}}^{\rm{T}}$

(17)

对矩阵 ${{T}} = {{\Sigma }}_{{{XX}}}^{ - 1/2}{{{\Sigma }}_{{{XY}}}}{{\Sigma }}_{{{YY}}}^{ - 1/2}$ 奇异值分解，得到左奇异矩阵 ${{{\alpha }}_L}$ 和右奇异矩阵 ${{{\eta }}_L}$ ，则可得到优化目标值：

${\mathop {{A}} \limits^ \frown} = {{{\alpha }}_L}{{\Sigma }}_{{{XX}}}^{ - 1/2}, \; {\mathop {{B}} \limits^ \frown} = {{{\eta }}_L}{{\Sigma }}_{{{YY}}}^{ - 1/2}$

(18)

经过矩阵A和B转换，使最终输出U和V实现最大相关，从而实现对X和Y的非线性典型相关分析学习。

ELM-CCA与DCCA具有相同的模型结构，二者均通过深度神经网络学习特征的非线性表示，然后对得到的深度特征进行线性CCA求解，最终将非线性模态相关性问题转化为线性相关分析。不同的是，在神经网络参数的优化过程中，DCCA首先由式(4)计算目标函数对深度特征的梯度，然后根据反向传播算法优化每层的权值。而在ELM-CCA中，每层之间的权值是通过前向逐层训练，由式(13)直接计算得到。相比DCCA，不需要反向微调，极大地提高了训练速度。

3 实验结果

为了验证本文提出的ELM-CCA算法在多模态特征提取中的有效性，我们在康奈尔大学抓取数据集^[17]上开展了实验对比。机器抓取是指机器人根据传感器采集到的信息来推断夹持器放置的位置，抓取过程涉及感知、规划、识别和控制等问题。在实施抓取操作之前，机器人首先需要对物体可抓取部分做出准确的识别，因此本文将提出的算法应用于机器抓取识别任务中。

康奈尔大学抓取数据集包括由机器人视觉感知部位RGB-D相机采集到的一系列图像，图4给出了部分图像样本。相比传统的2-D图像，采用RGB-D相机能够在获取彩色图像的同时得到每个像素的深度信息，提高了机器人抓取的成功率^[18]。文献[19]通过对物体深度信息进行处理，实现了目标抓取任务。近年来，相关文献的研究也表明了多模态特征融合的必要性^[20]，文献[21]提出采用多特征光学遥感图像提高目标的分类识别性能；文献[22]指出RGB-D融合的多应用场合。因此本文将对图像的颜色RGB模态和深度信息模态进行研究，寻找其相关信息。

3.1 实验数据

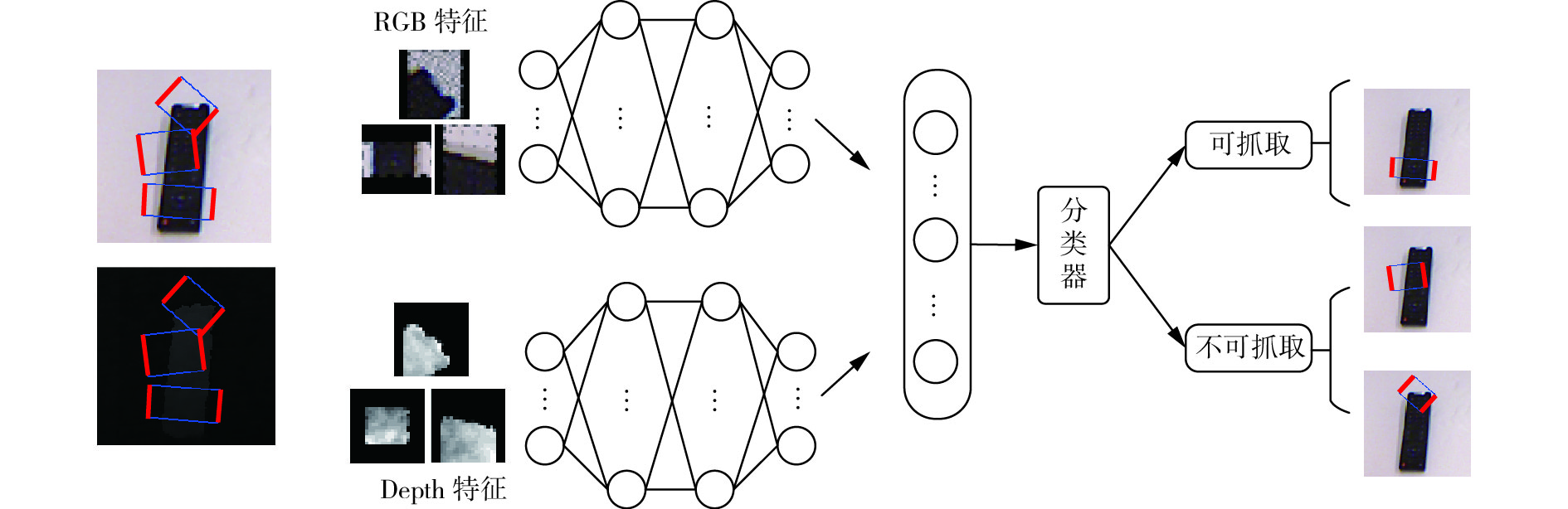
实验数据集包含885张RGB图像，这些图像来自于对240个不同物体的多角度拍摄。每张图片被多个已标签矩形框标记，共记8 019个，如图5所示，粗线对应夹持器抓取的位置。其中正矩形表示可抓取，负矩形表示当前状态不可抓取。

每个矩形框对应一个样本，同时对这些矩形内的图像提取颜色信息和深度信息，分别对应算法中的X和Y。颜色特征为三通道24×24像素的RGB图像，即 ${{X}} \in {\operatorname{R} ^{1\,\,728}}$ 。深度特征包含单通道图像深度信息，即 ${{Y}} \in {\operatorname{R} ^{576}}$ 。图5右所示为抓取识别任务的实验流程。

3.2 实验结果

为了体现本文算法的优越性，将实验结果与线性CCA、分数阶嵌入典型相关分析(fractional-order embedding canonical correlation analysis，FECCA)^[4]和DCCA进行比较。分别在相关度、时间和抓取识别任务3个方面验证了ELM-CCA的优势。

CCA是对随机变量线性映射的统计方法，FECCA使用分子阶思想，对传统CCA类内和类间协方差进行重新估计，以减小训练样本噪声造成的样本协方差偏离真实数据的问题。DCCA和ELM-CCA都属于非线性映射方法。上述方法的目标都是极大化两个随机变量之间的相关系数。因此，首先对以上算法学习的特征进行相关度的比较。图6为不同特征下，4种方法在测试集下得到的前100个最相关典型变量的相关系数之和。从图中可以看出，ELM-CCA学习到的特征相关度始终高于其他算法。尤其在低维时表现突出，当输出维度为100时，采用ELM-CCA得到的相关系数之和相比前两者优势最大。输出维度较高时，相关度基本趋于一致。

图7对DCCA和ELM-CCA在不同网络结构下，提取特征至100维时，进行了时间和相关度的比较，横坐标表示隐含层的规模。从图7(a)可以看出，随着网络层数和隐含层节点数增加，算法消耗的时间在显著增长。并且在每个网络结构下，DCCA算法消耗的时间都远远高于ELM-CCA。当隐含层层数低于4层，且每层节点数在2 000以内时，ELM-CCA的训练时间可保持在10 s之内。而DCCA在隐含层结构为1 000-1 000时，训练时间已经达到466 s，可以看出ELM-CCA在训练速度上取得了很大的优势。图7(b)为在各网络结构映射下得到的特征相关度，ELM-CCA学习到的特征相关度均高于DCCA，随着网络层数增多，相关度逐渐增加，当隐含层层数为3层时，得到的结果最好。因此选择该网络结构提取多模态特征，用于机器人抓取点的识别任务。

通过对原始RGB和深度特征的非线性映射，可以得到两个模态特征的最终表示。我们分别将原始特征与经过CCA、DCCA和ELM-CCA算法提取后的特征输入到分类器中，通过得到的识别准确率比较不同算法的学习性能。为了使结果更有说服力，我们在不同的分类器上进行了实验，选择了基于统计理论的SVM和基于神经网络的ELM。此外，我们还比较了使用单模态特征(即RGB和Depth)和多模态特征融合(即RGBD)对识别率的影响。

表1和表2分别给出了使用SVM分类器和ELM分类器得到的分类结果。从表中可以看出，尽管使用了不同的分类器，得到的识别率趋势是相同的，经过特征提取后的识别率要高于直接使用原始特征进行识别的结果。而DCCA和ELM-CCA经过非线性的学习后，体现出了比线性CCA和FECCA的优势，其中FECCA通过对类内和类间协方差重新估计，相比传统CCA，性能得到了改善。ELM-CCA在经过快速的特征学习后，相比DCCA，仍然取得了满意的识别率。图8所示为不同输出维度下，采用ELM分类器在RGBD特征输入下的识别结果。在低维时，识别率随着输出维度的增加显著提升，在输出维度达到20维时基本稳定，并且在不同维度下，ELM-CCA始终体现了较好的识别效果。

4 结束语

本文提出一种新的ELM-CCA非线性典型相关分析方法，并应用于机器人抓取点的识别任务中。对机器人采集到的原始图像提取RGB模态和深度模态，首先采用ELM分别的对每个模态进行无监督特征学习，得到非线性特征表示，然后将学习到的特征通过CCA极大化模态之间的相关性。该方法在保证了识别率较高的情况下还体现了强大的快速性。在实际应用中，为机器人实现快速准确的抓取操作奠定了基础。