手势语言作为一种常用的交流语言，通过不同手势的组合、不同手形的变化，能够表达多种复杂的含义，在非声音传递信息的方式中，如特警手语、聋哑人交流、远程指挥等方面，起到重要作用^[1]。特征提取是手势识别的关键环节，即通过对不同的手势进行数学描述，表示独特的特征关系。常用的特征有几何特征、形状特征、Hu矩特征等。

国外方面，Davis等^[2]采用不变矩和神经网络，进行数字手势的识别；Miyashita等^[3]针对静态手势具有平移和旋转性问题，采用基于边界信息特征描述的方法；Kapuściński等^[4]提出改进的梯度直方图方法进行静态手势识别，通过加强图像坐标系的局部方向，使之能够找到最佳的关键向量，提高识别率。国内方面，谭台哲等^[5]将深度与肤色信息结合，根据手指和手掌质心判断方向，从而完成对手势和左右手的识别，鲁棒性强；刘淑萍等^[6]在传统的HOG方法的基础上加入肤色模型和手指检测算法，将识别率提高20%；赵磊等^[7]对传统DTW算法进行改进，以欧氏距离为元素组成矩阵，结合事先录入的手势模板，实现手势识别。通过上述国内外研究现状的分析不难发现研究问题主要集中于空域特征的提取。实际上，频谱能在描述纹理特征时体现重要作用^[8]。常用的频域变换主要有傅里叶变换、小波变换等。前期研究中，大多仅采用空域特征或者仅采用小波变换系数特征，但由于传统小波变换在获取频谱特征时，不具有方向性，因此，拟采用对偶树复小波变换提取频域特征，实现–75°、–45°、–15°、15°、45°和75°等6个方向的特征度量，最后为提高特征的完备性，本文将空域特征与频域特征进行融合。

分类器通常采用人工神经网络，常用的有BP神经网络、支持向量机(SVM)等。经过许多学者研究证实，在图像识别方面，SVM比BP精度更高，且不易陷入过拟合状态^[9-12]。但是，由于SVM在高维空间中计算量远远大于BP，因此，当样本较多、特征维数较大时，SVM速度较慢。本文引入BD(best distance)优选SVM训练样本的算法，一方面减少样本数，提高训练速度，另一方面，优化样本质量，提高训练精度。

1 特征提取 1.1 空域特征

1)位置。由前面部分手势跟踪，可获取手势的位置信息，用掌的面积中心表示。设手掌像素的坐标为 $({x_i},{y_i})$ ，其中 $(i = 0,1, \cdots ,n - 1;{\rm{ }}j = 0,1, \cdots ,$ $m - 1)$ ，那么其质心 $(\bar x,\bar y)$ 表示为

$\overline x = \frac{1}{{mn}}\sum\limits_{i = 0}^{n - 1} {\sum\limits_{j = 0}^{m - 1} {{x_i}} } ,\quad \overline y = \frac{1}{{mn}}\sum\limits_{i = 0}^{n - 1} {\sum\limits_{j = 0}^{m - 1} {{y_j}} } $

2)长宽比。手所在的最小矩形，长度定义为L，宽度定义为W，长宽比r定义为

$r = W/L$

3)矩形度。手势所占面积S₀与最小外接矩形面积S_m之比。矩形度a表示为

$a = {S_0}/{S_m}$

4) Hu矩特征。Hu矩特征主要描述图像旋转的不变性，包含7个分量。对于一幅 $N \times M$ 的图像 $f(x,y)$ ，则其 $\left( {p + q} \right)$ 阶矩为

${M_{pq}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {{x^p}{y^q}f\left( {x,y} \right)} } $

通过计算函数的重心，得到：

$\bar x = {M_{10}}/{M_{00}},\bar y = {M_{01}}/{M_{00}}$

对中心矩进行归一化后，使用二阶和三阶矩构造7个h分量矩：

${h_1} = {\eta _{20}} + {\eta _{02}}$

${h_2} = {\left( {{\eta _{20}} - {\eta _{02}}} \right)^2} + 4{\eta _{11}}^2$

${h_3} = {\left( {{\eta _{30}} - 3{\eta _{12}}} \right)^2} + {\left( {3{\eta _{21}} - {\eta _{03}}} \right)^2}$

${h_4} = {\left( {{\eta _{30}} + {\eta _{12}}} \right)^2} + {\left( {{\eta _{21}} + {\eta _{03}}} \right)^2}$

$\begin{gathered} {h_5} = \left( {{\eta _{03}} - 3{\eta _{12}}} \right)\left( {{\eta _{30}} + {\eta _{12}}} \right) + \left[ {{{\left( {{\eta _{30}} + 3{\eta _{12}}} \right)}^2}} \right. - \\ \left. {{\rm{ }} 3{{\left( {{\eta _{21}} + {\eta _{03}}} \right)}^2}} \right]\left( {3{\eta _{21}} - {\eta _0}} \right)\left( {{\eta _{21}} + {\eta _{03}}} \right)\cdot \\ {\rm{ }}\left[ {3{{\left( {{\eta _{30}} + {\eta _{12}}} \right)}^2} - {{\left( {{\eta _{21}} + {\eta _{03}}} \right)}^2}} \right] \\ \end{gathered} $

$\begin{gathered} {h_6} = \left( {{\eta _{20}} - {\eta _{02}}} \right)\left[ {{{\left( {{\eta _{30}} + {\eta _{12}}} \right)}^2} - {{\left( {{\eta _{21}} + {\eta _{03}}} \right)}^2}} \right] + \\ {\rm{ }} 4{\eta _{11}}\left( {{\eta _{30}} + {\eta _{12}}} \right)\left( {{\eta _{21}} + {\eta _{03}}} \right) \\ \end{gathered} $

$\begin{gathered} {h_7} = \left( {3{\eta _{21}} - {\eta _{03}}} \right)\left( {{\eta _{30}} + {\eta _{12}}} \right)\left[ {{{\left( {{\eta _{30}} + {\eta _{12}}} \right)}^2}} \right. - \\ \left. { 3{{\left( {{\eta _{21}} + {\eta _{03}}} \right)}^2}} \right]{\rm{ + }}\left( {3{\eta _{21}} - {\eta _{30}}} \right)\left( {{\eta _{21}} + {\eta _{03}}} \right)\cdot \\ \left[ {3{{\left( {{\eta _{30}} + {\eta _{12}}} \right)}^2} - {{\left( {{\eta _{21}} + {\eta _{03}}} \right)}^2}} \right] \\ \end{gathered} $

1.2 单位的书写规则

用函数 ${\psi _h}(t)$ 和 ${\psi _g}(t)$ 将对偶树复小波定义为

${\psi _c}\left( t \right) = {\psi _h}\left( t \right) + j{\psi _g}\left( t \right)$

且满足希尔伯特变换，即：

${\psi _g}\left( \omega \right) = \left\{ \begin{gathered} - j{\psi _h}\left( \omega \right), \quad \omega > 0 \\ {\psi _h}\left( \omega \right) , \quad \omega < 0 \\ \end{gathered} \right.$

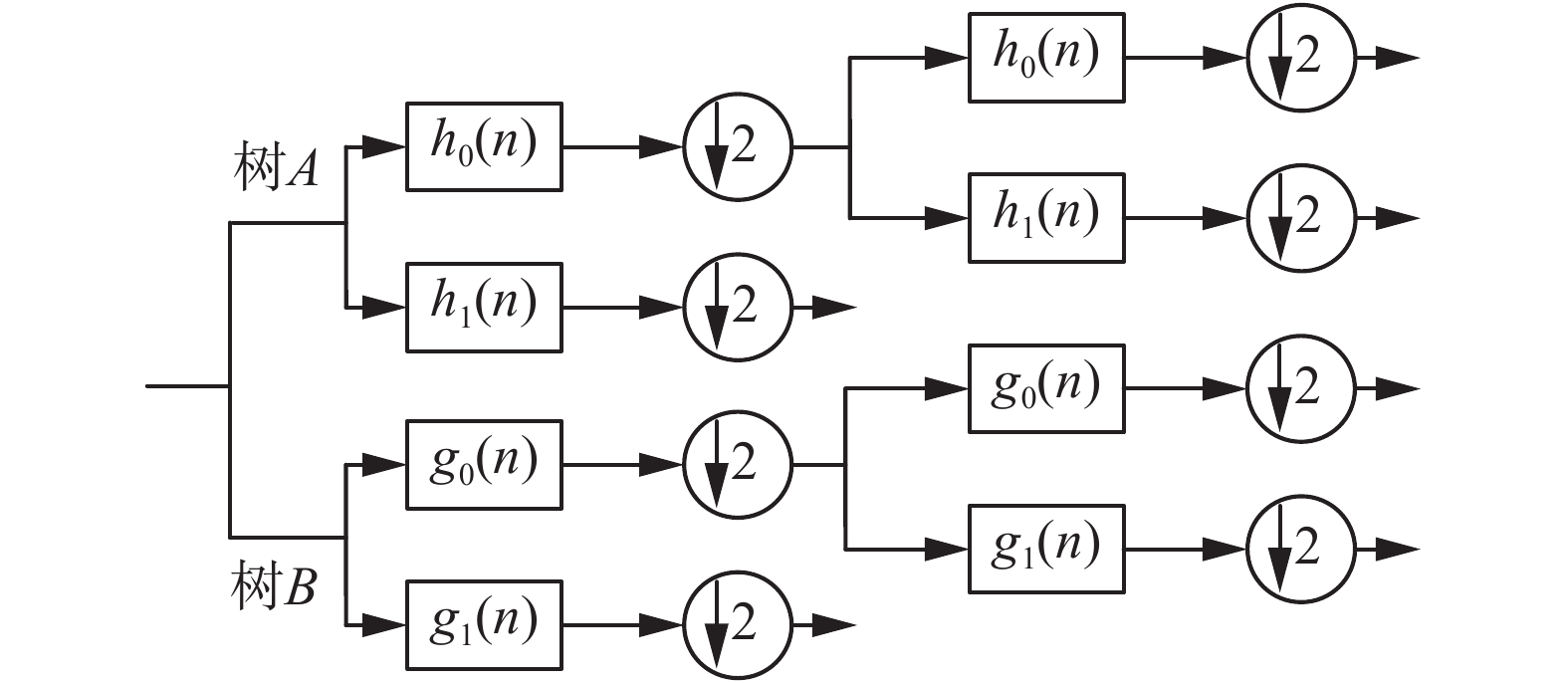
用树A和树B表示，结构图如图1所示。

通过 $\psi (t) = {\psi _h}(t) + j{\psi _g}(t)$ ，计算二维对偶树复小波变换：

$\begin{gathered} \psi \left( {x,y} \right) = \psi \left( x \right)\psi \left( y \right) = \\ \left[ {{\psi _h}\left( x \right) + j{\psi _g}\left( x \right)} \right]\left[ {{\psi _h}\left( y \right) + j{\psi _g}\left( y \right)} \right] = \\ {\psi _h}\left( x \right){\psi _h}\left( y \right) - {\psi _g}\left( x \right){\psi _g}\left( y \right) + \\ {\rm{ }} j\left[ {{\psi _g}\left( x \right){\psi _h}\left( y \right) + {\psi _h}\left( x \right){\psi _g}\left( y \right)} \right] \\ \end{gathered} $

输入图像后，采用滤波器 ${h_0}(n)$ 与 ${h_1}(n)$ 、 ${{\rm{g}}_0}(n)$ 与 ${g_1}(n)$ 进行两步分解操作，获得每个子带对应的系数，通过做差求取对偶树复小波变换的低频分量和高频分量。对偶树复小波变换后，实部与虚部分量方向相同，因此可进行6个方向的度量，分别对应 $ - 75^\circ $ 、 $ - 45^\circ $ 、 $ - 15^\circ $ 、 $75^\circ $ 、 $45^\circ $ 、 $15^\circ $ ，如图2所示。

2 BD-SVM分类器

根据传统SVM算法原理，根据几何特征，支持向量即同类距离最小，异类距离最大的两类样本，若训练样本未进行优化，则寻找支持向量的过程就会耗时严重，因此，改进思路聚集在对训练样本的几何特征上。本文将训练样本的点间距离作为度量，通过优化训练样本集，提高SVM的训练速度，也因样本集的品质提高，从而间接提高分类器的识别精度。具体数学描述如下。

将样本点分布于空间中，定义任意两点的距离为

$\begin{gathered} d\left( {{{{x}}_i},{{{x}}_j}} \right) = \sqrt {{{\left( {{{{x}}_i} - {{{x}}_j}} \right)}^{\rm{T}}}\left( {{{{x}}_i} - {{{x}}_j}} \right)} = \\\sqrt {2 - 2{{K}}\left( {{{{x}}_i},{{{x}}_j}} \right)} \\ \end{gathered} $

(16)

高维空间点定义为 ${z_k}$ ，则 ${z_k}$ 对应一对距离值 $(d_k^ + ,d_k^ - )$ ，具体表示如下：

$\left\{ {\begin{array}{*{20}{c}} {d_k^ + = \displaystyle\frac{1}{{{l^ + }}}\sum {d\left( {{z_k},{{{x}}_i}} \right)} } {d_k^ - = \displaystyle\frac{1}{{{l^ - }}}\sum {d\left( {{z_k},{{{x}}_j}} \right)} } \end{array}} \right.$

则存在临界值 ${c_1}$ 和 ${c_2}$ ，使得 $P\left( {d_k^ + > {c_1}} \right) = t$ ， $P\left( {d_k^ - < {c_2}} \right) = t$ ，支持向量就是满足 $\left\{ {{z_k}|d_k^ + > {c_1},d_k^ - < {c_2}} \right\}$ 的 ${z_k}$ 点。算法设计的具体步骤如下。

1)设置比例系数t(0<t<1)。

2)在高维空间中，按照式(1)计算距离矩阵 ${{D}} = \{ {({d_{ij}})_{l \times l}}\} $ 。

3)令 ${I_{{l^ + }}} = \displaystyle\frac{1}{{{l^ + }}}{e_{{l^ + } \times 1}}$ ， ${I_{{l^ - }}} = \displaystyle\frac{1}{{{l^ - }}}{e_{{l^ - } \times 1}}$ ，计算平均距离矩阵 ${{V}} = {\left[ {\begin{array}{*{20}{c}} {{{{V}}_{11}}}&{{{{V}}_{12}}} \\ {{{{V}}_{21}}}&{{{{V}}_{22}}} \end{array}} \right]_{\left( {{l^ + }{l^ - }} \right) \times 2}}$ 。

4)对矩阵V进行按序排列，其中，V₁₁和V₂₂降序，V₁₂和V₂₁升序，提取l·t个样本，得到新的训练样本集 $\left| {{T^{{\rm{new}}}}} \right|$ 。

5)在新样本集上利用SVM建立模型，并进行测试。

3 结果与分析 3.1 特征提取

静态手势识别选取60幅“1~9”手势的图像作为训练样本，30幅作为测试样本。包括空域及频域特征提取，BD-SVM分类器精度，输出识别正确率和分类时间。

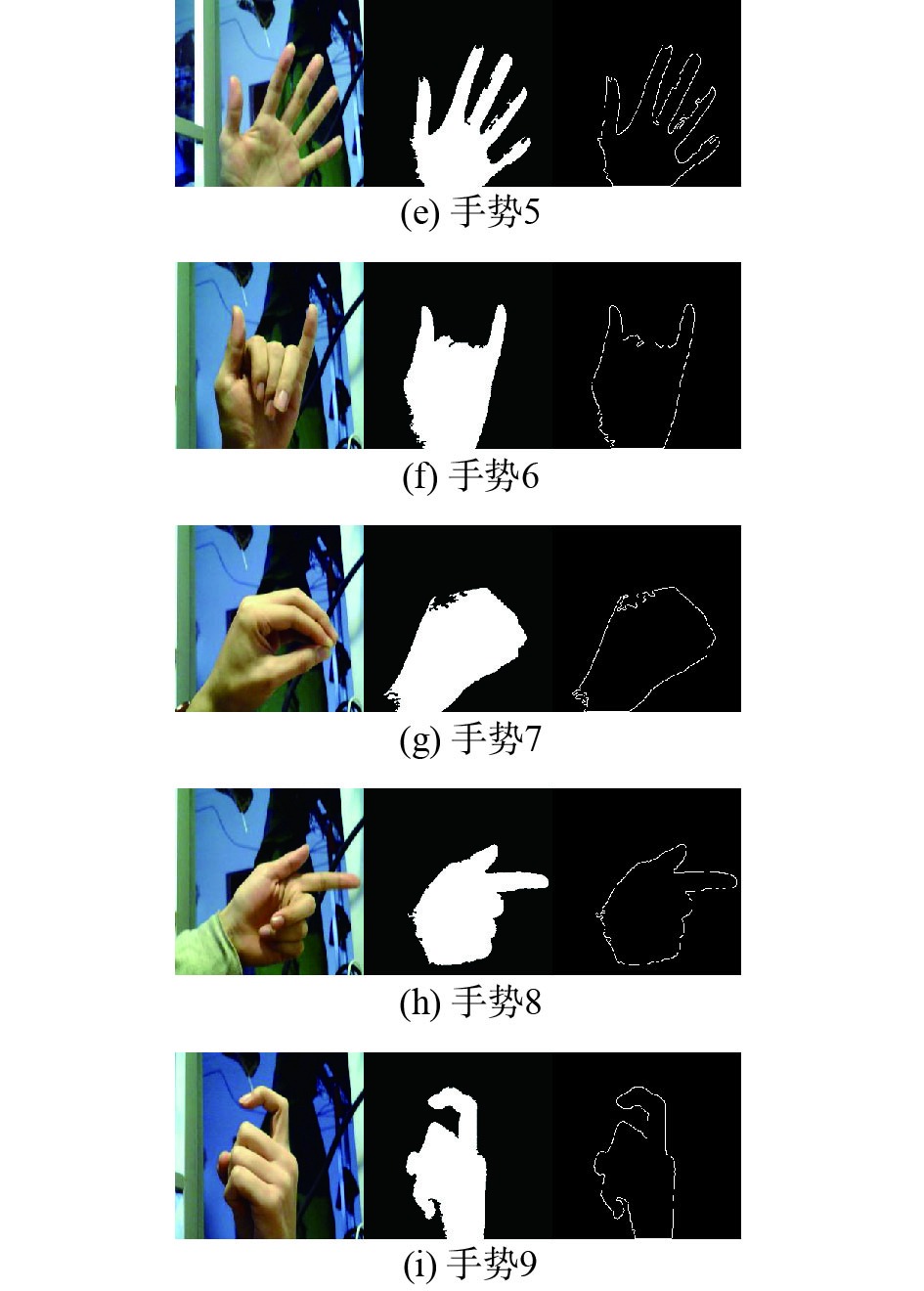
进行空域特征提取，首先需对输入的图像进行预处理，然后进行分割和检测，最后，计算相应的空域特征。某一样本“1~9”手势的预处理后的图像及分割检测后的图像如图3所示。

按照前文给出的公式，计算空域特征，包括位置、长宽比、矩形度、Hu矩的7个分量。取某一样本的“1~9”手势的特征，如表1所示。

对偶树复小波具有平移不变性和方向多样化的特性，按照对偶树复小波变换进行频域特征提取，dtwavexfm2函数中可以选择4个滤波器，本文选legall，进行变换分解。

以其中一幅手势图像为例，对偶树复小波特征提取的结果如下。某一示例图像“1”如图4所示，其他“2~9”手势特征提取过程相同。

经过分解后的结果如图5所示。

选取高频分量输出的16×16矩阵，作为该手势图像的特征参数，方便计算，将该矩阵进行归一化处理，然后，取主对角线元素作为特征，共计16个分量。

对于每个样本，将空域特征的11个分量与频域的16个分量进行融合，组成新的矢量，则新矢量的维度为27，然后，以60个样本作为训练集，输入分类器中训练，30个样本预测集，用于验证分类精度。

3.2 BD-SVM识别结果

本节主要测试手势“1~9”的识别效果。利用BD算法优化训练样本，设置BD-SVM的比例系数t为0.3，然后，将新的训练样本作为SVM训练集，最后，选取线性核函数、多项式核函数和径向基核函数分别进行实验。γ设置为0.1，惩罚参数设置为10，具体实验结果如下所示。

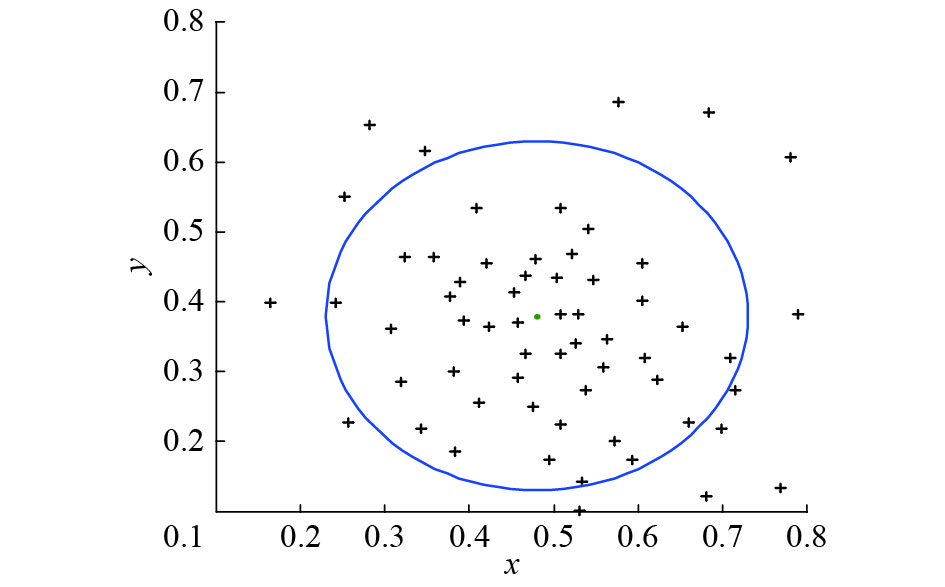
样本优选过程进行二维可视化后，如图6所示。

圈内的样本为优选后的样本，作为新的训练集，挑选出46个新的训练样本。

对于每个核函数，输出识别精度和识别时间，最后计算平均正确率和平均识别时间。采用线性核函数的识别结果如表2所示。

由表2得出，线性核函数的平均正确率为84%，平均识别时间为0.022 s。

采用多项式核函数的识别结果如表3所示。由表3得出，线性核函数的平均正确率为86.67%，平均识别时间为0.032 s。

采用径向基核函数的识别结果如表4所示。由表4得出，线性核函数的平均正确率为90.33%，平均识别时间为0.026 s。

通过实验得出，选择径向基核函数的识别率最高，运算速度也较快，因此，进行静态手势识别，采用径向基核函数。

4 结束语

本文主要采用空域特征和对偶树复小波相融合的特征，空域特征包含水平位置、竖直位置、长宽比、矩形度、Hu矩7个分量，计11维特征，频域特征采用对偶树复小波变换的16维特征，特征融合后，共计27维特征；采用BD算法进行训练样本优选，优选出46个新的训练样本，再将新的训练样本进行SVM分类器的训练，实验表明，采用径向基核函数识别精度最高，速度最快，“1~9”的静态手势识别效果最好。