2. 重庆邮电大学 计算智能重庆市重点实验室,重庆 400065
2. Chongqing Key Laboratory of Computation Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
目前,多媒体技术飞速发展,图像数量呈指数级增长,图像分类技术也得到了飞速发展。图像分类方法主要包括分类器的设计和特征提取两个部分,目前对图像分类的研究主要集中在分类器性能的改进和改善特征提取方法两方面。稀疏编码(字典学习)[1-10]是图像分类的有效技术之一,用于图像分类的字典学习算法也可以分为2类:1)学习字典把原始图像映射到有利于图像分类的空间上,用传统的分类器去分类;2)用稀疏系数所表示出来的样本属性进行分类。
在用于图像分类的字典学习算法中,字典和编码系数的设计从中起着关键作用[3]。基于稀疏表示的分类算法[4],将整个训练样本作为字典,利用测试样本在字典上的重构误差分类。在字典中的每个原子都是一个样本,由于样本数量的限制,字典原子中有相同或相似的,还有一些则不包含在内造成分类错误。而Aharon M等提出的KSVD算法[5]学习的字典具有自适应性,能够更好对信号进行稀疏表示。虽然,使用重构误差作为损失函数,可以用于图像分类,但是还有许多因素没有考虑到。Yang等[6]提出Fisher字典学习在自适应字典基础上,考虑到相同的样本之间的类内散度较小,类间散度大,在目标函数上加入了识别系数项,提高分类能力。Jiang等[7]提出的LC-KVD算法,在KSVD算法[5]基础上加入了标签约束项。在文献[8]中,由于分别学习特征影射矩阵和字典,会影响特征影射矩阵的判别信息,提出了同时学习投影矩阵和字典,为了能够提取更多的判别信息,加入图正则项。构建近邻图,近邻且同类相似度为1,近邻但不同类相似度为−1,其他为0。在文献[9]中图正则化中的相似度矩阵定义为两近邻样本的相似度为两样本之间的欧氏距离,不近邻样本之间的相似度为0。使用不同的相似矩阵,分类效果也不同。另一方面,由于字典学习[3-9]大多是使用编码系数的0或1范数作正则项,在训练和测试阶段效率较低,运行时间长。2014年在NIPS上Gu等[10]提出了字典对学习,联合学习一个综合字典和分析字典,用分析字典去分析编码,由于综合字典的重构效果比较好,使用综合字典去重构图像。它不仅减少了在训练和测试阶段的时间复杂度,也提高了模型的分类能力。但是,字典对学习模型没有考虑图像的几何近邻拓扑关系。为了提高模型的分类能力,基于同类样本的系数之间的距离小,不同类系数之间的距离大的思想,提出了基于图正则化字典对学习(GDPL)算法。
在最近的综合研究[11]中,用十倍交叉验证的方法评估轻度认知功能障碍(MCI)到阿尔兹海默症(AD)的预测,只有4种方法的实验结果比随机分类的结果好,因此,提出新的方法提高MCI-AD的预测是十分必要的。在图像分类中,并不是所有的特征都与识别分类有关,其中有一些是无关特征,将这些特征用于分类会出现过拟合现象。由于稀疏表示中表示系数具有稀疏性,将本文提出的图正则化字典对学习算法用于轻度认知功能障碍预测。
1 相关工作 1.1 字典学习设
| ${\min _{{{D}},{{A}}}}||{{X}} -{{DA}}||_F^2 + \lambda g({{A}}) + \eta f({{D}},{{A}},{{Y}})$ | (1) |
式中:
| $g({{A}}) = ||{{A}}|{|_p}$ | (2) |
式中:
在1.1中描述的判别式字典学习模型是学习一个共享字典,对系数的约束都是使用
| $\{ {{P}},{{D}}\} = {\min _{{{P}},{{D}}}}||{{X}} - {{DPX}}||_F^2 + f({{D}},{{P}},{{X}},{{Y}})$ | (3) |
式中:
| ${\min _{P,D}}\sum\limits_{k = 1}^K {||{{{X}}_k} - {{{D}}_k}{{{P}}_k}{{{X}}_k}||_F^2} $ |
因此,DPL模型的目标函数可以写为:
| $\begin{array}{c} \{ {{P}},{{D}}\} = {\mathop {\min }\limits_{{{P}},{{D}}} }\sum\limits_{k = 1}^K {||{{{X}}_k} - {{{D}}_k}{{{P}}_k}{{{X}}_k}||_F^2} + \lambda ||{{{P}}_k}\overline {{{{X}}_k}} ||_F^2\\ {\rm s.t.}||{d_i}||_2^2 \leqslant 1 \end{array}$ |
式中:
字典对学习只考虑图像的重构误差和不同类的分析字典和样本的投影系数尽可能的小,没有考虑原始样本的近邻几何结构,引入图正则化,使低维表示能够保留原始样本的近邻结构。
2.1 图正则化字典对学习在流形学习中,假设两个高维空间的相邻的两点,在其对应的低维空间仍保持其在高维空间的几何近邻拓扑关系。为了使样本之间可区分,并同时保持原始图像的几何近邻结构,且使同类样本在分析字典 P 上的投影系数之间距离小,不同类之间的距离大。对编码系数的图正则项约束表示为:
| $f(X) = \sum\limits_{u = 1}^n {\sum\limits_{v = 1}^n {||{{P}}{x_u} - {{P}}{x_v}||_2^2} } {{{S}}_{uv}}$ |
式中:n是所有样本总数;u 和 v 是第
在大多数图正则项,都是对数据集构建近邻图[9],用图的边的权值表示数据之间的关联度。但是本文利用样本总数去平衡类内和类间的距离,已经证明能够提高在字典上的编码系数的判别能力[12],因此,本文中相似度矩阵 S 是依据
| ${{{S}}_{uv}} = \left\{ {\begin{array}{l} {1/{n_{l({x_u})}}},\,\,\,\,\,\,\,\,\,\qquad{l({x_u}) = l\left( {{x_v}} \right)}\\ { - 1/(n - {n_{l({x_u})}})},\,\,\,{\rm otherwise} \end{array}} \right.$ |
式中:
在DPL算法的基础上,构建近邻图保持原始图像间的近邻关系,由此提出了图正则化字典对学习(GDPL)算法。GDPL算法的目标函数可写为:
| $\begin{split} {\rm{\{ }}{{{P}}^{\rm{*}}}{\rm{,}}{{{D}}^{\rm{*}}}{\rm{\} }} = & {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{P}}_k}{{{X}}_k}||_F^2 + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2)}+ \\ & \,\,\,\,\,\,\, \beta \displaystyle\sum\limits_{u = 1}^n {\sum\limits_{v = 1}^n {||{{P}}} } {x_u} - {{P}}{x_v}||_2^2{{{S}}_{uv}} \end{split}$ |
式中:
引入变量编码系数
| $\begin{array}{c} {\rm{\{ }}{{{P}}^{\rm{*}}}{\rm{,}}{{{D}}^{\rm{*}}}{\rm{\} }} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \alpha \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2} + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2) + (1 - \alpha )\beta \displaystyle\sum\limits_{u = 1}^n {\displaystyle\sum\limits_{v = 1}^n {||{{P}}} } {x_u} - {{P}}{x_v}||_F^2{{{S}}_{uv}} =\\ {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \alpha \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2} + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2) + (1 - \alpha )\beta \displaystyle\sum\limits_{u = 1}^n {\left( {\displaystyle\sum\limits_{v = 1}^n {\left( {{{({{P}}{x_u})}^2} - 2{{P}}{x_u}{{P}}{x_v} + {{({{P}}{x_v})}^2}} \right)} {{{S}}_{uv}}} \right)} = \\ {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \alpha \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2} + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2) + (1 - \alpha )\beta \displaystyle\sum\limits_{u = 1}^n {{c_u}{{({{P}}{x_u})}^2}} - \displaystyle\sum\limits_{u = 1}^n {\displaystyle\sum\limits_{v = 1}^n {{{P}}{x_u}{{P}}{x_v}{{{S}}_{uv}}} }= \\ {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \alpha \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2} + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2) + (1 - \alpha )\beta ({{PX}}){{C}}{({{PX}})^{\rm{T}}} - ({{PX}}){{S}}{({{PX}})^{\rm{T}}} = \\ {\rm{arg}}\mathop {{\rm{min}}}\limits_{{{P,D}}} \alpha \displaystyle\sum\limits_{k = 1}^K {(||{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2} + \lambda ||{{{P}}_k}{{\bar {{X}}}_k}||_F^2) + (1 - \alpha )\beta {\rm tr}({{PXL}}{{{X}}^{\rm{T}}}{{{P}}^{\rm{T}}}) \end{array}$ | (9) |
式中:
在流形学习中,假设两个高维空间的相邻的两随机初始化分析字典 P 和综合字典 D,之后,迭代更新编码系数 A 和
1) 固定综合字典
| ${{{A}}_k} = {({{D}}_k^{\rm{T}}{{{D}}_k} + \tau {{I}})^{ - 1}}({{D}}_k^{\rm{T}}{{{X}}_k} + \tau {{{P}}_k}{{{X}}_k})$ | (10) |
2) 固定编码系数
| $\left\{ {\begin{array}{l} {{{{P}}_k} = \arg \mathop {\min }\limits_{{P_k}} \alpha \displaystyle\sum\limits_{k = 1}^K {\tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2 + \lambda ||{{{P}}_k}{{{X}}_k}||_F^2} +}\\ { \beta {\rm tr}({{{P}}_k}{{XL}}{{{X}}^{\rm{T}}}{{P}}_k^{\rm{T}})}\\ {{{{D}}_k} = \arg \mathop {\min }\limits_{{{{D}}_k}} \alpha \displaystyle\sum\limits_{k = 1}^K {||{{{X}}_k} - {{{D}}_k}} {{{A}}_k}||_F^2}\\ {{\rm s.t.}||{d_i}||_2^2 \leqslant 1} \end{array}} \right.$ | (11) |
对
| $\begin{array}{c} {{{P}}_k} = \arg \mathop {\min }\limits_{{{{P}}_k}} \alpha \displaystyle\sum\limits_{k = 1}^K {\tau ||{{{P}}_k}{{{X}}_k} - {{{A}}_k}||_F^2 + \lambda ||{{{P}}_k}{{{X}}_k}||_F^2}+ \\ (1 - \alpha )\beta {\rm tr}({{{P}}_k}{{XL}}{{{X}}^{\rm{T}}}{{P}}_k^{\rm{T}}) \end{array}$ |
对
| $\begin{array}{c} \displaystyle\frac{\partial }{{\partial {{{P}}_k}}} = 2{{{P}}_k}(\alpha \tau {{{X}}_k}{{X}}_k^{\rm{T}} + \alpha \lambda {{\bar {{X}}}_k}\bar {{X}}_k^{\rm{T}} + \\ (1 - \alpha )\beta {{XL}}{{{X}}^{\rm{T}}} + \gamma {{I}}) - 2\alpha \tau {{{A}}_k}{{X}}_k^{\rm{T}} \end{array}$ |
令
| $\begin{array}{c} {{P}}_k^* = \alpha \tau {{{A}}_k}{{X}}_k^{\rm{T}}(\alpha \tau {{{X}}_k}{{X}}_k^{\rm{T}} + \alpha {\lambda _3}{{\bar {{X}}}_k}\bar {{X}}_k^{\rm{T}}+\\ \gamma{{I}} + (1 - \alpha )\beta {{XL}}{{{X}}^{\rm{T}}}{)^{ - 1}} \end{array}$ | (12) |
式中:
在公式(13)中用交替方向乘子算法(AMMD)[8]对 D 优化求解。具体的求解过程如下所示:
| $\left\{ {\begin{array}{l} {{{{D}}^{(r + 1)}} = \arg \mathop {\min }\limits_{{D}} \displaystyle\sum\limits_{k = 1}^K {{\rm{||}}{{{X}}_k} - {{{D}}_k}{{{A}}_k}||_F^2 + \rho ||{{{D}}_k} - {{S}}_k^{(r)} + {{K}}_k^{(r)}||_F^2} }\\ {{{{S}}^{(r + 1)}} = \arg \mathop {\min }\limits_{{S}} \displaystyle\sum\limits_{k = 1}^K {\rho ||{{D}}_k^{(r + 1)} - {{{S}}_k} + {{T}}_k^{^{(r)}}||_F^2{\rm s.t.}||{s_i}||_2^2 \leqslant 1} }\\ {{{{T}}^{(r + 1)}} = {{{T}}^{(r)}} +{{D}}_k^{(r + 1)} - {{S}}_k^{(r + 1)} } \end{array}} \right.$ | (13) |
对
| $\frac{\partial }{{\partial {{{D}}_k}}} = 2{{{D}}_k}({{{A}}_k}{{A}}_k^{\rm{T}} + \rho {{I}}) - 2({{{X}}_k}{{A}}_k^{\rm{T}} + \rho ({{S}}_k^r - {{T}}_k^r))$ |
令
| ${{{D}}_k} = ({{{X}}_k}{{A}}_k^{\rm{T}} + \rho ({{S}}_k^r - {{T}}_k^r)){({{{A}}_k}{{A}}_k^{\rm{T}} + \rho {{I}})^{ - 1}}$ | (14) |
对
| $\frac{\partial }{{\partial {{{S}}_k}}} = - 2\rho ({{D}}_k^{(r + 1)} + {{T}}_k^{(r)}) + 2\rho {{{S}}_k}$ |
令
| ${{{S}}_k} = {{D}}_k^{(r + 1)} + {{T}}_k^{(r)}$ | (15) |
由于算法中的图正则项,需要先用训练样本构建近邻图,计算出相似矩阵
算法1 GDPL训练算法
输入 训练样本
1) 利用样本标签信息构建近邻图。根据样本标签信息判断样本是否为近邻点。若
2) 初始化:随机生成综合字典
3)
While 未收敛(具体的在收敛性分析中)执行下面步骤:
1) 固定字典
2) 固定编码系数
3) 固定编码系数
End While
End For
输出 综合字典 D,分析字典 P。
2.4 分类方法在图像分类中,并不是所有的特征都与识别分类有关,其中有一些是无关特征,将这些特征用于分类会出现过拟合现象。另一方面,稀疏表示是在超完备字典中用尽可能少的原子去表示原来的图像信号,其中的表示系数具有稀疏性。用表示系数作为特征去分类,可以减少无关特征的影响,提高模型的判别能力。用ADNI1数据集进行验证,具体的实验结果在第4部分中,使用编码系数用分类器分类效果比直接使用分类器[14]的效果好。
在分类模型中,输入训练样本 X 使用算法1训练出来的综合字典 D 和分析字典 P,由 A,计算出训练集在分析字典上的投影系数即稀疏表示中的编码系数
本节主要对提出的图正则化字典对算法(GDPL)进行时间复杂度分析和收敛性分析,该算法通过联合学习一个综合字典和分析字典,将样本在分析字典上的投影作为表示系数,减小了算法的时间复杂度。
3.1 时间复杂度分析在GDPL算法中主要是计算训练阶段的时间复杂度。在训练阶段
在目标函数式(1)中对于
|
Download:
|
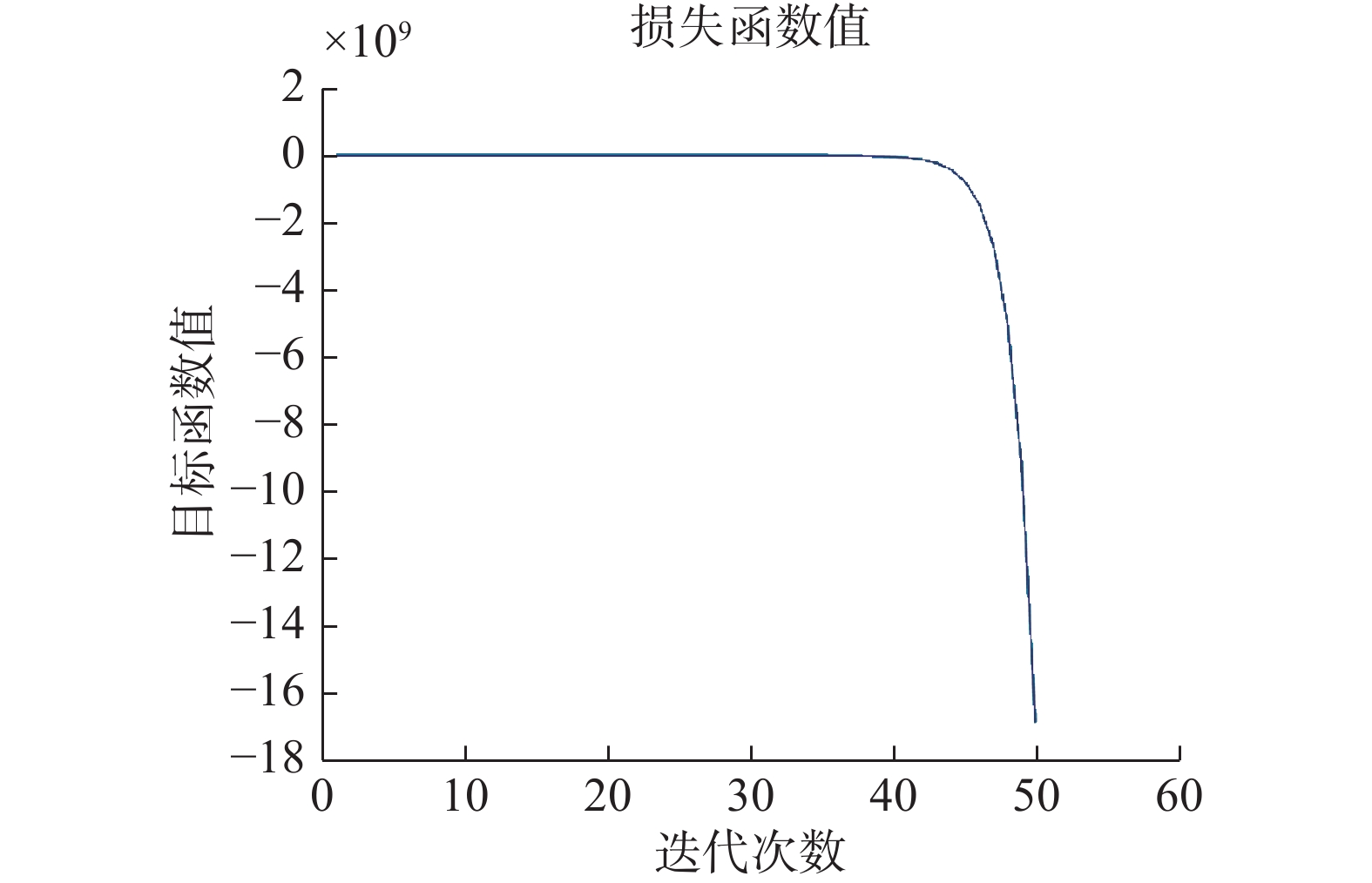
| 图 1 目标函数值随迭代次数变化 Fig. 1 The value of the objective function varies with the number of iterations | |
图1中单个样本的整个目标函数值在开始到40次的变化趋势是平行趋于0,之后变成一个比较大的负值,由于相似度矩阵不是半正定矩阵,由此使图正则项的值变成负值,并引起其他项的变化。并且由于图像的损失函数一般都不会小于0,所以,从图1可以看出算法在2~40次之间是局部收敛的。所以,有的实验在第2次迭代就达到最优值。
4 实验结果与分析为了验证图正则化字典对学习算法在图像分类中的性能,本文在ADNI1数据集上进行验证。ADNI由国际老年研究所、生物医学成像和生物工程研究所、美国食品和药物管理局、民营医药企业和非营利组织在2003年启动,资金为60万美元。ADNI的主要目标是测试是否能通过组合MRI、PET、其他生物标志物,以及临床和神经心理学评估来测定MCI和早期AD的进展。
在ADNI1[14]中,根据MCI患者在36个月之后的状态,将36个月之后仍表现出MCI的状态,则记为SMCI;36个月后表现为AD的病况,记为PMCI;没有36个月之后的信息的患者,记为uMCI。实验中只利用表1中显示的有标签的164个PMCI患者信息和100个SMCI患者信息,对MCI进展进行识别,提前预测AD。
| 表 1 PMCI和SMCI相关信息 Tab.1 PMCI and SMCI related information |
所有实验是使用中全局生物标志[14]和表1中显示的Age、MMSE、CDR-SB、RAVLT、FAQ、ADAS-cog信息的结合生物标志作为特征表示样本,使用算法1中学习的字典对
为了验证提出的基于图正则化的字典对学习方法的实验效果比其他的实验效果好,直接使用结合生物标志用SVM、LDA、KNN分类器分类,使用DPL方法训练出来的字典对上的稀疏系数作为特征用分类器(SVM、LDA、KNN)做出的实验效果,和使用GDPL方法训练出来的字典对上的稀疏系数作为特征用SVM、LDA、KNN分类的实验结果。最终的实验结果是取100次10倍交叉验证结果的平均值,对于具体实验数据的精确度取小数点后3位。
在使用字典对算法训练字典的过程中,算法中参数设置是选择一个参数变化,固定其他参数,进行遍历。选取3次十倍交叉验证平均准确率最好。经过遍历参数,算法中的参数设置如表2、3所示。
| 表 2 使用DPL稀疏系数作为特征的参数设置 Tab.2 Parameter setting using DPL algorithm |
| 表 3 使用GDPL稀疏系数作为特征的参数设置 Tab.3 Parameter setting of the GDPL algorithm |
1) 为了验证在基于图正则化的字典对(GDPL)算法学习的字典对上的系数作为特征效果比直接用结合生物标志作为特征的实验效果好。本文使用准确率(ACC)和ROC曲线下的面积(AUC)作为评价标准。
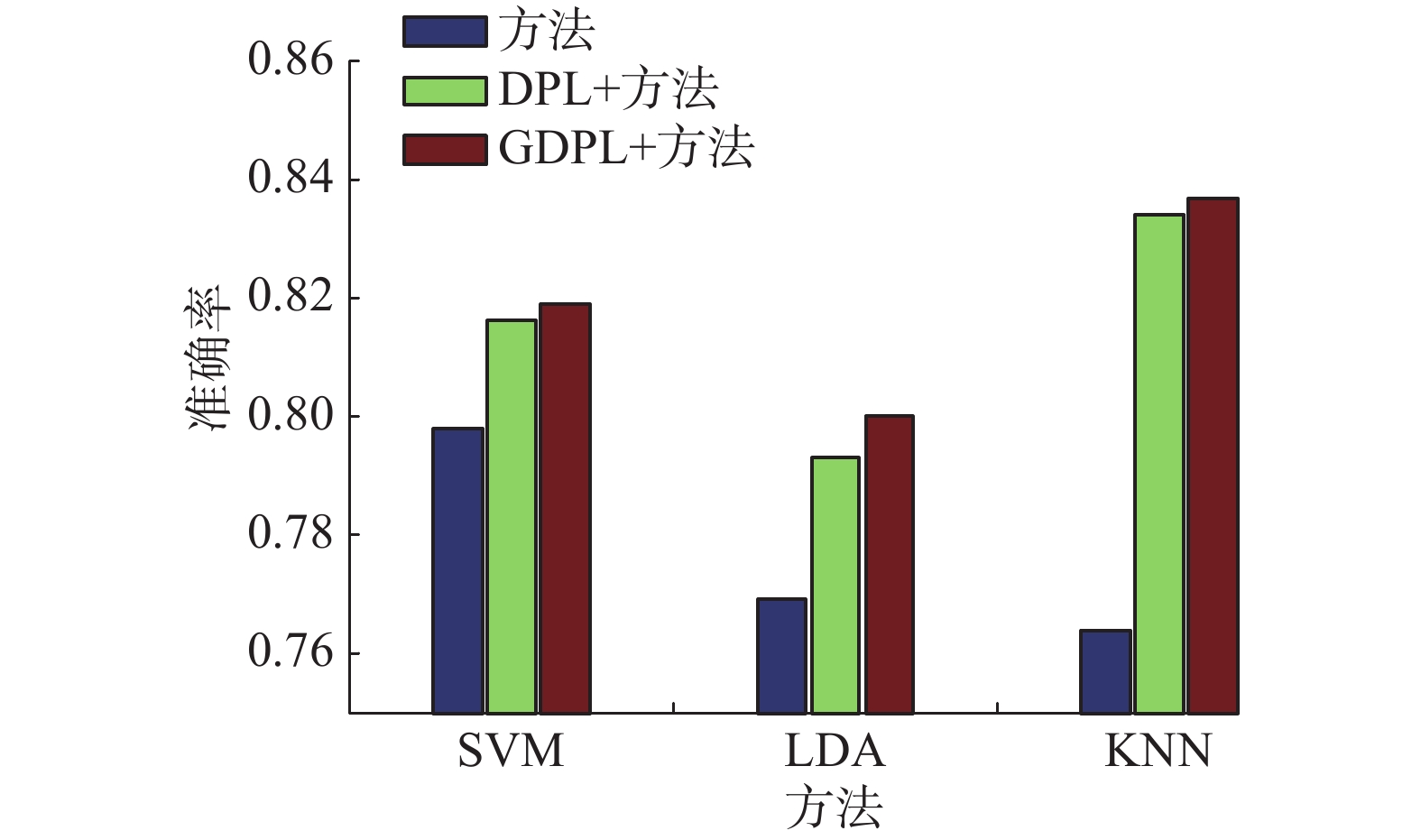
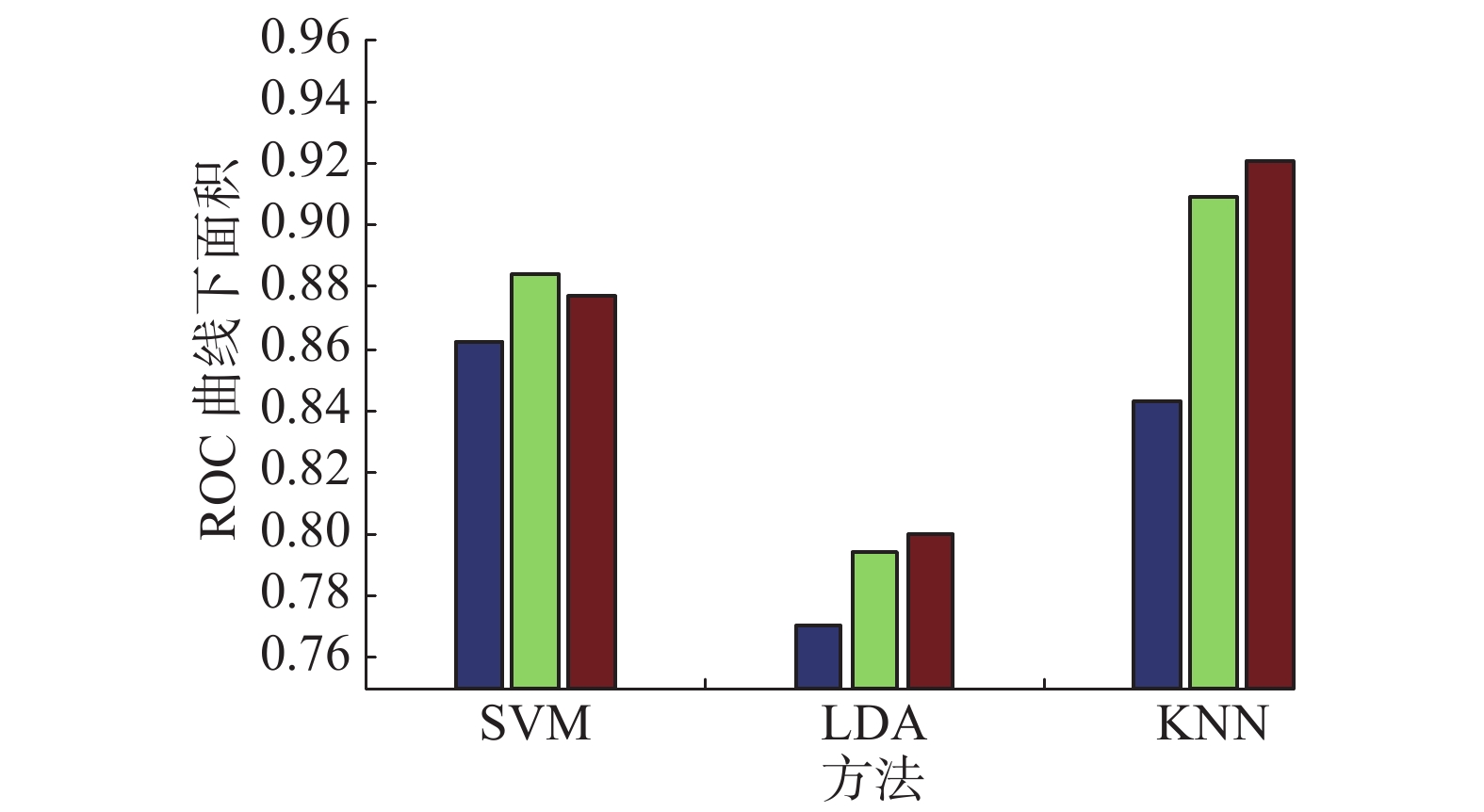
从图2可以看出直接用结合生物标志作为特征的准确率与使用字典对学习方法的准确率相差较大,使用SVM和GDPL+SVM的实验结果相差了2个百分点,K近邻(KNN)和GDPL+KNN相差了6个百分点。用GDPL方法的准确率比DPL方法的准确率高。从图2整体上看使用GDPL方法的实验效果比DPL方法和直接使用综合特征的效果好。图3从算法AUC性能评价,从中可以看出使用GDPL的稀疏系数作为特征的实验中,除了SVM外,其他的方法都比使用DPL的效果好,其中KNN的AUC最高到达92.1%。从图2、3中整体的结果可以看出GDPL方法的实验结果比DPL的实验结果好。
|
Download:
|
| 图 2 不同方法上的准确率 (ACC) Fig. 2 The accuracy of different methods | |
|
Download:
|
| 图 3 不同方法上的ROC曲线下的面积(AUC) Fig. 3 Area under ROC curve in different methods | |
2) 将结合生物标志直接作为特征用SVM、LDA、KNN分类,使用DPL方法的稀疏系数作为特征的分类方法记为DPL+SVM、DPL+LDA、DPL+KNN,和使用GDPL方法的稀疏系数作为特征的分类方法记为GDPL+SVM、GDPL+LDA、GDPL+KNN,所用实验结果都是记录使用100次十倍交叉验证的结果(平均值)画出的盒形图。使用准确率(ACC)、ROC曲线下面的面积(AUC)对于分类器的性能进行评估,具体实验结果在图4、5中显示。

|
Download:
|
| 图 4 使用100次十倍交叉验证的ACC画出的箱型图 Fig. 4 Box plot for the ACC of 100 times 10-fold cross-validation | |
|
Download:
|
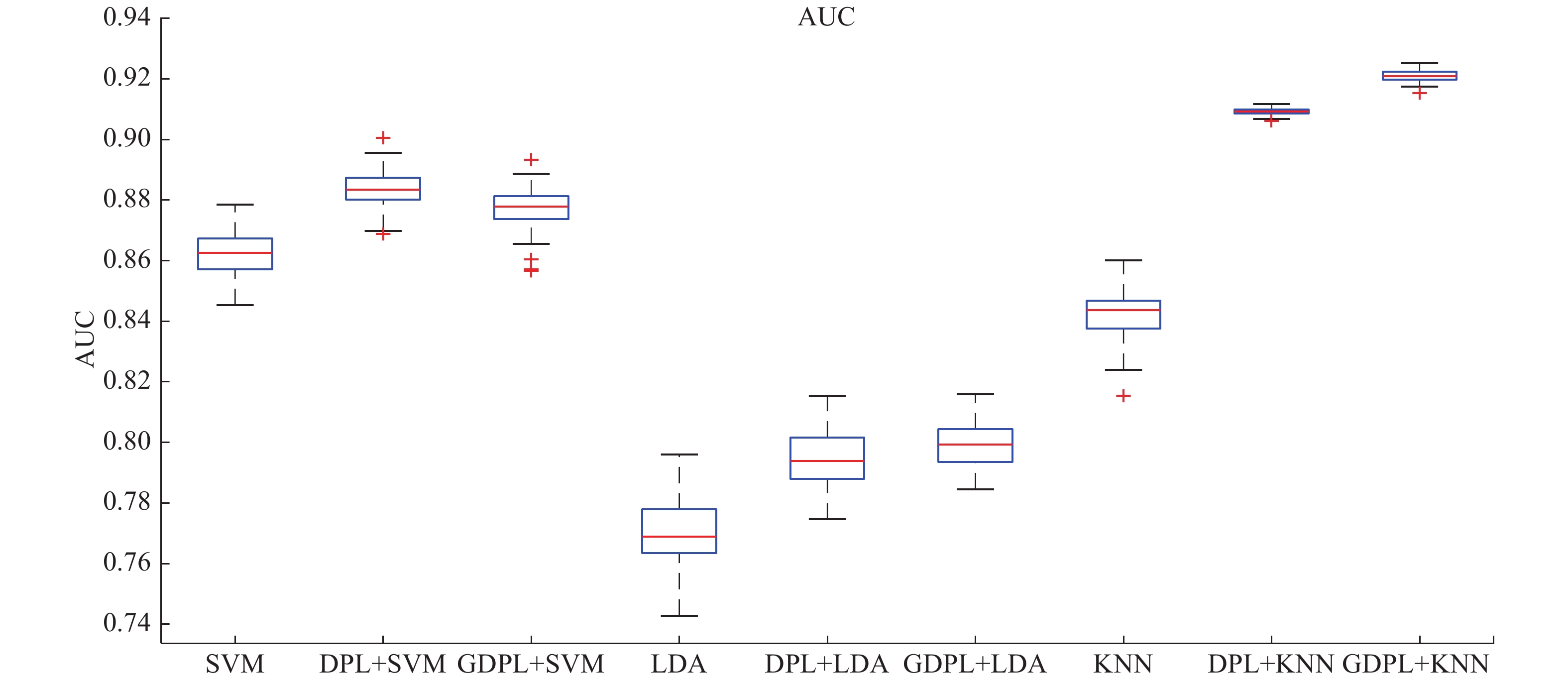
| 图 5 使用100次10倍交叉验证的AUC画出的箱型图 Fig. 5 Box plot for the AUC of 100 times 10-fold cross-validation | |
从图4中整体上可以看出使用GDPL算法的稀疏系数作为特征的平均准确率比DPL算法的稍微好一点,比直接使用结合生物标志作为特征的平均准确率高,GDPL+KNN算法的平均准确率最高达到了83.7%。图5显示ROC曲线下的面积(AUC)最好的是GDPL+KNN算法,AUC达到92.1%。在图4、5,100次实验结果中GDPL+KNN算法结果相对集中稳定。整体上看使用GDPL方法训练出来的字典对上的稀疏系数作为特征的实验结果比直接使用结合生物标志特征的结果好,GDPL+KNN实验结果最好,并且结果比较集中稳定,每次实验的结果的变化不大。
5 结束语本文实验结果表明在字典对学习算法中加入图正则项,可以提高字典对模型的识别能力,能够更好地对图像进行分类。另一方面,使用在字典对上的稀疏系数作为特征对轻度认知功能障碍预测可以取得更好的效果,并且在GDPL算法上的稀疏系数作为特征的实验结果比DPL上的实验结果好。随着科技的发展,图像资源越来越丰富,用户想在大量的图像中找到需要的图像信息比较困难。在现实生活中带标签的数据相对于不带标签的数据少很多,获得带标签的图像比较困难。并且训练样本较少不能获得足够的特征去学习字典,下一步可以将无标签的样本用于实验中,学习一个更完备的字典,提高模型的识别能力。可以进行半监督字典对学习,提高模型的判别能力。
| [1] |
邵冬华, 施志刚, 史军杰. 二次近邻稀疏重构法及人脸识别[J]. 重庆邮电大学学报 (自然科学版), 2017, 29(6): 844-850. SHAO Donghua, SHI Zhigang, SHI Junjie. Sparse reconstruction algorithm based on secondary nearest neighbor and face recognition[J]. Journal of Chongqing university of posts and telecommunications (natural science edition), 2017, 29(6): 844-850. (  0) 0)
|
| [2] |
王佐成, 杨娟, 薛丽霞. 基于二进神经网络的稀疏编码架构的图像无损压缩新方法[J]. 重庆邮电大学学报 (自然科学版), 2017, 29(3): 371-376. WANG Zuocheng, YANG Juan, XUE Lixia. A novel lossless image compression scheme based on binary neural networks with sparse coding[J]. Journal of Chongqing University of Posts and Telecommunications (natural science edition), 2017, 29(3): 371-376. (  0) 0)
|
| [3] |
WRIGHT J, MA Yi, MAIRAL J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044. DOI:10.1109/JPROC.2010.2044470 ( 0) 0)
|
| [4] |
WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 ( 0) 0)
|
| [5] |
AHARON M, ELAD M, BRUCKSTEIN A. rmK-SVD: an algorithm for designing overcomplete dictionaries for sparse representation
[J]. IEEE transactions on signal processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 ( 0) 0)
|
| [6] |
YANG Meng, ZHANG Lei, FENG Xiangchu, et al. Fisher discrimination dictionary learning for sparse representation[C]//Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain, 2011: 543–550.
( 0) 0)
|
| [7] |
JIANG Zhuolin, LIN Zhe, DAVIS L S. Label consistent K-SVD: learning a discriminative dictionary for recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(11): 2651-2664. DOI:10.1109/TPAMI.2013.88 ( 0) 0)
|
| [8] |
LU Jiwen, WANG Gang, DENG Weihong, et al. Simultaneous feature and dictionary learning for image set based face recognition[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland, 2014: 265–280.
( 0) 0)
|
| [9] |
YANG Yang, HUANG Zi, YANG Yi, et al. Local image tagging via graph regularized joint group sparsity[J]. Pattern recognition, 2013, 46(5): 1358-1368. DOI:10.1016/j.patcog.2012.10.026 ( 0) 0)
|
| [10] |
GU Shuhang, ZHANG Lei, ZUO Wangmeng, et al. Projective dictionary pair learning for pattern classification[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 793–801.
( 0) 0)
|
| [11] |
CUINGNET R, GERARDIN E, TESSIERAS J, et al. Automatic classification of patients with Alzheimer's disease from structural MRI: a comparison of ten methods using the ADNI database[J]. NeuroImage, 2011, 56(2): 766-781. DOI:10.1016/j.neuroimage.2010.06.013 ( 0) 0)
|
| [12] |
CHEN Yefei, SU Jianbo. Sparse embedded dictionary learning on face recognition[J]. Pattern recognition, 2017, 64: 51-59. DOI:10.1016/j.patcog.2016.11.001 ( 0) 0)
|
| [13] |
MAIRAL J, BACH F, PONCE J, et al. Supervised dictionary learning[J]. Paris: INRIA, 2008: 1-8. ( 0) 0)
|
| [14] |
TONG Tong, GAO Qinquan, GUERRERO R, et al. A novel grading biomarker for the prediction of conversion from mild cognitive impairment to Alzheimer's disease[J]. IEEE transactions on biomedical engineering, 2017, 64(1): 155-165. DOI:10.1109/TBME.2016.2549363 ( 0) 0)
|
| [15] |
WYMAN B T, HARVEY D J, CRAWFORD K, et al. Standardization of analysis sets for reporting results from ADNI MRI data[J]. Alzheimer's & dementia, 2013, 9(3): 332-337. ( 0) 0)
|
| [16] |
MORADI E, PEPE A, GASER C, et al. Machine learning framework for early MRI-based Alzheimer's conversion prediction in MCI subjects[J]. NeuroImage, 2015, 104: 398-412. DOI:10.1016/j.neuroimage.2014.10.002 ( 0) 0)
|
| [17] |
JANOUŠOVÁ E, VOUNOU M, WOLZ R, et al. Biomarker discovery for sparse classification of brain images in Alzheimer's disease[J]. Annals of the BMVA, 2012, 2012(2): 1-11. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


