随着信息技术的不断发展,数据获取越来越便捷,数据采集的密集化程度也越来越高。随之出现了一种具有函数特征的数据类型。如心理学研究中的脑电信号数据、生物技术中的基因微序列数据、化学计量中的光谱分析数据、经济研究中的股票分时成交价数据、环境监测中的污染物浓度数据等,均随着时间变化而表现出明显的曲线特征。当前文献中将这种数据类型称为函数型数据(functional data)[1]。
一般而言,函数型数据的曲线形式无法直接获取,通常仅能够观测到其离散样本点,并针对离散数据进行传统多元统计分析。当然,这种做法由于未能考虑到数据的函数特性(如连续、可导等),同时需要处理高维问题,往往不能取得很好的分析效果[2]。为此,针对数据的曲线特征,人们提出了各种分析方法[3-4],包括函数型主成分分析、函数型线性模型、函数型聚类分析等,将有限维的多元分析推广到无限维的函数型数据上来。
聚类分析是数据探索、数据压缩和展现的重要工具,本文讨论函数型数据的聚类算法。目前,函数型数据聚类分析方法大致分为两类[3]:一是原始数据法,该类方法直接针对离散样本点进行聚类,属于高维数据分析方法,文献[5]对这种做法进行了综述。二是投影方法,即以有限维的基底函数逼近曲线,将无限维的问题转化为有限维问题展开分析。依据对基底函数所对应的系数处理方式不同,又可分为滤波法和自适应法。滤波法将基底函数所对应的系数设定为固定参数,分曲线拟合和聚类分析两步展开:首先以有限维基底拟合曲线,对估计的参数执行传统聚类算法。包括利用自组织映射(SOM)算法进行聚类和拟合函数型数据[6];利用两阶段随机过程分别完成数据降维和聚类[7]等。根据基底函数选择利用B-样条基底函数拟合数据并根据传统聚类方法分析[8-9],利用正交基函数进行聚类分析[10]等。自适应法是将基底函数所对应的系数作为随机变量处理,将曲线拟合和聚类分析纳入一个目标函数,采用类似EM的算法,同时进行优化。如利用机器学习和神经网络模型SVR分析时空数据[11]、利用STM算法对时空数据进行聚类[12]以及时间序列数据[13]、经维度数据[14]等的聚类方法;基于K-medoids项目聚类的协同过滤推荐算法[15];基于多元函数型主成分分析(FPCA)方法进行的改进混合模型同时进行曲线拟合与聚类分析[16]。在随机过程中利用K-L散度度量,采用类似于EM算法进行聚类的算法[17]等。
尽管有众多其他的算法[6, 18],目前的函数型聚类分析仅考虑了类内部的差异,而忽视了类间的差异性。对传统离散数据的聚类研究表明[19],同时考虑类内与类间差异有助于提升聚类效果。
受此启发,本文提出一种加入类间因素的曲线聚类算法。本文的做法属于滤波法,包括B-样条基底拟合曲线、曲线距离确定、曲线聚类目标函数设定,以及加入类间因素的曲线聚类算法等。
1 加入类间因素的曲线聚类根据前面的描述,本文讨论的曲线聚类分析模型构建主要包含3个方面:1)由观测离散数据生成函数型数据,这里采用B-样条基底表述的方法;2)构造曲线之间的“距离”的表述,并通过用B-样条基底系数,将曲线距离转化为传统欧氏距离;3)以所构造的距离作为亲疏程度度量,并构建同时考虑类内差异和类间差异的目标函数,完成曲线聚类任务。
1.1 曲线生成假定数据
| ${y_{ij}} = {X_i}\left( {{t_{ij}}} \right) + {\varepsilon _{ij}},\quad j = 1,2,\cdots ,m$ | (1) |
式中:
| ${X_i}\left( t \right) = \sum\limits_{k = 1}^\infty {{\alpha _{ik}}{\phi _{ik}}\left( t \right)} $ | (2) |
称这种做法为基底函数法,它是一种将离散数据转化为曲线的常用平滑技术[3]。对待估计曲线
| ${X_i}\left( t \right) = \sum\limits_{k = 1}^K {{\alpha _{ik}}{\phi _{ik}}\left( t \right)} {\rm{ = }}{{{\alpha }}_i}^{\rm{T}}{{{\varPhi }}_i}\left( t \right)$ | (3) |
从而将无限维问题转化为有限维估计方式。进一步假定[9]:
1) 对不同曲线
2) 基底函数设定为等距节点B-样条基底。有
| ${X_i}\left( t \right){\rm{ = }}\sum\limits_{k = 1}^L {{\alpha _{ik}}{B_{k,M}}\left( t \right)} {\rm{ = }}{{{\alpha }}_i}^{\rm{T}}{{{B}}_M}\left( t \right)$ | (4) |
式中:
假定曲线
| ${d^2}\left( {i,j} \right) = {\left\| {{X_i} - {X_j}} \right\|^2}$ | (5) |
其中
| ${X_i}\left( t \right) - {X_j}\left( t \right) = {\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]^{\rm{T}}}{{{B}}_M}\left( t \right)$ | (6) |
结合式(6),式(5)可转化为
| ${d^2}\left( {i,j} \right) = {\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]^{\rm{T}}}{{K}}\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]$ | (7) |
式中
| ${{K}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\left\langle {{B_{\rm{1}}},{B_1}} \right\rangle }&{\left\langle {{B_{\rm{1}}},{B_2}} \right\rangle }&{\cdots }&{\left\langle {{B_{\rm{1}}},{B_L}} \right\rangle } \\ {\left\langle {{B_2},{B_1}} \right\rangle }&{\left\langle {{B_2},{B_2}} \right\rangle }&{\cdots }&{\left\langle {{B_2},{B_L}} \right\rangle } \\ {\cdots }&{\cdots }& \ddots &{\cdots } \\ {\left\langle {{B_L},{B_1}} \right\rangle }&{\left\langle {{B_L},{B_2}} \right\rangle }&{\cdots }&{\left\langle {{B_L},{B_L}} \right\rangle } \end{array}} \right]$ |
其中,K为
| $\begin{array}{c} {d^2}\left( {i,j} \right) = {\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]^{\rm{T}}}{{K}}\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]{\rm{ = }} \\ {\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]^{\rm{T}}}L{L^{\rm{T}}}\left[ {{{{\alpha }}_i} - {{{\alpha }}_j}} \right]{\rm} = \\ {\left[ {{L^{\rm{T}}}{{{\alpha }}_i} - {L^{\rm{T}}}{{{\alpha }}_j}} \right]^{\rm{T}}} \left[ {{L^{\rm{T}}}{{{\alpha }}_i} - {L^{\rm{T}}}{{{\alpha }}_j}} \right]{\rm{ = }} {\left[ {{{{b}}_i} - {{{b}}_j}} \right]^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_j}} \right] \end{array}$ | (8) |
需要说明的是,式(8)完成了从曲线距离到一般距离的转变,构成了将曲线聚类转化为传统多元聚类问题的基础。利用式(8),运用传统聚类算法对
由
聚类分析的目的是将同类型数据进行归类,同时对不同类型的数据进行区分。文献[19]针对传统离散数据提出的K-means聚类扩展方法兼顾了类内、类间差异。具体来讲,通过对数据集引入全局中心点实现类内差异最小化的同时类中心与全局中心点距离最大化。相比于K-means算法,这种做法提高了聚类效果[19]。
受此启发,本文将K-means聚类分析扩展到函数型聚类分析上。本文的曲线聚类目标函数为
| $F\left( {{{\varPhi ,U}}} \right){\rm{ = }}\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } \frac{{{{\left\| {{X_i}\left( t \right) - \bar X\left( t \right)} \right\|}^2}}}{{{{\left\| {\bar X\left( t \right) - \bar X\left( {{t_0}} \right)} \right\|}^2}}}$ | (9) |
式中:
| $F\left( {{{\varPhi ,U}}} \right){\rm{ = }}\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } \frac{{{{\left\| {{{{\alpha }}_i}^{\rm{T}}{{{B}}_M}\left( t \right) - \bar X\left( t \right)} \right\|}^2}}}{{{{\left\| {\bar X\left( t \right) - \bar X\left( {{t_0}} \right)} \right\|}^2}}}$ | (10) |
根据前面关于曲线距离的描述将式(7)~(8)代入式(10)得到
| $ \begin{aligned} {\rm{ }}F\left( {{{\varPhi }},{{U}}} \right){\rm{ = }}\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } \frac{{{{\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}} \end{aligned} $ | (11) |
式中:
目标函数确定后,式(11)中含有两个未知参数
1) 固定
2) 固定
针对1),为使目标函数式(11)达到最小,当目标函数分子中曲线与对应类中心曲线距离小时
| $ {u_{ik}}{\rm{ = }}\left\{ \begin{array}{l} 1,\quad \displaystyle\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {\frac{{{{\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}}} \leqslant {{D}}} \\ 0,{\text{其他}} \end{array} \right. $ | (12) |
式中:
针对2),假设
当
当
| $\begin{array}{l} \displaystyle\frac{{\partial F\left( {{{\varPhi }},{{\hat U}}} \right)}}{{\partial {{{b}}_ * }}} = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{u_{ik}}} } \frac{{\partial \left( {\displaystyle\frac{{{{\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}}} \right)}}{{\partial {{{b}}_ * }}}{\rm{ = }}\\ \qquad\qquad\qquad \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{u_{ik}}} } \displaystyle\frac{{{\rm{2}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}}{\rm} -\\ \qquad\qquad\qquad\displaystyle\frac{{{\rm{2}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]{{\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left( {{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]} \right)}^{\rm{2}}}}}{\rm{ = 0}} \end{array}$ |
得出
| $\begin{array}{l} \quad\;\; \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{u_{ik}}} } \displaystyle\frac{{{\rm{2}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}}{\rm{ = }}\\ \quad\;\; \displaystyle\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } \displaystyle\frac{{{\rm{2[}}{{{b}}_ * } - {{{b}}_0}]{{\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}^{\rm{T}}}\left[ {{{{b}}_i} - {{{b}}_ * }} \right]}}{{{{\left( {{{\left[ {{{{b}}_ * } - {{{b}}_0}} \right]}^{\rm{T}}}\left[ {{{{b}}_ * } - {{{b}}_0}} \right]} \right)}^{\rm{2}}}}} \end{array}$ |
进一步化简得到
| ${{{b}}_ * }{\rm{ = }}\displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{u_{ik}}} } {{\left[ {{{{b}}_i} - {{{b}}_0}} \right]}^{\rm{T}}}{{{b}}_i}}}{{\displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{u_{ik}}} } {{\left[ {{{{b}}_i} - {{\bf{b}}_0}} \right]}^{\rm{T}}}}}$ |
即
| $ {{{b}}_ * }{\rm{ = }}\left\{ \begin{gathered} {{{b}}_{\rm{0}}}, \;\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } \left[ {\left| {{{{b}}_ * }{{{b}}_ * }^{\rm{T}}} \right|{{\left( {{{{b}}_ * }{{{b}}_ * }^{\rm{T}}} \right)}^{ - 1}}{{{b}}_ * } - {{{b}}_0}} \right] = 0 \hfill \\ \frac{{\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } {{\left[ {{{{b}}_i} - {{{b}}_0}} \right]}^{\rm{T}}}{{{b}}_i}}}{{\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^K {{u_{ik}}} } {{\left[ {{{{b}}_i} - {{{b}}_0}} \right]}^{\rm{T}}}}},\;\;{\text{其他}} \hfill \\ \end{gathered} \right. $ | (13) |
在进行计算机编程时可以不断对步骤1)、2)进行迭代,直至找出最优
Input:
Initialize: Randomly choose an initial
Repeat
Fixed
Fixed
Until convergence.
进一步,由
为验证本文曲线聚类算法的效果,利用模拟数据与文献[9]中曲线聚类方法进行比较。模拟数据由两组高斯分布生成两类曲线构成。模拟过程中两类高斯分布均值取0.5和1,方差取0.7和1。在确定类别的前提下比较本文算法与文献[9]曲线聚类算法的聚类效果。聚类效果评价指标采用兰德指数(Rand index)评价算法的性能[20]。同时分析两组高斯分布的参数(均值和方差)对聚类的影响。分析结果显示:同均值异方差情况下两种曲线聚类方法聚类结果均存在一定的误判,异均值异方差情况下二者聚类也存在误判,异均值同方差情况下二者聚类未出现误判。以下针对这一现象做出分析。
该部分采用R软件进行数据模拟分析,每组包含
|
Download:
|
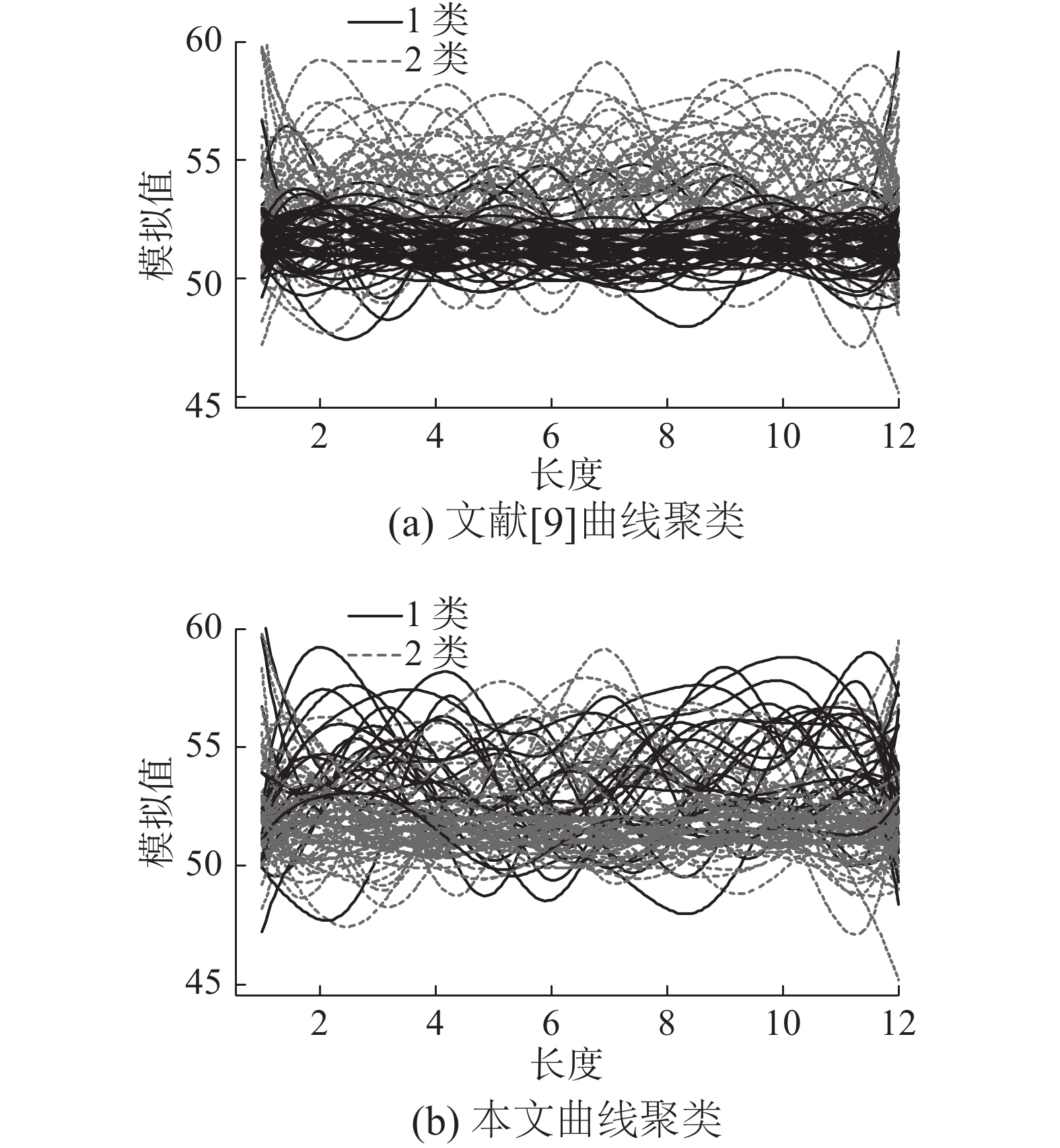
| 图 1 模拟数据曲线聚类对比 Fig. 1 Comparison with simulated data of curve's clustering | |
图1表明:两组高斯分布参数不同条件下,本文方法与文献[9]相比,图1(b)中1类曲线分布密集程度大于图1(a)中1类曲线。为避免模拟次数少或其他原因对聚类效果的影响,对3种类型的数据分别模拟一万次,比较两种方法的平均错判率,定义错判率=abs(1类个数−n)/n,模拟验证中m=12,n=50,错判率下降比例=文献[9]方法错判率-本文方法错判率。结果见表1。
| 表 1 3种类型模拟数据平均错判率 Tab.1 Average error rate of three types' simulated data |
表1、2表明:无论本文的曲线聚类还是文献[9]中的曲线聚类方法,类中心的变化与高斯分布中均值有关,而聚类效果好坏与高斯分布的方差有关。对比表1、2中的同均值异方差和异均值异方差的错判率及兰德指数可以得出:当两类高斯分布均值相同,方差不同时,两种方法对应的兰德指数相比于其他类型数据偏低。同时方差因素对聚类效果也会产生影响。综合比较表1、2中的3类数据错判率及兰德指数,可以得到:对于曲线聚类分析,聚类效果会同时受数据总体均值和方差的影响,对比分析表1、2均值相同方差不同的情形,可以得到:均值对聚类的影响程度要大于方差,同时表1、2对两种方法错判率对比结果显本文的方法能够降低聚类错判率从而提高聚类效果。
| 表 2 3种类型模拟数据兰德指数 Tab.2 Rand index of three types' simulated data |
空气质量,不仅关乎人类生存质量,同时也是衡量可持续发展能力和宜居程度的重要指标。NO2是一种重要的机动车尾气污染物,其污染程度涉及人们生活出行的健康。近年来,空气质量问题引起人们广泛的关注,大气污染监测数据成为人们了解空气质量的客观途径,也构成空气质量统计分析的数据基础。
作为示例,通过实时网络爬虫手段[21],采集兰州市铁路设计院空气质量监测站(交通污染控制点)的NO2小时浓度数据,采用本文的曲线聚类算法展开大气污染等级聚类分析,并与传统曲线聚类结果进行比较。我们分析的样本期为2013年6月1日—10月14日。
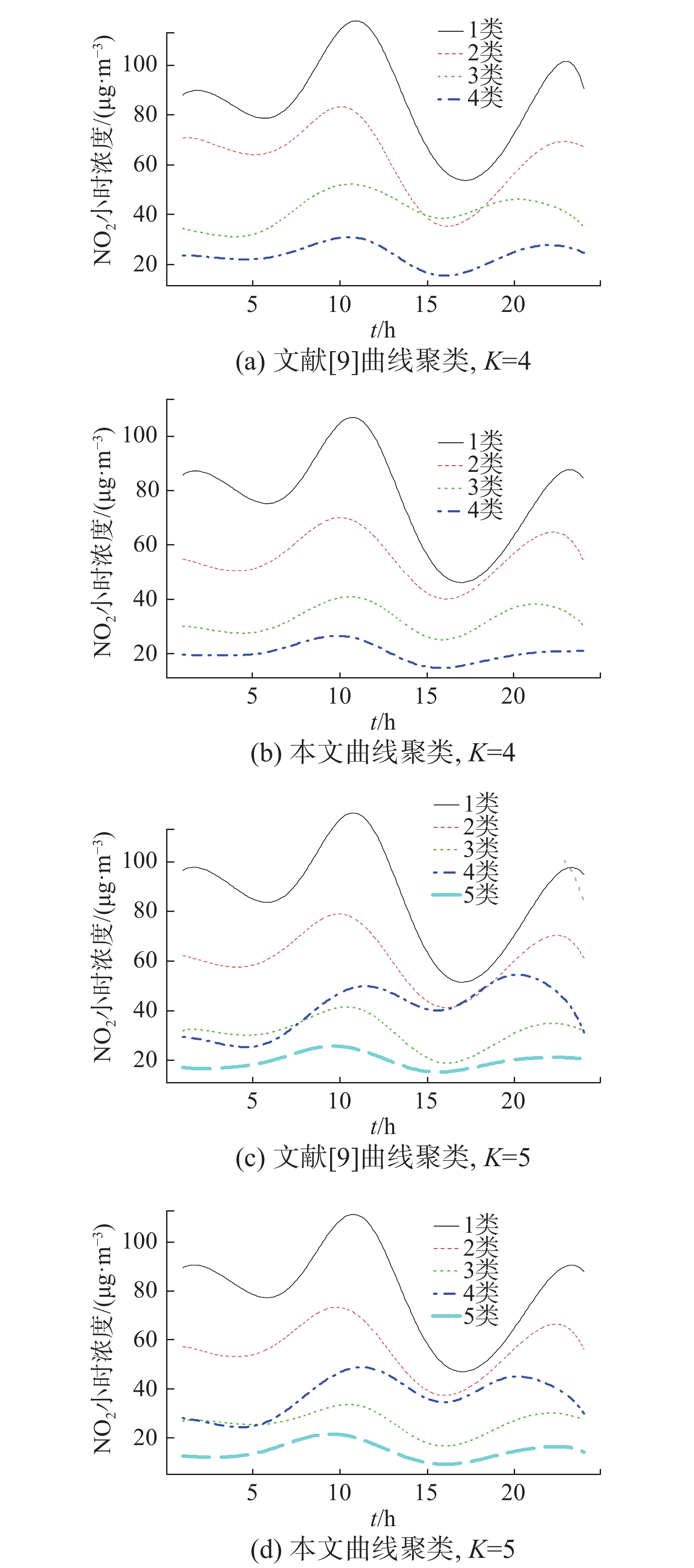
根据前面的方法,采用B-样条基底函数进行曲线聚类分析。为保证拟合结果光滑,两种聚类方法样条基底阶数M均设置为5,节点采用等距节点设置为11(文中采用广义交叉验证准则进行节点数量选择)。考虑相同类中心下,与文献[9]曲线聚类进行聚类效果对比,如图2所示。
|
Download:
|
| 图 2 曲线聚类类中心对比 Fig. 2 Comparison with curve cluster's center generated by different algorithms | |
图2表明,K=5时类中心聚类效果优于K=4,即随着类中心个数的增加,两种方法的聚类效果均有所提升,说明类中心个数的确定在曲线聚类中起到关键作用。但需要指出的是,本文方法的类中心分布曲线更为平滑,类间的类中心曲线分布更为分散,进一步说明本文提出的方法聚类效果优于已有聚类方法。此外,考虑到实际应用,可将图2中的不同类别曲线看作空气质量污染物等级划分[20]。对比图2(a)、(c)与图2(b)、(d)可以发现,在空气质量实时监测过程中,图2(a)、(c)出现不同等级交叉情况,这对空气质量等级划分及应对会造成影响[22]。图2(b)、(d)在进行空气质量分析过程中能够较好的对空气质量进行聚类。另外,相比于针对离散数据的传统K-means聚类分析[23],本文方法能够实时检测NO2小时浓度变化趋势,并依据该变化趋势对污染物进行等级划分。
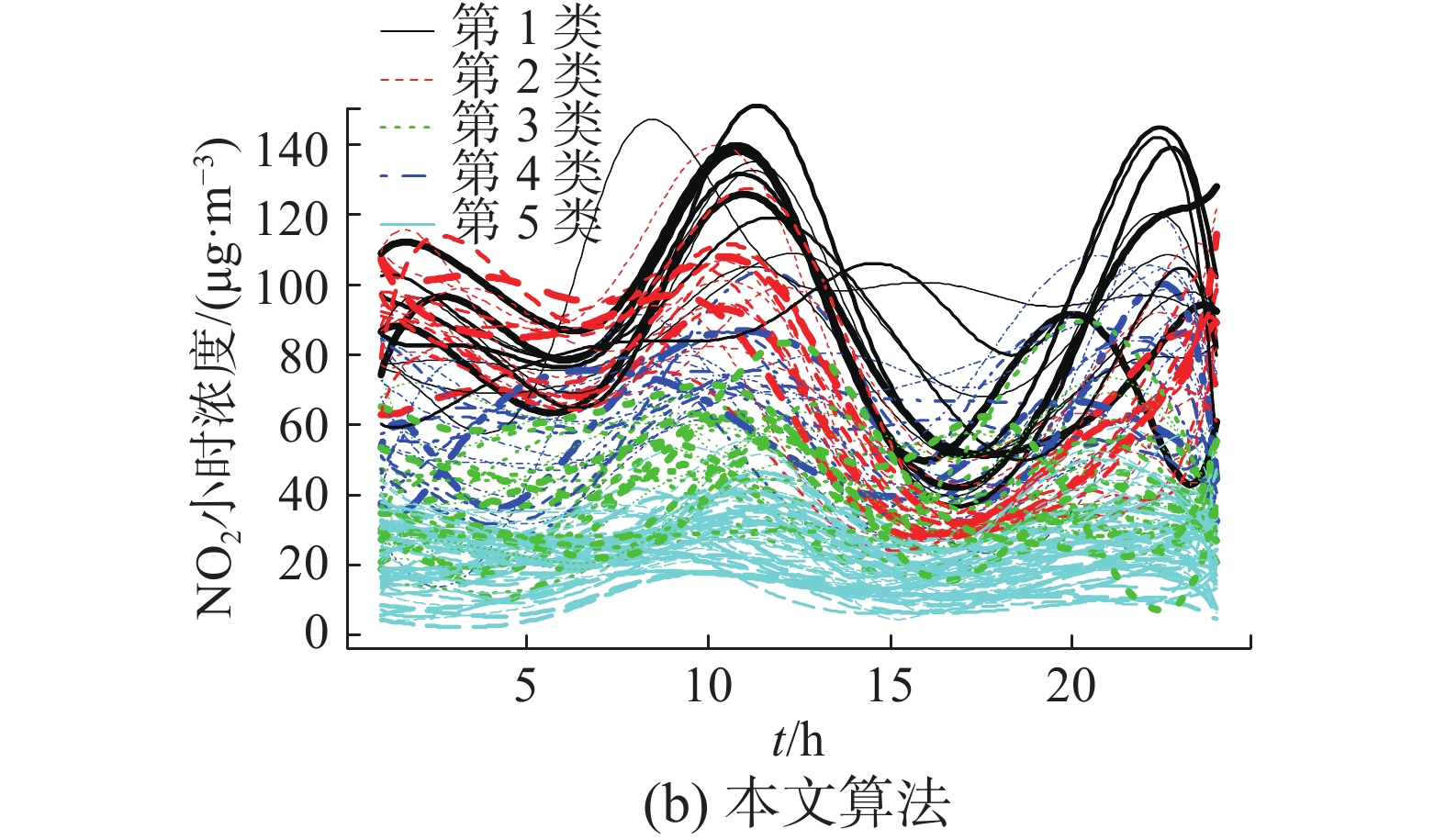
为便于展示,本文以K=5的曲线聚类结果为例,结果见图3。图3表明,相比于已有曲线聚类算法,利用本文曲线聚类算法类内曲线分布集中,类间差异化明显。这与图2中两种曲线聚类算法类中心比较结果相一致。说明本文方法具有较好的类间区分度。
|
Download:
|
| 图 3 NO2小时浓度数据曲线聚类对比 Fig. 3 Comparison with curve clustering of NO2 concentration | |
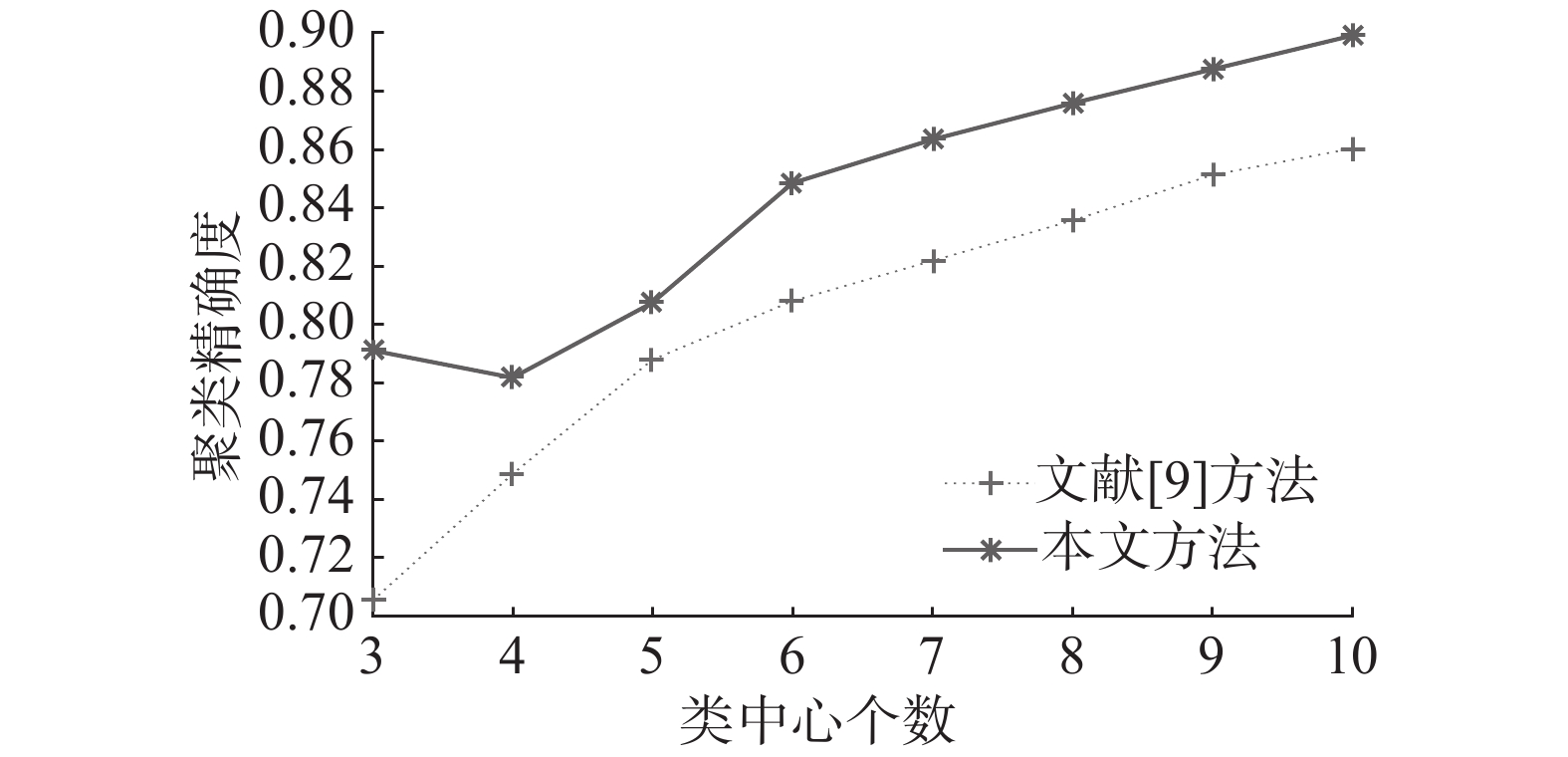
为进一步验证本文曲线聚类的聚类效果,对两种方法的分类精确度采用公式:类间差异/(类内差异+类间差异)进行对比,见图4。图4表明,随着类中心个数的增加,两种曲线聚类算法聚类效果均有所提高。本文曲线聚类的聚类效果要好于文献[9]的方法。通过与文献[9]方法进行比较,本文方法在4类的聚类效果低于3类聚类效果,随着类中心个数大于4类,聚类效果才逐步随着类中心个数增加聚类效果不断提升。说明本文方法存在一定的不稳定性。
|
Download:
|
| 图 4 聚类效果对比结果 Fig. 4 Comparison with clustering effects | |
本文基于已有曲线聚类方法,针对聚类效果不明显的问题,提出加入类间因素的扩展曲线聚类算法。加入类间因素能够同时保证两类数据类内差异较小和类间差异较大。模拟数据及实例应用表明,本文的曲线聚类算法有助于提高聚类效果。
需要说明的是,本文的目的是将同时考虑类内和类间差异的做法引入曲线聚类算法。但我们的做法属于两步法,即首先拟合曲线,然后进行聚类。这种做法很难达到两部分的统一优化[24]。为此,后续的工作是,在同时考虑类内和类间差异的情况下,进行自适应算法研究,即将曲线拟合和聚类分析纳入一个目标函数,同时进行优化。
| [1] |
RAMSAY J O. When the data are functions[J]. Psychometrika, 1982, 47(4): 379-396. DOI:10.1007/BF02293704 ( 0) 0)
|
| [2] |
JACQUES J, PREDA C. Functional data clustering: a survey[J]. Advances in data analysis and classification, 2014, 8(3): 231-255. DOI:10.1007/s11634-013-0158-y ( 0) 0)
|
| [3] |
RAMSAY J O, SILVERMAN B W. Functional data analysis[M]. 2nd ed. New York: Springer, 2005: 1–18.
( 0) 0)
|
| [4] |
FERRATY F, VIEU P. Nonparametric functional data analysis: theory and practice[M]. New York: Springer, 2006: 11–18.
( 0) 0)
|
| [5] |
BOUVEYRON C, BRUNET-SAUMARD C. Model-based clustering of high-dimensional data: a review[J]. Computational statistics & data analysis, 2014, 71: 52-78. ( 0) 0)
|
| [6] |
ROSSI F, CONAN-GUEZ B, GOLLI A E. Clustering functional data with the SOM algorithm[C]//proceedings of European Symposium on Artificial Neural Networks. Bruges, Belgium, 2004: 305–312.
( 0) 0)
|
| [7] |
PENG Jie, MüLLER H G. Distance-based clustering of sparsely observed stochastic processes, with applications to online auctions[J]. The annals of applied statistics, 2008, 2(3): 1056-1077. DOI:10.1214/08-AOAS172 ( 0) 0)
|
| [8] |
ABRAHAM C, CORNILLON P A, MATZNER-LØBER E, et al. Unsupervised curve clustering using B-splines[J]. Scandinavian journal of statistics, 2003, 30(3): 581-595. DOI:10.1111/sjos.2003.30.issue-3 ( 0) 0)
|
| [9] |
黄恒君. 基于B-样条基底展开的曲线聚类方法[J]. 统计与信息论坛, 2013, 28(9): 3-8. HUANG Hengjun. Curves clustering using B-splines expansion[J]. Statistics & information forum, 2013, 28(9): 3-8. DOI:10.3969/j.issn.1007-3116.2013.09.001 (  0) 0)
|
| [10] |
KAYANO M, DOZONO K, KONISHI S. Functional cluster analysis via orthonormalized gaussian basis expansions and its application[J]. Journal of classification, 2010, 27(2): 211-230. DOI:10.1007/s00357-010-9054-8 ( 0) 0)
|
| [11] |
王永坤, 王海洋, 潘平峻, 等. 面向公共安全的时空数据挖掘综述[J]. 重庆邮电大学学报 (自然科学版), 2018, 30(1): 40-52. WANG Yongkun, WANG Haiyang, PAN Pingjun, et al. A survey of data mining on spatial-temporal user behavior data for public safety[J]. Journal of chongqing university of posts and telecommunications (natural science edition), 2018, 30(1): 40-52. (  0) 0)
|
| [12] |
CHEAM A S M, MARBAC M, MCNICHOLAS P D. Model-based clustering for spatiotemporal data on air quality monitoring[J]. Environmetrics, 2017, 28(3): e2437. DOI:10.1002/env.v28.3 ( 0) 0)
|
| [13] |
BOUVEYRON C, JACQUES J. Model-based clustering of time series in group-specific functional subspaces[J]. Advances in data analysis and classification, 2011, 5(4): 281-300. DOI:10.1007/s11634-011-0095-6 ( 0) 0)
|
| [14] |
CHIOU J M, LI Pailing. Functional clustering and identifying substructures of longitudinal data[J]. Journal of the royal statistical society series B, 2007, 69(4): 679-699. DOI:10.1111/rssb.2007.69.issue-4 ( 0) 0)
|
| [15] |
王永, 万潇逸, 陶娅芝, 等. 基于K-medoids项目聚类的协同过滤推荐算法[J]. 重庆邮电大学学报 (自然科学版), 2017, 29(4): 521-526. WANG Yong, WAN Xiaoyi, TAO Yazhi, et al. Collaborative filtering recommendation algorithm based on K-medoids item clustering[J]. Journal of Chongqing university of posts and telecommunications (natural science edition), 2017, 29(4): 521-526. (  0) 0)
|
| [16] |
JACQUES J, PREDA C. Model-based clustering for multivariate functional data[J]. Computational statistics & data analysis, 2014, 71: 92-106. ( 0) 0)
|
| [17] |
JACQUES J, PREDA C. Funclust: a curves clustering method using functional random variables density approximation[J]. Neurocomputing, 2013, 112: 164-171. DOI:10.1016/j.neucom.2012.11.042 ( 0) 0)
|
| [18] |
卞则康, 王士同. 基于混合距离学习的鲁棒的模糊C均值聚类算法[J]. 智能系统学报, 2017, 12(4): 450-458. BIAN Zekang, WANG Shitong. Robust FCM clustering algorithm based on hybrid-distance learning[J]. CAAI transactions on intelligent systems, 2017, 12(4): 450-458. (  0) 0)
|
| [19] |
HUANG Xiaohui, YE Yunming, ZHANG Haijun. Extensions of kmeans-type algorithms: a new clustering framework by integrating intracluster compactness and intercluster separation[J]. IEEE transactions on neural networks and learning systems, 2014, 25(8): 1433-1446. DOI:10.1109/TNNLS.2013.2293795 ( 0) 0)
|
| [20] |
JAIN A K, DUBES R C. Algorithms for clustering data[M]. Upper Saddle River, NJ: Prentice-Hall, 1988: 227–229.
( 0) 0)
|
| [21] |
黄恒君, 漆威. 海量半结构化数据采集、存储及分析--基于实时空气质量数据处理的实践[J]. 统计研究, 2014, 31(5): 10-16. HUANG Hengjun, QI Wei. Massive semi-structured data: collection, storage and analysis--based on the practice of real-time air quality data processing[J]. Statistical research, 2014, 31(5): 10-16. DOI:10.3969/j.issn.1002-4565.2014.05.002 (  0) 0)
|
| [22] |
刘杰, 杨鹏, 吕文生, 等. 基于北京市6类污染物的环境空气质量评价方法[J]. 安全与环境学报, 2015, 15(1): 310-315. LIU Jie, YANG Peng, Lü Wensheng, et al. Environmental air quality evaluation method based on the six pollutants in the urban areas of Beijing[J]. Journal of safety and environment, 2015, 15(1): 310-315. (  0) 0)
|
| [23] |
郭云飞, 林红飞, 郑旭. 中国城市空气质量指标的聚类分析[J]. 统计与管理, 2016(8): 80-81. GUO Yunfei, LIN Hongfei, ZHENG Xu. Clustering analysis of urban air quality indexes in China[J]. Statistics and management, 2016(8): 80-81. (  0) 0)
|
| [24] |
YAMAMOTO M, HWANG H. Dimension-reduced clustering of functional data via subspace separation[J]. Journal of classification, 2017, 34(2): 294-326. DOI:10.1007/s00357-017-9232-z ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


