近年来，多智能体系统的一致性在生物系统、机器人编队、传感器网络、无人机编队、水下驱动装置和群决策等问题中都具有潜在的应用，所以吸引了从物理、数学、工程、生物学和社会学等各个领域的研究人员的广泛关注。现有的多智能体系统的一致性问题的研究成果大多建立在同质多智能体的基础上，即所有的多智能体都具有相同的动力学行为。然而，在实际中，因为外部的影响或交互的限制需要具有不同动态行为的多智能体完成一个共同的目标。因此，异质多智能体系统的一致性问题的研究具有更加重要的现实意义。

最近，异质多智能体的一致性问题得到了越来越多的关注。现有的研究异质多智能体系统的一致性主要考虑的是一阶和二阶结构的结合，而文献[1]中针对一阶智能体、二阶智能体和EL智能体组成的异质多智能体系统中分别对EL智能体参数确定和不确定情况下的一致性进行了研究。在协调控制中，根据发生的变化每个群体中的智能体必须达成一致。但是，由于环境、情形、合作的任务或者是时间的变化可能导致一致的状态不同。譬如对深陷火灾的多名人员进行搜救需要多智能体系统进行分工配合完成多个目标任务，因此，一个关键的问题就是设计合适的协议，使网络中的智能体达成多个共识状态。这就是多智能体系统的群一致性问题，关于系统中包含相同动力学特性智能体的群一致性问题取得了优秀的成果^[2-6]，文献[5-6]提出当各个子群满足入度平衡这个前提才能实现一阶智能体系统的群一致性，即允许拓扑结构中节点之间权重存在负值的情况，但是这个条件过于苛刻。近年来，异质多智能体系统的群一致性也取得了一定的进展。文献[7]中研究了在固定拓扑下的异质多智能体系统的群一致性；文献[8]中基于图论、矩阵理论和动力学理论研究了异质多智能体系统的群一致性问题，并且推广到了有向和切换拓扑中。文献[9]中考虑了部分的一阶智能体具有输入饱和，基于牵制控制提出了具有输入饱和的异质多智能体系统的群一致性；文献[10]中研究了具有输入延时的异质多智能体系统的动态分组一致性；文献[11]中利用自适应控制对不确定非线性动态结构进行线性化处理，利用牵制控制实现了多智能体系统的群一致性。

以上主要是研究线性的异质多智能体系统或者是具有相同非线性动态结构的群一致性，但是对于包含线性和非线性智能体组成的多智能体系统的群一致性却研究甚少，设计合适的控制协议实现包含非线性结构的异质多智能体系统的群一致性更具挑战，本文主要研究由一阶智能体、二阶智能体和非线性的EL结构智能体组成的异质多智能体系统的群一致性，针对无向的固定的通信拓扑情况，提出了基于牵制控制的群一致性控制协议。

1 预备知识和问题描述 1.1 代数图论

假设 $G = \left( {{{v}},{{\varepsilon }},{{A}}} \right)$ 是一个包含 $n$ 个节点的加权无向拓扑图，其中 ${{v}} = \left( {{v_1},{v_2},\cdots ,{v_n}} \right)$ 表示节点集； ${{\varepsilon }} = {{v}} \times {{v}}$ 表示边集； ${{A}} = {\left[ {{a_{ij}}} \right]_{n \times n}}$ 是加权邻接矩阵，如果 ${e_{ij}} \in \varepsilon $ ，则 ${a_{ij}} > 0$ ，否则， ${a_{ij}} = 0$ ，并且 ${a_{ij}} = {a_{ji}}$ 。如果存在边 ${e_{ij}} = \left( {{v_i},{v_j}} \right)$ ，则说明节点 ${v_i}$ 可以从节点 ${v_j}$ 中获得信息。 ${{{N}}_{{i}}} = \left\{ {{v_j}\left| {{e_{ji}} \in \varepsilon } \right.} \right\}$ 表示节点 ${v_i}$ 的邻居节点集。节点 ${v_i}$ 和 ${v_k}$ 之间存在一系列的边 $ \left( {{v_i},{v_2}} \right),\left( {{v_i},{v_2}} \right),\cdots ,$ $\left( {{v_{k - 1}},{v_k}} \right)$ ，则说明两节点之间存在一条路径^[12]，如果无向拓扑图中任意两个节点之间存在一条路径，则说明无向拓扑图是连通的。 ${{L}} = {{D}} - {{A}}$ 表示拓扑图的拉普拉斯矩阵，其中 $ {{D}} = {\rm diag}( {d_1},$ ${d_2},\cdots ,{d_n} )$ 表示拓扑图的度矩阵， ${d_i} = \displaystyle\sum\limits_{j = 1,j \ne i}^n {{a_{ij}}} $ 表示节点 $i$ 的度。 ${{L}} = $ ${\left[ {{l_{ij}}} \right]_{n \times n}}$ 可定义为

$ {l_{ij}} = \left\{ {\begin{array}{*{20}{l}} - {a_{ij}} \;\; , \; \;i \ne j \\ \displaystyle \sum\limits_{j = 1,j \ne i}^n {{a_{ij}}}\; \; , \;\; i = j \\ \end{array}} \right.$

式中 $ i,j = 1,2,\cdots ,n$ 。

1.2 问题描述

考虑一个具有 $n$ 个多智能体的异质多智能体系统，其中包含 $l$ 个一阶多智能体、 $m$ 个二阶多智能体和 $n - m - l$ 个EL智能体。一阶结构的多智能体满足：

${{{\dot x}}_{{i}}}\left( {{t}} \right) = {{{u}}_{{i}}}\left( {{t}} \right), \;\;i = 1,2,\cdots ,l$

(1)

式中： ${{{x}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^n}$ 表示智能体的位置向量， ${{{u}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^n}$ 表示第 $i$ 个智能体的控制输入。二阶结构的多智能体的动力学方程满足：

$ \left\{ \begin{array}{c} {{{{\dot x}}}_{{i}}}\left( {{t}} \right) = {{{v}}_{{i}}}\left( {{t}} \right) \\ \mathop {{{{{\dot v}}}_{{i}}}\left( {{t}} \right) = {{{u}}_{{i}}}\left( {{t}} \right)}\limits^. \\ \end{array} \right. $

(2)

式中： $i = l + 1,l + 2,\cdots ,m$ ； ${{{x}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^n}$ 表示智能体的位置向量， ${{{v}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^n}$ 表示智能体的速度向量， ${{{u}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^n}$ 表示第 $i$ 个智能体的控制输入。EL智能体的动力学方程满足：

$ \left\{ \begin{array}{l} {{{{\dot x}}}_{{i}}}\left( {{t}} \right) = {{{v}}_{{i}}}\left( {{t}} \right)\\ {{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right){{{{\dot v}}}_{{i}}} + {{{C}}_{{i}}}\left( {{{{x}}_{{i}}}{{,}}{{{v}}_{{i}}}} \right){{{v}}_{{i}}} = {{{u}}_{{i}}} \\ \end{array} \right. $

(3)

式中： $i = m + 1,m + 2,\cdots ,n$ ； ${{{x}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^{q \times 1}}$ 、 ${{{v}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^{q \times 1}}$ 和 ${{{u}}_{{i}}}\left( {{t}} \right) \in {{\bf{R}}^{q \times 1}}$ 分别表示第 $i$ 个智能体的位置信息、速度信息和控制输入； ${{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right) \in {{\bf{R}}^{p \times q}}$ 为惯性矩阵； ${{{C}}_{{i}}}\left( {{{{x}}_{{i}}}{{,}}{{{v}}_{{i}}}} \right)$ 为柯式力矩阵；EL智能体满足如下性质^[13]。

性质1　惯性矩阵 ${{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right)$ 具有上下界，即

$ 0 < {\lambda _m}\left\{ {{{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right)} \right\}{{I}} \leqslant {{{{ M}}}_{{\iota }}}\left( {{{{\xi }}_{{\iota }}}} \right) \leqslant {\lambda _M}\left\{ {{{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right)} \right\}{{I}} < \infty $

(4)

性质2　矩阵 $\mathop {{{{M}}_{{i}}}}\limits^{{.}} \left( {{{{x}}_{{i}}}} \right) - 2{{{C}}_{{i}}}\left( {{{{x}}_{{i}}}{{,}}{{{v}}_{{i}}}} \right)$ 是一个斜对称矩阵，对于任意给定的向量 ${{r}} \in {{{R}}^p}$ ，有：

$ {{{r}}^{\rm{T}}}\left( {\mathop {{{{M}}_{{i}}}}\limits^{{.}} \left( {{{{x}}_{{i}}}} \right) - {{2}}{{{C}}_{{i}}}\left( {{{{x}}_{{i}}}{{,}}{{{v}}_{{i}}}} \right)} \right){{r}} = 0 $

(5)

假定将异质多智能体网络分成 $k$ $\left( {k \geqslant 2} \right)$ 群,如果智能体属于第 $t$ 个群，则记 ${\sigma _i} = t,{x_{{\sigma _i}}}$ 是对智能体进行分群的常数，且当 ${\sigma _i} = {\sigma _j}$ 时，即表示同一个子群，并且有 ${x_{{\sigma _i}}} = {x_{{\sigma _j}}}$ ，否则， ${x_{{\sigma _i}}} \ne {x_{{\sigma _j}}}$ 。

定义1　对于任意给定的初始状态 ${{{x}}_{{i}}}\left( {{0}} \right) ,{{{v}}_{{i}}}\left( {{0}} \right)$ ，若异质智能体系统满足如下条件：

$ \left\{ \begin{array}{c} \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| = 0,{\rm if} {\sigma _i} \in {\sigma _j}, \\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| \ne 0,{\rm if}{\sigma _i} \ne {\sigma _j} , \\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{v}}_{{i}}}\left( {{t}} \right)} \right\| = 0,\forall i \in \left\{ {l + 1,l + 2,\cdots ,n} \right\} \\ \end{array} \right. $

(6)

则说明异质多智能体系统实现了 $k$ 群一致性。

注1 　本文是基于二维空间，所得结果都可以利用克罗内克积(Kronecker product)推广到 $n$ 维空间。

引理1^[14] 　对于定义在 ${{\bf{R}}^n}$ 上的动态系统 $\dot x = f\left( x \right)$ ，其中 $f\left( x \right)$ 为连续函数，设 $V\left( x \right):{{\rm R}^n} \to {\rm R}$ 是一阶光滑函数，且满足：

1)当 $\left\| x \right\| \to \infty $ 时， $V\left( x \right) \to \infty $ ；

2)对于任意的 $x \in {{\rm R}^n},\mathop V\limits^. \left( x \right) \leqslant 0$ 。

定义集合 ${{S}} = \left\{ {x \in {{\rm R}^n}:\mathop V\limits^. \left( x \right) = 0} \right\}$ ， ${{M}}$ 是 ${{S}}$ 中的最大不变集，则对于 $\forall {x_0} \in {{\rm R}^n}$ ，当 $t \to \infty $ 时， $x\left( t \right)$ 趋于不变集 ${{M}}$ 。

2 异质多智能体系统的群一致性控制

根据邻居个体之间的信息交互和EL动力学结构的性质，设计如下控制协议：

$ {{{u}}_{{i}}} = \left\{ \begin{array}{c} \displaystyle \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}}} - {b_i}\left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right)},\\ \displaystyle i = 1,2,\cdots ,l; \\ \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}} - {{\kappa }}} } {{{v}}_{{i}}} - {b_i}\left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right) ,\\ \displaystyle i = l + 1,2,\cdots ,m ; \\ \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}} - {{\lambda }}} } {{{v}}_{{i}}} - {b_i}\left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right),\\ \displaystyle i = m + 1,2,\cdots ,n \\ \end{array} \right. $

(7)

式中： ${{\kappa }}{\rm{,}}{{\lambda }}$ 是正定对角矩阵,当智能体 $i$ 为牵制个体，则可以获得静态虚拟领导者的状态信息，则 ${b_i} = 1$ ，否则 ${b_i} = 0$ 。各个群中的静态虚拟领导者的状态设为 $\left( {{x_{{\sigma _i}}},0} \right),{\sigma _i} = 1,2,\cdots ,k$ ， ${x_{{\sigma _i}}}$ 为该群智能体期望的状态。

定理1 　设智能体间的通信拓扑图是无向连通的，由式(1)~(3)组成的异质多智能体系统在控制协议(7)的作用下可实现群一致性，并且各群中智能体的状态都能够趋于期望的状态。

证明　根据控制器(7)，可以将式(1)~(3)改写为

$ \left\{ \begin{array}{c} \displaystyle{{{{\dot x}}}_{{i}}}\left( {{t}} \right) = \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}}} } {\rm{ - }}{b_i}\left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right),\qquad\quad \\ \displaystyle i = 1,2,\cdots ,l \\ {{{{\dot x}}}_{{i}}}\left( {{t}} \right) = {{{v}}_{{i}}}\left( {{t}} \right) \qquad\qquad\qquad\qquad\qquad\qquad\quad\quad\qquad\,\\ \displaystyle{{{{\dot v}}}_{{i}}}\left( {{t}} \right) = \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}} - } } {{\kappa }}{{{v}}_{{i}}} {\rm{ - }}{b_i}\left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right),\; \;\;\\ \displaystyle i = l + 1,l + 2,\cdots ,m \\ \displaystyle{{{{\dot x}}}_{{i}}}\left( {{t}} \right) = {{{v}}_{{i}}}\left( {{t}} \right) \qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\quad\;\\ \displaystyle {{{M}}_{{i}}}\left( {{{{x}}_{{i}}}} \right){{{{\dot v}}}_{{i}}} + {{{C}}_{{i}}}\left( {{{{x}}_{{i}}}{{,}}{{{v}}_{{i}}}} \right){{{v}}_{{i}}} = \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}} - }} \\ \displaystyle{{{\lambda }}} {{{v}}_{{i}}} {\rm{ - }}{b_i}( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} ),\qquad\qquad\qquad\qquad\quad\qquad\\ \displaystyle i = m + 1,m+2,\cdots ,n \\ \end{array} \right. $

(8)

令 ${{{e}}_{{i}}} = {{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}},i = 1,2,\cdots ,n$ ，则有：

$\begin{gathered} \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right)} + \sum\limits_{j = 1}^n {{l_{ij}} ={{{x}}_{{{{\sigma }}_{{j}}}}}} \\ \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{x}}_{{j}}} - {{{x}}_{{i}}}} \right) + \sum\limits_{j = 1,j \ne i}^n {{l_{ij}}{{{x}}_{{{{\sigma }}_{{j}}}}}} + {l_{ii}}{{{x}}_{{{{\sigma }}_{{i}}}}}} =\\ \sum\limits_{j = 1}^n {{a_{ij}}\left( {( {{{{x}}_{{j}}} - {{{x}}_{{{{\sigma }}_{{j}}}}}} ) - \left( {{{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right)} \right)} = \\ \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} \\ \end{gathered} $

(9)

根据式(9)，系统(8)可写为

$\left\{ \begin{gathered} {{{{\dot e}}}_{{i}}} = \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} {\rm{ - }}{b_i}{{{e}}_{{i}}},i = 1,2,\cdots ,l \qquad\qquad\\ {{{{\dot e}}}_{{i}}} = {{{v}}_{{i}}}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ \;{{{{\dot v}}}_{{i}}} = \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} - {{\kappa }}{{{v}}_{{i}}}{\rm{ - }}{b_i}{{{e}}_{{i}}},i = l + 1,l + 2,\cdots m \\ {{{{\dot e}}}_{{i}}} = {{{v}}_{{i}}} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ {{{M}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{{\dot v}}}_{{i}}} + {{{C}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}{{,}}{{{v}}_{{i}}}} \right){{{v}}_{{i}}}= \qquad\qquad\qquad\\ \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} - {{\lambda }}{{{v}}_{{i}}}{\rm{ - }}{b_i}{{{e}}_{{i}}},i = m + 1,m + 2,\cdots ,n \\ \end{gathered} \right.$

(10)

根据EL智能体性质1可选择李雅普诺夫函数如下：

$\begin{gathered} V = \sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{M}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{v}}_{{i}}} } + \sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{{v}}_{{i}}}} +\\ \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}{{\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)}^2}} } + \sum\limits_{i = 1}^n {{b_i}{{e}}_{{i}}^{\rm{T}}{{{e}}_{{i}}}} \\ \\ \end{gathered} $

(11)

对李雅普诺夫函数进行求导：

$\begin{gathered} \dot V = \sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{{\dot M}}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{v}}_{{i}}}} + 2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{M}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{{\dot v}}}_{{i}}}} + \\ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)\left( {{{{{\dot e}}}_{{i}}} - {{{{\dot e}}}_{{j}}}} \right)} } + 2\sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{{{\dot v}}}_{{i}}}} {\rm{ + }}2\sum\limits_{i = 1}^n {{b_i}{{e}}_{{i}}^{\rm{T}}{{{{\dot e}}}_{{i}}}} \\ \end{gathered} $

(12)

根据EL智能体的性质2，可知：

$\begin{gathered} \sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{{\dot M}}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{v}}_{{i}}}} + 2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{M}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{{\dot v}}}_{{i}}}} =\\ 2\sum\limits_{i = m + 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}{{v}}_{{i}}^{\rm{T}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} } - 2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{\lambda }}{{{v}}_{{i}}}} - 2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{b_i}{{{e}}_{{i}}}} \\ \end{gathered} $

(13)

又

$\begin{gathered} \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)\left( {{{{{\dot e}}}_{{j}}} - {{{{\dot e}}}_{{i}}}} \right)} } = \\ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{j}}} - } } \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{i}}}} } = \\ \sum\limits_{i = 1}^{\rm{n}} {\sum\limits_{j = 1}^l {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{j}}}} } + \sum\limits_{i = 1}^n {\sum\limits_{j = l + 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{v}}_{{j}}}} } - \\ \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{i}}}} } - \sum\limits_{i = l + 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{v}}_{{i}}}} } \\ \end{gathered} $

(14)

由于异质多智能体系统的通信拓扑是无向的， ${a_{ij}} = {a_{ji}}$ ，则有：

$\begin{gathered} \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^l {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{j}}}} } = - \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{{\dot e}}}_{{i}}}} } \\ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^l {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{v}}_{{i}}}} = - \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{v}}_{{j}}}} } } \\ \end{gathered} $

(15)

将式(15)代入式(14)可得：

$\begin{array}{ccccc} \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{\bf{i}}}} \right)\left( {{{{{\dot e}}}_{{j}}} - {{{\bf{\dot e}}}_{{i}}}} \right)} } = \\ - 2\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{\bf{i}}}} \right){{{{\dot e}}}_{\bf{i}}}} } {\rm{ }} - 2 \displaystyle\sum\limits_{i = l + 1}^n {\displaystyle\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right){{{v}}_{{i}}}} } \end{array}$

(16)

将式(13)、式(16)代入到式(12)可得：

$\begin{gathered} \mathop V\limits^. \left( t \right) = {\rm{ - }}2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{\lambda }}{{{v}}_{{i}}}} {\rm{ - }}2\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^n {{{{a}}_{{{ij}}}}{{\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)}^{\rm{T}}}{{{{\dot e}}}_{{i}}}} } + \\ 2\sum\limits_{i = 1}^l {{{{b}}_{{i}}}{{e}}_{{i}}^{\rm{T}}{{{{\dot e}}}_{{i}}}} - 2\sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{\kappa }}{{{v}}_{{i}}}} {\rm{ = }}\\ -2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{\lambda }}{{{v}}_{{i}}}} - 2{\sum\limits_{i = 1}^l {\left( {{{{{\dot e}}}_{{i}}}} \right)} ^2} - 2\sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{\kappa }}{{{v}}_{{i}}}} \leqslant 0 \\ \end{gathered} $

(17)

由引理1，最大不变集 ${{M}}$ 满足：

$\left\{ \begin{gathered} {{{{\dot e}}}_{{i}}} = 0,\quad i = 1,2,\cdots ,l \qquad\;\\ \!\! \! {{{v}}_{{i}}} = 0,\quad i = l + 1,l + 2,\cdots ,n \\ \end{gathered} \right.$

(18)

由式(10)和(18)可得，最大不变集 ${{M}}$ 满足：

$\left\{ \begin{gathered} \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} {\rm{ - }}{b_i}{{{e}}_{{i}}} = 0,\quad i = 1,2,\cdots ,l \\ {{{v}}_{{i}}} = 0,\quad i = l + 1,l + 2,\cdots ,n \qquad\qquad\\ \end{gathered} \right.$

(19)

显然有

$\sum\limits_{i = 1}^n {{{{e}}_{{i}}}\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} {\rm{ - }}} {b_i}{{{e}}_{{i}}} = 0$

(20)

$\sum\limits_{j = 1}^n {{{{e}}_{{j}}}\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} {\rm{ - }}} {b_i}{{{e}}_{{i}}} = 0$

(21)

联立式(20)和式(21)可得

$ - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}{{\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)}^2}} - 2\sum\limits_{i = 1}^n {{d_i}{{e}}_{{i}}^{\rm{2}}} } = 0$

(22)

由式(22)可得最大不变集 ${{M}}$ 为

$\left\{ {\begin{array}{*{20}{l}} {{{e}}_{{i}}}\left( {{t}} \right) = 0, &i = 1,2,\cdots ,n \\ {{{v}}_{{i}}}\left( {{t}} \right) = 0, &i = l + 1,l + 2,\cdots ,n \\ \end{array}} \right.$

(23)

将 ${{{e}}_{{i}}} = {{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}$ 代入到式(23)，可以知道对于 ${{x}}\left( {{0}} \right)$ 、 ${{v}}\left( {{0}} \right)$ ，当 $t \to \infty $ 有:

$\left\{ \begin{array}{c} \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| = 0,\;\; \;{\sigma _i} = {\sigma _j} \qquad\quad\quad\\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| \ne 0,\;\; \;{\sigma _i} \ne {\sigma _j} \qquad\quad\quad \\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{{{\sigma }}_{{i}}}}}} \right\| = 0,\;\;\; {\sigma _i} = {\sigma _j} \qquad\quad \quad\;\\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{v}}_{{i}}}\left( {{t}} \right)} \right\| = 0,\forall i \in \left\{ {l + 1,l + 2,\cdots ,n} \right\}\quad\quad \\ \end{array} \right.$

(24)

综上所述，由式(1)~(3)组成的异质多智能体系统在控制协议(7)的作用下可实现群一致性，并且各个子群的最终状态趋于该子群虚拟领导者的状态。

推论1 　通信拓扑图是无向连通的，控制协议(7)中不考虑牵制策略的作用下，由(1)~(3)组成的异质多智能体系统也能够实现群一致性。

证明　考虑李雅普诺夫函数：

$\begin{gathered} V = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}{{\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)}^2}} } + \sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{{v}}_{{i}}}}+ \\ \sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{{M}}_{{i}}}\left( {{{{e}}_{{i}}}{{ + }}{{{x}}_{{{{\sigma }}_{{i}}}}}} \right){{{v}}_{{i}}}} \\ \end{gathered} $

(25)

对李雅普诺夫函数求导化简后可得

$\begin{gathered} \dot V{\rm{ = }} - 2\sum\limits_{i = 1}^l {{{\left( {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} } \right)}^{\rm{T}}}\left( {\sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} } \right)}- \\ 2\sum\limits_{i = m + 1}^n {{{v}}_{{i}}^{\rm{T}}{{\lambda }}{{{v}}_{{i}}}} - 2\sum\limits_{i = l + 1}^m {{{v}}_{{i}}^{\rm{T}}{{\kappa }}{{{v}}_{{i}}}} \leqslant 0 \\ \end{gathered} $

(26)

同理由引理1可知，当 $\dot V = 0$ 时，有

$\left\{ \begin{gathered} {{{v}}_{{i}}} = 0,\quad i = l + 1,l + 2,\cdots ,n \qquad\\ \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} = 0, \quad i = 1,2,\cdots ,l \\ \end{gathered} \right.$

(27)

由式(27)可得：

$\sum\limits_{i = 1}^n {{{{e}}_{{i}}}} \sum\limits_{j = 1}^n {{a_{ij}}\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)} = 0$

(28)

$\sum\limits_{j = 1}^n {{{{e}}_{{j}}}} \sum\limits_{i = 1}^n {{a_{ij}}\left( {{{{e}}_{{i}}} - {{{e}}_{{j}}}} \right)} = 0$

(29)

式(28)、式(29)相加可得：

$ - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}{{\left( {{{{e}}_{{j}}} - {{{e}}_{{i}}}} \right)}^2} = 0} } $

(30)

由式(27)和式(30)可知，最大不变集 ${{M}}$ 可化为

$\left\{ {\begin{array}{*{20}{l}} {{{e}}_{{i}}} = {{{e}}_{{j}}},&i,j = 1,2,\cdots ,n \\ {{{v}}_{{i}}} = 0,&i = l + 1,l + 2,\cdots ,n \\ \end{array}} \right.$

(31)

将 ${{{e}}_{{i}}} = {{{x}}_{{i}}} - {{{x}}_{{{{\sigma }}_{{i}}}}}$ 代入到式(31)中，可以得到：

$\left\{ \begin{array}{c} \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| = 0,\;\;\;{\sigma _i} = {\sigma _j} \qquad\quad\quad\\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{x}}_{{i}}}\left( {{t}} \right) - {{{x}}_{{j}}}\left( {{t}} \right)} \right\| \ne 0,\;\;\;{\sigma _i} \ne {\sigma _j} \qquad\quad\quad \\ \forall i,j \in \left\{ {1,2,\cdots ,n} \right\},\forall {\sigma _i},{\sigma _j} \in \left\{ {1,2,\cdots ,k} \right\} \\ \mathop {\lim }\limits_{t \to \infty } \left\| {{{{v}}_{{i}}}\left( {{t}} \right)} \right\| = 0,\forall i \in \left\{ {l + 1,l + 2,\cdots ,n} \right\} \quad\quad\\ \end{array} \right.$

(32)

综上所述，推论1得证。

注2 　所提控制协议中只需满足无向固定拓扑是连通的条件就能实现异质多智能体系统的群一致性，从而放宽了文献[5-6]中实现群一致性的条件。

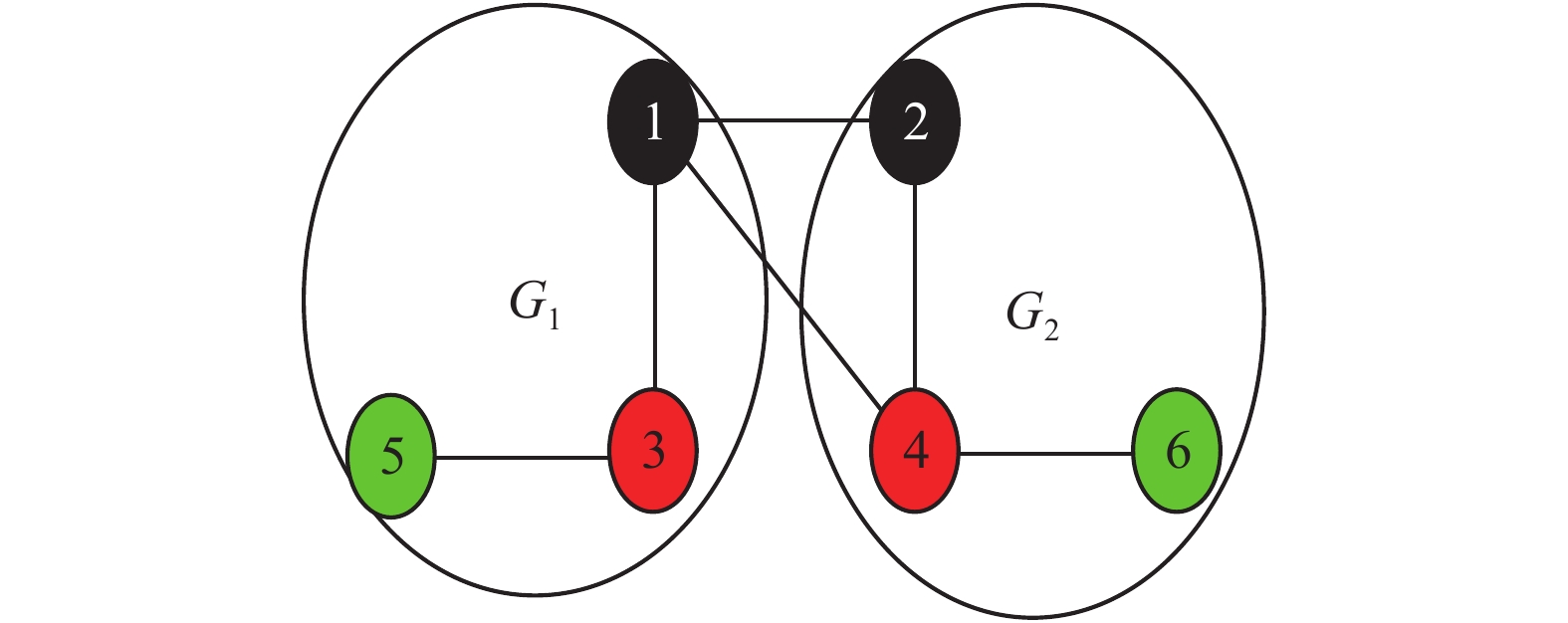
3 数值仿真

通过MATLAB仿真平台来验证所提群一致性控制协议的可行性，考虑一个由两个一阶结构的智能体(智能体1、2)、两个二阶结构的智能体(智能体3、4)和两个EL智能体(智能体5、6)构成的异质多智能体系统，它们的通信拓扑结构图如图1所示，将通信拓扑图分成两个群体 ${G_1}$ 和 ${G_2}$ ，每个群体中都包含不同结构的智能体。多智能体的状态信息 ${\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {{x_{i\left( 1 \right)}}}&{{x_{i\left( 2 \right)}}} \end{array}}\!\!\!\!\! \right]^{\rm{T}}},{{{x}}_{{i}}} = {{{v}}_{{i}}} = $ ${\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {{v_{i\left( 1 \right)}}}&{{v_{i\left( 2 \right)}}} \end{array}}\!\!\!\! \right]^{\rm{T}}}$ ；控制输入为 ${{{u}}_{{i}}} = {\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {{u_{i\left( 1 \right)}}}&{{u_{i\left( 2 \right)}}} \end{array}} \!\!\!\!\! \right]^{\rm{T}}}$ ,初始状态信息为

${{{x}}_{{1}}}\left( {{0}} \right) = {\left[ { - 1.5\;\;1.9} \right]^{\rm{T}}},{{{x}}_{{2}}}\left( {{0}} \right) = {\left[ {1.9\;\;1.5} \right]^{\rm{T}}} $ ， ${{{x}}_{{3}}}\left( {{0}} \right) = {\left[ { - 1.8\;\; - 1.5} \right]^{\rm{T}}},{{{x}}_{{4}}}\left( {{0}} \right) = {\left[ {0.1\;\;0.6} \right]^{\rm{T}}},{{{x}}_{{5}}}\left( {{0}} \right) = {\left[ {1.4\;\;1.9} \right]^{\rm{T}}}$ ， ${{{x}}_{{6}}} \left( {{0}} \right) ={\left[ { - 0.5\;\; - 1.8} \right]^{\rm{T}}},{{{v}}_{{3}}}\left( {{0}} \right) = {\left[ { - 0.2\;\;0.1} \right]^{\rm{T}}},{{{v}}_{{4}}}\left( {{0}} \right) = {\left[ { - 0.8\;\;1.9} \right]^{\rm{T}}}$ ， ${{{v}}_{{5}}}\left( {{0}} \right) = {\left[ {0.1\;\; - 0.3} \right]^{\rm{T}}},{{{v}}_{{6}}}\left( {{0}} \right) = {\left[ {0.6\;\;0.8} \right]^{\rm{T}}}$

${{\kappa }} = {\rm{diag}}\left[ {1,1} \right],{{\lambda }} = {\rm diag}\left[ {1,1} \right]$ 。 ${{{M}}_{{i}}} = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{12}}} \\ {{m_{21}}}&{{m_{22}}} \end{array}} \right]$ ； ${m_{11}} = {a_1} + 2{a_3}\cos {x_{i\left( 2 \right)}} + 2{a_4}\sin {x_{i\left( 2 \right)}}$ ， ${m_{12}} = {a_2} + {a_3}\cos {x_{i\left( 2 \right)}} + {a_4}\sin {x_{i\left( 2 \right)}}$ ， ${m_{21}} = {a_2} + {a_3}\cos {x_{i\left( 2 \right)}} + {a_4}\sin {x_{i\left( 2 \right)}}$ ， ${m_{22}} = {a_2};$ C_i = $\left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}} \\ {{c_{21}}}&{{c_{22}}} \end{array}} \right]$

${c_{11}} = {a_4}\cos {x_{i\left( 2 \right)}} - {a_3}\sin {x_{i\left( 2 \right)}}$ , ${c_{12}} = \left( {{a_4}\cos {x_{i\left( 2 \right)}} - {a_3}\sin {x_{i\left( 2 \right)}}} \right)\left( {{{\mathop x\limits^. }_{i\left( 1 \right)}} + {{\mathop x\limits^. }_{i\left( 2 \right)}}} \right)$ , ${c_{21}} = {a_3}\sin {x_{i\left( 2 \right)}} - {a_4}\cos {x_{i\left( 2 \right)}},$ ${c_{22}} = 0$ 。

其中： ${a_1} = {I_1} + {m_1}l_{c1}^2 + {I_e} + {m_e}l_{ce}^2 + {m_e}l_1^2,$ ${a_2} = {I_e} + {m_e}l_{ce}^2,$ ${a_3} = {m_e}{l_1}{l_{ce}}\cos {\delta _e},$ ${a_4} = {m_e}{l_1}{l_{ce}}\sin {\delta _e};$ ${m_1} = 1.2,$ ${l_1} = 1.2$ , ${m_e} = 2.5,$ ${\delta _e} \!=\! {30^o},$ ${I_1} \!=\! 0.15,$ ${l_{c1}} \!=\! 0.5,$ ${I_e} \!=\! 0.25,$ ${l_{ce}} \!=\! 0.6 $ 。

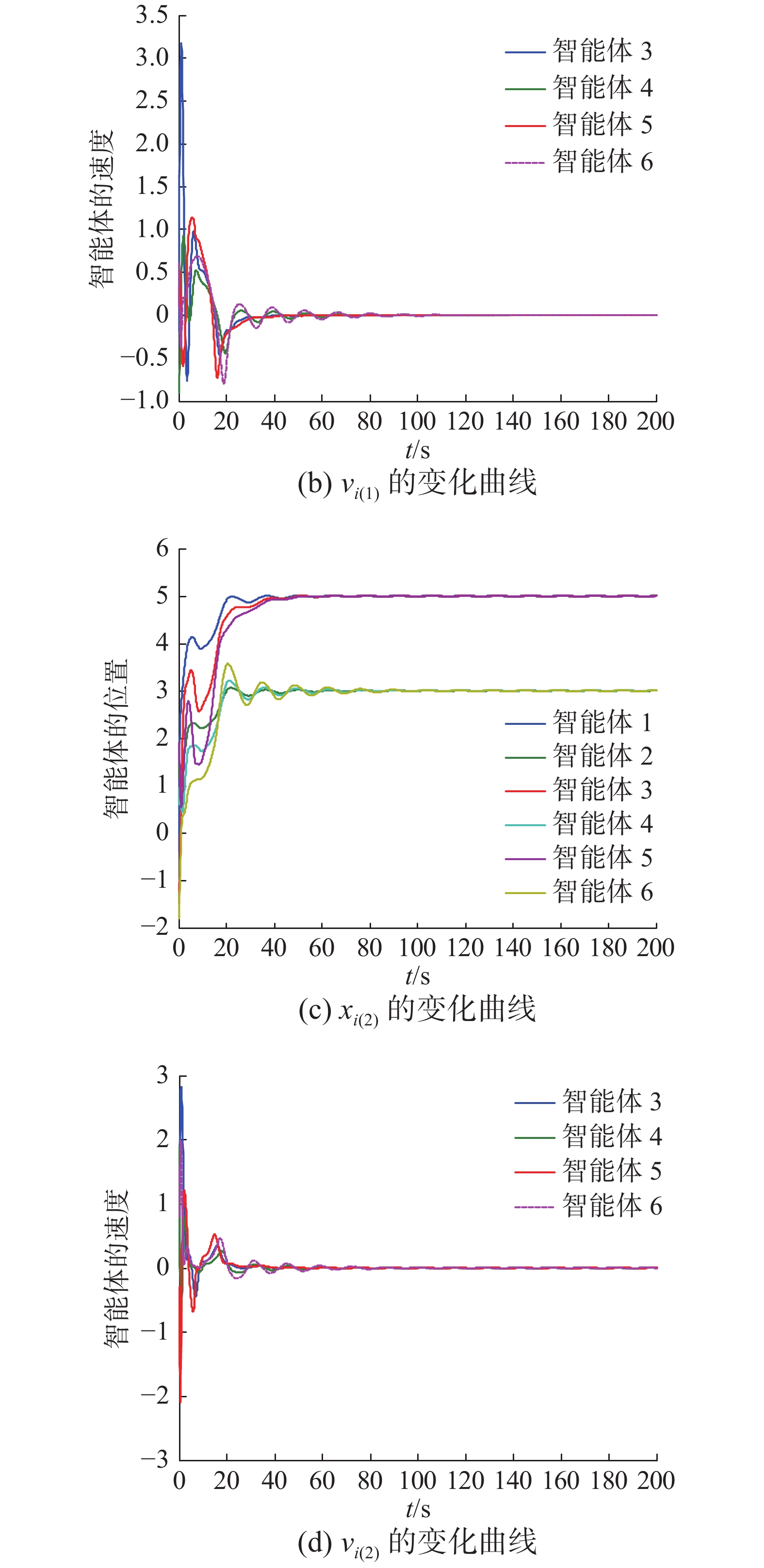
在各群中任意选择智能体为牵制节点，以智能体1、2为例。 ${G_1}$ 中的虚拟领导者的状态信息为 $\left( {5,0} \right)$ ， ${G_2}$ 中的虚拟领导者的状态信息为 $\left( {3,0} \right)$ 。在牵制节点的作用下异质多智能体系统的群一致性的仿真结果如图2所示。

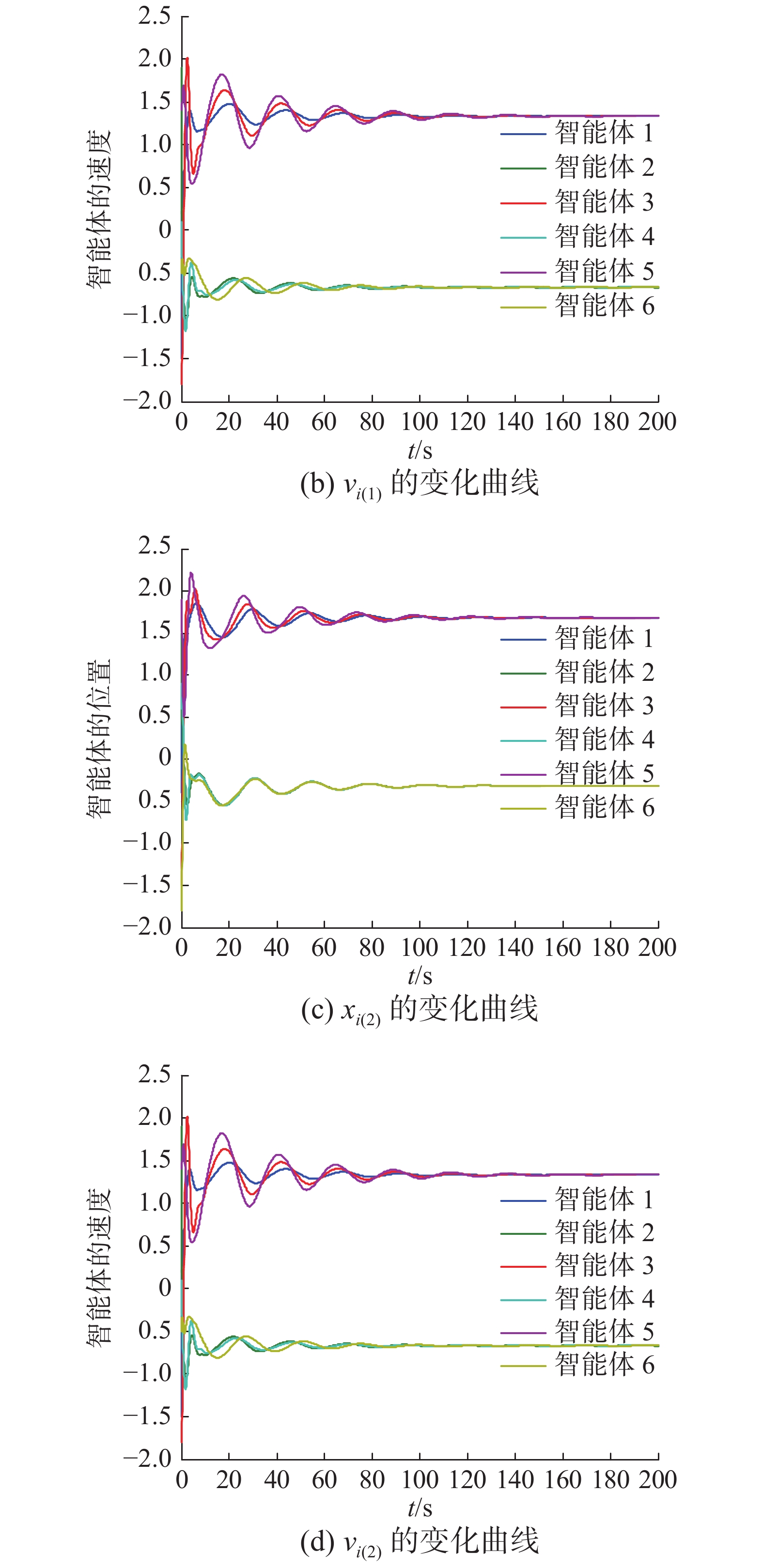
在同样的初始条件下，不考虑具有牵制控制的群一致性策略的仿真结果如图3所示。

由图2(a)和(c)可以看出，群 ${G_1}$ 中的智能体1、3和5位置状态最终都趋于5，群 ${G_2}$ 中的智能体2、4和6位置状态最终都趋于3，从图2(b)和(d)可以看出，群 ${G_1}$ 和 ${G_2}$ 中的智能体速度最终都趋于0。说明存在复杂的非线性结构的EL智能体构成的异质多智能体系统在基于牵制控制的控制协议作用下，在同一个群中的智能体的位置状态趋于同一个状态值，不同群的智能体的位置状态趋于不同的状态值，异质多智能体系统实现了群一致性，并且各群智能体状态最终收敛到虚拟领导者的状态，即期望的状态。由图3(a)和(c)可以看出，两个群体趋于不同的状态，实现了群一致，但相对于具有牵制控制的群一致性仿真结果相比,施加牵制控制的各个子群可以到达先前设定的预先期望状态，而未施加牵制控制的各个子群体最终的一致平衡状态不能趋于一个预先期望的状态。

4 结束语

本文研究了由一阶智能体、二阶智能体和EL智能体组成的异质多智能体系统的群一致性，为了实现各群中智能体状态能够趋于期望的状态，提出基于牵制控制的分布式控制协议，通过代数图论、李雅普诺夫和拉塞尔不变集原理证明了该种控制协议的充分条件，通过MATLAB仿真平台进行数值仿真，各群中智能体的状态信息趋于虚拟领导者的状态，即各群期望的状态信息。实现了由线性智能体和非线性智能体构成的异质多智能体系统的群一致性，从而实现对以往研究线性智能体构成的异质多智能体系统的群一致性的扩展。