植物是地球上最广泛存在的生命形式之一,与人类的生活密切相关。植物的分类鉴别对于探索植物的自身价值、生态监测以及生物多样性保护有着重要的意义。植物分类的主要依据是植物的外观特征,传统的识别方法需要业内专家对大量植物进行观察、测量,效率较低。由于植物外观特征能以数字图片方式获得,随着计算机图像识别技术的发展,借助计算机辅助处理进行植物分类,成为人们越来越关注的课题之一。
当前对植物识别方法的研究较多,但大多都是基于叶片几何特征的识别[1-3]。叶片几何特征是指叶片的外部形状和维度的各种参数特征,如叶片形状的圆形度、中心偏离半径,以及叶缘锯齿数等量化的数据。这类方法存在如下问题:1)进行几何特征提取的计算量很大,且不适用于所有的叶片样本;2)对植物图像要求较高,必须是单一背景下单个完整叶片图像,而实际能获得的植物图像通常是成片的,很难进行几何特征的度量。仅限于单个叶片的识别方法在图像采集上仍需耗费大量人工,不能有效提高植物识别的效率。为达到完全自动识别的效果,研究自然复杂背景下的植物识别是十分必要的。
人工在野外采集的植物图像通常背景复杂,且植物枝叶分布具有随机性,存在叶片重叠现象,单纯提取叶片特征的方法并不适用,利用边缘提取植物轮廓信息是合适的思路。边缘是数字图像中像素值明显变化的点的集合,边缘的显著变化通常表现了图像属性的重要变化。图像边缘检测能够剔除不相关的干扰信息,保留图像的主体结构,大幅度减少数据量,目前已在复杂植物图像的识别中有所应用。现有的边缘提取方法[4-6]很多,如 Roberts[7]算子、Sobel[8]算子、Prewitt[9]算子、Canny[10]算子和Laplacian[11]算子等。在这些经典算子的基础上,也有许多学者进行了改进工作[12-14]。这些传统边缘算子虽然在图像分割、图像检索等领域中获得了良好的性能,但是仍然存在方向较为固定、尺度单一等缺点,因此对复杂植物图像边缘特征的提取效果不尽如人意。针对传统边缘算子的固有缺陷,本文采用一种具有多尺度与多方向特性的可变局部边缘模式算子(varied local edge pattern,VLEP)提取绿色植物图像的纹理边缘信息,这种算子是灵活的圆形结构,半径和近邻点数目可以任意取值,因此可以提取不同尺度,不同方向的边缘特征,有效弥补了传统算子由于边缘方向过少,或尺度单一而容易丢失其他边缘信息的缺陷。
1 VLEP算子在复杂植物图像中,植物叶片的分布具有多方向性,而传统边缘算子的方形形式导致其通常只包含0°、90°两个方向,或者0°、45°、90°和135°这4个方向,因此在一定程度上忽略了其他方向上必要的边缘信息。人工采集植物图像时,拍摄距离等因素会影响叶片区域在图像上的尺度大小,传统边缘算子只覆盖2像素×2像素或3像素×3像素的图像单元,只能反映图像很小范围内的某个局部强度变化,而不同尺度的支持空间会包含不同的信息,因此其检测到的边缘特征并不完全。VLEP算子采用圆形结构,通过设置不同半径和近邻点数目,能获得多方向、多尺度的边缘特征。因此,VLEP算子能针对复杂背景下植物图像的特点,有效提取其边缘信息。
VLEP算子[15]是一种灵活的圆形可变局部边缘模式算子,用
对于局部边缘模式算子,

|
Download:
|
| 图 1 两组局部边缘模式算子 Fig. 1 Two groups of local edge pattern operators | |
局部非边缘检测算子包括P个均匀分布在R圆上的近邻点,其中P大于4且能被4整除,R为正实数。过圆心作两条相互垂直的第一方向线和第二方向线。对于第一类局部非边缘模式算子,位于第一方向线的两个近邻点赋值为1,位于第二方向线的两个近邻点赋值为–1,除此之外,其余近邻点均赋值为0,如图2(a)所示;对于第二类局部非边缘模式算子,位于第一方向线和第二方向线上的4个近邻点赋值为0,第一方向线和第二方向线将圆周平均分为4份,其中位于对角的两份圆周上的近邻点赋值为1,位于另一对角的两份圆周上的近邻点赋值为–1,如图2(b) 所示。图中两条虚线分别为第一方向线与第二方向线,以圆心为旋转中心,不断将两条方向线按顺时针或逆时针旋转固定角度
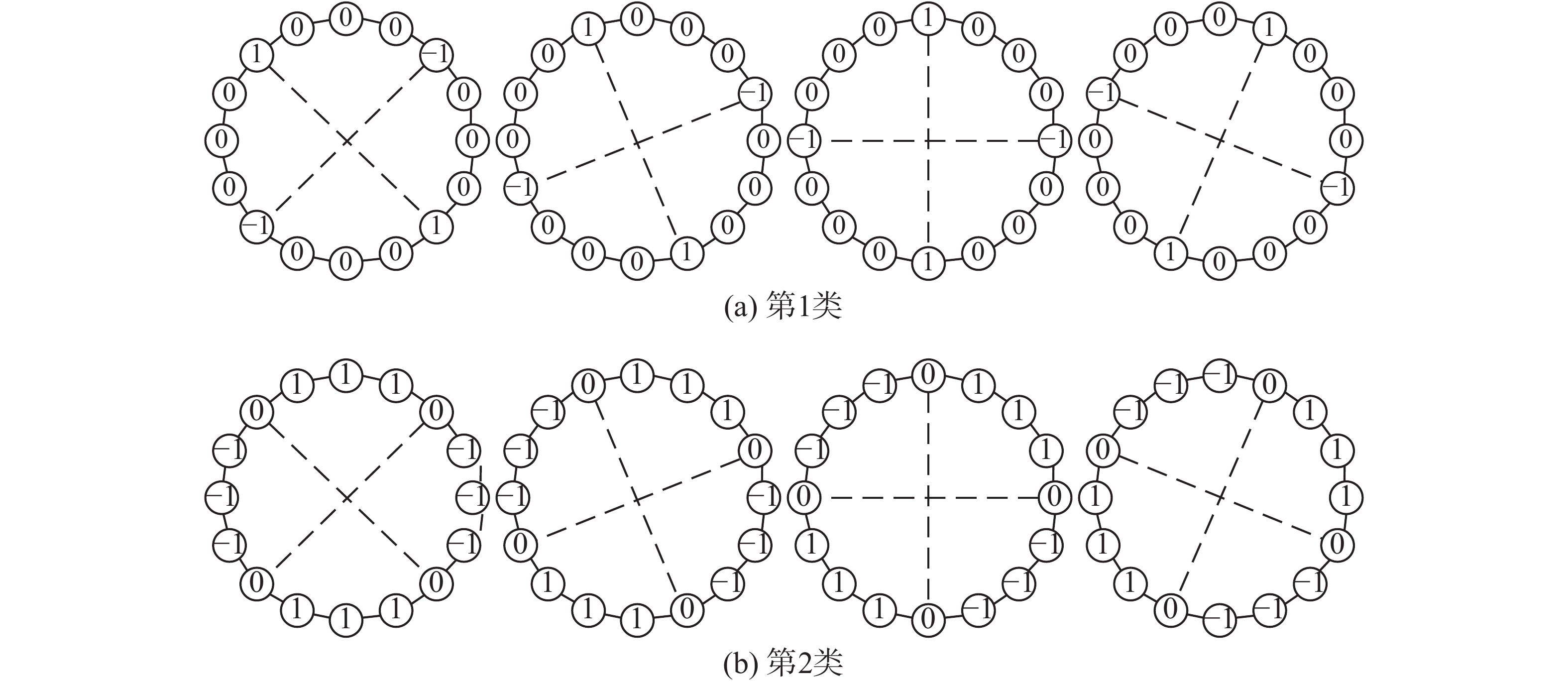
|
Download:
|
|
图 2 一组局部非边缘模式算子
|
|
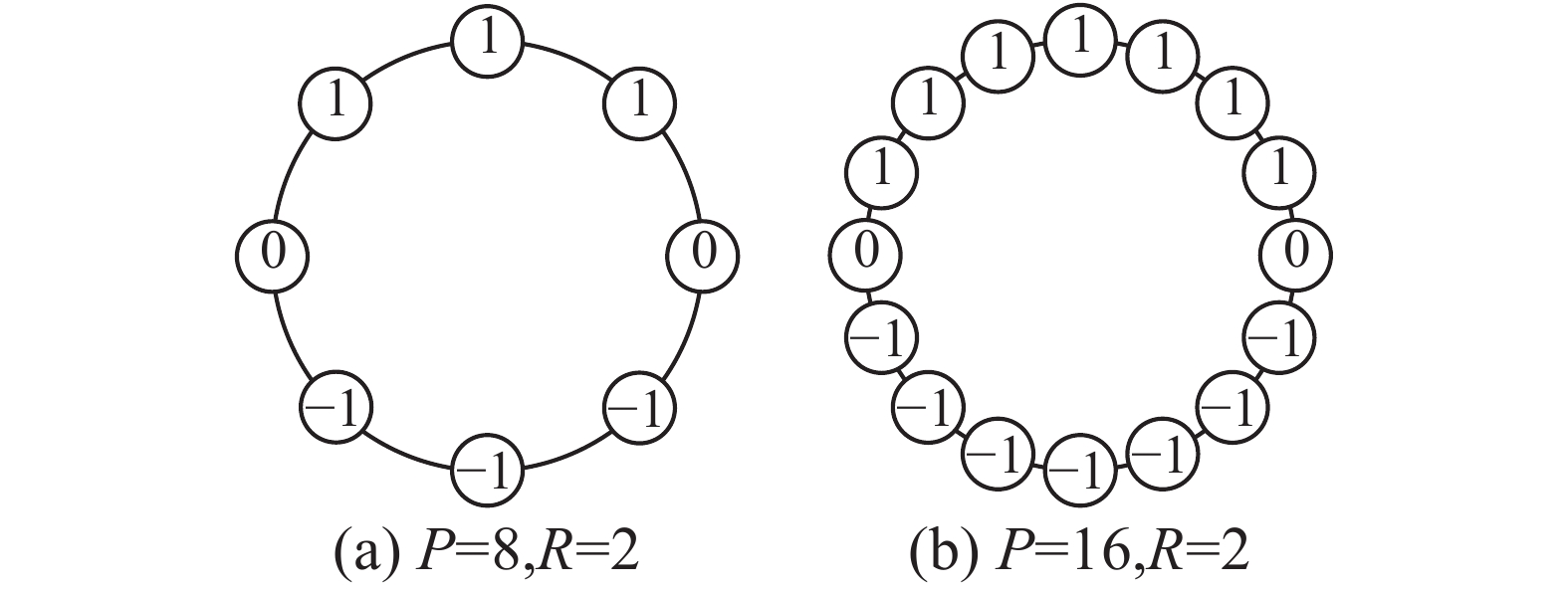
由于P、R取值的不同,VLEP算子可以刻画不同局部空间尺度和方向的纹理信息。不同尺度的VLEP算子,其近邻点P的个数相同,半径R不同,如图3所示。
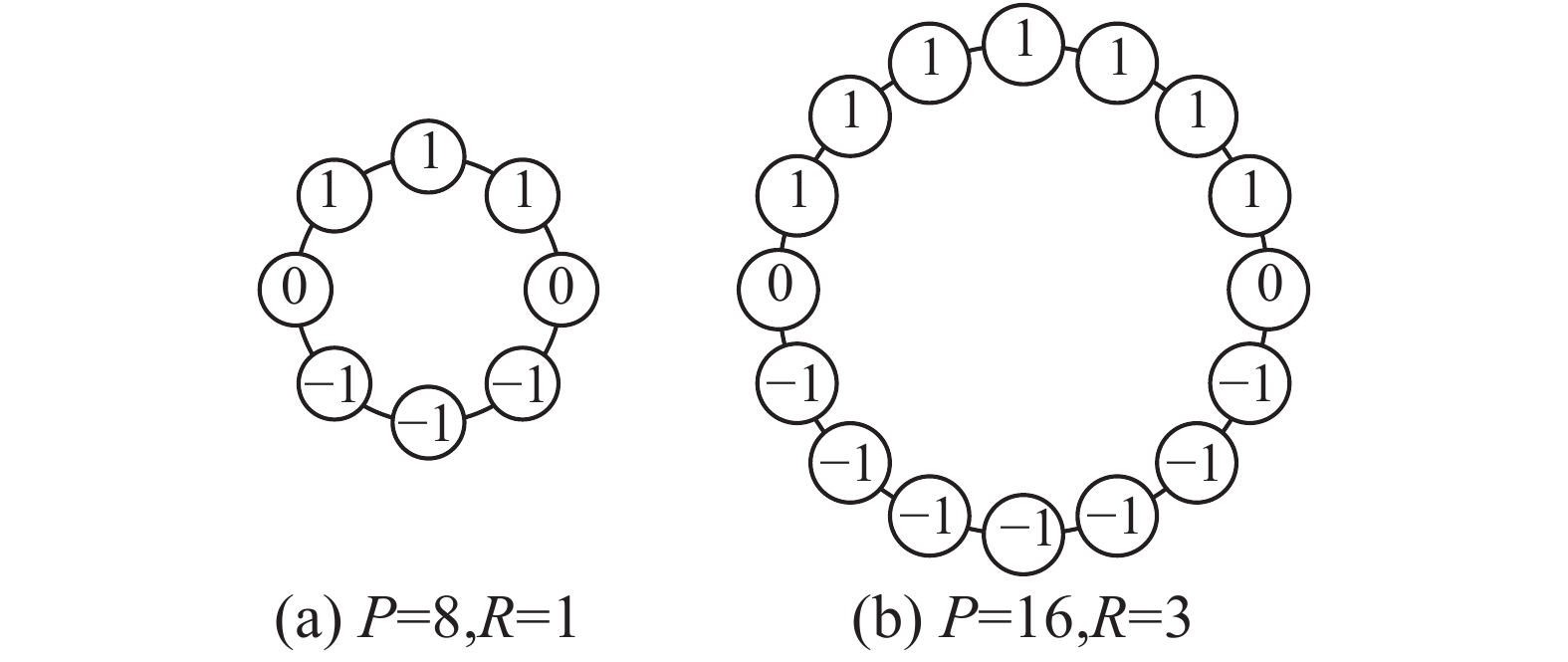
半径R越大,提取边缘特征的图像纹理基元尺寸越大。使用不同尺度的VLEP算子提取纹理边缘时,可以刻画出图像中不同的局部空间尺度的边缘信息。不同方向 (分辨率)的VLEP算子,其半径R相同,邻近点P的个数不同,如图4所示。近邻点P越大,对图像纹理基元提取边缘的方向越多,纹理特征越细致,分辨率越高。此外,VLEP算子的近邻点个数P与半径R可以同时不同,如图5所示,可以分别提取图像纹理边缘不同方向,不同尺度空间的信息。可见,VLEP算子具有多尺度和多方向特性,利用VLEP算子提取特征,可以有效解决传统算子由于边缘方向过少、尺度单一而丢失其他边缘信息的问题。

|
Download:
|
| 图 3 不同尺度VLEP算子实例 Fig. 3 An example of multi-scale VLEP operators | |
|
Download:
|
| 图 4 不同方向(分辨率)VLEP算子实例 Fig. 4 An example of multi-direction (or multi-resolution) VLEP operators | |
|
Download:
|
| 图 5 不同尺度与不同方向(分辨率)VLEP算子实例 Fig. 5 An example of multi-scale and multi-resolution VLEP operators | |
利用不同半径、近邻点和方向角的局部边缘算子
| $G_{P,R}^\theta (x,y) = {\rm{VLEP}}_{P,R}^\theta \otimes I(x,y)$ | (1) |
式中:
将图像位置
| $E_{P,R}^\varphi = \max (|G_{P,R}^\theta |) , \; \varphi \in \theta $ | (2) |
式中:
整个图像中每种边缘或非边缘模式各自出现的频率
| $T_{P,R}^\varphi = \frac{{\displaystyle\sum\limits_{x = 0}^{M - 1} {\displaystyle\sum\limits_{y = 0}^{N - 1} {f(x,y)} } }}{{M \times N}}$ | (3) |
式中:
| ${{{H}}_{P,R}} = (T_{P,R}^{{\varphi _1}}, \cdots ,T_{P,R}^{{\varphi _K}}, \cdots ,T_{P,R}^{{\varphi _m}})$ | (4) |
式中:
为了获得更紧致的特征向量,特征空间可以细分,每种类型的边缘和非边缘可以更详细地分类,每种类型的边缘和非边缘的细分阈值
首先,将所有训练图像的相同边缘类型或非边缘类型(或VLEP算子)的
| ${V_{\rm{th}}} = E_{P,R}^\varphi (\frac{N}{B} \times w + 1), \; (w = 1, 2, \cdots ,B - 1)$ | (5) |
式中:N代表所有训练图像中相同边缘或非边缘(或VLEP算子)类型的数目;B是每种类型的VLEP算子需要被进一步划分的类别数目,B需要提前设置;
细分阈值
| $\lambda = B\times(\frac{P}{2} + \frac{P}{4}\times A)$ | (6) |
式中:边缘VLEP算子是
| $ {{H}}_{P,R}' = (T_{P,R}^{{\varphi _{11}}}, \cdots \! ,T_{P,R}^{{\varphi _{1B}}}, \cdots \! T_{P,R}^{{\varphi _{k1}}}, \cdots \! ,T_{P,R}^{{\varphi _{kB}}}, \cdots \! ,T_{P,R}^{{\varphi _{m1}}}, \cdots \! ,T_{P,R}^{{\varphi _{mB}}})$ | (7) |
最近邻是一种简单有效的分类准则,通过最近邻分类器可以快速地计算两个直方图之间的相似性和差异性,例如最常用的欧氏距离、马氏距离。本文实验选用马氏距离作为衡量准则:
| $D\left( {\overline {{{H}}_k'} ,{{H}}_{\rm{test}}'} \right) = \sqrt {\left( {\overline {{{H}}_k'} - {{H}}_{\rm{test}}'} \right){S^{ - 1}}{{\left( {\overline {{{H}}_k'} - {{H}}_{\rm{test}}'} \right)}^{\rm{T}}}} $ | (8) |
式中:
目前,植物分类算法研究领域的一大问题是缺少一个公认的统一的数据平台。本文实验中所使用的绿色植物图像来自北京工商大学计算成像实验室拍摄的数据库,为了使数据更好地模拟真实世界的绿色植物环境,保证研究算法更具实用性,该图像库构建过程中考虑了多种因素,包括光照强度、叶片大小、拍摄背景、植株数量(多株与单株)、拍摄角度、拍摄距离等,这些因素虽然保证了数据更具实际意义,但同时也会增加物种识别的难度。图6展示了几幅数据库中的图例。本实验选取数据库中80类植物图像,其中,每类植物6幅图像作为训练图像,9幅作为测试图像,因此共有480幅训练图像,720幅测试图像。

|
Download:
|
| 图 6 绿色植物物种数据库图例(银杏树) Fig. 6 Some examples of the green plants database (ginkgo) | |
在阈值数相同(阈值数均为8)的情况下,利用不同P、R值的
| 表 1 相同阈值数下的
|
分析表1可知,在阈值数相同的情况下,近邻点个数P和半径R的选取会影响识别率。因此,P、R的取值具有最优组合,其中,近邻点个数
为了测试阈值细分的有效性,选用
| 表 2 不同阈值数下的
|
由表2可知,在算子半径R和近邻点P确定的情况下,阈值数越多,识别率越高。值得注意的是,阈值不能过多,阈值太多会划分出许多不具备区分性的特征子类,同时会导致落入有效特征子类的特征值过少,从而使特征直方图失去特征分类意义。在所测识别率中,使用
为了与传统边缘提取算法进行对比,本文使用Canny、Roberts、Prewitt、Sobel算子提取图像边缘特征,并同样进行32阈值细化,实验结果如表3所示。
| 表 3 对比算法识别率 Tab.3 Recognition results of contrast algorithms |
从表3可以看出,所提的可变局部边缘模式算子提取植物边缘特征的效果远远优于传统的边缘模式算子,识别率有大幅度的提高。可变局部边缘模式算子具有多方向特性,提取的图像边缘方向信息相对丰富,同时该算子具有多尺度特性,能提取大小不同尺度的纹理结构,因此,在边缘特征提取的表现上,要比传统算子有优势。
6 结束语本文针对传统边缘算子方向少、尺度固定的缺点,提出了一种基于灵活可变的圆形局部边缘模式的绿色植物物种识别算法,该算法由于所用边缘算子具有多尺度、多方向特性,能够提取更为丰富、完整的边缘信息。在自建绿色植物物种数据库上进行的一系列物种识别实验中,获得了满意的识别结果,这表明本文提出的算法可以有效弥补传统算子由于边缘方向过少,尺度单一而丢失其他边缘信息的缺陷。
| [1] |
胡秋萍. 基于叶片形状特征的植物识别技术研究[D]. 西安: 西安电子科技大学, 2014. HU Qiuping. The study of plant identification technology based on leaves’ shape features[D]. Xi’an: Xidian University, 2014. (  0) 0)
|
| [2] |
叶绪伦, 赵杰煜, 陈能仑. 结合LDA主题模型的植物叶片形状描述及分类[J]. 模式识别与人工智能, 2016, 29(3): 263-271. YE Xulun, ZHAO Jieyu, CHEN Nenglun. Leaf shape description and classification with LDA topic mode[J]. Pattern recognition and artificial intelligence, 2016, 29(3): 263-271. (  0) 0)
|
| [3] |
刘骥, 曹凤莲, 甘林昊. 基于叶片形状特征的植物识别方法[J]. 计算机应用, 2016, 36(s2): 200-202. LIU Ji, CAO Fenglian, GAN Linhao. Plant identification method based on leaf shape features[J]. Journal of computer applications, 2016, 36(s2): 200-202. (  0) 0)
|
| [4] |
SHRIVAKSHAN G T, CHANDRASEKAR C. A comparison of various edge detection techniques used in image processing[J]. International journal of computer science issues, 2012, 9(5): 269-276. ( 0) 0)
|
| [5] |
KAUR K, MALHOTRA S. A survey on edge detection using different techniques[J]. International journal of application or innovation in engineering and management, 2013, 2(4): 496-500. ( 0) 0)
|
| [6] |
ONN U, SINGLA P. A survey on conventional edge detection techniques[J]. Journal of algebra, 2014, 397: 1-17. DOI:10.1016/j.jalgebra.2013.08.022 ( 0) 0)
|
| [7] |
BERZINS V. Accuracy of Laplacian edge detectors[J]. Computer vision, graphics, and image processing, 1984, 27(2): 195-210. DOI:10.1016/S0734-189X(84)80043-2 ( 0) 0)
|
| [8] |
DUDA R O, HART P E. Pattern classification and scene analysis[M]. New York: Wiley, 1973.
( 0) 0)
|
| [9] |
MAINI R, SOHAL J S. Performance evaluation of Prewitt edge detector for noisy images[J]. GVIP journal, 2006, 6(3): 39-46. ( 0) 0)
|
| [10] |
OGAWA K, ITO Y, NAKANO K. Efficient Canny edge detection using a GPU[C]//2010 First International Conference on Networking and Computing. Hangzhou, China, 2010: 279–280.
( 0) 0)
|
| [11] |
VOLLMER J, MENCL R, MÜLLER H. Improved Laplacian smoothing of noisy surface meshes[J]. Computer graphics forum, 2010, 18(3): 131-138. ( 0) 0)
|
| [12] |
HUSSEIN W B, MOATY A A, HUSSEIN M A, et al. A novel edge detection method with application to the fat content prediction in marbled meat[J]. Pattern recognition, 2011, 44(12): 2959-2970. DOI:10.1016/j.patcog.2011.04.028 ( 0) 0)
|
| [13] |
DI Haibin, GAO Dengliang. Gray-level transformation and Canny edge detection for 3D seismic discontinuity enhancement[J]. Computers and geosciences, 2014, 72: 192-200. DOI:10.1016/j.cageo.2014.07.011 ( 0) 0)
|
| [14] |
GAO Wenshuo, ZHANG Xiaoguang, YANG Lei, et al. An improved Sobel edge detection operator[C]//2010 3rd IEEE International Conference on Computer Science and Information Technology. Chengdu, China, 2010: 67–71.
( 0) 0)
|
| [15] |
WANG Yu, ZHAO Yongsheng, CAI Qiang, et al. A varied local edge pattern descriptor and its application to texture classification[J]. Journal of visual communication and image representation, 2016, 34: 108-117. DOI:10.1016/j.jvcir.2015.11.001 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


