在传统中医学中,作为中医四诊之一的脉诊扮演了相当重要的角色,传统中医师通过手指感知病人的脉动来获取脉搏信息,从而对人体器官的健康状况进行判断。中医师之所以能够做到这点,是因为脉诊是对人的整体健康状况进行考察的一种信息获取方式,在临床诊断中,脉诊扮演了非常重要的角色,兼具研究和现实意义。脉搏信号是一种人体生物信号,其中包含了大量人体生物信息。从中医的观点来看,个体脉搏信息中的内容,很多都能直接被解读为单个个体的生理或者病理的信息[1]。因此,通过脉搏信号,我们可以了解个体身体的状况和变化。脉搏信息也能够为我们进行疾病的诊断提供一些基础的信息。
然而长期以来,脉诊都依赖于医生在病患身上采集信息之后,进行主观地判断。当然,在中医的研究上为了便于记忆,医师们将这些判断形象化为一些“脉象”。但是在临床诊断和教学中,医生与医生之间对于脉象的体会不同,会导致他们对病人脉象的区分标注不同,也就是说,因为医生的个体差异,比如个人经验的多寡,个人主观的因素,都会导致脉象判断的不同[2-3]。因此,这对于脉诊的客观化,以及中医的客观化,都是一个大的制约。
随着中医客观化工作的推进,脉诊技术也越来越走向客观化和仪器化。然而,如何对仪器所检测和收集到的信息进行解读,却又回到了原来脉诊诊断主观化的问题上来。因为传统的机器学习方法,依赖于对大量的脉诊数据进行标注,然后再利用标注的数据,从中学习到特征,从而构建起一个脉诊诊断的智能算法。假若标注的过程不够客观,就难免影响到最后的分类效果。
本文提出的方法,是先对脉搏信号数据进行预处理(去基线漂移和归一化),然后提取特征,最后用FCM聚类算法进行聚类,将结果与粗分类的结果进行对比。本文旨在提出一个无监督的客观化方法。在中医专家对数据进行标注之前,先根据信号的特征,进行粗线条的分类,为客观化提供依据。如果在更大规模的数据支持下,对特征进行进一步地优化,有理由预期无监督聚类分析可以得到更好的效果。
1 相关研究工作脉诊信号的模式分类研究,在脉诊客观化的过程中,扮演了核心的位置。脉诊信号的自动识别以及准确分类,是完成相关模式分类工作的预备条件。现阶段,在提取脉象信号特征的方法上,较常采用的是时域分析法[4],但脉象信号的时域特征存在一些自身的问题,如差异性小,区分脉象较为困难。所以,大多数研究人员都通过在时域特征之上结合频域特征的方法来获取脉象的特征频谱,从而将可显著区分的特征从信号的频域中找出,其中较为常用的方法为功率谱分析与倒谱分析[5]。
此外,为了更好地梳理脉象特征和生理病理两者间的关联,以做到令脉诊技术进一步客观化、智能化,很多学者也做了大量的研究工作。李娜等[6]对支气管哮喘与慢性胃炎患者脉图的比较研究,提取时域分析特征,通过实验证明了支气管哮喘与慢性胃炎在“寸”部存在脉图时域特征差异之间的相关性。张冬雨等[7]提出了两类基于ERP弹性测量距离的脉搏信号形态分类方法,用于脉搏信号的分类。实验证明,同现有的脉搏信号分类方法相比,他所提出的弹性核函数——高斯弹性测度距离核函数。对脉搏信号的分类和复杂时间序列的分类,都展现出较好的效果。
在神经网络被广泛应用到中医客观化的大背景下,用计算机进行脉诊特征分析,带来了进一步的效率和准确性的提升。人工神经网络是一种自适应的非线性动力系统,目前有不少学者利用人工神经网络对脉搏信号进行分类和识别,也取得了不错的效果。如郭红霞等[8]提出的基于小波包分析和BP神经网络的中医脉象识别方法,利用小波变换具有揭示信号时频两域细节和局部特征的能力,提出了将脉象信号的小波包分析和BP神经网络相结合以达到识别中医脉象的目的。小波包分解中的第3层从低频到高频的8个频带的信号能量,被用作脉冲识别的输入层,脉冲信号通过小波包分析,然后输入神经网络。通过该算法,步长函数和迭代的改进不仅缩短了网络训练时间,而且还利用小波包分解系数进行重建信号,并在此基础上获得更好的结果。此外,Zhang等[9]也通过小波变换提取时域和频域信息,进行了相似的实验,通过更细致地调校,网络的正确识别率有了进一步的提升。
然而,在上述方法中,无一不严重依赖于大量中医专家对脉搏数据的分类和标记,然而正如前文所提及,医生之间因为个体差异或者主观因素,会对脉象的判断有所不同,当数据量大,且分别来自不同医生的标注时,难免出现标注不准确的情况。这样的状况,对目前的中医客观化,特别是脉诊的客观化,起到了阻碍的作用。如果我们可以提出一种方法,减少人的主观判断信号的成分,直接从脉搏信息中进行特征提取,然后通过聚类的方法进行粗分类,这样的方法具备一定的理论价值。在当下医疗资源不均衡发展的现状中,医学仪器价格逐渐走低,而医学专家数量却十分有限,在解决医疗资源不匹配的问题上,粗分类可以扮演一个先期分诊的作用,使得它同时还具有一定实用价值。
2 中医脉诊的无监督分类方法文中提出的特征提取和分类的方法,是由3个主要步骤构成的:数据的预处理、特征提取过程和聚类过程。在这里,首先选择一个较好的特征来代言脉搏信号的相关数据,然后从训练数据中以一种无监督的形式,来进行聚类。
2.1 基于双树复小波变换的去除基线漂移方法脉象信号是一种相当复杂的生物医学信号,它的特点包括背景噪声大以及随机性强。脉象,体现了人身中的各类复杂的生理状态周期,它反映了人们在外部环境以及内部生理特征综合作用下的整体生理变化。因此,脉象信号具有非线性、整体性和可调性等特点。由于脉象信号受整体环境影响较大,不可避免的结果就是采集到的脉搏信号会因呼吸和仪器本身而引起基线漂移。目前,基线漂移的去除方法有很多种,如小波变换法、自适应滤波、插值拟合法、滑动平均滤波等[10-12]。其中被最广泛应用的是离散小波变换法,不过离散小波变换法因为具有对平移的高度敏感性以及容易出现频率混叠等缺点,为实验增加了一些不确定性因素。为了克服以上缺点,本论文则选取了双树复小波变换法来进行基线漂移的去除工作。
双树复小波(dual-tree complex wavelet transform)的概念最早由金斯伯里(Kingsbury)率先提出,该算法在双树滤波基础之上,又进行了一层优化,使其不单具备了一般复小波算法的优点,还可以完全重构原始信号,它属于对一维双树复小波的一种推广。
一维双树复小波:
| $ \psi (t) = {\psi _h}(t) + j{\psi _g}(t) $ | (1) |
式中
二维双树小波:
| $\begin{array}{c}\psi \left( {x,y} \right) = \psi \left( x \right)\psi \left( y \right) = \left[ {{\psi _h}\left( x \right) + j{\psi _g}\left( x \right)} \right]\left[ {{\psi _h}\left( y \right) + j{\psi _g}\left( y \right)} \right] = {\psi _h}\left( x \right){\psi _h}\left( y \right) - {\psi _g}\left( x \right){\psi _g}\left( y \right) + j\left[ {{\psi _g}\left( x \right){\psi _h}\left( y \right) + {\psi _h}\left( x \right){\psi _g}\left( y \right)} \right]\end{array}$ | (2) |
由一维双树复小波推广,其中双树实小波为
| $\psi_h (x){\psi _h}(y) - {\psi _g}(x) {\psi _g}(y)$ | (3) |
双树复小波方法采用了二叉树结构的两路变换,一树生成变换的实部,一树生成虚部(如图1所示)。该方法的思路主要是:首先对于第1层进行分解,如果两树滤波器间的延迟恰好等于一个采样间隔,那么就可通过区别b树种第1层的二抽取令其正好采样到a树种因二抽取所丢掉的采样值。

|
Download:
|
| 图 1 双树复小波二叉树结构 Fig. 1 Double tree complex wavelet binary tree structure | |
好的数据预处理,对脉搏信号的要求比较高,要求获取的脉搏信号稳定性比较好,并且具有比较好的可重复性。在单个个体的同一体质条件下,脉搏信号能够保持一定的持续性和稳定性。在这样的条件下,我们实施以去除基线漂移的处理,使得后续的信号分析工作成为可能。
2.2 基于小波变换的脉象信号的去噪与归一化原始的脉搏信号是不适合作为分类器的直接输入信息的,首先因为原始信号在未经处理前,维度过高,且有噪声干扰;其次没有进行归一化,相似性不易被捕捉到。为了改善后续的分析和识别,我们先将原始脉搏信号进行去噪处理,然后进行归一化过程,再利用一些通用的波形信号特征学习的手段,将波形信号转换成时空序列的表示,是数据预处理过程中很重要的一个步骤。在本文的实验中,首先基于小波变换,用非线性阈值法,从而对脉象信号进行一个去噪处理,然后再进行一个归一化的过程:我们将抽样频率统一调整为128 Hz每个心动周期,即将信号进行预处理之后,再进一步做一个归一化处理,其中包括对数据进行补零,然后将一个心动周期中的脉搏波信号长度进行调整,最后统一为128点。图2为补零操作完成后的一个心动周期,其中纵轴代表信号强度,横轴则示意了每个周期内采样点的数目(在图中第68个采样点后补零至第128个采样点)。

|
Download:
|
| 图 2 脉搏信号归一化单心动周期 Fig. 2 Pulse signal normalized single cardiac cycle | |
多种时域分析和频域分析的手段,比如经验模态分解方法、傅里叶变换和小波分析都被广泛地应用于脉搏信号的基本分析过程中[13]。尤其是傅里叶分析、小波分析这样的频域分析方法,对周期性的信号进行数值分析,将脉搏信号中复杂的周期性变化进行分解,得到不同频率的频谱变化,这样的做法,利用了脉象信号自身的周期性,很好地抓住了脉搏信号中的特点,从而使得后续的工作可以把从其间得到的频谱数据与人体的生理和病理相关状态关联起来[14-15]。
本文将采用梅尔倒谱系数这样更成熟而且高层的特征。在语音处理领域,梅尔倒谱系数(MFCC)是一个非常常用而且成熟的特征[16]。该特征根据人耳听觉的特征要点,用Mel标度频率域提取出来的倒谱参数,进行非线性转换,从而做到使得“处理之后的特征”,与“人类的真实听觉特征”相符。其优点在于:当用于信噪比较低的状况时,仍可做到较好的识别性能。MFCC这种特征的优良性质,在于它对于信号的性质并没有过高的要求,对于输入的信号也没有太多的预设和限定。所以MFCC特征与其他特征相比,具有更好的鲁棒性。因此本文选用它来对脉诊的输入信号进行特征提取的处理。
倒谱分析可以分为3步过程,首先,将原波形信号经过傅里叶变换得到频谱:
| ${X}[k]={H}[k]{E}[k]$ | (4) |
在两边取自然对数:
| $\log||{X}[k]||=\log||{H}[k]||+\log||{E}[k]||$ | (5) |
最后在两边取逆傅里叶变换得到
| $x[k]=h[k]+e[k] $ | (6) |
式中:x[k]就是倒谱,e[k]与h[k]分别是倒谱的高频和低频部分,其中的低频部分h[k]也就是本文真正关心的描述性特征。只需将频谱通过一组Mel滤波器就得到Mel频谱,在Mel频谱上面获得的倒谱系数h[k]就称为Mel频率倒谱系数。
MFCC特征的特点,是在频率坐标轴上非均匀的滤波。具体来说:在低频区有很多滤波器,分布较为密集,而在高频区域,滤波器的数目就变得较少,分布也变得稀疏(如图3)。这样的特点,可以把特征的关注点放在某些特定的频率,比较符合脉诊信号在中医诊断中的特点,因此可以较好地抓住相关信号的本质特征。
因为脉象识别本质上是一个模式识别问题,而在模式识别问题中,特征的提取是其中的关键一环。因此,在对原始的脉搏信号特征化过程中,选择时域信号当中最能够反映脉象的形态特点的参数,是一个关键点。在这里选取MFCC提取的特征作为输入向量,是为了更好地进行下一步,即脉诊信号的聚类工作。

|
Download:
|
| 图 3 MFCC非线性频谱(横轴与纵轴分别代表频率与滤波) Fig. 3 MFCC non-linear spectrum (horizontal for frequency, vertical for filter) | |
在前述过程中,通过对数据进行一些基本处理,提取出了信号的高层特征。整个流程(如图4)的最后一步是聚类过程。在聚类过程中,使用了Fuzzy C-means (FCM)聚类算法,它允许同一数据属于多个不同的类。FCM算法与K-means算法的不同,在于同一个数据并不单独属于一个分类,而是可能属于几个分类。

|
Download:
|
| 图 4 脉象信号处理流程 Fig. 4 Structure model of group organizations | |
传统的聚类算法通常需要预先确定聚类中心的数量,其缺点是容易降低聚类结果的客观性,不仅如此,传统算法得到的结果也容易陷入局部最优解。而本文采用的模糊C均值(fuzzy c-means,FCM)算法,与传统的算法相比,在客观性上进行了提升。它首先执行优化的模糊目标函数计算,以获得单个采样点相对于每个类别中心的隶属度,并以此来进一步确定这个采样点的归属。FCM在不少应用领域均被采用,比如医学诊断和目标识别等[17- 18]。
FCM算法的做法,是首先将n个向量xi(i=1,2,
| $ \sum\limits_{i = 1}^c {{u_{ij}}} = 1,\forall j = 1,2, \cdots ,n $ | (7) |
式中:uij表示了第j个元素属于第i个类群的隶属度值。因此,FCM的目标函数就是:
| $ J\left( {{{U}},{c_1}, \cdots ,{c_c}} \right) = \sum\limits_{i = 1}^c {{J_i}} = \sum\limits_{i = 1}^c {\sum\limits_j^n {u_{ij}^md_{ij}^2} } $ | (8) |
式中:uij的取值在[0,1];ci则表示模糊群第I类的聚类中心,dij=||ci-xj||则计算了第I类聚类中心与第j个采样点之间的欧式L2距离;此外m∈[1,∞)则是一个指数加权。
为了求出FCM目标函数的最小值,可以将其转换成下列函数,以进行最小化的求解:
| $\begin{array}{*{20}{c}}\bar J\left( {{{U}},\;{c_1}, \cdots ,{c_c},{\lambda _1}, \cdots ,{\lambda _n}} \right) = \\J\left( {{{U}},\;{c_1}, \cdots ,{c_c}} \right) + \displaystyle\sum\limits_{j = 1}^n {{\lambda _j}\left( {\displaystyle\sum\limits_{i = 1}^c {{u_{ij}} - 1} } \right) = } \\[8pt]{\displaystyle\sum\limits_{i = 1}^c {\sum\limits_j^n {u_{ij}^md_{ij}^2} } + \sum\limits_{j = 1}^n {{\lambda _j}\left( {\sum\limits_{i = 1}^c {{u_{ij}} - 1} } \right)} }\end{array}$ | (9) |
式中:λj,j=
| ${c_i} = \frac{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m{x_j}} }}{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m} }},\;\;\;\;{u_{ij}} = \frac{1}{{\displaystyle\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{2/\left( {m - 1} \right)}}} }}$ | (10) |
由上述求得的解不难看出,模糊c均值聚类算法可以被归结为一个简单的迭代过程。
3 实验结果本文所选用的实验环境是MATLAB运行在2.8 GHz Intel i5 CPU,8 GB内存平台下。本实验中采用的样本是69名健康大学生的脉搏数据,其中脉搏数据的频率为60~80次/min,而频率则主要分布在0~40 Hz的区间范围内,原始数据的采样频率为 512 Hz。通过降频处理,将原512 Hz频率的数据降低到了128 Hz。在预处理的过程中,进行了归一化和去均值,然后将一个心动周期中的脉搏波信号长度进行调整,最后通过补零统一调整为128点。为了将无监督聚类的效果进行评估,将归一化之后的信号进行粗分类为标记的4种基本类型(如图5),再通过聚类的方法进行试验。
在实验中,通过对比不同的特征源,分别使用基于线性距离度量特征(LD)、功率谱分析(PSA)、线性预测编码(LPC)、线性预测倒谱系数(LPCC)获取的特征,与MFCC倒谱分析获取的特征进行对比;同时使用传统的硬聚类的方法(k-MEANS、KNN)与模糊C均值的效果进行对比。

|
Download:
|
| 图 5 单脉搏信号粗分类基本类型 Fig. 5 Structure model of group organizations | |
另一方面,还比较了隶属度值对聚类结果的影响。隶属度函数A(x)越接近于1,表示x属于A的程度越高,A(x)越接近于0,则表示x属于A的程度越低。使用取值于区间[0,1]的隶属函数A(x)是FCM中最常用的,但是如果我们放宽FCM隶属度以及其归一化的条件,令所有的样本针对各个类的隶属度的总和值可以大于1,这样的改变,是否可以获得较好的结果呢?
在实验中,对比了当模糊C均值的隶属度等于1时,和当我们放宽条件,允许模糊C均值的隶属度值大于1时的结果。实验的结果显示,使用倒谱分析获取的特征源以及模糊C均值的方法进行聚类,对于脉象的识别准确率相对较高(如表1)。同时我们观察到,当放宽隶属度的条件,允许模糊C 均值的隶属度值大于1时,实验效果会更好一些。
| 表 1 多聚类方案与特征源实验效果对比 Tab.1 Comparison experiment of multi-clustering scheme and feature source % |
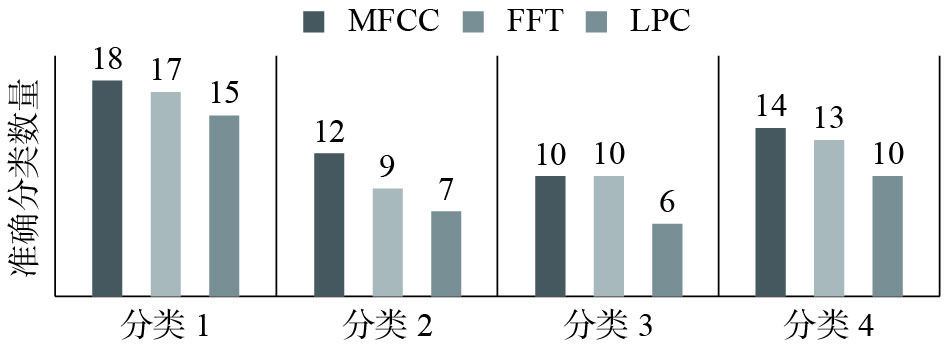
此外,单独考察了效果较好的3类特征提取方案(MFCC、FFT和LPC),观察它们在相同的聚类方案(FCM,隶属度>1)情况下,对每个单脉搏信号的准确分类数量(图6)。可以观察到,选用MFCC倒谱分析获取的特征,配合以模糊C均值的聚类方案,在所有的单个脉搏信号粗分类上,都获得了较佳的效果。
|
Download:
|
| 图 6 3种特征方案对单脉搏信号的准确分类数量 Fig. 6 Accurate classification of single pulse signals by three feature schemes | |
在中医研究中,脉象是对人体机能的状况进行分析的重要指标之一。一个有经验的中医,可以通过脉象的模式变换,判断出病症的紧迫性、位置和相应的性征。脉诊的客观化也是中医客观化研究中的一个重点。本文提出的一种客观化的方法,首先是通过脉象信号取漂移预处理,然后进行归一化,再通过频域信息特征的提取和分析,然后用其作为脉象信号识别过程中的输入向量,再采用模糊C均值的聚类方法,对脉象的信号进行识别。作为一种无监督的分析方法,它可以在没有中医专家的参与下,进行脉象信号的粗分类的识别。也可以作为有监督时特征提取的依据,进行进一步优化研究。
本文旨在提出了一个无监督的脉诊客观化方法。在中医专家对数据进行标注之前,先根据信号的特征,进行粗线条分类,为客观化提供依据。同时,在解决医疗资源不匹配的问题上,粗分类可以扮演一个先期分诊的作用,可以用于人群分类的脉诊预判断(比如孕妇与非孕妇,心脏病人与心脏健康人群)。在大数据的时代背景下,在医院拥有更大规模的数据情况后,可以将无监督的算法进一步细化,从而为节省医疗资源,提高分诊效率,做出进一步的贡献。
| [1] |
魏红, 徐刚. 从中医整体、动态、平衡观论脉诊客观化研究[J]. 中医杂志, 2014, 55(1): 25-27. WEI Hong, XU Gang. Research on objectifying pulse examination from overall, dynamic and balanced view of traditional Chinese medicine[J]. Journal of traditional Chinese medicine, 2014, 55(1): 25-27. (  0) 0)
|
| [2] |
刘磊, 吴秋峰, 张宏志, 等. 脉诊客观化研究综述[J]. 智能计算机与应用, 2013, 3(3): 20-24. LIU Lei, WU Qiufeng, ZHANG Hongzhi, et al. The objectification research of pulse diagnosis[J]. Intelligent computer and applications, 2013, 3(3): 20-24. (  0) 0)
|
| [3] |
洪光, 高丹. 中医脉诊客观化发展探析[J]. 国际中医中药杂志, 2016, 38(10): 869-871. HONG Guang, GAO Dan. Introduction and reflection on the current status of objectification of Chinese pulse diagnosis[J]. International journal of traditional Chinese medicine, 2016, 38(10): 869-871. DOI:10.3760/cma.j.issn.1673-4246.2016.10.002 (  0) 0)
|
| [4] |
李凯. 脉搏信号采集系统设计及算法研究[D]. 天津: 天津理工大学, 2014. LI Kai. Design of pulse signal collecting system and research of processing algorithm[D]. Tianjin, China: Tianjin University of Technology, 2014. (  0) 0)
|
| [5] |
彭涛. 脉象信号分析与中医脉象证型识别研究[D]. 苏州: 苏州大学, 2008. PENG Tao. Research on analysis of pulse signal and recognition of the tradition Chinese medicine syndrome[D]. Suzhou, China: Soochow University, 2008. (  0) 0)
|
| [6] |
李娜, 邹小娟, 王忆勤. 支气管哮喘与慢性胃炎患者寸口6部脉图的比较研究[J]. 世界科学技术–中医药现代化, 2015, 17(2): 343-349. LI Na, ZOU Xiaojuan, WANG Yiqin. Comparative study on Cun-Kou six-pulse diagram between chronic gastritis and bronchial asthma[J]. World science and technology-modernization of traditional Chinese medicine, 2015, 17(2): 343-349. (  0) 0)
|
| [7] |
张冬雨. 面向脉诊的脉搏信号与血流信号分类研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. ZHANG Dongyu. Research on classification of pulse signal and blood flow signal for pulse diagnosis[D]. Harbin, China: Harbin Institute of Technology, 2010. (  0) 0)
|
| [8] |
郭红霞, 王炳和, 张丽琼, 等. 基于小波包分析和BP神经网络的中医脉象识别方法[J]. 计算机应用研究, 2006, 23(6): 185-187. GUO Hongxia, WANG Binghe, ZHANG Liqiong, et al. Recognition method of TCM pulse-conditions based on wavelet packet analysis and BP neural networks[J]. Application research of computers, 2006, 23(6): 185-187. (  0) 0)
|
| [9] |
ZHANG Shiru, SUN Qingfu. Human pulse recognition based on wavelet transform and BP network[C]//Proceedings of 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). Ningbo, China, 2015: 1–4.
( 0) 0)
|
| [10] |
王群, 李敏, 庞枫骞, 等. 一种基于时变自回归模型的抗运动干扰心率提取算法[J]. 航天医学与医学工程, 2016, 29(1): 14-20. WANG Qun, LI Min, PANG Fengqian, et al. A motion-resistant heart rate extracting algorithm based on TVAR model[J]. Space medicine and medical engineering, 2016, 29(1): 14-20. (  0) 0)
|
| [11] |
于璐. 基于虚拟仪器的脉搏信号处理方法研究及应用[D]. 沈阳: 中国医科大学, 2009. YU Lu. Research and application of pulse signal processing methods based on virtual instrument[D]. Shenyang, China: China Medical University, 2009. (  0) 0)
|
| [12] |
王欣. 中医三部脉象信号的采集及其关联性研究[D]. 天津: 天津大学, 2014. WANG Xin. The relevance of Cun-guan-chi pulse based on a signal collection system[D]. Tianjin, China: Tianjin University, 2014. (  0) 0)
|
| [13] |
徐黎明, 宿明良, 张广福, 等. 关脉信号数学分析法对比研究[J]. 中国中医药信息杂志, 2005, 12(7): 16-19. XU Liming, SU Mingliang, ZHANG Guangfu, et al. Compared investigation of mathematical analyses for guan pulse tracings[J]. Chinese journal of information on TCM, 2005, 12(7): 16-19. (  0) 0)
|
| [14] |
焦琪玉. 脉象信号的特征提取与分类识别[D]. 长春: 长春理工大学, 2014. JIAO Qiyu. The pulse signals extraction and recognition[D]. Changchun, China: Changchun University of Science and Technology, 2014. (  0) 0)
|
| [15] |
张蔚波, 齐淑敏, 杜丽. 基于频域分析的脉搏波信号研究[J]. 山东建筑大学学报, 2010, 25(4): 419-422. ZHANG Weibo, QI Shumin, DU Li. Study of pulse wave based on frequency domain analysis[J]. Journal of Shandong jianzhu university, 2010, 25(4): 419-422. (  0) 0)
|
| [16] |
周红标. 融合语音和脉搏的多模态情感识别研究[J]. 微电子学与计算机, 2015, 32(6): 5-9. ZHOU Hongbiao. Research of multimodal emotion recognition based on speech and pulse signal[J]. Microelectronics and computer, 2015, 32(6): 5-9. (  0) 0)
|
| [17] |
朴尚哲, 超木日力格, 于剑. 模糊C均值算法的聚类有效性评价[J]. 模式识别与人工智能, 2015, 28(5): 452-461. PIAO Shangzhe, CHAOMURILIGE, YU Jian. Cluster validity indexes for FCM clustering algorithm[J]. PR and AI, 2015, 28(5): 452-461. (  0) 0)
|
| [18] |
康家银, 纪志成, 龚成龙. 一种核C-均值聚类算法及其应用[J]. 仪器仪表学报, 2010, 31(7): 1657-1663. KANG Jiayin, JI Zhicheng, GONG Chenglong. Kernelized fuzzy C-menas clustering algorithm and its application[J]. Chinese journal of scientific instrument, 2010, 31(7): 1657-1663. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


