藏棋是藏族人民的传统游戏,主要流传于我国西藏以及十大藏区,是藏族文化宝库中一颗璀璨的明珠[1],是人类社会文化的补充与完善,具有藏族独特的内涵和民族文化特征,深受藏族人民的喜爱[2-3]。藏棋棋种有几十种[4],“久”棋是其中的大棋种,保护及传承得也较好。“久”是藏语译音,是“方”的意思,还有一种说法是拼图的意思。“久”棋的对弈过程分为布局和战斗两个阶段,具有极强的趣味性、竞技性和生命力。布局阶段将棋子布满棋盘,不吃子、不移动棋子。战斗阶段通过移动棋子实现吃子。
“久”棋作为藏族棋类的大棋种,是具有相似棋规棋理的棋类游戏的出色代表,是中华民族的优秀棋类文化的代表。“久”棋分布极广,广泛流行于四川藏区、甘肃藏区等。经考证,青海盛行的夹棋、西藏盛行的国王与大臣棋、内蒙盛行的蒙古战旗、贵州都匀水族传统棋艺等棋种,甚至汉族地区民间的狼吃小羊棋,在棋规棋理上均与“久”棋类似。
机器博弈是人工智能领域最具挑战性的研究方向之一,是人工智能的果蝇[5]。1997年,IBM深蓝战胜了卡斯帕罗夫,国际象棋的计算机博弈取得了机器战胜棋类高手的优异成绩。2016年,谷歌Alpha Go将深度学习应用于围棋博弈,使用政策网络及价值网络对搜索树进行剪枝,取得了机器战胜人类高手的优异成绩[6-7]。Facebook的DarkForest将卷积神经网络和蒙特卡罗树搜索有机结合[8],也具备很高的棋力。2017年,谷歌推出了AlphaGo Zero,采用一种新的自对弈强化学习方法进行训练,训练开始时完全随机下棋,不需要人类棋手知识的指导。AlphaGo Zero仅仅将棋盘上的黑子和白子作为输入,使用一个神经网络进行训练。蒙特卡洛搜索树也更加简洁,仅仅使用一个神经网络进行着法预测和评估[9]。与围棋博弈研究不同,藏棋博弈研究尚处于起步阶段,其博弈算法研究具有很大的发展空间[10]。
现有的藏棋研究文献[11-13]主要关注藏式围棋及其他藏棋的历史、棋规等。也有部分文献[14-17]探讨了夹棋、王宫双门棋、褡裢、杰布杰曾的计算机应用研究。文献[14]首次进行了藏棋研究,开发了全国第一款藏族棋类软件,经考证,该棋种是流行于青海地区的夹棋;文献[15]讨论了王宫双门棋不规则棋盘状态空间表示、着法产生、终局判断等关键问题,给出了基本解决策略;文献[16]开发了“褡裢”,该款藏棋较为简单,适用于小朋友开发智力;文献[17]研究了对弈熵率在藏棋“杰布杰曾”上的应用,通过对弈双方熵率比较,得出国王取胜可能性较高的结论;文献[18]对藏式围棋的博弈搜索算法、局面评估算法等进行了初步研究,开发了一个藏式围棋博弈系统,并将其应用于教学研究中。
上述文献虽然对藏棋的计算机应用进行研究,但多是开发软件,将藏棋信息化,并没有真正从机器博弈的角度研究藏棋,“久”棋的研究文献更是接近于无。
“久”棋在四川阿坝藏族羌族自治州的保护及传承很好,2015年被列为四川省非物质文化遗产名录。本文作者在阿坝地区进行了深入调研及实地考察,采集了约300局有效的对弈数据。通过分析棋谱,提取了“久”棋中的几种常用棋型,分别为棋型命名为三角、三子、二子、对角、四子等。将作者录制的300局对弈数据采用SGF格式进行处理后,建立棋谱库。使用确定有限自动机识别当前盘面及棋谱,使用BM字符串匹配算法将当前盘面与棋谱进行匹配。本文提出了基于棋型的攻防策略进行“久”棋布局及战斗。本文开发了首款“久”棋博弈软件,该软件具有人人对弈、人机对弈、自动录制棋谱功能,邀请了“久”棋高手测试软件,测试结果表明该软件能够正常运行,但是棋力尚待提高。该软件在2016年四川省阿坝县第七届“体彩杯”藏棋比赛的人机对弈项目中运行稳定。
1 “久”棋的棋规“久”棋的棋盘有11路、14路等。常见的是14路棋盘,如图1所示。纵横14条等距平行线,正中的小方格里,有一对角线。布局从对角线开始,向外扩散,当棋盘上所有交叉点都被布满之后,取掉对角上的两颗棋子,进入战斗阶段。棋子只能放置在线与线的交叉点上,方格中不能放入棋子。

|
Download:
|
| 图 1 “久”棋的棋盘 Fig. 1 The board of JIU | |
1)猜先选定黑子或者白子,布局阶段白子先行,战斗阶段黑子先走。
2)布局:白子从棋盘中央对角线的两端任意选一个点布子,接着,黑子在对角线的另外一端布子。双方轮流放子,直至布满整个棋盘的交叉点。
3)战斗:布局完成后,取掉对角上的两颗棋子,进入战斗阶段。战斗阶段,黑子先行走棋。走棋的方式包括:①移动,棋子向紧邻的空交叉点移动一格,上、下、左、右4个方向可以任意移动;②单跳,在己方棋子行走的路线上有一个对方的棋子,而且与对方棋子相邻的点上没有棋子时就可以跳过对方的这个棋子把它吃掉;③连跳,连续多个单跳,吃掉己方行走路线上所有对方的子,棋子落到空交叉点上。在移动、单跳、或者连跳结束后,如果已方形成一个方(4个同色的棋子形成一个正方形),则在对方的任意位置吃掉对方一个子。因此,在布局及战斗中,已方要尽力成方,同时阻止对方成方。
4)阵型:“久”棋共有160种阵型及其变形。常见的有褡裢阵、拉萨阵、枪阵、经轮阵、鞋阵、烧阵、恰阵等。褡裢阵是“久”棋中非常重要的阵型,该阵型对棋的输赢影响重大。褡裢分为单褡裢和双褡裢,如图2所示。单褡裢阵由7个棋子或者8个棋子组成。7个棋子形成的褡裢阵如图2中左上、左下所示,该阵型中移动中间一颗黑棋就可成方。8个棋子形成的褡裢阵如图2中右上所示,将该阵型中最下方的两个棋子中的任意一个移动至空交叉点,即可成方。十个棋子形成的褡裢阵如图2右下方所示,该褡裢阵属于双褡裢,战斗力及防御能力比单褡裢更强。

|
Download:
|
| 图 2 褡裢 Fig. 2 Dalian | |
本文作者在阿坝地区进行了深入调研及实地考察,采集了约300局“久”棋高手的对弈记录。通过分析该记录,发现棋型对“久”棋胜负的影响很大,因此,研究棋型具有重要的意义。本文提取了常用棋型,设计了针对某棋型的应对策略。
1)三角棋型
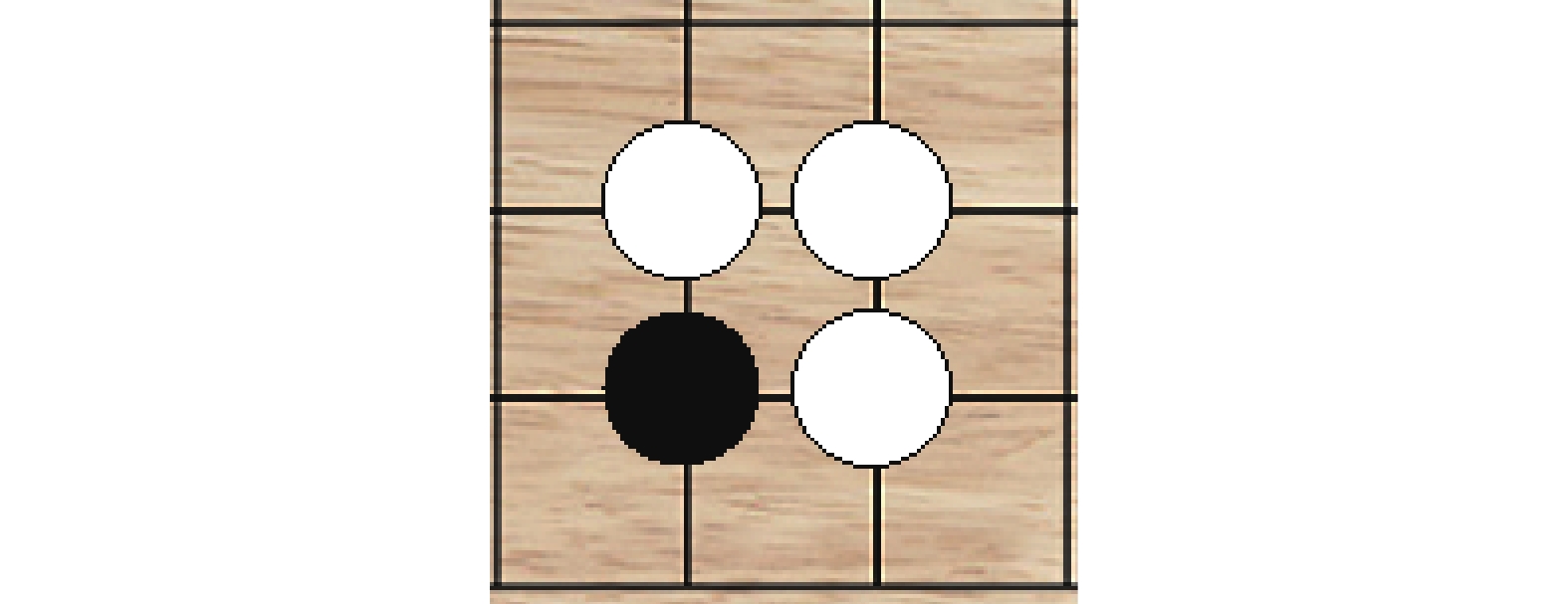
三角棋型是在对方成方之前,出现一个缺口的棋型,如图3中白色三子。应对策略是阻止白色棋子成方,把缺口填上,将黑子布置在图3所示位置。
|
Download:
|
| 图 3 三角棋型及其对策 Fig. 3 Triangle form and its tactics | |
2)三子棋型
三子棋型是在同一直线上摆放三个同色棋子,如图4中白子。若白棋走在图中黑子位置,白棋就能做出两个棋门,威力很大。因此,应对该棋型的策略是如图4所示,阻止白棋形成两个三角棋型。

|
Download:
|
| 图 4 三子棋型及其对策 Fig. 4 Trinity form and its tactics | |
3)二子棋型
二子棋型是指两个棋子周围均没有己方的棋子,如图5白色二子所示。

|
Download:
|
| 图 5 二子棋型 Fig. 5 Twain form | |
当某方出现该棋型时,若再下一子,就会变成三子棋型或者三角棋型。
因此,应对该棋型的策略是阻止该棋型成为三子棋型或者三角棋型。
4)对角棋型
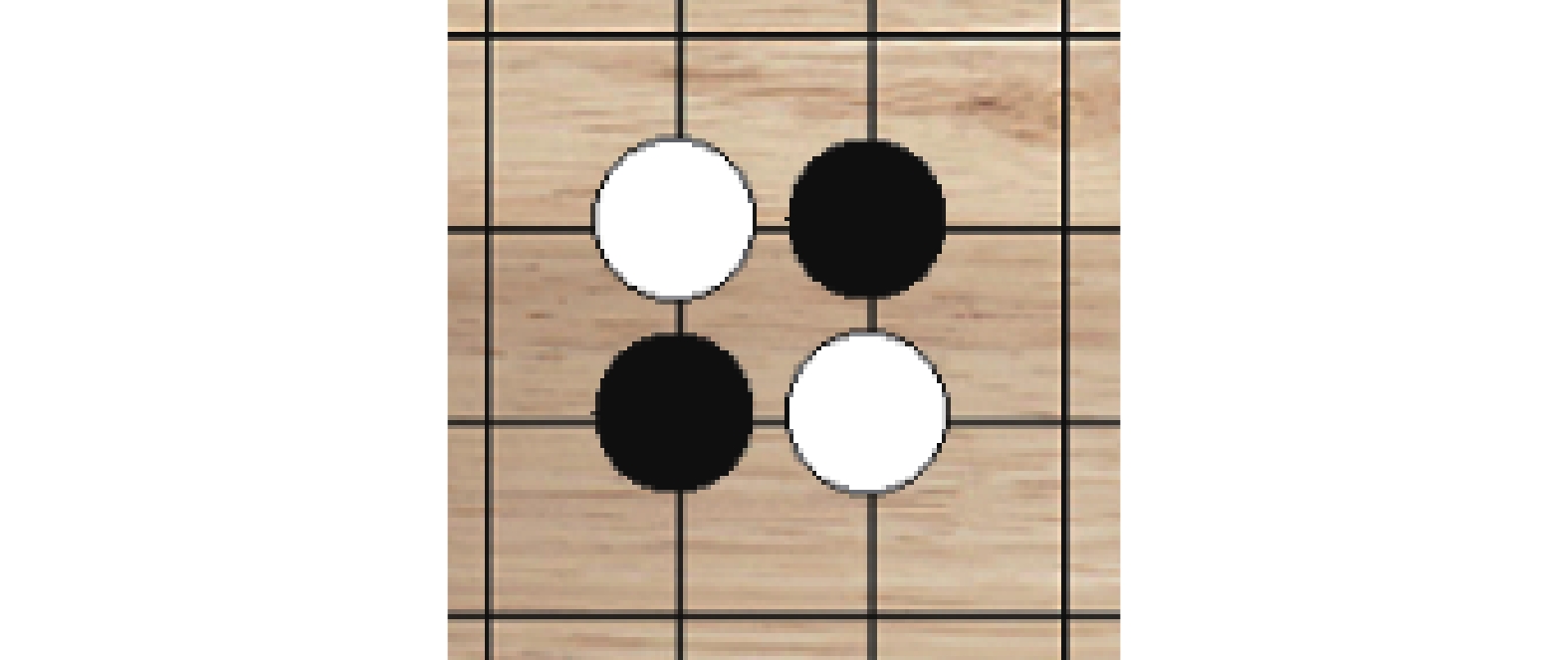
对角棋型是指棋盘上同色两子成90°夹着异色棋子的阵型。如图6中黑色二子夹着白色一子。此时,为了阻止黑色棋子布置在白色的对角成方,应将白色棋子下在图6中所示位置进行应对。
|
Download:
|
| 图 6 对角棋型及其对策 Fig. 6 Contrast form and its tactics | |
5)四子棋型
四子棋型是指同色四子形成一个方,如图7中白色的四颗棋子所示。四子棋型是整个战斗阶段中最强的阵型,褡裢、拉萨等阵型都是由此形成。一旦己方形成四子棋型,就可以吃掉棋盘上对方的任意一子。因此,在布局和战斗阶段,己方要尽力使自己形成四子棋型,阻止对方形成四子棋型。

|
Download:
|
| 图 7 四子棋型 Fig. 7 Square form | |
“久”棋中,布局的质量对胜负影响很大,而以棋盘中央对角线为中心的约40步棋的布局几乎决定了整个布局的质量,因此,在布局的前40步,使用模式匹配方法进行布局。具体来说,将录制的300局对弈数据采用SGF格式进行处理后,构建棋谱。使用确定有限自动机表示识别棋谱,使用BM字符串匹配算法进行模式匹配。
由于“久”棋的棋盘与围棋类似,因此借鉴围棋打谱的方式,仿照SGF的格式,建立“久”棋的棋谱文件。
3.1 确定有限自动机识别棋谱及当前盘面棋谱及当前盘面的识别是模式匹配中的重要环节。确定有限状态机(deterministic finite automaton,DFA)能够识别字符串,做出接受或者拒绝的判断[17]。下棋的若干步之间存在依赖关系,因此可以把每一个棋谱看作一个DFA。
把棋谱表示成一个确定有限自动机,如图8。

|
Download:
|
| 图 8 使用确定有限自动机识别棋谱过程 Fig. 8 Deterministic finite automaton to recognize chess record | |
图8中,
BM(Boyer Moore)算法是最为快速的模式匹配算法之一[18],因此,本文采用BM算法对棋谱及当前局面进行模式匹配。待匹配字符串为长度为
“久”棋中,模式匹配算法的伪代码如下:
private coordinate sgfmatch(inti) {
changtodfa;//把棋局的下子顺序变成DFA格式
List<Integer> matches =BoyerMoore.match(strb, str[i]); //使用BM算法对所有存在的棋谱与当前棋局相匹配
for (Integer integer : matches) {
i=str[i].charAt(integer+strb.length()+2)-'a';
j=str[i].charAt(integer+strb.length()+3)-'a';
}
}//去除所有相匹配的棋局的下子策略
4 基于棋型的攻防策略“久”棋布局阶段的质量对弈棋胜负影响很大,棋盘中央对角线附近约40步棋的棋子布局又直接决定一盘棋布局的好坏。战斗阶段,哪一方最先形成褡裢,哪一方就具有明显的赢棋优势。在布局及战斗阶段,好的棋型非常重要。本文设计了基于棋型的攻防策略,分别应用于“久”棋布局及战斗阶段。
4.1 基于矩阵的棋型识别方法对于上述提出的棋型,本文提出了基于矩阵的棋型识别方法,具体如下。以三角棋型为例,定义矩阵TS如式(1)所示:
| ${\bf{TS}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&1 \end{array}} \right]$ | (1) |
式中:0是该位置为空,1是该位置为白棋,2是该位置为黑棋。当前棋局的矩阵TB如式(2)所示。
| ${\bf{TB}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&2&0&1&0&0&0&0&0 \\ 0&0&0&0&0&0&1&1&1&0&0&0&0&0 \\ 0&0&0&0&0&2&0&2&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \end{array}} \right]$ | (2) |
把矩阵TS扩充成与TB规模相同的矩阵TSE,如式(3)所示:
| ${\bf{TSE}} = \left[ {\begin{array}{*{20}{c}} \!\!\! 0&1&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\! 1&1&0&0&0&0&0&0&0&0&0&0&0&0 \!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \! \!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \! \!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \! \!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\!\! \\ \!\!\! 0&0&0&0&0&0&0&0&0&0&0&0&0&0 \!\! \!\end{array}} \right]$ | (3) |
根据矩阵乘法的性质,把棋型矩阵扩展后的TSE和矩阵TB的转置矩阵相乘,如式(4):
| ${\bf{TR}} = {\bf{TSE}} \cdot {{\bf{TB}}^{\rm{T}}}$ | (4) |
如果相乘的结果TR和TSE相等,则当前的局面中存在三角棋型。同理,其他棋型也能通过上述的方法进行识别。
4.2 布局阶段的攻防策略布局阶段,设计3种策略:防守、攻击、连子,3种策略的优先级别从高到底,即防守策略有效时,进攻和连子策略不考虑,进攻策略有效时,连子策略不考虑。防守策略主要基于三子棋型、三角棋型及对角棋型。攻击策略主要基于二子模型。连子策略是在最新下的子的周围随机选择落点。
每种策略中,针对不同棋型,赋予不同的评估分值。防守策略中,三子棋型为5分,三角棋型为4分,对角棋型为3分。攻击策略中,二子棋型为5分。
4.3 战斗阶段的攻防策略在战斗阶段,使用式(5)的评估方法:
| ${\rm{Eva}} ={\rm{ move}} + {\rm{kill}} + {\rm{triple}} + {\rm{square}}$ | (5) |
式中:move为移动的评分,kill为单跳吃(连跳吃)的总评分,triple为是否阻止敌方成为四子棋型的总评分,suqare为己方在跳吃或者移动以后成为四子棋型的总评分。
根据上述的策略评估方法,在布局阶段和战斗阶段,可以选出较优的攻防策略。
5 “久”棋博弈软件的设计和实现“久”棋博弈软件由布局阶段和战斗阶段组成。软件的整体设计如图9所示。布局界面接受用户点击,把棋子下到界面上某位置,并标记下子的顺序。战斗界面接受用户的点击,实现提子和下子的功能,并判断下子后是否形成方,询问用户是否吃子。

|
Download:
|
| 图 9 程序结构 Fig. 9 Program structure | |
布局阶段的引擎由棋型匹配、防御策略、攻击策略、连子策略组成。
布局阶段的伪代码如下:
voidplaygame(){
FormGet();//从棋谱数据库中获取棋型
if(棋谱数据库中无棋型)
defense(b);//先采取防守策略
if(局面安全){//判断需不需要防守,局
面安全则进攻
attack(b);
}
elseif(没有防守的策略和进攻策略){
chain(b);//连子策略
}
}
//防守策略:
Publicbooleandefense(board b){
tribe(i,j); //检测三子棋型
triangle(i,j); //检测横三角棋型
contrast(i,j); //检测对角棋型
sortMapByValue(); //排序权值
}
//进攻策略:
Publicbooleanattack(board b){
twochess(i,j); //检测二子棋型
}
//连子策略:
public voidChain(board b) {
Getchain(); //随机选出最新下子方向
}
5.2 战斗引擎内核战斗阶段引擎由提取活动子、活动棋子所有方案计分、排序选出最高分的方案、实施方案4部分组成。战斗阶段伪代码如下:
Voidplaygame(){
activechess();//获取所有活动棋子
scoring();//计算活动棋子所有方案
getmaxscore();//排序取出最高分
carryout();//实施最高分策略
}
private void activechess(board b) {
for(inti=0;i<196;i++){
//是否能移动
if(moveable(b,pi,pj,pcolor))
record(pi, pj); //能移动就记录
//是否能跳吃
else if(eatable(b,pi,pj,pcolor))
record(pi, pj); //能吃子就记录
}
}
private void scoring(board b) {
if(eatable()) //判断4个方向是否能跳吃
if(eatable()){
scoring(); //跳吃后坐标进行递归
Eva=move+kill+triple+square;
}
if(moveable()) //判断4个方向上是否能走子
Eva=move+kill+triple+square;//走子计分
}
private void getmaxscore() {
for(inti=0;i<counts;i++){
compare(); //比较各个方案的积分,取出最大的积分
}
}
private void carryout(board b) {
while(解决方案未遍历完)
b.set(pi, pj); //把方案实施到棋盘上
}
6 测试及分析本文邀请四川省阿坝藏羌自治州阿坝县藏棋协会的原会长尼玛扎华先生、副会长甲花先生、拉萨藏棋协会的秘书长阿旺边巴老师、拉萨棋手白姆顿珠、中央民族大学藏族学生闹塔与软件对弈了100局,其中软件获胜25局。
邀请的测试选手均为“久”棋高手,尤其是阿坝藏棋协会的尼玛扎华先生及甲花先生的弈棋水平极高,本文的博弈软件提取的棋型还非常有限,采集的棋谱也较少,没有运用机器学习方法,因此棋力还不是很高。
此外,2016年,使用该软件在四川省阿坝藏族羌族自治州第七届“体彩杯”藏棋比赛中开展了人机对弈项目,进行了20局的人机对弈,软件运行稳定,表现良好。
7 结束语“久”棋是藏族棋类中保存及传承较好的棋类游戏之一,2015年,“久”棋被列为四川省非物质文化遗产名录。象棋、围棋的计算机博弈取得了机器战胜人类的优异成绩,但是“久”棋的机器博弈研究尚处于起步阶段。本文提取了“久”棋的常用棋型,提出了基于棋型的攻防策略,将基于BM的模式匹配算法应用于布局的前40步。开发了博弈软件,由于提取的棋型有限,采集的对弈数据较少,该软件的棋力无法与“久”棋高手对弈,但是运行稳定,功能齐全。AlphaGo Zero不需要人类知识,只训练一个神经网络,采用增强学习与蒙特卡洛树搜索相结合,完胜AlphaGo。借鉴AlphaGo Zero的思路,集合硬件设施条件,开展“久”棋的博弈研究工作,将有可能为未来“久”棋博弈研究提供重要思路。
| [1] |
刘强. 藏族传统棋艺现状及推广价值[J]. 当代体育科技, 2012, 2(27): 83-84. LIU Qiang. The status and promotion value of traditional Tibetan chess[J]. Contemporary sports technology, 2012, 2(27): 83-84. (  0) 0)
|
| [2] |
张月娟, 苟小江. 西藏高校引入藏族传统体育项目注意的问题[J]. 当代体育科技, 2014, 4(23): 130-132. ZHANG Yuejuan, GOU Xiaojiang. The attention of tibetan traditional sports introduced in Tibet college[J]. Contemporary sports technology, 2014, 4(23): 130-132. (  0) 0)
|
| [3] |
德康·索朗曲杰译, 约翰·帕日柏林著. 围棋在世界屋脊[J]. 西藏研究, 1994, 3: 153-157. ( 0) 0)
|
| [4] |
更堆. 浅淡西藏" 密芒”围棋的发现和相关传统藏棋种类[J]. 西藏大学学报: 汉文版, 2003, 18(3): 44-48. GENG Dui. On the discovery of Tibetan Chess (Mimang) and related traditional Tibetan chesses[J]. Journal of Tibet university: chinese edition, 2003, 18(3): 44-48. (  0) 0)
|
| [5] |
徐心和, 邓志立, 王骄, 等. 机器博弈研究面临的各种挑战[J]. 智能系统学报, 2008, 3(4): 288-293. XU Xinhe, DENG Zhili, WANG Jiao, et al. Various challenging issues faced to computer game research[J]. CAAI transactions on intelligent systems, 2008, 3(4): 288-293. (  0) 0)
|
| [6] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2016, 518: 529-533. ( 0) 0)
|
| [7] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529: 484-489. DOI:10.1038/nature16961 ( 0) 0)
|
| [8] |
TIAN Yuandong, ZHU Yan. Better computer goplayer with neural network and long-term prediction[EB/OL]. https://arxiv. org/abs/1511.0641.
( 0) 0)
|
| [9] |
SILVER D, SCHRITTWIESER Julian, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550: 354-358. DOI:10.1038/nature24270 ( 0) 0)
|
| [10] |
LI Xiali, DENG Songting. Review of research on computer games for Tibetan chess[C]//IEEE 14th Intl Conf on Dependable, Autonomic and Secure Computing. Auckland, New Zealand, 2016: 97–99.
( 0) 0)
|
| [11] |
李达伟, 关欣. 藏族传统体育项目探究[J]. 沈阳体育学院学报, 2011, 06: 130-132, 142. LI Dawei, GUAN Xin. Exploration on Tibetan traditional sports[J]. Journal of Shenyang sport university, 2011, 06: 130-132, 142. (  0) 0)
|
| [12] |
角巴东主. 对藏族民间棋艺抢救保护的思考[J]. 西藏艺术研究, 2007, 02: 78-82. JOPA Dondrub. Considerations on the rescuing and protecting Tibetan folk chess art[J]. Tibetan art studies, 2007, 02: 78-82. DOI:10.3969/j.issn.1004-6860.2007.02.016 (  0) 0)
|
| [13] |
陈斌. 文化哲学视域中的围棋与藏围棋[J]. 云南师范大学学报: 哲学社会科学版, 2006, 38(2): 1-5. CHEN Bin. A comparison of the i-go cultures between the han and the Tibetan from the perspective of cultural philosophy[J]. Journal of Yunnan normal university: philosophy and social sciences edition, 2006, 38(2): 1-5. (  0) 0)
|
| [14] |
尖扎夏贝. 藏族围棋软件的设计与实现[D]. 西宁: 青海民族大学毕业论文, 2011.
( 0) 0)
|
| [15] |
裴生雷. 王宫双门棋博弈系统中的关键问题研究[J]. 微计算机信息, 2012, 10: 461-462. PEI Shenglei. Study of key issues in the palace two-door chess game system[J]. Microcomputer information, 2012, 10: 461-462. (  0) 0)
|
| [16] |
仁增多杰, 安见才让. " 褡裢”藏棋的设计与实现[J]. 信息与电脑(理论版), 2014, 08: 106-107. ( 0) 0)
|
| [17] |
范忠雄. 对弈熵率在藏棋" 杰布杰曾”上的应用[J]. 西藏大学学报: 自然科学版, 2014, 01: 67-70. FAN Zhongxiong. Entropy rate of chess game-Tibetan Jiebujiezeng[J]. Journal of Tibet university: natural science, 2014, 01: 67-70. (  0) 0)
|
| [18] |
王昕杨. 藏式围棋博弈软件及其教育应用技术研究[D]. 北京: 中央民族大学硕士生毕业论文, 2016.
( 0) 0)
|
| [19] |
洪晓蕾. 模糊有限自动机及其最小化问题[D]. 成都: 四川师范大学, 2007: 1–15. HONG Xiaolei. Fuzzy finite automata and their minimizations[D]. Chengdu: Sichuan Normal University, 2007: 1–15. (  0) 0)
|
| [20] |
张红梅, 范明钰. 棋型匹配BM算法改进[J]. 计算机应用研究, 2009, 09: 3249-3252. ZHANG Hongmei, FAN Mingyu. Improved algorithm for BM string matching[J]. Application research of computers, 2009, 09: 3249-3252. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


