图像分割是图像处理中十分重要的研究内容，图像分割的质量将对后续的特征提取、图像识别等工作产生直接的影响。模糊C均值(FCM)算法^[1]是模糊聚类中最经典的方法，目前已广泛应用于医学、遥感影像分割^[2-6]等方面。考虑到实际应用中图像像素的归类具有不确定性，FCM算法利用模糊隶属度来衡量像素归属于某一类的程度，克服了传统硬聚类方法将像素归类一刀切的缺陷。然而，FCM算法在应用于图像分割时仍存在一些缺陷：计算复杂度高、对聚类初值和噪声敏感、未考虑空间邻域信息。

为弥补这些不足，国内外诸多学者进行了大量的研究工作以改进FCM算法的性能。针对FCM算法计算效率较低的问题，现有改进方法主要从减少迭代次数和降低数据集维度两方面进行加速，如基于图像灰度级的FCM算法^[7]，利用图像灰度级远小于像素个数的特性，采用一种线性加权和图像代替原图像进行迭代计算，大大减少了参与计算的像素个数，进而提高了计算速度，但算法的分割精度有所下降。针对FCM算法对初始聚类中心敏感的问题，Sikka等^[8]充分利用直方图的统计特性，通过检测直方图中各灰度区间内的局部峰点来确定初始聚类中心和聚类数，并对脑肿瘤图像进行分割，取得了比较准确的分割结果。鉴于智能优化算法具有良好的全局搜索能力，因此也有学者利用智能优化算法对FCM进行初始化^[9-10]，在加速迭代收敛的同时避免了算法陷入局部最优解。针对FCM算法中欧氏距离对噪声和异常点敏感的问题，国内外学者采用不同的距离测度对欧氏距离进行改进，如核诱导距离^{[5, 11]}、马氏距离^[12]等，以提升算法对噪声的鲁棒性。然而距离测度中各参数(如核函数带宽等)的选取对聚类分割性能具有较大的影响，且计算复杂度随图像规模的增大而增加。

针对FCM算法未考虑空间邻域信息的缺陷，许多学者提出了结合空间信息的改进算法。Ahmed等^[13]提出了一种基于空间邻域约束信息的FCM(fuzzy C-means with spatial constraints，FCM_S)算法，通过在FCM算法的目标函数中引入一空间惩罚项来调节邻域像素对中心像素的影响，提升了FCM算法的抗噪性能，但每次迭代中均需计算图像中各像素的邻域灰度，计算复杂度较高。为解决该问题，Chen等^[14]对其进行了改进，通过融合邻域像素的灰度均值与中值，提出了一种基于邻域均值和中值的空间FCM(FCM_S₁，FCM_S₂)算法，其分别对含有高斯噪声和椒盐噪声的图像具有较好的分割效果。随后，Cai等^[15]提出了一种融合局部空间与灰度差的快速广义FCM(fast generalized fuzzy C-means，FGFCM)算法，将各邻域窗口中像素的局部空间距离与灰度差信息同时引入到FCM算法中，在保证计算速度的条件下增强了算法对噪声的鲁棒性。但该方法引入了两个额外参数，需进行人为设置，且参数选取的好坏将直接影响算法的分割效果。文献[16]提出了一种基于灰度与空间特征的FCM图像分割算法，从修改像素空间隶属度的角度出发，利用像素的灰度相似度与空间邻域分布信息构造出新的空间隶属函数，提升了算法对噪声的抑制能力，具有良好的聚类性能。除此之外，近年来涌现出一些结合图像局部熵^[17-18]、非局部均值去噪^[19-20]、中智学^[21-22]等理论的先进方法。这些改进方法尽管在分割性能和抗噪性能方面取得了较大幅度的提高，但都具有较高的计算复杂度，实时性较差。

针对以上问题，本文采取一种自适应权重分配的策略，合理地为邻域窗口中的各像素赋予相应的权重；同时采用一种改进的距离测度代替原始的欧氏距离，进而提出一种自适应灰度加权的鲁棒模糊C-均值算法(adaptive gray-weighted based robust fuzzy C-means algorithm，AGWRFCM)。对不同图像的分割结果表明，该算法能够在不同强度的噪声条件下获得良好的分割性能。

1 模糊C均值算法

考虑由n个p维样本组成的数据集 ${{X}} = \{ {x_1},{x_2}, \cdots ,$ ${x_n}\} \in {{\rm{R}}^{n \times p}}$ ，FCM算法旨在最小化目标函数 ${J_m}$ 以完成对样本数据的模糊划分，即

${J_m}({{U}},{{V}}) = \sum\limits_{k = 1}^c {\sum\limits_{i = 1}^n {u_{ki}^m} } {\left\| {{{{x}}_i} - {{{v}}_k}} \right\|^2}$

(1)

式中： ${{U}} = \{ {u_{ki}}\} \in {{\rm{R}}^{n \times c}}$ 为隶属度矩阵，满足 $\displaystyle\sum\limits_{k = 1}^c {{u_{ki}}} = 1,$ $\forall i = 1,2, \cdots ,n$ ， ${{V}} = \{ {v_1},{v_2}, \cdots ,{v_c}\} $ 为聚类中心集合， $c \in [2,n]$ 为聚类数目， $m \in [1, + \infty )$ 为模糊指数，常取 $m = 2$ 。利用Lagrange乘子法对 ${J_m}$ 进行迭代更新，以实现目标函数的最小化，即

${u_{ki}} = \frac{{{{\left\| {{{{x}}_i} - {{{v}}_k}} \right\|}^{ - 2/(m - 1)}}}}{{\displaystyle\sum\limits_{j = 1}^c {{{\left\| {{{{x}}_i} - {{{v}}_j}} \right\|}^{ - 2/(m - 1)}}} }}$

(2)

${{{v}}_k} = \frac{{\displaystyle\sum\limits_{i = 1}^n {u_{ki}^m{{{x}}_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {u_{ki}^m} }}$

(3)

反复迭代式(2)~(3)，直至FCM算法收敛。

2 自适应灰度加权的鲁棒模糊C均值图像分割

现有的结合空间信息的FCM改进算法^[13-15]主要存在以下缺陷：1)这些算法并没有充分利用图像中像素分布的特点，在引入空间信息时未能充分考虑到邻域像素对中心像素灰度贡献的差异，对像素灰度的计算不够准确；2)这些算法均引入了额外的空间参数，用于控制邻域像素对中心像素的约束程度，而空间参数需根据经验或大量实验试错来进行确定，这样会极大地增加算法的处理时间，并且若参数选取不佳将会直接影响算法的分割效果^[19]；3)这些算法在计算像素与聚类中心之间的相似距离时均使用欧氏距离测度，难以准确地反映像素与聚类之间的关系，且对噪声和异常点较敏感。

针对以上缺陷，本文主要从两方面对FCM算法进行改进：首先，为充分考虑邻域像素对中心像素影响的差异性，采用一种自适应灰度加权的方法，根据局部窗口中各像素的灰度分布自适应地调节邻域像素对中心像素的权重，使其在计算中心像素的灰度时能够更充分地利用局部信息，以提升像素灰度的计算精度；其次，为更好地反映图像中各像素与聚类中心之间的相似性，用一种改进的距离测度取代传统的欧氏距离测度，以进一步增强算法对噪声的鲁棒性。

2.1 自适应灰度加权

对于一幅数字图像而言，其像素的灰度分布通常具有以下特点：平坦区域内部的灰度分布较为均匀，区域边缘或含噪区域的灰度差异较大，这在医学图像中表现尤为明显。由于人体组织结构的复杂性以及受医学成像中部分容积效应等因素的影响，使得获取的图像往往呈现出含噪较多、对比度低、灰度分布不均匀、目标边界不连续等特性^[18]。因此，在引入像素的空间信息时需考虑局部邻域内各像素对中心像素影响程度的差异性，以进一步提高图像分割的准确性。

首先，对于图像中的任一邻域窗口 ${{{N}}_i}$ ，定义局部灰度相似性测度 ${C_j}$ ，将当前邻域内的各像素与该邻域内所有像素的平均灰度进行比较，即

${C_j} = \left\| {{{{x}}_j} - \bar {{x}}} \right\|,j \in {{{N}}_i}$

(4)

$\bar {{x}} = \frac{1}{{{n_i}}}\sum\limits_{j \in {N_i}} {{{{x}}_j}} $

(5)

式中： ${{{x}}_j}$ 为邻域像素， $\bar {{x}}$ 为邻域像素的平均灰度， ${{{N}}_i}$ 表示以像素 $i$ 为中心的邻域， ${n_i}$ 表示以像素 $i$ 为中心的邻域窗口大小， $\left\| \cdot \right\|$ 表示任一范数。

由式(4)可以看出，对于灰度变化平缓的区域， ${C_j}$ 的值较小；而对于灰度发生突变的区域(如边缘、噪声等)， ${C_j}$ 的值较大。因此 ${C_j}$ 反映了局部邻域内像素灰度分布的均匀程度。

其次，对当前邻域中各像素的 ${C_j}$ 取平均值，作为该邻域的灰度分布度量，即

$\bar C{\rm{ = }}\frac{1}{{{n_i}}}\sum\limits_{j \in {N_i}} {{C_j}} $

(6)

在此基础上定义邻域像素的影响因子 ${\gamma _{ij}}$ ，将各邻域点的 ${C_j}$ 与当前邻域进行比较，即

${\gamma _{ij}} = {C_j} - \bar C,j \in {{{N}}_i}$

(7)

由式(7)可以看出，对于边缘点或噪声点， ${\gamma _{ij}}$ 的值较大，表明该点对当前邻域的影响较大；而对于非边缘点与非噪声点， ${\gamma _{ij}}$ 的值较小，表明该点对邻域的影响较小。因此 ${\gamma _{ij}}$ 决定了局部邻域内各像素灰度的影响程度。

在计算中心像素的灰度值时，对于 ${\gamma _{ij}}$ 值较大的点，应减小其对中心像素灰度计算的影响，反之应增大其影响程度。鉴于指数函数具有较快的衰减速度，故采用指数函数进一步控制邻域像素的影响权重，具体形式为

${w_{ij}} = \exp ( - {\gamma _{ij}}) = \exp ( - ({C_j} - \bar C))$

(8)

式中： ${w_{ij}}$ 为邻域像素 $j$ 相对于中心像素 $i$ 的权重。

由式(8)可知，对于边缘点或噪声点，其对中心像素的影响较大， ${w_{ij}}$ 的值更接近0，且随着 ${\gamma _{ij}}$ 的增加，权重下降幅度更大，从而进一步减小该邻域点的影响程度；而对于非边缘点与非噪声点， ${w_{ij}}$ 能够取得较大的值，从而增大其对中心像素的影响。因此 ${w_{ij}}$ 能够根据邻域像素的灰度差异自适应地为各像素赋予合适的权重，进而达到提高中心像素灰度计算准确性的目的。

最后，利用各邻域点的权重对邻域灰度作线性加权，将其作为该邻域中心像素的灰度值；同时为统一数据的量纲，将权重作归一化处理，得到最终的待聚类图像 ${\tilde {{x}}_i}$ ，即

${\tilde {{x}}_i} = \frac{{\displaystyle\sum\limits_{j \in {N_i}} {{w_{ij}}{{{x}}_j}} }}{{\displaystyle\sum\limits_{j \in {N_i}} {{w_{ij}}} }}$

(9)

2.2 距离测度的改进

传统的欧氏距离无法解决算法对噪声敏感的问题^[23]。核诱导距离^[11]的实质是将像素映射到高维特征空间中进行处理，以提升对高维数据的聚类性能。虽一定程度上弥补了欧氏距离的不足，但其难以克服噪声对聚类性能的影响，对噪声的抑制能力仍不够强，因此核诱导距离也无法从根本上解决对噪声敏感的问题。

为弥补这一不足，本文采用一种改进的距离测度，具体形式为

${d_R}({{{x}}_i},{{{v}}_k}) = \sqrt {1 - R({{{x}}_i},{{{v}}_k})} $

(10)

式中：

$R({{{x}}_i},{{{v}}_k}) = \exp ( - \beta {\left\| {{{{x}}_i} - {{{v}}_k}} \right\|^2})$

(11)

$\beta {\rm{ = (}}\frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left\| {{{{x}}_i} - \bar {{x}}} \right\|}^2}} }}{n}{)^{ - 1}}$

(12)

$\bar {{x}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{{x}}_i}} $

(13)

改进的距离测度建立在鲁棒统计理论的基础上，因此对噪声或异常值具有较强的稳定性^[24]。该距离测度虽然在形式上与核诱导距离类似，但其本质仍然是在原图像空间中进行处理，并未将像素映射到高维特征空间中^[24]。下文实验中将验证这一距离测度对噪声具有较强的鲁棒性，且均优于欧式距离与核诱导距离。

2.3 本文算法

根据以上分析，用 $d_R^2({{{x}}_i},{{{v}}_k})$ 代替式(1)中的 ${\left\| {{{{x}}_i} - {{{v}}_k}} \right\|^2}$ ，再用式(15)代替 $d_R^2({{{x}}_i},{{{v}}_k})$ 中的 ${x_i}$ ，得到本文算法的目标函数 ${J_{{\rm{AGWRFCM}}}}$ ，即

${J_{{\rm{AGWRFCM}}}} = \sum\limits_{k = 1}^c {\sum\limits_{i = 1}^n {u_{ki}^m} } d_R^2({\tilde {{x}}_i},{{{v}}_k})$

(14)

由Lagrange乘子法可得

${u_{ki}} = \frac{{{{[1 - R({{\tilde {{x}}}_i},{{{v}}_k})]}^{ - 1/(m - 1)}}}}{{\displaystyle\sum\limits_{j = 1}^c {{{[1 - R({{\tilde {{x}}}_i},{{{v}}_j})]}^{ - 1/(m - 1)}}} }}$

(15)

${{{v}}_k} = \frac{{\displaystyle\sum\limits_{i = 1}^n {u_{ki}^mR({{\tilde {{x}}}_i},{{{v}}_k}){{\tilde x}_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {u_{ki}^mR({{\tilde {{x}}}_i},{{{v}}_k})} }}$

(16)

AGWRFCM算法的具体步骤如下：

1) 设置聚类数目 $c$ ，模糊加权指数 $m$ ，迭代终止阈值 $\varepsilon $ ，最大迭代次数iter_max，邻域窗口大小 $\omega $ ，当前迭代次数 $t = 1$ ；

2) 初始化隶属度矩阵 ${{{U}}^{(0)}}$ 和聚类中心 ${{{V}}^{(0)}}$ ；

3) 根据式(10)~(15)计算新的灰度图像 ${\tilde {{x}}_i}$ ；

4) 根据式(22)计算新的聚类中心 ${{V}}$ ；

5) 根据式(21)计算新的隶属度矩阵 ${{U}}$ ；

6) 根据式(20)计算新的目标函数值 ${{J}}$ ；

7) 若 $\left\| {{{{J}}^{(t + 1)}} - {{{J}}^{(t)}}} \right\| < \varepsilon $ 或当前迭代次数 $t > $ iter_max，则终止迭代，输出隶属度矩阵 ${{U}}$ 和聚类中心 ${{V}}$ ；否则返回4)，继续下一次迭代。

3 实验结果与分析

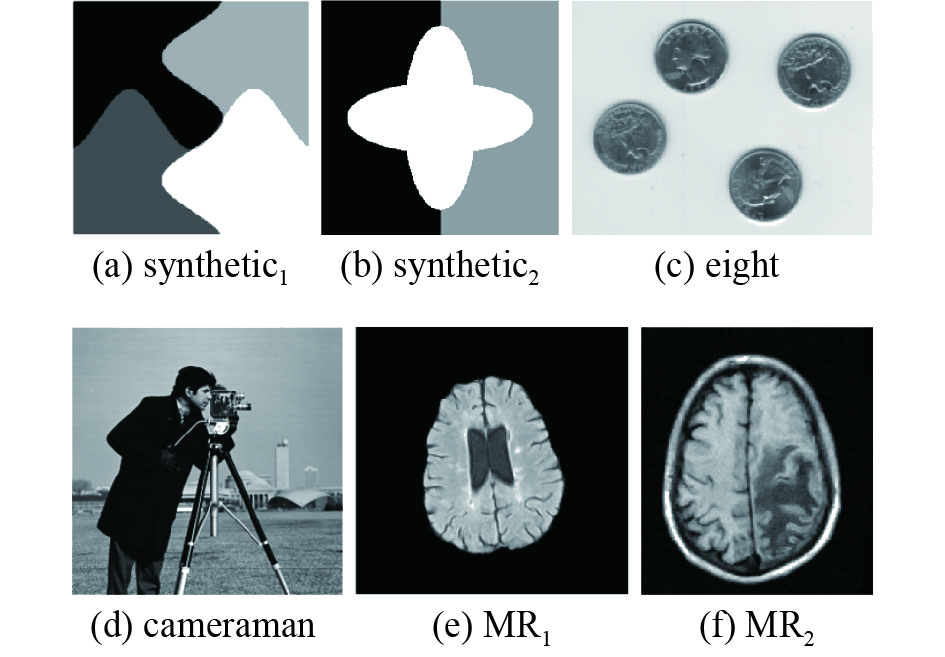
为验证本文算法的有效性，分别采用两组人工合成图像(synthetic₁和synthetic₂)、自然图像(eight和cameraman)和医学图像(MR₁和MR₂)进行实验，将本文算法与FCM_S₁^[14]、FCM_S₂^[14]、EnFCM^[7]、FGFCM^[15]、FLICM(模糊局部信息C-均值，fuzzy local information C-means)^[25]、文献[26](WFCM)几种算法进行对比，以测试算法的分割效果。实验中采用的测试图像如图1所示，几种对比算法中的参数根据文献[7, 14-15, 25-26]进行设置。为获得良好的实验效果，本文实验中的相关参数设置如下： $m = 2$ ， $\varepsilon = {10^{ - 5}}$ ， ${\rm{iter\_max}} = 500$ ，邻域窗口大小 $\omega = 3$ (即3×3邻域)，人工合成图像中 $c = 4$ ，自然图像和医学图像中 $c = 3$ 。其中，迭代终止阈值 $\varepsilon $ 为一较小数，其值通常根据人为经验进行选取。实验环境为MATLAB R2014a，Intel(R) Core(TM) i3-4160 CPU @3.60 GHz，4.00 GB内存。

3.1 分割性能测试

首先对人工合成图像(synthetic₁，244×244)进行分割实验(其中包含0、85、170、2 554个灰度值)。用分割精度(segmentation accuracy，SA^[25])作为算法分割性能的客观评价指标，其定义为

${\rm{SA}} = \sum\limits_{i = 1}^c {\frac{{{A_i} \cap {C_i}}}{{\displaystyle\sum\limits_{j = 1}^c {{C_j}} }}} $

(17)

式中： $c$ 为聚类数， ${A_i}$ 为由分割算法得到的属于第 $i$ 类的像素点集， ${C_i}$ 为标准图像中属于第 $i$ 类的像素点集， ${\rm{SA}}$ 表示正确分类的像素数占图像像素总数的比重。

对该合成图像添加均值为0，方差为25的高斯噪声，采用7种算法对其进行分割，结果如图2所示。通过对比可以看出，EnFCM算法的分割结果图中包含的噪声点最多，这是因为EnFCM算法中未引入像素的空间邻域信息，对噪声的抑制能力不强，因此该算法在含噪条件下的分割效果欠佳；FGFCM算法在EnFCM算法的基础上引入了邻域像素的空间信息和灰度差，一定程度上提升了算法的抗噪性，因此其分割效果优于EnFCM算法，但图像中仍含有较多的噪声点，在含噪条件下的分割性能还不够高；FCM_S₁、FCM_S₂算法结合了邻域像素的灰度均值和灰度中值，分割结果图中平坦区域较为平滑，但仍带有少量噪声，且图像边缘处存在大量的噪声点，因此分割结果不够理想；FLICM算法在目标函数中添加了包含空间局部信息的模糊因子，更多地考虑了像素的空间信息，因此分割质量较高，视觉效果较好。但其未能很好地保持边缘细节，导致图像中出现了较多的伪边缘，产生了过平滑现象，因此该算法的分割效果仍不够理想；WFCM算法通过引入当前像素及其周围像素的灰度差来反映各像素对分类的影响权重，其仍是对原图像进行分割处理，并且目标函数中采用的是欧氏距离测度^[26]，对噪声十分敏感，分割图像中仍包含大量噪声点，因此WFCM算法难以有效地分割含噪图像；而AGWRFCM算法是采用灰度加权后的新图像进行分割，同时采用改进的距离测度进行计算，分割结果十分接近原始图像，分割出的各区域连续性强，边缘更清晰，很好地平衡了噪声抑制和边缘保持之间的关系，不论是在视觉质量还是在分割性能方面均优于其他几种算法。

表1中同时给出了各算法在噪声强度逐级递增( $\sigma = 25,35,45,50$ )时的 ${\rm{SA}}$ 值。从中可以看出，随着噪声强度的增加，几种对比算法的分割精度明显下降，而AGWRFCM算法仍然能够取得较高的分割精度。

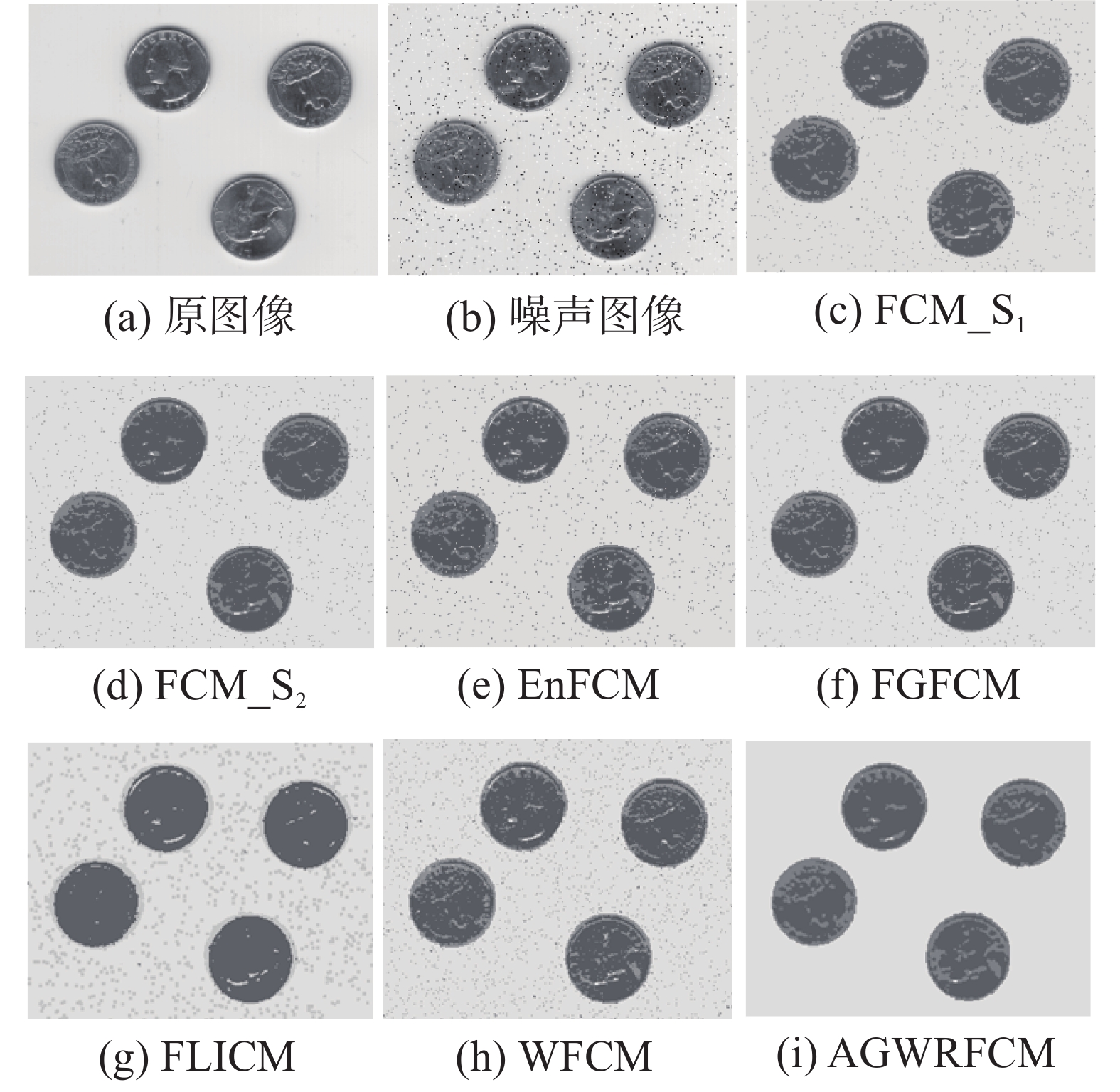
其次，对自然图像(eight，242×308)添加强度为0.02的椒盐噪声，使用7种算法分别对其进行分割，结果如图3所示。

从图3中可以看出，FCM_S₁、FCM_S₂、EnFCM、FLICM以及WFCM算法的分割结果图中均含有较多的噪声点，对噪声较为敏感，且FLICM算法未能很好地将硬币中的纹理细节分割出来，因此这些算法对硬币图像的分割效果均不佳；FGFCM算法虽能在一定程度上减弱噪声的影响，但其对噪声的抑制能力有限；而AGWRFCM算法可以很好地消除噪声的影响，且对硬币中的纹理细节分割较为合理，这表明本文算法能够获得较好的分割效果。

为进一步评价本文算法的分割性能，采用划分系数(partition coefficient， ${V_{\rm{pc}}}$ )^[27]、划分熵(partition entropy， ${V_{\rm{pe}}}$ )^[27]以及聚类有效性指数(Xie-Beni index， ${V_{\rm{xb}}}$ )^[28]3种评价指标对算法的聚类性能进行定量评价，分别定义为

${V_{\rm{pc}}} = \frac{{\displaystyle\sum\limits_{k = 1}^c {\sum\limits_{i = 1}^n {u_{ki}^2} } }}{n}$

(18)

${V_{\rm{pe}}} = - \frac{{\displaystyle\sum\limits_{k = 1}^c {\sum\limits_{i = 1}^n {{u_{ki}}\log {u_{ki}}} } }}{n}$

(19)

${V_{\rm{xb}}} = \frac{{\displaystyle\sum\limits_{k = 1}^c {\sum\limits_{i = 1}^n {u_{ki}^2{{\left\| {{{{x}}_i} - {{{v}}_k}} \right\|}^2}} } }}{{n({{\min }_{j \ne k}}\{ {{\left\| {{{{v}}_j} - {{{v}}_k}} \right\|}^2}\} )}}$

(20)

由式(18)～(20)可知， ${V_{\rm{pc}}}$ 和 ${V_{\rm{pe}}}$ 反映出划分矩阵的模糊程度， ${V_{\rm{pc}}}$ 越大，计算出的划分矩阵模糊性越小，像素的归类越明确，分割效果越好；同理， ${V_{\rm{pe}}}$ 越小，算法的分割性能越好。而 ${V_{\rm{xb}}}$ 则反映出各聚类之间的关联程度， ${V_{\rm{xb}}}$ 越小，同类中各像素之间的紧密性越高，不同类之间的关联性越低，其聚类性能越好。

表2列出了7种算法对自然图像eight的划分系数 ${V_{\rm{pc}}}$ 、划分熵 ${V_{\rm{pe}}}$ 以及聚类有效性指数 ${V_{\rm{xb}}}$ 。由表2可以看出，与其余5种算法相比，AGWRFCM算法具有更高的 ${V_{\rm{pc}}}$ 值和更低的 ${V_{\rm{pe}}}$ 值，这表明由AGWRFCM算法计算得到的隶属度矩阵划分性能更好，分割精度更高；同时AGWRFCM算法具有更高的 ${V_{\rm{xb}}}$ 值，表明类内像素的空间紧致性更好，不同类像素的空间分离性更强，因此AGWRFCM算法具有良好的聚类性能。

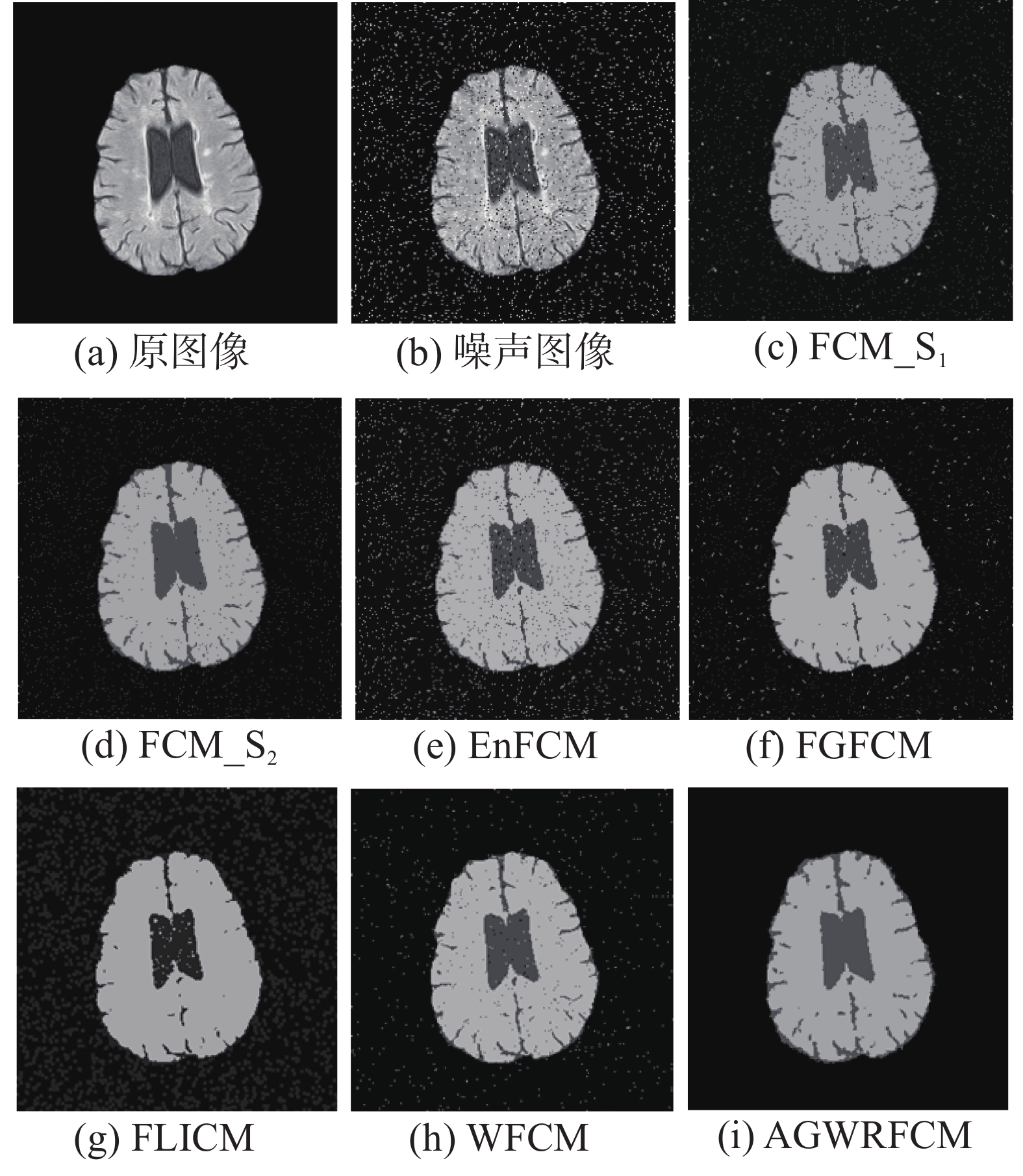
最后，对医学MR图像(MR1，256×256)^[29]添加强度为0.08的椒盐噪声，分割结果如图4所示，各算法的划分系数 ${V_{\rm{pc}}}$ 、划分熵 ${V_{\rm{pe}}}$ 以及聚类有效性指数 ${V_{\rm{xb}}}$ 如表3所示。

由图4可以看出，在分割含噪医学MR图像时，FCM_S₁、FCM_S₂、EnFCM、FGFCM、FLICM以及WFCM算法分割图中的背景噪声仍然较多，抗噪性能较差，且FLICM算法分割出的脑组织内部结构细节信息丢失较严重，因此无法精确地将MR脑组织分割出来；而AGWRFCM算法既能很好地抑制噪声，又能保留更多的图像细节，且表3中的数据也充分反映出AGWRFCM算法具有更优的聚类分割性能。因此，本文算法对医学图像也能够取得良好的分割效果。

3.2 改进距离测度的抗噪性测试

由于本文中采用了一种改进的距离测度来计算相似距离，因此为测试该距离测度对噪声的鲁棒性，需将其与传统的欧氏距离和核诱导距离进行对比，即在本文算法中分别使用欧氏距离(AGWFCM)、核诱导距离(AGWKFCM)和改进的距离测度(AGWRFCM)进行实验。

分别对人工合成图像(synthetic₂，256像素×256像素)、自然图像(cameraman，256像素×256像素)、医学MR图像(MR₂，386像素×331像素)^[29]添加不同强度的混合噪声，其中Mixed₁、Mixed₂、Mixed₃、Mixed₄分别表示均值为0，方差为10、20、30、40的高斯噪声与椒盐噪声的叠加，并采用峰值信噪比(peak signal-to-noise ratio，PSNR^[22])和平均结构相似度(mean structural similarity index，MSSIM^[30])对上述3种方法的抗噪性能进行客观评价，以进一步验证本文算法对噪声的鲁棒性。实验结果如表4～5所示。

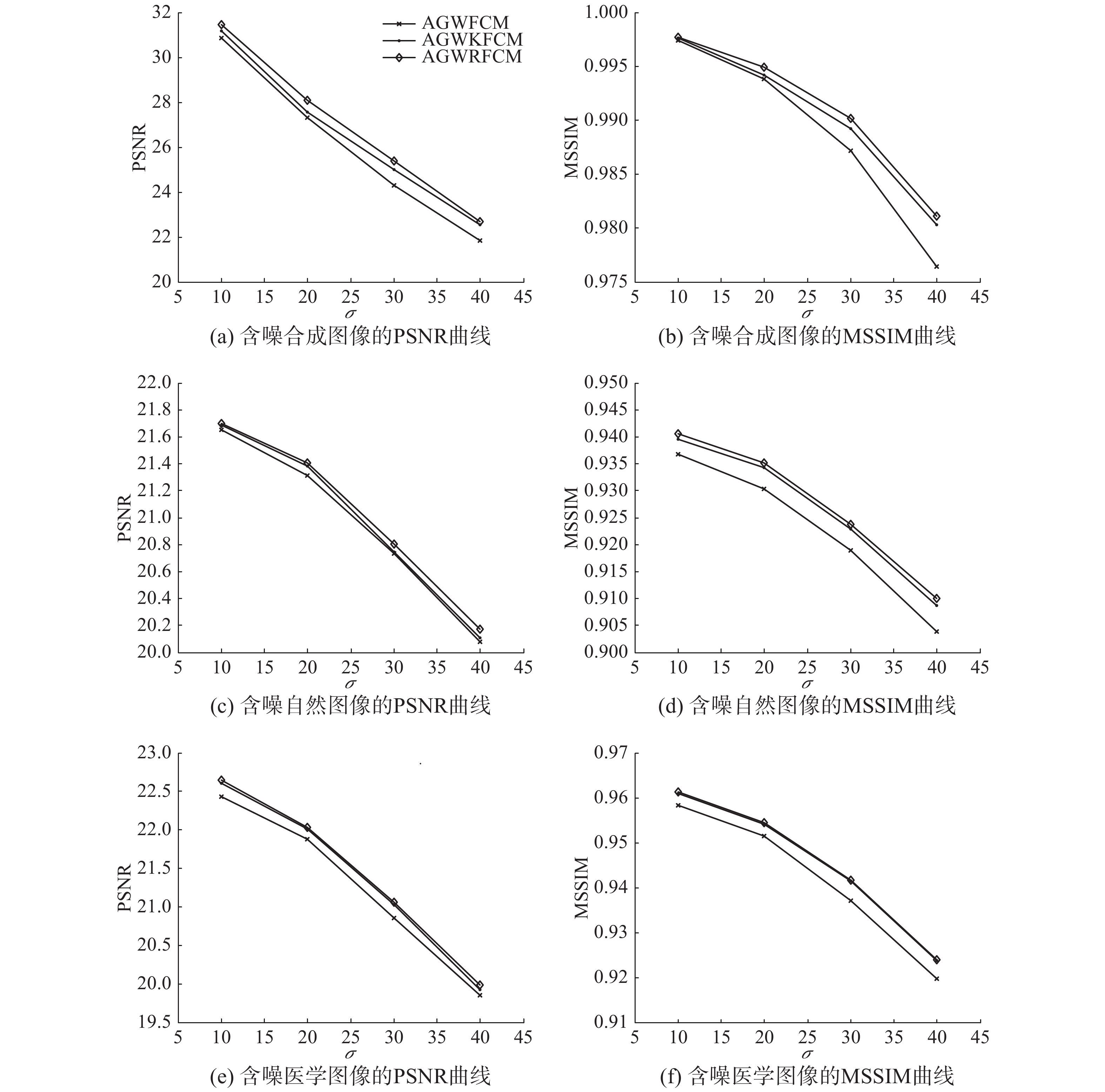
从表4和表5中可以看出，与传统的欧式距离和核诱导距离相比，改进的距离测度在对不同水平的噪声图像进行分割时均获得了更高的PSNR和MSSIM值，且随着噪声水平的提高，PSNR和MSSIM值增加的幅度越来越大。这是由于改进的距离测度能够克服噪声或野值数据对聚类性能的影响，从而增强算法的抗噪能力。据上分析可知采用改进距离测度的FCM算法具有更强的抗噪性。

图5同时给出了3种算法的PSNR和MSSIM曲线。从中可以更直观地看出，改进的距离测度相比于其余两种距离测度而言对噪声具有更强的鲁棒性。因此本文算法在抗噪性能上具有一定的优越性。

3.3 邻域窗口大小 $\omega $ 的选取

改进FCM算法涉及邻域窗口大小 $\omega $ 的选取，不同的窗口大小将会对图像分割的效果产生影响。因此有必要对不同噪声条件下 $\omega $ 的取值进行分析。

表6给出了在不同窗口大小 $\omega $ 下本文算法对人工合成图像synthetic₁的分割精度(其中图像的噪声方差 $\sigma $ 从10～90依次递增)。通过对比可以看出，当 $\sigma \leqslant 50$ 时，选取3×3窗口进行分割具有更高的分割精度；而当 $\sigma > 50$ 时，选取5×5或7×7窗口进行分割可以取得相对较高的分割精度，且随着噪声水平的增加，邻域窗口越大，分割精度越高。若此时仍选取3×3窗口，则分割精度将大幅下降，这是因为图像中包含大量的噪声，3×3窗口不足以抑制强度过高的噪声，因此分割性能较差。然而若邻域窗口选取过大，算法的分割时间将会越长，且容易过多地滤去图像中的纹理细节等特征，从而产生过平滑现象。

综上分析可得，对于较低水平的噪声，可选取3×3窗口进行分割；对于较高水平的噪声，为更好地维持分割精度与分割时间之间的平衡，选取5×5或7×7窗口进行分割较为合适。

3.4 运行时间对比

为比较不同算法的运行效率，表7中列出了7种分割算法对不同图像的处理时间，其中运行时间取10次运行结果的平均值。

从表7中可以看出，本文算法的运行时间远小于FLICM算法，与FCM_S₁、FCM_S₂以及WFCM算法相当，但不如EnFCM和FGFCM算法，这是因为EnFCM和FGFCM算法是基于灰度级的处理，参与计算的像素数远小于图像的像素总数，因此运行效率高于本文算法，但本文算法在视觉效果和分割质量方面均优于这两种算法。

4 结束语

本文提出了一种自适应灰度加权的鲁棒模糊C均值图像分割算法，该算法充分利用邻域像素对中心像素影响的差异性，对局部邻域内的各像素分配合适的权值，以提高像素灰度计算的准确性；同时采用一种改进的距离测度来计算像素与聚类中心之间的相似距离，以提高算法对噪声的鲁棒性。大量仿真结果表明，所提算法相比于经典FCM算法具有更优的分割效果和抗噪性能，且与其他分割算法相比也具有一定的竞争力。然而该算法在进行图像分割时需根据图像噪声的强度选取合适的窗口大小，以取得更好的分割效果，且算法的运行效率较低。因此下一步将致力于研究如何在噪声平滑与边缘保持之间取得更好的平衡，并进一步提升FCM算法的时间性能。