近年来，面向复杂非线性数据的模糊聚类问题得到了研究人员的广泛关注^[1-6]。在无监督学习环境中为了提高复杂非线性数据的可分性，一个重要的研究思路是使用非线性映射将数据映射到高维空间中。在众多非线性映射方法中，核方法作为经典的隐性映射方法得到了广泛的应用^[5-13]。研究表明，核方法通过使用核函数代替内积运算，将待分类数据隐性地映射到高维空间，从而有助于复杂非线性数据的学习。但是，核方法还存在着诸多局限性，尤其是如何针对不同的问题选择合适的核函数和相关参数，这都会影响算法的聚类效果。

模糊系统因其强大的不确定性系统建模能力、优良的可解释性和出色的泛化能力，近年来在复杂非线性数据学习问题中得到了大量的研究。在已有的经典模糊系统中，Takagi-Sugeno-Kang(TSK)^[14-17]模糊系统由于其良好的解释性和简洁性得到了广泛应用。在TSK模糊系统中，其规则前件部分通过显性映射方式(本文称之为模糊特征映射)，将输入数据映射到高维空间中去。从本质上讲，模糊特征映射可以视为一种特殊的非线性映射方式。基于此，本文将输入数据进行相应的非线性映射。在具体实现过程中我们发现，经模糊特征映射后的特征维数过高，这会增加计算量，同时也导致了数据的冗余。为此，本文通过引入多层递阶融合机制和主成分分析，提出新型的基于多层递阶融合的模糊特征映射新方法。并将之与经典模糊聚类技术相结合，进一步提出基于多层递阶融合模糊特征映射的模糊C均值聚类新方法。经实验验证，本文算法在处理复杂非线性数据时能够取得比传统模糊聚类算法更有效的聚类效果。

1 Takagi-Sugeno-Kang模糊系统及模糊特征映射

Takagi-Sugeno-Kang模糊系统模型^[18-23]是最重要的用于建模与智能控制的模糊模型之一。对于经典的TSK模糊模型，最常用的模糊推理规则的定义如下：

第k条模糊规则：

IF

${{{x}}_1} \;{\rm{is}} \; {{A}}_1^k \wedge {{{x}}_2} \;{\rm{is}} \; {{A}}_2^k \wedge \cdots {{{x}}_d} \wedge \;{\rm{is}} \; {{A}}_d^k$

THEN

${f^k}\left( {{x}} \right) = {{p}}_0^k + {{p}}_1^k{{{x}}_1} + \cdots + {{p}}_d^k{{{x}}_d},k = 1,2, \cdots ,K $

(1)

式中： ${{A}}_i^k$ 表示输入向量X第i维特征所对应的第k条模糊规则的模糊子集；K表示模糊规则数； $ \wedge $ 为模糊合取操作。每条规则都对应输入向量 ${{X}} = {\left[ {{{{x}}_1}\,\,{{{x}}_2}\,\, \cdots \,\,{{{x}}_d}} \right]^{\rm{T}}}$ ，并且把输入空间的模糊子集 ${{{A}}^k} \subset {{{R}}^d}$ 映射到输出空间的模糊集 ${f^k}\left( {{X}} \right)$ ，其中乘算子、加算子分别作为合取和析取操作算子，加法算子作为组合算子时，TSK模糊模型的输出可以表示为

${y^0} = \sum\limits_{k = 1}^K {\frac{{{\mu ^k}\left( {{X}} \right)}}{{\sum\limits_{{k'} = 1}^K {{\mu ^{{k'}}}\left( {{X}} \right)} }}} {f^k}\left( {{X}} \right) = \sum\limits_{k = 1}^K {{{\tilde \mu }^k}} \left( {{X}} \right){f^k}\left( {{X}} \right)$

(2)

式中： ${\mu ^k}\left( {{X}} \right)$ 和 ${\tilde \mu ^k}\left( {{X}} \right)$ 分别表示为模糊集 ${{{A}}^k}$ 相关的模糊隶属函数和归一化模糊隶属函数。这两个函数的计算公式分别为

${\mu ^k}\left( {{X}} \right) = \prod\limits_{i = 1}^d {{\mu _{{{A}}_i^k}}} \left( {{{{x}}_i}} \right)$

(3)

和

${\tilde \mu ^k}\left( {{X}} \right) = {{{\mu ^k}\left( {{X}} \right) } / {\sum\limits_{{k'} = 1}^K {{\mu ^{{k'}}}\left( {{X}} \right)} }}{\kern 1pt} $

(4)

通常采用高斯函数作为模糊隶属函数，其计算公式为

${\mu _{{{A}}_i^k}}\left( {{{{x}}_i}} \right) = \exp \left( {\frac{{ - {{\left( {{{{x}}_i} - {{c}}_i^k} \right)}^2}}}{{2{{\delta }}_i^k}}} \right)$

(5)

式中：参数 ${{c}}_i^k$ 和 ${{\delta }}_i^k$ 可以通过聚类技术或其他划分方法计算得出。通常使用模糊C均值(FCM)聚类算法进行数据集的初始划分，进而计算 ${{c}}_i^k$ 和 ${{\delta }}_i^k$ 公式为

${{c}}_i^k = {{\sum\limits_{j = 1}^N {{{{u}}_{jk}}{{{x}}_{ji}}} } / {\sum\limits_{j = 1}^N {{{{u}}_{jk}}} }}$

(6)

${{\delta }}_i^k = {{h \cdot \sum\limits_{j = 1}^N {{{{u}}_{jk}}{{\left( {{{{x}}_{ji}} - {{c}}_i^k} \right)}^2}} } / {\sum\limits_{j = 1}^N {{{{u}}_{jk}}} }}$

(7)

式中： ${{{u}}_{jk}}$ 表示通过FCM聚类计算出属于第k类的第j个输入数据 ${{{X}}_j} = {\left[ {{{{x}}_{j1}}\,\,{{{x}}_{j2}}\,\, \cdots \,\,{{{x}}_{jd}}} \right]^{\rm{T}}}$ 的模糊隶属度。在这里，h是高斯函数的核带宽参数。令：

${{{X}}_e} = {\left[ {1\,\,{{{X}}^{\rm{T}}}} \right]^{\rm{T}}}$

(8)

${{{\tilde X}}^k} = {\tilde \mu ^k}\left( {{X}} \right){{{X}}_e}{\kern 1pt} $

(9)

${{{X}}_g} = {\left[ {{{\left( {{{{{\tilde X}}}^1}} \right)}^{\rm{T}}}\,\,{{\left( {{{{{\tilde X}}}^2}} \right)}^{\rm{T}}}\,\, \cdots \,\,{{\left( {{{{{\tilde X}}}^K}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}$

(10)

${{{P}}^k} = {\left[ {{{p}}_0^k\,\,{{p}}_1^k\,\, \cdots \,\,{{p}}_d^k} \right]^{\rm{T}}}$

(11)

${{{P}}_g} = {\left[ {{{\left( {{{{P}}^{\rm{1}}}} \right)}^{\rm{T}}}\,\,{{\left( {{{{P}}^2}} \right)}^{\rm{T}}}\,\, \cdots \,\,{{\left( {{{{P}}^K}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}$

(12)

TSK模糊模型的训练问题转化为式(13)线性回归模型的参数学习问题^[24]：

${y^0} = {{P}}_g^{\rm{T}}{{{X}}_g}$

(13)

从式(13)中可以观察到，输入向量经式(8)～(10)计算，可以变换为一个 $(d + 1) * K$ 维的高维向量，本文中我们将这一转换过程称为模糊特征映射。与已有核方法中的隐性映射相比，模糊特征映射具有以下特点：1)它是一种显性映射方式，用户可以在高维特征空间中得到数据的显式表示方法；2)模糊特征映射基于模糊规则进行构建，而模糊规则本身具有较强的可解释性；3)输入向量经模糊特征映射后得到的高维特征向量的维数可以由模糊规则数确定，这有利于用户控制高维空间中数据的复杂程度。

2 基于多层递阶融合模糊特征映射的模糊C均值聚类算法 2.1 基于多层递阶融合的模糊特征映射新方法

原数据通过模糊特征映射，得到其在高维空间中的新表示。但是作为单层映射结构，会因映射后的特征维数过高使得数据变得混乱和冗余，继而影响算法后续的聚类效果。研究表明^[25-26]，将单层映射结构改造为多层映射结构，可以有效地提高算法对复杂非线性数据的学习能力。为此，本文引入多层递阶融合的概念来构造新型的映射，提出基于多层递阶融合的模糊特征映射新方法(MLHFFFM)。通过对每层模糊特征映射之后的高维特征表示进行PCA降维，再进行相应的信息补充，形成新的融合层，依次进入下一层的压缩融合过程，其结构如图1所示。

基于多层递阶融合的模糊特征映射新方法MLHFFFM算法描述如下：

输入　给定一个数据集D={X, Y}，设置初始模糊规则数K，分层融合层数S。

输出　经多层递阶融合后的数据矩阵 ${{X}}_{\rm{pca}}^{\left( {\rm{S}} \right)}$ 。

1) 对原数据进行第一层的模糊特征映射(初始层)

① 通过FCM算法计算出隶属度矩阵 ${{{u}}_{jk}}$ ；

② 经式(6)和式(7)分别计算出对应的 ${{c}}_i^k$ 和 ${{\delta }}_i^k$ (i=1, 2, $ \cdots $ , d，j=1, 2, $ \cdots $ , n，k=1, 2, $ \cdots $ , K)；

③ 通过高斯隶属度函数(5)和式(3)的计算得到 ${\mu ^k}\left( {{X}} \right)$ (k=1, 2, $ \cdots $ , K)；

④ 再经过式(8)～(10)的转化，得到映射后高维空间中的数据矩阵 ${{X}}_g^{(1)} \in {{{R}}^{N \times (d{\rm{ + 1)*}}K}}$ 。

2) 多层递阶融合

① 利用PCA对 ${{X}}_g^{(1)}$ 进行压缩，得到数据矩阵记为 ${{X}}_{\rm{pca}}^{\left( 2 \right)}$ ；

② For i=2:(S-1)；

③ 重复步骤1)，对原数据进行模糊特征映射，得到数据矩阵 ${{X}}_g^{\left( i \right)} \in {{{R}}^{N \times dK}}$ ；

④ ${{X}}_{\rm{lhffm}}^{\left( i \right)}{\rm{ = }}\left[ {{{X}}_{\rm{pca}}^{\left( i \right)}\,\,{{X}}_g^{\left( i \right)}} \right]$ ；

⑤ 利用PCA对 ${{X}}_{\rm{lhffm}}^{\left( i \right)}$ 进行压缩，得到数据矩阵记为 ${{X}}_{\rm{pca}}^{\left( {i{\rm{ + 1}}} \right)}$ ；

⑥ end；

2.2 基于多层递阶融合模糊特征映射的模糊C均值聚类算法MLHFFFM-FCM

本节中，将多层递阶融合模糊特征映射与经典模糊聚类算法FCM相结合，提出基于多层递阶融合模糊特征映射的模糊C均值聚类算法。MLHFFFM-FCM算法描述如下：

输入　给定一个数据集D={X, Y}，设置初始模糊规则数K，分层融合层数S。

1) 通过基于多层递阶融合的模糊特征映射，将输入数据X转化为 ${{X}}_{\rm{pca}}^{\left( {\rm{S}} \right)}$ 。

2) 对最终压缩融合获得的数据矩阵 ${{X}}_{\rm{pca}}^{\left( {\rm{S}} \right)}$ ，采用FCM算法聚类。

输出　模糊划分矩阵U。

3 实验研究与分析

为了验证MLHFFFM-FCM算法在复杂非线性数据分析上的有效性，本节从3个方面进行对比分析：1)各FCM演变算法之间聚类效果的对比实验；2)单层映射结构与多层递阶融合映射结构的聚类效果对比实验；3)关键参数敏感性的对比实验。

3.1 算法性能的评价指标

为了对各类算法的聚类性能进行对比，本文采用NMI(normalized mutual information)和RI(rand index)作为实验评价指标。这两个指标的值越接近1，说明算法聚类性能越好。其计算公式如下：

1) NMI

${\rm{NMI}}{\rm{ = }}\frac{{\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^C {{N_{i,j}}\log N \times {N_{i,j}}} } /{N_i} \times {N_j}}}{{\sqrt {\sum\limits_{i = 1}^C {{N_i}} \times \log {N_i}/N \times \sum\limits_{j = 1}^C {{N_j}} \times \log {N_j}/N} }}$

(14)

式中： ${N_{i,j}}$ 表示第 $i$ 个聚类与第 $j$ 类的契合程度， ${N_i}$ 表示第 $i$ 个聚类所包含数据样本量， ${N_j}$ 表示类 $j$ 所包含的数据样本量，而N表示整个数据样本大小。

2) RI

${\rm{RI}} = \frac{{{f_{00}} + {f_{11}}}}{{{{N(N - 1)} / 2}}}$

(15)

式中： ${f_{00}}$ 表示数据点具有不同的类标签并且属于不同类的配对点数目， $\sigma $ 则表示数据点具有相同的类标签并且属于同一类的配对点数目，而N表示整个数据样本的总量大小。以上两种方法，其取值范围均为[0, 1]，且均随着数值的增大，显示出算法的性能更为优越。

3.2 实验设置

我们采用UCI真实数据集(http://archive.ics.uci.edu/ml/)来评估本文算法。为了测试实验应用数据集的广泛性以及避免选取数据集的偶然性，选择其中7个具有代表性的数据集Ar₂、Diabetes、Zoo、Australian、Breast、Heart、Chronic_Kidney_Disease进行测试，其中数据集的相关信息如表1所示。同时本文选取5种经典的聚类算法与MLHFFFM-FCM算法进行对比实验，分别为FCM算法、PCA-FCM算法、ELM-FCM算法、KFCM-K算法以及KFCM-F算法。所有实验运行平台的配置如下：酷睿i3 3.6 GHz CPU，3.42 G RAM，32位 Windows 7操作系统，MATLAB R2012b编程环境。另外各算法相关说明及其参数设置如表2所示，其中各算法涉及的模糊指数m的寻优范围均为{1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0}。

3.3 聚类效果对比实验

为了验证MLHFFFM-FCM算法的有效性，本节对算法进行对比实验测试。在本实验中，将初始模糊规则数r设置为30，多层递阶融合层数设置为5层，并根据表2的实验相关参数设置，分别对各算法重复运行10次。最终的实验中各算法的参数取值情况和实验结果如表3和表4所示。

从表4中可以明显地看出，在聚类精度上，文中涉及的对比算法只能在某个或某几个数据集上取得较优的结果，而MLHFFFM-FCM算法不仅在所有的测试数据集上取得满意的结果，并且还有着明显的提高。这说明了MLHFFFM-FCM算法的有效性，也进一步说明了该算法处理复杂非线性数据的强大能力。

3.4 单层映射结构与多层递阶融合映射结构的聚类效果对比实验与分析

为了体现本文算法引入的多层递阶融合方法的优越性，本节实验针对多层递阶融合映射结构对FCM算法性能的影响进行实验与分析。实验在模糊规则数设置相同的情况下，分别采用单层映射结构和多层递阶融合映射结构对原输入数据进行非线性映射，将映射后的数据采用FCM进行聚类。实验最终的参数取值情况和结果如表5和表6所示，其中因受篇幅所限，仅在表6中给出RI指标结果，NMI与之有类似的结果，不再列出。

从表5和表6中可以明显地观察出，相比于单层映射结构，基于多层递阶融合映射结构的模糊聚类方法能够取得更好的学习效果。这是由于在单层映射之后的数据存在冗余信息，而在压缩之后又会导致信息缺失。但是多层递阶融合的映射结构是建立在单层映射结构的基础上，采用PCA技术对每一层模糊特征映射得到的高维特征表示进行压缩，再对应地结合每一层数据信息融合形成的。因此通过多层递阶融合的方法，可以有效地精简冗余信息，同时对每一层进行适当的信息弥补。这也充分体现了本文提出的多层递阶融合映射结构的优越。

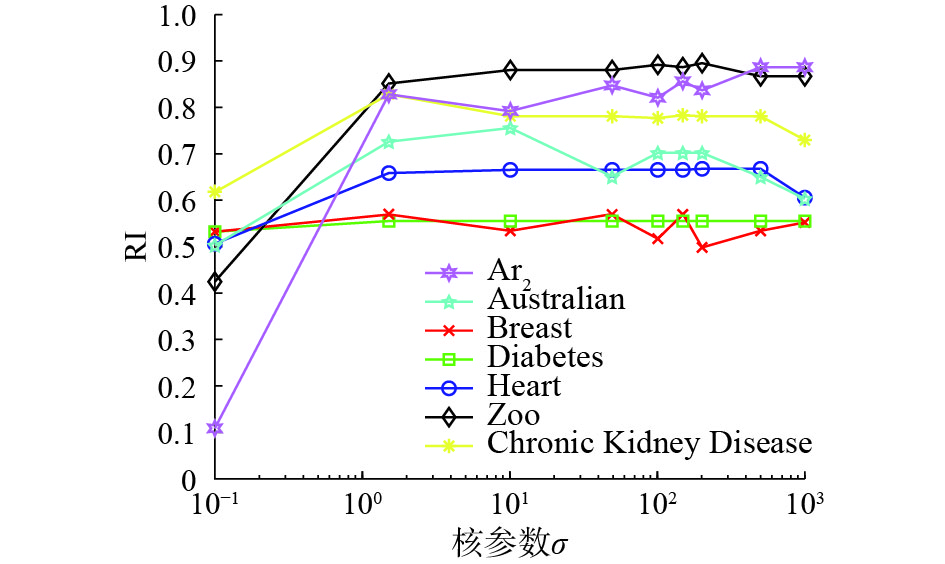
3.5 参数敏感性实验

模糊规则数r作为MLHFFFM-FCM算法中的关键参数，本节针对该参数进行参数敏感性实验。这里为了让实验结果能够直观地进行观察与对比，我们同时对KFCM-F算法中的关键参数 $\sigma $ 进行参数敏感性实验，进而研究模糊规则数这一关键参数对MLHFFFM-FCM算法性能的影响。实验中，MLHFFFM-FCM模糊规则数r的实验取值范围为{5, 10, 15, 20, 25, 30, 35, 40, 45, 50}，KFCM-F算法中核参数 $\sigma $ 的实验取值范围为{0.1, 1.5, 10, 50, 100, 150, 200, 500, 1 000}，实验最终结果分别如图2和图3所示。

从图2中不难看出，KFCM-F算法的性能随核参数 $\sigma $ 变化出现很大的波动，这说明核参数 $\sigma $ 对KFCM-F算法的性能有很大的影响。相反，由图3可以观察到，模糊规则数r对MLHFFFM-FCM算法性能的影响很小，算法性能始终保持稳定的状态，这说明MLHFFFM-FCM算法对模糊规则数r不敏感。结合上述实验也从另一个方面体现了采用本文提出的基于多层递阶融合映射方法的优越性，它不仅保证了算法的聚类效果，还克服了KFCM-F等算法对参数敏感的问题，这更有利于该算法在实际问题中的应用。

4 结束语

本文提出的MLHFFFM-FCM算法，是一种采用新型的显性映射方式来处理复杂非线性数据的无监督学习方法。相比于现有的核函数映射方法，MLHFFFM-FCM算法在取得良好聚类效果的同时，还对算法中模糊规则数不敏感，这更有利于算法在实际应用中的选用。但是本文提出的MLHFFFM-FCM算法仍然具有一定的缺陷，例如对于高维数据，其时间开销较大。如何有效克服这些问题，将是今后进一步研究的重点。