在过去几十年中,复杂网络研究吸引了许多来自不同科学领域学者的关注[1]。而以往的工作主要集中在对网络拓扑结构复杂性及其与网络动力学行为之间关系的研究,通过对复杂网络拓扑性质、复杂网络演化模型以及动力学行为的分析,揭示出隐藏在复杂系统中的一系列共同规律,对于把握复杂系统的宏观特征及调节复杂系统上的动力学行为都将具有重要意义[2-3]。随着对复杂网络研究的进一步深入,复杂网络可控性的研究得到了充分的关注与重视。Lin[4]给出了线性时不变控制系统“结构”和“结构可控性”的概念,并通过研究找到了结构可控性的充要条件;Liu等[5]基于线性时不变控制系统的结构可控性理论,对实际复杂系统进行了研究并建立了网络结构可控性模型;Jia[6-7]发现了两种不同的网络控制模式:集中式控制和分布式控制;同时基于控制能力和随机抽样算法对有向复杂网络的结构可控性做了进一步探索,随后一些研究者通过改变连接边的方向实现了网络可控性的优化[8-10]。目前复杂网络可控性研究已经取得了众多的重要成果,但复杂网络控制方面的研究仍然处于起步阶段,还有很多未解决的理论问题,例如结构可控性理论无法适用于无向网络、权重网络和时变网络的可控性等问题。针对结构可控性理论仅适用于有向网络的局限性,Yuan[11]引入了严格可控性(exact controllability)的概念,证明完全控制复杂网络所需的最少控制器数目由网络矩阵特征值的最大重数决定,并提出了利用矩阵初等变换甄别网络中需要被独立控制的节点的方法,通过对大量真实网络和模型网络的计算结果表明了严格可控性理论的有效性和实用性;Li[12]针对实际网络的分型特征,运用严格可控性理论对分型网络的可控性进行了分析。基于单层有向网络和无可控性进行的研究已取得了较大突破。但现实中的网络通常是相互依存的,例如,公交–地铁网络、电力–通信网络、电力–供水网络等,且通过研究已经发现相依网络的动态特性如级联失效[13-17]、扩散现象[18]、演化博弈动力学[19]、同步性[20]等,均明显区别于单层网络。怎样合理地控制相依网络将是面临的重要挑战。Yuan[21]运用严格可控性理论对多重网络的可控性进行了研究,发现在多关系网中存在主导关系网,其结构和连接权重对于整个网络的严格可控性起主导作用;在多层网中,不同层间的连接方式以及疏密程度对整个网络的严格可控能力都有重要的影响,并且发现在层间加入少量连接能够大大提高整个网络的可控能力。Nie[22]分析了多层网络中层间连边结构对网络可控性能的影响,研究发现层间连边比例较小时,网络最少驱动节点的数目随着连边度相关性的增加而减小,层间连边同配性强的网络易于控制;当层间连边比例较大时,则会出现相反的情况,层间连边异配性强的网络易于控制。然而以上研究仅分析了网络层间的连接方式及网络层间连接边的度相关性对无向相依网络可控性的影响,却未考虑到实际网络中存在有向网络相互依存的情况,例如在交通网络与供电网络中,某一时间内列车的运行方向是定向的,同时供电系统按照列车运行的线路提供电力支持保证其正常运行。在供电网络中某一处发生故障会通过网络之间的相依关系,将其传递到交通网络中从而导致经过这条线路的列车都无法运行,反之亦然。这样在某个网络中产生的故障会因为彼此间的相依关系,使得故障在两个网络之间相互蔓延,从而对网络造成更大的破坏,由此表明有向相依网络间的相依关系对整个有向相依网络有重要影响。为了探究有向网络间相依关系对网络的影响,本文首先构建了基本的有向相依网络模型,并结合严格可控性理论,给出了基于最少控制输入的可控性评判指标;其次,针对相依方式对有向相依网络可控性产生的影响,基于经典的有向随机网络(DER)和有向无标度网络(DSF),构建了DER-DER、DER-DSF、DSF-DSF 3类有向相依网络模型,并研究了随机相依方式下3类网络的可控性能;最后,基于随机相依方式下对网络可控性的分析,提出了3种有向网络的相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),且在既定的3种相依方式下对网络的可控性进行了仿真分析。
1 有向相依网络可控性 1.1 有向相依网络有向相依网络由两个有向子网络(子网络A和子网络B)通过双向连接线连接而成,
| $\begin{array}{*{20}{l}}{{F_A} = N_A^I/{N_A}}\\{{F_B} = N_B^I/{N_B}}\end{array}$ | (1) |
本文仅考虑相依子网络节点数相同的情况,即
|
Download:
|
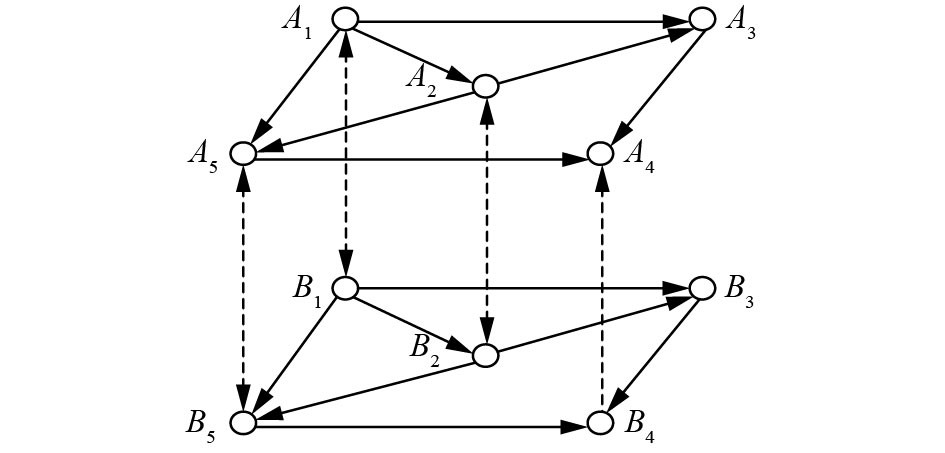
| 图 1 有向相依网络 Fig. 1 The interdependent directed network | |
如图1所示,定义了简单的有向相依网络模型,
在现代控制理论中,如果通过一些控制变量的输入能使一个系统从任意初始状态达到理想状态,我们称这个系统是可控的。这里只考虑线性时不变系统并且假设系统内部未发生动态变化。有向相依网络状态方程为
| ${\dot x} = {{Ax}}\left( {{t}} \right) + {{Bu}}\left( t \right)\; = \left[ \begin{gathered} \mathop A\nolimits_1 \;\;\mathop A\nolimits_{12} \\ \mathop A\nolimits_{21} \;\; \mathop A\nolimits_2 \\ \end{gathered} \right]{x}\left( {t} \right) + {B u}\left( {t} \right) $ | (2) |
向量
定理1 对于一个可控系统来说,最少控制输入个数是系统矩阵特征值中具有最大代数重数的特征值所对应的几何重数。
为了有效地衡量有向相依网络的可控性,本文采用
| $\mathop n\nolimits_D = \frac{{\mathop N\nolimits_D }}{{2N}}$ | (3) |
式中:
对于满足状态方程(2)的系统来说,其节点总数是不变的且为
| ${N_0} = N_1+N_2$ | (4) |
对于可控系统来说,必然存在一个得到外部控制输入作用节点的最小个数,记为
| ${N_0} = \min (N_1)+\max(N_2)$ | (5) |
从而可得
| $\frac{\min (N_1)}{N_0}=1-\frac{\max(N_2)}{N_0}$ | (6) |
在此定义最小控制比例
| $\mathop n\nolimits_D = \frac{{\min \left( {\mathop N\nolimits_1 } \right)}}{{\mathop N\nolimits_0 }}$ | (7) |
由式(7)可知:若
然而需要确定能够达到控制效果所需的最少控制输入个数。在这里将最小控制输入个数
| $\mathop N\nolimits_D = \min \left\{ {{\rm{rank}}({B})} \right\}$ | (8) |
若满足状态方程(2)的系统是可控的,那么由PHB判定定理可知,对矩阵A的任意特征值
| $2N = {\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {{A}},{{B}}} \right]$ | (9) |
式中I为单位矩阵。
根据矩阵不等式关系得:
| $\begin{gathered} 2N ={\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {A},{B}} \right] \leqslant \\ {\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {A}} \right] + {\rm{rank}}\left[ {B} \right] \\ \end{gathered} $ | (10) |
进一步得
| ${\rm{rank}}\left[ {B} \right] \geqslant 2N - {\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {A}} \right]$ | (11) |
上式满足恒成立关系,则:
| $\begin{gathered} {\rm{rank}}\left[ {B} \right] \geqslant \max \left\{ {2N - {\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {A}} \right]} \right\} = \\ \mathop {\max }\limits_i \left\{ {\mu \left( {\mathop \lambda \nolimits_i } \right)} \right\} = \mu \left( {\mathop \lambda \nolimits^M } \right) \\ \end{gathered} $ | (12) |
进一步可得
| $\begin{gathered} \min \left( { {\rm{rank}}\left[ {B} \right]} \right) \geqslant \max \left\{ {N - {\rm{rank}}\left[ {\mathop \lambda \nolimits_i {I} - {A}} \right]} \right\} = \\ \mathop {\max }\limits_i \left\{ {\mu \left( {\mathop \lambda \nolimits_i } \right)} \right\} = \mu \left( {\mathop \lambda \nolimits^M } \right) \\ \end{gathered} $ | (13) |
再由
| $\mathop N\nolimits_D = \mu \left( {\mathop \lambda \nolimits^M } \right)$ | (14) |
式中:
由
| $\mathop N\nolimits_D = \min \left( {{N_1}} \right)$ | (15) |
最后可得:
| $\mathop n\nolimits_D = \frac{{\mathop N\nolimits_D }}{{2N}}$ | (16) |
由此可知,当
|
Download:
|
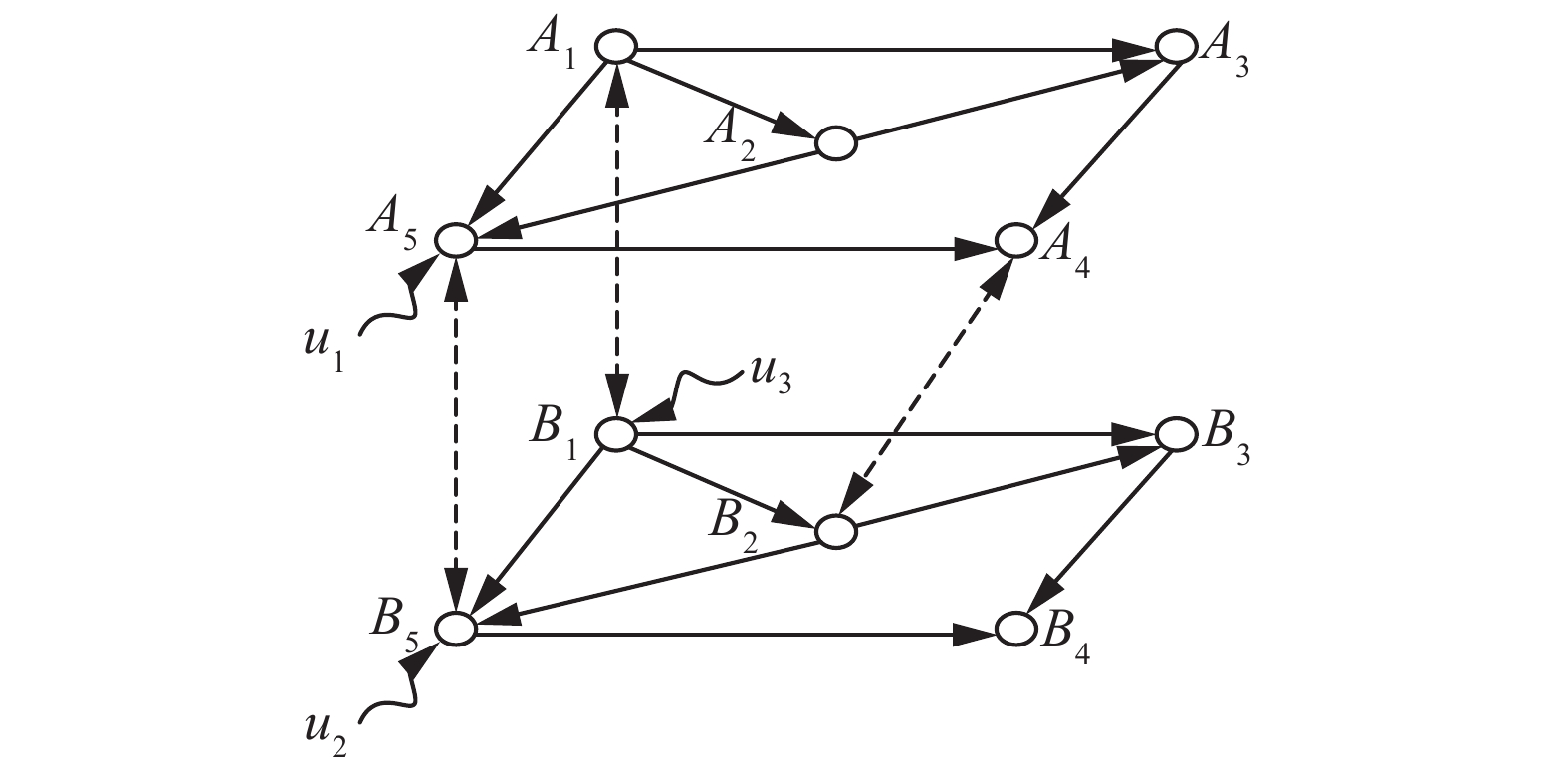
| 图 2 有向相依网络可控性 Fig. 2 Controllability of the interdependent directed network | |
如图2表示一个有向相依网络,其中子网络节点数
| ${A} = \left[ {\begin{array}{*{20}{c}} 0&1&1&0&1&0&0&0&1&0 \\ 0&0&0&0&1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0 \\ 0&0&0&1&0&0&1&0&0&0 \\ 0&0&0&0&0&0&1&1&0&1 \\ 0&0&0&0&1&0&0&1&0&1 \\ 0&0&0&0&0&0&0&0&1&0 \\ 1&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&1 \end{array}} \right]$ | (17) |
| ${{\lambda}} = \mathop {\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0&0&0&1&{ - 1}&0&0&0 \end{array}} \right]}\nolimits^{\rm T} $ | (18) |
通过观察特征值
本文基于经典的有向随机网络(DER)和有向无标度网络(DER),构建了DER-DER、DER-DSF、DSF-DSF 3类有向相依网络模型。同时在随机相依方式下,对不同相依比例的DER-DER网络可控性进行了独立仿真实验。
|
Download:
|
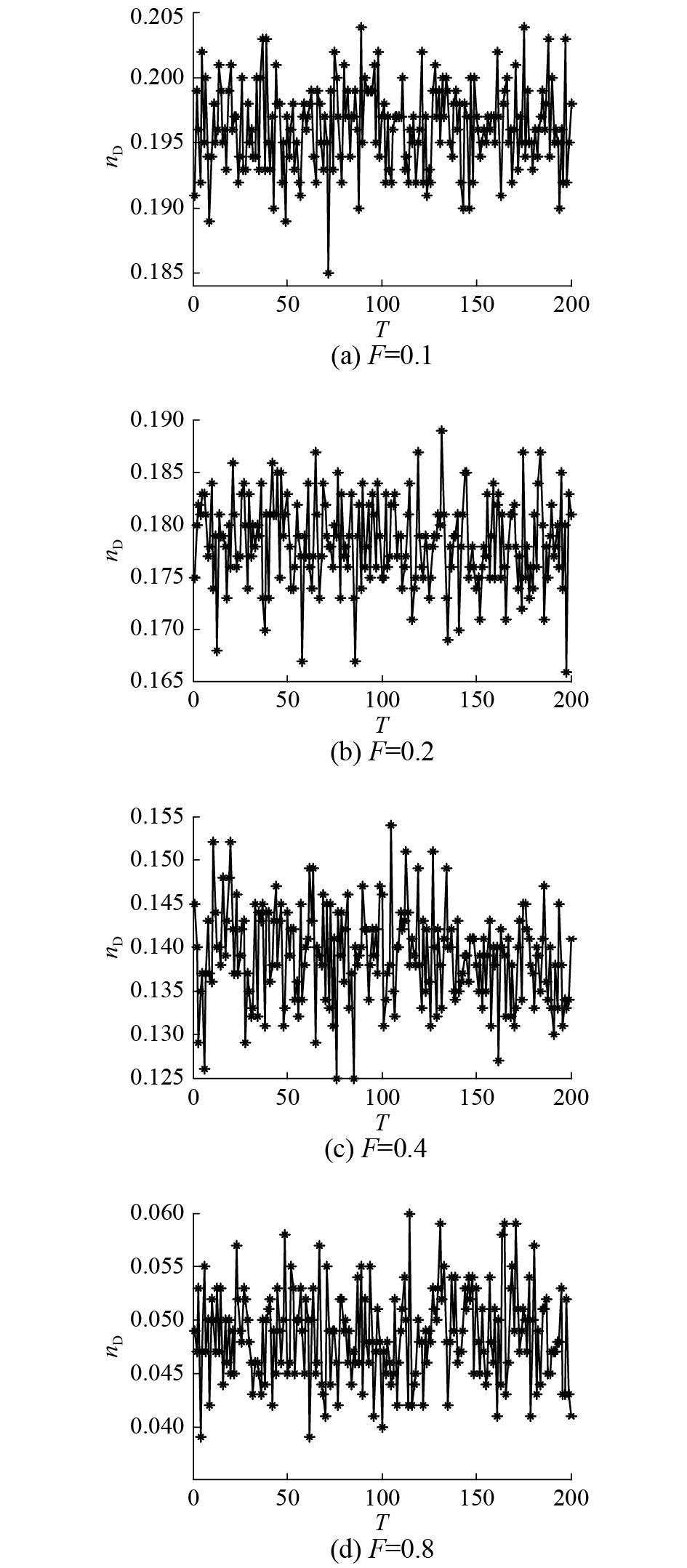
| 图 3 单一相依比例下DER-DER网络的可控性 Fig. 3 Controllability of DER-DER network with a single dependency ratio | |
在随机相依方式下,通过对4组不同相依比例的DER-DER网络可控性进行多次仿真,其中网络规模
通过对比以上4组不同相依比例下的网络可控性发现,随着相依比例F的逐渐增加,
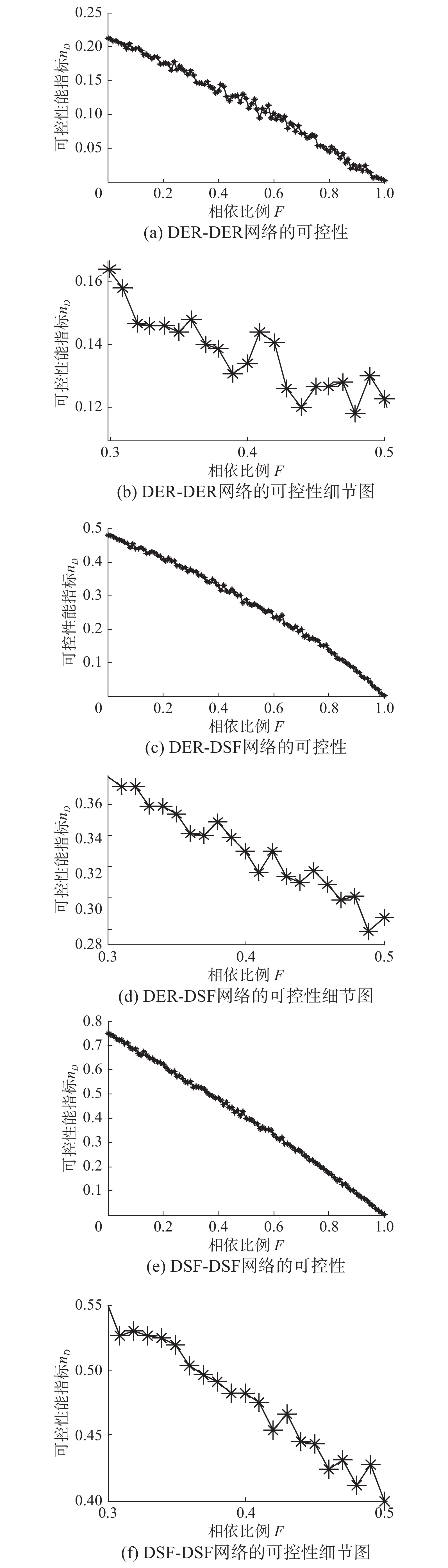
在随机相依方式下,通过对连续相依比例的DER-DER、DER-DSF、DSF-DSF这3类有向相依网络的可控性进行仿真,如图4(a)所示,就DER-DER有向相依网络而言,随着相依比例F的逐渐增加,
图4中,网络规模2N=1 000,其中DER网络,
|
Download:
|
| 图 4 连续相依比例下网络的可控性 Fig. 4 Controllability of the network under continuous dependency ratio | |
基于随机相依方式下对有向相依网络可控性的分析,本文提出了有向网络之间的3种相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),同时针对3种相依方式构建了如图5所示的简单有向相依网络模型并分析了其可控性。
图5中,网络节点总数

|
Download:
|
| 图 5 有向相依网络的相依方式 Fig. 5 Dependent way of the interdependent directed network | |
针对提出的3种有向网络相依方式,在DER-DER、DER-DSF、DSF-DSF 3类有向相依网络中对网络可控性进行了仿真对比。如图6(a)所示,在DER-DER有向相依网络中对3种既定相依方式而言,
图6中,网络规模2N=1 000,其中DER网络,

|
Download:
|
| 图 6 不同相依方式下有向相依网络可控性 Fig. 6 Controllability of the interdependent directed network under different dependent way | |
相互依存的复杂网络广泛存在于实际复杂系统中,且往往存在有向网络之间的相依,本文首先构建了基本的有向相依网络模型,并结合严格可控性理论,给出了基于最少控制输入的可控性评判指标;考虑相依方式对有向相依网络可控性产生的影响,本文基于经典的有向随机网络(DER)和有向无标度网络(DSF),构建了DER-DER、DER-DSF、DSF-DSF 三类有向相依网络模型,并在4组不同相依比例下,研究了随机相依方式下的DER-DER网络的可控性能,研究发现,随着相依比例的增加,网络可控性逐渐增强。但每组相依比例下的网络可控性均会在一定范围内出现大幅的波动。为了进一步证实相依方式影响着网络的可控性,通过在随机相依方式下对连续相依比例下的3类有向相依网络可控性进行了仿真,我们发现随着相依比例的逐渐增加,网络可控性总体均呈现逐渐增强的趋势,但由于相依方式的随机性,网络可控性在增强过程中会出现明显的波动情况,即有向网络的相依方式对网络可控性产生着重要影响。
基于分析本文提出了3种有向网络的相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),同时就提出的3种相依方式在3类有向相依网络中对网络可控性进行了仿真对比,且通过对比发现,在同一网络中同等相依比例下,基于最低入度与最低出度节点相依的有向相依网络可控性最强,而基于最高入度与最高出度节点相依的有向相依网络可控性最弱。研究证实了有向网络相依方式密切影响着网络的可控性,且得到3种相依方式下有向相依网络可控性的强弱关系,这为构建强可控性能的实际有向相依网络提供了参考依据。
| [1] |
MORENO Y, NEKOVEE M, PACHECO A F. Dynamics of rumor spreading in complex networks[J]. Physical review E, 2004, 69(6): 066130. DOI:10.1103/PhysRevE.69.066130 ( 0) 0)
|
| [2] |
NEWMAN M E, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 ( 0) 0)
|
| [3] |
SHEN J, ZHENG B. Cross-correlation in financial dynamics[J]. Europhysics letters, 2009, 86(4): 48005. DOI:10.1209/0295-5075/86/48005 ( 0) 0)
|
| [4] |
LIN Chingtai. Structural controllability[J]. IEEE transactions on automatic control, 1974, 19(3): 201-208. DOI:10.1109/TAC.1974.1100557 ( 0) 0)
|
| [5] |
LIU Yangyu, SLOTINE J J, BARABÁSI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167-173. DOI:10.1038/nature10011 ( 0) 0)
|
| [6] |
JIA Tao, LIU Yangyu, CSÓKA E, et al. Emergence of bimodality in controlling complex networks[J]. Nature communications, 2013, 4: 2002. DOI:10.1038/ncomms3002 ( 0) 0)
|
| [7] |
JIA Tao, BARABÁSI A L. Control capacity and a random sampling method in exploring controllability of complex networks[J]. Scientific reports, 2013, 3: 2354. DOI:10.1038/srep02354 ( 0) 0)
|
| [8] |
WANG Wenxu, NI Xuan, LAI Yingcheng, et al. Optimizing controllability of complex networks by minimum structural perturbations[J]. Physical review E, 2012, 85(2): 026115. DOI:10.1103/PhysRevE.85.026115 ( 0) 0)
|
| [9] |
XU Jiuqiang, WANG Jinfang, ZHAO Hai, et al. Improving controllability of complex networks by rewiring links regularly[C]//Proceedings of the 26th Chinese Control and Decision Conference. Changsha, China: IEEE, 2014: 642–645.
( 0) 0)
|
| [10] |
HOU Lvlin, LAO Songyang, SMALL M, et al. Enhancing complex network controllability by minimum link direction reversal[J]. Physics letters A, 2015, 379(20/21): 1321-1325. ( 0) 0)
|
| [11] |
YUAN Zhengzhong, ZHAO Chen, DI Zengru, et al. Exact controllability of complex networks[J]. Nature communications, 2013, 4: 2447. DOI:10.1038/ncomms3447 ( 0) 0)
|
| [12] |
LI Jingwen, YUAN Zhengzhong, FAN Ying, et al. Controllability of fractal networks: an analytical approach[J]. Europhysics letters, 2014, 105(5): 58001. DOI:10.1209/0295-5075/105/58001 ( 0) 0)
|
| [13] |
BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028. DOI:10.1038/nature08932 ( 0) 0)
|
| [14] |
WANG Jianwei, LI Yun, ZHENG Qiaofang. Cascading load model in interdependent networks with coupled strength[J]. Physica A: statistical mechanics and its applications, 2015, 430: 242-253. DOI:10.1016/j.physa.2015.02.072 ( 0) 0)
|
| [15] |
WANG Jianwei, JIANG Chen, QIAN Jianfei. Robustness of interdependent networks with different link patterns against cascading failures[J]. Physica A: statistical mechanics and its applications, 2014, 393: 535-541. DOI:10.1016/j.physa.2013.08.031 ( 0) 0)
|
| [16] |
CHENG Zunshui, CAO Jinde. Cascade of failures in interdependent networks coupled by different type networks[J]. Physica A: statistical mechanics and its applications, 2015, 430: 193-200. DOI:10.1016/j.physa.2015.02.090 ( 0) 0)
|
| [17] |
陈世明, 吕辉, 徐青刚, 等. 基于度的正/负相关相依网络模型及其鲁棒性研究[J]. 物理学报, 2015, 64(4): 048902. CHEN Shiming, LÜ Hui, XU Qinggang, et al. The model of interdependent network based on positive/negative correlation of the degree and its robustness study[J]. Acta physica sinica, 2015, 64(4): 048902. (  0) 0)
|
| [18] |
GÓMEZ S, DÍAZ-GUILERA A, GÓMEZ-GARDEÑES J, et al. Diffusion dynamics on multiplex networks[J]. Physical review letters, 2013, 110(2): 028701. DOI:10.1103/PhysRevLett.110.028701 ( 0) 0)
|
| [19] |
OHTSUKI H, NOWAK M A, PACHECO J M. Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs[J]. Physical review letters, 2007, 98(10): 108106. DOI:10.1103/PhysRevLett.98.108106 ( 0) 0)
|
| [20] |
BARRETO E, HUNT B, OTT E, et al. Synchronization in networks of networks: the onset of coherent collective behavior in systems of interacting populations of heterogeneous oscillators[J]. Physical review E, 2007, 77(3): 036107. ( 0) 0)
|
| [21] |
YUAN Zhengzhong, ZHAO Chen, WANG Wenxu, et al. Exact controllability of multiplex networks[J]. New journal of physics, 2014, 16(10): 103036. DOI:10.1088/1367-2630/16/10/103036 ( 0) 0)
|
| [22] |
NIE Sen, WANG Xuwen, WANG Binghong. Effect of degree correlation on exact controllability of multiplex networks[J]. Physica A: statistical mechanics and its applications, 2015, 436: 98-102. DOI:10.1016/j.physa.2015.05.038 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


