2. 数字化纺织服装技术教育部工程研究中心,上海 201602
2. Ministry of EducationCollege of Information Science and Technology Donghua University,
由于多机器人系统可以更好地实现信息和资源共享,具有更高的并行性和鲁棒性,可以完成更加复杂的任务,已经被应用到智能生产、未知环境探测、搬运清理、服务行业、搜索搜救、远程通信等很多领域中,具备很好的实用价值[1-2]。而一种良好的任务分配策略对整个系统起着重要的作用,因而成为学者们的研究热点。
针对不同的应用场景,国内外学者提出了许多有效的任务分配算法,大多都是基于行为机制、奖赏机制、市场机制以及群体智能[3-5]。袁等[6-7]提出改进的免疫网络算法解决了未知环境中机器人搬运箱子问题,取得一定效果。但以上算法大都适用于静态或任务信息事先已知的场景中,对于随着时间动态产生,且事先只能感知任务位置,无法具体判断任务量,需要机器人在任务执行时自主协作的场景中存在较大的局限。
生物免疫系统维持着生物系统的动态平衡,具有较强的学习性、记忆性和自适应性[8-9]。受此启发,本文借鉴独特型免疫网络,将多机器人系统和免疫系统进行类比,构建任务分配与协作模型,并利用事件驱动机制实现了多机器人动态的任务分配与协作,并引入焦躁模型来解决任务死锁问题,使多机器人系统能够在动态任务、且任务量无法事先确定的复杂场景中实现任务自适应分配与自主协作,构建一个智能协同的机器人网络[10]。将本文算法应用于需要协作的清理搜集任务中,仿真和实验表明本文算法能够有效解决此类动态任务分配问题。
1 多机器人任务分配与协作的免疫网络模型 1.1 生物免疫网络生物免疫系统维持着整个生物系统的动态平衡,非常适合于动态和鲁棒性系统研究,将其应用到实际工程,可以增强系统的稳定性。
1974年Jerne提出的独特型网络假说认为,生物系统可以维持本身的均衡,通过细胞间的相互作用,利用浓度最大的抗体消灭抗原[11]。
在此基础上,Farmer等[12]提出了相应的动态方程,并将免疫系统应用于工程应用。
| $\begin{array}{c}{A_i}\left( t \right) = {A_i}\left( {t - 1} \right) + \left( {\displaystyle\frac{\alpha }{N}\sum\limits_{j = 1}^N {{m_{ji}}{a_j}\left( {t - 1} \right)} - } \right.\\\left. {\displaystyle\frac{\alpha }{N}\sum\limits_{k = 1}^N {{m_{ik}}{a_k}\left( {t - 1} \right) + \beta {g_i} - {k_i}} } \right){a_i}\left( {t - 1} \right)\end{array}$ | (1) |
| ${a_i}\left( t \right) = 1/\left( {1 + \exp \left( {0.5 - {A_i}\left( t \right)} \right)} \right)$ | (2) |
式中:Ai(t)和ai(t)为分别为t时刻抗体i的激励水平和浓度;α、β为作用系数;ki表示抗体的消亡;N为抗体数目;mji和mik分别表示抗体间的激励和抑制;gi表示抗体和抗原间激励。
受此启发,为了实现的任务动态环境中的多机器人任务分配,参照生物免疫网络机理,将免疫网络与实际的多机器人系统进行类比,映射关系如表1,提出一种多机器人任务分配与协作模型。
1.2 任务分配与协作模型针对一定区域内的松散型清理搜集任务,需要通过多个同构或异构机器人独立或协作完成。设环境中存在m个机器人Ri(
| 表 1 机器人系统与生物免疫网络的映射关系 Tab.1 Mapping relationship between robot system and biological immune network |
1) 抗体与抗原激励
在初始时刻,机器人间的任务分配,主要是根据任务对机器人的激励进行选择,某个任务对某个机器人的激励较高,则其获得该任务的概率就较大。设第i个机器人Ri和第j个任务Tj之间的激励为gij,将其定义为
| ${g_{ij}} = \frac{{{\lambda _1}{f_i}{v_i} + {\lambda _2}{p_j}}}{{{\lambda _3}{d_{ij}}}}$ | (3) |
式中:λ1、λ2、λ3相应部分调整系数,fi和vi为相应机器人Ri的能力值和速度大小,dij为机器人Ri和任务Tj之间的距离大小,pj为任务Tj的优先等级。
2) 抗体与抗体激励
根据独特型免疫网络,抗体之间也存在激励。在机器人到达相应任务点后,若机器人Ri需要得到帮助,则其需要激励另外机器人,以使其尽快得到协作。若机器人Ri可以单独的执行被分配的任务,则其将会对其他机器人产生抑制作用,便不会产生激励作用。设机器人Ri对机器人Rj产生的激励为mij,将其定义为
| ${m_{ij}} = \frac{{{\lambda _4}{f_i}{v_i} + {\lambda _5}{v_j}}}{{{\lambda _6}{d_{ij}}}}$ | (4) |
式中:λ4、λ5、λ6为相应部分的调整系数,fi和vi为相应机器人Ri的能力值和速度值,dij为两机器人间的欧氏距离,当等待在某个任务处的机器人对空闲机器人激励越大,其前往协作的概率越大。
3) 综合激励
当机器要再次进行任务选择的时候,其需要根据受到的抗原和抗体的综合激励值来选择。综合激励由某个任务对该机器人的激励以及在该任务上处于等待的机器人对该机器人的激励共同构成,以此来完成机器人的任务分配与协作,设Aij为任务Tj对机器人Ri的综合激励,将其定义为
| ${A_{ij}} = \alpha \sum\limits_{k = 1}^N {{m_{ik}} + \beta {g_{ij}}} $ | (5) |
式中:α、β为相应部分调整参数,N为在任务Tj上等待的机器人数目,mik为机器人间产生的激励,gij为任务Tj和机器人Ri之间的激励值。机器人根据模型选择任务,如有任务处于待协作状态,等待在某个任务上的机器人越多,此任务被选择的概率越大,从而能尽快地得到协作。
2 事件驱动的多机器人动态任务分配算法利用文中提出的分配和协作模型,能实现任务的一次分配,在此基础上引入事件驱动的机制[13],使多机器人系统可以自适应地处理动态任务,并引入焦躁模型来解决任务死锁。
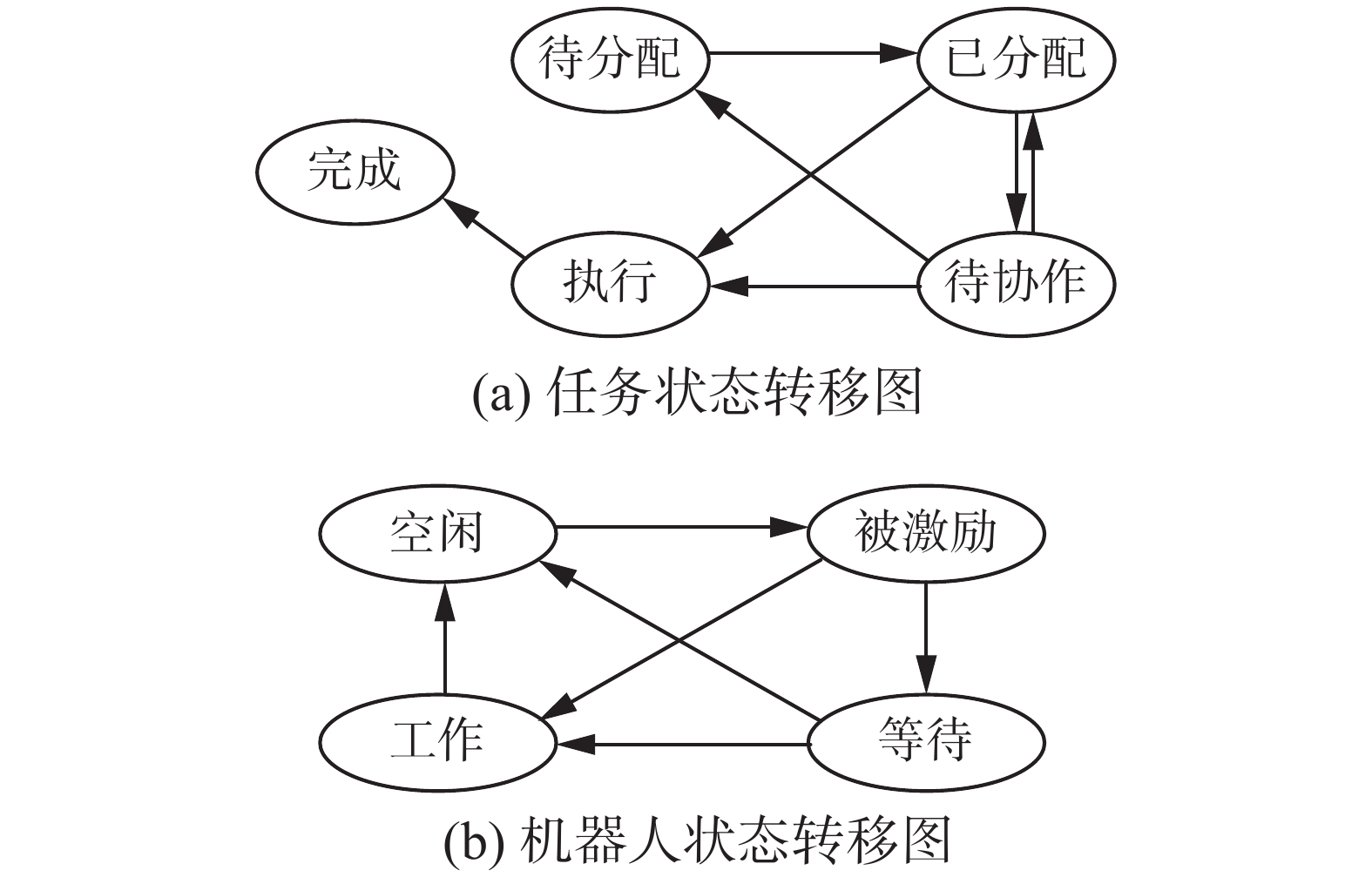
2.1 静态任务分配系统中设定机器人和任务的状态转移如图1所示,任务状态和机器人的状态相互对应,待分配任务激励空闲机器人转变为已分配状态,如果此机器人可以自行完成任务,则任务转变为执行态;否则任务转变为待协作,处于待协作状态的任务获得协作转变为已分配状态,若等待协作的机器人由于长时间没有得到协作而放弃任务,则任务由待协作状态重新回到待分配状态。
|
Download:
|
| 图 1 机器人和任务状态状态转移图 Fig. 1 Robot and task state transition diagram | |
初始时刻,所有任务处于未分配状态,机器人都处于空闲状态,每个机器人按照激励值选择最适合自己的任务,如果每个机器人选择的任务都不重复,则直接获得相应任务,转变为被激励态;如果出现冲突,则冲突的机器人中次优任务激励低者获得最优任务,次优任务激励相同时,随机分配最优任务,其余机器人重新选择任务。在任务分配时,每个机器人同一时刻只能得到一个任务,且当机器人处于闲暇状态时才能被任务所激励,任务处于等待和空闲状态时才可以对机器人产生激励作用。
2.2 动态任务分配静态任务分配方法只可以解决多机器人任务的一次分配,在此基础上引入事件驱动的机制,当系统需要再次进行任务分配或是有新的任务产生时,通过事件触发重新进行分配,以满足环境动态性的要求。
系统中,定义如下事件:
① 系统中有新的任务产生;
② 系统中有机器人状态由工作转变为空闲;
③ 系统中有机器人状态由等待转变为空闲;
④ 系统中有机器人状态由被激励转变为等待;
⑤ 系统中有机器人发生故障。
根据事件驱动的机制,当系统中有如上事件发生时,触发系统,处于空闲状态的机器人进行再次任务选择。
2.3 任务死锁解除对于一个多机器人系统而言,常常会发生任务死锁,即区域中所有机器人都因无法完成任务而处于等待状态[14]。对于智能系统而言,需要机器人能够自主地解除死锁,尽快恢复到工作状态。
为了使机器人能够自主解除死锁状态,引入一种焦躁模型。当机器人长时间由于无法完成任务而处于等待,激素分泌使其产生焦躁情绪,当达到一定的上限时,其将会放弃对该任务的等待,从而重新回到空闲状态,使其能够协助其余处于等待状态的机器人完成任务。
借鉴L.S.Farhy提出的激素分泌的规律[15],定义系统中引起焦躁情绪的激素分泌模型为
| $F\left( t \right) = \frac{1}{{{{\left( {T/t} \right)}^n} + 1}}$ | (6) |
式中:T为阈值,t为时间变量,n为Hill系数,且n≥1。
机器人处于等待状态而分泌激素,当其超过设定阈值C时,机器人会放弃等待的任务,回到空闲状态,且机器人会对该任务产生记忆,避免在该任务处于未分配状态时再次选择,陷入循环死锁状态。若该任务处于协作状态时,其对该机器人的激励将会被弱化,表达式如式(7)所示:
| $g{'_{ij}} = \eta \cdot {g_{ij}}$ | (7) |
式中:gij为抗原对抗体的激励表达式;η为调整参数,0<η<1。
2.4 算法流程在多机器人系统中,采用混合式的结构实现文中算法,服务端通过多进程模拟机器人,实现任务的分配,可以降低网络通信消耗,每个进程与一个实际的机器人通过网络通信,保持状态同步,多个机器并行运行。算法步骤如下:
① 初始化系统抗原抗体信息;
② 计算空闲机器人与待分配任务和待协作任务的综合激励值;
③ 各机器人自主解除冲突,选择合适的任务,并向任务处移动;
④ 机器人判断能否完成任务,若能跳到⑥,否则转到⑤;
⑤ 机器人状态更改,事件触发,转到②,等待合适的空闲机器协作;
⑥ 机器人独自或协作完成相应任务;
⑦ 系统终止,否则转到⑧;
⑧ 状态更新,事件触发,转到②。
算法的程序流程图如图2所示:

|
Download:
|
| 图 2 多机器人动态任务分配流程 Fig. 2 Multi-robot dynamic task allocation | |
多机器人系统的通信和计算消耗是任务分配算法中重要的衡量指标[14],对于维持整个系统的稳定起着重要的作用。为了和其他算法进行比较,以机器人数量n和任务量m的函数形式O(·)来描述通讯量和计算量。
通讯量表示机器人在一次任务选择时的信息交互量。从通信量来看,由于本系统采用混合式结构实现,每一个机器人都拥有服务子进程专门服务,每个服务子进程为相应机器人选择当前最合适的任务,在服务端进行任务冲突解决,并不需要机器人实际通信解除冲突。只在任务的下达和任务反馈时需要进行通信,所以一次任务分配中每个机器人的通信量是O(1)。
计算量表示机器人选择一次任务所需要计算的时间复杂度。机器人每次选择任务,都需要进行m次综合激励计算,选择合适的任务,然后需要进行n次比较解决任务冲突问题,当有k个机器人任务冲突,需要2k次计算解决任务冲突,故计算量是O(m+n+2k)。
按照任务分配类型,文中算法满足“同时”、“再分配”,“同时”指可以考虑多个待分配任务,“再分配”指任务能够进行重分配[16]。这种任务分配方法明显优于“顺序”、“无再分配”、无法适应动态环境的算法,故不做对比。本文算法ALLIANCE[4]、BLE[17]性能比较如表2所示。
| 表 2 任务分配算法性能 Tab.2 Task allocation algorithm performance |
为了验证基于事件驱动免疫网络算法的有效性,在MATLAB 2012b平台上,设置动态的清理搜集,进行多机器人实验。设计不同场景,分别验证文中算法的动态任务分配和协作性能,以及系统自主处理任务死锁能力。系统监测节点可以实时感知任务是否产生及产生的位置,而任务能否独自完成需要机器人任务执行过程中进行判断,事先无法获知。
3.1 仿真实验及其结果分析 3.1.1 实验环境参数仿真环境设定为10 m×10 m的区域,实验中以圆形“○”代表机器人,以正方形“□”表示任务,R1/1代表1号机器人,且其能力值为1,T1/1代表任务1,且其完成需要的能力值为1,机器人的移动速率设为v=0.1 m/s(可自行设定),任务优先级设为p=1(可自行设定,不失一般性)。算法中参数设置为:λ1=0.6,λ2=0.4,λ3=0.2,λ4=0.5,λ5=0.5,λ6=0.2,α=0.6,β=0.4,η=0.6,C=0.6,T=5,n=5。
设定两种仿真实验环境,环境1中,初始设定6个静态任务:T1/1,坐标(3, 2.5);T2/2,坐标(2, 7);T3/1,坐标(5.5, 4);T4/1,坐标(7, 2);T5/1,坐标(6, 6);T6/1,坐标(8, 8.5),在机器人运行过程中,设定两个动态任务:T7/1,坐标(5, 2);T8/1,坐标(8, 6)。在环境中设有4个同构机器人,分别放置在不同的位置:R1/1,坐标(0.1, 0.1);R2/1,坐标(9.9, 0.1);R3/1,坐标(9.9, 9.9);R4/1,坐标(0.1, 9.9)。
在环境2中,主要是为了验证算法的自主解死锁能力,不失一般性,在环境中设置两个静态任务:T1/2,坐标(2, 2);T2/3,坐标(6, 4)。设置两个机器人:R1/1,坐标(0.1, 0.1);R2/2,坐标(9.9, 0.1)。
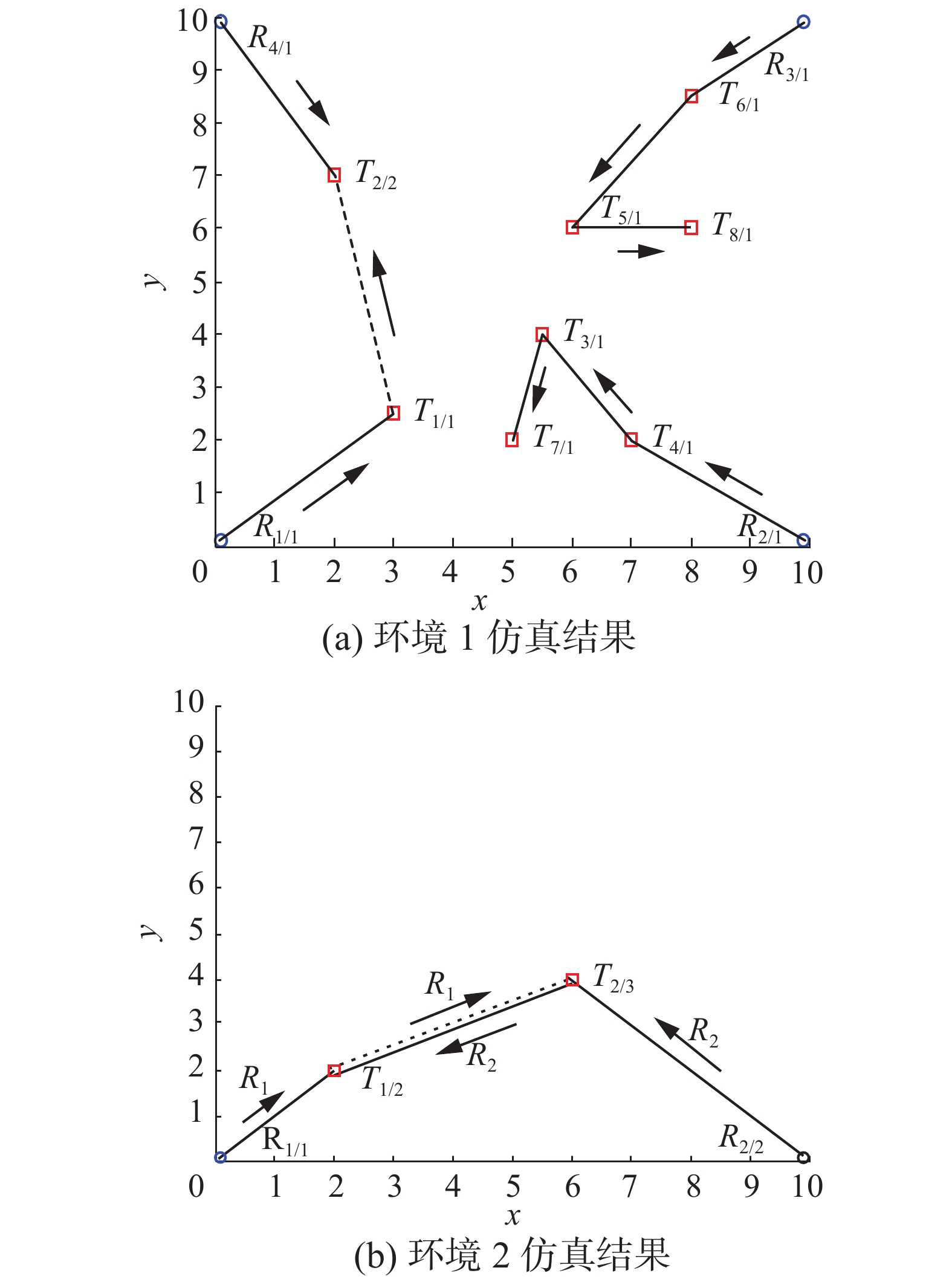
3.1.2 仿真实验结果分析如图3(a)所示为环境1的仿真结果。图中虚线代表前去协作过程,实线代表首次被某任务激励而前往过程。根据本文算法,在初始时刻,每个机器人被相应的任务所激励,机器人R1/1前往T1/1,R2/1前往T4/1,R3/1前往T6/1,R4/1前往T2/2,当机器人执行任务时,会判断是否可以独立完成,如果可以独自完成则开始执行任务,否则更改状态,触发请求协作。在第1次任务分配中,由于机器人速度相同,机器人R2/1和R3/1先于R1/1完成任务,进行第2次任务选择,而此时R4/1机器人在T2/2处等待协作,由于距离较远,机器人R2/1和R3/1被任务T3/1和T5/1所激励,R1/1完成T1/1后,初始的静态任务只剩下处于等待协作的T2/2,其被激励前往协作。在所有机器人都处于二次激励时,系统产生动态任务T7/1和T8/1,触发请求任务分配,然而此时没有处于闲暇状态的机器人,任务暂时不会被分配,在R2/1和R3/1完成T3/1和T5/1后被T7/1和T8/1再次激励,前往任务处进行处理。
|
Download:
|
| 图 3 仿真结果 Fig. 3 Simulation result | |
如图3(b)所示为环境2的仿真结果。初始时刻,机器人R1/1和R2/2分别被T1/2和T2/3所激励,机器人R1/1先到达任务处进行协作等待,同时开始分泌激素,R2/2随后到达T2/3,亦处于协作等待,同时开始分泌激素,随着时间的增加,机器人R1/1产生焦躁情绪而放弃等待,同时标记任务T1/2,随后R1/1前往协作处理T2/3,机器人R2/2得到协作,在任务T2/3完成后,机器人R2/2受到T1/2任务激励,前往完成,结果表明,系统能够可以成功解除死锁。
多次实验验证表明,基于事件驱动的免疫网络算法能够实现动态任务场景中多机器人的任务自主分配与协作,具有较强的适应性和鲁棒性。
3.2 多器人系统实验及其结果分析为了验证文中算法在实际多机器人动态任务分配系统中的有效性,利用多个khepera机器人,搭建多机器人障碍物环境,利用摄像头进行环境监测,当监测到系统中有任务(以红色物品代替)产生时,利用文中算法,激励相应的机器人前往完成任务,并采用人工势场法使机器人可以避开障碍,安全到达任务点。系统中机器人间利用网络与服务器通信。
图4(a)为系统中机器人系统初始图,当在系统中放置相应物品,将会触发系统进行任务分配,图4(b)为机器人被相应任务激励前往目标示意图。

|
Download:
|
| 图 4 实际机器人系统仿真图 Fig. 4 Actual robot system simulation | |
经过多次实验,设置不同任务,系统都能快速反应,激励相应的机器人进行任务的执行与协作,验证了文中算法在实际多机器人动态任务分配系统中具有较高的可行性。
4 结束语针对一类复杂的松散型动态任务,文中基于免疫网络和事件驱动机制,提出一种动态任务分配算法,解决了多机器人的动态任务分配与自主协作问题,并利用焦躁模型解决了任务分配过程中的死锁问题,仿真和实验表明本文算法在一类需要协作的动态任务分配问题中的有效性,具有较强的自适应性。将文中算法应用于实际场景的多机器人系统中,取得了较好的效果,表明将本文算法应用到实际的多机器人系统中有较高的可行性。课题后续将把重点放在分配模型的优化和实际应用的拓展上,在提高算法性能的同时,能够实现更大的实际价值。
| [1] |
TAVASOLI A, EGHTESAD M, JAFARIAN H. Two-time scale control and observer design for trajectory tracking of two cooperating robot manipulators moving a flexible beam[J]. Robotics and autonomous systems, 2009, 57(2): 212-221. DOI:10.1016/j.robot.2008.04.003 ( 0) 0)
|
| [2] |
DAHL T S, MATARIC M, SUKHATME G S. Multi-robot task allocation through vacancy chain scheduling[J]. Robotics and autonomous system, 2009, 57(6/7): 674-687. ( 0) 0)
|
| [3] |
ZHOU Pucheng, HONG Bingrong, WANG Yuehai, et al. Multi-agent cooperative pursuit based on extended contract net protocol[C]//Proceeding of 2004 International Conference on Machine Learning and Cybernetics. Shanghai, China, 2004: 169–173.
( 0) 0)
|
| [4] |
PARKER L E. ALLIANCE: an architecture for fault tolerant multirobot cooperation[J]. IEEE transactions on robotics and automation, 1998, 14(2): 220-240. DOI:10.1109/70.681242 ( 0) 0)
|
| [5] |
许建豪. 云计算中基于拍卖的虚拟机动态供应和分配算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(4): 585-592. XU Jianhao. Virtual machine dynamic supply and allocation algorithm based on auction in cloud computing[J]. Journal of Chongqing university of posts and telecommunications: natural science edition, 2016, 28(4): 585-592. (  0) 0)
|
| [6] |
袁明新, 叶兆莉, 程帅, 等. 干扰素调节的多机器人协作搬运免疫网络算法[J]. 智能系统学报, 2014, 9(1): 76-82. YUAN Mingxin, YE Zhaoli, CHENG Shuai, et al. Multi-robot cooperative handling based on immune network algorithm regulated by interferon[J]. CAAI transactions on intelligent systems, 2014, 9(1): 76-82. (  0) 0)
|
| [7] |
袁明新, 李平正, 江亚峰, 等. 基于胸腺肽调节机制的多机器人免疫任务分配[J]. 模式识别与人工智能, 2014, 27(5): 472-479. YUAN Mingxin, LI Pingzheng, JIANG Yafeng, et al. Immune task allocation for multi-robot system based on adjustment mechanism of thymic peptide[J]. Pattern recognition and artificial intelligence, 2014, 27(5): 472-479. DOI:10.3969/j.issn.1003-6059.2014.05.011 (  0) 0)
|
| [8] |
丁永生. 基于生物网络的智能控制与优化研究进展[J]. 控制工程, 2010, 17(4): 416-421, 536. DING Yongsheng. Research development of bio-network based intelligent control and optimization[J]. Control engineering of China, 2010, 17(4): 416-421, 536. DOI:10.3969/j.issn.1671-7848.2010.04.002 (  0) 0)
|
| [9] |
丁永生. 计算智能的新框架: 生物网络结构[J]. 智能系统学报, 2007, 2(2): 26-30. DING Yongsheng. A new scheme for computational intelligence: bio-network architecture[J]. CAAI transactions on intelligent systems, 2007, 2(2): 26-30. (  0) 0)
|
| [10] |
靳明双, 郜帅, 张宏科. 智慧协同网络研究进展[J]. 重庆邮电大学学报: 自然科学版, 2018, 30(1): 22-32. JIN Mingshuang, GAO shuai, ZHANG Hongke. Research progress of smart collaborative identifier networks[J]. Journal of Chongqing university of posts and telecommunications: natural science edition, 2018, 30(1): 22-32. (  0) 0)
|
| [11] |
JERNE N K. Towards a network theory of the immune system[J]. Annales d’immunologie, 1974, 125(1/2): 373-389. ( 0) 0)
|
| [12] |
FARMER J D, PACKARD N H, PERELSON A S. The immune system, adaptation, and machine learning[J]. Physica D: nonlinear phenomena, 1986, 22(1/2/3): 187-204. ( 0) 0)
|
| [13] |
陈蕊, 丁永生, 郝矿荣. 基于事件驱动的动态免疫分簇路由算法[J]. 计算机应用研究, 2016, 33(7): 2087-2090, 2109. CHEN Rui, DING Yongsheng, HAO Kuangrong. Event-driven dynamic immune clustering routing algorithm[J]. Application research of computers, 2016, 33(7): 2087-2090, 2109. DOI:10.3969/j.issn.1001-3695.2016.07.037 (  0) 0)
|
| [14] |
高云园, 韦巍. 未知环境中基于免疫网络的多机器人自主协作[J]. 浙江大学学报: 工学版, 2006, 40(5): 733-737. GAO Yunyuan, WEI Wei. Multi-robot self-determination cooperation based on immune network in an unknown environment[J]. Journal of Zhejiang university: engineering science, 2006, 40(5): 733-737. (  0) 0)
|
| [15] |
FARHY L S. Modeling of oscillations in endocrine networks with feedback[J]. Methods in Enzymology, 2004, 384: 54-81. DOI:10.1016/S0076-6879(04)84005-9 ( 0) 0)
|
| [16] |
GERKEY B P, MATARIĆ M J. A formal analysis and taxonomy of task allocation in multi-robot systems[J]. The international journal of robotics research, 2004, 23(9): 939-954. DOI:10.1177/0278364904045564 ( 0) 0)
|
| [17] |
WERGER B B, MATARIC M J. Broadcast of local eligibility: behavior-based control for strongly cooperative robot teams[C]//Proceedings of the 4th International Conference on Autonomous Agents. Barcelona, Spain, 2000: 21–22.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


