1985年，Powell提出多变量插值的径向基函数(radical basic function, RBF)方法。1988年，Moody和Darken^[1]提出了一种神经网络结构，即RBF神经网络。该网络能够以任意精度逼近任意连续函数，非线性拟合能力强，具有很强的鲁棒性，因此应用广泛，如海洋表面温度预测^[2]、网络安全态势预测^[3]、智能轮椅自适应控制^[4]、失业率预测^[5]、电力系统的可用输电能力在线估计^[6]、在线恶意垃圾邮件检测^[7]等。随着应用范围的推广，研究者们发现RBF神经网络仍存在一些不足，制约其进一步的发展和应用，故许多专家学者提出了一些改进算法，如有学者提出对神经网络的结构进行优化，相关学习算法主要有两大类：1)先构造复杂的网络结构，再通过训练精简网络结构，如韩敏等^[8]提出了一种改进的RAN算法，该方法采用样本的输入输出信息对网络进行初始化，再根据FPE剪枝策略对网络结构进行简化；2)先采用精简的网络结构，再通过训练增大网络规模，直至达到泛化要求，如Platt等^[9]提出了一种资源分配网络，该方法首先创建一个精简网络，当网络出现异常模式时，通过分配新单元和修改已有单元参数来进行学习，直至网络稳定。基于聚类的RBF神经网络隐含层数据中心一般通过K-means聚类算法获得，故有学者提出对该聚类方法进行优化以提高算法泛化性能^[10-12]。此外，还有一些学者研究各种基于进化算法的RBF神经网络^[13-15]。如Lacerda等^[13]提出使用遗传算法优化学习参数；Shekhar等^[14]提出使用模拟退火算法确定神经网络的连接权值；Alexandridis等^[15]提出使用粒子群算法和模糊均值法确定隐含层的中心，改进网络的结构等。

从上述文献综述可以发现，以往的研究主要围绕RBF神经网络的网络结构和参数设计展开，所解决问题的场景是采集到的数据能反映数据集的分布情况，但在实际应用中，信息采集器或传感器设备可能会出现故障，导致采集到的数据不完整。训练样本不完整，或多或少都会影响RBF神经网络的学习效率，使网络的推广能力变差。训练样本反映数据集总体分布的程度对算法的泛化性能有着重要的影响。到目前为止，样本数量和质量对RBF神经网络算法泛化性能影响方面的研究还不多。针对上述问题，本文将迁移学习思想引入RBF神经网络，提出已标签样本少时的RBF神经网络学习算法。所谓迁移学习，就是学习已有的源领域知识来解决目标领域中已标签样本数量较少甚至没有的学习问题^[16-17]。该思想已广泛应用于分类、回归、概率密度估计等各类机器学习领域。本文在文献[18]提出的 $\varepsilon \text{-} $ RBF算法的基础上，提出了具有迁移学习能力的RBF神经网络(ε-RBF with transfer learning ability， $\varepsilon \text{-} $ TLRBF)算法，通过引入 $\varepsilon $ 不敏感损失函数和学习源领域径向基函数的中心向量及核宽和源领域模型参数，帮助目标领域建立模型。

1 RBF神经网络

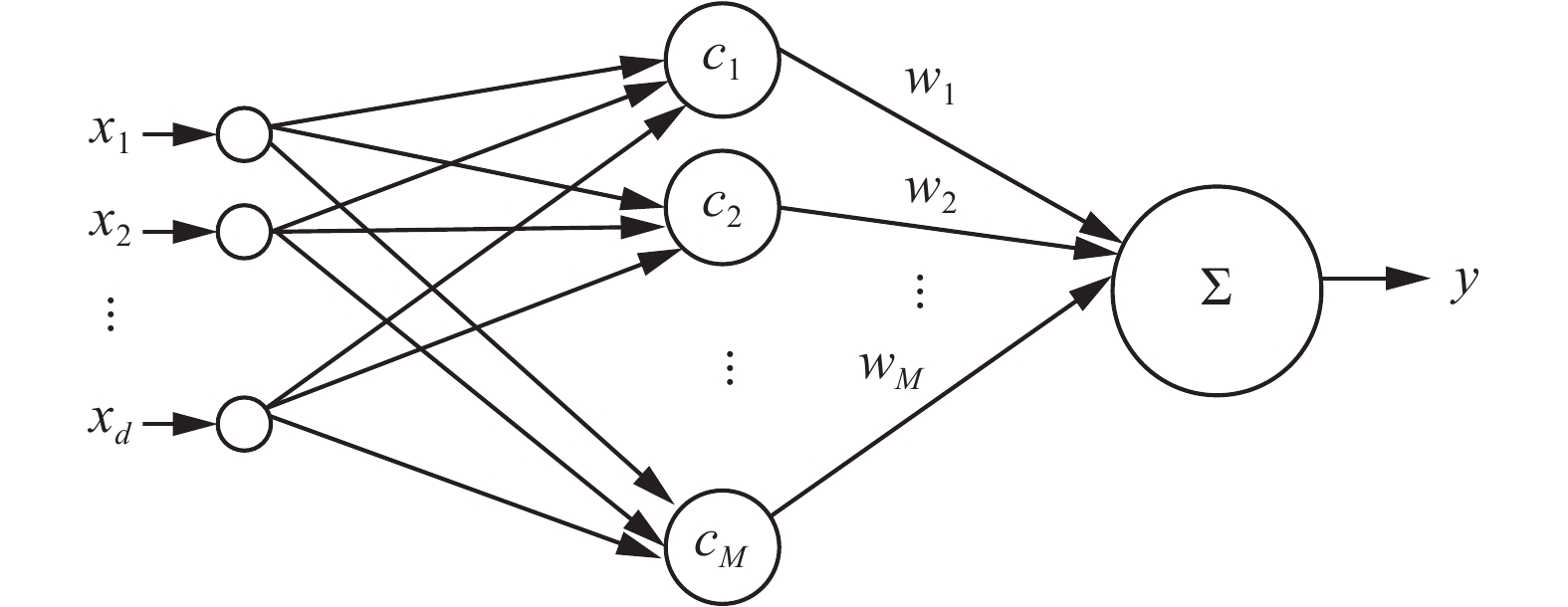
RBF神经网络由输入层、隐含层和输出层组成，由图1所示。其中， ${{{x}}_i} \in {R^d}$ ， $y \in R$ ，隐含层节点数为M，RBF神经网络完成 $f:{R^d} \to R$ 的非线性映射。

在RBF神经网络中，输入层接收训练样本；隐含层节点通过径向基函数执行一种非线性变化，将输入空间映射到一个新的空间，若该径向基函数定义为高斯函数，设 ${{{c}}_i} \in {R^d}$ 表示高斯函数的中心， ${\delta _i}$ 表示高斯函数的核宽，该函数可表示为

$\phi \left( {\left\| {{{x}} - {{{c}}_i}} \right\|} \right) = \exp \left( { - \frac{{{{\left\| {{{x}} - {{{c}}_i}} \right\|}^2}}}{{{\delta _i}}}} \right)$

(1)

输出层节点在该新空间实现线性加权组合。设 ${w_i}$ 为隐含层与输出层的连接权值， $\phi \left( \bullet \right)$ 为径向基函数， ${R^d} \to R$ 的映射函数为

$y = f\left( {{x}} \right) = \sum\limits_{i = 1}^M {{w_i}\phi \left( {\left\| {{{x}} - {{{c}}_i}} \right\|} \right)}\quad\quad i = 1,2, \cdots ,M$

(2)

2 RBF神经网络与线性模型

由第1节介绍可知，RBF神经网络的参数有3个，径向基函数的中心向量 ${{{c}}_i} = {\left[ {{c_{i1}}\,\,\,{c_{i2}}\,\,\, \cdots \,\,\, {c_{id}}} \right]^{\rm{T}}}$ ，核宽 ${\delta _i}$ 和隐含层与输出层的连接权值 ${w_i}$ 。其中， ${{{c}}_i}$ 、 ${\delta _i}$ 可利用模糊C均值(FCM)聚类技术确定，参数 ${w_i}$ 利用梯度下降学习算法获得。设 ${\mu _{ji}}$ 表示FCM聚类算法得到的样本 ${{{x}}_j}$ 对于第 $i$ 类的模糊隶属度， $h$ 是可调缩放参数，n表示训练样本规模，M表示隐含层节点数，径向基函数的中心 ${{{c}}_{ik}}$ 和核宽 ${\delta _i}$ 可由式(3)表示：

$c_{ik}^{} = \frac{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{ji}}{x_{jk}}} }}{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{ji}}} }},\delta _i^{} = h\frac{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{ji}}{{\left\| {{{{x}}_j} - {{{c}}_i}} \right\|}^2}} }}{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{ji}}} }}$

(3)

令 ${\tilde x^i} = \phi \left( {\left\| {{{x}} - {{{c}}_i}} \right\|} \right)$ ， $i = 1,2, \cdots ,M$

${{{\tilde x}}_g} = {\left[ {{{\tilde x}^1}\,\,{{\tilde x}^2}\,\, \cdots \,\,{{\tilde x}^M}} \right]^{\rm{T}}}$

(4)

通过式(3)得到径向基函数的中心 ${{{c}}_i}$ 和核宽 ${\delta _i}$ ，代入式(1)将输入样本映射到新空间 $f:{R^d} \to {R^M}$ ，输入层至隐含层的转换为非线性映射。

设 ${{{p}}_g} = {\left[ {{w_1}\,\,{w_2}\,\, \cdots \,\,{w_M}} \right]^{\rm{T}}}$ ，神经网络函数可表示为

$y = {{{p}}_g}^{\rm{T}}{{{\tilde x}}_g}$

(5)

由式(5)可知，当径向基函数隐含层被估计后，网络的输出可转换成一个线性模型。

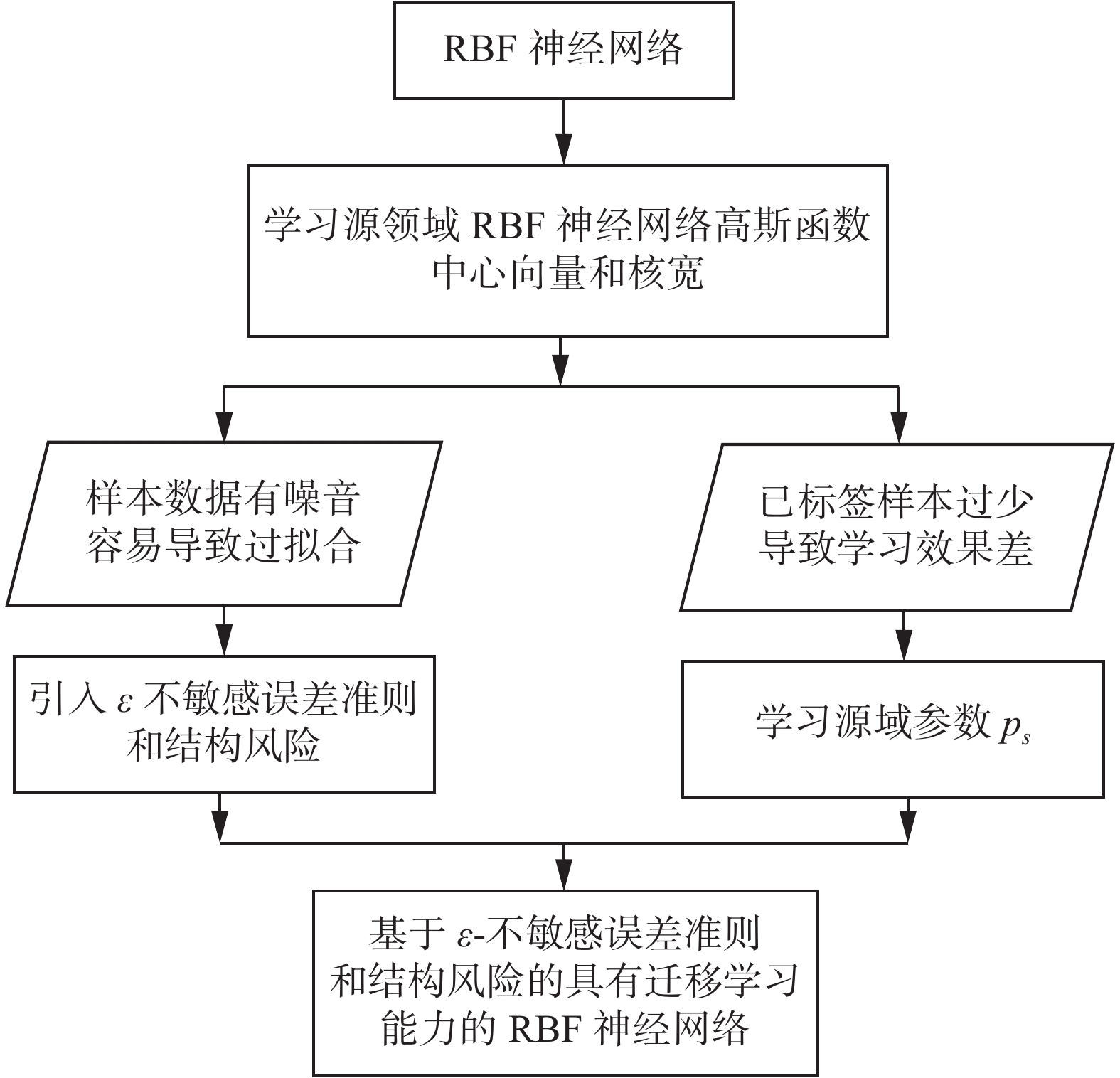
3 具有迁移学习能力的RBF神经网络

对于经典的RBF神经网络算法中的参数 ${w_i}$ ，常采用梯度下降学习策略。但该策略的缺陷是抗噪音能力差以及对小样本数据集的泛化能力差。针对上述两问题，本文提出算法在引入 $\varepsilon $ 不敏感损失函数提高算法的抗噪能力的基础上，通过学习已有源领域知识解决小样本泛化能力差的问题。通过第1、第2节分析可知，RBF神经网络学习分为两大部分：1)利用径向基函数映射到新空间；2)采用梯度下降法求参数 ${w_i}$ ，本文所提算法学习源领域已有知识也从这两方面进行考虑。因目标领域样本较少，不能反映数据集整体分布情况，故通过FCM聚类算法获得的聚类中心并不一定能反映目标域数据集的聚类中心，而源领域与目标领域存在一定的相似性，故 $\varepsilon \text{-}{\rm{TLRBF}}$ 算法首先学习源领域径向基函数的中心向量和核宽，接着引入 $\varepsilon $ 不敏感损失函数和结构风险项并学习源领域已知参数 ${w_i}$ ，建立目标领域模型，算法思路如图2所示。

下面具体介绍算法的实现。

设源领域高斯函数中心向量集 $C \!=\! \{ {{{c}}_1},{{{c}}_2}, \cdots ,{{{c}}_M}\} $ ，核宽集合 ${{\Delta }} = \{ {\delta _1},{\delta _2}, \cdots ,{\delta _M}\} $ ，源领域核宽可调缩放参数 ${h_s}$ ，模型参数 ${{{p}}_s}$ ，其中M为隐含层节点个数。目标领域数据集为 ${X_t} = \{ ({{{x}}_i},{y_i})\} _{i = 1}^n$ ，其中， ${{{x}}_i} \in {R^d}$ ，n为目标域样本数，且 $n > M$ 。

1)设 ${h_g}$ 为目标域核宽的可调参数，目标域中心向量集 ${C_g} = \{{{{c}}_{g1}},{{{c}}_{g2}}, \cdots ,{{{c}}_{gM}}\}$ 中每一个中心向量 ${{{c}}_{gi}}$ 学习源领域高斯函数中心向量 ${{{c}}_i}$ ，目标域高斯函数核宽 $\delta _{gi}^{}$ ，学习源领域核宽 ${\delta _i}$ 获得，如式(6)表示，实现输入层至隐含层 ${R^d} \to {R^M}$ 的非线性映射，得到新空间的数据集 ${\tilde X_g} = \{ ({{{\tilde x}}_{gi}},{y_i})\} _{i = 1}^n$ ，其中， ${{{\tilde x}}_{gi}} \in {R^M}$ 。

${{{c}}_{gi}} = {{{c}}_i},\delta _{gi}^{} = {h_g}\frac{{{\delta _i}}}{{{h_s}}},i = 1,2, \cdots ,M$

(6)

2)引入 $\varepsilon $ 不敏感损失函数和结构风险项并学习源领域已知参数 ${{{p}}_s}$ ，取代梯度下降法求目标领域模型参数 ${{{p}}_g}$ 。

首先，给出 $\varepsilon $ 不敏感损失函数的定义：

定义 (线性) $\varepsilon $ 不敏感损失函数 ${L^\varepsilon }\left( {{{x}},y,f} \right)$ 定义为^[19]

${L^\varepsilon }\left( {{{x}},y,f} \right) = {\left| {y - f\left( {{x}} \right)} \right|_\varepsilon } = \max \left( {0,{{\left| {y - f\left( {{x}} \right)} \right|}_\varepsilon }} \right)$

式中： ${{{x}}_i} \in {R^d}$ ， $y \in R$ 。

对于式(5)线性模型，其对应的 $\varepsilon $ 不敏感损失函数可表示为

$\begin{gathered} \sum\limits_{i = 1}^n {{{\left| {y_i^o - {y_i}} \right|}_\varepsilon }} = \sum\limits_{i = 1}^n {\max \left( {0,\left| {y_i^o - {y_i}} \right| - \varepsilon } \right)} = \\ \sum\limits_{i = 1}^n {\max \left( {0,\left| {{{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i}} \right| - \varepsilon } \right)} \\ \end{gathered} $

(7)

式中： $y_i^o$ 表示神经网络输出， ${y_i}$ 表示真实输出。

对于式(7)， ${{{p}}_g}^{\rm{T}}{{{\tilde x}}_{gi}} - {y_i} < \varepsilon $ 和 ${y_i} - {{{p}}_g}^{\rm{T}}{{{\tilde x}}_{gi}} < \varepsilon $ 的约束条件并不一定总能满足，故引入松弛因子 $\xi _i^{}$ 和 $\xi _i^*$ ，可得到如下约束条件：

$\left\{ {\begin{array}{*{20}{c}}{{y_i} - {{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} < \varepsilon + \xi _i^{}}\\{{{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i} < \varepsilon + \xi _i^*}\end{array}} \right.,\xi _i^{} \geqslant 0,\xi _i^* \geqslant 0$

(8)

本算法的目的是要使式(7)表示的 $\varepsilon $ 不敏感损失函数值最小，结合式(8)，可等价表示为

$\begin{gathered} \min \sum\limits_{i = 1}^n {\left( {{\xi _i} + \xi _i^*} \right)} \\ {\rm{s.t.}}\left\{ {\begin{array}{*{20}{c}} {{y_i} - {{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} < \varepsilon + \xi _i^{}} \\ {{{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i} < \varepsilon + \xi _i^*} \end{array}} \right.,{\xi _i} \geqslant 0,\xi _i^* \geqslant 0 \\ \end{gathered} $

(9)

接着，加入结构化风险项。支持向量机是结构风险最小化原则的一种实现，学习支持向量机的实现方法，引入正则化项 $\displaystyle\frac{1}{2}{{{w}}_g}^{\rm{T}}{{{w}}_g}$ ，使算法结构风险最小，故式(9)加入结构化风险项后可用式(10)表示：

$\begin{gathered} \mathop {\min }\limits_{{{p}},{\xi _i},{\xi _i}^*} \frac{1}{2}{\left\| {{{{p}}_g}} \right\|^2} + C\sum\limits_{i = 1}^n {\left( {{\xi _i} + {\xi _i}^*} \right)} \\{\rm{s.t.}}\left\{ {\begin{array}{*{20}{c}} {{y_i} - {{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} < \varepsilon + \xi _i^{}} \\ {{{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i} < \varepsilon + \xi _i^*} \end{array}} \right.,{\xi _i} \geqslant 0,\xi _i^* \geqslant 0,i = 1,2, \cdots ,n \\ \end{gathered} $

(10)

最后，为了使本文提出算法具有迁移学习能力，在学习源领域径向基函数的中心向量和核宽后，加入学习源领域模型参数 ${{{p}}_s}$ 项 ${\left\| {{{{p}}_s} - {{{p}}_g}} \right\|^2}$ ，故最终，所求解的问题可表示为

$\begin{gathered} \mathop {\min }\limits_{{{p}},{\xi _i},{\xi _i}^*} \frac{1}{2}{\left\| {{{{p}}_g}} \right\|^2} + C\sum\limits_{i = 1}^n {\left( {{\xi _i} + {\xi _i}^*} \right)} + \frac{\lambda }{2}{\left\| {{{{p}}_s} - {{{p}}_g}} \right\|^2} \\{\rm{s.t.}}\left\{ {\begin{array}{*{20}{c}} {{y_i} - {{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} < \varepsilon + \xi _i^{}} \\ {{{{p}}_g}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i} < \varepsilon + \xi _i^*} \end{array}} \right.,{\xi _i} \geqslant 0,\xi _i^* \geqslant 0,i = 1,2, \cdots ,n \\ \end{gathered} $

(11)

引入拉格朗日乘子，构造出式(11)的拉格朗日函数：

$\begin{gathered} L = \frac{1}{2}{\left\| {{{{p}}_g}} \right\|^2} + C\sum\limits_{i = 1}^n {\left( {{\xi _i} + {\xi _i}^*} \right)} + \frac{\lambda }{2}{\left\| {{{{p}}_s} - {{{p}}_g}} \right\|^2} + \\ \sum\limits_{i = 1}^n {{\alpha _i}\left( {{y_i} - {{{p}}_g}{}^{\rm{T}}{{{{\tilde x}}}_{gi}} - \varepsilon - {\xi _i}} \right)} + \sum\limits_{i = 1}^n {{\alpha _i}^*\left( {{{{p}}_g}{}^{\rm{T}}{{{{\tilde x}}}_{gi}} - {y_i} - \varepsilon - {\xi _i}^*} \right)} - \\ \sum\limits_{i = 1}^n {{\beta _i}} {\xi _i} - \sum\limits_{i = 1}^n {{\beta _i}^*} {\xi _i}^* \\ \end{gathered} $

(12)

式(12)相应的对偶问题形式为

$\begin{gathered} \mathop {\max }\limits_{{\alpha }} - \frac{{\displaystyle\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\alpha _i}^*} \right)\left( {{\alpha _j} - {\alpha _j}^*} \right){{{{\tilde x}}}_{gi}}^{\rm{T}}{{{{\tilde x}}}_{gj}}} } }}{{2\left( {1 + \lambda } \right)}} + \\ \sum\limits_{i = 1}^n {{\alpha _i}\left( {{y_i} - \varepsilon - \frac{\lambda }{{\left( {1 + \lambda } \right)}}{{{p}}_s}^{\rm{T}}{{{{\tilde x}}}_{gi}}} \right)} + \\ \sum\limits_{i = 1}^n {{\alpha _i}^*\left( { - {y_i} - \varepsilon + \frac{\lambda }{{\left( {1 + \lambda } \right)}}{{{p}}_s}^{\rm{T}}{{{{\tilde x}}}_{gi}}} \right)}\\ {\rm{s.t.}}\quad\quad 0 \leqslant {\alpha _i}^{(*)} \leqslant C \\ \end{gathered} $

(13)

利用式(13)得到最优解：

${{{p}}_g} = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {{\alpha _i} - {\alpha _i}^*} \right){{{{\tilde x}}}_{gi}}} + \lambda {{{p}}_s}}}{{\left( {1 + \lambda } \right)}}$

(14)

基于上述分析，基于 $\varepsilon $ 不敏感误差准则和结构风险最小的具有迁移学习能力的RBF神经网络学习算法步骤如下表所示：

1) 学习源领域径向基函数中心向量和核宽，确定h_g值，带入式(6)，得目标领域高斯函数中心向量c_gi和核宽δ_gi；

2) 将目标领域高斯核中心向量c_gi和核宽δ_gi带入式(1)得 ${{{\tilde x}}_{gi}}$ ；

3) 求解式(13)对应的二次规划问题；

4) 利用式(13)求得的二次规划最优解，根据式(14)求得隐含层和输出层之间的权值 ${{{p}}_g}$ ；

5) 利用公式 $y = {{{p}}_g}^{\rm{T}}{{{\tilde x}}_g}$ 求得网络层的输出。

上述算法参数设置除高斯函数核宽中的可调参数h_g外，还有式(13)需设置的3个参数，分别是 $C$ 、 $\varepsilon $ 、 $\lambda $ ，确定参数的方法是网格搜索策略，5重交叉验证获得。

4 实验研究 4.1 实验设置

本节利用模拟数据集和在谷氨酸发酵过程中采集的真实数据集对本文所提算法进行实验验证。在4.2节和4.3节分别描述模拟数据集和真实数据集的构成及实验结果分析。为了突显本文所提算法的优势，两组实验在3个场景下进行，场景1为目标域数据集RBF神经网络算法训练；场景2为源领域历史数据集和目标领域当前数据集RBF神经网络算法合并训练；场景3为加入源领域历史知识的目标领域数据集 $\varepsilon \text{-} {\rm{TLRBF}}$ 迁移学习训练。

为了有效评估算法的性能，采用如下性能指标^[18]：

$J = \sqrt {{{\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{y_i}' - {y_i}} \right)}^2}} }/{\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{y_i} - \bar y} \right)}^2}} } \right]}}} $

式中：N表示测试样本规模，y_i表示第i个样本的采样输出， ${y_i}'$ 表示第i个样本的径向基神经网络输出。

4.2 模拟数据集实验

在已标签数据较少而导致RBF神经网络预测精度降低的前提下，验证本文所提算法可通过学习相关历史领域知识提高预测精度。所设计的模拟数据集符合以下两个原则：1)当前数据集和历史数据集既存在相关性，又有自己的数据分布特点；2)当前目标域数据集已标签样本较少，无法反映出数据集的整体分布情况。

为了表征以上两个原则，采用函数 $Y = x\sin x $ ^[20]来表示历史场景。其中， $x \in [ - 10,10]$ 。按照此函数生成包含100个样本的历史场景数据集(DS₁)。采用函数 $y = r \times Y + N\left( {0,0.1} \right)$ 表示当前场景。其中， $N\left( {0,0.1} \right)$ 表示均值为0，标准差为0.1的白噪声； $r$ 表示当前场景与历史场景的相关系数， $r$ 值越大，表示相关性越高。实验中 $r$ 的取值为0.9,0.85,0.8,0.75,0.7,0.6。按照目标域场景函数生成包含20个样本的目标域场景数据集(DS₂)。按照 $y = r \times Y$ 函数生成200个测试样本作为测试集。图3表示源领域历史场景函数和相关系数为0.9、0.8、0.7时的目标域场景函数，由图可知，源领域场景函数和目标域场景函数既存在相关性，又存在不同，且系数最小，相关性越小。

实验在相关系数 $r$ 为不同值的前提下进行。因引入 $\varepsilon $ 不敏感损失函数和结构风险项对噪音的影响在文献[17]中已经进行验证，故本文算法学习源领域 $\varepsilon \text{-} $ RBF训练后的各参数值并验证所提算法的迁移学习能力。为每个 $r$ 值各随机生成30组目标域场景数据集，并分别在源领域模型预测、目标域数据集训练、目标域数据集和源领域历史数据集合并训练以及目标域数据集和源领域历史知识迁移学习训练4种情况下进行。 $\varepsilon \text{-} {\rm{TLRBF}}$ 隐含层节点数为15，需确定的参数有4个，h设置为从1~10之间按对数等分的30个值，C在集合 $\{ 1,10,100,500,1\;000\} $ 中取值， $\varepsilon $ 在集合 $\{ 0,{10^{ - 9}}, {10^{ - 8}},$ ${10^{ - 7}},{10^{ - 6}}\} $ 中取值， $\lambda $ 在集合 $\{ 1,3,5, \cdots ,39\} $ 中取值，参数最终值通过网格搜索策略5重交叉验证确定。表1给出了各种算法在模拟数据集上的泛化性能比较。图4给出了相关系数为0.75时的其中一组数据集的训练结果。

由表1和图4可以得出如下结论：

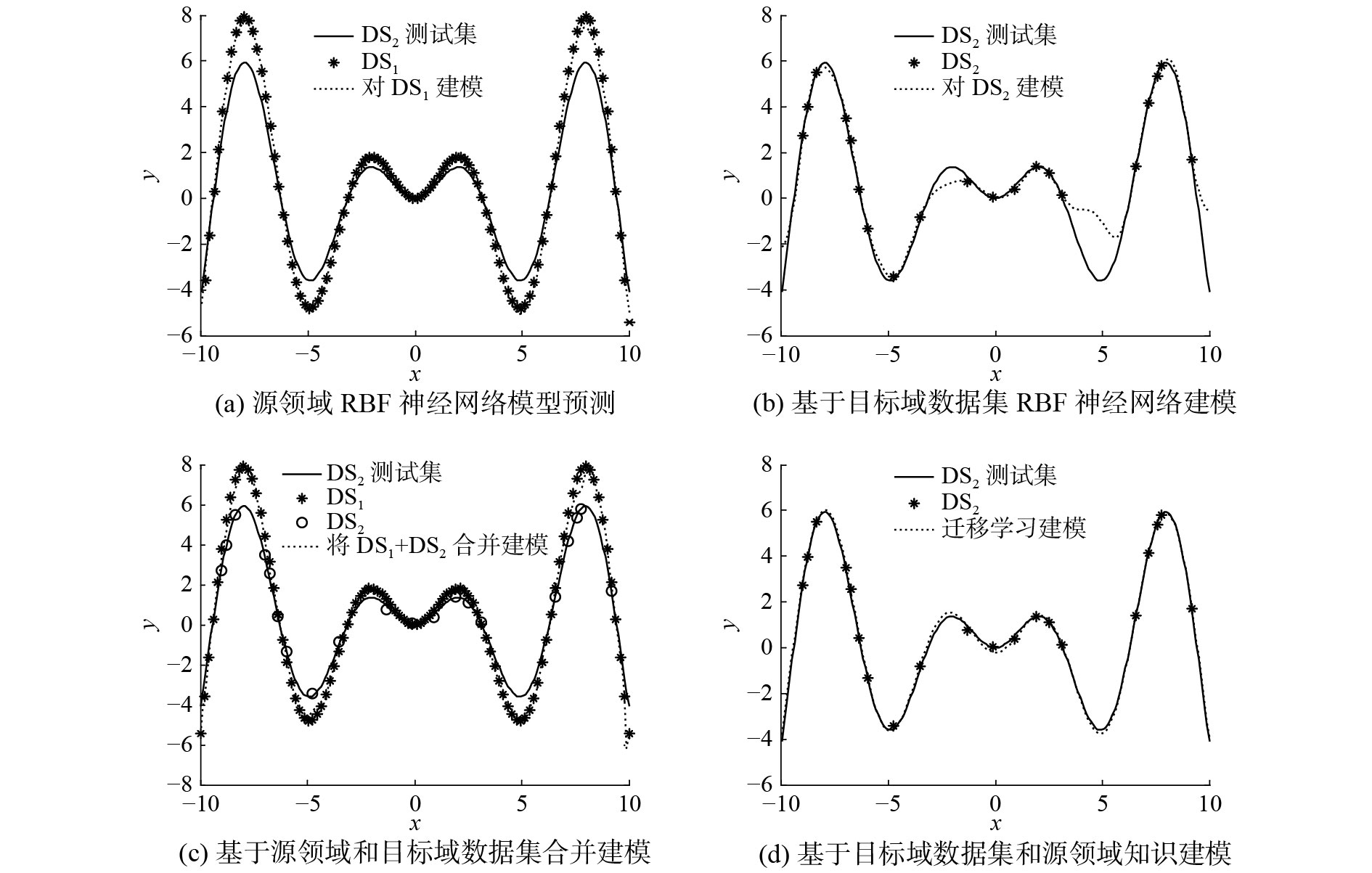
1) 观察表1和图1(a)可知，若直接使用源域模型对目标领域测试集进行预测，目标领域和源领域差异由r为0.9时的0.106 1增大到r为0.65时的0.521 9。随着r系数的减小，源领域与目标域数据分布差异增大，误差增幅明显。

2) 目标域数据集规模较小，存在某些数据段缺失的现象，不能反映目标域数据集的整体分布，如图4(b)所示。传统RBF神经网络算法可以对当前采样数据集逼近，但无法对缺失的地方进行弥补，导致仅用目标域数据集进行训练泛化性能不高，如表1和图4(b)所示。

3) 将源领域数据集和目标域数据集合并训练，算法性能较仅用源领域进行训练并没有明显提高，如表1和图4(c)所示。其原因是源领域数据集对目标领域数据集来说，规模很小，其对于建模的影响作为可容忍噪声忽略了。此外，一些高度机密的源领域历史数据集很难获取，合并训练并不一定能实现。

4) 从表1和图4(d)可知，基于历史知识的迁移学习算法具有较好的性能。和仅用目标领域数据集训练相比，缺失的部分通过历史知识的学习加以弥补，提高了泛化性能；和源领域及目标领域数据集合并训练相比，不仅提高了精度，且因为学习的是知识，而不是所有历史数据集参与训练，历史场景数据还具有保密性。

由此，可以得出结论，本文所提算法解决了RBF-NN算法不具有迁移学习能力的问题。

4.3 真实数据集实验

本部分实验数据来自工厂采集到的真实发酵数据集^[19]。该数据集记录了食品发酵过程中记录下的21批数据，每批数据有14条记录，共有294条记录。该数据集记录了发酵过程的采样时间(h)，葡萄糖浓度(Glucose concentration)，菌体浓度(Thalli concentration)和谷氨酸浓度(Glutamic acid concentration)。其输出为下一时刻的葡萄糖浓度(h+1)、菌体浓度(h+1)和谷氨酸浓度(h+1)。将前1～16批数据共224条记录作为源领域数据集；剩余的5批数据中，17～19批数据42条记录中，任意选取20条记录作为目标域数据集，数据集已标签样本较少，不能反映数据集的整体分布情况；20～21批数据作为目标域测试数据集。

实验中，用3个单输出系统进行仿真，且将RBF、 $\varepsilon $ -RBF、 $\varepsilon $ -TLRBF 3种算法进行比较。实验结果如图5和表2所示。

观察图5和表2，可以得出如下结论，因目标域训练集已标签数据较少，而RBF和 $\varepsilon $ -RBF算法没有迁移学习能力，故两算法泛化性能不理想，而学习了源领域知识的 $\varepsilon $ -TLRBF算法，弥补了数据量小和缺失数据的不足，泛化性能较好。

RBF神经网络算法基于最小平方误差准则，对小样本数据集或存在噪声的数据集容易过拟合而导致泛化性能下降。 $\varepsilon $ -RBF引入 $\varepsilon $ 不敏感准则和结构风险，对小样本数据集显示出了更鲁棒的性能，但对采样样本不能反映数据集整体分布的数据集泛化性能仍不理想。 $\varepsilon $ -TLRBF不仅引入 $\varepsilon $ 不敏感准则和结构风险项，还学习了源领域知识，能弥补缺失数据的不足，泛化性能较RBF和 $\varepsilon $ -RBF有很明显的改善。

5 结束语

已有RBF神经算法及其改进算法大多未考虑采样样本不能反映数据集整体分布而导致算法泛化性能降低的情况。本文通过采用知识迁移的思想，提出能充分学习源领域知识的具有迁移学习能力的RBF神经网络学习算法。本文所提方法并不需要大量源领域样本参与目标领域模型的建立，仅是学习源领域的高斯核中心向量及核宽以及源领域模型参数帮助数据存在一定程度的信息缺失的目标领域建立模型，这是传统的RBF神经网络学习算法所不具备的。通过合成数据实验以及真实发酵过程的仿真实验，验证了本文方法较之于传统方法具有更好适应性。但本文方法采用网格搜索策略和交叉验证方法来获得各个参数的值，加大了获取各参数最优值的工作量，在今后的工作中，将致力于研究两个领域间的相关性与 $\lambda $ 参数取值间的关系，以估计 $\lambda $ 参数的合理区间，减少获得最优参数的工作量。