多旅行商问题(multiple traveling salesman problem，MTSP)可直观描述为一个旅行商团队要分头遍历若干个城市，每个城市至少被一个旅行商访问一次且只访问一次，如何安排m(大于1)位旅行商遍历n(大于m)个城市，使得总的访问行程最小^[1]。该问题最常见的应用领域是车间调度领域，在生产线上的作业调度通常被建模为一个旅行商问题(traveling salesman problem，TSP)。如果生产经营扩展到有多条平行线，工作可以分配，这个问题可以建模为一个多旅行商MTSP^[2]；另一个经常被建模为多旅行商问题的就是车辆调度问题(VSP)^[3]。车辆调度问题是指对一些车辆进行调度，所有的车辆离开并回到原地点，使得每个地方只能而且必须被访问一次。

由于多旅行商问题的复杂性，必须根据实际问题的大小采用启发式解决方案^[4]。遗传算法(genetic algorithms，GA)^[5]是一种基于生物自然选择和基因遗传学原理的高效并行、随机全局优化搜索算法。Keshavarz等^[6]学者发现遗传算法对调度问题有很强的适应性，MTSP有效的遗传算子也激发了研究者的极大兴趣；张永库等^[7]研究了改进的遗传算法在模糊聚类中的表现；Katayama等^[8]提出的混合变异遗传算法在旅行商问题中的应用提高了遗传算法解决旅行商问题的性能。多旅行商问题在实际问题中有很广泛的应用。Huang等^[9]研究了多旅行推销员问题在热轧规划中的应用；江贺等^[10]研究了近年来出现的新NP-难解问题，即黑白旅行商问题(BWTSP)，给出了遗传算法解决问题的一种新思想；Trigui等^[11]提出一种解决多机器人系统多目标多旅行推销员问题的模糊逻辑方法。最近出现了多种解决TSP问题的方法，王宇平等^[12]提出的求解TSP的量子遗传算法使用了有关量子方面的知识。研究者们也在其他经典优化算法^[13]中找到了许多新思想。

遗传算法求解MTSP的关键是要根据问题设计一种好的染色体编码方法，而好的遗传算法染色体编码方案应该能够从候选解中减少或消除冗余的解。冗余解是指以一种以上的方式表示同一染色体，并多次出现在种群中的染色体编码方式。相同解的多次再现不仅增加了查找空间，而且降低了查找效率。

本文首先列出了传统的两个染色体方案(单染色体设计方案和双染色体方案)，以及最近提出的较新的两段式染色体设计方案；本文引入相对解空间概念，以此定量地衡量不同染色体方案给出的相对解空间大小关系，先给出对旅行商数目和城市数目在趋于无穷时的极限相对大小关系，接下来近似分析了旅行商数目与城市数目在不同情形下解空间的相对大小关系。

1 3种染色体方案

MTSP染色体的设计主要有以下3种^[1]。

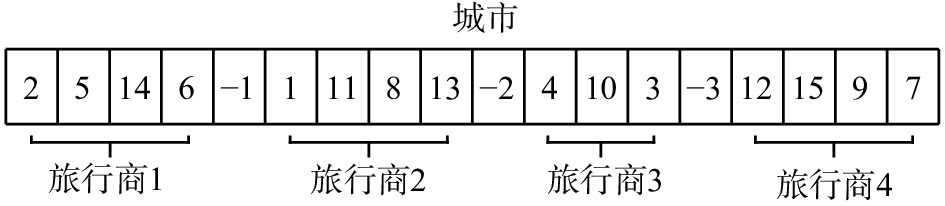
1.1 单染色体设计

图1描述了MTSP问题城市数n=15、旅行商数m=4时染色体编码的一种设计方法的一个实例。这种设计使用了一个染色体编码长度为n+m–1的染色体，因此被称为“单染色体”(one chromosome)设计。该设计方案中，n个城市用从1~n正整数编码表示，并进行无规则的排列，代表着n个城市的整数编码列被–1~–(m–1)这m–1个负整数分为m段，分别依次对应着有序的m个旅行商所访问的城市，因此这个长度为n+m–1的整数列的任何一种排列组合都可能是这个MTSP问题的解。以图1为例，第一个旅行商将访问编号为2、5、14、6的这几座城市，第二个旅行商将访问编号为1、11、8、13的这几座城市，依次类推。在这种染色体设计中，MTSP所有问题的解将可能是由(n+m–1)!个解构成的一个空间。这些解中有很多是冗余的，例如，旅行商1与旅行商2的访问城市全部按顺序相互调换位置后的解和现有解。

1.2 双染色体设计

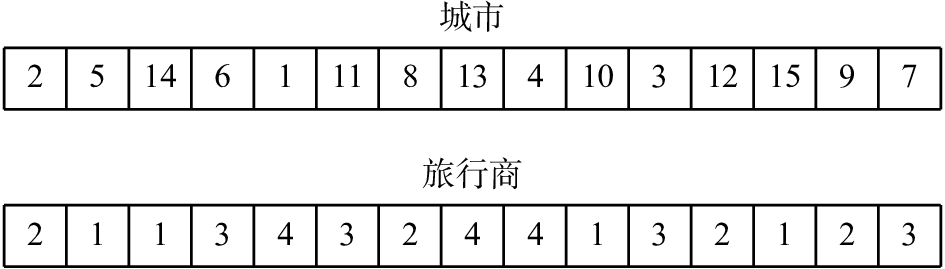
图2描述了同样一个MTSP问题由遗传算法中染色体编码方案的另一种设计方法。一般称它为“双染色体(two chromosomes)”设计。这种设计使用两个长度为n的染色体表示一个解。图2中，第一个染色体表示n个城市的一组排列，第二个染色体的每一位数对应上面相应的城市，由对应编码的旅行商来访问。例如，旅行商l访问的城市为5、14、10、15，旅行商2访问的城市为2、8、12、9。使用这种编码设计，对应的空间是由n!mⁿ个可能的解构成的一个集合。同样，这种编码方案也有许多冗余的解。例如，上述事例解中头两个基因位交换位置后得到的解与现有解就是相同的。

1.3 两段式染色体设计

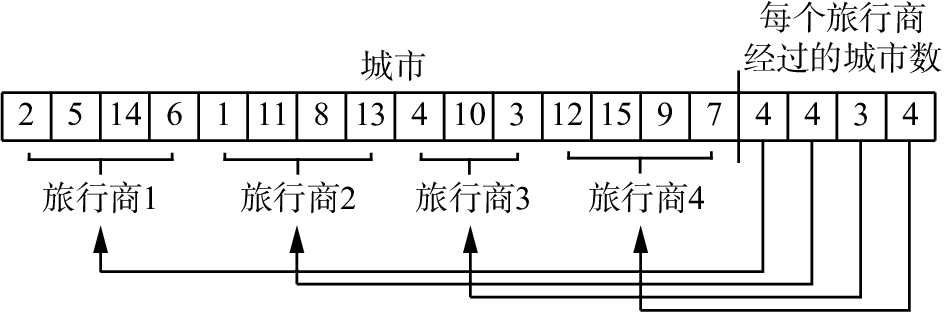
图3描述了一个新的染色体设计方案，它由前后两个部分组成，因此称为“两段式染色体(two-part chromosome)”设计。前段是整数l~n的一个排列，代表了n个城市的一个顺序排列；后段长度为m，按顺序分别表示m个旅行商在前段编码中对应访问的城市数，并且这m个数之和等于n。图3所示旅行商l访问前段中的头4个城市顺序分别为2、5、l4、6；旅行商3访问从第4+4+1个开始的连续3个城市，分别为4、10、3。使用新的两段式染色体设计，不仅减少了查找空间，而且由于固定了旅行商的顺序而消除了部分(但不是全部的)冗余的解。使用这种染色体编码设计，对于前段可能会有n!种排列，后段由于是一个和为n的正整数向量，因此需要 $C_{{{n - 1}}}^{{{m - 1}}}$ 种可能的m维正整数表示，才能满足要求。从而，可以得到解空间大小为 $C_{{{n - 1}}}^{{{m - 1}}}$ 。

2 3种染色体编码方案下的相对解空间分析

上一节介绍了遗传算法求解多旅行商问题的3种染色体编码方案。文献[1]给出了3种染色体编码方案对应的搜索空间的大小，仅是定性分析了3种方案的优劣，即两段式染色体方案对应的解空间优于前两种编码方案对应的解空间，而第一种单染色体设计方案优于双染色体编码方案。如果只是定性地了解3种编码方案对应解空间大小关系，对染色体编码方案和算法设计以及实际工程应用并没有太大的指导意义。因此本文首先引入相对解空间概念，然后详细地定量分析了3种染色体方案对应的解空间相对大小，这对多旅行商问题的研究和求解具有现实的指导意义。

2.1 相对解空间

3种染色体编码方案对应的解空间大小^[1]分别为

${C_{\rm{one}}}= \left( {m + n - 1} \right)!$

(1)

${C_{\rm{two}}}= n!{m^n}$

(2)

${C_{2 {\text{-}} {\rm{part}}}}= n!C_{n - 1}^{m - 1}$

(3)

式中：C_one表示单染色体编码对应的解空间规模，C_two表示双染色体编码对应的解空间规模， ${C_{2 \text{-} {\rm{part}}}}$ 表示两段式染色体解空间的规模。从3种编码方案解空间的代数表达式可以看出，它们都是城市数n和旅行商数目m的二元函数，自变量n和m的取值范围是正整数，且一般m<n(旅行商人数小于城市数)。

式(1)～(3)按大小排序有： $ {C_{2 \text{-} {\rm{part}}}} <{C_{\rm{one}}} <$ $ {C_{\rm{two}}}$ ^[1](n>m)，这几个代数式给出的解空间大小从数量上来讲是对解空间的绝对衡量，假若将其两两作比值运算(较大的作分母)，得到的结果是个相对值，当m和n取较大的正整数时，比值结果是一个小于1的真分数，我们称之为“相对解空间”，分别用C₃₁、C₃₂和C₁₂表示，即

${C_{31}}= \frac{{{C_{2 \text{-} {\rm{part}}}}}}{{{C_{\rm{one}}}}}= \frac{{n!C_{n - 1}^{m - 1}}}{{\left( {m + n - 1} \right)!}}$

(4)

${C_{32}}= \frac{{{C_{2 - {\rm{part}}}}}}{{{C_{\rm{two}}}}}= \frac{{n!C_{n - 1}^{m - 1}}}{{n!{m^n}}}$

(5)

${C_{12}}= \frac{{{C_{\rm{one}}}}}{{{C_{\rm{two}}}}}= \frac{{(m + n - 1)!}}{{n!{m^n}}}$

(6)

2.2 相对解空间的极限分析

在现实的工程应用中，比如车辆调度问题，m、n一般取值较大，因此随着自变量的增大或问题规模的扩大，我们需要了解相对解空间对应的比值结果的变化趋势，从而从数学表达式中讨论m和n取较大正整数时，相对解空间的极限行为，也可以认为是讨论m、n趋于无穷时的极限。

2.2.1 C₃₁的极限分析

1) m适当大时

在多旅行商问题中，城市数目与旅行商数目之间的差距一般都比较大，因此当讨论C₃₁的极限性质时，不妨假设 $n \gg m$ ，当n充分大、m应适当大时，对C₃₁取对数，分析可得：

$\begin{aligned}& \quad{{\rm{ln\;}}{C_{31}} = \sum\limits_{k = 1}^n {{\rm{ln\;}}} k + \sum\limits_{k = 1}^{n - 1} {{\rm{ln\;}}} k - \sum\limits_{k = 1}^{m + n - 1} {{\rm{ln\;}}} k - \sum\limits_{k = 1}^{n - m} {{\rm{ln\;}}} k - }\\& {\sum\limits_{k = 1}^{m - 1} {{\rm{ln\;}}} k = \sum\limits_{k = 1}^n {{\rm{ln\;}}} k + \sum\limits_{k = 1}^{n - 1} {{\rm{ln\;}}} k - \left( {\sum\limits_{k = 1}^{n - 1} {{\rm{ln\;}}} k + \sum\limits_{k = n}^{n + m - 1} {{\rm{ln\;}}} k} \right) - }\\&\quad {\left( {\sum\limits_{k = 1}^n {{\rm{ln\;}}} k - \sum\limits_{k = n - m + 1}^n {{\rm{ln\;}}} k} \right) - \sum\limits_{k = 1}^{m - 1} {{\rm{ln\;}}} k = - \sum\limits_{k = n}^{n + m - 1} {{\rm{ln\;}}} k + }\\& \quad\quad\quad\;\;{\sum\limits_{k = n - m + 1}^n {{\rm{ln\;}}} k - \sum\limits_{k = 1}^{m - 1} {{\rm{ln\;}}} k - < \sum\limits_{k = 1}^{m - 1} {{\rm{ln\;}}} k < 0}\\&\quad\quad\quad\quad\quad\; {{C_{31}} = {{\rm{e}}^{ - \ln \left( {m - 1} \right)!}} = \frac{1}{{\left( {m - 1} \right)!}}}\end{aligned}$

所以C₃₁<1。

C₃₁<1意味着第三种编码方案对应的解空间严格小于第一种方案对应的解空间，这严格证明了Carter^[1]给出的解空间的定性比较结果。当n足够大时，所需的旅行商数也有相应增大，因此当n充分大、m适当大时， ${C_{31}} \ll 1$ 。例如：m=10， ${C_{31}}{\rm{ }} < {{\rm{e}}^{ - \sum\limits_{k = 1}^9 {\ln } k}} \approx 2.76 \times {10^{ - 6}}$ 。

2) m是不大的常数时

(n–1)!可与(n+m–1)!相抵消，n!可与(n–m)!相抵消，所以当n趋于无穷时得出：

${C_{31}}= \frac{{{C_{t \text{-} {\rm{part}}}}}}{{{C_{\rm{one}}}}}= \frac{{n! n - 1!}}{{\left( {n + m - 1} \right)! \left( {n - m} \right)! \left( {m - 1} \right)!}} \to \frac{1}{{\left( {m - 1} \right)!}}$

即当旅行商人数m取不大的常数时，随着城市数目的增加，单染色体编码方案对应的空间约是两段式染色体方案解空间的(m–1)！倍，此结果与两种解空间的极限分析是一致的。

2.2.2 C₃₂的极限分析

1)m适当大时

依然假设 $n \gg m$ ，当n充分大、m适当大时，取对数分析可得：

$\begin{aligned}\begin{array}{l}\;{\kern 1pt} {\rm{ln\;}}{C_{32}} = \displaystyle\sum\limits_{k = 1}^{n - 1} {\ln\; } k - \displaystyle\sum\limits_{k = 1}^{n - m} {\ln\; } k - n{\rm{ln\;}}m - \displaystyle\sum\limits_{k = 1}^{m - 1} {\ln\; } k = \\\displaystyle\sum\limits_{k = n - m + 1}^{n - 1} {\ln\; } k - n{\rm{ln\;}}m - \displaystyle\sum\limits_{k = 1}^{m - 1} {\ln\; } k\end{array}\end{aligned}$

$\displaystyle \sum\limits_{k = n - m + 1}^{n - 1} {\ln\; } k$ 中有m-1项，通项是城市数n的对数，而nln m中有n项，ln m是旅行商数目的对数，并且当n充分大时， $\mathop {\lim }\nolimits_{n \to \infty } \displaystyle\frac{n}{{{\rm{ln\;}}n}}= + \infty $ ^[14]，所以当 $n \to \infty $ 时， $\displaystyle\sum\limits_{k = n - m + 1}^{n - 1} {\ln\; } k - n{\rm{ln\;}}m < 0$ 。因为

$\begin{array}{c} \mathop \sum \limits_{k= n - m + 1}^{n - 1} {\rm{ln\;}}k - n{\rm{ln\;}}m < \left( {m - 1} \right) \cdot {\rm{ln\;}}\left( {n - 1} \right) - n{\rm{ln\;}}m < \\m{\rm{ln\;}}n - n{\rm{ln\;}}m < 0\end{array}$

所以，ln ${C_{32}} < - \displaystyle \mathop \sum \limits_{k= 1}^{m - 1} {\rm{ln\;}}k < 0$ ，即C₃₂<1。

C₃₂<1同样意味着第三种编码方案对应的解空间小于第二种方案对应的解空间。同C₃₁的分析类似，当n足够大、m适当大时， ${C_{32}} \ll 1$ 。

2)m是不大的常数时

$\begin{array}{c}{C_{32}}= \displaystyle \frac{{{C_{t \text{-} {\rm part}}}}}{{{C_{{\rm two}}}}}= \frac{{n!C_{n - 1}^{m - 1}}}{{n!{m^n}}}= \frac{{\left( {n - 1} \right)!}}{{\left( {m - 1} \right)!\left( {n - m} \right)!{m^n}}}= \\\displaystyle \frac{{\left( {n - 1} \right)\left( {n - 2} \right) \cdots \left( {n - m + 1} \right)}}{{\left( {m - 1} \right)!{m^n}}} < \displaystyle \frac{{{n^m}}}{{\left( {m - 1} \right)!{m^n}}}\end{array}$

由此可知， ${C_{32}} < \displaystyle \frac{1}{{\left( {m - 1} \right)!}}$ 。

由对C₃₂的分析可知，当m取大于2的常数时，C₃₂< 1。此结果显示，第三种编码方案对应的解空间小于第二种编码方案对应的解空间，此结果与两种解空间的极限分析是一致的。

2.2.3 C₁₂的极限分析

假设 $n \gg m$ ，当n充分大、m，适当大时，对C₁₂取对数，即

$\begin{array}{c}\ln\;{C_{12}}= \displaystyle \mathop \sum \limits_{k= 1}^{n + m - 1} {\rm{ln\;}}k - \displaystyle \mathop \sum \limits_{k= 1}^n {\rm{ln\;}}k - n{\rm{ln\;}}m=\displaystyle \mathop \sum \limits_{k= n + 1}^{n + m - 1} {\rm{ln\;}}k - n{\rm{ln\;}}m <\\ \left( {m - 1} \right)\ln\; \left( {n + m - 1} \right) - n{\rm{ln\;}}m\end{array}$

当n充分大时， $\mathop {\lim }\nolimits_{n \to \infty } \displaystyle\frac{n}{{{\rm{ln\;}}n}}= + \infty $ ，因此 $ {\rm{ln\;}}{C_{12}} < 0$ ， ${C_{12}} < 1$ 。C₁₂的大小说明第一种编码方案对应的解空间小于第二种编码方案对应的解空间。

至此，在合理适当的条件下：n适当大，对3种解空间的相对大小给出详细严密的论证，很好地补充了文献[1]中定性的结论，即 ${C_{\rm two}} > $ $ {C_{\rm one}} > {C_{2 \text{-} \rm part}}$ ，而且由分析可知，当n充分大、m适当大时， ${C_{\rm two}} \gg {C_{\rm one}} \gg {C_{2 \text{-} \rm part}}$ 。

以上分析中，对一般的m和n给出的是相对解空间理论上的对比，但是如果只知道相对大小，对实际问题应用几乎没有实质性的帮助，例如求C₃₁的极限，实质上m为常数，n逐渐增大，也就是说，在某一个多旅行商问题中，我们保持商人的数目不变，增大工程的规模，让城市数目逐渐增大，这也就意味着单个商人访问的城市数目随着城市数目的增多而无限增加下去，这显然不符合实际情况，因为每个旅行商访问的城市数目是有上限的，即最大负荷能力。因此单一用这个极限结果去估计解空间的大小，虽然能得出严密的定量分析结果，但是其代表的实际意义是不乏片面性的。

我们不仅需要知道染色体编码方案 ${C_{2 - \rm part}}$ 对应的解空间小，更重要的是需要知道到底小多少，这也是本文最初的研究目的。通过研究发现，对一般性的m和n，很难给出解空间的具体差距，因此本文在旅行商数m与城市数n之间成几种典型函数关系的条件下给出相对解空间的差距，包括城市数n与旅行商数m的线性关系、幂函数关系和指数关系。

2.3 相对搜索空间的粗略估计

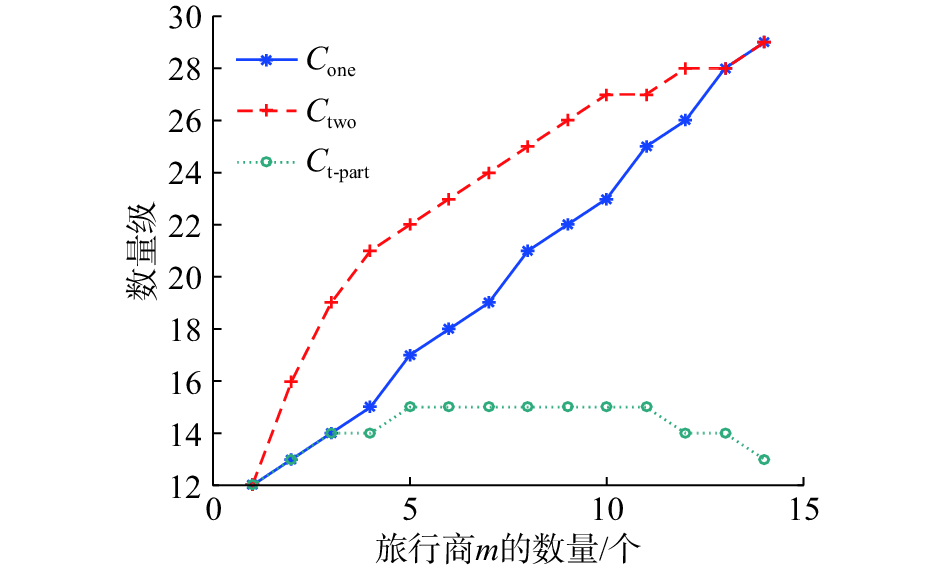
图4描述了l5个城市，是旅行商数量从l增加到14时，3种染色体编码设计的搜索空间的变化示意图。图4的纵轴表示搜索空间的数量级。由图4可以看出，在旅行商逐步增加的情况下，单染色体编码对应的搜索空间数量的增加由快到慢；双染色体编码对应的搜索空间数量的增加比较平稳；而两段式染色体编码对应的搜索空间数量呈现两端相当、中间略微增加的大体对称的情况。因此图4与2.2节的解空间分析结果显示出了两段式染色体编码设计的初步优越性。

众所周知，当城市数目逐步增加时，旅行商人数也应该相应增加，而m一般会随n的变化而变化。以下详细讨论m与n有特定关系时的相对搜索空间。例如：n=10m，n=m²，n=e^m三种情形下，相对搜索空间的变化趋势。

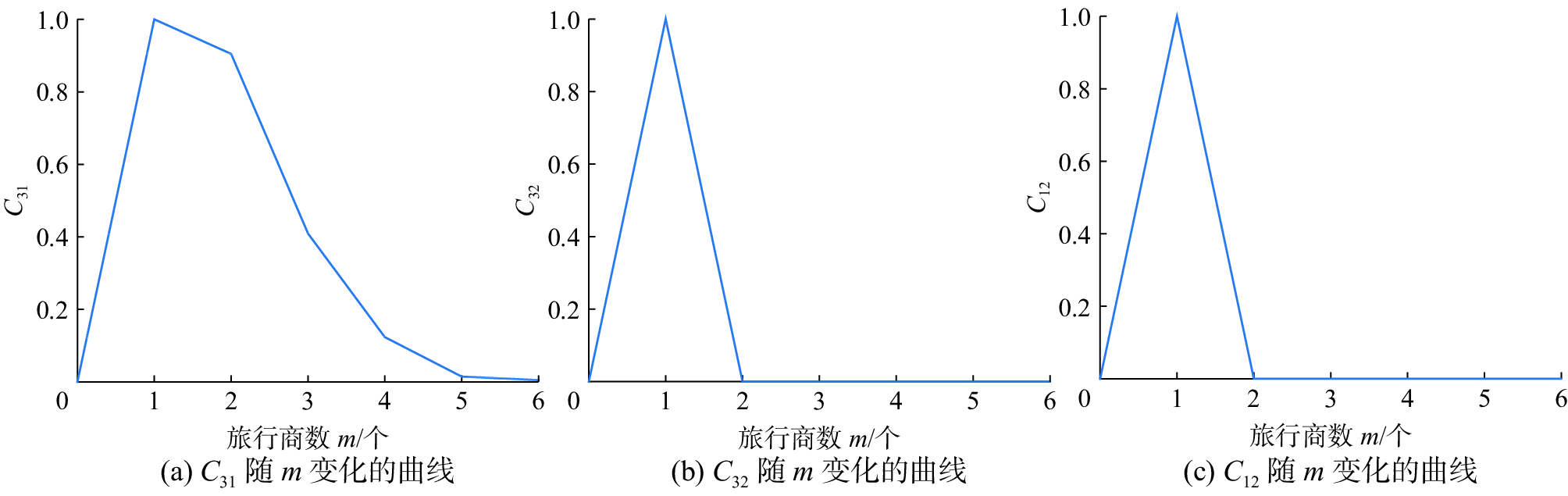
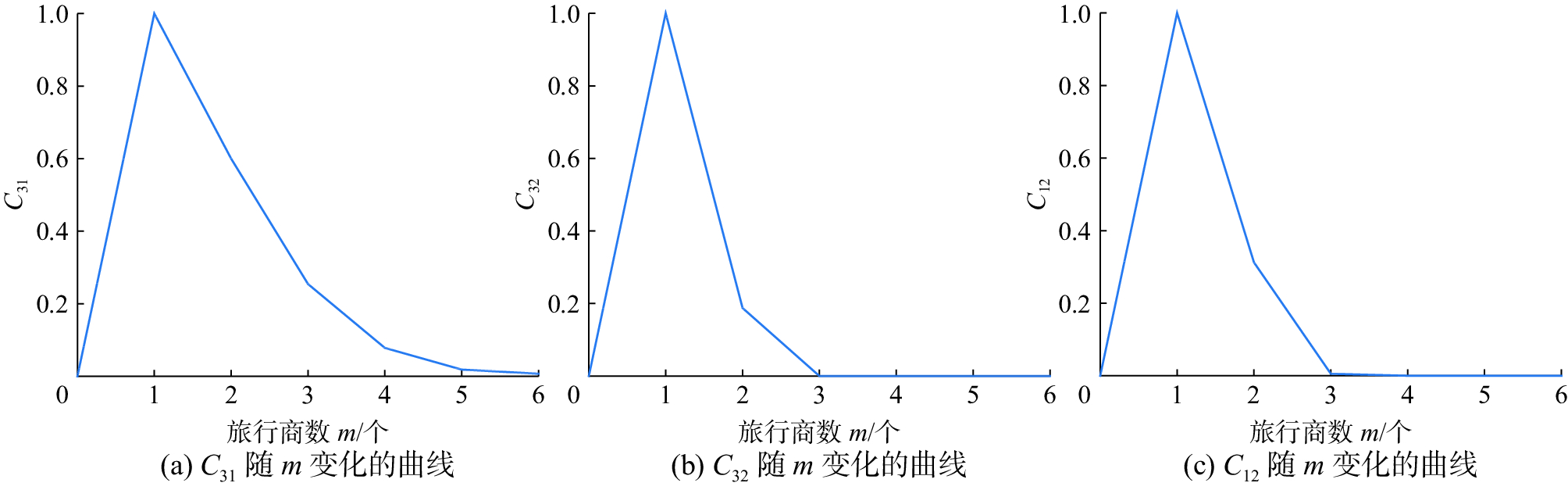
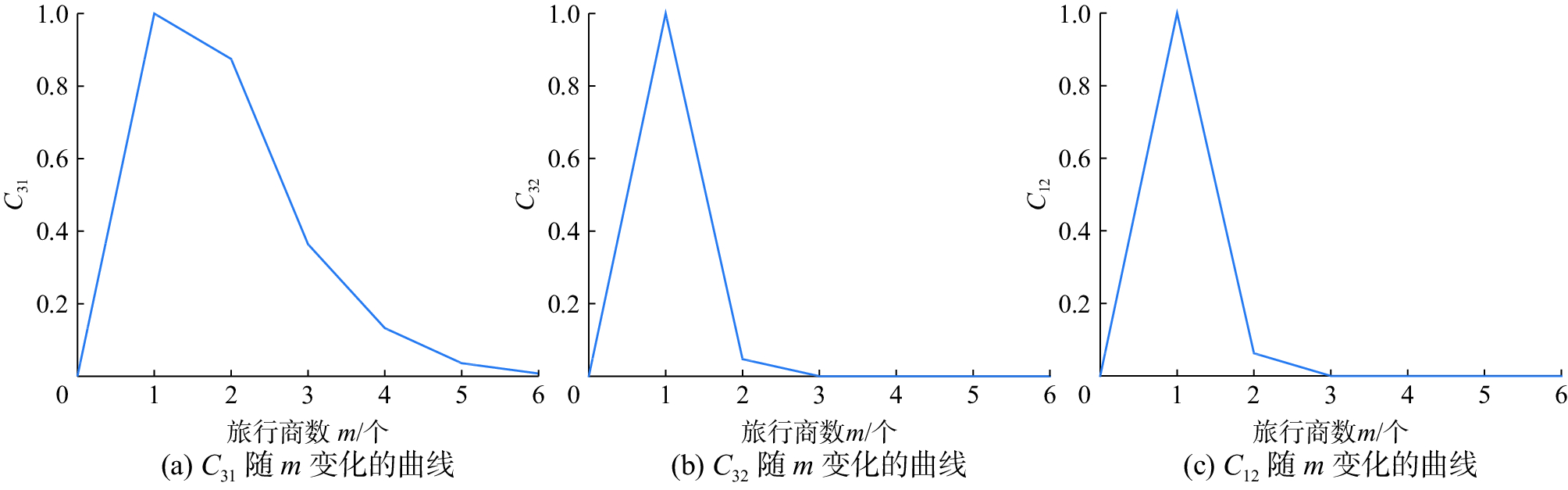
从图5~7所示的3组函数图像可以看出，3种情形下的相对搜索空间变化，总体来说，从相对搜索空间上比较，在n=10m和n=m²情形下，C₃₁和C₃₂在前期的差别不大，纵轴随着m的增大很快收敛，且C₁₂在n=m²情形下比在n=10m情形下收敛得更快些；在n=e^m情形下C₃₂相对搜索空间和C₁₂相对搜索空间比其他两种情形收敛更快，但C₃₁在前期收敛得有些缓慢，而在n=e^m情形下明显比其他两种情形收敛更快。从同一情形下看3种相对搜索空间的变化时，可以看出C₃₁、C₃₂和C₁₂都是纵轴随着m的增大很快收敛，C₃₂和C₁₂收敛较快些，在m≤6时就能定性地看出收敛；C₃₁收敛最慢，在m取较大值时能判断出也是收敛的。从两种判断方法中我们能够看出收敛，但是很难直观地从函数图像上直接看出m取较大值时的收敛状况，也即只能定性得出收敛的结论，这与前面的结论亦是吻合的。

2.4 分情形下的相对解空间大小分析 2.4.1 Stirling公式

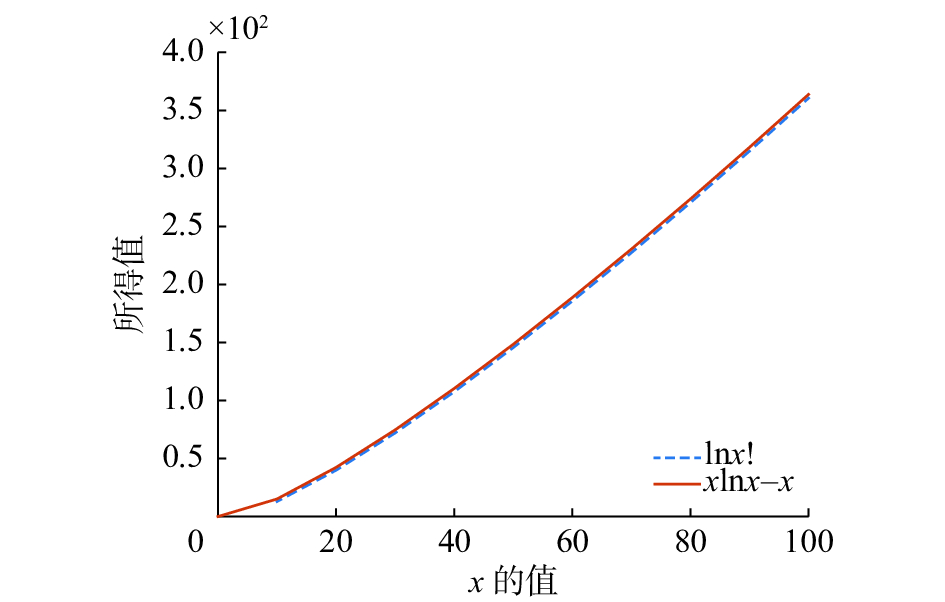
相对解空间表达式中出现阶乘项，增加了相应的分析和对比运算，而我们在此要讨论的是m、n取较大正整数时相对解空间的变化属性，因此本文用Stirling公式来近似化简分式^[14](当n取充分大的正整数时，用多项式代替阶乘运算)，图8为阶乘项和等价的多项式项的变化示意图。Stirling 公式为

$\mathop {{\rm{lim}}}\nolimits_{n \to \infty } \displaystyle\frac{{n!}}{{\sqrt {2{\text{π}} n} {{\left( {\displaystyle\frac{n}{{\rm{e}}}} \right)}^n}}}= 1$

(7)

2.4.2 n=10m时相对解空间分析

当n=10m时：

$\begin{array}{l}{C_{31}}= \displaystyle\frac{{{C_{2 \text{-} {\rm part}}}}}{{{C_{\rm one}}}}= \displaystyle\frac{{n!C_{n - 1}^{m - 1}}}{{\left( {m + n - 1} \right)!}}\sim \displaystyle\frac{{\sqrt {2{\text{π}} n} {{\left( {\displaystyle\frac{n}{{\rm{e}}}} \right)}^n}\sqrt {2\pi \left( {n - 1} \right)} {{\left( {\displaystyle\frac{{n - 1}}{{\rm{e}}}} \right)}^{n - 1}}}}{{\sqrt {2{\text{π}} \left( {m + n - 1} \right)} {{\left( {\displaystyle\frac{{m + n - 1}}{{\rm{e}}}} \right)}^{m + n - 1}}\sqrt {2{\text{π}} \left( {m - 1} \right)} {{\left( {\displaystyle\frac{{m - 1}}{{\rm{e}}}} \right)}^{m - 1}}\sqrt {2{\text{π}} \left( {n - m} \right)} {{\left( {\displaystyle\frac{{n - m}}{{\rm{e}}}} \right)}^{n - m}}}}\sim \\\displaystyle \sqrt {\displaystyle\frac{{5\left( {10m - 1} \right)}}{{9\pi \left( {11m - 1} \right)\left( {m - 1} \right)}}} \cdot \displaystyle\frac{{{m^m}{{\left( {m - \displaystyle\frac{1}{{10}}} \right)}^{10m - 1}}}}{{{{\left( {m - \displaystyle\frac{1}{{11}}} \right)}^{11m - 1}}{{\left( {m - 1} \right)}^{m - 1}}}} \cdot \displaystyle\frac{{{{10}^{20m - 1}} \cdot {{\rm e}^{m - 1}}}}{{{{11}^{11m - 1}} \cdot {9^{9m}}}}\end{array}$

(8)

式（8）是一个关于m的分式，可分为3个部分。当m取较大值时，第一部分 $\sqrt {\displaystyle \displaystyle\frac{{5\left( {10m - 1} \right)}}{{9{\text{π}} \left( {11m - 1} \right)\left( {m - 1} \right)}}} $ 可以用 $\displaystyle\sqrt {\frac{1}{{2{\text{π}} m}}} $ 近似代替，第二部分 $ \displaystyle\frac{{{m^m}{{\left( {m - \displaystyle\frac{1}{{10}}} \right)}^{10m - 1}}}}{{{{\left( {m - \displaystyle\frac{1}{{11}}} \right)}^{11m - 1}}{{\left( {m - 1} \right)}^{m - 1}}}}$ 是幂指数次项，在m较大时可以用 $ \displaystyle\frac{1}{{{m^{m - 1}}}}$ 代替，第三部分 $\displaystyle \displaystyle\frac{{{{10}^{20m - 1}} \cdot {{\rm e}^{m - 1}}}}{{{{11}^{11m - 1}} \cdot {9^{9m}}}}$ 可以化简为 ${{\rm e}^{m - 1}}$ 。在这三项中，增长速度主要体现在第二项和第三项幂指数项，也就是说，我们评价整个代数表达式随着m的增大其增长速度可以用第二项和第三项代替。

在计算机程序设计中，衡量一个算法的好坏，通常会用到时间复杂度和空间复杂度。性按照某一速度增长。它只表示增长的速度(Order)，这个时间或空间复杂度并不是与程序复杂性严格相等的数学表达式，它只抽象表示增长速度的类型，通常用大O表示法。本文中的解空间的大小也称为空间复杂度，也同样用算法设计中的空间复杂度表示法(大O表示法)来衡量本文中讨论的3种染色体设计方案的相对解空间。

因增长速度主要体现在第二项和第三项幂指数项，也就是说，我们评价整个代数表达式随着m的增大其增长速度可以用第二项和第三项代替。于是，式(8)化简结果为

${C_{31}}= \frac{{{C_{2 \text{-} {\rm part}}}}}{{{C_{{\rm one}}}}}\sim \sqrt {\frac{1}{{2{\text{π}} m}}} {\left( {\frac{{\rm{e}}}{m}} \right)^m}$

(9)

式（9）的结果可以用 ${\left( {\displaystyle \frac{{\rm{e}}}{m}} \right)^m}$ 来代表其收敛速度，则该等式可表示为

${C_{{\rm one}}}= {C_{2 \text{-} {\rm part}}} \cdot O\left( {{{\left( {\frac{m}{{\rm{e}}}} \right)}^m}} \right)$

(10)

同样

${C_{32}}= \frac{{{C_{2 \text{-} {\rm part}}}}}{{{C_{{\rm two}}}}}= \frac{{n!C_{n - 1}^{m - 1}}}{{n!{m^n}}}$

(11)

当m取较大正整数时，指数项可以用二项展开式的前两项近似替代，具体过程不在此赘述，以下相似替代过程将不特殊说明，式(11)化简为

${C_{32}}\sim \sqrt {\frac{1}{{2{\text{π}} m}}} \cdot \frac{1}{{{m^{10m}}}} \cdot \frac{{{{10}^{10m - 1}}}}{{{9^{9m}}}}$

(12)

则该等式可表示为

${{\rm{C}}_{\rm {two}}}= {C_{2 \text{-} {\rm part}}} \cdot {{O}}\left( {{m^{10m}}} \right)$

(13)

对于C₁₂同样可得到：

$\begin{array}{l}{C_{12}}= \displaystyle\frac{{{C_{\rm one}}}}{{{C_{\rm two}}}}= \displaystyle\frac{{m + n - 1!}}{{n{m^n}}}= \displaystyle\frac{{\left( {11m - 1} \right)!}}{{\left( {10m} \right)!{m^{10m}}}}\sim \\\displaystyle \frac{{\sqrt {2{\text{π}} \left( {11m - 1} \right)} {{\left( {\displaystyle\frac{{11m - 1}}{e}} \right)}^{11m - 1}}}}{{\sqrt {2{\text{π}} \left( {10m} \right)} {{\left( {\displaystyle\frac{{10m}}{e}} \right)}^{10m}}{m^{10m}}}}\sim \sqrt {\displaystyle\frac{{11}}{{10}}} \cdot \displaystyle\frac{1}{{{m^{9m}}}} \cdot \displaystyle\frac{1}{{{{\rm e}^{m - 1}}}}\end{array}$

(14)

则该等式可表示为

${C_{{\rm two}}}= {C_{{\rm one}}} \cdot O\left( {{m^{9m}} \cdot {{\rm e}^m}} \right)$

(15)

由前两个关系式：

${C_{{\rm one}}}= {C_{2 \text{-} {\rm part}}} \cdot {{O}}\left( {{{\left( {\frac{m}{{\rm{{\rm e}}}}} \right)}^m}} \right)$

(16)

${{\rm{C}}_{{\rm two}}}= {C_{2 \text{-} {\rm part}}} \cdot {{O}}\left( {{m^{10m}}} \right)$

(17)

用等式(17)除以等式(16)可得

$\frac{{{C_{\rm two}}}}{{{C_{\rm one}}}}= \frac{{{C_{2 - \rm part}} \cdot {{O}}\left( {{m^{10m}}} \right)}}{{{C_{2 - \rm part}} \cdot O\left( {{{\left( {\displaystyle\frac{m}{{\rm{e}}}} \right)}^m}} \right)}}= {{O}}\left( {{m^{9m}} \cdot {{\rm e}^m}} \right)$

(18)

式（18）等价于 ${C_{\rm two}}= {C_{\rm one}} \cdot O\left( {{m^{9m}} \cdot {{\rm {e}}^m}} \right)$ ，这与上述推导中的等式(15)是吻合的，由此该方法计算三者解空间大小在逻辑上是严密的，从式(15)～(17)可知， ${C_{\rm two}}= {C_{\rm one}} \cdot O\left( {{m^{9m}} \cdot {{\rm e}^m}} \right)={C_{2 \text{-} \rm part}} \cdot $ $ {O}\left( {{m^{10m}}} \right)$ ，可以看出，随着问题规模的逐渐增大，3种编码方案对应解空间的差距呈幂指函数的关系。由此可以看出，两段式染色体编码方案的优越性。

2.4.3 平方关系下的相对解空间分析

上一小节讨论了3种染色体方案在城市数目与旅行商人数为线性关系时，解空间的相对大小关系，实际上，在线性关系n=km下，系数k代表的是平均每个商人访问的城市数目。因此讨论相对解空间时，让m逐渐递增时，k是作为常数处理的，也就是说，平均每个商人访问的城市数目是大体不变的。在现实的工程问题中，随着工程规模的增加，即待访问城市数目的急剧增多，旅行商的人数也应该随之增加。考虑这个实际问题时，不应该单纯依靠旅行商人数的增加来完成所有城市的访问，也应该随着城市的增加，相应地增大每个商人的工作负载，即访问城市的数目。于是，我们应该找到一个函数来表示城市数目和旅行商人数的关系，满足随着城市数目的增多，旅行商人数也随之增加，同时平均每个商人访问的城市数目也随之相应增加。考虑到城市数与旅行商人数的关系和商人访问城市效率的不同，本文选择两种常见的不同增速关系，即二次幂函数与指数增长关系。

本节讨论n与m在二次函数关系下相对解空间的收敛速度。

将n=m²代入式（19）：

$\begin{array}{l}{C_{31}}= \displaystyle \frac{{{C_{2 \text{-} \rm part}}}}{{{C_{\rm one}}}}= \displaystyle \frac{{n!C_{n - 1}^{m - 1}}}{{\left( {m + n - 1} \right)!}}= \displaystyle \frac{{{m^2}!\left( {{m^2} - 1} \right)!}}{{\left( {{m^2} + m - 1} \right)!\left( {m - 1} \right)!({m^2} - m)!}}\sim \\ \displaystyle \frac{{\sqrt {2{\text{π}} {m^2}} {{\left( {\displaystyle\frac{{{m^2}}}{{\rm{e}}}} \right)}^{{m^2}}}\sqrt {2{\text{π}} ({m^2} - 1)} {{\left( {\displaystyle\frac{{{m^2} - 1}}{{\rm{e}}}} \right)}^{{m^2} - 1}}}}{{\sqrt {2{\text{π}} \left( {{m^2} + m - 1} \right)} {{\left( {\displaystyle\frac{{{m^2} + m - 1}}{{\rm{e}}}} \right)}^{{m^2} + m - 1}}\sqrt {2{\text{π}} \left( {m - 1} \right)} {{\left( {\displaystyle\frac{{m - 1}}{{\rm{e}}}} \right)}^{{{m}} - 1}}\sqrt {2{\text{π}} \left( {{m^2} - m} \right)} {{\left( {\displaystyle\frac{{{m^2} - m}}{{\rm{e}}}} \right)}^{{m^2} - {{m}}}}}}\end{array}$

(19)

同样用二项展开式的前两项去近似代替指数项部分，式（19）可简化为

${C_{31}}\sim \frac{1}{{\sqrt {2{\text{π}} m} }} \cdot \frac{1}{{{m^m}}} \cdot {{\rm{e}}^{m - 1}}$

(20)

式（20）的收敛速度主要取决于第二项幂指数因式 $\displaystyle\frac{1}{{{m^m}}}$ 和第三项 ${{\rm{e}}^m}$ ，所以式（20）关系可表示为

${C_{\rm one}}= {C_{2 \text{-} \rm part}} \cdot O\left( {{{\left( {\frac{m}{{\rm{e}}}} \right)}^m}} \right)$

(21)

同样将n=m²代入式（22）：

$\begin{array}{l}\quad\quad{C_{32}}= \displaystyle\frac{{{C_{2 \text{-} \rm part}}}}{{{C_{\rm two}}}}= \displaystyle\frac{{n!C_{n - 1}^{m - 1}}}{{n!{m^n}}}= \displaystyle\frac{{\left( {n - 1} \right)!}}{{\left( {m - 1} \right)!\left( {n - m} \right)!{m^n}}}=\\ \quad\quad\quad\quad\quad\quad\;\displaystyle\frac{{\left( {{m^2} - 1} \right)!}}{{\left( {m - 1} \right)!\left( {{m^2} - {\rm{m}}} \right)!{m^{{m^2}}}}}\sim \\\displaystyle\frac{{\sqrt {2{\text{π}} \left( {{m^2} - 1} \right)} {{\left( {\displaystyle\frac{{{m^2} - 1}}{{\rm{e}}}} \right)}^{{m^2} - 1}}}}{{\sqrt {2{\text{π}} \left( {m - 1} \right)} {{\left( {\displaystyle\frac{{m - 1}}{{\rm{e}}}} \right)}^{m - 1}}\sqrt {2{\text{π}} \left( {{m^2} - m} \right)} {{\left( {\displaystyle\frac{{{m^2} - m}}{{\rm{e}}}} \right)}^{{m^2} - {{m}}}}{m^{{m^2}}}}}\sim \\\quad\quad\quad\quad\quad\quad\displaystyle \frac{1}{{\sqrt {2{\text{π}} \left( {m - 1} \right)} }} \cdot \frac{1}{{{m^{{m^2} - m}}}} \cdot \frac{1}{m}\end{array}$

(22)

式（22）的增长速度仍取决于第二项的幂指数项，所以式（22）关系可表示为

${C_{\rm two}}= {C_{2 \text{-} \rm part}} \cdot O\left( {{m^{{m^2} - m}}} \right)$

(23)

继而将n=m²代入C₁₂化简得到

${C_{\rm two}}= {C_{\rm one}} \cdot O\left( {\frac{{{m^{{m^2}}} - 2m}}{{{{\rm{e}}^m}}}} \right)$

(24)

由式(21)、(23)、(24)可得 $ {C_{{\rm{two}}}} = {C_{{\rm{one}}}} \cdot $ $ O\left( {\displaystyle\frac{{{m^{{m^2}}} - 2m}}{{{{\rm{e}}^m}}}} \right) = $ ${C_{2 - \rm part}} \cdot O\left( {{m^{{m^2} - m}}} \right)$ ，看出在旅行商人数和城市数为二次关系时，双染色体编码对应的解空间是两段式染色体编码对应的解空间的增长速度的 ${m^{{m^2} - m}}$ 倍，因此不同染色体编码方案的选择对问题的求解经常起主要的作用，可以指导实际问题的求解。

2.4.4 指数关系下的相对解空间分析

本节讨论n与m在指数函数关系下相对解空间的收敛速度。

将n=e^m代入式（4）：

$\begin{array}{c}{C_{31}}= \displaystyle \frac{{{C_{t - \rm part}}}}{{{C_{\rm one}}}}= \displaystyle \frac{{n!C_{n - 1}^{m - 1}}}{{\left( {m + n - 1} \right)!}}\sim \displaystyle \frac{{\sqrt {2{\text{π}} {{\rm{e}}^m}} {{\left( {\displaystyle\frac{{{{\rm{e}}^{m}}}}{{\rm{e}}}} \right)}^{{{\rm{e}}^m}}}\sqrt {2{\text{π}} \left( {{{\rm e}^m} - 1} \right)} {{\left( {\displaystyle\frac{{{{\rm{e}}^m} - 1}}{{\rm{e}}}} \right)}^{{{\rm{e}}^m} - 1}}}}{{\sqrt {2{\text{π}} \left( {m + {{\rm{e}}^{m}} - 1} \right)} {{\left( {\displaystyle\frac{{m + {{\rm{e}}^m} - 1}}{{\rm{e}}}} \right)}^{m + {{\rm{e}}^m} - 1}}\sqrt {2{\text{π}} \left( {m - 1} \right)} {{\left( {\displaystyle\frac{{m - 1}}{{\rm{e}}}} \right)}^{m - 1}}\sqrt {2{\text{π}} \left( {{{\rm{e}}^m} - m} \right)} {{\left( {\displaystyle\frac{{{{\rm{e}}^m} - m}}{{\rm{e}}}} \right)}^{{{\rm{e}}^m} - m}}}}\sim \\ \displaystyle \frac{1}{{\sqrt {2{\text{π}} m} }} \cdot \displaystyle \frac{1}{{{m^m}}} \cdot {{\rm{e}}^{m - 1}}\end{array}$

(25)

同样用二项展开式的前两项取近似代替指数项部分，式（25）可化简为

${C_{31}}\sim \frac{1}{{\sqrt {2{\text{π}} m} }} \cdot \frac{1}{{{m^m}}} \cdot {{\rm{e}}^{m - 1}}$

(26)

式（26）的收敛速度主要取决于第二项幂指数因式 $\displaystyle\frac{1}{{{m^m}}}$ ，所以式（26）关系可表示为

${C_{\rm one}}= {C_{2 \text{-} \rm part}} \cdot O\left( {{{\left( {\frac{m}{{\rm{e}}}} \right)}^m}} \right)$

(27)

同样将n=e^m代入式（5）得

${C_{32}}= \frac{{{C_{2 \text{-} \rm part}}}}{{{C_{\rm two}}}}= \frac{{n!C_{n - 1}^{m - 1}}}{{n!{m^n}}}= \frac{{\left( {n - 1} \right)!}}{{\left( {m - 1} \right)!\left( {n - m} \right)!{m^n}}}$

(28)

式(28)的增长速度仍是取决于第二项的幂指数项，所以式（28）关系可表示为

${C_{\rm two}}= {C_{2 \text{-} \rm part}} \cdot O\left( {{m^{{{\rm{e}}^m}}}} \right)$

(29)

继而将n=e^m代入C₁₂化简得到：

${C_{\rm two}}= {C_{\rm one}} \cdot O\left( {\frac{{{m^{{{\rm{e}}^m} - m}}}}{{{{\rm{e}}^m}}}} \right)$

(30)

由式（27）、（29）、（30）可得 ${C_{\rm two}}= {C_{\rm one}} \cdot O $ $\left( {\displaystyle\frac{{{m^{{{\rm{e}}^m} - m}}}}{{{{\rm{e}}^m}}}} \right) = $ $ {C_{2 \text{-} {\rm{part}}}} \cdot O\left( {{m^{{{\rm{e}}^m}}}} \right)$ ，可以看出在旅行商人数和城市数为指数关系时，双染色体编码对应的解空间是两段式染色体编码对应的解空间的增长速度的 ${m^{{{\rm{e}}^m}}}$ 倍，不同染色体编码方案的选择对问题的求解效率有非常重要的影响，因此本文得到的对3种编码方案对应解空间的大小分析对实际问题的求解提供了定量的指导意义。

3 结束语

本文首先介绍了多旅行商问题的概念和3种染色体编码方案，已有文献只是定性地给出3种编码方案对应解空间的大小关系，并没有给出严格证明。本文首先给出相对解空间的概念，然后在城市数充分大和城市数大于旅行商人数的条件下，在极限意义下严格证明了3种解空间的相对大小关系，最后利用Stirling公式严密分析了几种染色体编码方案中旅行商人数和城市数目在不同关系下相对解空间的大小，得出了相对解空间的理论增长速度，给实际工程问题求解中染色体编码方案的选择提供了科学的参考依据和指导意义。

基于3种染色体方案求解多旅行商问题的相对解空间大小关系分析，就目前方案给出的解空间仍然有冗余解存在。两段式染色体方案在单染色体方案和双染色体方案基础之上消除了相当大的一部分冗余，虽然没有完全消除，但是给了我们很大启发，去寻找更加合理的新的染色体编码方案以进一步减小解空间的冗余。