人脸识别^[1-2]一直是模式识别和人工智能领域研究的热点问题。在此背景下，国内外公司竞相进入该领域，如苹果公司推出的手机人脸识别解锁，支付宝的刷脸登录等。解决人脸识别问题的关键环节是特征提取，特征提取的好坏直接影响分类器识别准确率的高低。目前常用图像特征有LBP纹理特征^[3]、HOG方向梯度直方图特征^[4]和Haar-like特征^[5]，这三种特征虽然在人脸识别中获得了不错的效果，但是也存在特征提取过程比较复杂，识别效率较低等不足。与传统的人脸识别算法相比，卷积神经网络可以将原始图像直接作为输入，减少数据的预处理过程，通过自学习的方式完成特征提取，不仅有效降低了人脸特征提取的时间消耗，而且提取的人脸特征具有很高的辨识度。为了克服传统人脸识别算法特征提取带来的长时间消耗、低识别度的问题，本文提出一种基于卷积神经网络特征提取和贝叶斯分类器相结合的人脸识别算法，利用卷积神经网络提取人脸特征，利用主成分分析法（PCA）对提取的特征进行降维，采用贝叶斯分类器进行判别分类，最后在ORL人脸数据集上进行实验分析，验证该方法提取特征辨识度高和低耗时的优点。

1 相关工作 1.1 卷积神经网络

卷积神经网络^[6-7]作为一种高效的深度学习识别算法，近些年引起了广泛关注，其在语音识别、语音分析和图像处理等领域都获得了巨大成功。在图像处理领域，卷积神经网络可直接将多维的图像数据输入网络，有效避免了复杂的特征提取和预处理过程。

1.1.1 卷积层

卷积层^[8]一般为特征提取层，由多个二维的特征图组成，每个特征图由许多共享权值的神经元组成。特征图中每个神经元通过卷积核与上一层特征图的局部区域相连接。卷积层特征图的计算表达式如式(1)所示。

$x_j^l = f(\sum\limits_{i \in M_{j}} {x_i^{l - 1}k_{ij}^l} + b_j^l)$

(1)

式中： $l$ 表示层数； $j$ 表示 $l$ 层的第 $j$ 个特征图； $f$ 代表激活函数； $k$ 表示卷积核； ${M_j}$ 表示输入特征图的一个选择； $b$ 表示对应的偏置。

1.1.2 亚采样层

亚采样层利用图像的局部相关原理，对卷积层输入的特征图在相邻小区域内进行聚合统计，在减少数据量的同时，保留有用信息。常用的亚采样操作有均值池化(average pooling)、最大值池化(max pooling)和随机池化(stochastic pooling)。亚采样操作之后，输入特征图的宽度和高度均缩小为原来的 $1/n$ ，特征图的个数和上一层一致。亚采样层特征图的计算表达式如式(2)所示。

$x_j^l = f(\beta _j^l{\rm{down}}(x_j^{l - 1}) + b_j^l)$

(2)

式中： ${\rm{down}}( \cdot )$ 表示亚采样函数； $\beta $ 表示乘性偏置； $b$ 表示加性偏置。

1.2 PCA算法

PCA即主成分分析法^[9]，是一种基于统计思想的降维方法。它通过正交变换，将与其分量相关的原随机向量转化为与其分量不相关的新随机向量，达到降维的目的。

设 $p$ 维的随机向量 ${{x}} = {[{x_1}\;{x_2} \cdots {x_p}]^{\rm{T}}}$ ， $N$ 个训练样本 ${{{x}}_i} = {[{x_{i1}}\;{x_{i2}} \cdots {x_{ip}}]^{\rm{T}}},i = 1,2 \cdots ,N$ ， $N > p$ ，则训练样本的均值 $u$ 可由式(3)计算出来。

$u = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} $

(3)

把训练样本每一个图像均值化之后得到样本矩阵Z，Z的计算表达式如式(4)所示。

${{Z}} = [{x_1} - u\;{x_2} - u \cdots {x_n} - u]$

(4)

此时，可得到训练样本的协方差矩阵 ${{C}}$ ， ${{C}}$ 的表达式如式(5)所示。

${{C}} = \frac{{{{Z}} \cdot {{{Z}}^{\rm{T}}}}}{N}$

(5)

协方差矩阵的维数为 $p \times p$ 。

主成分分析法所要寻找的最优投影子空间由协方差矩阵 ${{C}}$ 的非零特征值对应的特征向量组成。在利用PCA降维过程中，一般通过特征值的累积贡献率 $\alpha $ 来确定主成分维数 $k$ ， $\alpha $ 可由式(6)计算。

$\alpha = \frac{{\displaystyle\sum\limits_{i = 1}^k {{\lambda _i}} }}{{\displaystyle\sum\limits_{i = 1}^p {{\lambda _i}} }}$

(6)

假设求得的特征空间矩阵为 ${{U}} = [{u_1}\;{u_2} \cdots {u_k}]$ ，那么将训练样本向 ${{U}}$ 上投影，可以得到投影矩阵 ${{Q}}$ ， ${{Q}}$ 的计算表达式如式(7)所示。

${{Q}} = {{{U}}^{\rm{T}}}{{Z}}$

(7)

${{Q}}$ 即为降维之后的数据。

1.3 朴素贝叶斯分类器

朴素贝叶斯^[10]分类器是一个简单、高效的分类器。它主要是根据先验概率预测样本属于某一类别的概率，选取概率最大的类别作为预测类别。整个朴素贝叶斯算法的过程分为两个阶段：分类器训练阶段、判别分类阶段。分类器训练阶段的目的是生成分类器；判别分类阶段则是根据训练得到的分类器，对一个未知的样本进行预测分类。朴素贝叶斯分类器的数学模型可表示为：假设 $x({x_1},{x_2}, \cdots ,{x_n})$ 为一个待分类的样本，类别集合表示为 $C = \{ {y_1},{y_2}, \cdots ,{y_m}\} $ ，要对样本 $x$ 判别分类，则需分别计算 $P({y_1}|x),P({y_2}|x), \cdots , P({y_n}|x)$ ，那么 $x$ 的预测类别计算表达式如式(8)所示。

$P({y_k}|x) = {\rm{max}}\{ P({y_1}|x), P({y_2}|x), \cdots ,P({y_m}|x)\}$

(8)

${y_k}$ 即为贝叶斯分类器判别的未知样本 $x$ 的类别。

计算上述条件概率的步骤：

1) 构造已知类别的训练样本集合；

2) 统计训练集中各个特征属性在每个类别中的条件概率估计，即计算式(9)所示概率：

$P({x_1}|{y_1}),P({x_2}|{y_1}), \cdots P({x_n}|{y_1})$

(9)

3) 假定各个特征属性是独立的，根据贝叶斯定理,可得条件概率计算表达式，即

$P({y_i}|x) = P(x|{y_i})P({y_i})/P(x)$

(10)

4) $P(x)$ 对所有类别都是一样的，因此只要将分子最大化即可，简化后的条件概率表达式为

$P(x|{y_i})P({y_i}) = P({y_i})\prod\limits_{j = 1}^n {P({x_j}|{y_i})} $

(11)

2 算法详细设计 2.1 算法框架

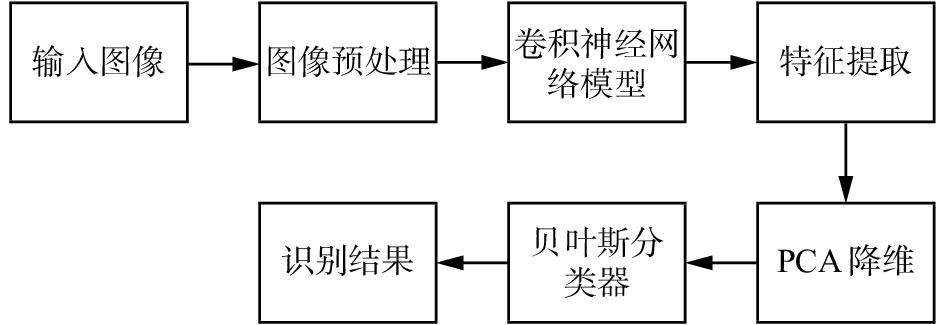
基于卷积特征和贝叶斯分类器的人脸识别方法的主要思想是通过训练好的卷积神经网络模型提取人脸特征，利用PCA对提取的人脸特征进行降维，最后利用贝叶斯分类器进行判别分类。算法框架如图1所示。

从图1可知，算法主要分为两个阶段：学习阶段和测试阶段。学习阶段：利用训练图像样本集合对卷积神经网络模型进行训练，然后用训练好的网络模型提取训练集所有样本图像的特征，通过PCA降维处理之后，用降维后的特征集训练贝叶斯分类器。测试阶段：对待识别的图像预处理之后，通过卷积神经网络提取人脸特征，利用PCA降维，最后将降维之后的特征送入贝叶斯分类器即可得到该样本的预测类别。

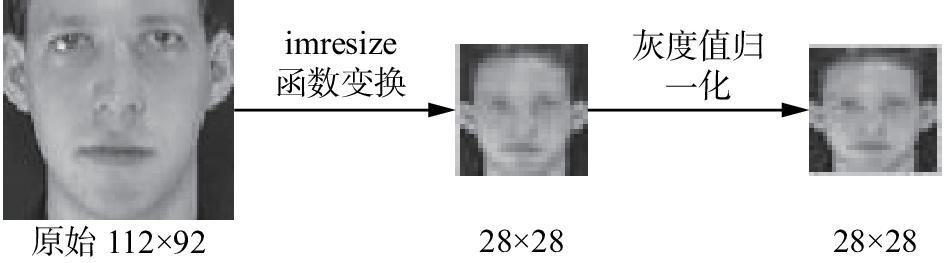
2.2 数据预处理

本文采用ORL人脸数据集作为实验数据集。在训练算法模型之前，对数据集中的人脸图像进行预处理，步骤如下：

1) 调整图像尺寸。通过imresize函数对训练集和测试集中每一幅图像进行缩放处理，由原始的112×92变为28×28。

2) 归一化图像。ORL数据集中的图像为灰度图像，其颜色灰度值一般在0~255，将缩放后图像的原始像素值除以255归一化到[0, 1]。

假设向量 ${{x}}$ 表示原始图像、向量 ${{x}}'$ 表示归一化后的图像，则归一化操作如式(12)。

${{x}}' = {{x}}/255$

(12)

整个数据预处理的过程如图2所示。

2.3 卷积神经网络结构

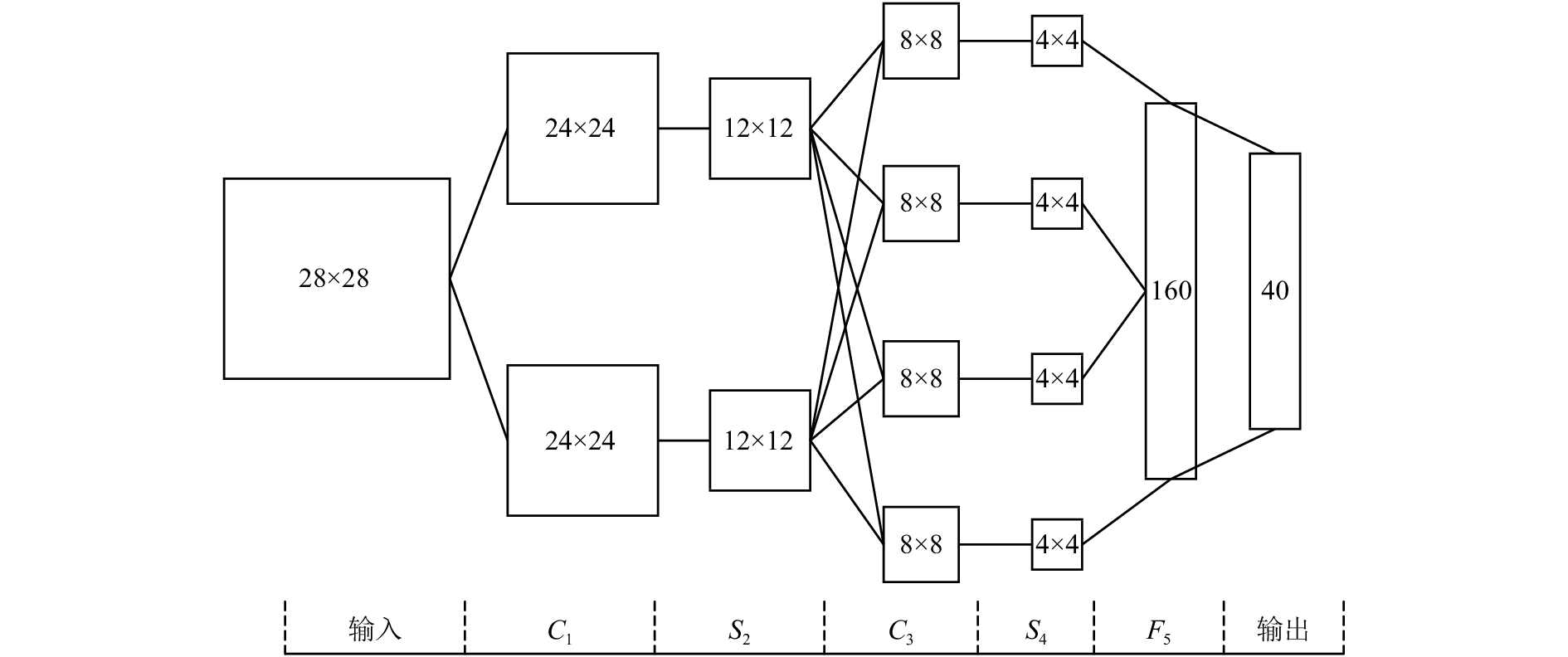
根据前面的介绍可知，卷积神经网络一般是由输入层、卷积层、亚采样层、全连接层和输出层组成。对于卷积神经网络的结构设计，目前都是以经验为基础，缺乏科学的理论指导。依据ORL数据集中人脸图像的尺寸及类别，本文经过大量实验之后设计了一个合适的卷积神经网络结构用于提取ORL人脸特征，网络层次结构如图3所示。

从图3可知，网络的主要参数设置如下：

1) 输入层为28×28的灰度图像；

2) 卷积层C₁通过6个5×5的卷积核对输入层的灰度图像进行卷积操作，得到6个24×24的特征图；

3) 亚采样层S₂在2×2的区域内对C₁层的特征图执行均值亚采样，得到6个12×12的特征图；

4) 卷积层C₃通过10个5×5的卷积核对S₂层的特征图进行卷积操作，得到10个8×8的特征图；

5) 亚采样层S₄在2×2的区域内对C₃层的特征图执行均值亚采样，得到10个4×4的特征图。此时将S₄层的所有特征图连接为一个160维的特征向量；

6) 学习率为1.7，批处理块大小为2，网络阈值函数为sigmoid。

3 实验结果

为了验证本文所提算法的有效性，在ORL数据集中进行了人脸识别实验。

ORL人脸数据集^[11]中部分人脸图像如图4所示。

ORL数据集中包含40个不同人物的脸部图像，每个人物包含10张图像，总共400张图像，每个图像原始大小均为112像素×92像素。每个类别中的脸部图像在不同的时间拍摄得到，主要存在光线、面部表情和面部细节上的一些差异。本文随机选取每一个类别图像中的8张作为训练样本，剩下的2张图像作为测试样本，训练集与测试集的比例为4∶1。

3.1 网络结构设计 3.1.1 卷积核尺寸选择

卷积核的尺寸决定了卷积层输出特征图的大小。假设卷积层输入图像的大小为 ${{n}}\times{{n}}$ ，卷积核的大小为 ${{m}}\times{{m}}$ ，卷积之后特征图的大小为 ${{s}}\times{{s}}$ ，则s可通过式(13)算出。

${s} = {n} + 1 - {m}$

(13)

ORL人脸图像经2.2节预处理后大小变为28×28，为确保卷积后的特征图大小为整数，将C₁和C₃层卷积核大小设置为5×5。

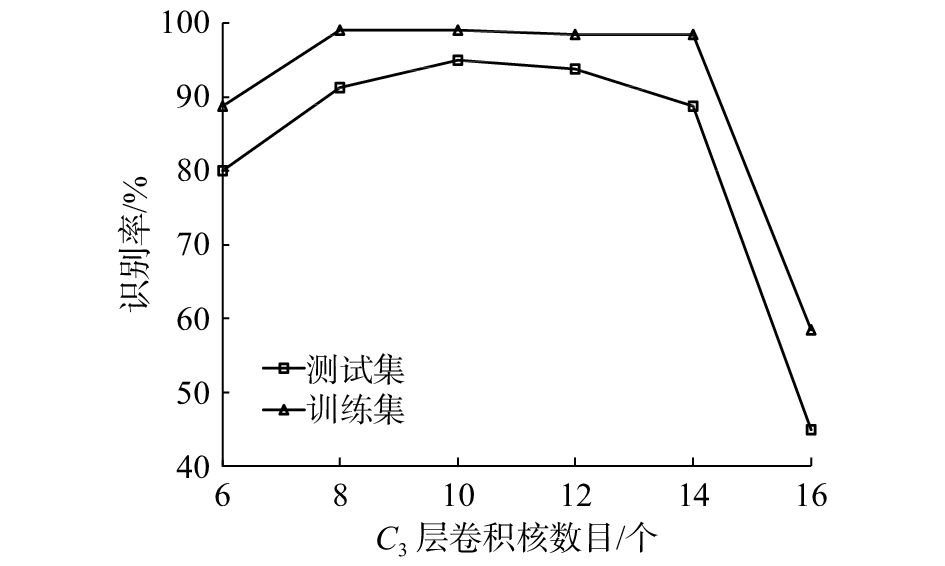
3.1.2 C₃层卷积核个数选择

卷积神经网络识别准确率与卷积核的个数密切相关。卷积核个数越多，提取的图像特征越丰富，但同时会增加网络训练时间。为选取C₃层合适的卷积核个数，保持C₁层卷积核个数不变，训练迭代次数为60次，改变C₃层卷积核的个数，分别使用训练集和测试集对变化后网络结构的识别准确率进行验证。实验结果如图5所示。

图5的实验结果表明，卷积核个数与网络识别正确率并非正比关系。当C₃层卷积核个数为10时，测试集的识别准确率达到最高。若继续增加卷积核个数，网络中对应的权重W个数也随之增多，但由于ORL数据集样本的个数较少，可选取的训练集样本有限，已无法满足网络学习的需要，因此测试集的识别准确率开始下降。

3.1.3 C₁层卷积核个数选择

由3.1.2节实验结果可知，C₃层有10个卷积核时，测试集的识别准确率均达到最高。为选取C₁层合适的卷积核个数，保持C₃层卷积核个数不变，训练迭代次数为60次，改变C₁层卷积核的个数，分别使用训练集和测试集对变化后的网络结构进行实验验证。实验结果如图6所示。

图6的实验结果同样表明，卷积核个数与网络最终识别正确率并非正比关系。当C₁层卷积核个数为6时，测试集的识别准确率达到最高。若继续增加卷积核，网络需要学习的参数也增多，但由于ORL数据集样本的个数较少，选取的训练集样本有限，已无法满足网络学习的需要，因此测试集的识别准确率开始下降。

3.1.4 学习率

学习率不仅决定卷积神经网络学习过程中训练误差的收敛速度，而且影响网络的识别正确率。学习率越大，权值变化越快，训练误差收敛越快。学习率越低，权值变化越慢，收敛越慢，网络训练时间就会增加。但学习率过大或过小，均可能导致训练误差无法收敛。为研究学习率与网络识别正确率的关系，网络结构参数设置为：C₁层6个卷积核，C₃层10个卷积核，统计不同学习率下的训练集和测试集的识别正确率，实验结果如图7所示。

从图7可以看出，随着学习率的增大，训练集和测试集的识别率也相应提高。当学习率为1.7时，训练集和测试集的识别率最高。此后继续增大学习率，识别率反而下降。因此，本文将学习率设定为1.7。

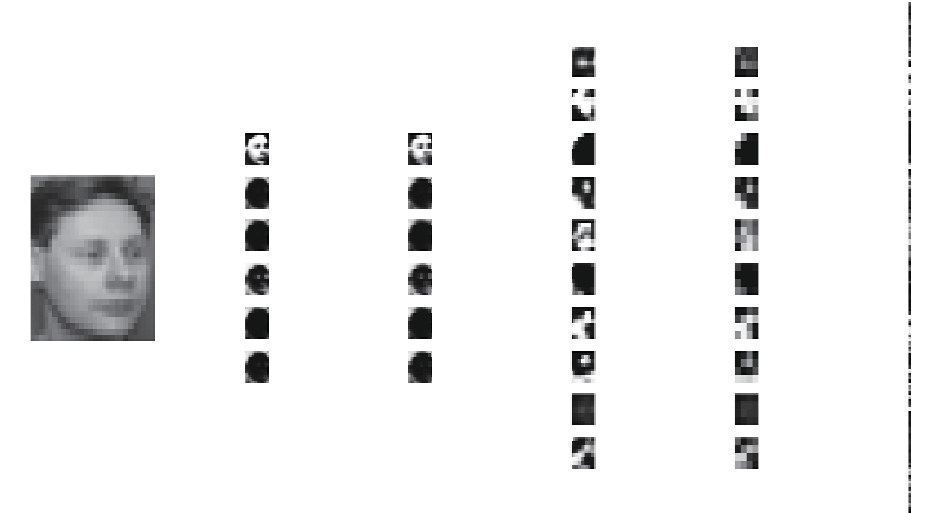
3.2 卷积激活特征

通过训练好的卷积神经网络结构即可完成特征提取。为更加直观地展示卷积神经网络不同层提取到的具体人脸特征，本文对卷积神经网络每一层的人脸特征图进行可视化，实验结果如图8所示。

图8分别展示了本文所设计的卷积神经网络结构从输入层到全连接层每一层提取到的人脸特征图。第一层将缩放和归一化后的28×28大小的图像直接作为网络的输入，经过C₁层卷积操作后得到6个24×24的特征图，第三层的池化层S₂在2×2的小区域内进行均值亚采样操作后，得到6个12×12的特征图，第四层C₃为卷积层，第五层S₄为卷积池化层，分别采用C₁和S₂相同的处理方式，经过C₃、S₄层的卷积与亚采样处理后，可得到10个4×4的特征图，网络最后一层为全连接层，全连接层将最后一层的10个特征图连成一维的特征向量，该特征向量即为提取到的人脸特征，通过PCA降维之后送入贝叶斯分类器即可完成判别分类。

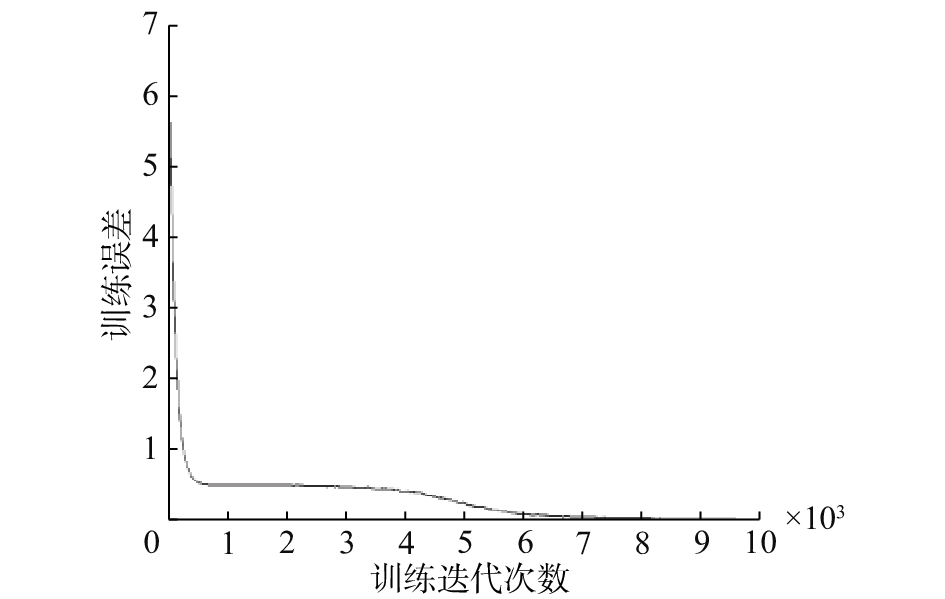
3.3 卷积神经网络

由于卷积神经网络结构本身也具备分类器的功能。为检验单独用卷积神经网络的识别效果，本文利用卷积神经网络对ORL数据集中的人脸进行识别。卷积神经网络训练过程代价函数误差曲线变化如图9所示。

从图9可以看出，在训练过程中，卷积神经网络的输出误差一直在减小，最终不再变化，此时卷积神经网络已达到收敛状态。用训练好的网络模型对ORL数据集80张测试样本的识别准确率为96.25%，对全部样本的识别准确率为98.75%，达到了预期的目标。

3.4 PCA降维

通过卷积神经网络提取到的人脸特征为160维，维数较高，为降低人脸特征维数，本文采用PCA对160维的特征进行降维处理，为研究主成分特征值累计贡献率对识别性能的影响，本文分别研究了不同累积贡献率下基于卷积特征和贝叶斯分类器人脸识别方法的识别效果，特征值累积贡献率与识别率的关系曲线如图10所示。

令 $\alpha $ 表示特征值累积贡献率，从图10可知，当 $\alpha $ 的取值从100%减少到95%过程中，识别准确率逐渐增加，当 $\alpha = $ 95%时，识别准确率最高，当 $\alpha $ 取值继续减小时，识别准确率逐渐开始下降。这主要是因为，当 $\alpha $ 的取值从100%减少到95%过程中，卷积特征经PCA变换时，冗余信息被去除的越来越多，当 $\alpha $ 取值为95%时，冗余信息几乎被全部剔除，获得的识别准确率也最高；当 $\alpha $ 继续减少时，卷积特征中的部分有用信息也被剔除，导致识别效果越来越差。因此，在利用PCA进行降维压缩时，主成分的维数选择至关重要。在本文人脸识别实验中，选取 $\alpha = $ 95%时的主成分维数，那么经PCA变换之后，原来160维的卷积特征就变为41维的特征，降维效果比较显著。

3.5 对比实验

本文提出的方法在ORL人脸数据集中获得了良好的识别效果，该方法在选取的80张测试图像中获得了97.5%的高识别率，在全部人脸图像的识别正确率可达99.00%。为进一步验证本文所提算法的有效性和优越性，将此方法与几种传统的人脸识别算法在ORL数据集全部样本的识别效果进行对比，结果如表1所示。

表1的实验结果可以表明：本文提出的基于卷积特征和贝叶斯分类器的人脸识别算法，在ORL人脸库的识别效果好于传统的人脸识别算法；本文方法相对2DPCA的识别准确率提高了0.7%，比FisherFace方法识别准确率提高了0.5%，比Eigenface的识别准确率提高了1.5%，比ICA识别方法的识别准确率提高了5.25%，比单独卷积神经网络的识别准确率高0.25%。这一系列实验结果表明，卷积神经网络提取的人脸特征具有较高的辨识度，与PCA和贝叶斯分类器结合可进一步提高人脸识别正确率。

3.6 结果分析

为了克服传统人脸识别算法特征提取带来的长时间消耗、低识别度的问题，本文提出一种卷积神经网络、PCA和贝叶斯分类器相结合的方法，用卷积神经网络提取人脸特征，用PCA对提取的特征降维压缩，通过朴素贝叶斯判别分类，在ORL人脸数据集中获得了良好的识别效果。该方法在选取的80张测试图像中获得了97.5%的高识别率，在全部人脸图像的识别正确率可达到99.00%，且识别效果好于几种经典的人脸识别算法以及单独的卷积神经网络算法。因此卷积神经网络提取到的人脸特征具有更强的辨识度，在判别分类的过程中表现出了强大的优势。

4 结束语

当前人脸识别仍是学术界和工业界研究的热点问题。为降低人脸特征提取的复杂性，本文将当下最为流行的深度学习模型卷积神经网络引入人脸识别任务，提出基于卷积神经网络和贝叶斯分类器以及主成分分析法的人脸识别算法模型，首先利用卷积神经网络提取人脸特征，其次通过PCA对人脸特征进行降维处理，最后通过朴素贝叶斯进行判别分类。通过实验与分析可以看出，本文所提的算法不仅简化了特征提取的过程，而且提高了人脸识别的准确率，为人脸识别算法的研究提供一种新思路。