如何充分提取图像纹理特征是人脸识别技术的核心^[1-2]。一般，人们习惯将纹理特征分成全局特征^[3-5]与局部特征两大类。全局特征由于描述的是整个人脸图像特征，包括颜色、纹理和形状特征，会有大量的冗余信息。局部特征是指用一些特征点来简单有效地表示人脸特征信息，具有对遮挡情况良好的稳定性和对背景与前景的可区分性。局部二值模式 (local binary pattern，LBP)^[6]是最常见和最有效的人脸特征提取方法之一，但对光照和噪声变化比较敏感，识别效果还不理想，之后涌现出很多新的改进方法^[7-11]。Jabid等^[12]于2010年提出了局部方向模式算法，即LDP(local directional pattern)算法，是在LBP特征图的基础上，与Kirsch算子卷积得到的人脸特征信息，表现出对光照和噪声较强的鲁棒性，由于特征模式数还比较大，加上卷积所耗费的时间，LDP算法识别时间会很长。之后不断出现一些新的改进算法^[13-22]，比如：2105年朱明旱^[16]提出的改进局部方向数字模式(improved local directional number pattern，ILDN)的算法，是一种采用16邻域和24邻域两种边缘模板的局部方向模式，虽然识别效果有所改善，但多尺度多半径特征提取，卷积次数明显增加，大量增加了训练时间；吴迪等^[17-18]提出显著型局部方向模式(significance local directional pattern，SLDP)和显著型局部方向差值模式(significance difference local directional pattern，SDLDP)算法，需要对两组编码进行求和取平均，这样会造成区分度降低；2015年Rivera等^[19]提出LDTP(local directional texture pattern)算法，将原始空间采用中心对称方式提取方向信息，在强度空间提取最大边缘响应值，虽然人脸特征信息会增加，但原始空间的方向会导致算法的不稳定性增加；2015年李照奎等^[20]在LDP基础上提出差值局部方向模式 (DLDP)算法，来提取相邻卷积后的人脸灰度值之间的特征信息，引出了差值空间的新思路，相比LDP的强度空间，表现出对光照、噪声、遮挡更强的鲁棒性；但按照LDP编码方式，不仅特征模式数较高，而且只单一地考虑近邻边缘响应值之间的强度变化，会造成特征提取不充分；2018年Khadiri^[21]提出3值模式LDTP (local directional ternary pattern)的算法，由于会选择一个固定的阈值，不同情况下，阈值会有波动，算子的适用性不强；王晓华等^[22]于2016年提出梯度中心对称局部方向模式(GCS-LDP)算法，采用的方式是提取方向信息和人脸强度信息，但在强度空间上编码时，采取中心对称作差的方式，提取的方向信息会造成编码不稳定。

本文提出一种双差值局部方向模式(DDLDP)人脸表示方法。首先，利用作差运算减少光照和噪声等外界影响因素对像素值产生的影响，因为影响因子对相邻像素点的影响是连续的，相邻之间像素值作差正好可以相互抵消一部分外界因素的影响，但还不够。通过不同半径领域像素值之间的差值和同一半径领域像素值之间的差值运算，选取两个运算差值中的最大值，外界因素造成两个最大差值的变化相比两个最大差值本身固有的变化，基本可忽略不计，从而达到减少噪声和光照对其的影响。其次，双差值运算不仅提取了相邻卷积后的人脸灰度值之间的内在梯度信息，而且提取了相邻不同半径人脸灰度响应值之间的外在方向信息，内在梯度信息和外在方向信息的结合使提取的人脸特征更加丰富。最后，由于编码值是2位8进制数，模式数为64，相比DLDP算法，特征维度将会减少。

1 DDLDP 1.1 DLDP码

为了提取更多细节的人脸信息，DLDP算法是在LDP算法基础上，通过计算近领边缘响应值之间的强度变化，揭示了图像潜在的结构信息，本质上是强度空间到梯度空间人脸信息的一种跨越，使人脸特征信息得到更充分的提取。具体步骤如下。

1)将图像3×3子领域I与8个Kirsch算子卷积，得到相应8个方向的边缘响应 ${{ m}_i}$ (i=0, 1, ···, 7)，表达式为

${ m}_i = { I}\times{{ M}_i}$

(1)

2)将近领边缘响应值 ${ m}_{i}$ 之间按照一定顺序作差并取绝对值，得到相应8个差值 ${n_j}$ ( j=0, 1, ···, 7)，同样也相应地对应到8个方向。计算方法见式(2)：

${n_j} = \left\{\!\!\! \begin{array}{l}\left| {{m_{i + 1}} - {m_i}} \right|,\quad j \in [0,6]\\\left| {{m_0} - {m_7}} \right|,\quad j = 7\end{array} \right.$

(2)

3)将绝对人脸灰度响应差值 ${n_j}$ 按照从小到大的顺序，选择第k位的值 ${n_k}$ 作为判别点，再将大于等于 ${n_k}$ 的所有 ${n_j}$ 值所对应的j位取1，剩下的8-j位取0。表达式如式（3）、（4）：

${\rm DLDP}\left( {{I}} \right) = \sum\limits_{j = 0}^{\frac{N}{2}-{1}} {s({n_j} - {n_k})} {2^j}$

(3)

$s(x) = \left\{\!\!\!\! \begin{array}{l}1,\quad x > = 0\\0,\quad {\text{其他}}\end{array} \right.$

(4)

4)图1给出了k=3时，计算DLDP码的一个实例。

1.2 DDLDP码

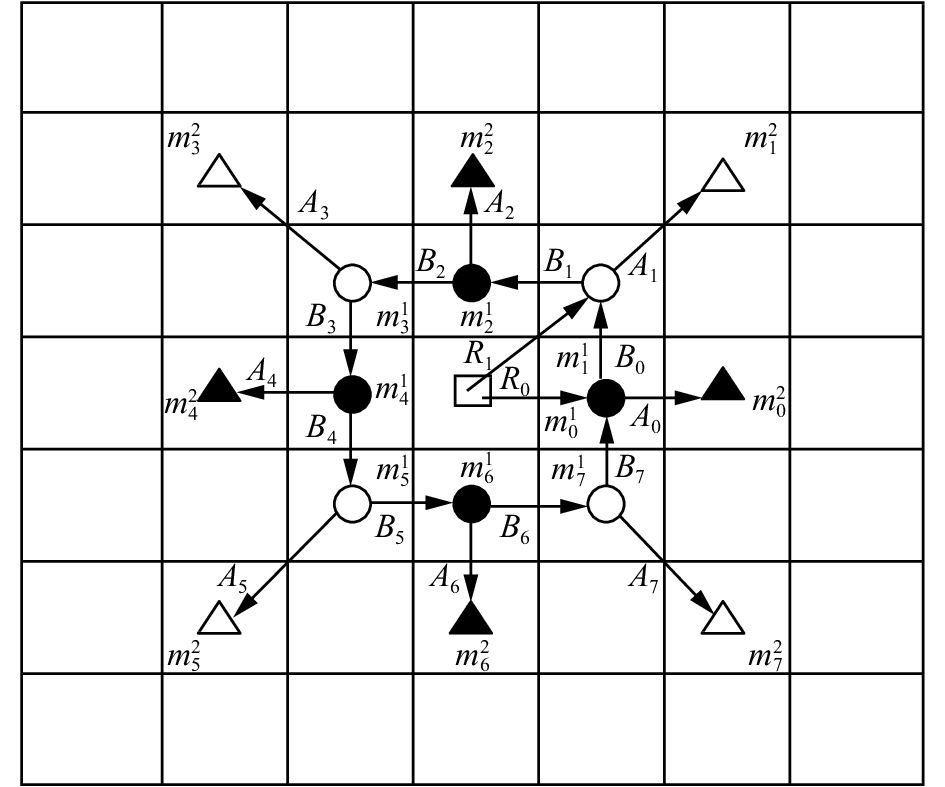
DLDP算法是对LDP算法存在问题的一种改进算法，本质上揭示了像素块之间内在关系，虽然相邻像素值之间作差可以减少对光照、噪声的影响，但作用有限，人脸特征提取本质没有很大的变化，人脸特征提取还不够充分，识别效果还不够好，模式数较大。本文提出的DDLDP算法，考虑了不同半径边缘响应值之间的外在方向关系，把边缘响应值之间内在关系和外在关系结合，使人脸特征得到更加充分的提取，并且减少了人脸的特征维度，缩短了识别时间，降低了光照和噪声对人脸的影响。DDLDP算法原理如图2所示。

DDLDP算法具体步骤：首先，将半径为1的3×3领域人脸灰度值 ${{ I}_1}$ 与同样大小半径的Kirsch算子 ${ M}_i^1$ 进行卷积。同理，将半径为2的5×5领域人脸灰度值 ${{ I}_2}$ 与 ${ M}_i^2$ 卷积，分别得到两组人脸灰度卷积值 $m_i^1$ 和 $m_j^2$ (i, j=0, 1, ···, 7)。如图3所示列举了其中正东方向不同半径的Kirsch算子。

计算方法见式(5)、(6)

${ m}_i^1 = {{ I}_1}*{ M}_{_i}^1$

(5)

${ m}_j^2 = {{ I}_2}*{ M}_j^2$

(6)

式中： ${{ I}_1}$ 和 ${{ I}_2}$ 表示输入图像； ${ M}_i^1$ 表示半径为1第i个Kirsch模板算子； ${ M}_j^2$ 表示半径为1第i个Kirsch模板算子； ${ m}_i^1$ 表示半径为1的边缘响应值； ${ m}_j^2$ 表示半径为2的边缘响应值。

然后，将半径为1得到的人脸灰度响应值 ${ m}_i^1$ (i=0, 1, ···, 7)，用前后相邻作差的方式，得到8个绝对人脸灰度响应差值 $A_i$ (i=0, 1, ···, 7)，再将不同半径大小的相邻边缘值，用上下相邻作差的方式，得到8个绝对人脸灰度响应差值 $B_j$ ( j=0, 1, ···, 7)。计算方法见式(7)、(8)：

${{ A}_i} = \left\{\!\!\!\! \begin{array}{l}|{ {m}}_0^1 - { {m}}_7^1|,\quad i = 7\\|{ {m}}_{i + 1}^1 - { {m}}_i^1|,\quad {i \in [0,6]}\end{array} \right.$

(7)

$B_j = |{ {m}}_j^1 - { {m}}_j^2|,\quad j \in [0,7]$

(8)

最后，分别将两组值 $A_i$ 和 $B_j$ 中最大人脸灰度响应值对应的编号下标位置i和j，构成二位八进制DDLDP码，如式(9)～(11)所示：

$i = \arg \max \left\{ {{A_i}|0 \leqslant i \leqslant 7} \right\}$

(9)

$j = \arg \max \left\{ {{B_j}|0 \leqslant j \leqslant 7} \right\}$

(10)

${\rm{DDLD}}{{\rm{P}}_{}}(I) = i \times {8^1} + j \times {8^0}$

(11)

可得，DDLDP码模式数为64。图4所示详细地展示了DDLDP算法编码流程。

1.3 DDLDP优势分析

DDLDP是对DLDP算法的一种改进算法，其采用的双差值运算不仅表现对光照和噪声更强的鲁棒性，而且人脸特征得到更加充分的提取。证明过程如下。首先，假设 ${{a}} = {{m}}_1^1$ ， ${{b}} = {{m}}_2^1$ ， ${{c}} = {{m}}_1^2$ ；由式(7)、(8)得： $A_1 = |{{a}} - {{b}}|$ ， $B_1 = |{{a}} - {{c}}|$ ；外界因素对其影响: ${{{a}}'} = {{m}}_1^1 + \varepsilon _1^1$ ， ${{{b}}'} = {{m}}_2^1 + \varepsilon _2^1$ ， ${{{c}}'} = {{m}}_1^2 + \varepsilon _1^2$ ；同理，由式(7)、(8)得： $A_1' = |{{{a}}} - {{b}} + \varepsilon _{_1}^1 - \varepsilon _{_2}^1|$ ， $B_1' = |{{a}} - {{c}} + \varepsilon _{_1}^1 - \varepsilon _{_1}^2|$ 。

因为 $|\varepsilon _1^1 - \varepsilon _2^1| \leqslant \varepsilon _1^1$ ， ${\rm{|}}\varepsilon _1^1 - \varepsilon _2^1{\rm{|}} \leqslant \varepsilon _2^1$ ，所以作差可以抵消部分影响。又由相邻像素值的连续性可知， $|\varepsilon _1^1 - \varepsilon _2^1|$ 和 ${\rm{|}}\varepsilon _1^1 - \varepsilon _1^2{\rm{|}}$ 很小，由式(9)、(10)可得，选择最大 $\partial = \max \{ {A_i}|0 \leqslant i \leqslant 7\} $ 和 $\beta = \max \{ {B_j}|0 \leqslant j \leqslant 7\} $ ；可得， $\partial \gg |\varepsilon _i^1 - \varepsilon _{i + 1}^1|$ ， $\beta \gg |\varepsilon _i^1 - \varepsilon _i^2{\rm{|}}$ 。外界因素造成两个最大差值的变化相比两个最大差值本身固有的变化，基本可忽略不计。因此，双差值运算在对噪声和光照的鲁棒性方面具有更好的效果。

双差值运算既提取了相邻人脸灰度响应值之间的内在梯度信息，也提取了相邻不同半径人脸灰度响应值之间的外在方向信息。图5具体展示了特征提取图和人脸直方图。由图5可知，DDLDP算法的特征提取图纹理轮廓更加清晰，人脸提取更加充分；DDLDP算法直方图数据分布波动更小，表现出对噪声和光照等外界因素的鲁棒性；并且DDLDP算法的特征模式数为64，相比DLDP和LDP算法，特征维度更小。

2 人脸描述

DDLDP人脸识别算法流程图见图6，具体步骤描述如下。

1)对人脸库进行预处理，最主要是对人脸以眼部为中心进行裁剪，以提取有效的人脸部分I。

2)对预处理后的人脸图像采用DDLDP算法进行特征提取。DDLDP算法具体编码方式见1.2节。

3)因为不同的分块有不同的识别效果，所以对每一张图像进行分块处理。本文对人脸图像进行从块行大小1~13、块列大小1~13的循环分块，并从中选择最佳分块方式。每一个子块用符号 ${{ I}^*}_{\left( {x,y} \right)}$ 表示，其中，x,y $ \in $ [1,13]。

4)考虑到人脸不同部位的特征信息不同，计算出图像每个子块各像素点的局部信息熵，计算方法见公式(12)。

$H\left( {{{ I}^*}_{(x,y)}} \right) = - \sum\limits_i^t {{P_i}\log \left( {{P_i}} \right)} $

(12)

式中：P_i表示第i个灰度级出现的概率，i $ \in $ [0，63]。

5)根据分块后每个像素点的局部信息熵的熵值，计算出分块子图的贡献度即权值。计算方法见式(13)：

$W\left( {x,y} \right) = \frac{1}{{P \times Q}}\sum\limits_{x = 1}^P {\sum\limits_{y = 1}^Q {H\left( {{{ I}^*}_{(x,y)}} \right)} } $

(13)

式中：P和Q分别代表分块的行数和列数；x，y $ \in $ [1，13]。

6)将所有分块的统计直方图特征信息串接，融合成一个直方图。计算方法见式(14)：

${H^*} = \sum\limits_{x = 1}^P {} \sum\limits_{y = 1}^Q {{ I}_{(x,y)}^* \times } W\left( {x,y} \right)$

(14)

7)再通过PCA^[4]对特征向量进行降维处理。

8)最后，通过Chi平方统计^[23]分类识别，求得识别率。计算方法见式(15)：

$\chi _n^2({\bf S{H}^*},{\bf M{H}^*}) = \sum\limits_{j = 0}^{P \times Q} {\frac{{{{({\bf S{H}^*}(j) - {\bf M{H}^*}(j))}^2}}}{{{\bf S{H}^*}(j) + {\bf M{H}^*}(j)}}} $

(15)

式中：j表示对应第几个子块；SH^*和MH^*分别代表测试与训练样本待比较的特征向量。对于卡方而言，匹配度越高，距离越小，则卡方值越低，同理，反之。

3 实验仿真与分析

对YALE人脸库、ORL人脸库和AR人脸库进行相关实验。耶鲁大学创建的YALE人脸库有15个志愿者，共165张图像，图片大小为100×100。选择的人脸情况为不同的光照、不同的表情和不同遮挡等。ORL人脸库有40个人，每个人10幅图像，共400幅人脸图像，其人脸表情、细节、姿态、年龄、性别、种族等均有变化，图片的大小为112×92。美国普渡大学的AR人脸库来自126个人，该人脸库分为姿态(不同笑的程度)、光照(不同光照方向和大小)、遮挡A(戴眼镜)和遮挡B(带围巾)等4种变化。具体人脸库图片如图7所示。

3.1 分块数的选择

因为人脸特征信息分布不均匀，所以对人脸进行不同的分块会有不同的识别效果，分块数太少会有大量的信息冗余，分块数太多会丢失人脸特征的空间信息，这都会导致人脸识别效果不佳。所以对图像进行处理后，为了选择出最佳识别率，本文对人脸图像进行从块行大小1~13、块列大小1~13的循环分块。其中，在YALE和ORL库上随机抽取每个人3张图片构成训练集，在AR库上都选第1张构成训练集，剩下的构成测试集。最终识别率由重复实验50次的平均值来表示，再选择最合适的分块方式，具体实验结果如图8所示。由图8可知，在YALE库中，当行分块固定不变，列分块3~10时，识别效果最佳，呈现中间高，两端低的变化情况；当列分块固定不变，行数7~13时，识别率最好，呈现前段低，后端高的情况，获得最高识别率的分块大小为11×10(行分块数为11，列分块数为10)。在ORL库中，当行分块固定不变，列分块1~4时，基本上识别率快速增加，列分块5~13时识别率缓慢下降；当列分块固定不变时，除行分块数为1时，识别率较差外，其他分块识别效果呈波动变化，ORL人脸库上获得最高识别率的分块方式为7×4；同理，AR表情集、光照集、遮挡A和遮挡B获得最高识别率的分块方式分别为4×11、6×8、7×5和13×10。

3.2 实验识别率与实验分析

为了体现DDLDP算法的优势，选择如下算法进行对比：LDP^[12]、LDN^[14]、CSLDP^[15]、SDLDP^[18]、LDTP^[19]、DLDP^[20]、GCSLDP^[22]。在YALE库上训练样本为4时，LDP、DLDP和SDLDP对应最佳分块为13×13，GCSLDP和LDN对应的最佳分块为12×13，LDTP对应最佳分块为13×12，CSLDP对应最佳分块为11×11。在ORL库上训练样本为4时，LDP、DLDP、GCSLDP、SDLDP对应最佳分块为6×3，LDTP对应最佳分块为7×3，LDN对应最佳分块为5×3，CSLDP对应最佳分块为7×2；同样在AR人脸库中各算法都取对应最佳分块情况下的实验结果，YALE和ORL人脸库训练样本数为2~4，分别如表1~3所示。

由表1~3可得，在YALE、ORL、AR人脸库上，对比LDP、LDN、CSLDP、DLDP、SDLDP、LDTP和GCSLDP算法，DDLDP算法识别率最高。特别是在AR库遮挡情况下，DDLDP算法明显高于其他算法。所以在姿态、光照、表情和遮挡情况下，所提方法具有更强的识别能力。LDP、LDN和CSLDP算法，利用与8个Kirsch算子卷积，得到8个方向的边缘响应值，只是编码方式不同，在提取人脸信息方面，单一地利用了梯度空间原始信息。DLDP算法利用与8个Kirsch算子卷积，得到8个方向的边缘响应值，然后，将近邻边缘响应值之间相应作差，在提取人脸信息方面，单一地利用了相邻边缘邻域梯度差空间信息。SDLDP算法利用DLDP差值运算的思想对井型领域的特征提取方式进行改进，但对两组梯度值取平均，编码区分度会降低。LDTP算法是原始灰度空间采用中心对称方式提取方向信息，在强度空间提取最大边缘响应值，虽然人脸特征信息会增加，但原始空间的方向会导致算法的不稳定性因素增加。GCSLDP算法先对8个边缘响应值采用CSLDP算法编码方式，再选取边缘响应值中最大值，虽然利用了梯度空间信息和梯度差空间信息，但只是考虑像素邻域内在的空间信息，没有考虑不同邻域半径像素值之间的外在空间信息。DDLDP算法既考虑卷积后相邻人脸灰度响应值之间的内在空间梯度信息，又考虑不同半径相邻人脸灰度值响应之间的外在空间方向信息，使人脸特征信息得到进一步的提取，所以在人脸识别效果上高于其他算法。

3.3 噪声实验

为了验证DDLDP算法的抗噪性，选择在ORL人脸库进行噪声实验，选择均值为0的高斯白噪声作为噪声模型。其实验噪声的大小从0开始每次增加0.000 1，增加5次，对比实验效果。噪声ORL人脸库具体操作同3.2节。为了直观体现DDLDP算法的抗噪性，本文引入式(16)来表示算法识别率下降速度。

$\alpha = \frac{{x - y}}{x} \times 100\text{%} $

(16)

式中：x表示原本的识别率；y表示加噪声后的识别率；α表示加入噪声后，各算法识别率的下降比例。α越小，表示抗噪能力越强；反之，α越大，表示抗噪能力越弱。加噪声后，各算法识别率结果见表4所示。由表4可得，在噪声实验中，随着高斯白噪声归一化方差逐渐增大，当高斯白噪声归一化方差增大到0.000 5时，对比LDP、LDN、CSLDP、DLDP、SDLDP、LDTP、GCSLDP、DDLDP算法，DDLDP算法的δ值最小，体现本文算法对噪声更强的鲁棒性。且在噪声条件下，相比其他算法，DDLDP算法的识别率一直最高，具有更强的抗噪性。

4 结束语

针对差值局部方向模式(DLDP)特征提取不够充分和对光照、噪声敏感的问题，本文提出的双差值局部方向模式人脸识别方法相比其他算法，DDLDP算法通过双作差运算不仅提取了相邻卷积后的人脸灰度值之间的内在空间梯度信息，而且提取了相邻不同半径人脸像素点之间的外在方向信息，边缘响应值之间内在关系与外在关系的结合使人脸特征得到了更充分的提取。在YALE、ORL、AR人脸库上，DDLDP算法均取得了较高的识别效果。在噪声实验中，DDLDP算法也表现出更强的鲁棒性，证明了该算法的有效性。接下来的工作是研究不相邻边缘响应值对识别率的影响。