随着大数据与互联网加时代的到来，动态流数据成为了一种主流的数据类型，当前已经被广泛地应用于金融股票交易、天气和环境监测、计算机网络监控等众多领域^[1]。在上述应用中，在线计算^[2-3]是动态流数据的主要计算形式，其主要特点是实时数据快速地加载入内存，而CPU需要对内存中的实时数据实施快速计算，并且实时反馈计算结果。而传统的离线计算^[4]方式需要外部存储器积淀数据后再进行科学计算，对于数据实时性和流动性的要求相对较低，因此传统计算方法不能完全适应在线计算的新要求。研究更加高效的在线计算方法已经成为了当前大数据领域的一项重要课题。

近年来，以SPARK^[5]为代表的内存计算平台的推出与发展，较快推动了动态在线计算的发展。不确定性问题是机器学习领域的经典难题，如何在在线计算过程中进行不确定性问题的动态推理及求解也逐渐成为一项具有挑战性的新议题。

三支决策理论^[6]是基于粒计算粗糙集理论提出和发展起来的一种处理不确定、不完整信息决策的新方法。其初始目的是为粗糙集理论中的3个分类区域，即正域、负域和边界域，提供合理的决策语义解释。近年来随着该理论的深入研究与发展，三支决策被认为是在信息不足或者获取足够信息的代价较高背景下的合理选择。该理论与人类的认知习惯相似，具有认知方面的优势，近年来，三支决策理论在垃圾邮件过滤^[7]、文本挖掘^[8]、图像识别^[9]、属性约简^[10]、聚类^[11]等应用领域^[12-14]也都取得了广泛的成果。

目前主要代表性的理论成果包括：基于代价敏感度量的决策粗糙集三支决策^[15]、模糊集三支决策^[16]、区间集三支决策^[17]、概率粗糙集三支决策^[18]、博弈粗糙集三支决策^[19]、信息熵三支决策^[20]、GINI系数三支决策^[21]等。

同时针对动态数据环境下的动态计算也是另一项主要研究内容。文献[22]首次提出一种离线动态计算方法，其对更新后的数据对象进行重新计算，算法执行效率不高。为了提高动态计算的效率，许多学者研究了粗糙集及三支决策的离线增量学习方法。其主要成果有：Liu等^[23]提出了一种基于矩阵的动态不完备信息系统的增量方法；Li等^[24]通过分析动态数据库中新数据的不断更新，提出了基于粗糙集理论的增量学习方法；Zhang等^[25]等给出了邻域粗糙集模型下多对象增加删除时近似集快速更新的方法；Luo等^[26]考虑到信息系统中数据对象动态插入，讨论介绍了概率粗糙集模型中条件概率的动态估计策略，进而给出了概率三支近似的增量更新算法。然而研究表明，上述动态学习研究都是以离线计算为研究背景，而以在线计算为背景的动态三支决策研究较少。

本文以上述三支决策动态计算研究为基础，系统性地研究了在线计算中动态数据变化形式及动态决策的变化规律，提出一种有别于传统经典计算的三支决策在线快速计算学习方法，并进行实验验证。

1 相关工作 1.1 概率粗糙集三支决策模型

概率粗糙集是构造三支决策的基础原型，首先我们回顾一下概率粗糙集三支决策的相关基本理论^[20]。

信息系统 ${\rm{IS}}$ 是一个四元组， ${\rm IS} = (U,A,V,f)$ ，其中 $U$ 代表论域中对象 $x$ 的集合； $A = R \cup D$ 代表属性集合，R为条件属性集合( $U/R = \{ {R_1},{R_2} \cdot \cdot \cdot ,{R_m}\} $ 为R属性确定的不可区分关系形成的等价类集合)，D为决策属性集合( $U/D = \{ {D_1},{D_2} \cdot \cdot \cdot ,{D_n}\} $ 为D属性确定的不可区分关系形成的等价类集合)；V代表A中各属性的取值范围； $f$ 代表从对象到属性取值的信息函数，即 $f:U \times A \to V$ 。

定义 1 　在信息系统 ${\rm{IS}}$ 中，设 ${D_j}$ 为论域U的子集，即 ${D_j} \subseteq {U}$ ，给定一个等价类 $\left[ x \right] \subseteq {U}$ 属于 ${D_j}$ 的条件概率可定义为 $\Pr ({{D}_{j}}|{[x])} = \displaystyle\frac{{|{{D}_{j}} \cap [x]|}}{{|[x]|}}$ 。

注： $| \cdot |$ 表示集合的基数。

定义 2　设 ${D_j}$ 为论域U的子集，即 ${D_j} \subseteq U$ ，给定一对阈值(α，β)，并且满足 $0 \leqslant \beta < \alpha \leqslant 1$ ，则(α，β)-正域、负域和边界域可以定义为

$\begin{aligned}& {\rm{PO}}{{\rm{S}}_{(\alpha ,\, \bullet )}}({D_j}) = \{ x \in U|\Pr ({D_j}|[x]) \geqslant \alpha \} \\ &{\rm{NE}}{{\rm{G}}_{( \bullet ,\,\beta )}}({D_j}) = \{ x \in U|\Pr ({D_j}|[x]) \leqslant \beta \} \\ &{\rm{BN}}{{\rm{D}}_{(\alpha ,\,\beta )}}({D_j}) = \{ x \in U|\beta < \Pr ({D_j}|[x]) < \alpha \} \end{aligned}$

通过定义2中的(α，β)-正域、负域和边界域，可分别生成相应的接受、拒绝和延迟决策规则。

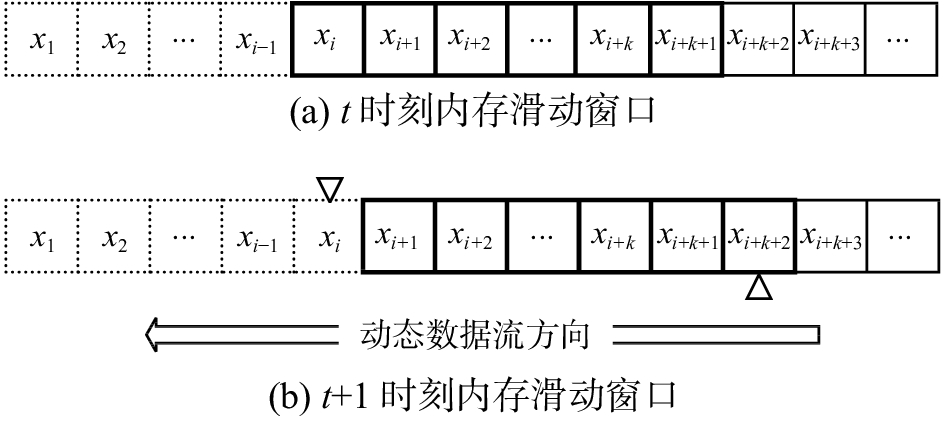
1.2 三支决策在线快速计算模型

滑动窗口技术^[27-28]可以有效处理动态流数据下的数据挖掘与知识更新问题。在线计算的动态特点是，随着新数据不断进入，同时由于内存空间的限制，旧数据也被不断被删除，内存中包含的计算数据既增又减。由此，三支决策在线计算的数据变化模式可以用滑动窗口的方式进行描述。

给定t时刻的决策信息系统表： ${\rm{I}}{{\rm{S}}^{(t)}} =$ $ \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，其中 ${U^{(t)}}/{C^{(t)}} = \left\{ {{R_1}^{(t)},{R_2}^{(t)},{R_3}^{(t)}, \cdots, {R_m}^{(t)}} \right\}$ ， ${U^{(t)}}/{D^{(t)}} = \left\{ {{D_1}^{(t)},{D_2}^{(t)},{D_3}^{(t)}, \cdots, {D_n}^{(t)}} \right\}$ 。将决策表空间看作内存空间，即当前决策表中为内存中实时计算的数据。当t+1时刻有新的数据对象动态进出决策表时，内存空间发生数据动态变化，其变化机制如下。

设t时刻内存滑动窗口如图1(a)所示，其中粗实线框(即 ${x_i},{x_{i+1}},\cdots,{x_{i + k + 1}}$ 数据对象)为当前t时刻内存滑动窗口空间，长度为k；虚线框(即 ${x_1},{x_2},\cdots,$ ${x_{i - 1}}$ 数据对象)为历史遗弃数据；细实线框(即 ${x_{i + k + 2}},{x_{i + k + 3}},\cdots$ 数据对象)为待移入内存数据。如图1(b)所示，t+1时刻单个对象 ${x_{i + k + 2}}$ (图中上三角标识)移入内存滑动窗口中，同时前一时刻最陈旧的决策对象 ${x_{i - 1}}$ (图中下三角标识)被移出，内存滑动窗口发生更新。

基于三支决策理论以及上述在线内存数据变化模型，可以获取如下动态单对象三支决策在线内存计算变化模型。

给定t+1时刻决策表 ${{\rm IS}^{(t + 1)}}$ ，当有新数据对象集 ${\rm{\{ }}\overline x {\rm{\} }}$ 移入，同时必然有旧数据对象集 ${\rm{\{ }}\underline x {\rm{\} }}$ 移出，则更新后的决策信息系统中条件等价类和决策类可能分别发生如下变化：

$\begin{aligned}& R_i^{(t + 1)} = \\ & \left\{{\begin{array}{l}\!\!\! {R_i^{(t)} - \{ \underline x \} ,}\,\, {(x,\underline x ) \in R_i^{(t + 1)},\,\,(x,\overline x ) \notin R_i^{(t + 1)},}\,\, {1 \leqslant i \leqslant m}\\\!\!\! {R_i^{(t)} \cup \{ \overline x \} ,} \,\, {{\rm{ (}}x,\underline x ) \notin R_i^{(t + 1)},\,\,(x,\overline x ) \in R_i^{(t + 1)},}\,\, {1 \leqslant i \leqslant m}\\\!\!\! {R_i^{(t)} \cup \{ \overline x \} - \{ \underline x \} ,} \,\, {(x,\underline x ) \in R_i^{(t + 1)},\,\,(x,\overline x ) \in R_i^{(t + 1)},} \,\,{1 \leqslant i \leqslant m}\\\!\!\! {R_i^{(t)},}\,\, {{\rm{ (}}x,\underline x ) \notin R_i^{(t + 1)},\,\,(x,\overline x ) \notin R_i^{(t + 1)},}\,\, {1 \leqslant i \leqslant m}\end{array}} \right.\end{aligned}$

(1)

$\begin{aligned}& D_j^{(t + 1)} = \\ & \left\{ {\begin{array}{l}\!\!\! {D_j^{(t)} - \{ \underline x \} ,} \,\, {{\rm{ (}}x,\overline x ) \in D_j^{(t + 1)},\,\,(x,\underline x ) \notin D_j^{(t + 1)},}\,\, {1 \leqslant j \leqslant n}\\\!\!\! {{D_j}^{(t)} \cup \{ \overline x \} ,} \,\, {{\rm{ (}}x,\overline x ) \in D_j^{(t + 1)},\,\,(x,\underline x ) \notin D_j^{(t + 1)},} \,\, {1 \leqslant j \leqslant n}\\\!\!\! {{D_j}^{(t)} \cup \{ \bar x\} - \{ \underline x \} ,}\,\, {{\rm{ (}}x,\overline x ) \in D_j^{(t + 1)},\,\,(x,\underline x ) \in D_j^{(t + 1)},}\,\, {1 \leqslant j \leqslant n}\\\!\!\! {{D_j}^{(t)},} \,\,{{\rm{ (}}x,\overline x ) \notin D_j^{(t + 1)},\,\,(x,\underline x ) \notin D_j^{(t + 1)},} \,\, {1 \leqslant j \leqslant n}\end{array} }\right. \end{aligned}$

(2)

可见，决策信息系统在动态环境中，伴随着数据对象在内存窗口的移入移出变化，必然会导致相关条件分类与决策分类发生相应变化，其条件概率及三支区域必然也会发生变化。本文首先系统地讨论在线数据的动态变化情况下条件概率及三支区域的变化，并以此为基础提出三支决策在线快速计算算法。

2 三支决策在线快速计算方法

上述模型实现了动态流数据在线计算的动态变化机制。在经典计算中，对于信息系统的每一次数据更新，采用等价类的重新划分与计算，开销较大。基于内存滑动窗口的三支决策动态变化情况需要借鉴增量学习的思想，对于移入移出数据进行同步处理，从而能够加快三支决策在线计算状态下条件概率与三支区域的更新速度，保证了动态三支决策更新的实时性与高效性。

2.1 条件概率快速估计方法

如何利用已有的决策知识，实现条件概率的动态估计是基于三支决策知识更新的基础。

由定义2可知，计算概率粗糙集三支决策的原理是：首先计算每条决策规则的条件概率，然后将每条决策规则的条件概率与三支决策阈值α、β进行比较，然后才能确定每个条件等价类属于哪个三支决策区域。可见，每条决策规则的条件概率计算，是概率粗糙集三支决策的关键步骤。

定理 1　给定t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} \!=\! \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，t+1时刻信息系统更新为 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，在此期间，基于内存滑动窗口机制，移入单数据对象 $\overline x $ ，同时移出单数据对象 $\underline x $ ，当动态数据对象符合以下变化模式时，条件概率呈增大趋势，即 $\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.) > \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.)$ 。

变化模式1： $ (\overline x \! \notin \! R_i^{(t + 1)} \! \wedge \! \overline x \! \notin \! D_j^{(t + 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \notin D_j^{(t)}) $

变化模式2： $ (\overline x \! \notin \! R_i^{(t + 1)} \! \wedge \! \overline x \! \in \! D_j^{(t + 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)}) $

变化模式3： $ (\overline x \in R_i^{(t + 1)} \! \wedge \! \overline x \! \in \! D_j^{(t \!+\! 1)}) \wedge \left\{ \begin{aligned}& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)}) \\ & (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)})\\ & (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)})\end{aligned} \right. $

证明　若移入对象 $\overline x $ 及移出对象 $\underline x $ 满足变化模式1，则有 $R_i^{(t + 1)} = R_i^{(t)}$ $ - \{ \underline x \} ,D_j^{(t + 1)} = D_j^{(t)}$ 。根据定义1及给定t + 1时刻决策表 ${{\rm IS}^{(t + 1)}}$ 的数据变化公式(1)和(2)，可推断出 $t + 1$ 时刻条件概率 $\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.)$ 更新为

$\begin{aligned} \Pr ({D_j}^{(t + 1)} &\left| {{R_i}^{(t + 1)}} \right.) = \displaystyle\frac{{\Big|{D_j}^{(t + 1)} \cap {R_i}^{(t + 1)}\Big|}}{{|{R_i}^{(t + 1)}|}} =\displaystyle\frac{{\Big|(D_j^{(t)}) \cap (R_i^{(t)} -{x} \} )\Big|}}{{\Big|R_i^{(t)} - \{ \underline x \} \Big|}} = \\ & \displaystyle\frac{{\Big|(D_j^{(t)}) \cap (R_i^{(t)})\Big|}}{{|R_i^{(t)}| - 1}} > \displaystyle\frac{{\Big|D_j^{(t)} \cap R_i^{(t)}\Big|}}{{|R_i^{(t)}|}} = \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.) \end{aligned} $

其余变化模式的证明过程与变化模式1类似，在此省略。

定理 2　给定t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，t+1时刻信息系统更新为 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，在此期间，基于动态流数据滑动窗口机制，移入单数据对象 $\overline x $ ，同时移出单数据对象 $\underline x $ ，当流数据对象符合以下变化模式时，条件概率呈减小趋势，即 $\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.) < \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.)$ 。

变化模式4： $ (\overline x \! \notin \! R_i^{(t + 1)} \! \wedge \! \overline x \! \notin \! D_j^{(t + 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)}) $

变化模式5： $ (\overline x \! \notin \! R_i^{(t \! + \! 1)} \! \wedge \! \overline x \! \in \! D_j^{(t \! + \! 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)}) $

变化模式6： $ (\overline x \! \in \! R_i^{(t + 1)} \! \wedge \! \overline x \! \notin \! D_j^{(t \! + \! 1)}) \! \wedge \! \left\{ \begin{aligned}& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)}) \\& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)})\\& (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)})\end{aligned} \right. $

证明　若移入对象 $\overline x $ 及移出对象 $\underline x $ 遵循变化模式4，则有 $R_i^{(t + 1)} = R_i^{(t)} - \{ \underline x \} ,D_j^{(t + 1)} = D_j^{(t)} - \{ \underline x \} $ 。根据定义1及给定 $t + 1$ 时刻决策表 ${{\rm IS}^{(t + 1)}}$ 的数据变化公式(1)、(2)，可推断出 $t + 1$ 时刻条件概率 ${\rm{Pr}} ({D_j}^{(t + 1)}| $ ${{R_i}^{(t + 1)}})$ 更新为

$\begin{array}{c}\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.) = \displaystyle\frac{{\Big|{D_j}^{(t + 1)} \cap {R_i}^{(t + 1)}\Big|}}{{|{R_i}^{(t + 1)}|}} = \\ \displaystyle\frac{{\Big|(D_j^{(t)} - \left\{ {\underline x } \right\}) \cap (R_i^{(t)} - \left\{ {\underline x } \right\})\Big|}}{{\Big|R_i^{(t)} - \left\{ {\underline x } \right\}\Big|}} = \\ \displaystyle\frac{{\Big|D_j^{(t)} \cap R_i^{(t)}\Big| - 1}}{{|R_i^{(t)}| - 1}} < \frac{{\Big|D_j^{(t)} \cap R_i^{(t)}\Big|}}{{|R_i^{(t)}|}} = \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.) \end{array} $

其余变化模式的证明过程与变化模式4类似，在此省略。

定理3　给定t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，t+1时刻信息系统更新为 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，在此期间，基于动态流数据滑动窗口机制，移入单数据对象 $\overline x $ ，同时移出单数据对象 $\underline x $ ，当流数据对象符合变化模式5~8时，条件概率保持不变，即 $\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.) = \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.)$ 。

变化模式5： $ (\overline x \! \notin \! R_i^{(t + 1)} \! \wedge \! \overline x \! \notin \! D_j^{(t \! + \! 1)}) \! \wedge \! \left\{ \begin{aligned}& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)})\\& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)})\end{aligned} \right. $

变化模式6： $ (\overline x \! \notin \! R_i^{(t \!+\! 1)} \! \wedge \! \overline x \! \in \! D_j^{(t \!+\! 1)}) \! \wedge \! \left\{ \begin{aligned}& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)})\\& (\underline x \! \notin \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)})\end{aligned} \right. $

变化模式7： $ (\overline x \! \in \! R_i^{(t \!+\! 1)} \! \wedge \! \overline x \! \notin \! D_j^{(t \!+\! 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \notin \! D_j^{(t)}) $

变化模式8： $ (\overline x \! \in \! R_i^{(t \!+\! 1)} \! \wedge \! \overline x \! \in \! D_j^{(t \!+\! 1)}) \! \wedge \! (\underline x \! \in \! R_i^{(t)} \! \wedge \! \underline x \! \in \! D_j^{(t)}) $

证明　若移入对象 $\overline x $ 及移出对象 $\underline x $ 遵循变化模式5： $(\overline x \notin R_i^{(t + 1)} \wedge \overline x \notin D_j^{(t + 1)}) \wedge (\underline x \notin R_i^{(t)} \wedge \underline x \notin D_j^{(t)})$ ，则有 $R_i^{(t + 1)} = R_i^{(t)} \wedge D_j^{(t + 1)} = D_j^{(t)}$ 。根据定义1及给定 $t + 1$ 时刻决策表 ${{\rm IS}^{(t + 1)}}$ 的数据变化公式(1)和公式(2)，可推断出 $t + 1$ 时刻条件概率 $\Pr ({D_j}^{(t + 1)}\left| {{R_i}^{(t + 1)}} \right.)$ 更新为

$\begin{aligned} \Pr ({D_j}^{(t + 1)} & \left| {{R_i}^{(t + 1)}} \right.) = \frac{{|{D_j}^{(t + 1)} \cap {R_i}^{(t + 1)}|}}{{|{R_i}^{(t + 1)}|}} = \\ & \frac{{|(D_j^{(t)} \cap R_i^{(t)})|}}{{|R_i^{(t)}|}} = \Pr ({D_j}^{(t)}\left| {{R_i}^{(t)}} \right.)\end{aligned}$

其余变化模式的证明过程与变化模式5类似，在此省略。通过定理1~3可知，随着决策系统中数据对象同步移入移出的更新，原有决策规则的条件概率的变化趋势可以通过局部更新数据的计算进行快速估计。这样既避免了原有数据对象的重复学习，又利用同步更新大大提高了条件概率的计算效率，实现了三支决策条件概率的在线计算，进而使得三支决策区域的在线更新成为可能。

2.2 三支决策区域在线更新方法

三支决策的在线快速计算，即充分利用t时刻信息系统的获取的三支决策知识以及t+1时刻变化数据的动态变化信息，快速且准确地计算三支决策的区域变化。其计算的原理是根据2.1节定理1~3获得的各个决策规则的条件概率变化趋势及特定条件概率取值，推导出三支决策区域在t+1时刻的变化规律。

推论1　给定t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ 和t+1时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，若定理1描述的变化模式成立，三支决策区域更新如下：

$1)\;{\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}, \quad {p_1} \\ & {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {p_2} \\ & {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {p_3} \end{aligned} \right.$ 其中　　 $\begin{aligned}& {p_1}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \\ & {p_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha \\ & {p_3}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha \end{aligned} $

$2)\;{\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}, \quad {b_1} \\ & {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}, \quad {b_2} \\ & {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {b_3}\end{aligned} \right.$ 其中　　 $\begin{aligned}& {b_1}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha \\ & {b_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \\ & {b_3}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \end{aligned} $

$3)\;{\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)},\quad {n_1}\\ & {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t + 1)},\quad {n_2}\\ & {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)},\quad {n_3}\end{aligned} \right.$ 其中　　 $\begin{aligned}& {n_1}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha \\& {n_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \\& {n_3}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta\end{aligned} $

证明　1)对于 $ {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$

①假设 ${p_1}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)})$ 成立，由定义2得 $\Pr (D_j^{(t)}|R_i^{(t)}) > \alpha $ 。由定理1可知 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) > $ $ \Pr (D_j^{(t)}|R_i^{(t)})> \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ，则接受域更新为 ${{\rm POS}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = $ ${{\rm POS}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}$ 。

②假设 ${p_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha $ 成立，由定义2得 $\beta < \Pr (D_j^{(t)}|R_i^{(t)}) < \alpha $ 。因为 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ，则接受域更新为 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = $ ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}$ 。

③假设 ${p_3}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha $ 成立，由定义2得 $\Pr (D_j^{(t)}|R_i^{(t)}) \leqslant \beta $ 。因为 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant $ $ \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ，则接受域更新为 ${{\rm POS}_{(\alpha ,\beta )}} $ $(D_j^{(t + 1)}) ={\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}$ 。

2)对于 $ {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$

①假设 ${b_1}:R_i^{(t)}\! \subseteq \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)})\! \wedge \! \Pr (D_j^{(t + 1)}|R_i^{(t + 1)})\! \geqslant \!\alpha $ 成立，由定义2得 $\beta \! < \! \Pr (D_j^{(t)}|R_i^{(t)}) < \alpha $ 。因为 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \! \geqslant $ $ \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，则边界域更新为 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}} $ $(D_j^{(t + 1)}) ={\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}$ 。

②假设 ${b_2}:R_i^{(t)} \! \subseteq \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \wedge \! \beta \! < \! \Pr (D_j^{(t \!+\! 1)}|R_i^{(t + 1)}) \! < \! $ $ \alpha $ 成立，由定义2得 $\beta < \Pr (D_j^{(t)}| $ $R_i^{(t)}) < \alpha $ ，因为 $\beta < \Pr (D_j^{(t + 1)}|$ $R_i^{(t + 1)}) < \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，则边界域更新为 ${{\rm BND}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}$ 。

③假设 ${b_3}:R_i^{(t)} \!\subseteq \! {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \wedge \! \beta \! < \! \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < $ $ \alpha $ 成立，由定义2得 $\Pr (D_j^{(t)}|R_i^{(t)}) < \beta $ ，因为 $\beta < \Pr (D_j^{(t + 1)}|$ $R_i^{(t + 1)}) < \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，则边界域更新为 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = $ ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}$ 。

3)对于 $ {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$

①假设 ${n_1}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha $ 成立，由定义2得 $\Pr (D_j^{(t)}|R_i^{(t)}) \! \geqslant \! \alpha $ ，因为 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \! \geqslant \! \alpha $ ，即 $R_i^{(t + 1)} \! \subseteq \! {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，则拒绝域更新为 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) \!=\! $ $ {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}$ 。

②假设 ${n_2}:R_i^{(t)} \! \subseteq \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \wedge \! \beta \! < \! \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < $ $ \alpha $ 成立，由定义2得 $\beta \! < \! \Pr (D_j^{(t)}|R_i^{(t)}) \! < \! \alpha $ ，因为 $\beta < \Pr (D_j^{(t + 1)}|$ $R_i^{(t + 1)}) < \alpha $ ，即 $R_i^{(t + 1)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ，则拒绝域更新为 ${\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t + 1)}) = {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t + 1)}$ 。

③假设 ${n_3}:R_i^{(t)} \subseteq {\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta $ 成立，由定义2得 $\Pr (D_j^{(t)}|R_i^{(t)}) \! < \! \beta $ ，因为 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \! \leqslant \! \beta $ ，即 $R_i^{(t \!+\! 1)} \!\! \subseteq \!\! {\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t \!+\! 1)})$ ，则拒绝域更新为 ${\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t \!+\! 1)}) \!= $ ${\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t \!+\! 1)}$ 。

证毕。

推论2　给定t时刻信息系统 ${\operatorname{IS} ^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ 和t+1时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，若定理2描述的变化模式成立，则三支决策区域更新为

$1)\;{\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}, \quad {p_1} \\ & {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}, \quad {p_2} \\ & {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}, \quad {p_3} \end{aligned} \right.$ 式中：　　 $\begin{aligned}& {p_1}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \geqslant \alpha \\ & {p_2}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \\ & {p_3}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta \end{aligned}$

$2)\;{\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {b_1} \\ & {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}, \quad {b_2} \\ & {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)}, \quad {b_3}\end{aligned} \right.$ 式中：　　 $\begin{aligned} &{b_1}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \\ &{b_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \beta < \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) < \alpha \\ &{b_3}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta \end{aligned}$

$3)\;{\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) = \left\{ \begin{aligned}& {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {n_1} \\ & {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \cup R_i^{(t + 1)}, \quad {n_2} \\ & {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) - R_i^{(t)} \cup R_i^{(t + 1)}, \quad {n_3} \end{aligned} \right.$ 式中：　　 $\begin{aligned}& {{n_1}:R_i^{(t)} \subseteq {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta }\\ & {{n_2}:R_i^{(t)} \subseteq {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \wedge \Pr (D_j^{(t + 1)}|R_i^{(t + 1)}) \leqslant \beta }\\ & {{n_3}:R_i^{(t)} \subseteq {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)})}\end{aligned}$

证明　证明过程与推论1类似，此处略。证毕。

推论3 　给定t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ 和t+1时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t{\rm{ + }}1)}} = \left\{ {{U^{(t{\rm{ + 1}})}},{C^{(t{\rm{ + }}1)}} \cup {D^{(t{\rm{ + }}1)}}} \right\}$ ，若定理3描述的变化模式成立，三支决策区域更新为：

$\begin{aligned} & {\rm{POS}}:R_i^{(t)} \! \subseteq \! {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \Rightarrow \! {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) \! = \! {\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)}); \\ & {\rm{BND}}:R_i^{(t)} \! \subseteq \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \Rightarrow \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)}) \! = \! {\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)}); \\ & {\rm{NEG}}:R_i^{(t)} \! \subseteq \! {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}) \! \Rightarrow \! {\operatorname{NEG} _{(\alpha ,\beta )}}(D_j^{(t + 1)}) \! = \! {\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)}){\text{。}} \end{aligned} $

证明　根据定理3，条件概率 $\Pr ({D_j}^{(t + 1)}\left| {{C_i}^{(t + 1)}} \right.)$ 保持不变，由定义2可知此时三支决策区域亦是保持不变的。证毕。

2.3 三支决策在线快速计算算法

根据2.1节中的定理1~3推导出的概率粗糙集的条件概率变化趋势，以及2.2节中的三支决策区域的快速计算3种情形展开讨论。

本节设计了三支决策在线快速计算算法(online computing algorithm)，并从算法时间复杂度角度与基于三支决策理论的经典计算算法作对比，从理论上分析在线快速计算算法的优势。

算法1　三支决策在线快速计算算法

输入　 t时刻信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，条件等价类和决策等价类 $R_i^{(t)}$ 、 $D_j^{(t)}(i = 1,2, \cdots ,m;j =$ $ 1,2, \cdots ,n)$ ，条件概率 $\Pr (D_j^{(t)}|R_i^{(t)})(i \!=\! 1,2, \cdots ,m; j \!=\! 1,2, \cdots ,$ $n)$ ，三支决策接受域、拒绝域和边界域 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)})$ 、 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)})$ 及 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，新增决策对象 $\overline x $ 及被移出对象 $\underline x $ ，三支决策阈值(α，β)。

输出　 t+1时刻三支决策区域 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 、 ${{\rm BND}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 及 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 。

1) 通过 $\overline x $ 及 $\underline x $ 的等价类从属关系，更新t+1时刻的条件等价类和决策等价类 $R_i^{(t + 1)}$ 和 $D_j^{(t + 1)}$ ;

2) 根据定理1~3评估t+1时刻条件概率 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)})$ 的变化趋势;

3) 根据推论1~3更新t+1时刻三支决策区域 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 、 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 、 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ;

4) 更新t+1时刻每个等价类的条件概率值 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)})$ 及条件、决策等价类 ${R^{(t + 1)}}$ 、 ${D^{(t + 1)}}$ ，返回1)。

在线快速计算中，若给定内存部分信息系统IS，包含m个条件等价类和n个决策等价类，其中 $m = |{U^{(t)}}/A|({U^{(t)}} \subseteq U)$ ， $n = |D|$ ，等价类的计算时间复杂度为 $O(|{U^{(t)}}/A| \cdot |A| + |D|)$ 。步骤2)评估条件概率变化趋势，其时间复杂度为 $O(1)$ ，这时可以忽略不计的。步骤3)为更新三支区域，即区域内的对象可能发生转移，区域未发生变化是最好的情况，在这种情况下两种算法的时间复杂度均可视为 $O(1)$ ；最坏的情况，此算法中需要转移对象两次，以 $|{R_i}|$ 和 $|{R_j}|$ 表示移入对象 $\overline x $ 和被移出对象 $\underline x $ 的条件和决策等价类，则区域更新的时间复杂度为 $O(|{R_i}| + |{R_j}|)$ 。步骤4)中，在 $|{R_i}|$ 和 $|{D_j}|$ 已知的情况下，重新计算条件概率的时间复杂度几乎是可以忽略不计的。综上，在线快速计算的时间复杂度为 $O(|{U^{(t)}}/A| \cdot |A| + |D|) + O(|{R_i}| + |{R_j}|)$ 。

为了说明上述在线三支决策算法的特点与优势，本文将根据文献[22]中提出的基于概率粗糙集三支决策理论的经典计算思想，设计三支决策经典计算算法(classical computing algorithm)。

算法2　基于三支决策的经典计算算法

输入　 t时刻下信息系统 ${\rm{I}}{{\rm{S}}^{(t)}} = \left\{ {{U^{(t)}},{C^{(t)}} \cup {D^{(t)}}} \right\}$ ，条件等价类和决策等价类 $R_i^{(t)}$ 、 $D_j^{(t)}$ $(i = 1,2, \cdots ,m;j = 1,$ $2, \cdots ,n)$ ，条件概率 $\Pr (D_j^{(t)}|R_i^{(t)})$ $(i = 1,2, \cdots ,m; j = 1,2, \cdots ,$ n)，三支决策接受域、拒绝域和边界域 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t)})$ 、 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t)})$ 、 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t)})$ ，新增决策对象 $\overline x $ 及被移出对象 $\underline x $ ，三支决策阈值(α，β)。

输出　 t+1时刻的三支决策区域及决策规则 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 、 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 和 ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 。

/* 根据移入对象 $\overline x $ 、移出对象 $\underline x $ 进行三支决策更新计算*/

1) 通过 $\overline x $ 和 $\underline x $ 的等价类从属关系，更新t+1时刻的条件等价类和决策等价类 $R_i^{(t + 1)}$ 和 $D_j^{(t + 1)}$ ;

2) 根据定义1重新计算t+1时刻条件概率 $\Pr (D_j^{(t + 1)}|R_i^{(t + 1)})$ 值;

3) 根据定义2重新计算t+1时刻三支决策接受域、拒绝域和边界域 ${\rm{PO}}{{\rm{S}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 、 ${\rm{BN}}{{\rm{D}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ ， ${\rm{NE}}{{\rm{G}}_{(\alpha ,\beta )}}(D_j^{(t + 1)})$ 。

经典计算算法中，若给定内存部分信息系统IS，包含m个条件等价类和n个决策等价类，其中 $m = |{U^{(t)}}/A|({U^{(t)}} \subseteq U)$ ， $n = |D|$ ，等价类的计算时间复杂度为 $O(|{U^{(t)}}/A| \cdot |A| + |D|)$ ；重新计算条件概率的时间复杂度为 $O(|{U^{(t)}}/A| \cdot |D|)$ ；根据条件概率大小与阈值的比较，更新三支区域的时间复杂度亦为 $O(|{U^{(t)}}/A| \cdot |D|)$ 。因此，经典计算算法的时间复杂度为 $O(|{U^{(t)}}/A| \cdot |A| + |D|) + O(2|{U^{(t)}}/A| \cdot |D|)$ 。

假设原t时刻信息系统为 ${{\rm IS}^{(t)}}$ ，新增对象集为 $\{ \overline x \} $ ，上述两种算法的时间复杂度分别为：

经典计算算法：

$O(|{U^{(t)}}/A| \cdot |A| + |D|) + O(2|{U^{(t)}}/A| \cdot |D|)$

在线快速计算：

$O(|{U^{(t)}}/A| \cdot |A| + |D|) + O(|{R_i}| + |{R_j}|)$

从时间复杂度分析可知，在线快速计算的效率明显优于经典计算算法。从算法执行过程亦可看出，由于经典计算算法对于决策对象的每一次更新，都进行等价类划分和条件概率的重新计算，其开销甚是庞大；而在线计算利用内存滑动窗口模型，同步处理移入移出数据，对当前实时变化的数据进行局部计算，实现条件概率及三支区域的快速估计与更新，其运算效率明显高于经典计算算法。

综上，从理论分析可知在线快速计算的运行效率明显优于经典计算算法。接下来，我们将从实验的角度评估两算法的实际表现。

3 实验与结果

2.3节通过理论证明了三支决策在线快速计算算法的时间复杂度优于经典计算算法。本章将通过与三支决策经典计算算法的对比实验来验证三支决策在线快速计算算法的时间消耗优势。

本实验环境为：双核、4 GB内存的PC，运行Microsoft Windows 7操作系统，算法程序使用Java编程，Java开发包为JDK1.6版本。

3.1 数据集

为了验证在线快速计算的性能，我们从UCI数据库中选择了8个较大数据集，分别为Skin-NoSkin、Shuttle、IRIS、Zoo、Haberman、Breast-cancer、Letter、Magic，所有的数据均为数值型或类别型，表1为数据集的基本信息。

3.2 实验和结果

为排除偶然因素的影响，所有实验都进行了10次，最终结果是10次实验的平均值。我们任意设定的三支决策阈值 $(\alpha ,\beta )$ 为(0.75，0.3)。

1)算法执行时间对比实验

假设存储空间保持为100条记录，我们比较在线快速计算、经典计算算法的性能时，逐渐增加上述8个数据集在内存中存储数据的比例。当进入决策信息系统的在线计算数据总量累计达到总数据量的10%~100%时，分别测试不同情况下，两种算法在三支决策区域更新中的平均执行时间。实验结果如图2所示。

由图2显然可以看出，在每个数据集下，随着进入内存中动态数据比例的增大，在线快速计算与经典计算算法的平均执行时间亦逐渐增大，但经典计算算法的增幅明显更大。可见，在线快速计算的平均执行时间相对更少。

此外，为了更加精确地展现在线快速计算的优势及其稳定性，我们将在占数据总量50%的情况下，从t时刻到t+5时刻，测试两类算法的平均执行时间并对比其稳定性。结果见表2，单位为ms。可以观察到，对于同一数据集，对比经典计算算法，在线快速计算可以大大节约算法执行时间。

同时，在不同数据集上，在线快速计算执行时间的均值和方差比经典计算算法更小，显示了其具有更好的效率及稳定性。

2)不同内存容量算法执行时间对比

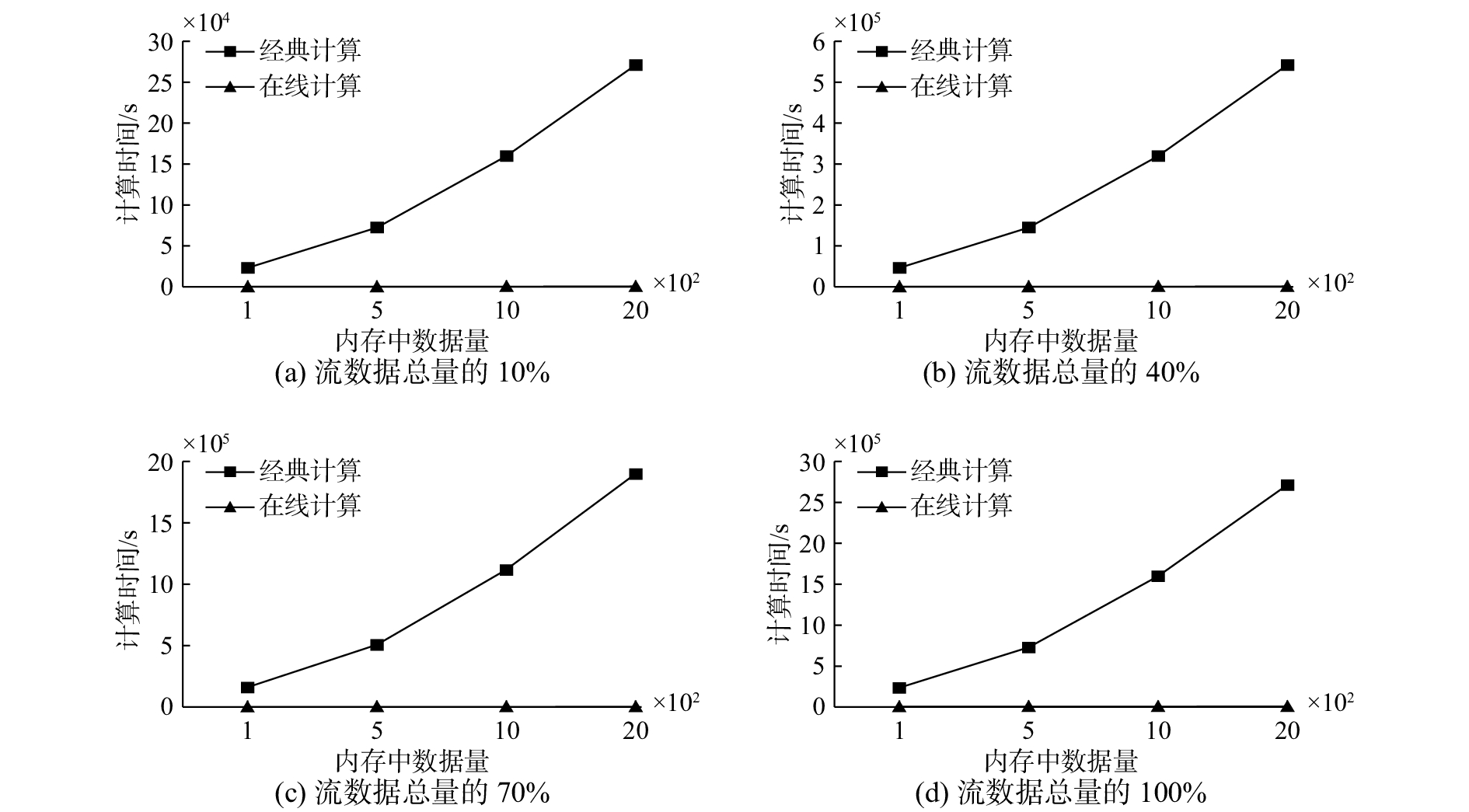
由于在线计算方法以内存计算为依托，内存空间的容量对于三支决策在线快速计算的执行效果是否有影响，是一个值得研究的问题。因此我们选择以上8个UCI数据集中规模较大且复杂程度较高的Breast-cancer数据集，构造和实验1相似的对比实验，但是将内存容量分别为设定为100、500、1 000、2 000条记录，当上述数据集实施两种算法实验的数据总量累计达到总数据量的10%、40%、70%和100%时，分别记录这两种算法此时的平均执行时间。

由图3可以观察到，在相同实验数据累积量下，随着内存空间的增加，经典计算算法的平均执行时间几乎呈指数级速度增长，而在线快速计算的时间消耗较为平稳。

由算法的时间复杂度可知，随着决策系统的每一次更新，经典计算算法需要进行所有数据等价类的重新划分及条件概率的重新计算，此过程每次都需要执行时间复杂度为 $O(2|{U}^{(t)}/{ A}|\cdot |{D}|)$ 的步骤，其时间消耗极大，且与内存中的数据量及复杂程度密切相关；而在线快速计算由于只需要对当前实时变化的数据对象进行局部计算，避免了历史数据的重复学习，最多只需执行时间复杂度为 $O({\rm U}^{(t)}/{\rm A}|\cdot |{\rm D}|)$ 的步骤，大大节省了此更新过程的开销。

综上可知，在不同内存空间下，在线快速计算的效率均远高于经典计算算法，且这一优势随着内存空间的增加更加明显。

3)不同阈值在线快速计算执行时间对比

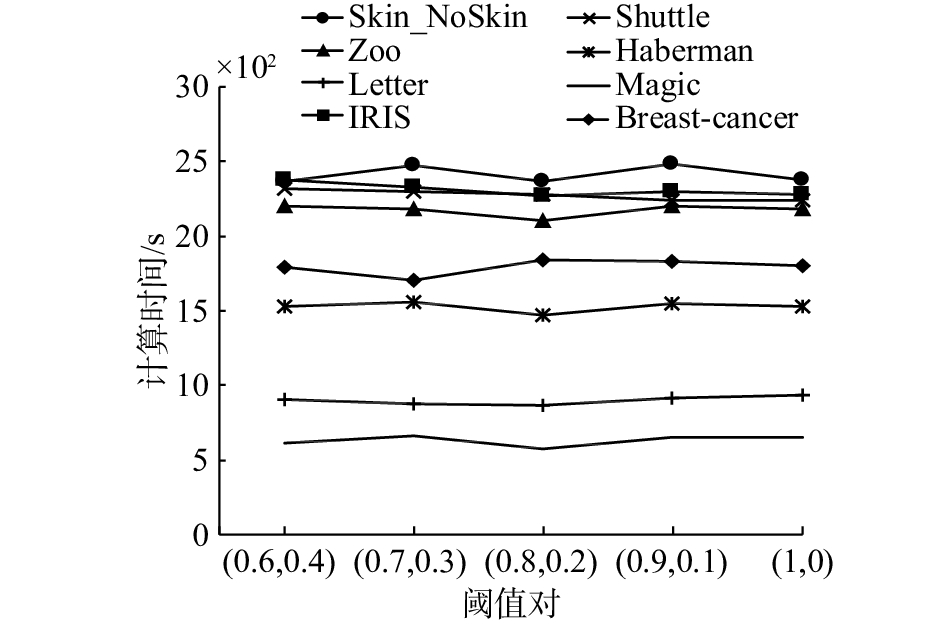
由于三支决策是一种典型的概率粗糙集参数化模型，实验结果可能会受参数设置的影响。设置内存空间为100 b，并选取了5对阈值，分别测出在线快速计算在8个数据集下执行完毕平均所需时间，从而验证在线快速计算的性能与选取阈值的关系。图4显示了算法平均执行时间随不同阈值对的变化趋势，不难看出，算法的执行时间随着阈值的改变有轻微的波动，总体来说比较稳定。由此也进一步验证了在线快速计算的时间复杂度主要取决于动态数据的规模及其复杂程度。

4 结束语

动态在线计算是一种常见的数据计算方法，本文提出一种内存滑动窗口机制对在线计算的数据变化模式进行统一建模，并根据上述模型，推导出不同类型数据变化模式下的三支决策条件概率及三支区域的变化规律。最后本研究提出一种新型的动态在线快速计算算法，该算法能够获得与经典三支决策算法相同的决策结果。由于本算法只需要对当前的变化数据进行局部实时计算，有效避免了历史数据的重复学习，大大提高了三支决策更新效率。为验证本文所提出的在线快速计算的优势，与经典计算算法在8个UCI公共数据集上进行实验对比。实验结果表明，在线快速计算比经典计算算法效率更高，稳定性更好。本研究表明，概率粗糙集三支决策领域采用在线计算方法进行快速计算是可行的。我们将在未来的工作中，继续探讨概率粗糙集三支决策的多对象动态在线快速计算以及其在实际在线计算场景中的应用。