近年来,随着SLAM研究的不断深入,使三维重建成为了机器人研究领域的热潮[1]。从本质上来说,SLAM所有的计算都是对传感器数据的处理,因此不同传感器的基本方程的参数化有很大的差别。常见的SLAM传感器有IMU、激光传感器。IMU通常包含陀螺仪和加速度计。陀螺仪具有良好的动态响应,但会产生累计误差;加速度计虽然不会产生累计误差,但易受到机器运行时的振动干扰;激光传感器精度高、探测范围广,但价格昂贵、功耗大;相机主要分为单目相机、双目相机和RGB-D[2]相机,单目相机无法直接获取图像深度信息,需要通过移动相机来产生深度;双目相机通过视差计算深度,在推算图像中物体距离时计算量大,实时性较差;典型的RGB-D相机,如Kinect,具有价格低廉、信息丰富、更新速度快、能直接获取图像深度等优点,因此其成为了RGB-D SLAM系统的主流视觉传感器,受到广大视觉SLAM研究者的青睐。因此,国内外学者对Kinect在室内移动机器人上的应用研究取得了一定的研究成果。
一个完整的RGB-D SLAM系统应该包含传感器数据、视觉里程计、非线性优化、建图与回环检测等主要5个部分。视觉里程计的作用是估计相机运动,其中包括特征点检测与提取、相邻帧间配准、迭代最近点等。非线性优化是从带有噪声的传感器数据中优化机器人运行轨迹和在运行过程中增量式构建环境地图。回环检测[3]是机器人通过识别图像间的相似性来判断是否回到之前到过的位置。在视觉里程计部分,通常采用ICP算法去估计相机的运动。然而传统的ICP算法[4]搜寻对应点对相当耗时,且容易出现大量误匹配点对。针对以上问题,许多学者提出了优秀的改进ICP算法。文献[5]针对多场景三维重建问题,在基于2D局部特征匹配的基础上,提出了一种新颖且高效的3D配准方法。该方法将三维点云转换为2D轴承角图像,然后在两幅图像之间利用SURF特征搜寻匹配的像素对,获取3D点云的对应点,再通过基于SVD的方法求出最优旋转矩阵,将点云与矩阵对齐来重建3D模型。该方法虽大大减少了算法运算时间,但在精度上却不如传统ICP算法。文献[6]针对服务机器人手眼协调抓取提出了一种利用RGB-D传感器对家庭常见物体进行3-D建模的方法。该方法仅需环绕物体采取数十帧即可重建三维模型,但无法估计相机位姿。
针对以上研究现状,本文提出了一种新的室内移动机器人视觉SLAM方法。通过Kinect相机获取室内环境信息,对获取的彩色图像进行特征提取与匹配,结合标定后的Kinect内参与像素点深度值,得到对应的空间对应点云,运用RANSAC方法筛选出可靠的内点进行初始位姿估计完成初匹配。在精匹配过程中,初匹配的结果作为精匹配的初值,通过添加点对间距离和角度阈值双重限制,剔除误匹配点对,提高点云配准的精度。在优化端的关键帧选取中引入权重,通过回环检测消除累积误差,实现三维地图的优化与更新。
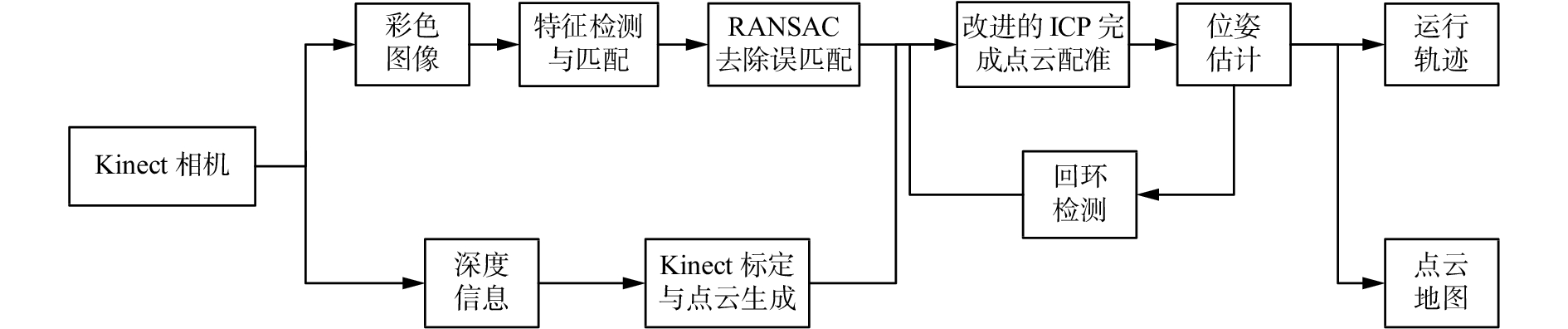
1 基于Kinect的改进移动机器人V-SLAM算法基本原理 1.1 系统结构本文提出的室内移动机器人视觉SLAM系统框架如图1所示,在进行传感器数据采集之前,需对Kinect传感器进行标定以获取相机内部参数,对获取到的彩色图像进行特征检测与提取,进行初步筛选后,利用RANSAC算法剔除离群点获取初始位姿估计,再用改进的ICP算法完成点云的精准匹配,在关键帧选取中引入权重,通过回环检测消除累积误差,实现三维点云地图的优化与更新,最终获得机器人运行轨迹和室内环境点云地图。
|
Download:
|
| 图 1 室内环境下基于移动机器人的RGB-D SLAM系统框架图 Fig. 1 The frame of RGB-D SLAM system for mobile robot in indoor environment | |
SLAM包含两个问题,一个是“定位”,一个是“建图”。解决定位问题的关键是在相机获取了机器人所在的室内环境信息后,如何根据相邻图像的信息,粗略估计出相机运动,这一过程也被称为视觉里程计。视觉里程计的实现方法主要分为特征法和直接法。特征法运行稳定,对光照、动态物体不敏感,是目前比较成熟的解决方案,因此本文采用特征法。
随着在计算机视觉领域的长年探索,研究者们提出了许多优秀的图像特征检测方法。如著名的FAST[7]、SIFT[8]以及SURF[9]。FAST特征点检测计算速度快,但FAST不具有方向性。SURF算法采用盒子滤波器,积分图像的运用减少了采用盒子滤波进行卷积的时间,盒子滤波可以加速卷积运算过程,在尺度空间建立上比SIFT更迅速。由于图像特征检测与匹配仅仅是整个SLAM系统诸多环节中的一个,为了满足实时性,采用具有旋转和尺度不变性的SURF特征。在提取了图像特征以后,需确定两个点集元素的对应关系。最简单的方法是暴力匹配(brute-force matcher,BFM),然而当特征点数量很大时,暴力匹配法的运算量将变得很大,运行过程非常耗时,因此选用更适合于匹配点数量极多情况的快速近似最近邻[10](fast library for approximate nearest neighbour,FLANN)算法。
利用SURF算法进行特征点检测与匹配的主要过程如下:
1) 对图像关键点进行检测;
2) 使用“金字塔”构建尺度空间;
3) 关键点定位;
4) 确定每个关键点的主方向;
5) 生成特征描述子;
6) 运用FLANN对特征描述子进行匹配。
1.3 Kinect标定与点云生成彩色图像和深度图像需结合Kinect内参生成三维点云。Kinect相机在出厂之后具有固定的内参,但这些参数会随着温度、湿度、气压等环境因素的变化而改变,在使用前有必要进行相机标定[11]。本文采用文献[12]的方法对Kinect进行标定。在相机完成标定之后,图像中任意一点可结合该点深度值得到其对应的三维空间点坐标,进而生成三维点云数据。二维图像中的像素点(其中d指深度数据)与其空间点的对应关系为
| $v = \frac{{y \cdot {f_y}}}{z} + {c_y}$ | (1) |
| $u = \frac{{x \cdot {f_x}}}{z} + {c_x}$ | (2) |
| $d = z \cdot s$ | (3) |
式中:
| ${{C}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{f_x}} \\ 0 \\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0 \\ {{f_y}} \\ 0 \end{array}}&{\begin{array}{*{20}{c}} {{c_x}} \\ {{c_y}} \\ 1 \end{array}} \end{array}} \right]$ | (4) |
ICP算法依赖良好的初值选取,如果初值选取不合适,迭代易陷入局部最优,以至不能达到全局最优效果。RANSAC是一种随机参数估计算法,通过随机抽选样本子集、计算模型参数、设定阈值等步骤获取最佳模型参数[13]。本文采用RANSAC算法对两组相邻RGB图的特征点进行粗匹配,通过预先设定一个阈值d将全部匹配点对区分为内点和外点,剔除大于此阈值的匹配点对即剔除了外点对粗匹配的影响。将筛选后的内点进行最小二乘法下对Kinect相机的初始位姿估计,可将源点集
| ${{{P}}_{i + 1}} = {{{P}}_i}{{T}}_i^{i + 1}$ | (5) |
传统ICP算法通过解决最小二乘均方差问题,求解包含旋转矩阵R和平移矩阵t的刚体变换T,从而实现相机相邻位姿的运动估计。传统ICP算法步骤如下。
1) 为源点集
| ${P'} = \left\{ {{p_1},{p_2}, \cdots, {p_n}} \right\}$ | (6) |
| ${Q'} = \left\{ {{q_1},{q_2}, \cdots, {q_n}} \right\}$ | (7) |
2) 通过最小化均方目标函数来求解刚体变换T。
| ${d_m} = \frac{1}{n}\sum\limits_{i = 1}^{n}{\left\| {{q_j} - \left( {{{R}}{p_i} + {{t}}} \right)} \right\|^2}$ | (8) |
| ${{T}} = \left[\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{R}}_{3 \times 3}}} \\ 0 \end{array}}&{\begin{array}{*{20}{c}} {{{{t}}_{3 \times 1}}} \\ 1 \end{array}} \end{array}} \!\!\!\!\!\!\!\!\right]$ | (9) |
式中:R为旋转矩阵,t为平移矩阵。
3) 运用刚体变换转换点云。
| ${{{P}}_{m + 1}} = {{{R}}_{m + 1}}{{{P}}_m} + {{{t}}_{m + 1}}$ | (10) |
式中m表示迭代次数。
4) 当满足
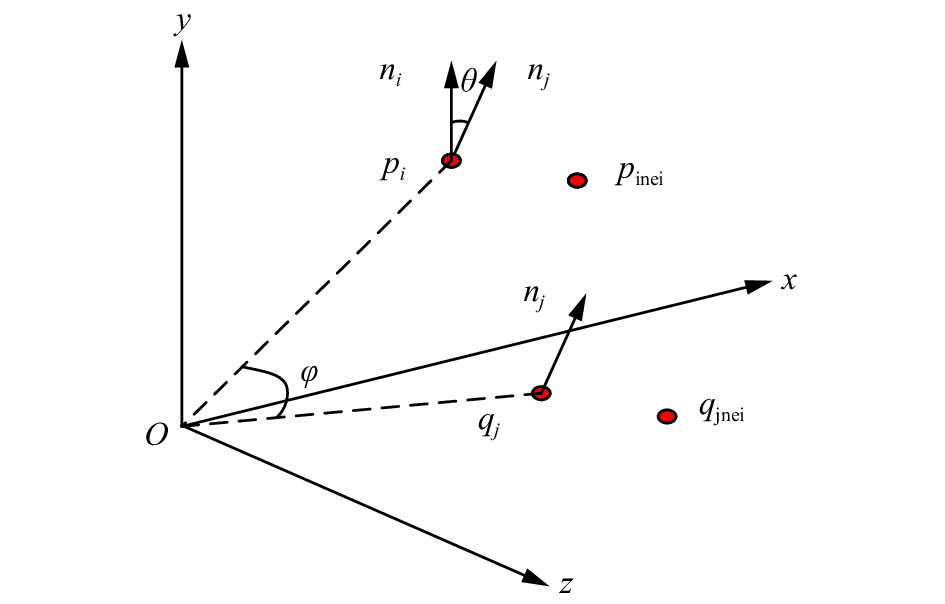
通过RANSAC算法进行特征点的粗匹配可粗略地重合相邻两帧点云。传统的ICP算法是基于两组点云完全重合这一假设理论,然而在实际应用中点云P中的一点并不能总在点云Q中找到其对应点,传统ICP算法存在大量错误匹配点对,算法易陷入局部最优,甚至不能收敛。为了减少配准误差,提高点云配准精度,需要利用改进的ICP算法对点云进行精确配准。在精匹配过程中,粗匹配的结果作为精匹配的初值,采用点对间欧氏距离阈值法和角度阈值法对误匹配点对进行剔除,以筛选出满足阈值条件的点对,进行精确相机位姿估计。所提阈值法原理如图2所示。
|
Download:
|
| 图 2 欧氏距离阈值法及角度阈值法原理示意图 Fig. 2 Euclidean distance threshold method and angle threshold method | |
1) 欧氏距离阈值
正确的匹配点对,两点对之间的欧氏距离不应过大。本文添加了点对间欧氏距离阈值限制,去除小于平均点对距离的匹配,且认为同一片点云下任一点与其邻点的拓扑结构不会随刚体变换而变化。因此在粗匹配后,配对点云
| $\left| {{p_i} - {q_j}} \right| < u$ | (11) |
| $\left| {\frac{{\bigl\| {{p_i} - {p_{{\rm{inei}}}}} \bigr\| - \left\| {{q_j} - {q_{{\rm{jnei}}}}} \right\|}}{{\bigl\| {{p_i} - {p_{{\rm{inei}}}}} \bigr\| + \left\| {{q_j} - {q_{{\rm{jnei}}}}} \right\|}}} \right| \leqslant \delta $ | (12) |
式中:
2) 角度阈值
经过欧氏距离阈值法可剔除大部分点云数据噪声点,再结合角度阈值,能进一步检测点对匹配的正确性,提高点云初值选取的正确率。本文采用了点到切平面的最近搜索算法,对于给定点
| $\cos \theta = \frac{{{{{{n}}_i}} \times {{{{n}}_j}} }}{{\left| { {{{{n}}_i}} } \right| \times \left| {{{{{n}}_j}} } \right|}} > \omega $ | (13) |
| $\left| {\sin \varphi - \sin \theta } \right| < \tau $ | (14) |
式中:
1) 在点集
2) 在目标点集
3) 应用角度阈值法进一步剔除误匹配点对,得到精配对点集
4) 采用奇异值分解(singular value decomposition,SVD)求得点集
5) 根据式
6) 重复3)~5),直到满足式(15):
| $\left\{ {\begin{aligned} & {{d_m} - {d_{m + 1}} < \varepsilon } \\ & {{d_m} = \displaystyle\frac{1}{n}\sum\limits_{i = 1}^{n} {{\left\| {{{{Q}}_{im}} - {{{P}}_{im}}} \right\|}^2}} \end{aligned}} \right.$ | (15) |
Kinect相机以一定的帧率采集室内环境信息,即使相机固定不动,程序的内存占用也会越来越高。在RGB-D SLAM系统中,过多的关键帧会增加闭环检测与全局优化的计算耗时,过少的关键帧会导致关键帧间间隙增大,造成帧间配准易出现失败的情况。为了满足帧间配准的成功率和系统实时性要求,引入一种关键帧选取机制。在关键帧选取上,旋转的变化比平移更加敏感,因此在旋转出现微小变化或平移相对大一段距离后添加关键帧。当新帧到来时,检测其图像特征并与前一关键帧进行变换计算,如果变换超过阈值
| $\varphi = {\left\| {{\lambda _1}{{\left[ {{\rm{\Delta }}x\,\,\,\,{\rm{\Delta }}y\,\,\,\,{\rm{\Delta }}z} \right]}^{\rm{T}}}} \right\|_2} + {\lambda _2}{\left\| {\left( {\alpha ,\beta ,\gamma } \right)} \right\|_2}$ | (16) |
式中:
在进行机器人同时定位与地图构建过程中,两帧之间的位姿变换可通过式(5)计算得到,各时刻相对于起始时刻的变换矩阵可通过式(17)获得:
| ${{T}}_0^k = {{T}}_0^1 \times {{T}}_1^2 \times \cdots \times {{T}}_{(k - 1)}^k$ | (17) |
在各个位姿转换过程中均存在误差,如果不进行优化,随着转换过程的叠加,会产生累计误差。本文采用g2o优化算法[14]对位姿转换过程中产生的累计误差进行优化,误差函数
| ${{F}}\left( {{x}} \right) = \sum\limits_{\left( {i,j} \right) \in C} {{e^{\rm{T}}}\left( {{x_i},{x_j},{z_{ij}}} \right){{{\varOmega}} _{ij}}e\left( {{x_i},{x_j},{z_{ij}}} \right)} $ | (18) |
| ${{{x}}^*} = \arg {\min _x}{{F}}\left( {{x}} \right)$ | (19) |
式中:
本文实验平台由3个主要部分组成:第一部分为一台Intel双核4.0 GHz主频的笔记本电脑,装配以Linux为内核的Ubuntu 14.04操作系统;第二部分为Kinect XBOX360,图像分辨率为640×480,最高帧率为30帧/秒,水平视场角为52°;第三部分为Pioneer3-DX机器人。实验环境为一间约80 m2的小型实验室,图3(a)为实验真实场景,图3(b)为实验设备。

|
Download:
|
| 图 3 实验场景及实验设备 Fig. 3 Experimental scene and experimental installation | |
在实验过程中,Pioneer3-DX机器人搭载笔记本电脑与Kinect相机,并以0.1 m/s的速度在实验室内移动,Kinect相机通过获取室内环境的彩色信息与深度信息,利用关键帧的选取机制,对新来的关键帧进行图像特征检测与提取,结合相机标定内参与像素点深度值,生成三维点云数据。采用改进的基于RANSAC的ICP点云配准算法将两片相邻点云进行配准,获取相机位姿估计。实验过程中各参数设置为:
在实验场景中,图4(a)为相机获取到的第一帧数据(包含彩色信息和深度信息),图4(b)为相机获取到的第二帧数据,两帧数据的视角只在水平方向发生了较小的平移。图5为利用标定后的Kinect相机获取到的第一帧彩色信息,结合像素点深度值生成的彩色点云数据。图6(a)为未经RANSAC算法的匹配点对,两帧数据只在水平方向上发生了移动,因此只有水平的匹配线才是正确的匹配。图6(b)为经RANSAC算法后的匹配点对,可以看出,剔除误匹配后,基本消除了噪声对匹配结果的影响,提高了点对匹配正确率。

|
Download:
|
| 图 4 室内环境的两帧数据 Fig. 4 Two frames in indoor environment | |

|
Download:
|
| 图 5 第一帧数据的三维彩色点云图 Fig. 5 3-D color point cloud of the first frame data | |

|
Download:
|
| 图 6 粗匹配实验结果 Fig. 6 The experimental results of coarse matching | |
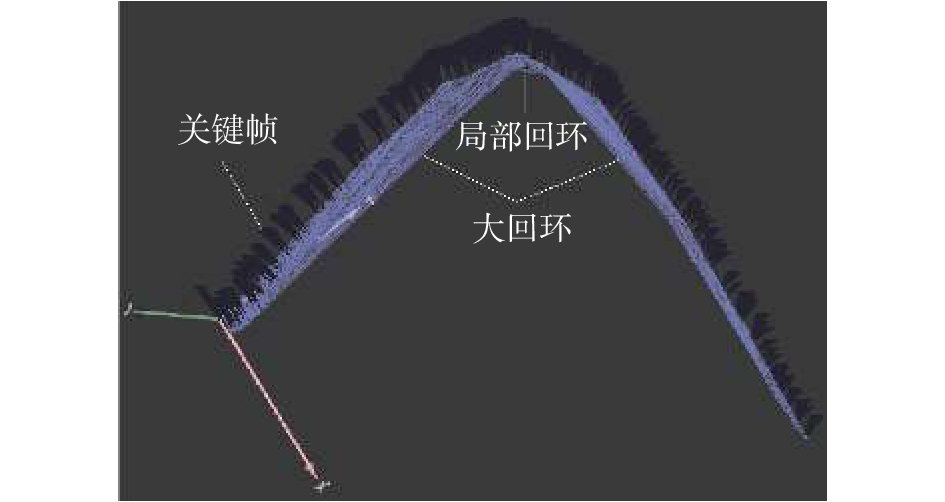
图7(a)为采用文献[6]的方法进行三维重建的效果图,所重构出的点云图中的货物架、AGV小车以及墙板等物体存在轮廓不清晰的情况,左边窗帘冗余点较多。图7(b)为采用本文改进后的ICP算法进行三维重建的效果图。相比之下,利用本文算法得到的点云图精度明显提高,货物架、AGV小车以及墙板等物体轮廓变得清晰,窗帘上的冗余点明显得到减少。图8为采用g2o算法对地图进行优化与更新,深蓝部分为关键帧,其顶点表示相机的各个姿态,连接两顶点的边即表示两点之间的位姿变换。局部回环表示当前帧与就近

|
Download:
|
| 图 7 室内环境三维重建结果 Fig. 7 The experimental results of 3D reconstruction in indoor environment | |
|
Download:
|
| 图 8 g2o优化图 Fig. 8 g2o optimization diagram | |
|
Download:
|
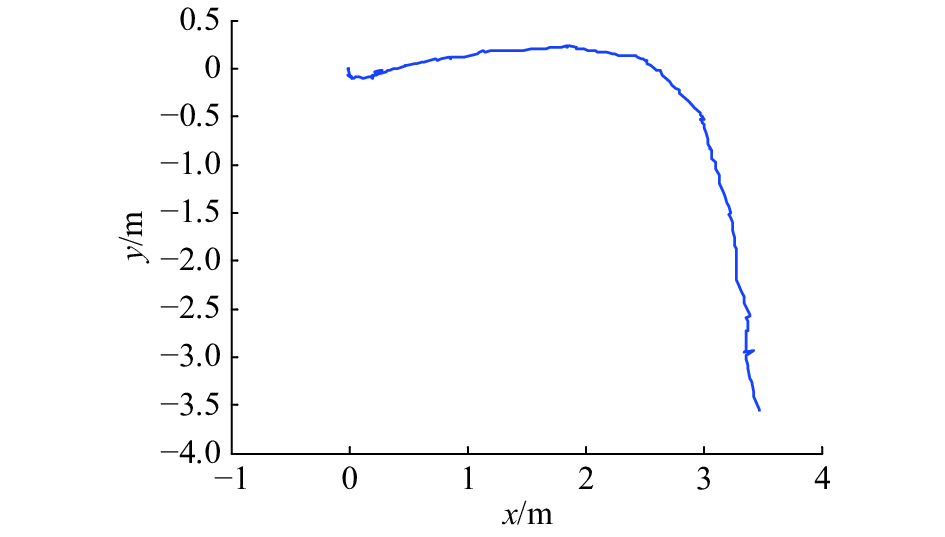
| 图 9 机器人运行轨迹估计 Fig. 9 Robot trajectory estimation | |
本文提出了一种新的基于Kinect的室内移动机器人同时定位与地图构建系统。针对相机位姿估计过程中,点云配准精度不高,易陷入局部最优等问题,提出了一种新的欧氏距离与角度阈值的双重限制法,提高了点云配准精度,减少了配准误差。结合关键帧选取机制和g2o优化算法,实现了三维地图的优化与更新。在真实室内环境下进行在线实验,实验结果证明了本文算法的有效性与可行性。进一步改进工作将集中在:1)进一步研究欧氏距离与角度阈值的选取标准;2)提出移动机器人在同一环境下持续运动所产生的关键帧冗余的情况的解决方案。
| [1] |
ENDRES F, HESS J, STURM J, et al. 3-D mapping with an RGB-D camera[J]. IEEE transactions on robotics, 2014, 30(1): 177-187. DOI:10.1109/TRO.2013.2279412 ( 0) 0)
|
| [2] |
KERL C, STURM J, CREMERS D. Dense visual SLAM for RGB-D cameras[C]//Proceedings of 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan, 2014: 2100–2106.
( 0) 0)
|
| [3] |
HOU Yi, ZHANG Hong, ZHOU Shilin. Convolutional neural network-based image representation for visual loop closure detection[C]//Proceedings of 2015 IEEE International Conference on Information and Automation. Lijiang, China, 2015: 2238–2245.
( 0) 0)
|
| [4] |
解则晓, 徐尚. 三维点云数据拼接中ICP及其改进算法综述[J]. 中国海洋大学学报: 自然科学版, 2010, 40(1): 99-103. XIE Zexiao, XU Shang. A survey on the ICP algorithm and its variants in registration of 3D point clouds[J]. Periodical of ocean university of China, 2010, 40(1): 99-103. (  0) 0)
|
| [5] |
LIN C C, TAI Y C, LEE J J, et al. A novel point cloud registration using 2D image features[J]. Eurasip journal on advances in signal processing, 2017, 2017: 5. DOI:10.1186/s13634-016-0435-y ( 0) 0)
|
| [6] |
杨扬, 曹其新, 朱笑笑, 等. 面向机器人手眼协调抓取的3维建模方法[J]. 机器人, 2013, 35(2): 151-155. YANG Yang, CAO Qixin, ZHU Xiaoxiao, et al. A 3D modeling method for robot’s hand-eye coordinated grasping[J]. Robot, 2013, 35(2): 151-155. (  0) 0)
|
| [7] |
ROSTEN E, PORTER R, DRUMMOND T. Faster and better: a machine learning approach to corner detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(1): 105-119. DOI:10.1109/TPAMI.2008.275 ( 0) 0)
|
| [8] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 ( 0) 0)
|
| [9] |
BAY H, ESS A, TUYTELAARS T, et al. speeded-up robust features (SURF)[J]. Computer vision and image understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 ( 0) 0)
|
| [10] |
MUJA M, LOWE D G. Scalable nearest neighbor algorithms for high dimensional data[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 36(11): 2227-2240. DOI:10.1109/TPAMI.2014.2321376 ( 0) 0)
|
| [11] |
陈胜勇, 刘盛. 基于OpenCV的计算机视觉技术实现[M]. 北京: 科学出版社, 2008.
( 0) 0)
|
| [12] |
DANIEL H C, KANNALA J, HEIKKILÄ J. Joint depth and color camera calibration with distortion correction[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(10): 2058-2064. DOI:10.1109/TPAMI.2012.125 ( 0) 0)
|
| [13] |
朱德海, 郭浩, 苏伟. 点云库PCL学习教程[M]. 北京: 北京航空航天大学出版社, 2012.
( 0) 0)
|
| [14] |
KUMMERLE R, GRISETTI G, STRASDAT H, et al. G2o: a general framework for graph optimization[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai, China, 2011: 3607–3613.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


