自1982年汪培庄^[1]提出因素空间(factors space，FS)理论，时至今日，35年来理论与应用的发展，充分展示了FS理论在解释随机性根源和概率规律的数学实质，融合随机数学与模糊数学的技术方面思想的深刻性，奠定了FS理论作为知识工程的思想框架的地位。

FS理论的早期成果可见汪培庄文集^[2]。1994年汪培庄、李洪兴合著^[3]《知识表示的数学理论》一书系统地论述了FS理论在知识获取、知识表示、知识管理和知识利用方面的数学思想与原理。《模糊计算系统与模糊计算机》^[4]及其相关的工程实践标志着FS理论与智能工程设计理念的完美结合，其中给出的概念内涵和外延相互转换的可操作方法，实现了决策树算法和粗糙集算法没有实现的“双向转换的目的”。其后，李洪兴^[5]关于《因素空间理论与知识表示的数学框架》长达5年的系列讨论，不仅推进了FS理论的发展，也奠定了FS理论在知识发现与智能工程领域广泛应用的基础。袁学海^[6-8]从范畴论的角度对FS的结构问题进行了深入讨论；在FS理论的应用方面，刘增良^[9-13]在因素神经网络技术，军事信息战与网络战领域的研究成绩斐然。此外，基于FS理论的专家系统^[14-15]、多传感器决策融合^[16]、控制仿真^[17-19]、模式识别^[20-21]、安全科学^[22-24]等应用领域的研究，体现了FS作为智能科学的数学空间理论的价值和发展前景。

在KDD问题的研究中，1998年何清^[25]讨论了基于FS和模糊聚类的概念形成方法，2013年汪培庄发表《因素空间与因素库》一文^[26]，推动FS理论在KDD领域的应用。近年来，关于FS与数据科学的关系^[27]，基于FS理论的分类算法^[28-29]、文本挖掘方法^[30-31]等相关研究也有一定的进展。

FS理论生根于数学，反映认识论特点，是KDD和概念格生成的一种自然有效的数学方法。然而，早期奠基性工作建立在模糊数学的基础上，融合了随机数学和抽象代数的思想、方法和语言；FS理论的高起点在保证数学严谨性的同时，也为其普及推广树立了一道屏障。FS的经典定义可见文献[3]，此后的理论与应用研究基本上遵循了这一定义的思想和描述。近年来，随着FS领域应用和教学的深入，出现了对FS定义的领域适应性描述和扩展^[32-33]。2013年汪培庄在讨论FS在数据科学中的应用问题时，对FS的定义进行了修正^[26]。

为能够相对通俗地诠释FS理论的基本思想和原理，2015年包研科^[34]基于认知本体论原理，梳理了FS理论中的基本概念和术语，给出了有别于FS经典定义的描述。这一描述充分体现了汪培庄“因素是分析的维度，是变异的指标和变量名称，是矛盾的编码，是事物形成和描述的基因。以因素为轴所张成的坐标空间就是因素空间，它为事物描述和思维形式提供了普适性的坐标框架”^[27]的论述精神。文献[34]对FS的定义，最大的变化是对因素的顺序关系、算符的意义给出了符合认知本体论原理的描述，形式上同经典定义有所不同，并再次触发了对FS结构问题的思考。

本文的工作是文献[34]的延续，进一步讨论FS的结构问题。

1 预备知识

为方便对本文工作的理解，作为预备知识，简要介绍文献[34]中给出的原理、概念与术语、公理和关键命题，部分内容笔者根据近期研究予以必要的重述。复述与重述不做标识，有需要了解期间变化的读者可同文献[34]进行比对。

1.1 认知本体论原理

因素是认知工具，因素分析应遵循认知本体论原理，因素空间的结构应体现和摹写人类自身的认知结构与思维运动规律。

认知由概念表达，概念是人类思维体系中最基本的构筑单位。概念通常由内涵与外延两个逻辑术语表达。内涵往往采用“上位概念+本位属性”的逻辑形式描述，而外延则是概念所描述的事项的集合。

认知形成的标志是概念的形成，其间的思维运动，主要由分析和综合两种思维方法构成。分析的信息加工与处理技术是解析，实现方式是将事物拆分为更小的单元进行管理和研究，或者表述为“发现事物的个性特征”。综合的信息加工与处理技术是概括，实现方式是将一些具有相同属性的事物归纳为更大的单元进行管理和研究，或者表述为“对事物的一类属性进行综合”。

对一个概念的解析称为概念分化，是下位学习。对一些事物的共有属性进行概括，利用学习者已有的认知结构形成新的概念称为概念同化，是上位学习。

在认知科学的基本概念与原理的基础上，关于FS的认知本体论原理，本文吸收了冯嘉礼^[35]关于《思维与智能科学中的性质论方法》的一些思想原理，参考了文献[36]的讨论。后续关于FS数学结构的讨论遵循下列认知本体论原理：

1) 一个因素总是特定论域上的因素，离开论域谈论因素是没有意义的。更进一步，一个因素总是特定论域上特定问题的因素，离开问题无从讨论因素的认知功能。论域、因素和由因素形成的关于问题的认知结果构成一个特定的思维空间。

2) 概念的分化与同化动态平衡。在概念形成过程中，思维在解析与概括的交替运用中发展。解析强化内涵知识，促进概念分化；概括丰富外延认知，促进概念同化。在这个过程中，内涵与外延存在反变关系，即内涵扩张必然减小外延，反之内涵缩减将导致外延扩张。一个概念的形成，是一定认知阶段上分化与同化的暂时平衡。

3) 概念的内涵与外延对合，即内涵与外延所描述的事项一致。在概念形成过程中，解析与概括之间的差异是思维的技术性差异，不同技术产生的信息在思维运动中以概念的内涵与外延对合为目标纠缠运动，辩证统一。

1.2 基本概念

基于认知本体论原理的FS的基本概念、术语和符号约定如下：

1) 论域是一个关于问题的本体论研究对象的非空可列集合，记为 $U$ 。因素是定义在论域 $U$ 上的一个满映射，记为

$f:U \to {I_f}$

式中：集合 ${I_f}$ 称为 $f$ 的相空间(寓意必须考虑映射像的分布特征)，描述论域 $U$ 上的一类本体论性态。

约定两个特殊因素：

①零因素，记为 $o$ ，其相空间 ${I_o} = \{ {\rm{NoN}}\} $ 非空，相态NoN用来描述所研究问题的“原始概念”或“根节点”，在论域 $U$ 上关于NoN的讨论都是下位学习。

另外，约定NoN是任何一个因素 $f$ 的相空间 ${I_f}$ 中的共有元素，寓意任何一个因素 $f$ 在应用中都有被“空置”的可能，此时NoN可以表示因素 $f$ 的缺失值。

②全因素，记为 $e$ ，其相空间 ${I_e}$ 同论域 $U$ 对等，即 ${I_e}$ 和 $U$ 之间存在一一映射，表示因素e能够“完全个体化”认知论域中的任何一个对象。

因素 $o$ 和 $e$ 称为非平凡因素，除此之外均为平凡因素。

2) 从某一个因素 $f$ 的相空间 ${I_f}$ 到论域 $U$ 的幂集 $ \mathcal{F} $ (U)上的映射 ${\mathop f \limits^ \leftharpoonup}$ 称为因素 $f$ 的回溯，满足

$\forall x \in {I_f},{\mathop f \limits^ \leftharpoonup}(x) = {[x]_f} \in \mathcal{F}(U)$

式中： ${[x]_f}$ 表示由因素 $f$ 的某一相态 $x$ 在 $U$ 限定出的等价类；幂集 $ \mathcal{F} $ (U)称为因素分析的背景空间。回溯的性质如下：

① $\forall x \in {I_f},f({\mathop f \limits^ \leftharpoonup} (x)) = x$ 。

② $\forall {[x]_f} \subseteq U,{\mathop f \limits^ \leftharpoonup} (f({[x]_f})) = {[x]_f}$ 。

③ $\forall x,y \in {I_f},x \ne y,{\mathop f \limits^ \leftharpoonup} (x) \cap {\mathop f \limits^ \leftharpoonup} (y) = \text{Ø} $ 。

注：回溯是一种拟逆映射，同一般逆映射不同之处在于 ${\mathop f \limits^ \leftharpoonup}(x)$ 表示在论域 $U$ 寻找以x标识的对象的等价类。

3) 两个因素 $f$ 和 $g$ 认知等效称为相等，定义为

$f = g \Leftrightarrow \left\{ {\begin{array}{l}{{I_f} \risingdotseq {I_g}{\text{(集合对等)}}}\\{{\mathop f \limits^ \leftharpoonup} (f(u)) = {\mathop g \limits^ \leftharpoonup} (g(u)),\forall u \in U}\end{array}} \right.$

4) 因素在 $U$ 上的认知能力约简为描述概念分化的解析力和描述概念同化的概括力，并以解析力主导因素的序关系，定义

$g \leqslant f \Leftrightarrow \forall x \in {I_f},\exists y \in {I_g},{\text{使}}{\mathop f \limits^ \leftharpoonup} (x) \subseteq {\mathop g \limits^ \leftharpoonup} (y)$

称为因素 $g$ 小于或等于因素 $f$ ，表示 $f$ 比 $g$ 或有更强的解析力。

因素之间的 $ \leqslant $ 关系是偏序关系，并以论域上子集合之间的关系 $ \subseteq $ 为背景关系。

5) 因素 $f$ 与 $g$ 的析运算是因素之间交互效应的描述与分析工具，记为 $f \wedge g$ ，主要服务于概念分化。析因素 $f \wedge g$ 是由 $f$ 和 $g$ 构造出的有更强解析力的新因素，定义为

$\overleftarrow {f \wedge g} (x,y) = {\mathop f \limits^ \leftharpoonup} (x) \cap {\mathop g \limits^ \leftharpoonup} (y),\forall (x,y) \in {I_f} \times {I_g}$

6) 因素 $f$ 与 $g$ 的合运算是思维过程中的信息汇总与认知概括工具，记为 $f \vee g$ ，主要服务于概念同化。合因素 $f \vee g$ 可以理解为比因素 $f$ 和 $g$ 有更强概括力的新因素，定义为

$\overleftarrow {f \wedge g} (x,y) = {\mathop f \limits^ \leftharpoonup} (x) \cup {\mathop g \limits^ \leftharpoonup} (y),\forall (x,y) \in {I_f} \times {I_g}$

7) 因素 $f$ 的补因素以及 $f$ 与 $g$ 的差运算是思维过程中的信息分离工具。补因素实现视角的转换，记为 $f'$ ，定义为

$g = f' \Leftrightarrow \forall x \in {I_f},\exists y \in {I_g},{\mathop g \limits^ \leftharpoonup} (y) = U - {\mathop f \limits^ \leftharpoonup} (x)$

差运算的目的是“从一个因素中排除另一个因素的干涉效应”，记为 $f - g$ ，定义为

$f - g \Leftrightarrow f \wedge g'$

1.3 基本命题

约定如下两个公理：

公理1(发现公理)　 ${\mathop o \limits^ \leftharpoonup} ({\rm{NoN}}) = U,{\mathop e \limits^ \leftharpoonup} (x) = \text{Ø} $ 。

公理2(顺序公理)　 $o \leqslant f \leqslant e$ 。

注：由全元素的定义，公理 ${\mathop e \limits^ \leftharpoonup} (x) = \text{Ø} $ 的意义是 $e$ 的回溯不能在论域 $U$ 发现以 $x$ 标识的对象的等价类。

在前述概念(定义)和两个公理的基础上，可以证明下列命题：

命题1(对合定理)　 ${\mathop f \limits^ \leftharpoonup} = {\mathop g \limits^ \leftharpoonup} \Leftrightarrow f = g$ 。

命题2(反变关系定理)　 $g \leqslant f \Leftrightarrow {\mathop f \limits^ \leftharpoonup} \leqslant {\mathop g \limits^ \leftharpoonup} $ 。

命题3(幂等律)　 $f \wedge f = f,f \vee f = f$ 。

命题4(交换律)　 $f \wedge g = g \wedge f,f \vee g = g \vee f$ 。

命题5(结合律)　 $(f \wedge g) \wedge h = f \wedge (g \wedge h)$ ， $(f \vee g) \vee $ $h = f \vee (g \vee h)$ 。

命题6(分配律)　 $f \wedge (g \vee h) = (f \wedge g) \vee (f \wedge h)$ ， $f \vee $ $ (g \wedge h) = (f \vee g) \wedge (f \vee h)$ 。

命题7(第一吸收律)　 $f \vee g \leqslant f,f \vee g \leqslant g$ ； $f \leqslant g \wedge f,g \leqslant g \wedge f$ 。

命题8(第二吸收律)　若 $g \leqslant f$ ，则 $f \wedge g = f$ ， $f \vee g = g$ 。反之亦真。

命题9(第三吸收律)　 $f \! \vee \! (f \! \wedge \! g) \!=\! f$ ， $f \! \wedge \! (f \vee g) \!=\! f$ 。

命题10(排序定理)　 $o \leqslant f \vee g \leqslant f,g \leqslant f \wedge g \leqslant e$ 。

命题11(第一对偶律)　 $o = e',e = o'$ 。

命题12(第二对偶律)　 $(f \wedge g)' = f' \vee g'$ ， $(f \vee g)' = $ $ f' \wedge g'$ 。

1.4 因素空间

在一个论域 $U$ 上，可以定义多个因素 $\{ {f_j}\} _{j = 1}^N$ ，称为 $U$ 上一个因素族，并作为一个代数系统进行讨论，是借助因素分析实现论域上知识发现的基础。

定义1　设 $F$ 表示定义在论域 $U$ 上的所有因素的集合，则称代数系统 $(F, \vee , \wedge , ' )$ 是论域U上一个因素空间，记为FS。

定义中3种代数运算 $ \vee , \wedge , ' $ 的概念和性质承接1.2和1.3节的讨论。

由零因素的定义，显然 $o \in F$ 。由论域的可列性和全因素的定义， ${I_e} \risingdotseq U$ ，至少 $U$ 中对象的“编号”是一个定义在 $U$ 上的全因素，即存在 $e \in F$ 。

定义2　设 $f$ 和 $g$ 是论域 $U$ 上两个因素，若 $U/f \ne U/g$ ，则称 $f$ 和 $g$ 是自为因素。

定义3　设 $\{ {f_j}\} _{j = 1}^N$ 是论域 $U$ 上一个平凡因素族， $\forall i \ne j = 1,2, \cdots ,N$ ， ${f_i}$ 和 ${f_j}$ 是自为因素，则称 $\{ {f_j}\} _{j = 1}^N$ 是可基因素族，记为BF。

定义4　设BF是因素空间 $(F, \vee , \wedge , ' )$ 上的一个有限可基因素族，则称各个因素相空间的笛卡尔积

${I_1} \times {I_2} \times \cdots \times {I_N}$

为定义在论域 $U$ 上的一个信息系统，不妨记为 $(U,{\rm{BF}})$ 。

定义5　设BF为因素空间 $(F, \vee , \wedge , ' )$ 中的可列可基因素族，若

$\mathop {\lim }\limits_{N \to \infty } \mathop V\nolimits_{j = 1}^N {f_j} = o {\text{且}} \mathop {\lim }\limits_{N \to \infty } \mathop \Lambda \nolimits_{j = 1}^N {f_j} = e$

${f_j} \in {\rm{BF}}$ ，则称BF为论域 $U$ 上的一个完备因素族，记为 ${\rm{CFF}}$ 。

称 $({\rm{CFF}}, \vee , \wedge , ' )$ 为完备因素空间，简称因素空间，仍记为FS。

称 $(U,{\rm{CFF}})$ 是一个完备信息系统，记为CIS。

在不引起误会的场合，不必刻意区分FS和CIS的不同，即一个因素空间既是一个完备信息系统。

显然，当论域 $U$ 为有限集时，存在自然数 $N < \infty $ ，使 $\mathop V\nolimits_{j = 1}^N {f_j} = o$ 且 $\mathop \Lambda \nolimits_{j = 1}^N {f_j} = e$ 。

定义6　设(S, $ \mathcal{F} $ ,P)是一个概率空间，H是定义在样本空间 $S$ 上的所有二阶矩随机变量的集合， $H = \{ X|E(|X{|^2}) < \infty \} $ ，则称 $(H, \vee , \wedge , ' )$ 为正则因素空间，记为CFS。

引进CFS的目的是方便描述结构化数据分析问题。文献[34]中讨论了因素概念的外延，随机变量是基本的数量化因素。若有限个二阶矩随机变量 ${X_j},j = 1,2, \cdots ,N$ 各自有不同的概率分布，则 $\{ {X_j}\} _{j = 1}^N = $ BF，于是 $(S,\{ {X_j}\} _{j = 1}^N)$ 就是一个结构化信息系统。CFS在结构化数据分析的应用中，只需将样本空间 $S$ 理解为论域，而 $\sigma - $ 代数 $ \mathcal{F} $ 等价于 $ \mathcal{F} $ (S)，相应概念的对应关系可作如下约定：

1) $X = o$ 表示对 $X$ 的观测缺失。

2) $X = e$ 表示对 $X$ 的观测不能发现随机性 波动(取常数值)。

3) $X \vee Y$ 表示对 $(X,Y)$ 的联合概率分布 $F(x,y)$ 的观测。

4) $X \wedge Y$ 表示 $(X,Y)$ 对条件分布乘积 ${F_{X|Y}}(x|y) \cdot $ ${F_{Y|X}}(y|x)$ 的观测。

5) $\bar X$ 表示对 $1 - {F_X}(x)$ 的观测。

在一个论域 $U$ 上的知识发现问题，通常存在各种不同的主题 ${T_i},i = 1,2, \cdots ,N$ ，每一个主题下所有可能结果的集合就是这一主题的样本空间 ${S_i}$ ，相应的存在一个正则因素空间 ${\rm{CF}}{{\rm{S}}_i}$ ，则论域 $U$ 上的因素空间

${\rm{FS}} = {\rm{CF}}{{\rm{S}}_1} \times {\rm{CF}}{{\rm{S}}_2} \times \cdots \times {\rm{CF}}{{\rm{S}}_N}$

相应的，信息系统

$(U,{\rm{BF}}) = (U,{\rm{B}}{{\rm{F}}_1} \times {\rm{B}}{{\rm{F}}_2} \times \cdots \times {\rm{B}}{{\rm{F}}_N})$

CFS的概念有助于FS分析方法与技术体系的建构，有助于理解因素空间同概率空间、希尔伯特空间和张量空间的关系。

前述讨论是对因素空间宏观结构的一种公理化诠释，其意义在于为信息系统分析提供了一个统一的语境场。

2 因素空间的结构 2.1 交错自同构变换与回旋格

通常认为，格是认知描述与形式概念分析理想的代数系统^{[2, 36]}。

本文引进格上的交错自同构变换和回旋格的概念，然后给出FS对偶回旋定理，构成对FS代数结构的新认知。

定义7　设 $ \leqslant $ 为非空集合 $L$ 上的偏序关系， $(L, \leqslant )$ 为有界偏序格，其中， $\forall x,y \in L$ ， $x \vee y = \sup \{ x,y\} $ ， $x \wedge y = \inf \{ x,y\} $ ，泛下界为0，泛上界为1。

若 $L$ 上存在变换 $\tau $ ，满足条件：

1) $\forall x \in L,x \ne 0,1,\tau (x) = x$ 。

2) $\forall x,y \in L$ ， $\tau (x \vee y) = x \wedge y$ ， $\tau (x \wedge y) = x \vee y$ 。

3) $\tau (0) = 1,\tau (1) = 0$ 。

则称 $\tau $ 为 $(L, \leqslant )$ 上的交错自同构变换(staggered automorphism transform)。

下面诠释格上交错自同构变换的几何意义。

不妨设 $L = \{ {x_j}\} _{j = 1}^n,{x_j} \ne 0,1$ ，在 $(L, \leqslant )$ 中，格点是分层的。按组合计数 $C_n^k,k = 1,2, \cdots ,n$ ，同层的格点集合记为

${\{ {x_j}\} ^{(1)}} = L,{\{ \wedge {x_j}\} ^{(k)}} = \{ \wedge _{s = 1}^k{x_{{j_s}}}\} ,{\{ \vee {x_j}\} ^{(k)}} = \{ \vee _{s = 1}^k{x_{{j_s}}}\} $

式中 $k = 1,2, \cdots ,n$ 。于是，格中的偏序关系为

$0 \leqslant \cdots \leqslant {\{ \wedge {x_j}\} ^{(k)}} \leqslant \cdots \leqslant {\{ {x_j}\} ^{(1)}} \leqslant \cdots \leqslant {\{ \vee {x_j}\} ^{(k)}} \leqslant \cdots \leqslant 1 \cdots$

(1)

在每一个层的格点集合中取一个元素，由关系 $ \leqslant $ 构成一个序链。

若将式(1)理解为一条定宽的纸带，从左到右摹写式(1)中的格层与偏序关系，最左端为0，最右端为1。

根据交错自同构变换的3个条件，将 $\tau $ 的像摹写在纸带(1)的反面，得到一种同 $ \leqslant $ 等价(认知等效)的偏序关系 $ \preccurlyeq $ ，即纸带(1)的反面为

$1 \preccurlyeq \cdots \preccurlyeq {\{ \vee {x_j}\} ^{(k)}} \preccurlyeq \cdots \preccurlyeq {\{ {x_j}\} ^{(1)}} \preccurlyeq \cdots \preccurlyeq {\{ \wedge {x_j}\} ^{(k)}} \preccurlyeq \cdots \preccurlyeq 0 \cdots $

(2)

记为

$(L, \leqslant ,\tau ) = (L, \preccurlyeq )$

显然，两个偏序格 $(L, \leqslant )$ 和 $(L, \preccurlyeq )$ 的代数格同一，均为 $(L, \vee , \wedge )$ 。

在格 $(L, \vee , \wedge )$ 上，由于式(1)左端的0和式(2)右端的0同一，式(1)右端的1和式(2)左端的1同一，所以这一纸带是对合的，但是需要扭转纸带粘合两端，粘合后一面显示0，另一面显示1。于是，L上的两种偏序关系 $ \leqslant $ 和 $ \preccurlyeq $ 融合为一体，即在泛界点0或1处，偏序关系 $ \leqslant $ 和 $ \preccurlyeq $ 均“不失意”的无障碍连通。

综上所述，一个存在交错自同构变换的偏序格 $(L, \leqslant )$ ，其代数格 $(L, \vee , \wedge )$ 的几何构型是一个麦乌比斯环(mobius strip)。

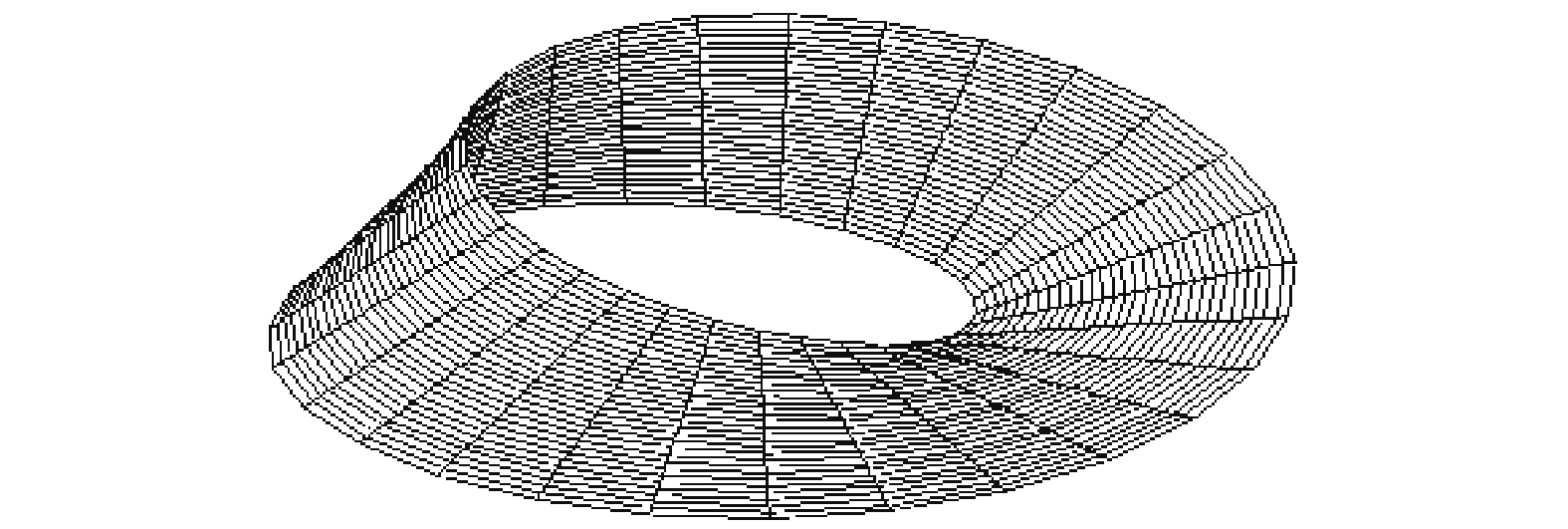
定义8　设 $ \leqslant $ 和 $ \preccurlyeq $ 是非空集合 $L$ 上的两个不同的偏序关系，若 $(L, \preccurlyeq )$ 是有界偏序格 $(L, \leqslant )$ 上交错自同构变换的像，则称 $(L, \leqslant )$ 的代数格 $(L, \vee , \wedge )$ 为回旋格(convolution lattice)，其几何构型如图1。

显然，回旋格的定义当 $L$ 为可列集时仍是适用的。引进回旋格的概念，旨在揭示因素空间深刻、丰富而有趣的性质。

2.2 对偶回旋定理

关于CFS的代数结构，文献[34]已经证明： $({\rm{CFF}}, \leqslant )$ 是一个偏序格。 $({\rm{CFF}}, \vee , \wedge )$ 是一个有界代数格，满足分配律。 $({\rm{CFF}}, \vee , \wedge , ' )$ 是一个布尔格。

上述结论的建立，数学原理基于认知原理，遵循概念内涵与外延的对合性与反变关系原理，因素解析能力的大小主导因素的序关系，偏序格 $({\rm{CFF}}, \leqslant )$ 受顺序公理、对合定理、反变关系定理和排序定理的影响，同数学上经典的偏序格不尽相同。因此，在代数格 $({\rm{CFF}}, \vee , \wedge )$ 中，虽然形式运算性质同数学经典的代数格描述一致，但内在运算机理有所不同。

在布尔格 $({\rm{CFF}}, \vee , \wedge , ' )$ 中，结构与体系的核心在于因素大小的定义和顺序公理的约定。下面引进 $({\rm{CFF}}, \vee , \wedge , ' )$ 上的交错自同构变换:

1) 将因素大小的定义

$f \leqslant g \Leftrightarrow {\mathop g \limits^ \leftharpoonup} (y) \subseteq {\mathop f \limits^ \leftharpoonup} (x)$

变异为

$g \preccurlyeq f \Leftrightarrow {\mathop g \limits^ \leftharpoonup} (y) \subseteq {\mathop f \limits^ \leftharpoonup} (x)$

2) 将顺序公理

$o \leqslant f \leqslant e$

变异为

$e \preccurlyeq f \preccurlyeq o$

式中 $o$ 和 $e$ 的意义不变。

由变异式(1)可知，因素之间的关系 $ \leqslant $ 和 $ \preccurlyeq $ 有相同的背景关系；由变异式(2)可知， $ \leqslant $ 和 $ \preccurlyeq $ 的认知意义不同， $ \leqslant $ 代表了认知的解析过程， $ \preccurlyeq $ 代表了认知的概括过程。因此， $ \leqslant $ 和 $ \preccurlyeq $ 背景关系的一致和认知意义的不同，反映的是概念的对合性和概念分化、同化过程的技术差异。

3) 代数运算 $ \vee , \wedge $ 的定义不变

在上述3个约定下，需要系统的修改、重述1.3节涉及序关系的命题，其他命题形式不变。修改后的相关命题如下：

命题2’(外延限制定理)　 $f \preccurlyeq g \Leftrightarrow {\mathop f \limits^ \leftharpoonup} \preccurlyeq {\mathop g \limits^ \leftharpoonup} $ 。

认知本体论的解释：命题2’由命题2描述概念内涵与外延的反变关系转变为描述对外延的限制。

命题7’(第一吸收律)　 $f \wedge g \preccurlyeq f,f \wedge g \preccurlyeq g$ ； $f \preccurlyeq $ $ g \vee f,g \preccurlyeq g \vee f$ 。

命题8’(第二吸收律)　若 $g \preccurlyeq f$ ，则 $f \wedge g = g$ ， $f \vee g = f$ 。反之亦真。

认知本体论的解释：命题7’和命题8’修改了序关系与代数运算的联系规则，将因素固有的概括功能从“隐性”表达转变为“显性”表达。

命题10’(排序定理)　 $e \preccurlyeq f \wedge g \preccurlyeq f,g \preccurlyeq f \vee g \preccurlyeq o$ 。

从命题10到命题10’实现了 $({\rm{CFF}}, \vee , \wedge )$ 从偏序关系 $ \leqslant $ 到偏序关系 $ \preccurlyeq $ 的交错自同构变换。

基于偏序关系 $ \preccurlyeq $ 的背景关系，容易证明命题2’、命题7’、命题8’和命题10’，限于篇幅，不再赘述证明过程。在偏序关系 $ \preccurlyeq $ 约定的结构体系上， $({\rm{CFF}}, \vee , \wedge , ' )$ 仍是一个布尔格。

综上所述，得到下面的定理1。

定理1(对偶回旋定理)　 $({\rm{CFF}}, \vee , \wedge , ' )$ 是一个回旋布尔格。

因素是认知工具，FS是认知科学的数学模型。有别于Boole代数，FS的本质在于其回旋性，反映了概念形成过程中分化与同化的双向统一性，具体地讲：

1) FS的回旋性反映概念内涵与外延的对合性。在论域上，最小元 $o$ 形成完全概括性认知，最大元 $e$ 形成彻底的个性化认知。因此，在对论域形成的终极认知即“论域中的每一个对象都是不同的个体，同时所有对象又是一个整体”的意义上，因素 $o$ 和 $e$ 是等效的。在解析过程中，零因素 $o$ 是析运算的单位元，也是合运算的零元。反过来，在概括过程中，全因素 $e$ 是析运算的零元，也是合运算的单位元。当终极认知形成之时，必有 $o = e$ 。

2) FS的回旋性反映概念内涵与外延的反变关系。这种反变关系在实际的认知过程中，往往表现为概念的分化与同化的纠缠，对于理解一个事物而言，究竟是概念分化多一些好，还是同化多一些好？概念的分化与同化的纠缠，反映概念形成过程中因素的解析力和概括力交互作用的过程。从论域为一个整体的角度，解析导致“论域划分”，破坏整体性；从论域中对象的个体性出发，概括是在论域划分的基础上重构整体性。同理，从“属性限定”揭示一类事物共同特征的角度讲是概括；而从概念的结构、即“属性限定”为概念分化技术的角度讲是解析。在认知过程中，概括与解析各具所长，往往交互作用，殊途同归。由因素认知一个概念不外乎借助因素的解析力和概括力，辨识概念的内涵(属性限定)，界定概念的外延(论域划分)，并使两种过程形成同一认知。

在FS中，因素运算的认知性质由解析力主导，准确地揭示了概念的内涵与外延的反变关系。但是，概括力的隐化导致因素操作的代数性质同经典Boole代数理论中的部分运算性质形式不同。这种情况恰是FS的价值所在。由因素描述的认知过程中，概括和解析不是两种截然分开的过程，仅仅是间或性的哪个表现更强势一些，解析能力的提升(降低)导致概括能力的降低(提升)，总合觉察力不变。

因此，由解析力主导的有界偏序格 $({\rm{CFF}}, \leqslant )$ 同概括力主导的有界偏序格 $({\rm{CFF}}, \preccurlyeq )$ ，在因素空间 $({\rm{CFF}}, \vee , \wedge , ' )$ 中不是“双面结构”。对偶回旋定理是对概念形成过程中，由内涵与外延的对合性和反变关系引导的信息表达、加工和信息运动过程的数学抽象。

3 结论与展望

本文工作对文献[34]的核心概念进行梳理，简化了公理性约定，凝练并重述核心命题，承接前期工作的理论与思想。着眼因素空间的理论与方法在信息科学领域的应用，重述因素空间的定义，提出了自为因素、可基因素族、完备因素空间和正则因素空间的概念，初步地、明确勾勒出因素空间与信息系统之间的关系。

本文对FS理论的贡献在于交错自同构变换、回旋格和对偶回旋定理，突破了经典论述关于FS结构的认知，为认知科学讨论若干基本概念之间关系和思维运动的问题给出了可借鉴数学模型，为FS理论在人工智能领域的研究与应用提供了新的切入点。

据此，本文对FS理论与应用研究的展望如下：

1) 进一步构建FS理论“四位一体”的思想框架。在本文的讨论中，一个中心思想就是“人工智能是人类认知模式的数学重构”，在这个过程中，关于人工智能的数学思想、原理与算法必须同人的认知模式高度契合，理论研究的思想框架必须同人类问题解决过程中的思维场高度契合，并同机器实现的技术特征高度契合。这一思想暗涵于本文之中，可以想象在以 $U,{\rm{FS}},{\rm{BF}},$ $ \mathcal{F} $ (U)为顶点的四面体中，底面 $\Delta ({\rm{FS}},{\rm{BF}},$ $ \mathcal{F} $ (U))表示因素分析理论，侧面 $\Delta (U,{\rm{BF}},$ $ \mathcal{F} $ (U))表示商空间理论，侧面 $\Delta (U,{\rm{FS}},$ $ \mathcal{F} $ (U))表示张量分析理论，侧面 $\Delta (U,{\rm{FS}},{\rm{BF}})$ 表示数据分析理论，每个棱表示两个顶点之间的双向信息通道。这个四面体构成完整的FS理论的思想框架。

在这个思想框架中，论域 $U$ 是问题空间，是研究主题之源；因素空间FS是关于问题或主题的要素与要素关系的数学系统，是数据分析理论的上位体系，为信息系统 $(U,{\rm{BF}})$ 理论提供可靠的数学原理支撑；从张量代数同认知科学结合的观点看，论域的离散拓扑 $ \mathcal{F} $ (U)与因素空间FS应当同构。在本文的概念体系中，一个信息系统 $(U,{\rm{BF}})$ 等价于因素空间中的可基因素族BF，因此商空间 $U/{\rm{BF}}$ 就是在FS与 $ \mathcal{F} $ (U)同构关系下的知识库，而得到这一知识库的技术路径依赖于数据分析理论和 $(U,{\rm{BF}})$ 及其数据库上的KDD技术。

2) 发展基于FS对偶回旋定理的因素分析技术体系。本文发现的FS对偶回旋定理，明确了因素空间中信息的运动过程存在麦比乌斯环特征。佩捷、王兰新在《从麦比乌斯到陈省身——麦比乌斯变换与麦比乌斯带》一书中，较为系统地介绍了在代数几何、拓扑学的研究中发现的麦比乌斯带有趣的性质。麦比乌斯带的存在源自实数域R的乘法群R^*的不连通性，这一性质更深刻的等价描述如下^[37]：

设 $n$ 维向量丛集 $GL(n,{\bf{R}}) \subset GL(n + 1,{\bf{R}})$ ，记 $G{L_\infty } = $ $ { \cup _n}GL(n,{\bf{R}})$ 。设A是希尔伯特空间H中的斜伴随算子，即在通常的范数 $\left\| {{A}} \right\| = {\sup _{|x| = 1}}\left| {{{Ax}}} \right|$ 下，交错内积

$ \left\langle {{Ax}},{{y}} \right\rangle = - \left\langle {{x}},{{Ay}} \right\rangle ,\forall {{x}},{{y}} \in H$

成立，等价于 ${{A}}$ 在有限维零空间的正交补空间上可逆，记A为所有 $H$ 中斜伴随算子 ${{A}}$ 的拓扑空间。则 $G{L_\infty }$ 同伦等价于A。

另外，格代数与麦比乌斯代数存在天然的联系^[37-40]。

这表明，从纯数学的角度看，FS对偶回旋定理所描述的数学性质以不同的形式存在已久。但是，本文再发现的过程却贯通了认知科学与数学深刻的内在联系，巩固了FS理论作为人工智能研究的思想框架和认知科学研究的数学模型的地位。众多的文献给出了麦比乌斯变换群在其他数学分支，如数论、组合数学、微分几何、黎曼几何、罗巴切夫斯基几何、模与丛论中的应用，以及在图像处理领域、通信科学、密码学、量子物理学、遗传生物学、有机化学、乃至机械与工程领域中的应用，无不昭示着FS对偶回旋定理潜在的理论与应用价值。

3) 发展基于麦乌比斯环0的数据分析方法与算法。因素 $o$ 和 $e$ 是FS认知能力的两个极点，是不动点。若用一个有一定带宽的信息通道来描述FS和对偶回旋定理所揭示的认知过程，非常有趣的是，这一信息通道恰为一个麦乌比斯环0。记FS中任意一个状态点(n维向量)为 $\varphi $ ，则 $\varphi $ 的能量态可以借助量子计算理论的量子比特叠加态

$|\varphi > = \alpha \cdot |o > + \beta \cdot |e > $

表达，其中 $\alpha $ 和 $\beta $ 分别是极点 $o$ 和 $e$ 对 $\varphi $ 的引力系数，满足 ${\alpha ^2} + {\beta ^2} = 1$ 。这个发现，为在FS理论的数据挖掘与信息处理算法建构过程中嵌入量子计算技术，将状态关系的度量和分析提升为状态—能量关系的度量和分析提供了可靠的切入点^[41-42]。