2. 国网浙江省电力公司 经济技术研究院,浙江 杭州 310000
2. Economic Research Institute, State Grid Zhejiang Electric Power Company, Hangzhou 310000, China
电网是加快工业进步、提高居民生活质量、保持社会稳定健康发展的基础。因此,电网的发展具有重要的意义。电网企业的责任是确保安全、经济、清洁和可持续的能源供应,从而为社会、经济的健康发展,人民生活水平的逐步提高保驾护航。其中,产能输出和运营指标管理作为电网企业经营活动的中枢,是企业发展的重中之重,能对企业整体运营状况、管控经营、监控战略产生实效。此外,通过挖掘数据资产的潜在价值,不仅能提升企业各部门的专业管理能力,而且还能促进企业安全、有序、健康、高效地运营,对决策制定发挥重要的辅助作用。然而,确定和下达经营决策的合理性取决于预测这些指标未来变化情况的准确性,由于预测电网企业运行运营指标是面向未来的,且影响指标变化的因素较多,因此预测过程具有很大的随机性和不确定性。结合电网企业的实际情况设计合适的预测方法,将直接关系到预测实施的精度。
目前,常用的传统预测方法有指数平滑法(exponential smoothing,ES)[1]、线性回归分析法(linear regression analysis,LRA)[2]、时间序列法(time series method,TS)[3]等,ES认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延,且它认为最近的过去态势,在某种程度上会持续到未来,所以将较大的权数放在最近的资料上。LRA利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间的关系进行建模的一种回归分析。TS则通过编制和分析时间序列,根据时间序列所反映出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年内可能达到的水平。虽然这些传统方法在预测应用中略有成效,但是它们预测对象单一、过度依赖历史数据,且无法考虑到未来预测过程中存在的不确定性因素。
因此,针对以上问题,一些学者尝试将神经网络应用到预测中去,使得预测系统具有一定的智能信息处理能力,取得了不错的预测效果。但是,由于神经网络采用的是经验风险最小化原则,容易陷入局部极小点且收敛速度慢,这极大地限制了该方法在实际过程中的应用。基于支持向量机的预测模型[4]很好地克服了神经网络的这一缺点,SVM采用结构风险最小化原则,整个求解过程转化为凸二次规划问题,能得到全局最优解。但是,由于SVM是借助二次规划来求解支持向量,而求解二次规划将涉及m阶矩阵的计算(m为样本的个数),当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。因此,其不适用于大规模训练样本。
为此,本文提出一种双非凸回归(double nonconvex regression,DNR)算法用于标量电力数据预测。该方法首先将稀疏编码技术[5]转化为回归预测应用,再采用lp范数替换原始的重构误差l2范数以及表示系数l1范数等约束,以获得更为灵活的模型目标泛函形式。最后,利用交替方向乘子法(alternating direction method of multipliers,ADMM)[6]优化求解目标函数;其中,为获得快速的子问题优化效果,提出一种改进的迭代阈值方法用于求解lp约束子问题,保证全局最优解并可实现并行实施方案。在电网企业运行运营指标真实数据上的实验结果表明该方法切实可行,且具有很高的预测精度。
1 双非凸回归算法稀疏编码技术[5]已在模式识别领域得到广泛的应用,其通过误差平方最小化和稀疏性范数约束搜寻目标量的最佳逼近系数。原始的稀疏回归模型可以描述为
| $\min \left\| {{x} - {{A\alpha }}} \right\|_2^2 + \lambda {\left\| {{\alpha }} \right\|_0}$ | (1) |
式中:x∈Rm×1、A∈Rm×n和α∈Rn×1分别表示查询向量、观测矩阵和表示系数,伪范数||·||0用于计算系数矢量α的非零值个数。在分类问题中,式(1)的具体意义为:观测数据A包含n个m维特征样本,未知样本x通过表示系数α进行重构,要求α具有有限个非零元素且对应于同类观测样本。然而,在电力数据预测(或称为回归)问题中,常见的数据如电力产能、运营利润等都是标量值,而影响其具体取值的特征量为矢量形式。因此,本文将式(1)转化为回归问题,即x∈Rm×1表示m个已知目标样本,A∈Rm×n表示m个观测特征样本,每个样本的维数为n,而系数α∈Rn×1则表示每个特征子元素的重构贡献度。通过训练样本计算得到最优的α系数,可用于预测任意未知特征样本a为y=aTα。
遗憾的是,受l0伪范数约束影响,最小化式(1)是一个NP难问题,仅能在有限样本集中运行实施[7]。一般将之调整为Lasso问题,即通过l1范数替换l0范数
| $\min \left\| {{x} - {A\alpha }} \right\|_2^2 + \lambda {\left\| {\alpha } \right\|_1}$ | (2) |
已有理论表明,在一定的不连贯条件下[7],l1最小化问题很大概率等价于l0最小化问题。而且,l1范数是最逼近于l0范数的凸约束形式,有利于模型的优化求解。
此外,式(1)和式(2)中所采用的l2范数最小化重构误差仅适合于高斯分布噪声环境[8-9]。为适应特定的样本或特征干扰,常采用等价于拉普拉斯分布的l1范数约束进行误差最小化[5],即
| $\min \left\| {{x} - {A \alpha }} \right\|_1^{} + \lambda {\left\| {\alpha } \right\|_1}$ | (3) |
然而,当矩阵A的不连贯条件无法满足,或重构误差并不适应于常规的高斯分布或拉普拉斯分布时,模型(3)的求解结果往往是次优的。针对此问题,本文采用lp范数(p∈(0, 1]))替换式(3)中的l1范数约束,即
| $\min \left\| {{x} - {A \alpha }} \right\|_q^q + \lambda \left\| {\alpha } \right\|_p^p$ | (4) |
为便于区分,在重构误差中以符号q表示lp范数约束。式(4)为本文所提回归模型的目标函数,对误差项和正则项都采用非凸函数约束,因此称之为双非凸回归算法(double nonconvex regression, DNR),其中对α约束lp范数较l1更接近于l0,使得重构系数α具有更强的稀疏性;对误差约束lp范数使之更贴近于椭圆分布[10],具有较高斯分布和拉普拉斯分布更为宽泛的适用范围。
2 模型优化求解针对常规的单lp约束稀疏回归问题,迭代重加权最小二乘(IRLS)[11]、迭代重加权l1最小化(IRL1)[12]、交替方向乘子[6]以及迭代阈值收缩(IST)[13]等求解算法都得到了成功应用。然而,对于式(4)所示双非凸约束模型,所述求解算法都无法直接应用。如果强行将迭代重加权型算法扩展为双加权凸约束形式,所得解也非常容易陷入局部最优;ADMM算法能够进行有效地多变量拆分,但是要求各子优化问题具有闭式解或快速求解策略;IST具有高效的收敛性能,但前提需将目标函数中的观测矩阵A变换至正交形式。结合所述分析,本节采用ADMM算法和IST算法融合策略进行目标函数式(4)的求解优化。首先,通过ADMM变量拆分,获得部分子问题的闭式解;其次,提出改进的迭代阈值算法进行非凸子问题优化;最后,给出完整的模型求解算法并分析其运算复杂度。
2.1 ADMM变量拆分考虑到DNR模型包含两个非凸lp范数约束,需要引入两个辅助变量用于问题简化,将式(4)转化为等价约束优化式
| $\begin{array}{c}\min \left\| {{{x}} - {{A}}{{\beta} }} \right\|_q^q + \lambda \left\| {{\beta} } \right\|_p^p\\{\rm{s.t.}}\;{x} - {A\alpha } = {e},{\alpha } = {\beta }\end{array}$ | (5) |
并得到其增广拉格朗日形式
| $\begin{array}{c}{L_{{\mu _e},{\mu _\beta }}}({{e}},{{\alpha }},{{\beta }}) = ||{{e}}||_q^q + \lambda ||{{\beta }}||_p^p + \displaystyle\frac{\mu _e}{2}||{{x}} - {{A\alpha }} - {{e}}||_2^2 + \displaystyle\frac{\mu _\beta }{2}||{{\alpha }} - {{\beta} }||_2^2 + {{\gamma} }_e^{\rm{T}}({{x}} -{ {A\alpha} } - {{e}}) + {{\gamma }}_\beta ^{\rm{T}}({{\alpha} } - {{\beta }})\end{array}$ | (6) |
式中:μe、μβ>0为惩罚参数,γe和γβ为拉格朗日乘子系数。根据ADMM变量分离规则,式(6)包含以下迭代步骤:
1) 固定α和γβ,βk+1的更新子问题为
| $\begin{array}{c}{{{\beta }}_{k + 1}} = \arg \mathop {\min }\limits_{{\beta }} {L_{{\mu _\beta }}}({{\beta} },{{\alpha }},{{{\gamma} }_\beta }) = \\\displaystyle\frac{\lambda }{{{\mu _\beta }}}||{{\beta} }||_p^p + \frac{1}{2}||{{\beta} } - {{\alpha} } - \frac{{{{{\gamma} }_\beta }}}{{{\mu _\beta }}}||_2^2\end{array}$ | (7) |
2) 固定α和γe,ek+1的更新子问题为
| $\begin{array}{c}{{{e}}_{k + 1}} = \arg \mathop {\min }\limits_{{e}} {L_{{\mu _e}}}({{e}},{\alpha },{{{\gamma} }_e}) = \displaystyle\frac{1}{{{\mu _e}}}||{{e}}||_q^q + \frac{1}{2}||{{e}} - {{x + A\alpha }} - \frac{{{{{\gamma} }_e}}}{{{{\mu} _e}}}||_2^2\end{array}$ | (8) |
3) 固定e、β、γe和γβ,αk+1的更新子问题为
| $\begin{array}{c}{{{\alpha} }_{k + 1}} = \arg \mathop {\min }\limits_{{e}} {L_{{\mu _e},{\mu _\beta }}}({{e}},{{\beta} },{{{\gamma }}_e},{{{\gamma }}_\beta }) = \\\displaystyle\frac{{{{\mu} _e}}}{2}||{{A\alpha }} -{ {x + e}} - \frac{{{{{\gamma} }_e}}}{{{{\mu} _e}}}||_2^2 + \frac{{{{\mu} _\beta }}}{2}||{{\alpha }} - {{\beta}}+\frac{{{{{\gamma} }_\beta }}}{{{{\mu} _\beta }}}||_2^2\end{array}$ | (9) |
4) 根据计算所得的β、e和α1,更新γe和γβ
| $\begin{array}{c}{\gamma }_e^{k + 1} = {\gamma }_e^k + {{\mu} _e}({x} - {A\alpha } - {e})\\{\gamma }_\beta ^{k + 1} = {\gamma }_\beta ^k + {{\mu} _\beta }({\alpha } - {\beta })\end{array}$ | (10) |
上述迭代步骤中,式(10)是ADMM固有的乘子升级规则。式(9)通过微分后可得αk+1的解析解:
| ${{\alpha }^{k + 1}} = {C}({\mu _e}{{A}^{\text{T}}}({x} - {e}) + {{A}^{\text{T}}}{{\gamma }_e} + {\mu _\beta }{\beta } - {{\gamma }_\beta })$ | (11) |
式中:在给定μe和μβ的前提下,逆算子C=(μeATA+μβI)-1是常量,可提前计算并缓存,加速算法的求解效率。因此,非凸子问题(7)和(8)是求解式(6)的关键步骤。考虑到p次lp范数约束
| $\min f({\delta} ) = \frac{1}{2}\left\| {{\delta} - {\sigma} } \right\|_2^2 + \lambda {\left\| {\delta} \right\|^p}$ | (12) |
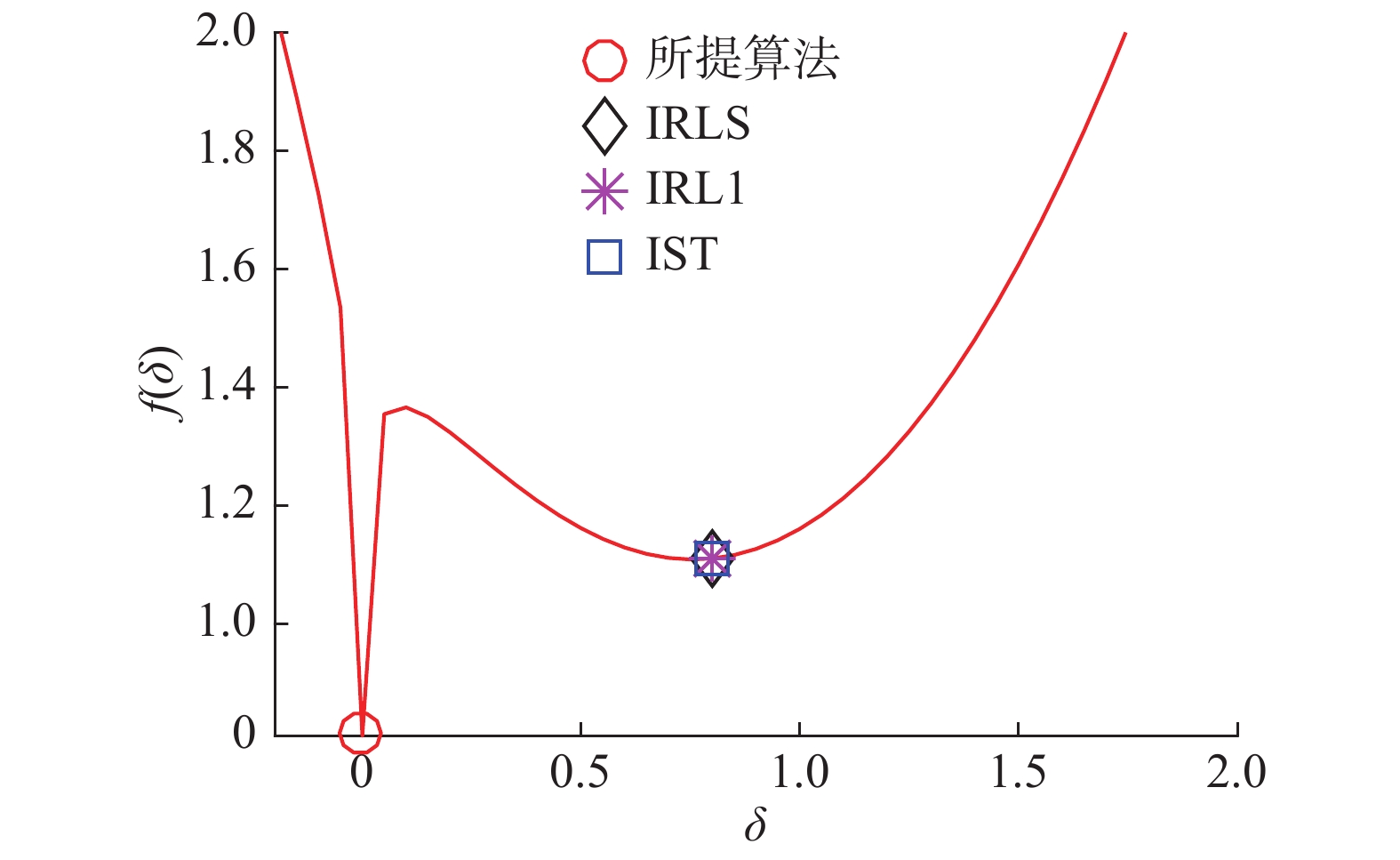
当p=1时,可由经典的软阈值算法[14]进行有效求解。针对本文的非凸情况(0<p<1),IRLS、IRL1、IST等求解算法都存在局部次优解的缺陷。如图1所示,当σ=0.9,p=0.2且λ=1时,IRLS、IRL1和IST都陷入了局部最小值。为解决该问题,本文提出一种改进的阈值迭代方法,在保证高效求解的同时能够获得全局最优值。
|
Download:
|
| 图 1 几种算法对典型非凸问题式(12)的最优解 Fig. 1 Several algorithms for the optimal solution to the typical nonconvex problem in formula (12) | |
根据式(12)的对称性以及阈值收缩规则[13],当σ>0时,最优解范围为[0,σ];当σ<0时,最优解范围为[σ, 0]。不失一般性,本节仅考虑σ>0的情形。设p=0.6,λ=2.5,图2给出了不同σ值下的f(δ)最优解情况。由图2中可见,f (δ)的最小值取决于某临界σ值τσ,当σ<τσ时,minf (δ)位于δ=0;当σ≥τσ时,minf (δ)位于δ>0的某个点。因此,求解式(12)的核心由τσ和δ两个关键值确定。

|
Download:
|
| 图 2 不同σ值下非凸问题f (δ)的最优解 Fig. 2 The optimal solution of non-convex problem f (δ) under different σ values | |
式(12)的一阶和二阶微分别为
| $f'(\delta ) = \delta - \sigma + \lambda p{\delta ^{p - 1}}$ | (13) |
| $f''(\delta ) = 1 + \lambda p(p - 1){\delta ^{p - 2}}$ | (14) |
设f"(δ(λ, p))=0,可得δ(λ, p)=(λp(1-p))1/(2-p)。结合图2可知,当δ∈(0, δ(λ, p))时,f(δ)是凹函数;当δ∈(δ(λ, p), +∞)时,则f(δ)是凸函数。进一步,为保证f(δ)在(δ(λ, p), +∞)具有最小值,需满足f'(δ(λ, p))≤0,文献[13]令f'(δ(λ, p))=0并计算出τσIST用于迭代阈值求解。然而,该阈值设法存在问题,如图1所示,IST计算所得的解满足上述所有规则,且σ≥τσIST时保证
| ${\delta ^*} - \sigma + \lambda p{\delta ^*}^{p - 1} = 0$ | (15) |
在(δ(λ, p), +∞)中具有唯一的最小值。然而,f(δ*)具体取值依然高于f(0)。
从图2可见,存在特定的τσ使得f(δ*)=f(0),当σ<τσ时,δ=0为f(δ)的最小值;当σ≥τσ时,f(δ)最小值在δ>0的某个位置。因此,正确的阈值τσ和δ*计算公式应该为
| $\frac{1}{2}{({\delta ^*} - \tau _\sigma ^{})^2} + \lambda {({\delta ^*})^p} = \frac{1}{2}{(\tau _\sigma ^{})^2}$ | (16) |
| ${\delta ^*} - \tau _\sigma ^{} + \lambda p{({\delta ^*})^{p - 1}} = 0$ | (17) |
将式(17)中的τσ值代入式(16)可得
| ${\delta ^{*p}}(2\lambda (1 - p) - {({\delta ^*})^{2 - p}}) = 0$ | (18) |
其最优解δ*∈(δ(λ, p), +∞)为δ*=(2λp(1-p))1/(2-p),并可进一步计算出τσ为
| ${\tau _\sigma } = {[2\lambda (1 - p)]^{\frac{1}{{2 - p}}}} + \lambda p{[2\lambda (1 - p)]^{\frac{{p - 1}}{{2 - p}}}}$ | (19) |
根据式(15)和式(19),所提的迭代阈值规则如算法1描述。算法1主要更改了阈值计算策略,基本步骤与文献[13]类似,当J=2时能够获得令人满意的收敛结果。
结合算法1与ADMM优化框架,完整的DNR优化步骤按式(7)~(10)循环进行,具体的收敛条件按文献[6]设定。值得注意的是,式(7)与式(8)由算法1并行计算实施,其计算复杂度仅为O(n),而式(9)的计算复杂度在逆算子缓存的前提下为O(max(n2, nm))。假设ADMM迭代次数为t,则完整的算法复杂度为O(tnmax(n, m)),远远优于IRLS、IRL1等算法的O(n3)。
算法1 改进的迭代阈值规则
输入 参数σ,λ ,p,J;
输出 δ*。
1) 按式(19)计算τσ值;
2) 如|σ|<τσ;则令δ*=0;
3) f反之,令k=0,δk=σ;
4) for k=1, 2,
5)
6) End
7) δ*=sgn(σ)δJ;
3 实验分析分别对电力企业运行中的全负荷电能输出(兆瓦时)以及运营指标中的月利润总额进行预测。首先对电力企业的产能输出和运营数据进行实证分析,然后将所提算法与经典的SVM[15]、BP神经网络[16]和非凸非光滑约束NNR方法[7]进行精度对比。
3.1 电能输出预测通过某电力企业复循环动力装置(包括两个燃气涡轮,一个汽轮机以及两个热回收系统)6年运行数据作为预测样本,共含该企业全负荷运行674天所产生的9 568个采样点,样本特征包括环境温度(AT)、大气压力(AP)、相对湿度(RH)、排汽压力(V) 4个维度。随机选择{10%, 20%, 30%, 40%, 50%}个采集数据作为训练样本,其余作为测试数据。实验精度由绝对误差均值(MAE)和均方误差(RMSE)两者表示,其计算式分别为
| ${\text{MAE}} = (|{p_1} - {r_1}| + |{p_2} - {r_2}| + \cdots + |{p_n} - {r_n}|)/n$ |
| ${\text{RMSE}} = \sqrt {({{({p_1} - {r_1})}^2} + {{({p_2} - {r_2})}^2} + \cdots + {{({p_n} - {r_n})}^2})/n} $ |
式中:p和r分别为预测值和真实值,n为测试样本总量。
表1给出了SVM、BP神经网络、NNR以及DNR三种对比算法在不同训练样本量下的预测精度对比,其中DNR的参数值p=q=1。从表1可见,DNR算法在不同的训练数下都具有最低的误差均值和均方误差值,展示了更为优秀的预测精度。而且,DNR算法在30%~50%训练样本量下的精度非常接近,MAE基本稳定在4.95左右,而BP神经网络、SVM和NNR在不同样本量下的预测值跨度相对较大,说明DNR具有更高的算法稳定性,对输入训练样本量要求更小。同时,DNR计算所得的AT、AP、RH、V这4个特征表示系数绝对值分别为0.767、0.085、0.102、0.426,即4个特征的预测贡献度依次为AT>V>RH≈AP,与文献[17]的理论分析结果吻合。此外,SVM、BP、NNR、DNR 3种算法在50%训练量下的完整预测时间分别为2.91 s、0.48 s、0.32 s和0.06 s,可见DNR具有明显更高的运行效率。最后,表2和表3分别给出了DNR算法在不同p、q值下的预测精度。从中可见,随着p、q值的优选变化,DNR的预测精度得以进一步提升,验证了非凸约束的优越性,且最优值处于p、q∈[0.5, 0.8],与文献[18]的理论结论吻合。
| 表 1 电能输出预测精度对比 Tab.1 Comparison of prediction accuracy of energy output |
| 表 2 DNR算法不同q值下的电能输出预测精度 Tab.2 Predicting accuracy of energy output in different q of DNR algorithm |
| 表 3 DNR算法不同p值下的电能输出预测精度 Tab.3 DNR algorithm power output prediction accuracy in different p |
选取某电网企业自2013年1月—2014年12月期间的流动资产周转率(次),购电成本(万元),可控费用(万元),货币资金,主营业务利润率,单位资产售电量,每万元电网资产运行维护成本等真实数据作为训练样本集,2015年1月—2015年12月期间的运营指标数据作为测试样本集。表4为部分训练样本集数据。
| 表 4 部分训练样本集数据 Tab.4 Partial training sample data set |
实验中通过DNR、SVM、BP神经网络和NNR这3种预测方法对2013年1月—2014年12月连续2年的月利润总额进行拟合,对2015年1月—2015年12月1年的月利润总额进行预测,并比较三者的预测精度,其结果如图3~6以及表5所示。
| 表 5 DNR、SVM、BP和NNR在运营数据中的预测对比 Tab.5 Predictive comparison of DNR, SVM, BP and NNR in operational data |
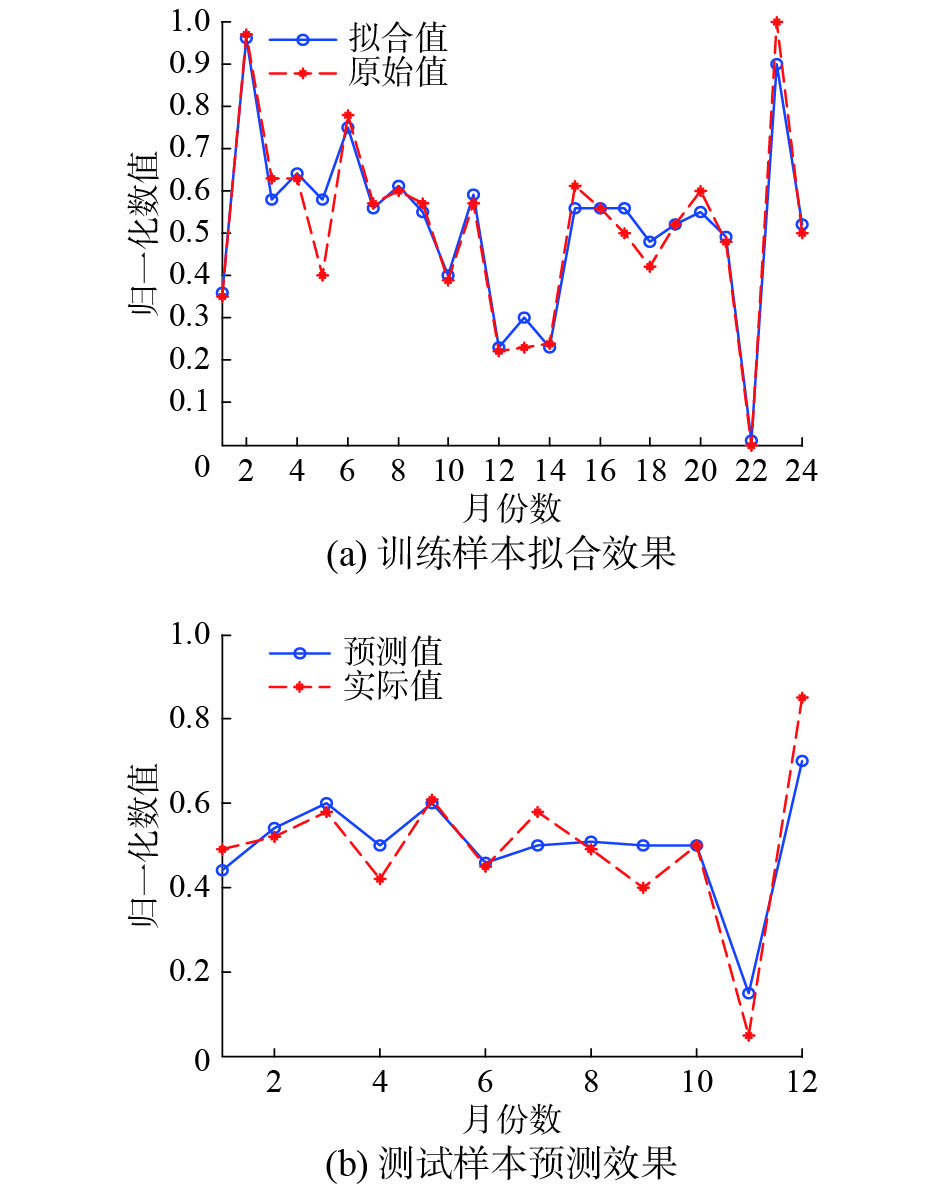
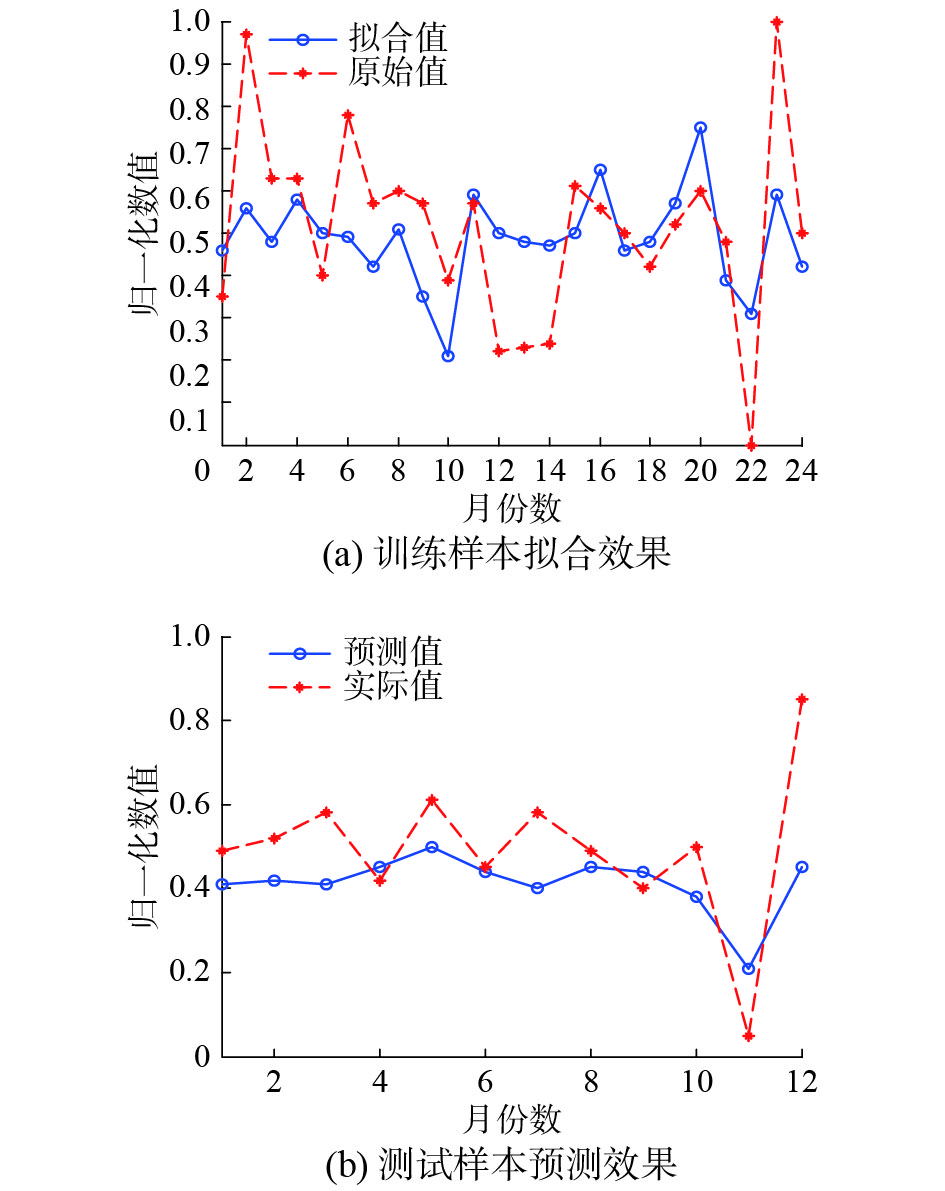
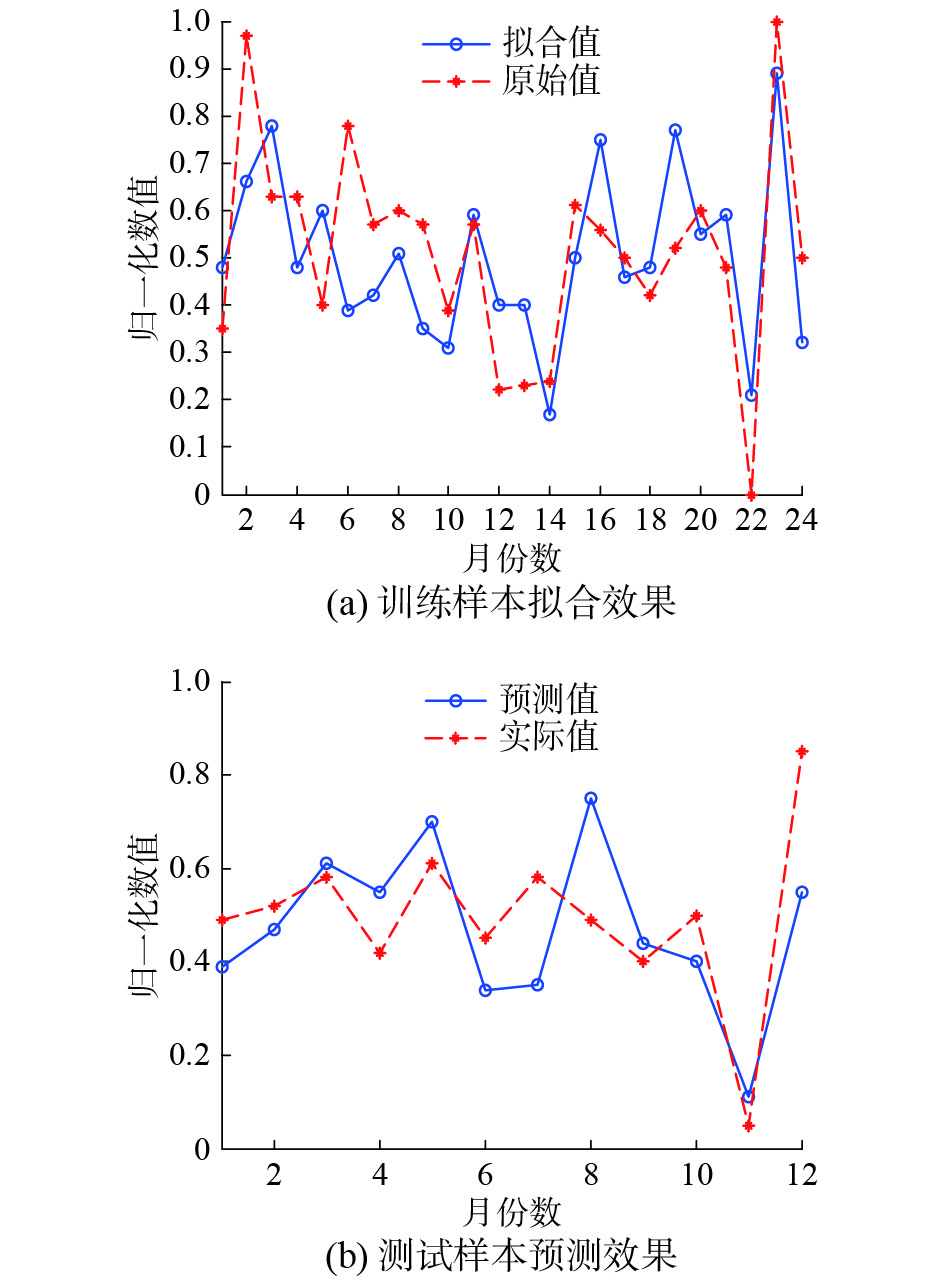
由图3可知,DNR对24个月数据的拟合值基本贴合原始值的走势,表现出优秀的拟合能力。图4中SVM的拟合能力一般,特别是第1个月~第11个月的拟合值与原始值相差较大。图5中BP神经网络对数据的拟合值符合原始值的一般走向,只是在数值上存在一定程度上的等比例缩小。由图6可以看出NNR的拟合和预测误差较大。而对于DNR、SVM和BP神经网络的预测效果,通过图3~6的预测对比可知DNR更为接近地预测出了2015年1月—2015年10月的月利润总额。虽然其对11月~12月这两个月的数据预测不甚理想,但整体利润趋势与实际值吻合。相较而言,BP神经网络对这两个月的数据预测较精准,但1月~4月的预测值却与实际值相差甚远。SVM的预测值与实际值虽大致在同一数值层上,但整体预测值离精确点相去较远。此外,NNR虽与实际值走势相似,但存在多个严重偏离真实值的预测值。
|
Download:
|
| 图 3 DNR对训练样本的拟合效果及对测试样本的预测效果对比 Fig. 3 Comparison of the fitting effect of DNR on training samples and the prediction effect of test samples | |
|
Download:
|
| 图 4 SVM对训练样本的拟合效果及对测试样本的预测效果对比 Fig. 4 Comparison of test samples and training samples’s fitting effect by SVM | |

|
Download:
|
| 图 5 BP神经网络对训练样本的拟合效果及对测试样本的预测效果对比 Fig. 5 Comparison of test samples and training samples’s fitting effect by BP neural network | |
|
Download:
|
| 图 6 NNR对训练样本的拟合效果及对测试样本的预测效果对比 Fig. 6 Comparison of test samples and training samples’s fitting effect by NNR | |
综上所述,DNR和BP神经网络在运营数据中对训练样本的拟合效果优于SVM。虽然DNR和BP神经网络的拟合效果接近,但对于测试样本的预测结果对比图中明显可以看出,DNR的预测结果最佳。NNR因为存在多个高偏离度的预测点而次于SVM。BP神经网络的预测效果最差。
此外,由表5可知,不论训练样本还是测试样本,DNR的MEA和RMSE值均小于SVM BP神经网络和NNR的误差均值和均方差,再次验证了图3~6的拟合效果和预测效果,并且DNR的运行时间(单位:s)也远远少于SVM、BP神经网络和NNR。
4 结束语电网企业运行和运营数据预测是一个极为复杂的课题,数据采集过程中仪器老化产生的测量误差、人工疏忽导致的漏检误标等因素使得预测过程具有很大的随机性和不确定性。本文提出一种称为非凸回归的预测算法,改进了经典稀疏回归法中的模型约束形式,对重构误差和稀疏系数引入lp(0<p≤1)正则化项约束,使之包含更为稀疏的目标项并具有更为灵活的扩展应用能力。通过交替方向乘子法对该回归模型进行求解,并对其中的子问题提出一种新的阈值优化规则,确保目标函数具有快速的非凸优化求解能力。实验结果表明,与支持向量机BP神经网络和非凸约束算法NNR相比,本文所提方法具有较高的预测精度和更好的预测效果,且运行效率高。
| [1] |
TAYLOR J W. Multi-item sales forecasting with total and split exponential smoothing[J]. Journal of the operational research society, 2011, 62(3): 555-563. DOI:10.1057/jors.2010.95 ( 0) 0)
|
| [2] |
彭敏, 张泰玮, 黄佳佳, 等. 基于回归模型与谱聚类的微博突发话题检测方法[J]. 计算机工程, 2015, 41(12): 176-181. PENG Min, ZHANG Taiwei, HUANG Jiajia, et al. Microblog sudden topic detection method based on regression models and spectral clustering[J]. Computer engineering, 2015, 41(12): 176-181. (  0) 0)
|
| [3] |
ARYA F K, ZHANG Lan. Time series analysis of water quality parameters at Stillaguamish River using order series method[J]. Stochastic environmental research and risk assessment, 2015, 29(1): 227-239. DOI:10.1007/s00477-014-0907-2 ( 0) 0)
|
| [4] |
丁宏飞, 李演洪, 刘博, 等. 基于BP神经网络与SVM的快速路行程时间组合预测研究[J]. 计算机应用研究, 2016, 33(10): 2929-2932, 2936. DING Hongfei, LI Yanhong, LIU Bo, et al. Expressway’s travel time prediction based on combined BP neural network and support vector machine approach[J]. Application research of computers, 2016, 33(10): 2929-2932, 2936. DOI:10.3969/j.issn.1001-3695.2016.10.012 (  0) 0)
|
| [5] |
ZHENG Jianwei, YANG Ping, CHEN Shengyong, et al. Iterative re-constrained group sparse face recognition with adaptive weights learning[J]. IEEE transactions on image processing, 2017, 26(5): 2408-2423. DOI:10.1109/TIP.2017.2681841 ( 0) 0)
|
| [6] |
CHEN Liang, SUN Defeng, TOH K C. A note on the convergence of ADMM for linearly constrained convex optimization problems[J]. Computational optimization and applications, 2017, 66(2): 327-343. DOI:10.1007/s10589-016-9864-7 ( 0) 0)
|
| [7] |
CUI Zhuoxu, FAN Qibin. A nonconvex nonsmooth regularization method for compressed sensing and low rank matrix completion[J]. Digital signal processing, 2017, 62: 101-111. DOI:10.1016/j.dsp.2016.11.006 ( 0) 0)
|
| [8] |
YANG Meng, ZHANG Lei, YANG Jian, et al. Regularized robust coding for face recognition[J]. IEEE transactions on image processing, 2013, 22(5): 1753-1766. DOI:10.1109/TIP.2012.2235849 ( 0) 0)
|
| [9] |
WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 ( 0) 0)
|
| [10] |
LUO Lei, YANG Jian, QIAN Jianjun, et al. Robust image regression based on the extended matrix variate power exponential distribution of dependent noise[J]. IEEE transactions on neural networks and learning systems, 2017, 28(9): 2168-2182. DOI:10.1109/TNNLS.2016.2573644 ( 0) 0)
|
| [11] |
郑建炜, 黄琼芳, 杨平, 等. 特征加权组稀疏判别投影分析算法[J]. 自动化学报, 2016, 42(5): 746-759. ZHENG Jianwei, HUANG Qiongfang, YANG Ping, et al. Feature weighted group sparse discriminative projection algorithm[J]. Acta automatica sinica, 2016, 42(5): 746-759. (  0) 0)
|
| [12] |
CANDÈS E J, WAKIN M B, BOYD S P. Enhancing sparsity by reweighted l1 minimization[J]. Journal of Fourier analysis and applications, 2008, 14(5): 877-905. ( 0) 0)
|
| [13] |
SHE Yiyuan. Thresholding-based iterative selection procedures for model selection and shrinkage[J]. Electronic journal of statistics, 2009, 3: 384-415. DOI:10.1214/08-EJS348 ( 0) 0)
|
| [14] |
CAI Jianfeng, CANDÈS E J, SHEN Zouwei. A singular value thresholding algorithm for matrix completion[J]. SIAM journal on optimization, 2010, 20(4): 1956-1982. DOI:10.1137/080738970 ( 0) 0)
|
| [15] |
CHAÂBANE N. A novel auto-regressive fractionally integrated moving average-least-squares support vector machine model for electricity spot prices prediction[J]. Journal of applied statistics, 2014, 41(3): 635-651. DOI:10.1080/02664763.2013.847068 ( 0) 0)
|
| [16] |
LIU Ke, GUO Wenyan, SHEN Xiaoliu, et al. Research on the forecast model of electricity power industry loan based on GA-BP neural network[J]. Energy procedia, 2012, 14: 1918-1924. DOI:10.1016/j.egypro.2011.12.1188 ( 0) 0)
|
| [17] |
TÜFEKCI P. Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods[J]. International journal of electrical power and energy systems, 2014, 60: 126-140. DOI:10.1016/j.ijepes.2014.02.027 ( 0) 0)
|
| [18] |
ZHANG Yong, YE Wanzhou, ZHANG Jianjun. Sparse signal recovery by accelerated lq (0<q<1) thresholding algorithm
[J]. International journal of computer mathematics, 2017, 94(12): 2481-2491. DOI:10.1080/00207160.2017.1284314 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


