符号网络[1-2]是指具有正边或负边的网络,其中正边表示积极的、正面的意义,负边表示消极的、负面的意义。在现实生活中,可以将很多网络抽象为符号网络。例如,国际关系网[3]中合作和敌对的关系、社交网络[4]中朋友和敌人关系、生物网络[5]中促进和抑制作用等。1946年Heider[6]提出三角形关系中正关系与负关系的相互作用模式,将符号网络带入大家的视线。随着符号网络的兴起,网络的全局平衡性引起众多学者的关注。根据计算得到的全局平衡性可以有效地进行个性化推荐、态度预测等。一般全局平衡性用不平衡度来衡量,不平衡度是指一个网络从不平衡到平衡的距离,若将这些引起不平衡的边的符号取反,网络就变为平衡网络。然而对于大多数符号网络而言,结构平衡定理太过严苛。Leskovec等[7]也证实了弱结构平衡定理更适合真实网络。因此本文从弱结构平衡定理出发,来研究网络的弱不平衡性。孙一翔[8]提出Meme-SB算法,将结构平衡定理的能量函数作为适应值函数,利用混合遗传算法求得真实符号网络的不平衡度。在Meme-SB算法基础上,本文提出了WSB-EA算法,将研究范围扩展到符号网络的弱不平衡性。即将弱结构平衡定理的能量函数当作适应值函数,利用进化算法原理,初始化种群,选择、交叉、变异,最终得到网络的弱不平衡度。4个小型数据集的实验表明,WSB-EA算法比其他算法能够更快收敛得到最优解。在实验最后部分计算得到两大符号网络Epinions和Slashdot的弱不平衡度。
1 背景知识从20世纪40年代,Heider提出三角形关系中正关系与负关系的相互作用模式,到Cartwright等[9]用图论语言描述这一理论将其推广到整个网络。越来越多的研究者对符号网络的结构和演化问题感兴趣,致力于研究社会群体的派系结构和发展过程。然而,有很大一部分真实网络并不符合Heider提出的结构平衡理论,由此Davis[10]放宽结构平衡理论的约束条件,提出弱结构平衡理论。
1.1 弱结构平衡定理符号网络用数学符号G(V, E)表示,V表示网络节点集合,E表示网络边的集合。其中任意一条边
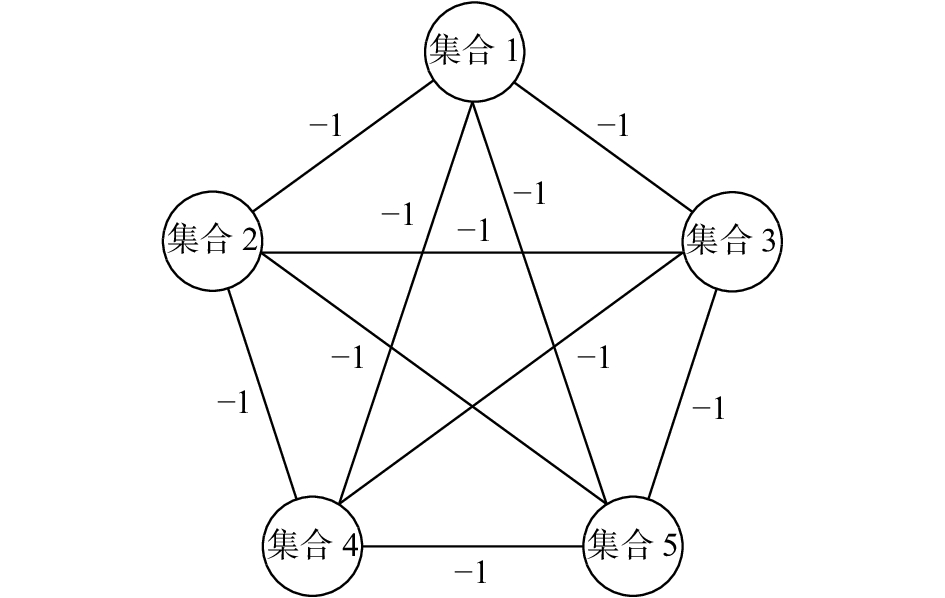
然而对于大多数符号网络而言,结构平衡定理的要求太过严苛。之后Davis放宽结构平衡理论的约束条件,提出了弱结构平衡理论。这一理论将图1(d)三条边都是负号这样的三角结构也认为是平衡结构。因此产生了一个新的概念,K-平衡网络。这一理论认为,一个符号网络是弱平衡的,当且仅当可以将这一网络中的节点分为k个子集,子集内部都是正边,子集之间都是负边。结构平衡定理是弱结构平衡定理中k为2的特殊情况。K-平衡网络的结构如图2所示,图中集合内部连边都是正边,集合之间连边都是负边。
|
Download:
|
| 图 2 弱结构平衡网络 Fig. 2 Weak balance network structure | |
根据弱结构平衡定理,计算符号网络的弱不平衡度就是寻找一种集合划分,使得集合内部之间的负边数和集合外部之间的正边数最少。例如,节点1和节点2之间的连边为正,如果将这两个节点分到同一个集合,这两个节点就没有对弱不平衡度做出“贡献”,如果把它们分到不同的集合,就需要计算这两个节点对弱不平衡度做的“贡献”。同理,两个节点之间的边是负边时,将其分到同一集合,也要计算这一部分的“贡献”。因此计算弱不平衡度就是遍历整个符号网络,找到所有对弱不平衡度做出“贡献”的节点对。由此提出弱结构平衡定理的能量函数:
| $h\left( s \right) = \sum\limits_{ij} {\left( {1 - {J_{ij}}\delta \left( {{s_i},{s_j}} \right)} \right)} /2$ | (1) |
在弱结构平衡定理中,一个无向符号网络被分为k个子集。因此,网络中每个节点都有一个所属的子集编号,在式中用si来表示这一编号。δ(si, sj)的计算结果由si和sj决定,如果si和sj的值相同则计算结果为+1,否则为–1。
由此,求解符号网络的弱结构平衡问题就转变为最小化能量函数的优化问题。能量函数的最小值代表了导致符号网络弱不平衡的最少边的数目。若将这些边的符号取反,可以将此网络转变为弱结构平衡网络。如果能量函数值为0,说明此网络已是弱结构平衡网络。
1.3 进化算法进化算法[11-12]或称演化算法(evolutionary algorithms, EAS),是一个算法簇,它们产生的灵感都来自于大自然的生物进化,但它有很多的变化,有不同的遗传基因表达方式,不同的交叉和变异算子,特殊算子的引用,以及不同的再生和选择方法。与传统的基于微积分的方法和穷举法等优化算法相比,进化计算是一种成熟的具有高鲁棒性和广泛适用性的全局优化方法,具有自组织、自适应、自学习的特性,能够不受问题性质的限制,有效地处理传统优化算法难以解决的复杂问题。
2 WSB-EA算法描述 2.1 WSB-EA算法主要流程根据问题定义以及进化算法原理,本文将弱结构平衡定理的能量函数作为目标函数,在Meme-SB算法的基础上,初始化种群,经过选择、交叉、变异得到最优解。具体框架如算法1所示。
算法1 WSB-EA算法
输入 邻接矩阵J,种群规模P,迭代次数M;
输出 最优解的适应值,即网络弱不平衡度。
1)
2) Pop←Population(P, true); //初始化种群
3) a=0;
4) repeat
5) individual = Pop.getFittest();//计算得到
种群最优个体
6) Pop←evolvePopulation(Pop, individual); //种群进化,选择、交叉、变异操作
7) a=a+1;
8) until a=M //达到最大进化次数时停止
2.2 编码本文使用的编码方式是整数编码[13]。种群中的染色体由
一般进化算法中的初始化方法都是随机产生每条染色体,但这样的初始化方式效率不高。如果初始化的染色体对应的适应值很低,要经过很多次迭代才能得到最优解,收敛速度太慢。因此本文使用一种简单的启发式方法,保证在初始化时每一个节点与它的邻居节点对能量函数没有“贡献”。即在初始化之后,随机选择一个节点,如果此节点与它的邻居节点对能量函数没有“贡献”,则不改变这一节点的取值,否则将其改为它的正邻居节点所属的子集编号。这样的操作重复n次,并且保证每次选择的节点是之前没有选择过的。
2.4 遗传操作本文的遗传操作过程如算法2所示。遗传过程分为3步:首先将上一代种群中的优秀个体保存到新一代种群中,这个过程称为精英保留;接下来利用锦标赛方式选取父代染色体,经过单路交叉;单点变异得到新一代种群。
算法2 evolvePopulation (individual)算法
输入 原始种群Pop,最优个体individual,锦标赛规模tournamentSize,交叉概率uniformRate,变异概率mutationRate;
输出 新一代种群newPop。
1) newPop.saveIndividua(0, individual); //精英保留
2) for( j=0; j< Pop.size();j++)
3) indiv1 =tournamentSelection(Pop); //选择父本1
4) indiv2 = tournamentSelection(Pop);
5) newIndiv=crossover(indiv1, indiv2); //交叉算法
6) newPop.saveIndividua ( j, newIndiv);
7) for( j=0; j< Pop.size();j++)
8) mutate(newPop.getIndividual( j)); //变异算法
2.4.1 选择操作在进化算法中轮盘赌是最常用也是最简单的选择算子。但对于本文而言,轮盘赌不利于保持种群多样性。为了解决这一问题,本文选用锦标赛方法选取优秀个体进行繁衍。首先确定锦标赛规模t,随机从种群中选择出t个个体,计算这些个体的适应值,将适应值最小的个体作为父代进行繁衍。
2.4.2 交叉操作一般在进化算法中经常使用的两点交叉算子很有可能会破坏父代染色体中优秀的基因结构,因此为了保存父代染色体中的优秀基因结构,本文选择单路交叉方式[14]作为交叉算子。首先通过锦标赛选择算法选择两个优秀父代A、B。随机产生一个0 ~ k–1的整数m,记录A中所有m所在的位置,然后将B对应位置的基因值改为m。例如,图3中,每一条染色体有15个基因,选择两条父代染色体,随机产生一个数2,将B中对应位置的取值都改为2。

|
Download:
|
| 图 3 单路交叉 Fig. 3 Single cross | |
本文的变异算子是单点变异。从父代种群中随机选择一条染色体,然后从这一染色体中随机选取一个基因,对其重新赋值,但要保证变异之后染色体的能量函数值没有增加。这样的操作要循环n次,因此变异也可以看作一种局部搜索,将染色体变异为它的邻居染色体,试图找到局部最优的染色体。
2.5 符号网络存储符号网络在计算机中一般有3种存储方式:邻接矩阵、三元组和链表方式。邻接矩阵是普遍使用的一种方式。然而对于大型符号网络来说,邻接矩阵达到105×105的数量级,存储这样的邻接矩阵对内存要求太高。因此本文选择邻接链表[15] 来存储网络信息。首先为每一个节点都创建一条链表,头结点是节点本身,后面链接与这一节点有联系的节点信息,包括节点编号以及边的符号。例如,图4中,这一链表存储节点1的连边信息。节点1与节点2的连边为1,节点1与节点6的连边为–1。虽然每条边都存储了两次,但相对于邻接矩阵的存储方式,大大降低了内存占用。

|
Download:
|
| 图 4 二维链表示例 Fig. 4 Two-dimension link structure | |
在一般的遗传算法中,每一次的交叉和变异之后都需重新计算一次适应值,这样重复操作使得算法的时间复杂度太高。基于此,本文在定理1的基础上提出一种增量计算的方式,在重新计算适应值时,只计算个体中因基因改变使得适应值增减的部分。
定理1 假设个体ind在位置h处变异,sh由old变为new,则个体ind的新适应值h(ind)new为
| ${h_{\rm {new}}} = {h_{\rm {old}}} + \sum\limits_{{v_j} \in N\left( {{v_h}} \right)} {{J_{hj}}\left( {\delta \left( {{\rm {new}},{s_j}} \right) - \delta \left( {{\rm {old}},{s_j}} \right)} \right)} $ |
其中
| $\begin{array}{c}{{\textbf{证明}}}\qquad\qquad h = \displaystyle\sum\limits_{{v_i},{v_j} \in E} {{J_{ij}}\delta \left( {{s_i},{s_j}} \right)} = \qquad\qquad\qquad \\ \displaystyle\sum\limits_{{v_h},{v_j} \in E} {{J_{hj}}\delta \left( {{s_h},{s_j}} \right)} + \sum\limits_{{v_i},{v_j} \in E \wedge i! = h} {{J_{ij}}\delta \left( {{s_i},{s_j}} \right)} = \\ \displaystyle\sum\limits_{{v_j} \in N\left( {{v_h}} \right)} {{J_{hj}}\delta \left( {{s_h},{s_j}} \right)} + \sum\limits_{{v_i},{v_j} \in E \wedge i! = h} {{J_{ij}}\delta \left( {{s_i},{s_j}} \right)} \end{array}$ | (2) |
由于式(2)等号右侧第2部分在变异前后不变,所以
| $\begin{array}{c}{h_{\rm {new}}} - {h_{\rm {old}}} =\\ \displaystyle \sum\limits_{{v_j} \in N\left( {{v_h}} \right)} {{J_{hj}}\delta \left( {{\rm {new}},{s_j}} \right)} - \sum\limits_{{v_j} \in E\left( {{v_h}} \right)} {{J_{hj}}\delta \left( {{\rm {old}},{s_j}} \right)} =\\ \displaystyle \sum\limits_{{v_j} \in N\left( {{v_h}} \right)} {{J_{hj}}\left( {\delta \left( {{\rm {new}},{s_j}} \right) - \delta \left( {{\rm {old}},{s_j}} \right)} \right)} \end{array}$ |
上述推导表明,当个体ind在h位置变异后,新的适应值通过旧适应值加一个增量就可以得到,而这个增量只需要遍历vh的邻居节点就可以算出,这样计算一个个体的适应值的时间复杂度从O(m)降为O(davg),其中davg为平均度数。
基于定理1,计算新的适应值就可以简便为计算改变子集编号的节点与其邻居节点对适应值的“贡献”。具体分为两种情况:1)原本对适应值没有“贡献”的边,在改变基因之后对适应值有“贡献”;2)原本对适应值有“贡献”的边,在改变之后对适应值没有“贡献”。增量计算大大地降低了时间复杂度,在交叉算法中的增量计算只需循环若干次,而在变异算法中只需运行一次。
算法具体操作如算法3所示。算法第1行将increaseFitness设置为0,第2行是将c赋值为被改变基因所对应的节点的链表头结点,为了找到这个节点的所有邻居,之后遍历整个链表。算法第4 ~ 8行是在判断邻居为正邻居之后,再次判断如果邻居的基因与旧基因相同,但与新基因不同时,increaseFitness加2;如果邻居的基因与旧基因不同,但与新基因相同时,increaseFitness减2。算法第9 ~ 13行是在判断邻居为负邻居之后,再次判断如果邻居的基因与旧基因相同,但与新基因不同时,increaseFitness减2;如果邻居的基因与旧基因不同,但与新基因相同时,increaseFitness加2。
算法3 ncreaseFitness()算法
输入 需要计算适应值的个体individual,基因改变位置id,旧基因old,新基因new;
输出 增加的适应值increaseFitness。
1) increaseFitness=0;
2) c =Data.node[id].first;
3) 遍历节点id的所有邻居节点;
4) if (正邻居)
5) if(getGene(c.data)==old&&getGene(c.data)!=new)
6) increaseFitness= increaseFitness+2;
7) else if(getGene(c.data)!=old&&getGene(c.data)== new)
8) increaseFitness= increaseFitness-2;
9) else if(负邻居)
10) if(getGene(c.data)==old&&getGene (c.data) !=new)
11) increaseFitness= increaseFitness-2;
12) else if(getGene(c.data)!=old&&getGene (c.data) == new)
13) increaseFitness= increaseFitness+2;
2.7 复杂性分析在整个算法中,时间复杂度最高的是遗传操作这一部分,因此只分析这一部分的时间复杂度。首先定义几个基础概念,节点个数n、边个数m、种群规模M、锦标赛规模t以及迭代次数G。选择父本的时间复杂度是O(t)。交叉算法所花费的时间复杂度是O(n)。变异算子的时间复杂度是O(1)。计算适应值的时间复杂度分两种情况,若不用增量计算,计算适应值时要遍历整个网络的所有边,此时的时间复杂度是O(m)。如果使用增量计算的方式,在计算适应值时只需遍历网络中的若干条边。假设改变的是节点i的子集编号,而节点i的度数为di,则需遍历di条边。在网络中每个节点的度数是不相等的,因此用平均度davg来代表某一个节点的度最合理。所以此时的时间复杂度是O(davg)。总体算法的时间复杂度是O(MG(n+m))。
3 实验结果与分析 3.1 参数设置表1列出了WSB-EA算法中使用到的所有参数及其取值。算法的运行环境是Intel(R)Core(TM)i3-2330m,运行内存4 GB,操作系统Windows7旗舰版,使用的软件是eclipse4.5。
| 表 1 参数设置 Tab.1 Parameter setting |
本文使用的小型数据集有4个:斯洛文尼亚政党网络(SPP)、Gahuku-Gama部落网络(GGS)、社交圈网络(SC)和yeast网络(yeast)。
斯洛文尼亚政党网络:这是一个由斯洛文尼亚10个议会政党之间的关系组成的网络,1994年由一些研究政治的学者提出[16]。10个议会政党的英文名字缩写分别是SKD、ZLSD、SDSS、LDS、ZS-ESS、ZS、DS、SLS、SPS-SNS和SNS。这一网络中有10个节点,45条连边。
Gahuku-Gama部落网络[17]:这一网络中有16个节点,代表16个部落。边数为59,代表部落之间的联盟和对抗。
社交圈网络:这一网络是根据现实生活中人与人之间的关系得到的实际网络,节点有28个,边数为42,代表节点之间的朋友关系或敌人关系。
Yeast网络:这是一个酵母菌的基因调控网络[18],该网络包含690个节点和1 080条边。由于这一网络的节点个数较多,在实验中将种群规模增加到500。
为了验证WSB-EA算法的准确性以及健壮性,在这4个数据集上与孙一翔提出的Meme-SB算法和没有使用增量计算的WSB-EA算法的实验结果作对比分析。每一个数据集都做30次实验,记录求得最小适应值时的迭代次数和时间。实验结果如表2所示。同时,为了验证增量计算对算法的贡献,将WSB-EA算法与没有使用增量计算的WSB-EA算法进行时间比较,即得到迭代相同的次数所用的时间。结果如表3所示。
| 表 2 对比实验结果1 Tab.2 Comparison results 1 |
| 表 3 对比实验结果2 Tab.3 Comparison results 2 |
从表2可知,无论是只有10个节点的SPP网络还是有690个节点的yeast网络,在求得相同适应值的情况下,WSB-EA算法的迭代次数较少,也就说明WSB-EA算法能更快收敛到最优解。这也证明了,本文使用的锦标赛选择、单路交叉、单点变异和局部搜索这些遗传操作,不仅保证了算法的正确性,还加快了寻找最优解的速度。
从表3的实验结果可以看出,没有增量计算的WSB-EA算法的运行时间大大超过了有增量计算的WSB-EA算法。在规模比较小的SPP、GGS、SC网络上时间差距没有太大,因为这3个网络节点少,有无增量计算没有太大差别。但是当节点个数增加,在yeast网络上增量计算就体现出了优势。这也验证了本文提出的增量计算对与求解大型符号网络的弱不平衡度有很大的帮助。
接下来使用WSB-EA算法求得4个网络的弱不平衡度。在实验开始前无法获得k的取值,因此只能在实验之初先测试k的取值,即先取不同的k值,看哪一个k值在算法运行时的收敛效果好。做法是选取k值从3 ~ 20,每一个k值都做10次实验,迭代次数设置为50。比较最后适应值,适应值最小的k值就是最适合的k的取值。确定每一个网络的k的取值之后,对每个网络作30次实验,求解这个网络的弱不平衡性,实验结果如表4所示。由表2和表4中的适应值这一列可以看出,弱不平衡度值更小,也就说明,弱不平衡定理更适合真实符号网络,更具有现实意义。由表4中k的取值这一列可知,k的取值都不大,所以对于一个网络而言,在处于弱结构平衡时不会被划分成太多的阵营。
| 表 4 4种小型符号网络的弱不平衡度实验结果 Tab.4 The experimental results of unbalanced degree of four small signed networks |
本文使用的大型数据集有两个:Epinions网络[7]和Slashdot网络[7]。根据数据集的规模来修改迭代次数和种群规模这两个参数。由于数据集中节点个数太多,以及内存的限制,种群规模只能设置为200,所以很大程度地增大迭代次数,设置为10万次。
Epinions网络:Epinions网络是从Epinions获取的,Epinions网站是一般消费者评论网站,成立于1999年。游客可以对各种物品进行评价,也可以通过阅读各种物品的评价来帮助他们作出购买决策。该网络有131 828个节点,841 372条边。每条连边表示节点之间的信任关系。此数据集是有向网络,因此预处理数据时需将其改为无向网络,即将节点之间关系冲突的连边删除,例如节点1认可节点2评论,但节点2不认可节点1的评论,在预处理数据时要删除这样的连边。
Slashdot网络:Slashdot网络是从Slashdot网站获取的,Slashdot网站是一个资讯科技网站。它每天都会更新主页的新闻数次,网站使用者可以对公布在该站的新闻发表意见。该网络有81871个节点,545 671条边。预处理的方法与处理Epinions数据集方法一样。
在大型符号网络上,将WSB-EA算法与HRT-SB算法的实验结果进行比较。对于每一个数据集做30次实验,求解网络的弱不平衡度,实验结果如表5所示。表5中前3列由WSB-EA算法计算得出,最后一列数据由HRT-SB算法[19]得出。由表5可知,对于大型符号网络而言,即使节点个数有10万这么多,k的取值仍然不大。也就是说,无论这个网络有多大规模,划分的阵营个数都不会太多。由弱不平衡比可知,每一个网络中不平衡的边占很少一部分,整个网络是处于弱结构平衡的。由弱不平衡度和不平衡度这两列数据可以看出,弱不平衡度的值是远远小于不平衡度的值的,也说明了弱结构平衡定理相对于结构平衡定理来说,更适合研究符号网络的结构性质。
| 表 5 两种大型符号网络的弱不平衡度实验结果 Tab.5 The experimental results of unbalanced degree of two large signed network |
在符号网络中,结构平衡是一个很重要的研究领域,然而现实世界中存在的大多数网络都不是严格的结构平衡网络。因此研究网络的弱结构平衡性就显得尤为重要。在前人的基础上,本文提出了弱结构平衡定理的能量函数,利用进化算法的繁衍得到网络的弱不平衡度。通过大量的对比实验证明,本文提出的WSB-EA算法实验效果不错,且能更快得到最优解。然而,由于本文提出的算法是用来解决大型网络的,当网络节点太多的时候,想要找到最优解需要的时间太长,因此在未来的工作中可以继续改进算法的进化能力,让算法可以更快地找到最优解,及在后续工作中可以寻找WSB-EA算法的应用领域。例如,将晋商文化中的商帮当作节点,商帮之间的经济往来当作联系,将此组成晋商网络,分析网络中商帮之间的相互作用关系,以及如何达到一种稳定的发展态势,将这些信息整合,为现代企业发展提供参考。
| [1] |
程苏琦, 沈华伟, 张国清, 等. 符号网络研究综述[J]. 软件学报, 2014, 25(1): 1-15. CHENG Suqi, SHEN Huawei, ZHANG Guoqing, et al. Survey of signed network research[J]. Journal of software, 2014, 25(1): 1-15. (  0) 0)
|
| [2] |
蓝梦微, 李翠平, 王绍卿, 等. 符号社会网络中正负关系预测算法研究综述[J]. 计算机研究与发展, 2015, 52(2): 410-422. LAN Mengwei, LI Cuiping, WANG Shaoqing, et al. Survey of sign prediction algorithms in signed social networks[J]. Journal of computer research and development, 2015, 52(2): 410-422. (  0) 0)
|
| [3] |
AMARAL L A N, SCALA A, BARTHELEMY M, et al. Classes of behavior of small-world networks[J]. arXiv: cond-mat/0001458, 2000.
( 0) 0)
|
| [4] |
MOORE M. An international application of Heider’s balance theory[J]. European journal of social psychology, 1978, 8(3): 401-405. DOI:10.1002/(ISSN)1099-0992 ( 0) 0)
|
| [5] |
PARISIEN C, ANDERSON C H, ELIASMITH C. Solving the problem of negative synaptic weights in cortical models[J]. Neural computation, 2008, 20(6): 1473-1494. DOI:10.1162/neco.2008.07-06-295 ( 0) 0)
|
| [6] |
HEIDER F. Attitudes and cognitive organization[J]. The journal of psychology, 1946, 21(1): 107-112. DOI:10.1080/00223980.1946.9917275 ( 0) 0)
|
| [7] |
LESKOVEC J, HUTTENLOCHER D, KLEINBERG J. Signed networks in social media[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. Atlanta, USA, 2010: 1361–1370.
( 0) 0)
|
| [8] |
孙一翔. 基于进化算法的符号网络结构平衡分析[D]. 西安: 西安电子科技大学, 2014: 25–36. SUN Yixiang. Structural balance analysis in signed networks based on evolutionary algorithm[D]. Xi'an: Xidian University, 2014: 25–36. (  0) 0)
|
| [9] |
CARTWRIGHT D, HARARY F. Structural balance: a generalization of Heider’s theory[J]. Psychological review, 1956, 63(5): 277-293. DOI:10.1037/h0046049 ( 0) 0)
|
| [10] |
DAVIS J A. Clustering and structural balance in graphs[J]. Human relations, 1967, 20(2): 181-187. DOI:10.1177/001872676702000206 ( 0) 0)
|
| [11] |
FOGEL D B. An introduction to simulated evolutionary optimization[J]. IEEE transactions on neural networks, 1994, 5(1): 3-14. DOI:10.1109/72.265956 ( 0) 0)
|
| [12] |
FOGEL D B. Evolutionary algorithms in theory and practice[J]. Complexity, 1997, 2(4): 26-27. DOI:10.1002/(ISSN)1099-0526 ( 0) 0)
|
| [13] |
廖美英, 郭荷清, 张勇军. 一种整数编码的改进遗传算法[J]. 计算机工程与应用, 2003, 39(1): 103-105, 120. LIAO Meiying, GUO Heqing, ZHANG Yongjun. An ameliorative integer coded genetic algorithm[J]. Computer engineering and applications, 2003, 39(1): 103-105, 120. DOI:10.3321/j.issn:1002-8331.2003.01.034 (  0) 0)
|
| [14] |
邓琨, 张健沛, 杨静. 利用改进遗传算法进行复杂网络社团发现[J]. 哈尔滨工程大学学报, 2013, 34(11): 1438-1444. DENG Kun, ZHANG Jianpei, YANG Jing. Community detection in complex networks using an improved genetic algorithm[J]. Journal of Harbin engineering university, 2013, 34(11): 1438-1444. (  0) 0)
|
| [15] |
YANG Bo, CHEUNG W, LIU Jiming. Community mining from signed social networks[J]. IEEE transactions on knowledge and data engineering, 2007, 19(10): 1333-1348. DOI:10.1109/TKDE.2007.1061 ( 0) 0)
|
| [16] |
KROPIVNIK S, MRVAR A. An analysis of the slovene parliamentary parties network[M]//FERLIGOJ A, KRAMBERGER A. Developments in Statistics and Methodology. FDV, Ljubljana: Metodološki Zvezki, 1996.
( 0) 0)
|
| [17] |
READ K E. Cultures of the central highlands, new guinea[J]. Southwestern journal of anthropology, 1954, 10(1): 1-43. DOI:10.1086/soutjanth.10.1.3629074 ( 0) 0)
|
| [18] |
MILO R, SHEN-ORR S, ITZKOVITZ S, et al. Network motifs: simple building blocks of complex networks[J]. Science, 2002, 298(5594): 824-827. DOI:10.1126/science.298.5594.824 ( 0) 0)
|
| [19] |
FACCHETTI G, IACONO G, ALTAFINI C. Computing global structural balance in large-scale signed social networks[J]. Proceedings of the national academy of sciences of the United States of America, 2011, 108(52): 20953-20958. DOI:10.1073/pnas.1109521108 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13



