随着现代控制系统规模的不断扩大,系统的机械复杂度和环境复杂度越来越高,整个系统往往呈现出复杂的非线性和不确定性。不确定性的存在使得传统控制理论很难或者无法设计出满足性能要求的控制系统。近些年来,很多学者针对不确定系统设计了各种各样的控制系统[1-4],并取得了较好的效果。
滑模控制的基本原理是根据系统当前的状态有目的地改变系统的“结构”,使系统按照预定的“滑动模态”的状态轨迹运动,故称滑模控制是一种变结构控制。由于滑模控制具有“不变性”,当系统处于滑动模态运动状态时,系统动力学行为完全由设计的“滑动模态”决定,而与系统内部参数的不确定性和外部扰动无关,此时系统具有完全鲁棒性,使其在不确定系统的控制中得到广泛应用[5-7],并取得了较好的效果。但是滑模控制存在一个较为严重的缺点,就是当系统状态轨迹到达滑模面后,难以严格地沿着滑模面向平衡点移动,而是会在滑模面两侧来回穿越,即发生抖振。一方面,抖振的存在会很容易激发系统的未建模特性,从而使控制性能下降甚至导致系统发散;另一方面,抖振的存在对于控制系统的硬件也具有一定的损伤,导致控制系统的寿命大大缩短。对此,文献[8]利用BP神经网络的输出来调整离散指数趋近律中的到达速度常数和趋近速度指数;文献[9]针对板球系统,设计了一种基于蚁群的直接自适应模糊滑模控制器;文献[10]针对磁轴承系统,设计了一种自适应滑模控制器;文献[11]针对一类不确定系统,设计了一种将CMAC与滑模控制相结合的基于自组织小波CMAC的不确定非线性系统鲁棒自适应终端滑模控制。
本文针对一类不确定系统的跟踪控制问题,设计了一种将GBF-CMAC和滑模控制相结合的控制系统。利用符号函数和分层结构减少了神经网络所需存储器的数量,进一步提出了一种神经网络参数的自适应学习律。并将设计的控制器用于含有不确定性和欠驱动结构的高阶柔性直线系统的跟踪控制。
1 分层结构GBF-CMAC神经网络设计CMAC本质是一种基于表格查询技术的[12],局部连接的类感知器型联想记忆神经网络。由于CMAC具有局部连接、收敛速度快和逼近精度高等优点,所以在控制领域(尤其是机器人控制系统中)得到广泛应用[13-15]。其中Chiang等[16]将Albus提出的CMAC的常数型基函数推广到了一般类型的基函数,并引入了可微型基函数,GBF-CMAC即为其中一种。
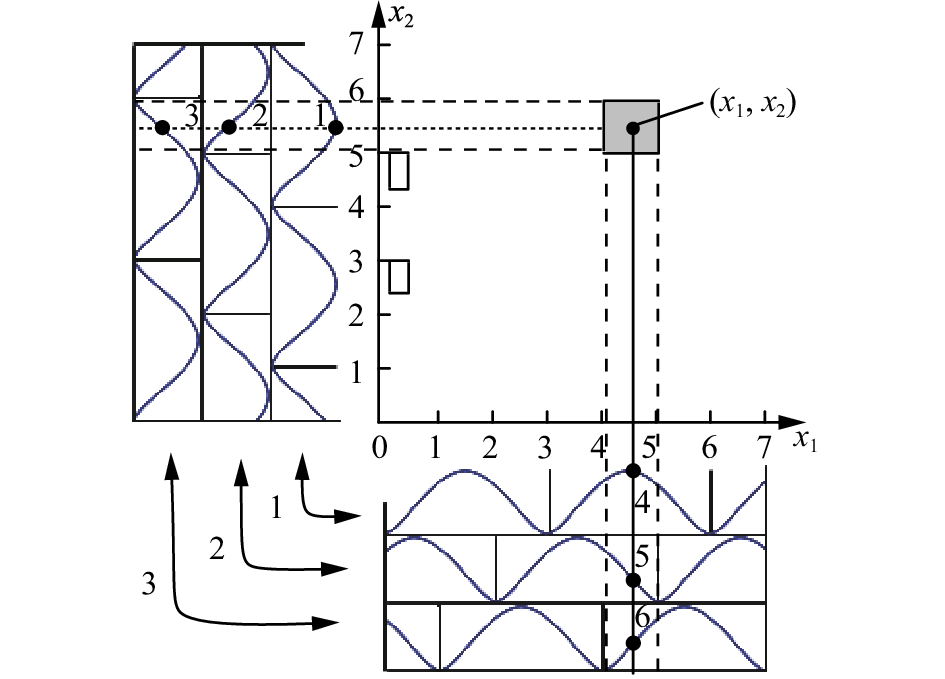
GBF-CMAC神经网络映射原理如图1所示,其中GBF-CMAC的基本参数为:输入维数
|
Download:
|
| 图 1 GBF-CMAC映射原理 Fig. 1 Mapping principle of GBF-CMAC | |
CMAC包含5层(输入层I、离散层S、联想层A、存储层M和输出层O)和4个映射(离散映射I→S、联想映射S→A、存储映射A→M和输出映射M→O)。4个映射过程进一步可以分为两部分。
1) 存储器寻址过程计算权值选择向量
2) 输出过程就是将
GBF-CMAC在传统CMAC的映射过程中附加了一个基函数的计算。基函数矩阵
| $b{({x_{\rm{I}}})_{{p_j}}} = \prod\limits_{k = 1}^n {\exp \left[\frac{{ - {{({x_{{\rm{I}},k}} - {\mu _{k,j,l_j^k}})}^2}}}{{\sigma _{k,j,l_j^k}^2}}\right]},\quad j = 1,2, \cdots ,{N_{\rm{e}}}$ | (1) |
式中:
GBF-CMAC的输出如式(2)所示:
| ${{y}} = {{a}}({{{x}}_{\rm{I}}}){{B}}({{{x}}_{\rm{I}}}){{w}}$ | (2) |
式中:
由上述可知,GBF-CMAC所需存储器的个数
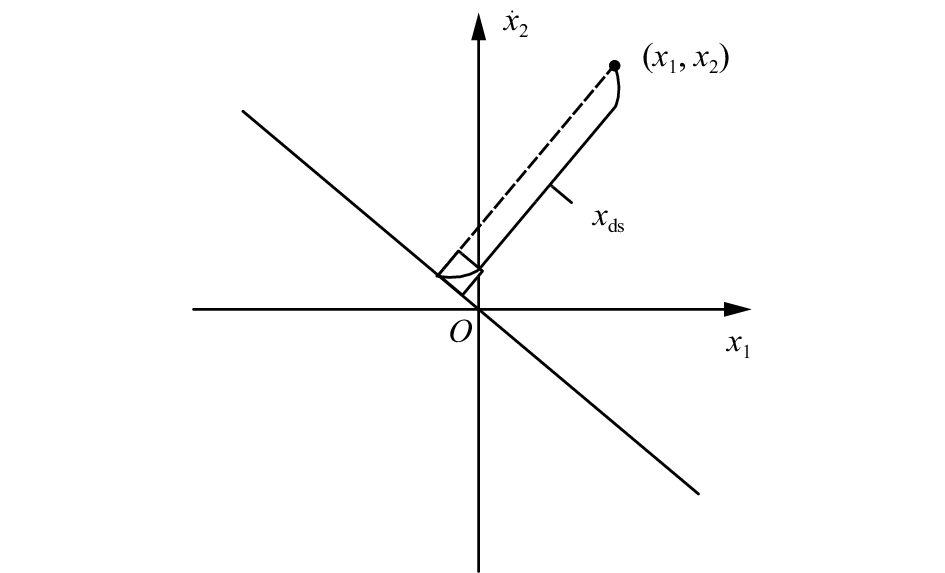
以二维输入为例,利用符号距离减少神经网络输入维数的原理如图2所示,过程为:
1) 若原网络的输入形如
2) 设过原点的直线为
| ${x_{{\rm{ds}}}} = \frac{{{x_1} + \lambda {x_2}}}{{\sqrt {1 + {\lambda ^2}} }}$ | (3) |
|
Download:
|
| 图 2 符号距离原理图 Fig. 2 Principle of signed distance | |
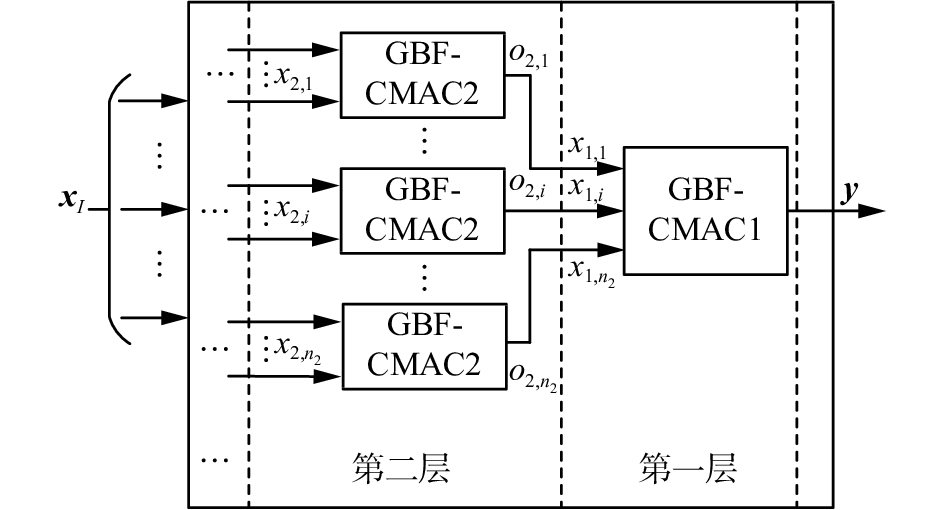
分层结构GBF-CMAC原理如图3所示。假设网络输入维数为
|
Download:
|
| 图 3 分层结构GBF-CMAC原理图 Fig. 3 Principle of hierarchical GBF-CMAC | |
分层结构GBF-CMAC学习过程的参数更新一般采用反向传播和梯度下降法[20-21]。在此基础上,本文提出了一种分层结构多GBF-CMAC的参数自适应学习律。不失一般性,现以输出维数
性能指标如式(4):
| $E = \frac{1}{2}{({y_{\rm{d}}} - y)^2}$ | (4) |
式中:
第一层GBF-CMAC的个数为
| $\begin{array}{c} \Delta {w_{{p_j}}} = - \displaystyle\frac{\alpha }{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}\frac{{\partial E}}{{\partial {w_{{p_j}}}}} = \\ -\displaystyle\frac{\alpha }{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}\frac{{\partial E}}{{\partial y}}\frac{{\partial {{y}}}}{{\partial {w_{{p_j}}}}} = \frac{{\alpha ({y_d} - {{y}})b{{({{{x}}_1})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}\end{array}$ | (5) |
| $\begin{array}{c}\Delta {\mu _{i,j,l_j^i}} = \displaystyle\frac{\partial }{{\partial {\mu _{i,j,l_j^i}}}}\left( {\frac{{\alpha ({y_{\rm{d}}} - y)b{{({{{x}}_1})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}} \right) = \\ \displaystyle\frac{{2\alpha ({y_d} - y)}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}\left( {1 - \frac{{{N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}} \right) \times \\ \exp \left[ {\displaystyle\frac{{ - {{({{{x}}_{1,i}} - {\mu _{i,j,l_j^i}})}^2}}}{{\sigma _{i,j,l_j^i}^2}}} \right]\left( {\displaystyle\frac{{{{{x}}_{1,i}} - {\mu _{i,j,l_j^i}}}}{{\sigma _{i,j,l_j^i}^2}}} \right)\end{array}$ | (6) |
| $\begin{array}{c}\Delta {\sigma _{i,j,l_j^i}} = \displaystyle\frac{\partial }{{\partial {\sigma _{i,j,l_j^i}}}}\frac{{\alpha ({y_{\rm{d}}} - y)b{{({{{x}}_1})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}=\\ \displaystyle\frac{{2\alpha ({y_{\rm{d}}} - y)}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}\left( {1 - \frac{{{N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_1})}_{{p_j}}}}}} \right) \times \\ \exp \left[ {\displaystyle\frac{{ - {{({{{x}}_{1,i}} - {\mu _{i,j,l_j^i}})}^2}}}{{\sigma _{i,j,l_j^i}^2}}} \right]\left( {\displaystyle\frac{{{{({{{x}}_{I,i}} - {\mu _{i,j,l_j^i}})}^2}}}{{\sigma _{i,j,l_j^i}^3}}} \right)\end{array}$ | (7) |
式中:
该层网络除了计算各参数的修正量外,还需要计算
| $ - \frac{{\partial E}}{{\partial {{{x}}_{1,i}}}} = \sum\limits_{j = 1}^{{N_{\rm{e}}}} {\left( {2{w_{{p_j}}}b{{({{{x}}_{1,i}})}_{{p_j}}}\frac{{{{{x}}_{1,i}} - {\mu _{i,j,l_j^i}}}}{{\sigma _{i,j,l_j^i}^2}}} \right)} = {\delta _{1,i}}$ | (8) |
式中:
第二层GBF-CMAC的个数为
| $\begin{aligned}\Delta {w_{{p_j}}} = - \displaystyle\frac{\alpha }{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\frac{{\partial E}}{{\partial {w_{{p_j}}}}} =\quad\quad\quad \\- \displaystyle\frac{\alpha }{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\frac{{\partial E}}{{\partial {o_{2,i}}}}\frac{{\partial {o_{2,i}}}}{{\partial {w_{{p_j}}}}} =\quad\quad\quad\;\; \\ - \displaystyle\frac{\alpha }{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\frac{{\partial E}}{{\partial {{{x}}_{1,i}}}}\frac{{\partial {o_{2,i}}}}{{\partial {w_{{p_j}}}}} = \frac{{\alpha {\delta _{1,i}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\end{aligned}$ | (9) |
| $\begin{array}{c}\Delta {\mu _{{f_i},j,l_j^{{f_i}}}} = \displaystyle\frac{\partial }{{\partial {\mu _{{f_i},j,l_j^{{f_i}}}}}}\left( {\frac{{\alpha {\delta _{1,i}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}} \right) =\\ \displaystyle\frac{{2\alpha {\delta _{1,i}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\left( {1 - \frac{{{N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}} \right) \times \\\exp \left[ {\displaystyle\frac{{ - {{({{{x}}_{2,i,{f_i}}} - {\mu _{{f_i},j,l_j^{{f_i}}}})}^2}}}{{\sigma _{{f_i},j,l_j^{{f_i}}}^2}}} \right]\left( {\displaystyle\frac{{{{{x}}_{2,i,{f_i}}} - {\mu _{{f_i},j,l_j^{{f_i}}}}}}{{\sigma _{{f_i},j,l_j^{{f_i}}}^2}}} \right)\end{array}$ | (10) |
| $\begin{array}{c}\Delta {\sigma _{{f_i},j,l_j^{{f_i}}}} = \displaystyle\frac{\partial }{{\partial {\sigma _{{f_i},j,l_j^{{f_i}}}}}}\left( {\frac{{\alpha {\delta _{1,i}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}} \right) =\\\displaystyle\frac{{2\alpha {\delta _{1,i}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}\left( {1 - \frac{{{N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}{{U + {N_{\rm{e}}}b{{({{{x}}_{2,i}})}_{{p_j}}}}}} \right) \times \\\exp \left[ {\displaystyle\frac{{ - {{({{{x}}_{2,i,{f_i}}} - {\mu _{{f_i},j,l_j^{{f_i}}}})}^2}}}{{\sigma _{{f_i},j,l_j^{{f_i}}}^2}}} \right]\left[ {\displaystyle\frac{{{{\left( {{{{x}}_{2,i,{f_i}}} - {\mu _{{f_i},j,l_j^{{f_i}}}}} \right)}^2}}}{{\sigma _{{f_i},j,l_j^{{f_i}}}^3}}} \right]\end{array}$ | (11) |
式中:
1)在分层结构多GBF-CMAC神经网络中,对于具有封闭性质的GBF-CMAC神经网络结构参数(
2)在分层结构的多GBF-CMAC神经网络中,对于具有开放性质的网络参数(输入变量和输出变量),对于每个GBF-CMAC都作了有区别的命名。分层结构的多GBF-CMAC神经网络整体:输入向量为
3)在分层结构多GBF-CMAC神经网络中,对于临时参数(存储器地址
4)在分层结构多GBF-CMAC神经网络中,由于本文只讨论两层结构GBF-CMAC的参数学习律,故
考虑如下形式的不确定系统:
| $\left\{\!\! {\begin{array}{*{20}{c}}{{\dot{ x}} = {{Ax}} + {{b}}u + {{{\tau }}_{\rm{d}}}}\\{{{y}} = {{Cx}}}\qquad\qquad\qquad\end{array}} \right.$ | (12) |
式中:
对上述不确定系统的输出跟踪控制问题,滑模控制器的设计如下。
1) 定义系统误差
从系统状态方程式(12)可知系统的状态向量包含两部分:第一部分为系统输出
| ${{e}} = {[{x_{{\rm{d,}}1}} - {x_1}\;{\dot x_{{\rm{d,}}1}} - {\dot x_1}\cdots {x_{{\rm{d,}}n}} - {x_n}\;{\dot x_{{\rm{d,}}n}} - {\dot x_n}]^{\rm{T}}}$ | (13) |
| $\dot {{e}} = {[{\dot x_{{\rm{d,}}1}} - {\dot x_1}\;{\ddot x_{{\rm{d,}}1}} - {\ddot x_1} \cdots {\dot x_{{\rm{d,}}n}} - {\dot x_n}\;{\ddot x_{{\rm{d,}}n}} - {\ddot x_n}]^{\rm{T}}}$ | (14) |
式中
2) 设计滑模面
为保证系统的输出跟踪满足一定的性能品质,设计的滑模面及其导数如式(15)、(16)所示:
| ${{s}}({{x}}) = {{\Lambda e}}$ | (15) |
| ${\dot{ s}}({{x}}) = {{\Lambda }}{\dot{ e}}$ | (16) |
式中:
3) 设计滑模控制器
滑模面的有限时间可达条件如式(17)所示:
| ${s_i}{\dot s_i} < - {k_i}{\rm{, }}\forall {k_i} > 0,\quad i = 1,2, \cdots ,2n$ | (17) |
采用等速趋近律设计的滑模控制器如式(18)所示:
| $\left\{\!\! {\begin{array}{*{20}{l}}{u = {{{b}}_{li}}{{v}} - {{{b}}_{li}}{{Ax}} }\\{{{v}} = {{{\dot{ x}}}_{\rm{d}}} + {{bk}}{\mathop{\rm sat}\nolimits} ({{s}}/\delta )}\end{array}} \right.$ | (18) |
式中:
| ${\rm{sat}}({{s}}/\delta ){\rm{ = }}\left\{\!\! {\begin{array}{l}{1,\quad \displaystyle\frac{{s}}\delta \geqslant 1}\\{{{s}}/\delta ,\quad - {\rm{1 < }}\displaystyle \frac{s}{\delta}< 1}\\{ - 1,\quad \displaystyle \frac{s}{\delta} \leqslant - 1}\end{array}} \right.$ | (19) |
采用积分类型的滑模面就可以构成积分滑模控制。针对上述不确定系统,设计的积分滑模面如式(20)所示。采用指数趋近律设计的积分滑模控制器如式(21)所示。
| ${{s}}({{x}}) = {{{x}}_{\rm{d}}} - \int_0^t {\left( {{\dot{ x}} - {{\varLambda }_{\rm{I}}}{{e}}} \right){\rm{d}}t} $ | (20) |
式中:
| $\left\{ {\begin{split}& {u = {{{b}}_{li}}{{v}} - {{{b}}_{li}}{{{\Lambda }}_{\rm{I}}}{{x}} }\\& {{{v}} = {{{\dot{ x}}}_{\rm{d}}} + {{{\Lambda }}_{\rm{I}}}{{e}} + {{b}}({{ps}} + {{{k}}_{\rm{I}}}{\rm{sat}}({{s}}/{\delta _{\rm{I}}}))}\end{split}} \right.$ | (21) |
式中 :
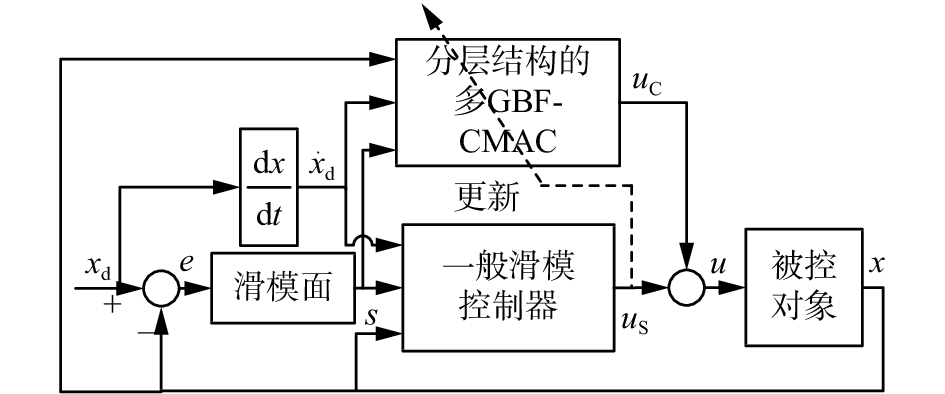
神经网络用于控制系统设计时,一种典型的结构是利用神经网络逼近非线性映射的能力,将神经网络与其他控制器并联组成复合控制器。针对上述不确定系统的输出控制问题,设计GBF-CMAC和滑模控制结合的控制系统结构如图4所示。
|
Download:
|
| 图 4 控制系统结构图 Fig. 4 Structure of control system | |
总控制量u(t)为式(22)所示:
| $u(t) = \gamma (t){u_{{S}}}(t) + (1 - \gamma (t)){u_{{C}}}(t)$ | (22) |
式中:
| $\gamma (t) = \left\{ {\begin{array}{*{20}{c}} \!\!\! {1, \; \; t < 2\,\,{\rm{s}}} \\ \!\!\! {0,\; \; t \geqslant 2\,\,{\rm{s}}} \end{array}} \right.$ | (23) |
将设计的控制系统用于高阶柔性直线系统的跟踪控制[22],实际系统如图5所示,系统状态空间表达式如式(24)所示。该系统是一种典型的欠驱动系统,其部分小车无法直接控制,而只能通过各个小车之间的耦合作用实现控制的目的。

|
Download:
|
| 图 5 高阶柔性直线系统 Fig. 5 High-order flexible linear system | |
| $\left\{ {\begin{aligned}& {{\dot{ x}}(t) = {{Ax}}(t) + {{b}}u(t) + {{{\tau }}_{\rm{d}}}(t)}\\& {{{y}}(t) = {{Cx}}(t)}\end{aligned}} \right.$ | (24) |
式中:
| ${\tau _i} = \exp \left[ { - {{\left( {\frac{{t - 5}}{{0.2}}} \right)}^2}} \right], \quad i = 1,2, \cdots ,6$ | (25) |
| ${{A}} = \left[ {\begin{array}{*{20}{r}} {0}\;\;\;\;&1&{ 0 }\;\;\;\;&{ 0}&0\;\;\;\;&{ 0}\;\;\;\;\;\;\; \\ { - 213.0 }&0&{140.8}&0&{ 0}\;\;\;\;&0\;\;\;\;\;\;\; \\ 0\;\;\;\;&{ 0} &{ 0}\;\;\;\;&{ 1}&0\;\;\;\;&0 \;\;\;\;\;\;\;\\ {150.6 }&{0 }&{ - 301.2 }&{ 0}&{ 150.6 }&{ 0} \;\;\;\;\;\;\;\\ 0\;\;\;\;&0&{0 }\;\;\;\;&0&{ 0}\;\;\;\;&{ 1} \;\;\;\;\;\;\;\\ { 0}\;\;\;\;&{ 0 }&{150.6}&0&{ - 150.6}&{ - 3.94} \end{array}} \right]$ |
| ${{b}} = {\left[ {\begin{array}{*{20}{c}} 0&{4600}&0&0&0&0 \end{array}} \right]^{\rm{T}}}$ |
| ${{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&0&1&0&0&0 \\ 0&0&0&0&1&0 \end{array}} \right]$ |
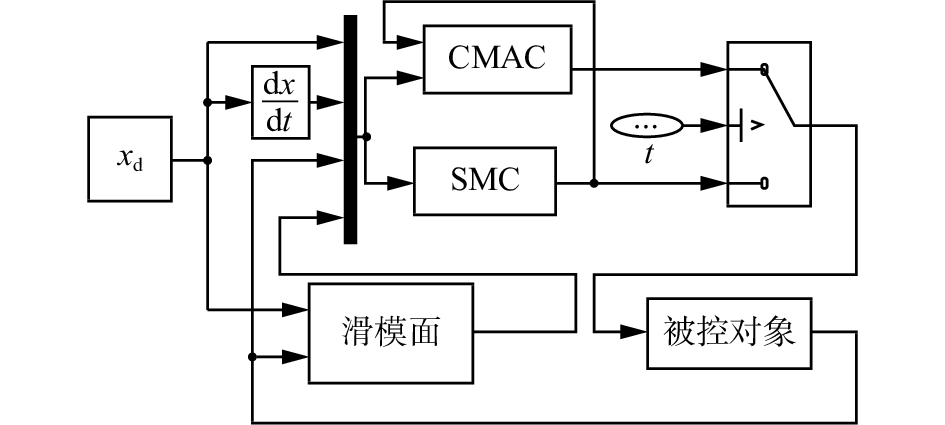
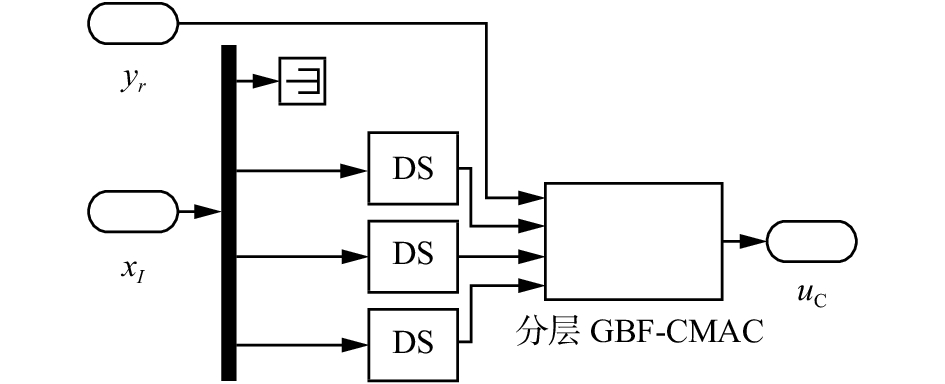
跟踪控制系统MATLAB/SIMULINK仿真图如图6~8所示。图6为控制系统总体结构图;图7所示为滑模面计算子系统,其中利用一个切换开关可以实现一般滑模面和积分滑模面之间的切换;图8为GBF-CMAC子系统,包括符号函数计算部分和分层GBF-CMAC两部分。
|
Download:
|
| 图 6 控制系统总体仿真结构图 Fig. 6 Simulation of control system | |

|
Download:
|
| 图 7 滑模面计算图 Fig. 7 Calculation of sliding surface | |
|
Download:
|
| 图 8 高斯基函数小脑模型关节控制器 Fig. 8 GBF-CMAC | |
仿真控制参数为:仿真时间
一般滑模控制器的参数设置为
传统CMAC的参数设为
GBF-CMAC部分首先利用符号函数将18维输入变成9维输入,然后利用4个GBF-CMAC构成两层结构,其参数设置为:
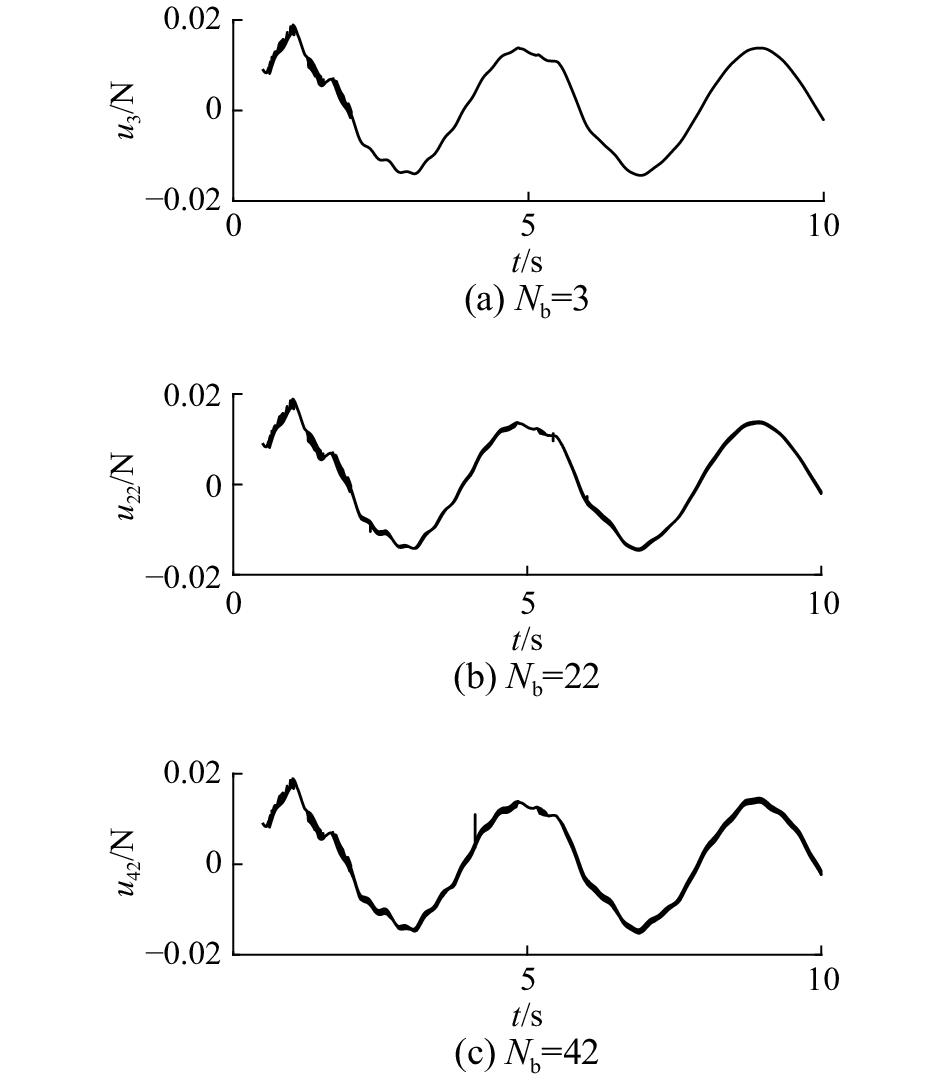
1) 复合控制器中神经网络不同分块数(3、22、42)下控制效果对比实验
|
Download:
|
| 图 9 3种控制器输出对比 Fig. 9 Output contrast of three controllers | |

|
Download:
|
| 图 10 3种控制器跟踪误差 Fig. 10 Tracking error of three controllers | |
综合图9和图10可以看出,神经网络的参数
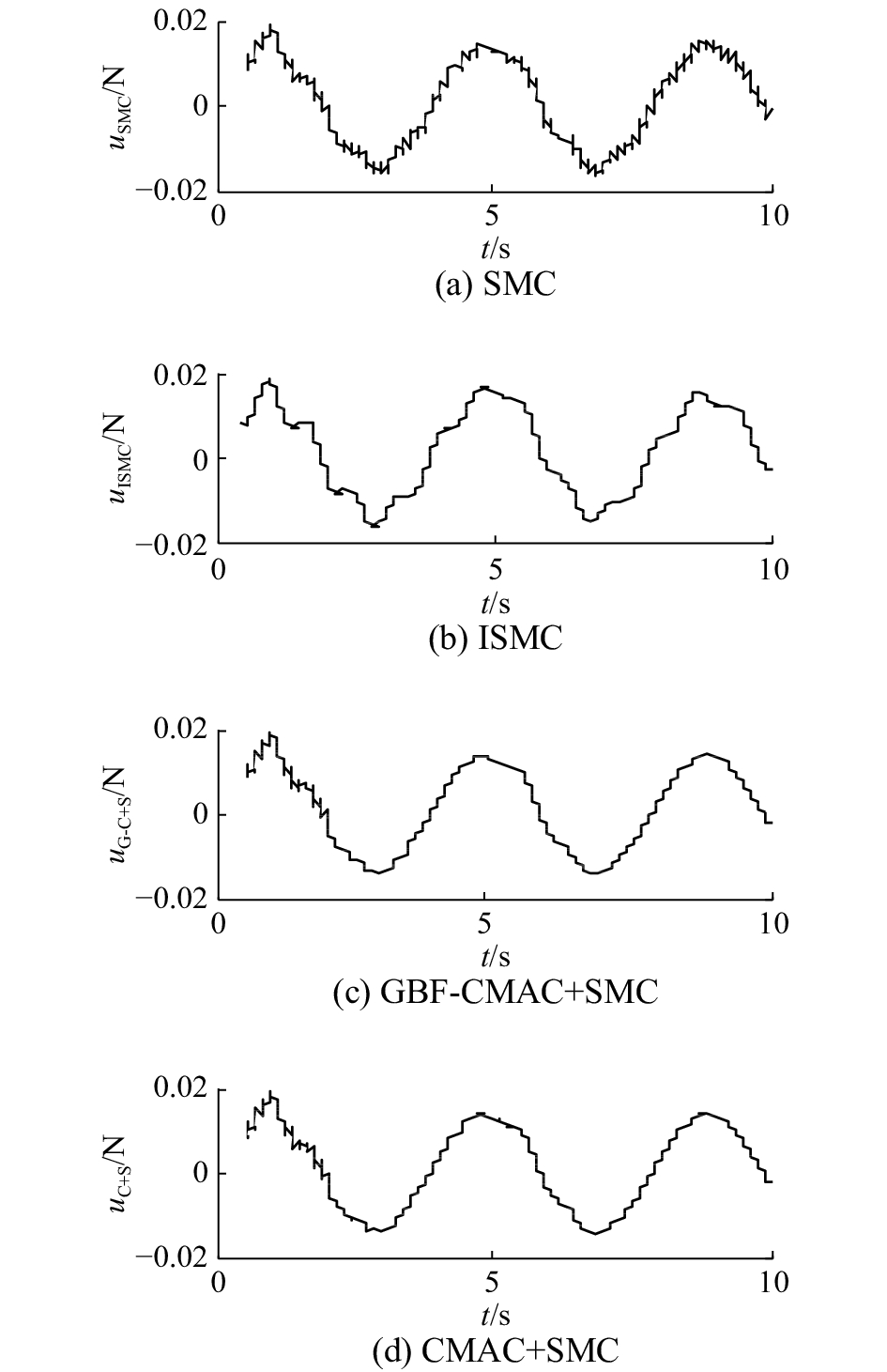
2) 一般滑模控制、积分滑模控制、传统CMAC复合控制和改进GBF-CMAC复合控制对比实验
|
Download:
|
| 图 11 4种控制器输出对比 Fig. 11 Output contrast of four controller | |
|
Download:
|
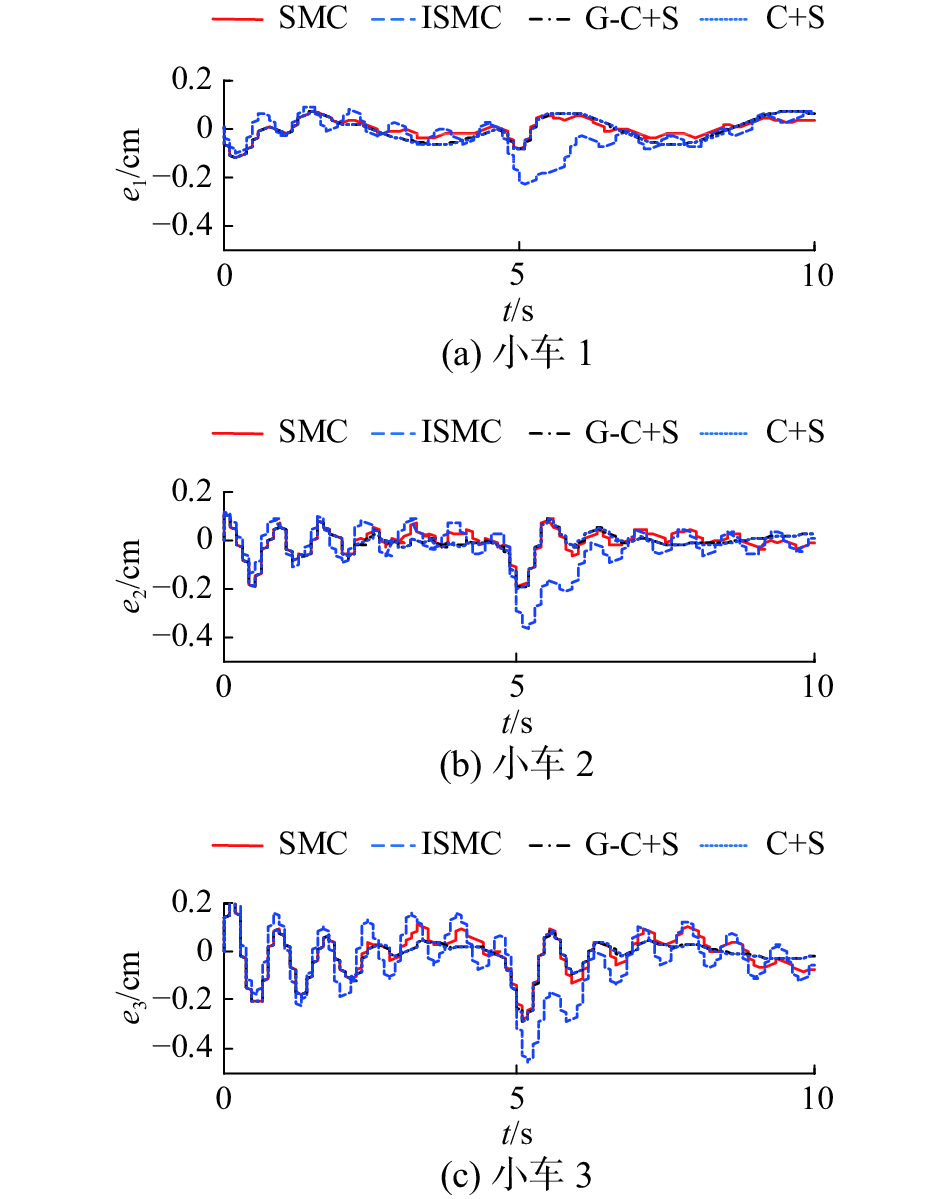
| 图 12 4种控制器跟踪误差 Fig. 12 Tracking error of four controllers | |
从图11和图12可以看出,一般滑模控制抖振程度最大;积分滑模控制抖振程度小,但鲁棒性和跟踪精度最差;本文设计的改进GBF-CMAC复合控制器,不仅抖振基本消除,而且具有较好的鲁棒性,同时输出跟踪精度要比一般滑模控制、积分滑模控制和传统CMAC复合控制器好。
4 结束语针对一类不确定系统,设计了将GBF-CMAC与滑模控制结合的复合控制器,采用符号函数和分层结构减少了GBF-CMAC所需存储器的数量,提出了一种分层结构多GBF-CMAC参数的自适应学习律。并将设计的复合控制器应用于高阶柔性直线系统的输出跟踪控制中。从实验结果可以看出,本文所提的复合控制器不仅具有较好的鲁棒性,并基本消除抖振现象,而且跟踪精度比一般滑模控制和积分滑模控制要好。此外,结果显示可以通过调节复合控制器中神经网络的参数对控制系统抖振程度、鲁棒性和跟踪精度进行调节,从而可以在抖振程度、鲁棒性和跟踪精度之间进行最优选择。
| [1] |
梁涛年, 陈建军. 分数阶参数不确定系统的PIλ控制器
[J]. 控制理论与应用, 2011, 28(3): 400-406. LIANG Taonian, CHEN Jianjun. Design of fractional order PIλ controller for fractional order systems with uncertain parameters [J]. Control theory & applications, 2011, 28(3): 400-406. (  0) 0)
|
| [2] |
叶思隽, 王新民, 张清江, 等. 不确定系统混合H2/H∞鲁棒控制的直接迭代LMI方法
[J]. 控制理论与应用, 2011, 28(2): 247-255. YE Sijun, WANG Xinmin, ZHANG Qingjiang, et al. Direct iterative LMI-based approach of mixed H-two/H-infinity robust control for uncertain systems[J]. Control theory & applications, 2011, 28(2): 247-255. (  0) 0)
|
| [3] |
齐丽强, 孙明轩, 管海娃. 非参数不确定系统的有限时间迭代学习控制[J]. 自动化学报, 2013, 40(7): 1320-1327. QI LiQiang, SUN MingXuan, GUAN HaiWa. Finite-time iterative learning control for systems with nonparametric uncertainties[J]. Acta automatica sinica, 2013, 40(7): 1320-1327. (  0) 0)
|
| [4] |
于靖, 陈谋, 姜长生. 基于干扰观测器的非线性不确定系统自适应滑模控制[J]. 控制理论与应用, 2014, 31(8): 993-999. YU Jing, CHEN Mou, JIANG Changsheng, Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer[J]. Control theory & applications, 2014, 31(8): 993-999. (  0) 0)
|
| [5] |
王琦, 陈龙胜. 非仿射纯反馈不确定系统预设性能鲁棒自适应控制[J]. 电机与控制学报, 2017, 21(2): 109-116. WANG Qi, CHEN Longsheng. Prescribed performance adaptive robust control for a class of uncertain non-affine pure feedback system[J]. Electric machines and control, 2017, 21(2): 109-116. (  0) 0)
|
| [6] |
王艳敏, 冯勇, 夏红伟, 等. 多输入不确定系统的平滑非奇异终端滑模控制[J]. 控制与决策, 2015, 30(1): 161-165. WANG Yanmin, FENG Yong, XIA Hongwei, et al. Smooth nonsingular terminal sliding mode control of uncertain multi-input systems[J]. Control and decision, 2015, 30(1): 161-165. (  0) 0)
|
| [7] |
胡盛斌. 非线性多关节机械人系统滑模控制[M]. 北京: 国防工业出版社, 2015.
( 0) 0)
|
| [8] |
姚灵灵, 贺乃宝, 高倩, 等. 四旋翼偏航系统的优化神经网络滑模控制[J]. 机械设计与制造, 2016(10): 147-150. YAO Lingling, HE Naibao, GAO Qian, et al. Optimized neural network sliding mode control for the yaw system associated with quad-rotor[J]. Machinery design & manufacture, 2016(10): 147-150. DOI:10.3969/j.issn.1001-3997.2016.10.038 (  0) 0)
|
| [9] |
翟晨汐, 李洪兴. 板球系统的直接自适应模糊滑模控制[J]. 计算机仿真, 2016, 33(2): 383-388, 432. ZHAI Chenxi, LI Hongxing. Direct adaptive fuzzy sliding-mode control for ball and plate system[J]. Computer simulation, 2016, 33(2): 383-388, 432. DOI:10.3969/j.issn.1006-9348.2016.02.080 (  0) 0)
|
| [10] |
楼晓春, 吴国庆. 主动磁轴承系统的自适应滑模控制[J]. 电工技术学报, 2012, 27(1): 142-147. LOU Xiaochun, WU Guoqing. Adaptive sliding mode control for an active magnetic bearing system[J]. Transactions of China electrotechnical society, 2012, 27(1): 142-147. (  0) 0)
|
| [11] |
张强, 于宏亮, 许德智, 等. 基于自组织小波小脑模型关节控制器的不确定非线性系统鲁棒自适应终端滑模控制[J]. 控制理论与应用, 2016, 33(3): 387-397. ZHANG Qiang, YU Hongliang, XU Dezhi, et al. A robust adaptive integral terminal sliding mode control for uncertain nonlinear systems using self-organizing wavelet cerebella model articulation controller[J]. Control theory & applications, 2016, 33(3): 387-397. (  0) 0)
|
| [12] |
ALBUS J S. Data storage in the cerebellar model articulation controller (CMAC)[J]. Journal of dynamic systems, measurement, and control, 1975, 97(3): 228-233. DOI:10.1115/1.3426923 ( 0) 0)
|
| [13] |
鲍春雷, 王斌锐, 金英连, 等. 气动肌肉关节的无模型自适应CMAC迟滞补偿控制[J]. 机器人, 2015, 37(3): 298-303, 309. BAO Chunlei, WANG Binrui, JIN Yinglian, et al. Model free adaptive CMAC hysteresis compensation control of the pneumatic muscle joint[J]. Robot, 2015, 37(3): 298-303, 309. (  0) 0)
|
| [14] |
LIN C M, LI H Y. Intelligent control using the wavelet fuzzy CMAC backstepping control system for two-axis linear piezoelectric ceramic motor drive systems[J]. IEEE transactions on fuzzy systems, 2014, 22(4): 791-802. DOI:10.1109/TFUZZ.2013.2272648 ( 0) 0)
|
| [15] |
ZHANG Ping, LIU Xin, DU Guanglong. Online robot auto-calibration using IMU with CMAC and EKF[C]//Proceedings of 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems. Shenyang China, 2015.
( 0) 0)
|
| [16] |
CHIANG C T, LIN C S. CMAC with general basis functions[J]. Neural networks, 1996, 9(7): 1199-1211. DOI:10.1016/0893-6080(96)00132-3 ( 0) 0)
|
| [17] |
YEH M F. Single-input CMAC control system[J]. Neurocomputing, 2007, 70(16/17/18): 2638-2644. ( 0) 0)
|
| [18] |
RODRÍGUEZ F O, DE JESÚS RUBIO J, GASPAR C R M, et al. Hierarchical fuzzy CMAC control for nonlinear systems[J]. Neural computing and applications, 2013, 23(1): 323-331. ( 0) 0)
|
| [19] |
YU Wen, RODRIGUEZ F O, MORENO-ARMENDARIZ M A. Hierarchical fuzzy CMAC for nonlinear systems modeling[J]. IEEE transactions on fuzzy systems, 2008, 16(5): 1302-1314. DOI:10.1109/TFUZZ.2008.926579 ( 0) 0)
|
| [20] |
段培永, 邵惠鹤. 基于广义基函数的CMAC学习算法的改进及收敛性分析[J]. 自动化学报, 1999, 25(2): 258-263. DUAN Peiyong, SHAO Huihe. Improved algorithm of CMAC with general basis function and its convergence analysis[J]. Acta automatica sinica, 1999, 25(2): 258-263. (  0) 0)
|
| [21] |
NGO T Q, PHUONG T V. Robust adaptive self-organizing wavelet fuzzy CMAC tracking control for de-icing robot manipulator[J]. International journal of computers communications & control, 2015, 10(4): 567-578. ( 0) 0)
|
| [22] |
M210使用手册[M]. 美国: 易希普公司, 2014.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


