近几十年来，博弈论得到了许多研究人员的关注，逐渐成为了经济学中的标准分析工具之一，并且在经济学、军事科学和其他社会科学中得到了广泛的应用。在博弈问题中，非合作博弈纳什均衡是其最核心的研究内容。1951年，Nash^[1]在提出的“纳什定理”中揭示并证明了纳什均衡解的存在，但是Nash并没有给出求解纳什均衡的一般性方法。传统的求解方法如Lemke-Howson算法^[2]、牛顿算法^[3]、同伦算法^[4]等均存在一定的局限性；特别是对于高维的博弈模型(如3维及以上的矩阵策略)，传统算法的计算复杂求解成本较高。除了传统的优化方法，许多学者还利用遗传算法^[5]、免疫算法^[6]、粒子群算法^[7]、蚁群算法^[8]等启发式算法来求解博弈纳什均衡问题，这为求解非合作博弈问题提供了一种新的有效途径和方法。

教与学优化算法(teaching-learning-based optimization，TLBO)是Rao等^[9-10]于2011年提出，它是一种模拟教师教学与学生学习的群体智能优化算法。由于该算法参数设置少、操作简便、寻优性能好，引起了国内外学者的重视。目前它已被成功应用于各个领域，如LQR控制器优化设计^[11]、热交换器优化设计^[12]、人工神经网络优化^[13]等。

一般来说，原始的TLBO算法容易出现“早熟收敛”的现象，从而易于陷入局部最优。为了提高TLBO算法的寻优性能，很多学者提出了改进算法。比如，Rao等^[14]提出了ETLBO算法，该算法将精英策略引入TLBO算法中，保留每代中的最优解，并随机对精英个体进行变异操作，其主要目的是提高算法的收敛速度和寻优精度；Yu等^[15]提出了ITLBO算法，该算法在TLBO算法中引入教学反馈阶段和差分算法中的交叉变异策略，并在算法后期加入混沌扰动机制；Zou等^[16]提出了DGSTLBO算法，该算法在教学阶段引入动态分组教学策略，在学习阶段加入量子行为策略，以增加种群的多样性和避免算法早熟收敛；Chen等^[17]提出了VTTLBO算法，该算法将种群的数量以先增后减的方式来进行动态调整。在种群数量增加阶段利用高斯分布生成个体，并在减少阶段进行相同个体的去重操作，其主要目的是减少计算成本以及增强算法的收敛精度和速度。Wu等^[18]提出了NIWTLBO算法，在该算法中，利用非线性惯性权重因子来控制个体的学习速率，同时使用动态惯性权重因子代替原有随机数，仿真结果表明此改进策略提高了算法的收敛速率和寻优性能。Shahbeig等^[19]提出了TLBO-PSO算法，该算法将改进的变异模糊自适应的PSO算法与TLBO算法进行结合，目的在于提高算法的寻优精度从而解决多目标优化问题。上述研究结果均表明，将改进策略引入TLBO算法中可以提高算法的寻优性能。

为了能更进一步提高TLBO的搜索性能，本文提出一种基于混沌搜索和权重学习的教与学优化(TLBO-CSWL)算法。仿真结果表明，所提算法的整体优化性能明显优于其他所比较的算法。最后，将改进的算法应用于非合作博弈纳什均衡问题的求解。

1 预备知识 1.1 标准的教与学优化算法

标准TLBO算法^[9-10]主要包括两个阶段，教学阶段与学习阶段。

1.1.1 教学阶段

${{{X}}_i} = ({x_{i,1}},{x_{i,2}}, \cdots ,{x_{i,D}}),{i = 1,2, \cdots ,{\rm{NP}}}$ ，表示第i个个体，其中，D为优化问题的维数，NP表示种群规模。种群的平均值表示为 ${{{X}}_{{\rm{mean}}}} = \sum\limits_{i = 1}^{{\rm{NP}}} {{{{X}}_i}} /{\rm{NP}}$ ，其中当前适应度值最好的个体被选为教师，即X_teacher。在教学阶段，每个个体基于教师与种群的平均值之差进行学习。新的个体更新公式为

${{{X}}_{i,{\rm{new}}}} = {{{X}}_{i,{\rm{old}}}} + r \cdot \left( {{{{X}}_{{\rm{teacher}}}} - {T_F} \cdot {{{X}}_{{\rm{mean}}}}} \right)$

(1)

式中：X_{i, old}表示第i个个体学习之前的个体； $r$ 为[0, 1]之间的均匀随机数，表示学习步长；T_F=round[1+rand(0, 1)]，取值1或2，表示教学因子。若X_{i, new}的适应度值优于X_{i, old}，则更新个体；否则，不更新。

1.1.2 学习阶段

在TLBO算法的学习阶段中，个体的更新公式为

$\left\{ \begin{array}{l}{{{X}}_{p,{\rm{new}}}} = {{{X}}_{p,{\rm{old}}}} + r \cdot \left( {{{{X}}_p} - {{{X}}_l}} \right),\quad\;\;f\left( {{{{X}}_p}} \right) < f\left( {{{{X}}_l}} \right) \\ \\{{{X}}_{p,{\rm{new}}}} = {{{X}}_{p{\rm{,old}}}} + r \cdot \left( {{{{X}}_l} - {{{X}}_p}} \right),\quad\;\;f\left( {{{{X}}_l}} \right) < f\left( {{{{X}}_p}} \right)\\ \end{array} \right.$

(2)

式中：p≠l, $p,\;l \in \left( {1,2, \cdots ,{\rm{NP}}} \right)$ ；f (X)为适应度函数。若X_{p, new}的适应度值优于X_p,old，则更新个体；否则，不更新。

1.2 混沌映射

混沌是指确定性动力学系统产生的一种不可预测的、类似随机性的运动，最显著的特点是初值敏感性。混沌模型不仅具有随机性、初值敏感性，同时还有一个很重要的性质是遍历性。由于混沌序列是遍历的，它已被越来越多地应用到智能优化算法中。其主要被用来初始化种群^[20]，以及能够对个体进行随机次数的扰动使其跳出局部最优^[21]，从而在个体周围进行遍历搜索。借鉴文献[21]中的混沌扰动策略，所提算法利用Logistics搜索策略来对个体进行更新，公式为

${x_{{\rm{new}}}} = {x_{{\rm{old}}}} \cdot \mu \cdot \left( {1 - {x_{{\rm{old}}}}} \right)$

(3)

式中：x_old和x_new分别表示混沌映射之前和混沌映射之后的变量，x∈[0, 1]; $\mu $ ∈[0, 4]为控制参数，当 $\mu $ =4时，Logistics映射将处于完全混沌状态。

2 基于混沌搜索和权重学习的教与学优化算法 2.1 权重学习

在原始的TLBO算法中，教学阶段主要是使用当前最佳个体来指导种群进化，这将会造成算法陷入局部最优。因此，本文提出一种权重学习的策略，基于个体适应度值产生一个可以代表种群适应度水平的综合个体X_weight，并且引导其他个体向其学习。这可以缓解算法“早熟”现象的发生。

1) 计算种群的最大适应度值及每个个体的权重

${f_{\max }} = \max \left( {f\left( {{{{X}}_i}} \right)} \right)$

(4)

${{{w}}_i} = \frac{{\left| {f\left( {{{{X}}_i}} \right) - {f_{\max }}} \right|}}{{\displaystyle\sum\limits_{i = 1}^{{\rm{NP}}} {\left| {f\left( {{{{X}}_i}} \right) - {f_{\max }}} \right|} }}$

(5)

2) 计算加权平均个体

${{{x}}_{{\rm{weight}},j}} = \sum\limits_{i = 1}^{{\rm{NP}}} {{{{w}}_i} \times } {{{x}}_{i,j}}, \quad{j = 1,2, \cdots ,D} $

(6)

3) 改进后的教学阶段更新公式为

$\begin{aligned}{{{X}}_{i,{\rm{new}}}} = &{{{X}}_{i,{\rm{old}}}} + r \cdot \left( {{{{X}}_{{\rm{teacher}}}} - {T_F} \cdot {{{X}}_{{\rm{mean}}}}} \right) +\\ & r \cdot \left( {{{{X}}_{{\rm{weight}}}} - {{{X}}_{i,{\rm{old}}}}} \right)\end{aligned}$

(7)

式中r =N(0.5, 0.2)。若X_{i, new}的适应度值优于X_{i, old}, 则更新个体；否则，不更新。

2.2 混沌搜索

为了提高TLBO算法的全局搜索能力，将混沌搜索策略加入到该算法中。混沌搜索的执行步骤如下：

1) 对种群中的所有个体进行适应度值降序排列(最小化问题)；

2) 随机取出一个排名前10的个体；

3) 利用式(3)对选择的个体进行混沌扰动，产生混沌个体X_chaos；

4)若X_chaos的适应度值优于X_i，则更新个体；否则，不更新。

2.3 TLBO-CSWL算法的实现步骤

1) 初始化：设定种群大小NP，维数D，最大评价次数，初始化种群。

2) 教学阶段：根据式(7)对个体进行更新。

3) 学习阶段：利用正态分布随机数代替式(2)的均匀随机数，然后根据式(2)对个体进行更新。

4) 混沌搜索：利用2.2部分随机对个体进行混沌扰动操作，并更新个体。

5) 判定程序是否达到最大评价次数，若没有达到，则转至2)；如达到，则执行6)。

6) 输出最优解。

3 仿真测试

为验证TLBO-CSWL算法的有效性，本文选取了文献[17]中的18个测试函数，其中f₁~f₅为单峰函数，f₆~f₁₀为多峰函数，f₁₁~f₁₈为旋转函数。改进算法分别与jDE^[22]、SaDE^[23]、PSOwFIPS^[24]、CLPSO^[25]、TLBO^[9-10]、ETLBO^[14]、VTTLBO^[17]等算法进行对比。根据文献[17]的设定, 最大的函数评价次数均为50 000。对于每个测试函数，所有算法均独立运行30次。为了保证结论的可靠性，采用Friedman^[26]、Dunn^[27]、Holm和 Hochberg^[28]检验来对结果进行统计分析，其中，显著水平设定为5%。

3.1 TLBO-CSWL算法与其他算法的比较 3.1.1 与其他算法在10维测试上的比较

在该实验中，所有算法的种群规模设定为30，仿真结果如表1所示。由表1可知，TLBO-CSWL在函数f₁、f₂、f₃、f₄、f₆、f₁₁、f₁₂、f₁₄、f₁₅、f₁₇上均有很好的寻优效果，性能明显优于其他所比较算法。但在函数f₅、f₁₀、f₁₃、f₁₈上，所有其他算法的寻优性能都略优于TLBO-CSWL算法，其主要原因有两个方面：1)虽然所提算法使用正态分布和权重学习来提高原始TLBO的搜索效率，但在某种程度上却降低了算法的全局搜索能力；2)每种算法都有自身的寻优特性，到目前为止，没有一种算法能够在所有的测试函数上都能表现得最好，因此，所提算法在某些测试函数上表现的差，也符合没有免费午餐定理^[29]。而对于其余测试函数，TLBO-CSWL所获得的结果与所比较算法中获得的最好结果相同。同时，利用非参数的统计方法来对实验结果进行分析，所得结果见表2、3所示。从表2可知，TLBO-CSWL算法的整体性能是最好的。从表3可以看出，所提算法的整体性能要显著好于PSOwFIPS算法和CLPSO算法。另外，虽然TLBO-CSWL的整体性能在统计意义上没有显著好于SaDE、ETLBO、TLBO、jDE、VTTLBO，但是从结果来看，所提算法的整体性能优于其他算法。

3.1.2 与其他算法在30维测试上的比较

在该实验中，所有算法的种群规模设定为40。仿真结果见表4，从表4可以看出本文算法获得的平均结果在f₁、f₂、f₃、f₄、f₆、f₇、f₁₁、f₁₂、f₁₄、f₁₅上均明显优于其他所比较算法。对于函数f₅，除了CLPSO外，其他比较算法的整体性能都要好于TLBO-CSWL。对于函数f₁₀，从结果来看，TLBO及其改进算法的性能比改进的差分进化算法差，这主要是由算法的本身搜索特性所决定的。对于函数f₁₃，虽然TLBO-CSWL的性能比jDE、SaDE和PSOwFIPS差，但比CLPSO和TLBO及其改进算法要好。对于函数f₁₈，TLBO-CSWL的性能表现要比其他所比较算法差，其主要原因可能是所提方法虽然可以加快TLBO的收敛速度，但也损失了算法一部分全局搜索的能力。在其余测试函数中，TLBO-CSWL的寻优结果与所比较算法中获得的最好的结果相同。统计分析结果见表5和表6。由表5可知，本文所提出的TLBO-CSWL算法与其他算法相比具有优越的整体性能。由表6可知，TLBO-CSWL算法的性能要显著性优于PSOwFIPS算法和CLPSO算法。此外，虽然TLBO-CSWL的寻优性能在统计学意义上没有显著性地优于其他比较算法，但是结合以上分析可知，TLBO-CSWL算法在解决18个测试函数问题上整体表现得最好。

3.2 TLBO-CSWL算法分析

为了验证所提算法的有效性，利用18个30维测试函数来对TLBO-CSWL和它的变种算法TLBO-CSWL-1(使用均匀随机数)、TLBO-CSWL-2(没有混沌搜索)进行测试。其中，种群规模设定为40，最大评价次数50 000。针对每个测试函数，每个算法均独立运行30次。同时，利用Friedman、Bonfeeroni-Dunn、Holm以及Hochberg检验等非参数的统计方法对结果进行统计分析，其中显著性水平设定为5%。

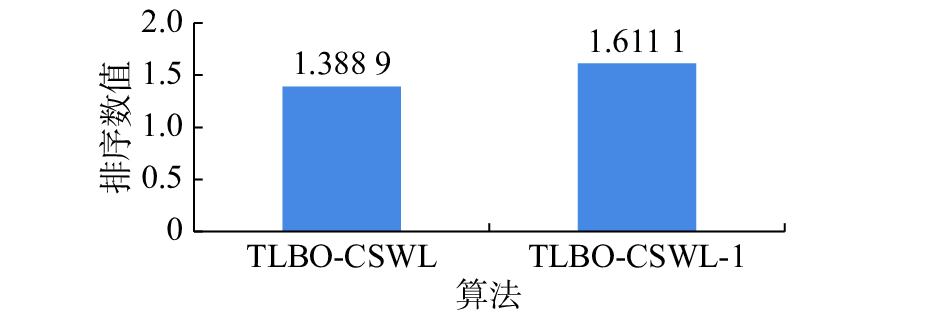
3.2.1 与变种算法TLBO-CSWL-1的比较

为了验证策略正态随机数的有效性，将对TLBO-CSWL-1与TLBO-CSWL进行仿真测试。结果见表7。由表7可知，TLBO-CSWL算法所得到的平均结果在f₂、f₆、f₁₀、f₁₄和f₁₈上要比TLBO-CSWL-1好，而对于其余的测试函数，两者结果相同；这说明TLBO-CSWL算法具有更好的寻优性能。统计分析结果见表8，由表8可知TLBO-CSWL和TLBO-CSWL-1在统计学意义上虽然不存在显著性差异，但是从Friedman测试所得到的排序结果来看(见图1)，TLBO-CSWL的整体性能要好于TLBO-CSWL-1。以上统计分析结果表明，利用正态分布产生随机数替代原有均匀随机数的策略对于提升TLBO算法的性能是有效的。

3.2.2 与变种算法TLBO-CSWL-2的比较

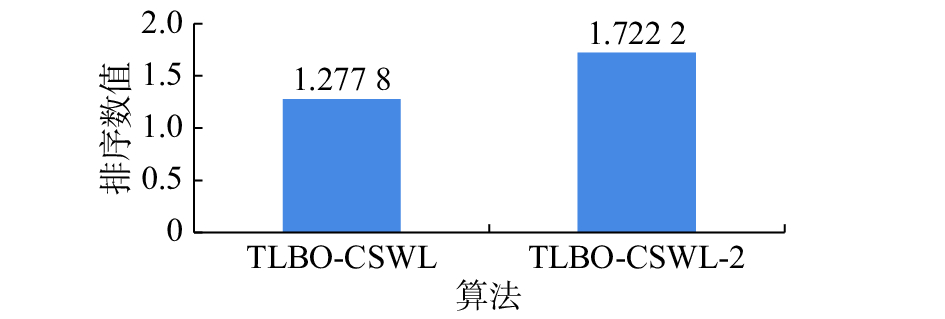
本文对不加混沌搜索的TLBO-CSWL-2和TLBO-CSWL在同样的18个测试函数上进行仿真测试。结果如表7所示。从表7可以看出所提出的TLBO-CSWL算法在f₂、f₅、f₆、f₇、f₁₀、f₁₃、f₁₄和f₁₈上的寻优结果要比TLBO-CSWL-2好，而在其余测试函数上，两者的寻优结果相同；以上表明TLBO-CSWL算法的性能要好于TLBO-CSWL-2算法。统计分析结果见表9，由表9可知TLBO-CSWL和TLBO-CSWL-2在统计学意义上不存在显著性差异。但是，从图2的Friedman测试所得到的排序结果来看，与TLBO-CSWL-2相比，TLBO-CSWL具有更好的整体性能。以上统计分析表明，混沌搜索策略对于提升TLBO算法的性能是有效的。

4 在非合作博弈问题中的应用

在本实验中，将所提算法应用于非合作博弈纳什均衡问题的求解。

4.1 博弈问题的描述

N人有限非合作博弈纳什均衡问题，主要是求解一种混合策略使得博弈双方均基于一定的概率来选择自己的每一个纯策略，使得博弈双方的利益均最大化，此时博弈模型处于稳定的状态。参考文献[7]中的问题描述，对于2人有限非合作博弈问题：设局中人1的混合策略为 ${ x} = ({x_1},{x_2}, \cdots ,{x_m})$ ，局中人2的混合策略为 ${ y} = ({y_1},{y_2}, \cdots ,{y_n})$ 。A_m×n, B_m×n分别为局中人1和局中人2的支付矩阵，则局中人1和局中人2的期望支付分别为 ${{x}}{{A}}{{{y}}^{\rm{T}}}$ 和 ${{x}}{{B}}{{{y}}^{\rm{T}}}$ 。( $ { x}^*$ , $ { y}^*$ )为双矩阵博弈问题的一个纳什均衡解的充分必要条件，即

$\left\{ \begin{array}{l}\!\!\!\!\!{{ x}^*}{{A}}{{ y}^{*{\rm T}}} \geqslant { x}{{A}}{{ y}^{*{\rm T}}},\;\forall { x}\\\!\!\!\!\!{{ x}^*}{{B}}{{ y}^{*{\rm T}}} \geqslant { x}{{B}}{{ y}^{*{\rm T}}},\;\forall { y}\end{array} \right.$

(8)

算法中的每一个个体的取值表示所有局中人的混合策略，则双矩阵博弈问题z=(x, y)的适应度函数可以表示为

$\begin{aligned}f\left( {{z}} \right) =& \max \left\{ {\mathop {\max }\limits_{0 \leqslant i \leqslant n} \left( {{{{A}}_i}{{{y}}^{\rm{T}}} - {{x}}{{A}}{{{y}}^{\rm{T}}}} \right),0} \right\} + \\ & \max \left\{ {\mathop {\max }\limits_{0 \leqslant j \leqslant m} \left( {{{x}}{{{B}}_j} - {{x}}{{B}}{{{y}}^{\rm{T}}}} \right),0} \right\}\end{aligned}$

(9)

式(9)中，A_i表示A_m×n的第i行，B_j表示B_m×n的第j列。

根据纳什均衡的定义和性质^[1]可知，混合局势 ${ z}^* $ =( ${ x}^* $ ， ${ y}^* $ )为双矩阵博弈问题的一个纳什均衡解的充分必要条件为：存在 ${ z}^* $ =( ${ x}^* $ ， ${ y}^* $ )，使得f( ${ z}^* $ )=0；且对于任意的 ${ z} $ ≠ ${ z}^* $ ，都有f ( ${ z} $ )>0。

4.2 案例研究

本文选取2个双矩阵博弈问题^[30-31]。

例1　博弈模型1, ${\varGamma _1} \equiv \left( {{x_1},{y_1};{{{A}}_1},{{{B}}_1}} \right)$ ，支付矩阵为

${{{A}}_1} = \left[ {\begin{array}{*{20}{c}} 1&2&0 \\ 0&1&2 \\ 2&0&1 \end{array}} \right], \;\;\; {{{B}}_1} = \left[ {\begin{array}{*{20}{c}} 1&0&2 \\ 2&1&0 \\ 0&2&1 \end{array}} \right]$

例2　博弈模型2, ${\varGamma _2} \equiv \left( {{x_2},{y_2};{{{A}}_2},{{{B}}_2}} \right)$ ，支付矩阵为

${{{A}}_2} = \left[ {\begin{array}{*{20}{c}} 0&4&5 \\ 4&0&5 \\ 3&3&6 \end{array}} \right], \;\;\; {{{B}}_2} = \left[ {\begin{array}{*{20}{c}} 4&0&3 \\ 0&4&3 \\ 5&5&6 \end{array}} \right]$

为了求解以上两个问题，选取jDE、SaDE、CLPSO、TLBO、TLBO-CSWL来对其进行求解。对于所有的算法，种群大小均设定为40，最大的评价次数为2 000，每个问题均独立运行30次。并使用Wilcoxon秩和检验方法^[32]来对实验结果进行统计分析。

实验结果和统计分析结果见表10，其中，“+”表示所提算法优于其比较算法；“–”表示所提算法差于其比较算法 ；“≈”表示TLBO-CSWL算法与其他算法性能相似。从表10的统计结果可知，TLBO-CSWL算法在2个博弈问题上的求解结果均优于jDE、SaDE、CLPSO、TLBO算法，说明TLBO-CSWL算法在解决非合作博弈问题上表现得最好。另外，对于博弈问题1和2，所有算法的最好结果见表11和表12。从表11可以看出，相对于其他算法，TLBO-CSWL算法能够得到更好的纳什均衡解。同时对于博弈模型1，本文算法求解的适应度函数精度明显优于其他算法。另外，从表12可以看出，TLBO-CSWL比其他算法能找到更好的纳什均衡解，适应度函数的精度显著好于其他所有算法，这说明TLBO-CSWL算法在计算结果的精度比其他算法有了较大的改进。

上述分析表明，将本文提出的TLBO-CSWL算法应用到非合作博弈问题，取得了较满意的结果。

5 结束语

本文针对教与学优化算法容易早熟收敛的问题，提出了一种基于混沌搜索和权重学习的教与学优化(TLBO-CSWL)算法。在该算法中，利用当前种群的加权平均值来指导种群的进化，并且使用正态分布随机数替代均匀随机数来提高原始TLBO算法的寻优性能；另外，将混沌搜索策略加到所提算法中，以此来提高算法的全局搜索能力。实验仿真结果表明，所提算法的整体性能在所有比较算法中是最好的。同时，采用TLBO-CSWL算法与其变种算法TLBO-CSWL-1、TLBO-CSWL-2进行比较分析，仿真结果显示本文所提出的改进策略对于提升TLBO算法的性能是有效的。最后，将TLBO-CSWL算法应用于求解非合作博弈纳什均衡问题，其结果表明所提算法得到的结果要好于其他算法。