地图构建作为机器人自主导航的基础，是指移动机器人在未知环境下依据自身携带的传感器信息建立地图模型^[1]。常用的地图模型有栅格地图^[2]、几何地图^[3]以及拓扑地图^[4]等。然而，地图构建问题与定位问题紧密相关，定位的结果用于地图构建，而已经构建好的地图又能实现精确定位，因此同时定位与地图构建(SLAM^[5])被提出并受到广泛研究和应用。目前，SLAM技术大都基于概率理论，比如卡尔曼滤波^[6]及扩展卡尔曼滤波^[7]、最大似然估计^[8]、粒子滤波^[9]和Markov定位^[10]等。文献[11]将UT和UKF运用到高斯项更新及采样粒子权重计算过程中，提出一种无迹高斯混合概率假设密度SLAM算法；文献[12]在雁群粒子群算法的基础上采用分数阶微积分和混沌思想训练模糊自适应扩展卡尔曼滤波，从而实现同时定位与地图创建；文献[13]在基本SLAM算法的迭代过程中引入元胞自动机(CA)，建立“SLAM-CA生长–重定位”的闭环作用机制。

Rao-Blackwellized粒子滤波算法是目前解决SLAM问题的有效方法，它将SLAM问题分解成机器人的位姿估计和地图估计，采用粒子滤波器和扩展卡尔曼滤波器估计概率，但仍存在算法运行时间长，粒子退化严重等不足；此后很多改进的RBPF算法被提出，如文献[14]提出一种基于高斯分布的RBPF-SLAM算法，通过高斯分布分散高权重粒子获得新粒子，虽然算法能在粒子减少的条件下保持可靠估计，但忽略对低权重粒子的考虑，抑制样本匮乏现象还存在不足；文献[15]提出一种粒子群优化遗传重采样的改进RBPF-SLAM算法，采用粒子群优化策略调整粒子集，并对权重较小的粒子进行变异操作，但粒子群的引入容易陷入局部最优，加上重采样中只针对权重较小粒子操作，对缓解粒子退化无法产生满意的效果。文献[16]采用改进的提议分布并结合基于等级的自适应局部重采样(APRR)算法，设计了一种基于退火参数优化混合提议分布的RBPF算法，对高权重和低权重粒子只进行复制操作，对增加粒子多样性缓解粒子退化效果不佳。

考虑这些不足，本文从解决RBPF算法运行时间长、提议分布精度不高以及重采样过程的粒子退化出发，将量子粒子群算法^[17]引入到Rao-Blackwellized粒子滤波算法，提出一种QPSO-RBPF-SLAM算法，一方面在基本提议分布中加入观测信息，使改进的提议分布更加接近真实状态，另一方面在重采样中根据QPSO算法更新粒子位姿，对高低权值粒子进行自适应交叉变异操作。QPSO-RBPF-SLAM保持了粒子的多样性，有效缓解了粒子退化，同时算法能在减少运算时间和粒子数的条件下获得可靠的估计，整体性能得到较大提高，能够精确估计出机器人的位姿并获得高精度的地图。

1 RBPF-SLAM

移动机器人SLAM实质上是一个Markov链的过程：在一个未知环境中机器人从起始位置出发，在运动过程中，使用里程计记录自身运动的信息( ${{{u}}_{1:t}} = {{{u}}_1},{{{u}}_2}, \cdots ,{{{u}}_t}$ )和外部传感器获取的环境信息( ${{{z}}_{1:t}} = {{{z}}_1},{{{z}}_2}, \cdots \!,{{{z}}_t}$ )，估计机器人的轨迹( ${{{x}}_{1:t}} = {{{x}}_1},{{{x}}_2}, \cdots\!,{{{x}}_t}$ )与构建增量式环境地图 ${{{m}}_t}$ ，同时使用创建好的地图及传感器的信息实现自定位。根据贝叶斯滤波递归原理，从概率学的角度得出SLAM的递归公式为

$\begin{aligned}\!\!\!\!\! & {\rm Bel}({{{x}}_t},{{{m}}_t}) = p({{{x}}_t},{{{m}}_t}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}}) = \eta p({{{z}}_t}\left| {{{{x}}_t},{{{m}}_t}}\right.) \cdot \\\!\!\!\!\! & \iint {p({{{x}}_t},{{{m}}_t}\left| {{{{x}}_{t - 1}},{{{m}}_{t - 1}}} \right.,{{{u}}_{t - 1}})} \cdot {\rm Bel}({{{x}}_{t - 1}},{{{m}}_{t - 1}}){\rm{d}}{{{x}}_{t - 1}}{\rm{d}}{{{m}}_{t - 1}} \\ \end{aligned} $

(1)

式中 $\eta $ 表示归一化常量。

SLAM中包含运动模型 $p({{{x}}_t}\left| {{{{x}}_{t - 1}}} \right.,{{{u}}_{t - 1}})$ 与观测模型 $p({{{z}}_t}\left| {{{{x}}_t},{{m}}} \right.)$ 两种模型。运动模型表示在给定上一时刻移动机器人轨迹 ${{{x}}_{t - 1}}$ 和控制命令 ${{{u}}_{t - 1}}$ 条件下，机器人获得新位姿 ${{{x}}_t}$ 的概率密度；而观测模型表示在给定移动机器人地图m与位姿 ${{{x}}_t}$ 的条件下，传感器获取环境的不确定性。

基于Rao-Blackwellized粒子滤波SLAM算法的思想：计算机器人轨迹 ${{{x}}_{1:t}}$ 和地图m的后验概率 $p({{{x}}_{1:t}},{{m}}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}})$ ，将其分解为式(2)所示的轨迹估计和地图估计两个后验概率乘积。

$p({{{x}}_{1:t}},{{m}}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}}) = p({{{x}}_{1:t}}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}}) \cdot p({{m}}\left| {{{{x}}_{1:t}},{{{z}}_{1:t}}} \right.)$

(2)

首先对机器人的轨迹进行估计，利用Rao-Blackwellized粒子滤波器实现，其中每个粒子代表机器人一条可能的行走轨迹。

然后再结合观测模型对地图进行更新。将地图表示为服从高斯分布的特征路标的集合，因此对地图的估计可通过特征路标估计得到，这里采用扩展卡尔曼滤波来实现。

因此，在粒子代表的轨迹上利用传感器实时观察获得的路标信息构成最后的地图。

利用Rao-Blackwellized 滤波器在传感器观测信息与里程计信息基础下构建增量式地图的步骤可以分为4步：

1) 初始化：当t=0时，选取N个粒子，每个粒子的权重为 $\omega _0^{(i)} = 1/N$ 。

2) 采样：机器人的运动模型作为提议分布 $\pi $ ，从上一代粒子集合 $\left\{ {{{x}}_{t{\rm{ - }}1}^{(i)}} \right\}$ 采样得到下一代粒子集合 $\left\{ {{{x}}_t^{(i)}} \right\}$ 。

3) 粒子权重：为了弥补采样时提议分布跟目标分布的差距，需要计算每一个独立粒子的权重 $\omega _t^{(i)}$ ，由重要性采样公式得出式(3)：

$\omega _t^{(i)} = \frac{{p({{x}}_{1:t}^{(i)}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}})}}{{\pi ({{x}}_{1:t}^{(i)}\left| {{{{z}}_{1:t}}} \right.,{{{u}}_{1:t - 1}})}}, \quad i = 1,2,\; \cdots ,N$

(3)

4) 重采样：根据式(4)计算有效粒子数，同时设定阈值 ${N_{\rm th}}$ 。

${N_{\rm eff}} = 1/\sum\limits_{i = 1}^N {{{(\widetilde {{\omega ^{(i)}}})}^2}} $

(4)

当 ${N_{\rm eff}} < {N_{\rm th}}$ 时，进行重采样。重采样完成后保证所有的粒子具有相同的权重。其中， ${\widetilde {{\omega ^{(i)}}}}$ 表示归一化权重。

5) 地图更新：每一粒子用其轨迹 ${{x}}_{1:t}^{(i)}$ 和观测信息 ${{{z}}_{1:t}}$ 来计算相应的 $p({{{m}}^{(i)}}\left| {{{x}}_{1:t}^{(i)},{{{z}}_{1:t}}} \right.)$ 实现地图的更新。

2 QPSO-RBPF-SLAM

在重要性采样中，需要依据提议分布对下一代粒子集进行采样，而基本RBPF-SLAM中常采用运动模型作为提议分布，使得粒子退化严重，导致丢失权值较大的粒子从而创建的地图精度不高。为了解决提议分布精度不高的问题，结合里程计信息和外部传感观测信息作为混合提议分布如式(5)所示：

${\pi '}({{{x}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{x}}_{t - 1}^{(i)},{{{z}}_t},{{{u}}_{t - 1}}) =\displaystyle\frac{{p({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{{x}}_t}) \cdot p({{{x}}_t}\left| {{{x}}_{t - 1}^{(i)}} \right.,{{{u}}_{t - 1}})}}{{p({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{x}}_{t - 1}^{(i)},{{{u}}_{t - 1}})}} $

(5)

然而此混合提议分布无法直接进行采样操作，需要目标提议分布的一个近似化正态分布实现。式(6)所示的正态分布参数 $N\left({{u}}_t^{(i)},\sum\nolimits_t^{(i)}\right) $ 通过带权重的蒙特卡罗采样方法估计得出。

$\left\{ \begin{array}{l} {{u}}_t^{(i)} = \displaystyle\frac{1}{{{\eta ^{(i)}}}}\sum\limits_{j = 1}^M {{{{x}}_j}} \cdot p \left({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{{x}}_j}\right) \\ \sum\nolimits _t^{(i)} = \displaystyle\frac{1}{{{\eta ^{(i)}}}}\sum\limits_{j = 1}^M {p\left({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{{x}}_j}\right)} \cdot \left({{{x}}_j} - {{u}}_t^{(i)}\right){\left({{{x}}_j} - {{u}}_t^{(i)}\right)^{\rm{T}}} \end{array} \right.$

(6)

式中： ${\eta ^{(i)}} = \displaystyle\sum\limits_{j = 1}^M {p\left({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} ,\right.{{{x}}_j}\right)} $ 为归一化因子，M表示常数。

在混合提议分布下，粒子权重通过式(7)得出：

$\begin{array}{c} \omega _t^{(i)} = \omega _{t - 1}^{(i)} \cdot k\displaystyle\sum\limits_{j = 1}^M {p({{{z}}_t}\left| {{{m}}_{t - 1}^{(i)}} \right.,{{{x}}_j})} = \omega _{t - 1}^{(i)} \cdot k{\eta ^{(i)}} \end{array} $

(7)

式中k表示常数。

基本粒子群优化算法(PSO)由于粒子速度的局限性而不能在整个可行空间进行搜索，无法保证算法全局收敛，故在重采样过程中引入量子粒子群算法更新粒子集。量子粒子群算法是一种将量子系统的特点与粒子群算法相结合的新兴群体智能算法，将粒子群引入量子空间并确定粒子在空间中的位置，通过量子束缚态描述粒子的聚集性，保证了粒子在整个可行解区域的搜索，保证收敛到全局最优解。利用QPSO算法驱使粒子快速地靠近于似然函数高的区域，优化调整机器人位姿状态的粒子集 $\left\{ {{{x}}_t^{(i)}} \right\}$ ，则粒子位置更新如式(8)所示：

$ \left\{ \begin{aligned} & {{{X}}_{i,j}}(t \!+\! 1) \!=\! {{{p}}_{i,j}}(t) \pm \alpha \cdot \left| {{{\bf mbest}_j}(t) - {{{X}}_{i,j}}(t)} \right|\ln \left(\displaystyle\frac{1}{{{{{u}}_{i,j}}(t)}}\right) \\& {{{p}}_{i,j}}(t) = {f_j}(t) \cdot {{{P}}_{i,j}}(t) + \left| {1 - {f_j}(t)} \right| \cdot {{{P}}_{g,j}}(t) \\& {u_{i,j}}(t) \sim U(0,1) \\& {f_j}(t) \sim U(0,1) \\ \end{aligned} \right.$

(8)

式中： ${{{X}}_{i,j}}(t)$ 、 ${{{X}}_{i,j}}(t{\rm{ + }}1)$ 分别表示当前时刻和下一时刻粒子的位置； ${{{p}}_{i,j}}(t)$ 表示吸引子； ${{{P}}_{i,j}}(t)$ 表示第t次迭代时第i个粒子的个体最好位置； ${{{P}}_{g,j}}(t)$ 表示第t次迭代时所有粒子中的全局最好位置； ${{\bf mbest}_j}(t)$ 表示第t次迭代时所有粒子当前最好位置的平均值; $\alpha $ 为收缩–扩张系数。

同时，为了防止粒子退化以及保持粒子的多样性，对所得的粒子集进行优化调整，基本思想是：根据权重阈值将粒子划分为高权重粒子、低权重粒子以及中等权重粒子，保留中等权重粒子，对具有高权重和低权重的粒子进行自适应交叉变异操作。根据式(9)设置合适的高权重阈值 ${\omega _{\rm H_0}}$ 和低权重阈值 ${\omega _{\rm L_0}}$ ，取两阈值之间的粒子作为中等权重的粒子。

${\omega _{\rm H_0}} = \frac{2}{N},\quad {\omega _{\rm L_0}} = \frac{1}{{2N}}$

(9)

选择 $F({{{X}}_i}) = \omega _t^{(i)}$ 作为粒子的适应度函数，则t时刻的交叉操作与变异操作如下。

交叉操作：在高权重和低权重的粒子集中随机选取两个个体作为父辈粒子进行配对，按照式(10)所示的自适应交叉率 ${P_c}$ 进行交叉操作得到两个新个体。

${P_c} = \left\{ \begin{aligned}& {P_{c1}}, \quad F' < {F_{{\rm{avg}}}} \\& {P_{c2}} + \displaystyle\frac{{{P_{c1}} - {P_{c2}}}}{{1 + \exp \left\{ {\beta \left[ {\displaystyle\frac{{2({F'} - {F_{{\rm{avg}}}})}}{{{F_{\max }} - {F_{{\rm{avg}}}}}}} \right]} \right\}}}, \quad F' \geqslant {F_{{\rm{avg}}}} \\ \end{aligned} \right.$

(10)

变异操作：从交叉后得到的新粒子集中随机选择的一个父辈粒子按照式(11)所示自适应变异率 ${P_m}$ 进行变异操作产生新粒子。

${P_m} = \left\{ \begin{aligned}& {P_{m1}}, \quad F < {F_{{\rm{avg}}}} \\& {P_{m2}} +\displaystyle \frac{{{P_{m1}} - {P_{m2}}}}{{1 + \exp \left\{ {\beta \left[ {\displaystyle\frac{{2(F - {F_{{\rm{avg}}}})}}{{{F_{\max }} - {F_{{\rm{avg}}}}}}} \right]} \right\}}}, \quad F \geqslant {F_{{\rm{avg}}}} \\ \end{aligned} \right.$

(11)

式中： ${F_{{\rm{avg}}}}$ 表示每代群体中粒子的平均适应度值； ${F_{\max }}$ 表示群体中粒子的最大适应度值； $F'$ 、F分别表示参与交叉操作的两个粒子中较大的适应度值以及参与变异操作的粒子的适应度值； $\beta $ 表示常数。

QPSO-RBPF-SLAM算法流程：

1) 当t=0时，选取N个粒子，每个粒子的权重为 $\omega _0^{(i)} = 1/N$ ；设置相关参数，即自适应交叉率 ${P_c}$ 以及自适应变异率 ${P_m}$ 。

2) 根据式(5)计算混合提议分布，进行采样操作得出粒子集。

3) 根据式(8)对粒子集 $\left\{ {{{x}}_t^{(i)}} \right\}$ 进行QPSO迭代优化。

4) 根据式(7)计算粒子权重，并依据设定的高低权重阈值来划分粒子。

5) 根据式(4)重采样条件，判断是否需要进行重采样操作。若需要重采样，则执行6)；否则，执行8)。

6) 保留中等权重粒子，将高权重和低权重粒子根据式(10)、式(11)进行自适应交叉和变异操作。

7) 中等权重粒子和交叉变异后的粒子组成新粒子集进行重采样，并返回3)实现QPSO重复优化。

8) 根据机器人轨迹 ${{x}}_{1:t}^{(i)}$ 和观测信息 ${{{z}}_{1:t}}$ 更新栅格地图。

3 实验 3.1 仿真实验

为了说明本文改进算法的有效性，在MATLAB平台进行了仿真实验。

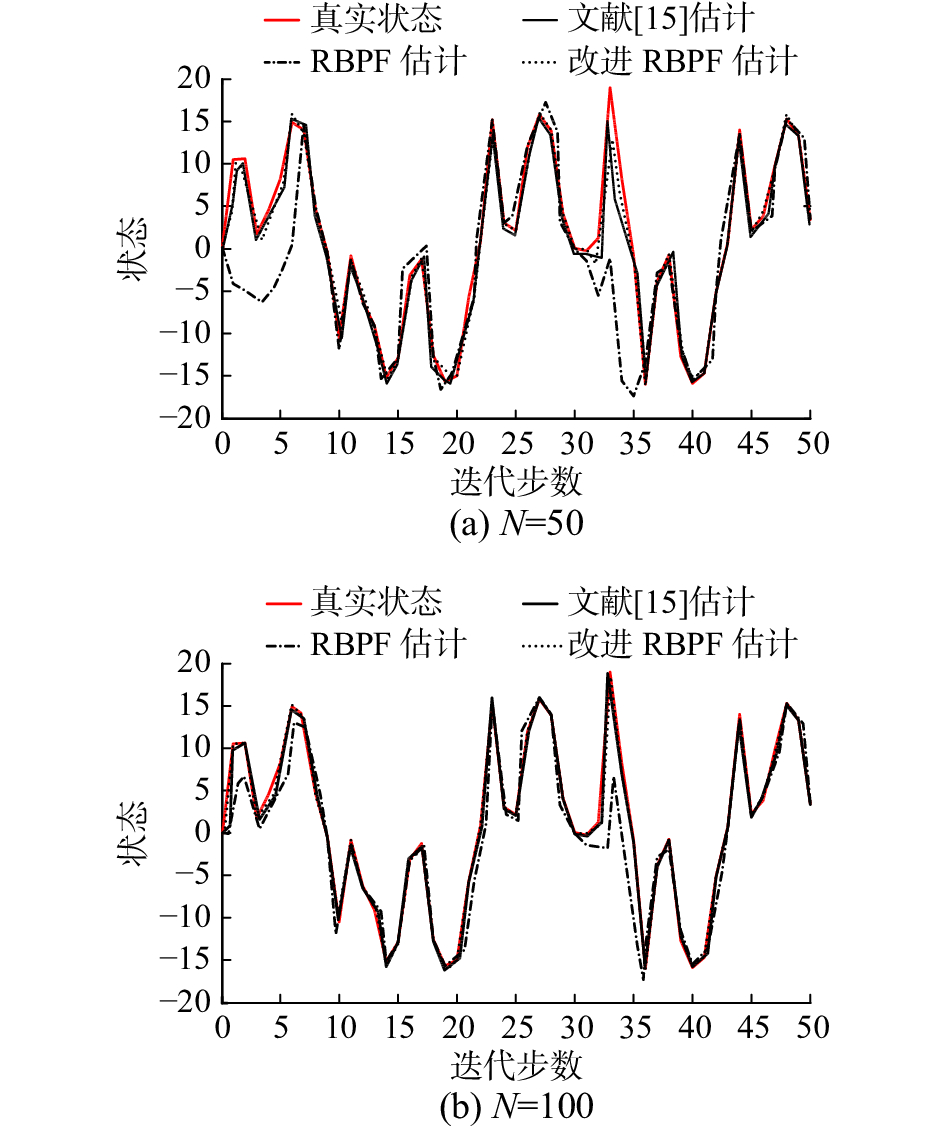
首先对机器人自身位姿估计。设置机器人实际行走轨迹中真实的位姿状态，利用基本RBPF、文献[15]算法和改进RBPF在粒子数N取50和100时对真实的位姿进行估计。其中， ${P_{c1}}$ =0.8、 ${P_{c2}}$ =0.6、 ${P_{m1}}$ =0.1、 ${P_{m2}}$ =0.01。

由图1和表1可知，在粒子数相同的条件下，改进RBPF算法的均方根误差较小，与真实状态接近；随着粒子数的增加，虽然算法运行时间延长，但估计的结果则更加接近真实状态；与RBPF算法和文献[15]算法采用100个粒子所获得的估计结果相比，改进的RBPF算法采用50个粒子能够获得较好的估计效果，故改进的RBPF算法能利用较少的粒子获得可靠且较精确的估计。

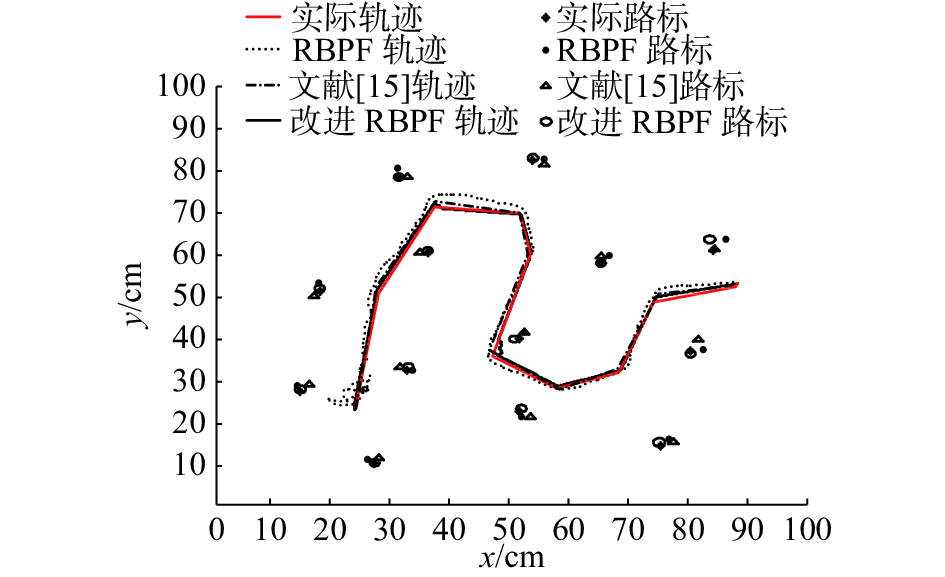
其次，比较RBPF算法、文献[15]算法和改进RBPF算法下对机器人轨迹和路标的估计结果。如图2所示，设定100 cm×100 cm的区域，星形表示实际路标，红线表示实际轨迹；黑线表示利用改进RBPF算法得到的轨迹估计，圆形表示对应的路标估计；虚线表示利用文献[15]算法得到的轨迹估计，三角形表示对应的路标估计；点线表示利用RBPF算法得到的轨迹估计，黑色小点表示对应的路标估计。

由图2和表2可知，改进的RBPF算法在进行轨迹和路标估计时所用粒子数和运行时间比RBPF算法和文献[15]算法少。在轨迹估计方面，改进的RBPF算法得到的轨迹与机器人实际轨迹误差较小，而RBPF算法和文献[15]算法得到的轨迹波动较大；在路标估计方面，利用改进的RBPF算法得到的路标估计与实际路标较为接近，而RBPF算法和文献[15]算法得到的路标估计则在一定程度上远离实际路标。因此，与RBPF算法和文献[15]算法相比，改进的RBPF算法在机器人轨迹估计和路标估计方面能够得到更加满意的效果。

下面利用维多利亚公园数据集对RBPF算法、文献[15]算法和改进的RBPF算法的性能进一步验证。由于悉尼维多利亚公园数据集并未提供相关噪声参数的信息，故将噪声参数设置为：车辆速度控制噪声为1.0 m/s，驾驶角控制噪声为2.0°；路标观测的角度噪声为2.5°，测距噪声为1.6 m。3种算法分别采用20个粒子、15个粒子和10个粒子来描述车辆轨迹和环境地图。

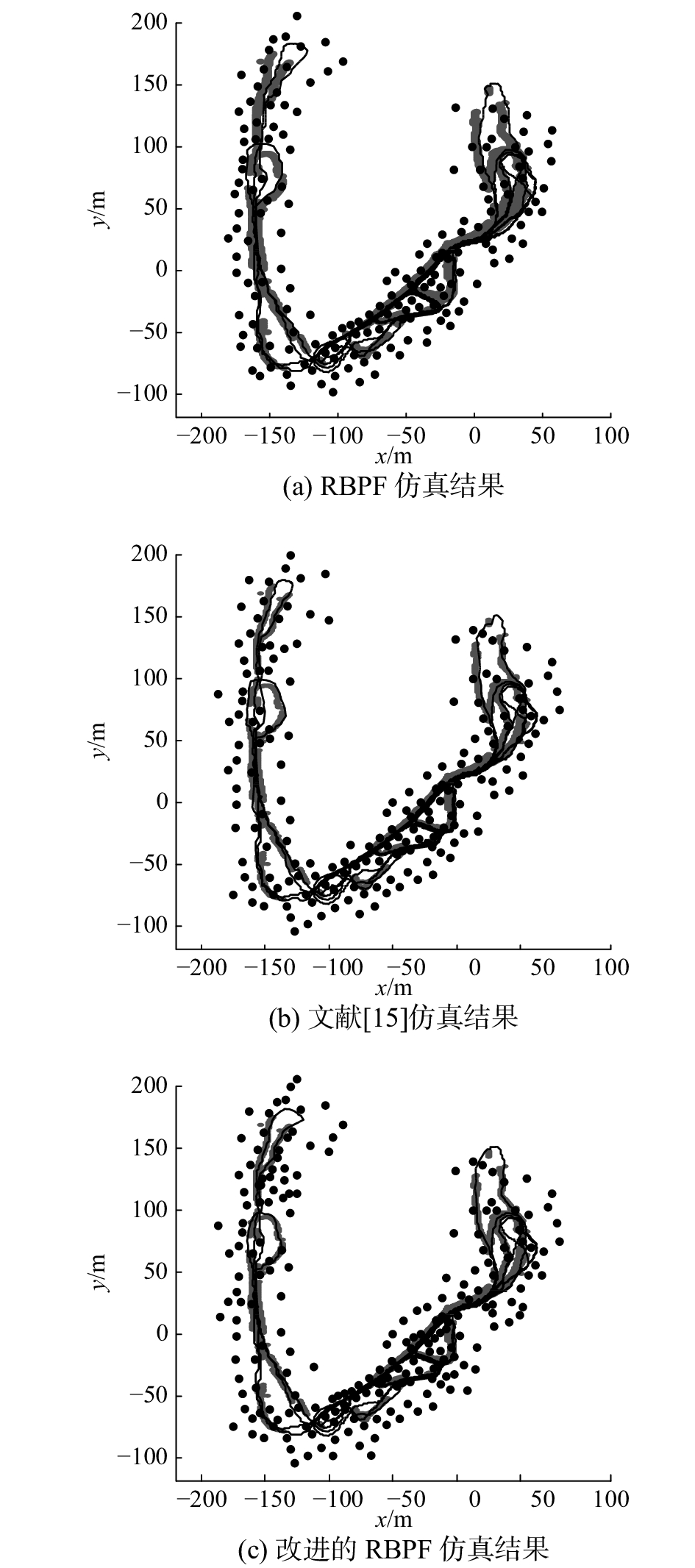
RBPF算法、文献[15]算法和改进的RBPF算法的仿真结果如图3所示。其中，灰色粗线表示GPS路径(即真实路径)，黑色细线表示估计路径，黑点表示估计路标。

由图3可知，3种算法在不同程度上估计出GPS路径，但RBPF算法采用20个粒子得到的轨迹在部分区域出现明显的不匹配现象，偏差较大；文献[15]算法采用15个粒子得到的轨迹相比RBPF算法不匹配现象减少；而改进的RBPF算法采用10个粒子得到的轨迹与GPS路径之间的误差较小，吻合度更高。同时，RBPF算法和文献[15]算法出现粒子匮乏问题而导致估计的路标个数不完全，而改进的RBPF算法能精确地估计所有设定的路标。

由上述仿真可知，RBPF算法的提议分布缺少观测信息且所有粒子都有参与重采样，算法整体计算过程简单但效果不佳，会出现粒子退化现象导致最后创建的地图精度不高；文献[15]对提议分布进行改进，引入粒子群算法更新粒子集，并对所有权重较低粒子进行重采样，计算复杂度有所提升；而改进的RBPF算法通过量子粒子群算法，只考虑粒子的位置量，且针对部分粒子进行重采样，整体计算复杂度介于RBPF算法和文献[15]算法之间，但由于改进的RBPF算法能以较少粒子数获得更好的估计结果，使得算法整体运行时间降低。整体而言，改进的RBPF算法具有更好的有效性和优越性。

3.2 实际验证

为了验证本文改进算法的实际性，在室内环境下利用旅行家2号移动机器人进行实际验证，完成同时定位与地图构建。该机器人内部有里程计，并随身携带URG-hokuyo激光传感器。在PC机上运行Liunx(Ubuntu 12.04)的ROS系统。

选取安徽工程大学电气工程学院实验室部分区域作为本次实验的室内环境。如图4所示，选取的区域为8 m×1.5 m，机器人以0.2 m/s的速度移动，利用里程计信息和激光数据信息实时构建栅格地图。

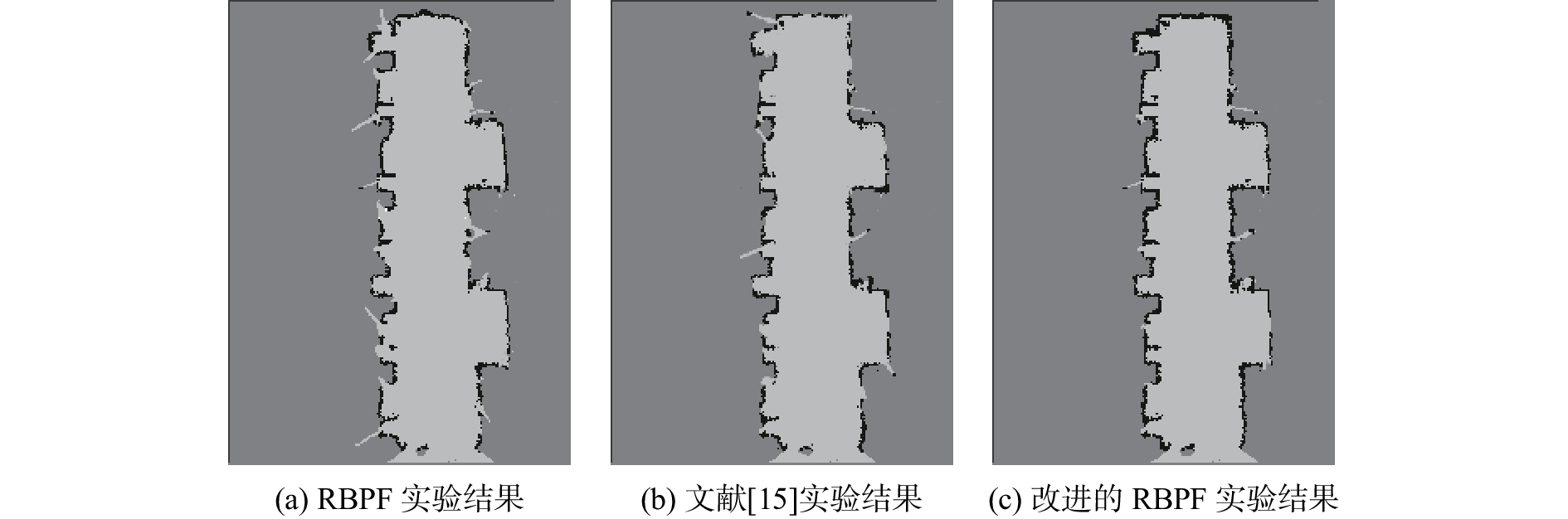
由图5和表3可知，RBPF-SALM算法采用了39个粒子，粒子退化严重，降低粒子多样性，创建的地图不够精确；文献[15]算法采用了24个粒子，创建的地图有所改善，但效果不显著；改进的RBPF-SALM算法只使用了16个粒子获得了比RBPF-SALM算法和文献[15]算法更精确的地图，同时轨迹和路标估计的均方根误差、运行时间也大大缩减。

4 结束语

为解决RBPF算法中粒子退化和多样性降低问题，本文提出一种QPSO-RBPF-SLAM算法。将机器人运动模型和观测模型作为提议分布，在重采样过程中结合量子粒子群思想和遗传算法，利用QPSO算法更新粒子位姿，根据权值划分粒子种类引入自适应交叉变异操作对所得粒子集进行优化、调整。同时，在机器人ROS平台上利用旅行家2号机器人进行实验，以较少的粒子数和较短时间在精确估计机器人位姿的同时能够创建较高精度的栅格地图。下一步，在获得的高精度栅格地图的基础上对移动机器人进行路径规划研究。